Skip to main content
SpringerLink
Log in

Modified partial update EDS algorithms for adaptive filtering

  • Published:
Analog Integrated Circuits and Signal Processing Aims and scope Submit manuscript

Abstract

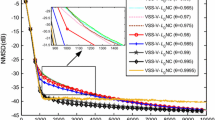
Partial update (PU) Euclidean direction search (EDS) algorithms have been developed to reduce the computational complexity of the full update EDS. In this paper, the PU EDS is modified to achieve better performance. The performance is analyzed for a time-invariant system and for a time-varying system. Theoretical steady-state mean and mean squared error results of the modified PU EDS are derived for both time-invariant system and time-varying system. Computer simulations are presented to support the theoretical analyses. The modified PU EDS can achieve similar performance to the full update EDS while reducing the computational complexity significantly. The performance of the modified PU EDS is also compared with the PU recursive least squares (RLS) algorithm and the PU conjugate gradient in computer simulations. The performance of modified PU EDS is comparable to PU RLS, and it needs less computational cost.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Bose, T. (2004) Digital signal and image processing. Wiley, New York

    Google Scholar 

  2. Doğançay, K. (2008) Partial-update adaptive signal processing. Academic Press, Champaign, IL

    Google Scholar 

  3. Naylor, P. A., & Khong, A. W. H. (2004). Affine projection and recursive least squares adaptive filters employing partial updates, in Proceeings of Thirty-Eighth Asilomar Conference on Signal, System & Computers, pp. 950–954.

  4. Khong, A. W. H., & Naylor, P. A. (2007). Selective-tap adaptive filtering with performance analysis for identification of time-varying systems. IEEE Transactions on Audio, Speech, and Language Processing 15(5):1681–1695

    Article  Google Scholar 

  5. Xie, B., & Bose, T. (2011). Partial update conjugate gradient algorithms for adaptive filtering, in Proceeings of PECCS.

  6. Xie, B., & Bose, T. (2011). Tracking performance of the MMax conjugate gradient algorithm, in Proceedings of SDR-WInnComm.

  7. Xie, B., & Bose, T. (2010). Partial update EDS algorithms for adaptive filtering, in Proceedings of ICASSP.

  8. Zhang, Z. K., Bose, T., Xiao, L., & Thamvichai, R. (2006). Performance analysis of the deficient length EDS adaptive algorithms, in Proceedings of APCCAS, pp. 222–226.

  9. Chang, P. S., & Willson, A. N. (2000). Analysis of conjugate gradient algorithms for adaptive filtering. IEEE Transactions on Signal Processing 48(2):409–418

    Article  MATH  Google Scholar 

  10. Haykin, S. (2002). Adaptive filter theory, 4th ed. Prentice Hall, New Jersey

    Google Scholar 

  11. Mayyas, K. (2005). Performance analysis of the deficient length LMS adaptive algorithm. IEEE Transactions Signal Processing 53(8):2727–2734

    Article  MathSciNet  Google Scholar 

  12. Sayed, A. H. (2003). Fundamentals of adaptive filtering. Wiley, New York

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Virginia Polytechnic Institute and State University, 210 Burruss Hall, Blacksburg, VA, 24061, USA

    Bei Xie

  2. University of Arizona, 1401 E University Blvd, Tucson, AZ, 85721, USA

    Tamal Bose

Authors
  1. Bei Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tamal Bose
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bei Xie.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xie, B., Bose, T. Modified partial update EDS algorithms for adaptive filtering. Analog Integr Circ Sig Process 78, 657–667 (2014). https://doi.org/10.1007/s10470-013-0108-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10470-013-0108-9

Keywords

Search

Navigation