Skip to main content
SpringerLink
Log in

Prediction of Vibrational Behavior of Composite Cylindrical Shells under Various Boundary Conditions

  • Published:
Applied Composite Materials Aims and scope Submit manuscript

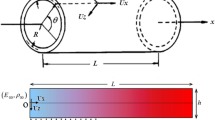
Abstract

In this paper, a unified analytical approach is applied to investigate the vibrational behavior of composite cylindrical shells. Theoretical formulation is established based on Sanders’ thin shell theory. The modal forms are assumed to have the axial dependency in the form of Fourier series whose derivatives are legitimized using Stoke's transformation. The Influence of some commonly used boundary conditions and the effect of variations in shell geometrical parameters on the shell frequencies are studied. The results obtained for a number of particular cases show good agreement with those available in the open literature. The simplicity and the capability of the present method are also discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Leissa, A.W., Vibration of shells. NASA SP-288 US Govt Printing Office (1973)

  2. Egle, D.M., Bray, F.M.: An experimental study of free vibration of cylindrical shells with discrete longitudinal stiffening. School of Aero-Space and Mechanical Engineering, University of Oklahoma, NSF Grant, Final Report, GK-1490, November (1968)

  3. Sharma, C.B.: Calculation of natural frequencies of fixed-free circular cylindrical shells. J. Sounds Vibration 35(1), 55–76 (1974)

    Article  MATH  ADS  Google Scholar 

  4. Sharma, C.B., Darvizeh, M.: Free vibration characteristics of laminated, orthographic clamped-free cylindrical shells, developments in mechanics. In: Proceedings of the 19th Midwestern Mechanics Conference, vol. 13, Department of Engineering Mechanics, The Ohio State University, Columbus, Ohio, September 9–11 (1985)

  5. Darvizeh, M.: Free vibration characteristics of orthotropic thin circular cylindrical shell, PhD thesis, UMIST, (1985)

  6. Sharma, C.B., Darvizeh, M., Darvizeh, A.: Free vibration response of multilayered orthotropic fluid-filled circular cylindrical shells. Compos. Struct. 34, 349–55 (1990)

    Article  Google Scholar 

  7. Birman, V.: Exact solution of axisymmetric problems of laminated cylindrical shells with arbitrary boundary conditions: higher-order theory. Mech. Res. Commun. 19(3), 219–225 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  8. Lam, K.Y., Loy, C.T.: Influence of boundary conditions and fiber orientation and the natural frequencies of thin orthotropic laminated cylindrical shells. Compos. Struct. 31, 21–30 (1995)

    Article  Google Scholar 

  9. Lam, K.Y., Loy, C.T.: Influence of boundary conditions for a thin laminated rotating cylindrical shell. Compos. Struct. 41, 215–228 (1998)

    Article  Google Scholar 

  10. Bert, C.W., Malik, M.: Differential quadrature method: a powerful new technique for analysis of composite structures. Compos. Struct. 39, 179–189 (1997)

    Article  Google Scholar 

  11. Sharma, C.B., Darvizeh, M., Darvizeh, A.: Free vibration behavior of helically wound cylindrical shells. Compos. Struct. 44, 55–62 (1999)

    Article  Google Scholar 

  12. Haftchenari, H., Darizeh, M., Darizeh, A., Ansari, R., Sharma, C.B.: Dynamic analysis of composite shells using Differential Quadrature Method (DQM). Compos. Struct. 78, 292–298 (2007)

    Article  Google Scholar 

  13. Ganesan, N., Kadoli, R.: Buckling and dynamic analysis of piezothermoelastic composite cylindrical shell. Compos. Struct. 59, 45–60 (2003)

    Article  Google Scholar 

  14. Kadoli, R., Ganesan, N.: Free vibration and buckling analysis of composite cylindrical shells conveying hot fluid. Compos. Struct. 60, 19–32 (2003)

    Article  Google Scholar 

  15. Darvizeh, M., Haftchenari, H., Darvizeh, A., Ansari, R., Sharma, C.B.: The effect of boundary conditions on the dynamic stability of orthotropic cylinders using a modified exact analysis. Compos. Struct. 74, 495–502 (2006)

    Article  Google Scholar 

  16. Sanders, J.L.: NASA Report 24. An improved first approximation theory for thin shells (1959)

  17. Ansari, R., Darvizeh, M.: Prediction of dynamic behaviour of FGM shells under arbitrary boundary conditions. Compos. Struct. 85(4), 284–292 (2008)

    Article  Google Scholar 

  18. Sewall, J.L., Naumann, E.C.: An experimental and analytical vibration study of thin cylindrical shells with and without longitudinal stiffeners NASA TN D-4705, (1968)

  19. Zhang, X.M.: Vibration analysis of cross-ply laminated composite cylindrical shells using the wave propagation approach. Appl. Acoust. 62, 1221–1228 (2001)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Guilan, P.O. Box 3756, Rasht, Iran

    Milad Hemmatnezhad, Reza Ansari & Mansour Darvizeh

Authors
  1. Milad Hemmatnezhad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reza Ansari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mansour Darvizeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Reza Ansari.

Appendices

Appendix A

$$ \begin{array}{*{20}{c}} {u\left( {x,\theta ,t} \right) = \left( {{A_{0n}} + \sum\limits_{m = 1}^\infty {{A_{mn}}} \cos \frac{{m\pi x}}{L}} \right)\cos n\theta \sin \omega t,\quad 0 \leqslant x \leqslant L,} \hfill \\ {{u_{,x}} = - \left( {\frac{\pi }{L}} \right)\sum\limits_{m = 1}^\infty {m{A_{mn}}} \sin \frac{{m\pi x}}{L}\cos n\theta \sin \omega t,\quad 0 < x < L,} \hfill \\ {\quad \quad \quad {u_{,x}}\left( {0,\theta } \right) = \left( {\frac{{{\pi ^2}}}{{2L}}} \right){{\overline u }_0}\cos n\theta ,\quad {u_{,x}}\left( {L,\theta } \right) = \left( {\frac{{{\pi ^2}}}{{2L}}} \right){{\overline u }_L}\cos n\theta ,} \hfill \\ {{u_{,xx}} = {{\left( {\frac{\pi }{L}} \right)}^2}\left[ {\frac{{{{\overline u }_0} + {{\overline u }_L}}}{2} + \sum\limits_{m = 1}^\infty {\left\{ {{{\overline u }_0} + {{\overline u }_L}{{\left( { - 1} \right)}^m} - {m^2}{A_{mn}}} \right\}\cos \frac{{m\pi x}}{L}} } \right]\cos n\theta \sin \omega t,\quad 0 \leqslant x \leqslant L,} \hfill \\ {v\left( {x,\theta ,t} \right) = \sum\limits_{m = 1}^\infty {{B_{mn}}\sin \left( {m\pi x/L} \right)\sin n\theta \sin \omega t,\quad 0 < x < L,} } \hfill \\ {\quad \quad \quad \quad v\left( {0,\theta } \right) = - \left( {\frac{\pi }{2}} \right){v_0}\sin n\theta ,\quad v\left( {L,\theta } \right) = - \left( {\frac{\pi }{2}} \right){v_L}\sin n\theta ,} \hfill \\ {{v_{,x}} = \left( {\frac{\pi }{L}} \right)\left[ {\frac{{{v_0} + {v_L}}}{2} + \sum\limits_{m = 1}^\infty {\left\{ {{v_0} + {v_L}{{\left( { - 1} \right)}^m} + m{B_{mn}}} \right\}\cos \frac{{m\pi x}}{L}} } \right]\sin n\theta \sin \omega t,\quad 0 \leqslant x \leqslant L,} \hfill \\ {{v_{,xx}} = - {{\left( {\frac{\pi }{L}} \right)}^2}\left[ {\sum\limits_{m = 1}^\infty {\left\{ {{v_0}m + {v_L}m{{\left( { - 1} \right)}^m} + {m^2}{B_{mn}}} \right\}\sin \frac{{m\pi x}}{L}} } \right]\sin n\theta \sin \omega t,\quad 0 < x < L,} \hfill \\ {\quad \quad \quad \quad {v_{,xx}}\left( {0,\theta } \right) = - \left( {\frac{{{\pi ^3}}}{{2{L^2}}}} \right){{\overline{\overline v} }_0}\sin n\theta ,\quad {v_{,xx}}\left( {L,\theta } \right) = - \left( {\frac{{{\pi ^3}}}{{2{L^2}}}} \right){{\overline{\overline v} }_L}\sin n\theta ,} \hfill \\ {w\left( {x,\theta ,t} \right) = \sum\limits_{m = 1}^\infty {{C_{mn}}\sin \left( {m\pi x/L} \right)\cos n\theta \sin \omega t,\quad 0 < x < L,} } \hfill \\ {\quad \quad \quad \quad w\left( {0,\theta } \right) = - \left( {\frac{\pi }{2}} \right){w_0}\cos n\theta ,\quad v\left( {L,\theta } \right) = - \left( {\frac{\pi }{2}} \right){w_L}\cos n\theta ,} \hfill \\ {{w_{,x}} = \left( {\frac{\pi }{L}} \right)\left[ {\frac{{{w_0} + {w_L}}}{2} + \sum\limits_{m = 1}^\infty {\left\{ {{w_0} + {w_L}{{\left( { - 1} \right)}^m} + m{C_{mn}}} \right\}\cos \frac{{m\pi x}}{L}} } \right]\cos n\theta \sin \omega t,\quad 0 \leqslant x \leqslant L,} \hfill \\ {{w_{,xx}} = - {{\left( {\frac{\pi }{L}} \right)}^2}\left[ {\sum\limits_{m = 1}^\infty {\left\{ {{w_0}m + {w_L}m{{\left( { - 1} \right)}^m} + {m^2}{C_{mn}}} \right\}\sin \frac{{m\pi x}}{L}} } \right]\cos n\theta \sin \omega t,\quad 0 < x < L,} \hfill \\ {\quad \quad \quad \quad {w_{,xx}}\left( {0,\theta } \right) = - \left( {\frac{{{\pi ^3}}}{{2{L^2}}}} \right){{\overline{\overline w} }_0}\cos n\theta ,\quad {w_{,xx}}\left( {L,\theta } \right) = - \left( {\frac{{{\pi ^3}}}{{2{L^2}}}} \right){{\overline{\overline w} }_L}\cos n\theta ,} \hfill \\ {{w_{,xxx}} = {{\left( {\frac{\pi }{L}} \right)}^3}\left[ {\frac{{{{\overline{\overline w} }_0} + {{\overline{\overline w} }_L}}}{2} + \sum\limits_{m = 1}^\infty {\left\{ {{{\overline{\overline w} }_0} + {{\overline{\overline w} }_L}{{\left( { - 1} \right)}^m} - {m^2}{w_0} - {m^2}{w_L}{{\left( { - 1} \right)}^m} + {m^3}{C_{mn}}} \right\}\cos \frac{{m\pi x}}{L}} } \right]} \hfill \\ {\quad \quad \quad \quad \quad \quad \quad \quad \quad \times \cos n\theta \sin \omega t,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0 \leqslant x \leqslant L,} \hfill \\ {{w_{,xxxx}} = {{\left( {\frac{\pi }{L}} \right)}^4}\left[ {\sum\limits_{m = 1}^\infty {\left\{ { - m{{\overline{\overline w} }_0} - m{{\overline{\overline w} }_L}{{\left( { - 1} \right)}^m} + {m^3}{w_0} + {m^3}{w_L}{{\left( { - 1} \right)}^m} + {m^4}{C_{mn}}} \right\}\sin \frac{{m\pi x}}{L}} } \right]} \hfill \\ {\quad \quad \quad \quad \quad \quad \quad \quad \quad \times \cos n\theta \sin \omega t,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 0 < x < L,} \hfill \\ {{w_{,xxxx}}\left( {0,\theta } \right) = {{\overline{\overline {\overline{\overline w} }} }_0}\cos n\theta ,\quad \quad \quad \quad \quad \quad {w_{,xxxx}}\left( {L,\theta } \right) = {{\overline{\overline {\overline{\overline w} }} }_L}\cos n\theta } \hfill \\ \end{array} $$

The successive derivatives with respect to θ and t are simply achieved. For example, the successive derivatives of u(x, θ, t) with respect to θ are as follows

$$ \begin{gathered} {u_{,\theta }} = - n\left( {{A_{0n}} + \sum\limits_{m = 1}^\infty {{A_{mn}}\cos \frac{{m\pi x}}{L}} } \right)\sin n\theta \sin \omega t, \hfill \\ {u_{,\theta \theta }} = - {n^2}\left( {{A_{0n}} + \sum\limits_{m = 1}^\infty {{A_{mn}}\cos \frac{{m\pi x}}{L}} } \right)\cos n\theta \sin \omega t \hfill \\ \end{gathered} $$

Appendix B

$$ \begin{array}{*{20}{c}} {{K_{11}} = R{A_{11}}{{\left( {\frac{{m\pi }}{L}} \right)}^2} + {A_{66}}\frac{{{n^2}}}{R}} \hfill \\ {{K_{12}} = - \left( {{A_{12}} + {A_{66}} + \frac{{{B_{12}}}}{R} + \frac{{{B_{66}}}}{{2R}}} \right)\left( {\frac{{mn\pi }}{L}} \right)} \hfill \\ {{K_{13}} = - {A_{12}}\left( {\frac{{m\pi }}{L}} \right) - R{B_{11}}{{\left( {\frac{{m\pi }}{L}} \right)}^3} + \left( {{B_{12}} - {B_{66}}} \right)\left( {\frac{{m\pi {n^2}}}{{RL}}} \right)} \hfill \\ {{K_{22}} = \left( {R{A_{66}} + \frac{{3{B_{66}}}}{2} + \frac{{{D_{66}}}}{{2R}}} \right){{\left( {\frac{{m\pi }}{L}} \right)}^2} + \left( {R{A_{22}} + 2{B_{22}} + \frac{{{D_{22}}}}{R}} \right){{\left( {\frac{n}{R}} \right)}^2}} \hfill \\ {{K_{33}} = {{\left( {\frac{{m\pi }}{L}} \right)}^2}{{\left( {2{B_{12}} + R{D_{11}}(\frac{{m\pi }}{L}} \right)}^2} + \left. {2\frac{{{D_{12}} + {D_{66}}}}{R}{n^2}} \right)} \hfill \\ { + 2{B_{22}}{{\left( {\frac{n}{R}} \right)}^2} + \frac{{{A_{22}}}}{R} + {D_{22}}\frac{{{n^4}}}{{{R^3}}}} \hfill \\ {{K_{01}} = {A_{66}}\frac{{{n^2}}}{R}} \hfill \\ \end{array} $$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hemmatnezhad, M., Ansari, R. & Darvizeh, M. Prediction of Vibrational Behavior of Composite Cylindrical Shells under Various Boundary Conditions. Appl Compos Mater 17, 225–241 (2010). https://doi.org/10.1007/s10443-009-9108-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10443-009-9108-4

Keywords

Search

Navigation