Modelling and Subject-Specific Validation of the Heart-Arterial Tree System

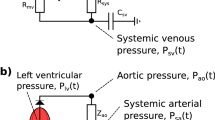
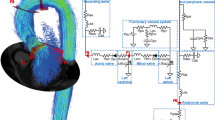
Abstract

A modeling approach integrated with a novel subject-specific characterization is here proposed for the assessment of hemodynamic values of the arterial tree. A 1D model is adopted to characterize large-to-medium arteries, while the left ventricle, aortic valve and distal micro-circulation sectors are described by lumped submodels. A new velocity profile and a new formulation of the non-linear viscoelastic constitutive relation suitable for the {Q, A} modeling are also proposed. The model is firstly verified semi-quantitatively against literature data. A simple but effective procedure for obtaining subject-specific model characterization from non-invasive measurements is then designed. A detailed subject-specific validation against in vivo measurements from a population of six healthy young men is also performed. Several key quantities of heart dynamics—mean ejected flow, ejection fraction, and left-ventricular end-diastolic, end-systolic and stroke volumes—and the pressure waveforms (at the central, radial, brachial, femoral, and posterior tibial sites) are compared with measured data. Mean errors around 5 and 8%, obtained for the heart and arterial quantities, respectively, testify the effectiveness of the model and its subject-specific characterization.

Appendices

Appendix

Coefficients of the constitutive Eq. (13)

$$\begin{aligned}&B_1=-\frac{1}{a_3^3} \bigl (a_5^3+PWV^6 \rho ^3+3 PWV^4 \rho ^2 a_5+3 a_5^2 PWV^2 \rho \bigr ) \quad \Biggl [\frac{\text {N}}{\text {m}^2}\Biggr ]\\&B_2=\frac{3\rho PWV^2}{A_0 a_3^3}\bigl (\rho ^2 PWV^4 +2 \rho a_5 PWV^2 +a_5^2\bigr ) \quad \Biggl [\frac{\text {N}}{\text {m}^4}\Biggr ]\\&B_3=-\frac{3 \rho ^2 PWV^4}{A_0^2 a_3^3} \bigl (a_5+\rho PWV^2 \bigr ) \quad \Biggl [\frac{\text {N}}{\text {m}^6}\Biggr ],\quad B_4=\Biggl (\frac{\rho PWV^2}{a_3 A_0}\Biggr )^3 \quad \Biggl [\frac{\text {N}}{\text {m}^8}\Biggr ]. \end{aligned}$$

Numerical Method

The model described in the second section is solved using the Runge-Kutta Discontinuous-Galerkin method12: first, space is discretized by a Discontinuous-Galerkin approach, then time evolution is described by a second-order Runge-Kutta scheme.

Conservative Form

In the conservative form, model (1) and (17) reads

$$\begin{aligned} \frac{\partial \mathbf {U}}{\partial t}+\frac{\partial \mathbf {F}(\mathbf {U})}{\partial x}+\mathbf {S}(\mathbf {U})=0 \end{aligned}$$

(29)

where $\mathbf {U}=[A(x,t),Q(x,t)]^T$ are the conservative variables, whereas the corresponding fluxes and source terms are

$$\begin{aligned} \mathbf {F}(\mathbf {U})= \left[ \begin{array}{l} Q \\ \beta \frac{Q^2}{A} +\displaystyle \sum _{j=2}^{4}\frac{j\!-\!1}{\rho {j}}A^jB_j -\frac{B_5}{\rho } \sqrt{A} \frac{\partial Q}{\partial x} \end{array}\right],\quad \mathbf {S}(\mathbf {U})=\left[\begin{array}{l} 0\\ \displaystyle \sum _{j=1}^{4}\frac{A^j}{\rho {j}}\frac{\text{ d }B_j}{\text{ d }x} +\frac{B_5}{\rho \sqrt{A}} \frac{\partial Q}{\partial x} \frac{\partial A}{\partial x}\!-\!N_4\!-\!A\,b_x \end{array}\right], \end{aligned}$$

where $b_x=g \sin (\gamma )$ is the longitudinal projection of the gravitational acceleration.

To solve system (29) in a one-dimensional generic domain $\Omega$ discretized into $N_{el}$ elemental non-overlapping regions $\Omega _e=[x_e^l,x_e^r]$—such that $x_{e+1}^l=x_e^r$ for $e=1,\ldots,N_{el}$ and $\cup _{e=1}^{N_{el}} \Omega _e=\Omega$—the weak form of Eq. (29) is written

$$\begin{aligned} \Biggl (\frac{\partial \mathbf {U}}{\partial t},\varvec{\psi } \Biggr )_\Omega +\Biggl (\frac{\partial \mathbf {F}}{\partial x},\varvec{\psi } \Biggr )_\Omega +\Bigl (\mathbf {S},\varvec{\psi } \Bigr )_\Omega =0 \end{aligned}$$

(30)

where $\varvec{\psi }$ is a set of arbitrary test functions in $\Omega$ and $(\mathbf {v},\mathbf {p})_\Omega =\int _\Omega \mathbf {v}\mathbf {p} \text {dx}$ is the standard $\mathbf {L}^2(\Omega )$ inner product between two generic function $\mathbf {v}$ and $\mathbf {p}$ whose domain is the closed interval $\Omega$. Decomposing the integrals in Eq. (30) into the elemental regions and integrating by part the second term, one obtains

$$\begin{aligned} \sum _{e=1}^{N_{el}} \Biggl [\Biggl (\frac{\partial \mathbf {U}}{\partial t},\varvec{\psi } \Biggr )_{\Omega _e} -\Biggl (\mathbf {F},\frac{d \varvec{\psi }}{d x} \Biggr )_{\Omega _e} +\bigl [ \mathbf {F} \varvec{\psi }\bigr ]_{\partial \Omega _e} +\Bigl (\mathbf {S},\varvec{\psi } \Bigr )_{\Omega _e}\Biggr ] =0. \end{aligned}$$

(31)

In order to discretize the problem in space, U is assumed to belong to the finite dimensional space of the $\mathbf {L}^2(\Omega )$ functions—that are polynomials of degree 1 on each element $\Omega _e$—obtaining the approximate solution $\mathbf {U}_h$ (subscript $h$ marks an element of such a space). Even if the solution $\mathbf {U}_h$ can be discontinuous at boundaries between elemental regions, information propagates by upwinding the fluxes $\mathbf {F}$ on the third term of Eq. (31).

The approximate solution $\mathbf {U}_h=\mathbf {U}_h(x,t)$ on the element $\Omega _e$ can be represented as

$$\begin{aligned} \mathbf {U}_h(x_e(\xi ),t)=\sum _{i=1}^2 \alpha _i(t) \phi _i(\xi ) \end{aligned}$$

where $\alpha _i$ are the time dependent unknown weights, $\phi _i(\xi )$ are the trial functions on the reference element $\hat{\Omega }=[-1,1]$, and the following affine mapping between $\hat{\Omega }$ and $\Omega _e$ is introduced

$$\begin{aligned} x_e(\xi )=x_e^l \frac{1-\xi }{2}+x_e^r \frac{1+\xi }{2}. \end{aligned}$$

We choose first-degree Lagrange functions as expansion polynomial basis, $\phi _1(\xi )\!=\!(1-\xi )/2$, $\phi _2(\xi )\!=\!(1+\xi )/2$, and, following the usual Galerkin approach, the discrete test functions $\varvec{\psi }_h$ are chosen in the same discrete space as the numerical solution $\mathbf {U}_h$.

Introducing the approximate solution $\mathbf {U}_h$ and the discrete test function into relation (31), one obtains the weak formulation as

$$\begin{aligned} \sum _{e=1}^{N_{el}} \Biggl [\Biggl (\frac{\partial \mathbf {U}_h}{\partial t},\varvec{\psi }_h \Biggr )_{\Omega _e}-\Biggl (\mathbf {F}(\mathbf {U}_h),\frac{d \varvec{\psi }_h}{d x}\Biggr )_{\Omega _e} +\bigl [ \mathbf {F}_{LF} \,\varvec{\psi }_h\bigr ]_{\partial \Omega _e}+\Bigl (\mathbf {S}(\mathbf {U}_h),\varvec{\psi }_h\Bigr )_{\Omega _e}\Biggr ] =0 \end{aligned}$$

(32)

where $\mathbf {F}_{LF}$ are the upwinded numerical fluxes. They are obtained using the Lax-Friedrichs method as

$$\begin{aligned} \mathbf {F}_{LF}=\frac{1}{2} (\mathbf {F}(\mathbf {U}^-)+\mathbf {F}(\mathbf {U}^+)-\lambda _{max} (\mathbf {U}^+-\mathbf {U}^-)) \end{aligned}$$

where $\mathbf {U}^+$ ($\mathbf {U}^-$, resp.) are the variables on the right (left, resp.) side of the boundary and $\lambda _{max}$ is the maximum eigenvalue of the matrix $\mathbf {H}(\mathbf {U})$ of the quasi-linear form (see eq. (7.2.1), below).

The formulation (32) is then advanced in time by a second-order Runge-Kutta explicit method. The choice of such a low-order time-advancing scheme is coherent with the spatial discretization, in which the order of the expansion polynomial is one. This method is stable if the well-known Courant-Friedrichs-Lewy (CFL) condition is satisfied.

Boundary Conditions

When characteristics have slopes of opposite signs—as in the present situation, see below –, the differential system (1) and (17) needs only one physical condition at each domain boundary. However, the solution of the numerical problem requires to prescribe both variables at each boundary. For this reason, extra relations (called compatibility equations) have to be written at each boundary by projecting the differential equations along the outgoing characteristics.

Quasi-Linear Form

In order to formulate the compatibility conditions, system (29) is written in the quasi-linear form

$$\begin{aligned} \frac{\partial \mathbf {U}}{\partial t}+ \mathbf {H}(\mathbf {U})\frac{\partial \mathbf {U}}{\partial x}+\mathbf {S}_2(\mathbf {U})=0 \end{aligned}$$

(33)

where the terms

$$\begin{aligned} \mathbf {H}(\mathbf {U})=\left[\begin{array}{ll} 0&1 \\ \frac{1}{\rho }\displaystyle \sum _{j=1}^4jA^jB_{j+1} -\beta \frac{Q^2}{A^2}&2 \beta \frac{Q}{A} \end{array}\right],\quad \mathbf {S}_2(\mathbf {U})=\left[\begin{array}{l} 0\\ \frac{1}{\rho }\displaystyle \sum _{j=1}^4jA^j\frac{\text{ d }B_{j}}{\text{ d }x} -N_4 -A\,b_x \end{array}\right] \end{aligned}$$

are obtained by neglecting viscoelasticity. Notice that the characteristic variables move along the corresponding characteristic directions for a spatial distance equal to the product of the time step by the local wave celerity. Being both time step and celerity small, the spatial distance is very small thus allowing the viscoelastic effect to be neglected.

Let $\varvec{\Lambda }$ and $\mathbf {L}$ be the eigenvalue and left eigenvector matrices of $\mathbf {H}(\mathbf {U})$, respectively, so that $\mathbf {L} \mathbf {H} \mathbf {L}^{-1} = \varvec{\Lambda }$. They read

$$\begin{aligned} \varvec{\Lambda }(\mathbf {U})=\left[\begin{array}{ll} \lambda _1&0 \\ 0&\lambda _2 \end{array}\right] \quad \mathbf {L}(\mathbf {U})=\left[\begin{array}{ll} -\lambda _2&0 \\ -\lambda _1&0 \end{array}\right]. \end{aligned}$$

(34)

In the present case, the eigenvalues read

$$\begin{aligned} \lambda _1=\beta \frac{Q(x,t)}{A(x,t)}-c(x,t), \qquad \qquad \lambda _2=\beta \frac{Q(x,t)}{A(x,t)}+c(x,t) \end{aligned}$$

where

$$\begin{aligned} c(x,t)=\sqrt{\frac{A}{\rho }(B_2+2 B_3 A+3 B_4 A^2)+(\beta -1) \beta \frac{Q^2}{A^2}} \end{aligned}$$

is the celerity of the propagation when the fluid is at rest. At least in physiological condition, the system results strictly hyperbolic because $c$ is always greater than $\beta Q/A$, entailing $\lambda _1<0$ (backward propagation) and $\lambda _2>0$ (forward propagation).

Compatibility Conditions

The characteristic variables $\mathbf {W}$ are defined as

$$\begin{aligned} \frac{\partial \mathbf {W}}{\partial \mathbf {U}}=\mathbf {L}(\mathbf {U}). \end{aligned}$$

(35)

Due to the structure of the matrix $\mathbf {L}$, it is not possible to obtain the characteristic variables analytically. Therefore, pseudo-characteristic variables are introduced by linearising Eq. (35).

By pre-multiplying the vectorial Eq. (33) by the left eigenvector matrix, one obtains

$$\begin{aligned} \mathbf {L}(\mathbf {U}) \frac{\partial \mathbf {U}}{\partial t}+ \mathbf {L}(\mathbf {U}) \mathbf {H}(\mathbf {U})\frac{\partial \mathbf {U}}{\partial x}+\mathbf {L}(\mathbf {U}) \mathbf {S}_2(\mathbf {U})=0 \end{aligned}$$

and then

$$\begin{aligned} \mathbf {L}(\mathbf {U}) \frac{\partial \mathbf {U}}{\partial t}+\varvec{\Lambda }(\mathbf {U}) \mathbf {L}(\mathbf {U}) \frac{\partial \mathbf {U}}{\partial x}+\mathbf {L}(\mathbf {U}) \mathbf {S}_2(\mathbf {U})=0. \end{aligned}$$

(36)

In order to introduce the total derivative, the first term of Eq. (36) is rewritten as

$$\begin{aligned} \mathbf {L}(\mathbf {U}) \frac{\partial \mathbf {U}}{\partial t}=\frac{\partial }{\partial t} \Bigl ( \mathbf {L}(\mathbf {U}) \mathbf {U} \Bigr )- \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial t} \end{aligned}$$

and the second term as

$$\begin{aligned} \varvec{\Lambda }(\mathbf {U}) \mathbf {L}(\mathbf {U}) \frac{\partial \mathbf {U}}{\partial x}=\varvec{\Lambda }(\mathbf {U}) \frac{\partial }{\partial x} \Bigl ( \mathbf {L}(\mathbf {U}) \mathbf {U} \Bigr )- \varvec{\Lambda }(\mathbf {U}) \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial x}, \end{aligned}$$

obtaining

$$\begin{aligned} \frac{\partial }{\partial t} \Bigl ( \mathbf {L} (\mathbf {U})\mathbf {U}\Bigr )+ \varvec{\Lambda }(\mathbf {U}) \frac{\partial }{\partial x} \Bigl ( \mathbf {L}(\mathbf {U}) \mathbf {U} \Bigr )- \varvec{\Lambda }(\mathbf {U}) \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial x}- \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial t}+ \mathbf {L}(\mathbf {U}) \mathbf {S}_2(\mathbf {U})=0. \end{aligned}$$

By introducing the total derivative $\mathrm{D} / \mathrm{D} t$, the last equation becomes

$$\begin{aligned} \frac{D\mathbf {L}(\mathbf {U}) \mathbf {U}}{D t}- \varvec{\Lambda }(\mathbf {U}) \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial x}- \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial t}+ \mathbf {L}(\mathbf {U}) \mathbf {S}_2(\mathbf {U})=0. \end{aligned}$$

(37)

If time is now discretized so that $\Delta t=t_{n+1}-t_{n}$ is the time step (the subscript $n$ denotes the $n$-th time instant), the total derivative can be approximated as

$$\begin{aligned} \frac{D}{D t}\Bigl ({\mathbf {L}}_{n+1}{\mathbf {U}}_{n+1}\Bigr )\approx \frac{{\mathbf {L}}_{n+1}{\mathbf {U}}_{n+1}-{\mathbf {L}}_{n}^{\star }{\mathbf {U}}_{n}^{\star }}{\Delta t}=\frac{{\mathbf {L}}_{n} {\mathbf {U}}_{n+1}-{\mathbf {L}}_{n}^{\star }{\mathbf {U}}_{n}^{\star }}{\Delta t}+\frac{\bigl ({\mathbf {L}}_{n+1} -{\mathbf {L}}_{n}\bigr ){\mathbf {U}}_{n+1}}{\Delta t} \end{aligned}$$

(38)

where the superscript $\star$ refers to the point located at the distance from the boundary equal to $c \cdot \Delta t$. By assuming that

$$\begin{aligned} \frac{\bigl (\mathbf {L}_{n+1} -\mathbf {L}_{n}\bigr )\mathbf {U}_{n+1}}{\Delta t} \approx \mathbf {U} \frac{\partial \mathbf {L}(\mathbf {U})}{\partial t} \end{aligned}$$

the departure of the pseudo-characteristic from a generic state $\mathbf {U}_n^{\star }$ is taken as

$$\begin{aligned} \mathbf {L}_n \mathbf {U}_{n+1}=\mathbf {L}_n^{\star } \mathbf {U}_{n}^{\star }+\Delta t \, \Bigl ( \varvec{\Lambda }_n^{\star } \frac{\partial \mathbf {L}_n^{\star }}{\partial x} \mathbf {U}_{n}^{\star }-\mathbf {L}_n^{\star } \mathbf {S}_2(\mathbf {U}_n^{\star }) \Bigl ) \end{aligned}$$

(39)

where $\mathbf {L}_n=\mathbf {L}(\mathbf {U}_n)$ and $\varvec{\Lambda }_n=\varvec{\Lambda }(\mathbf {U}_n)$.

Finally, because the pseudo-characteristics at the initial state are set null, Eq. (39) needs to be balanced by subtracting the initial condition to the dependent variables,29 i.e.

$$\begin{aligned} \mathbf {L}_n (\mathbf {U}_{n+1}-\mathbf {U}_{0})=\mathbf {L}_n^{\star } (\mathbf {U}_{n}^{\star }-\mathbf {U}_{0}^{\star })+\Delta t \, \Bigl (\varvec{\Lambda }_n^{\star } \frac{\partial \mathbf {L}_n^{\star }}{\partial x} (\mathbf {U}_{n}^{\star }-\mathbf {U}_{0}^{\star })-\mathbf {L}_n^{\star } (\mathbf {S}_2(\mathbf {U}_n^{\star })-\mathbf {S}_2(\mathbf {U}_0^{\star })) \Bigl ) \end{aligned}$$

(40)

where the subscript $0$ refers to the initial condition. Since the reference condition (uniform pressure of 100 mmHg and no flow) is assumed as initial condition, the same subscript $0$ is used to define both quantities.

The formulation (40) has to be coupled with the physical boundary conditions at every (internal and external) boundary. The corresponding non-linear systems are solved by an adaptive trust-region-dogleg method.