Skip to main content
SpringerLink
Log in

Numerical investigation on fluid forces of piggyback circular cylinders in tandem arrangement at low Reynolds numbers

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

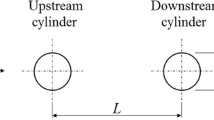
Abstract

Numerical simulations of flows past the piggyback circular cylinders in tandem arrangement are performed by solving the variational multiscale formulation of the incompressible Navier–Stokes equations using in-house finite element method (FEM) codes. The effects of the gap-spacing-to-diameter (G/D) and the two diameter ratio (d/D) on the flow characteristics and the reductions of the root-mean-square (RMS) drag and lift coefficients are considered for Reynolds numbers (Res) are 100 and 200. The validation shows the fluid force coefficients obtained by the in-house FEM codes are in good agreement with the results in the existing literatures. The obtained results show that, with a proper placement of the smaller cylinder (\(d/D=0.2\)) behind the larger cylinder, the RMS drag and lift coefficients largely decrease compared to those of the single circular cylinder. When \(d/D=0.2\), the largest reductions of the RMS lift coefficient of the larger cylinder and the RMS total lift coefficient appear at \(G/D=1.2\) as Re \(=100\) and at \(G/D=1.0\) as Re \(=200\). It is observed that the proper placement of the smaller cylinder causes the surrounding vorticity to take opposite sign with the vorticity in the outer region so as to suppress and postpone the vortex shedding in the wake, and that the different positions of the vortex shedding at two Res cause that the largest reductions of the RMS lift coefficient of the larger cylinder and the RMS total lift coefficient appear at different G/D as Re is different. When d/D varies, the variation of the RMS total lift coefficient behaves differently at two Res. It decreases with d/D increasing at Re \(=100\), while it no longer monotonously varies with d/D, but reaches a minimum in the considered range of d/D at Re \(=200\). Moreover, the larger d/D results in stronger suppression and postponement of the vortex shedding in the wake.

Graphic abstract

The effects of the gap-spacing-to-diameter and the two-diameter ratio on the flow characteristics and the reductions of the root-mean-square (RMS) drag and lift coefficients are investigated by stabilized finite element method. With a proper placement of the smaller cylinder behind the larger cylinder, the RMS drag and lift coefficients are smaller than those of the single circular cylinder. The proper placement of the smaller cylinder causes the surrounding vorticity to take opposite sign with the vorticity in the outer region so as to suppress and postpone the vortex shedding in the wake.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Wu, B., Bachina, D., Fan, D., et al.: Vortex-induced vibration of a piggyback pipeline half buried in the seabed. J. Sound Vibr. 449, 182–195 (2019)

    Article  Google Scholar 

  2. Brankovic, M., To/rnes, K., Zeitoun, H., et al.: Dynamic stability response of piggyback pipelines. In: Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering (2010)

  3. Zeitoun, H., Sutherland, J., Brankovic, M., et al., Physical modelling of hydrodynamic loads on piggyback pipelines in combined wave and current conditions. In: Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering (2010)

  4. Igarashi, T.: Characteristics of a flow around two circular cylinders of different diameters arranged in tandem. Bull. JSME 25(201), 349–357 (1982)

    Article  Google Scholar 

  5. Wong, P., Ko, N.: Flows past two circular cylinders of different diameters. J. Wind Eng. Ind. Aerodynam. 41, 563–564 (1992)

  6. Wong, P., Leung, R., Ko, N.: Interaction of flow structures within bistable flow behind two circular cylinders of different diameters. Exp. Therm. Fluid Sci. 12(8), 33–44 (1996)

    Google Scholar 

  7. Sreenivasan, K., Strykowski, P.: On the formation and suppression of vortex ‘shedding’ at low reynolds numbers. J. Fluid Mech. 218, 71 (1990)

  8. Sengupta, T., Talla, S., Dipankar, A.: Suppression of vortex shedding behind a circular cylinder by another control cylinder at low reynolds numbers. J. Fluid Mech. 573, 171–190 (2007)

    Article  Google Scholar 

  9. Haniu, H., Sakamoto, H.: Optimum suppression of fluid forces acting on a circular cylinder. J. Fluids Eng. 116(2), 221 (1994)

    Article  Google Scholar 

  10. Xu, Y., Owen, J., Dalton, C.: The suppression of lift on a circular cylinder due to vortex shedding at moderate reynolds numbers. J. Fluids Struct. 15(3–4), 617–628 (2001)

    Google Scholar 

  11. Kamemoto, K., Tsutsui, T., Igarashi, T.: Interactive flow around two circular cylinders of different diameters at close proximity. Experiment and numerical analysis by vortex method. J. Wind Eng. Ind. Aerodynam. 69–71, 279–291 (1997)

    Google Scholar 

  12. Cheng, L., Teng, B., Zhao, M., et al.: Numerical simulation of viscous flow past two circular cylinders of different diameters. Appl. Ocean Res. 27(1), 39–55 (2005)

    Article  Google Scholar 

  13. Cheng, L., Teng, B., Zhao, M., et al.: Hydrodynamic forces on dual cylinders of different diameters in steady currents. J. Fluids Struct. 23(1), 59–83 (2007)

    Article  Google Scholar 

  14. Duan, M., Gu, J., Song, Z.: Hydrodynamics and vortex shedding characteristics of two tandem cylinders of different diameters in steady flow. Ships Offshore Struct. 12, 1–14 (2015)

    Google Scholar 

  15. Zhao, M., Cheng, L., Thapa, J., et al.: Three-dimensional flow around two circular cylinders of different diameters in a close proximity. Phys. Fluids 27(8), 39–55 (2015)

    Article  Google Scholar 

  16. Cheng, L., Bin, T., Zhao, M.: Numerical modeling of flow and hydrodynamic forces around a piggyback pipeline near the seabed. J. Waterway Port Coast. Ocean Eng. 133(4), 286–295 (2007)

    Article  Google Scholar 

  17. Gao, F., Cui, J., Zang, Z.: Physical modeling and swirling strength analysis of vortex shedding from near-bed piggyback pipelines. Appl. Ocean Res. 40, 50–59 (2013)

    Article  Google Scholar 

  18. Hughes, T.J.R.: Multiscale phenomena: Greens̈ functions, the dirichlet-to-neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Comput. Methods Appl. Mech. Eng. 127(1–4), 387–401 (1995)

    Article  MathSciNet  Google Scholar 

  19. Feijo, G., Mazzei, L., Hughes, T.J.R., et al.: The variational multiscale method—a paradigm for computational mechanics. Comput. Methods Appl. Mech. Eng. 166(1–2), 3–24 (1998)

    MathSciNet  MATH  Google Scholar 

  20. Hu, X.Q., Chen, L.F.: A pod-based variational multiscale method for large eddy simulation of turbulent channel flows. Int. J. Comput. Methods 14(5), 1750049 (2017)

    Article  MathSciNet  Google Scholar 

  21. Chen, G.X., Wu, L.F.: Boundary shear flow past a cylinder near a wall. Appl. Ocean Res. 92, 101923 (2019)

    Article  Google Scholar 

  22. Hulshoff, S.J., Wang, Y.T., Chen, L.F.: 2D residual-based les of flow around a pipeline close to a flat seabed. Comput. Meth. Appl. Mech. Eng. 363, 112788 (2020)

  23. Wang, Y.T., Sun, S.Y., Chen, L.F., et al.: The effect of boundary shear flow on hydrodynamic forces of a pipeline over a fully scoured seabed. Ocean Eng. 206, 107326 (2020)

    Article  Google Scholar 

  24. Hughes, T.J.R., Oberai, A.A., Holmen, J., et al.: Sensitivity of the scale partition for variational multiscale large-eddy simulation of channel flow. Phys. Fluids 16(3), 824–827 (2004)

    Article  Google Scholar 

  25. Khurram, R.A., Masud, A.: A multiscale finite element method for the incompressible Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 195(13–16), 1750–1777 (2006)

    MathSciNet  MATH  Google Scholar 

  26. Sangalli, G., Hughes, T.J.R.: Variational multiscale analysis: the fine-scale green’s function, projection, optimization, localization, and stabilized methods. SIAM J. Numer. Anal. 45(2), 539–557 (2007)

    Article  MathSciNet  Google Scholar 

  27. Franca, L.P., Tezduyar, T.E., Behr, M.A.: Stabilized finite element methods for the velocity–pressure–stress formulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 104(1), 31–48 (1993)

    Article  MathSciNet  Google Scholar 

  28. Hughes, T.J.R., Johan, Z., Shakib, F.: A new finite element formulation for computational fluid dynamics: X. the compressible euler and Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 89(1–3), 141–219 (1991)

    MathSciNet  Google Scholar 

  29. Calderer, R., Masud, A.: A variational multiscale method for incompressible turbulent flows: bubble functions and fine scale fields. Comput. Methods Appl. Mech. Eng. 200(33–36), 2577–2593 (2011)

    MathSciNet  MATH  Google Scholar 

  30. Goraya, S.A., Masud, A., Zhu, L.: Interface-capturing method for free-surface plunging and breaking waves. J. Eng. Mech. 145(11), 04019088 (2019)

    Article  Google Scholar 

  31. Whiting, C., Hulbert, G., Jansen, K.: A generalized-alpha method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Comput. Methods Appl. Mech. Eng. 190, 305–319 (2000)

    Article  Google Scholar 

  32. Michler, C., Calo, V., Bazilevs, Y., et al.: Isogeometric variational multiscale modeling of wall-bounded turbulent flows with weakly enforced boundary conditions on unstretched meshes. Comput. Methods Appl. Mech. Eng. 199(13–16), 780–790 (2010)

    MathSciNet  MATH  Google Scholar 

  33. Tan, Z.R., Lin, L.M.: DNS in evolution of vorticity and sign relationship in wake transition of a circular cylinder: (pure) mode A. Acta Mech. Sin. 35(6), 1131–1149 (2019)

  34. Kang, S.: Characteristics of flow over two circular cylinders in a side-by-side arrangement at low reynolds numbers. Phys. Fluids 15(9), 2486–2498 (2003)

    Article  Google Scholar 

  35. Sigrist, J., Hamdouni, A., Placzek, A.: Numerical simulation of vortex shedding past a circular cylinder in a cross-flow at low Reynolds number with finite volume-technique: Part 1—forced oscillations. In: Proceedings of the ASME Pressure Vessel and Piping Division Conference, pp. 11–20 (2007)

  36. Zhong, X.F., Wu, Y.X., Lin, L.M.: Effect of perforation on flow past a circular cylinder at Re =100: vortex-shedding pattern and force history. Acta Mech. Sin. 34(2), 238–256 (2018)

    Article  Google Scholar 

  37. Zhong, X.F., Wu, Y.X., Lin, L.M.: Effect of perforation on flow past a conic cylinder at Re = 100: vortex-shedding pattern and force history. Acta Mech. Sin. 34(5), 812–829 (2018)

    Article  MathSciNet  Google Scholar 

  38. Sotiropoulos, F., Borazjani, I.: Vortex-induced vibrations of two cylinders in tandem arrangement in the proximitycwake interference region. J. Fluid Mech. 621, 321–364 (2009)

  39. Wu, G.X., Jiao, H.: Analysis of fluctuating force acting on two cylinders in different arrangements through lattice Boltzmann method. J. Fluids Struct. 82, 101–120 (2018)

    Article  Google Scholar 

Download references

Acknowledgements

The project was supported by the Natural Science Foundation of Jiangsu Province (Grant SBK2018040999), the Natural Science Research of Jiangsu Higher Education Institutions of China (Grant 18KJB570001) and the National Natural Science Foundation of China (Grants 51879123 and 91852111).

Author information

Authors and Affiliations

  1. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Jiangsu, 212003, China

    Linfeng Chen

  2. Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai, 200072, China

    Yuhong Dong

Authors
  1. Linfeng Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuhong Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Linfeng Chen.

Additional information

Executive Editor: Guo-Wei He.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, L., Dong, Y. Numerical investigation on fluid forces of piggyback circular cylinders in tandem arrangement at low Reynolds numbers. Acta Mech. Sin. 37, 599–612 (2021). https://doi.org/10.1007/s10409-020-01037-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-020-01037-z

Keywords

Search

Navigation