1 Introduction

The continuum approximation may break down as the characteristic dimensions of the mechanical device approach the mean free path (for gases) or molecular scale (for liquids) (Szeri 2011). Non-continuum effects on fluid flow are characterised by thermal creep, intermolecular forces, and the appearance of slip flow at solid boundaries (Gad-el-Hak 1999). For gas flows, when a Knudsen number (i.e. the ratio of the mean free path to the characteristic length scale of the flow) is in the range \(\text {Kn}\ge 10^{-3}\), the traditional no-slip boundary condition is no longer valid (Gad-el-Hak 1999), and similarly for liquid flows (Barrat and Bocquet 1999; Priezjev 2013; Omori et al. 2019). An important application at these scales is found in micro-electro-mechanical systems (MEMS) as sensors and actuators in a flow. For example, the typical flight height of the read/write head of a computer hard disk drive is on the order of \(1{\sim }10\,\text {nm}\). For such thin film flows, the Reynolds lubrication equation (Reynolds 1886) with a no-slip boundary condition is known to predict too much shear stress, and therefore lubrication models that take into account the velocity slip on the wall have been developed (Burgdorfer 1959; Shukla et al. 1980; Hsia and Domoto 1983; Mitsuya 1993; Wu and Bogy 2003; Bahukudumbi and Beskok 2003; Aurelian et al. 2011; Bailey et al. 2017).

Although the velocity slips on solid boundaries are typically observed at small scales, there may be situations where flows in large clearances (i.e. not thin or non-negligible gaps) are affected by velocity slips. For example, the air flow in micro bearings typically takes \(\text {Kn}\sim 10^{-2}\) (Gad-el-Hak 1999), while the gap between the shaft and the housing is generally not expected to be sufficiently small (Maureau et al. 1997) to justify the thin-gap approximation. Maureau et al. (1997) analytically solved the lubrication problem between the circular shaft and the housing of a micro bearing in the Stokes regime with a slip boundary condition. They reported that the effect of velocity slip appears as a disappearance of the recirculation flow when the gap width is not negligible, while the recirculation zone becomes larger with the increase in the clearance. Later, Nieto et al. (2013) analysed the Stokes flow in an eccentric channel with a nonlinear slip boundary condition as a function of local shear rate, and the effect of the inhomogeneous slip length shows interesting implications on the velocity inversion and recirculation zone. Therefore, the flow patterns under velocity slip may be different from those predicted by the bare lubrication theory in thin gaps under no-slip boundary conditions.

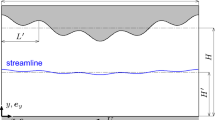
The mathematical treatment adopted in Maureau et al. (1997) to solve the Stokes flow problem in a non-negligible gap is similar to that developed by Kamal (1966) and Ashino and Yoshida (1975) using a conformal mapping from the bipolar coordinates (i.e. the region between two eccentric circles) to a rectangular system. Meanwhile, for lubrication in a gap of arbitrary shape (or even a region between deformable surfaces), the Reynolds lubrication equation is most widely used, and modifications of the equation with slip boundary condition were attempted; Aurelian et al. (2011) developed a modified Reynolds lubrication equation with the slip lengths in both wall-tangential and wall-normal directions, and Bailey et al. (2017) considered the effects of the fluid compressibility and velocity slip on the axisymmetric system. However, taking the aspect ratio of the gap region as \(\varepsilon\) (\(=H/L\) for the geometry in Fig. 1), the Reynolds lubrication equations were derived for a gap of \(\varepsilon \ll 1\) by retaining the \(O[\varepsilon ^0]\) terms in the Stokes equation. Therefore, in the situation of a non-negligible gap (i.e. \(\varepsilon \lesssim 1\)) bounded by (slip/no-slip) walls of arbitrary shape, a simple lubrication model is not possible and an additional higher order term needs to be considered in the Reynolds lubrication equation.

Fig. 1
figure 1

Schematic of a flow in a gap between two moving rigid surfaces

Full size image

One of the present authors showed that a higher order component of lubrication pressure can be considered through a reduced Stokes equation under the no-slip condition (Takeuchi and Gu 2019). Retaining the \(O[\varepsilon ^2]\) terms in the case of a non-negligible gap, Takeuchi and Gu (2019) showed that the pressure can be decomposed into (i) a base component satisfying the Reynolds lubrication equation and (ii) a higher order component that predominantly varies in the surface-normal direction. Their model contains an interesting aspect: the higher order term takes the form of the longitudinal variation of the local velocity of the Couette–Poiseuille flow driven by (i) and the moving walls. The validity of the higher order lubrication model was established for the case of non-negligible gap width of various geometries under the no-slip condition (Takeuchi and Gu 2019), and the feasibility of the model was studied for membrane permeation driven by lubrication pressure (Takeuchi et al. 2021a, 2021b; Yamada et al. 2021).

In this paper, we derive a higher order lubrication model of slip flow (under the linear slip boundary condition) in a non-negligible gap width, where the longitudinal variation of the gap is assumed to be small. The newly developed lubrication model has a unique property that the effect of velocity slip is capsuled as an apparent displacement of no-slip walls. The model is validated through comparison with a fully resolved numerical analysis of the Navier-Stokes equation under a boundary condition with locally varying slip length. Through modelling of the lubrication pressures under constant and locally varying slip lengths, the qualitative difference in the lubrication pressures by the slip characteristics is discussed.

2 Governing equations and boundary conditions

The following discussion is based on the gap and the boundary conditions illustrated in Fig. 1. For simplicity, the lower wall is flat. The x coordinate is taken along this wall, and the coordinate y is in the wall-normal direction. The velocities in the x and y directions are introduced as u and v, respectively. The wall velocities are \((U_{\text {b}},V_{\text {b}})\) on the lower wall and \((U_{\text {t}},V_{\text {t}})\) on the upper wall. The length scales in the longitudinal (x) and wall-normal (y) directions are taken as \(L\) and \(H\), respectively, and the aspect ratio of the narrow gap is introduced as \(\varepsilon =H/L\). The reference velocities in the x and y directions are denoted as U and V.

The scaled variables \(u_*=u/U,\ v_*=v/V,\ t_*=L/U,\ x_*=x/L,\ y_*=y/H\) and \(p_*=p/P_{\text {ref}}\) are introduced in the equation of continuity and in the incompressible Navier–Stokes equations, where t is the time and \(P_{\text {ref}}={\varepsilon ^{-2}}{\mu U} L^{-1}\). Then, the scaled equation of continuity,

$$\begin{aligned} \frac{\partial ^{} u_*}{\partial x_*^{}} +\frac{\partial ^{} v_*}{\partial y_*^{}} =0 \ \end{aligned}$$
(1)

gives the estimation \(V=\varepsilon U\). The scaled Navier–Stokes equations are obtained as (Leal 2007)

$$\begin{aligned}&\varepsilon ^2 {\textrm{Re}} \left( \frac{\partial ^{} u_*}{\partial t_*^{}} +\varvec{u}_*\!\cdot \!\nabla u_* \right) =- \frac{\partial ^{} p_*}{\partial x_*^{}} + \varepsilon ^2 \frac{\partial ^2 u_*}{\partial x_* ^2} +\frac{\partial ^2 u_*}{\partial y_* ^2} \\&\varepsilon ^4 {\textrm{Re}} \left( \frac{\partial ^{} v_*}{\partial t_*^{}} +\varvec{u}_*\!\cdot \!\nabla v_* \right) =- \frac{\partial ^{} p_*}{\partial y_*^{}} + \varepsilon ^4 \frac{\partial ^2 v_*}{\partial x_* ^2} + \varepsilon ^2 \frac{\partial ^2 v_*}{\partial y_* ^2} \end{aligned}$$

where \(\text {Re}=\rho U L/\mu\) is the Reynolds number. The characteristic aspect of this formulation may be that, because the reference pressure is defined with the viscous scale (\(P_{\text {ref}}\)), the Reynolds number appears in front of the inertia term multiplied with \(\varepsilon ^2\) and \(\varepsilon ^4\). By eliminating all the terms smaller than the order of \(\varepsilon ^2\) but retaining only the \(O[\varepsilon ^0]\) terms, the above equations are reduced to

$$\begin{aligned} \frac{\partial ^{} p}{\partial x^{}} =\mu \frac{\partial ^2 u}{\partial y ^2},\quad \frac{\partial ^{} p}{\partial y^{}} =0 \ \end{aligned}$$

which are the basic equations for the Reynolds lubrication equation (Reynolds 1886; Leal 2007).

On the other hand, assuming \(\text {Re}\ll 1\) and retaining the terms of \(O[\varepsilon ^2]\), we have the following set of equations:

$$\begin{aligned} & \frac{\partial ^{} p_*}{\partial x_*^{}}= \, {} \varepsilon ^2 \frac{\partial ^2 u_*}{\partial x_* ^2} + \frac{\partial ^2 u_*}{\partial y_* ^2} \ \end{aligned}$$
(2a)
$$\begin{aligned} & \frac{\partial ^{} p_*}{\partial y_*^{}}= {\qquad\qquad} \varepsilon ^2 \frac{\partial ^2 v_*}{\partial y_* ^2} \ \end{aligned}$$
(2b)

By using the gap width h(x), the first term in the right-hand side (RHS) of Eq. (2a) is re-evaluated as follows:

$$\begin{aligned} \varepsilon ^2 \frac{\partial ^2 u_*}{\partial x_* ^2} = \,\varepsilon ^2 \left[ \frac{\partial ^2 u_*}{\partial h_* ^2}\left( \frac{{\textrm{d}}^{} h_*}{{\textrm{d}} x_*^{}} \right) ^2 + \frac{\partial ^{} u_*}{\partial h_*^{}} \frac{{\textrm{d}}^2 h_*}{{\textrm{d}} x_*^2} \right] \ \end{aligned}$$
(3)

where \(h_*=h/H\). This equation indicates that, when both the gradient of the interface profile and its curvature

$$\begin{aligned} \kappa = \frac{{{\textrm{d}}^{2} h}/{{\textrm{d}} x^{2}} }{\left[ 1+\left( {{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} \right) ^2\right] ^{3/2}} \simeq \frac{{\textrm{d}}^{2} h}{{\textrm{d}} x^{2}} \end{aligned}$$

are small, the term \({\partial ^{2} u}/{\partial x^{2}}\) is smaller than the order of \(\varepsilon ^2\), which enables elimination of the second-order x-derivative of u from Eq. (2a). Therefore, in the present study, we employ the following set of equations for lubrication:

$$\begin{aligned}{} & {} \frac{\partial ^{} p}{\partial x^{}} =\mu \frac{\partial ^2 u}{\partial y ^2} \ \end{aligned}$$
(4a)
$$\begin{aligned}{} & {} \frac{\partial ^{} p}{\partial y^{}} =\mu \frac{\partial ^2 v}{\partial y ^2} \ \end{aligned}$$
(4b)

for a non-negligible gap of moderately undulating surface profile.

The isothermal slip boundary condition of the fluid velocity is specified by the following equation (Chen et al. 2014):

$$\begin{aligned} (\varvec{u}-\varvec{U})\cdot \varvec{t} =\ell \,\big [\,\varvec{t}\cdot (2\varvec{d})\cdot \varvec{n}\,\big ] \ \end{aligned}$$
(5)

where \(\varvec{u}\) and \(\varvec{U}\) are the fluid velocity and wall velocity vectors, respectively, \(\varvec{t}\) and \(\varvec{n}\) are the wall-tangential and wall-normal unit vectors, respectively, \(\ell\) is the slip length on the wall and \(\varvec{d}\) is the deformation rate tensor defined as \((\nabla \varvec{u}+(\nabla \varvec{u})^T)/2\). By introducing \(\varvec{t}\) and \(\varvec{n}\) as

$$\begin{aligned} \varvec{t} \simeq \frac{\varvec{e}_x + ({{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} )\varvec{e}_y}{\sqrt{1+({{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} )^2}}, \ \quad \varvec{n} \simeq \frac{\varvec{e}_y - ({{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} )\varvec{e}_x}{\sqrt{1+({{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} )^2}} \ \end{aligned},$$

where \(\varvec{e}_x\) and \(\varvec{e}_y\) are the basis in the x and y directions, and assuming \(|{{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} |\ll 1\), the above slip boundary condition is simplified as follows:

$$\begin{aligned}{} & {} u|_{y=h}-U_{\text {t}}=-\ell (x) \left. \frac{\partial ^{} u}{\partial y^{}} \right| _{y=h} \ , \end{aligned}$$
(6a)
$$\begin{aligned}{} & {} u|_{y=0}-U_{\text {b}}=+\ell (x) \left. \frac{\partial ^{} u}{\partial y^{}} \right| _{y=0} \ \end{aligned}$$
(6b)

Here, the slip length is denoted as a function of x for the purpose of the validation in the subsequent section. By assuming the wall is impenetrable to the fluid and also \(|{{\textrm{d}}^{} h}/{{\textrm{d}} x^{}} |\ll 1\), the y component of the fluid on the upper and lower walls is given as follows:

$$\begin{aligned} v|_{y=h}=\, & {} V_{\text {t}}\ \end{aligned}$$
(7a)
$$\begin{aligned} v|_{y=0}= \,& {} V_{\text {b}}\ \end{aligned}$$
(7b)

3 Modelling of lubrication with slip boundary condition

By solving Eqs. (1) and (4), a lubrication model is constructed to describe the pressure variation in both the longitudinal and surface-normal directions. The following two lemmas are introduced:

Lemma 1

The local pressure gradient in the x direction, \({\partial ^{} p}/{\partial x^{}}\), is regarded as a function of x (and is negligibly relevant to y).

Lemma 2

The pressure can be separated into the base and adjusting components:

$$\begin{aligned} p(x, y)=p_{\text {base}}(x)+p_{\text {adj}}(x, y) \ \end{aligned}$$
(8)

where no more independent function of x is separable from \(p_{\text {adj}}\).

The proofs of the lemmas are found in Takeuchi and Gu (2019), which are valid regardless of the specific wall boundary conditions.

By Lemma 1, we obtain the following form of u by integrating Eq. (4a) twice with respect to y:

$$\begin{aligned} u=\frac{1}{\mu }\frac{\partial ^{} p}{\partial x^{}} \frac{y^2}{2} + f_1(x)y + f_2(x) \ \end{aligned}$$
(9)

From the boundary conditions, Eq. (6), the integral constants \(f_1\) and \(f_2\) are given as

$$\begin{aligned} f_1(x)= & {} \frac{U_{\text {r}}}{h+2\ell } - \frac{h}{2\mu } \frac{\partial ^{} p}{\partial x^{}} \ , \end{aligned}$$
(10a)
$$\begin{aligned} f_2(x)= & {} \frac{\ell \,U_{\text {r}}}{h+2\ell } + U_{\text {b}}- \ell \frac{h}{2\mu } \frac{\partial ^{} p}{\partial x^{}} \ \end{aligned}$$
(10b)

where \(U_{\text {r}}=U_{\text {t}}-U_{\text {b}}\). From \({\partial ^{} v}/{\partial y^{}} =-{\partial ^{} u}/{\partial x^{}}\) with Eq. (9)

$$\begin{aligned} v=-\frac{1}{\mu }\frac{\partial ^2 p}{\partial x ^2} \frac{y^3}{6} - \frac{{\textrm{d}}^{} f_1}{{\textrm{d}} x^{}} \frac{y^2}{2} -\frac{{\textrm{d}}^{} f_2}{{\textrm{d}} x^{}} y +V_{\text {b}}\end{aligned}$$

is obtained, where one of the boundary conditions \(v|_{y=0}=V_{\text {b}}\) is used. The other velocity condition on the boundary, \(v|_{y=h}=V_{\text {t}}\), imposes the following relation:

$$\begin{aligned} V_{\text {r}}= -\frac{h^3}{6\mu } \left. \frac{\partial ^2 p}{\partial x ^2} \right| _{y=h} -\frac{h^2}{2} \frac{{\textrm{d}}^{} f_1}{{\textrm{d}} x^{}} -h\frac{{\textrm{d}}^{} f_2}{{\textrm{d}} x^{}} \ \end{aligned}$$

where \(V_{\text {r}}=V_{\text {t}}-V_{\text {b}}\). Hereafter, the wall pressure that satisfies the above equation is denoted as \(p_{\text {w}}(x)\). Substituting Eq. (10) into the above equation, the following equation for \(p_{\text {w}}\) is obtained:

$$\begin{aligned}&\frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{h^3}{12\mu }\frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \right] + h\frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{\ell \,h}{2\mu } \frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \right] \nonumber \\&\quad = \frac{h^2}{2}\frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{U_{\text {r}}}{h+2\ell }\right] + h \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{\ell \, U_{\text {r}}}{h+2\ell } + U_{\text {b}}\right] + V_{\text {r}}\ \end{aligned}$$
(11)

This is the Reynolds lubrication equation with the slip solid boundary condition. By taking \(\ell \rightarrow 0\), the above equations is reduced to the traditional Reynolds lubrication equation with no-slip boundary condition.

By integrating Eq. (4b) with respect to y and using Lemma 2, \({\partial ^{} v}/{\partial y^{}}\) is related to \(p_{\text {adj}}\) as

$$\begin{aligned} p(x,y)= & {} \mu \frac{\partial ^{} v}{\partial y^{}} +f_3(x) \\= & {} p_{\text {base}}(x)+p_{\text {adj}}(x,y) \\ \therefore \quad \frac{\partial ^{} v}{\partial y^{}}= & {} \frac{p_{\text {base}}(x)-f_3(x)}{\mu }+\frac{p_{\text {adj}}(x,y)}{\mu } \ \end{aligned}$$

where \(f_3\) is an integral constant. Comparing the above equation with \(-{\partial ^{} u}/{\partial x^{}}\), the following relation is obtained:

$$\begin{aligned} - \frac{\partial ^{} }{\partial x^{}} \left[ \frac{1}{\mu }\frac{\partial ^{} p}{\partial x^{}} \frac{y^2}{2} + f_1(x)y \right] = \frac{p_{\text {adj}}}{\mu } \ \end{aligned}$$
(12)

From the above equation, the order of magnitude of \({\partial ^{} p_{\text {adj}}}/{\partial x^{}}\) is found to be \(\mu U L^{-2}\), while those of \({\partial ^{} p}/{\partial x^{}}\) and \({{\textrm{d}}^{} p_{\text {w}}}/{{\textrm{d}} x^{}}\) are found to be \(\varepsilon ^{-2} \mu U L^{-2}\) from Eqs. (4a) and (11). Therefore, considering Lemma 1, the x derivatives of p and \(p_{\text {w}}\) are related as

$$\begin{aligned} \frac{\partial ^{} p}{\partial x^{}} \simeq \frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \quad \text {and}\quad \frac{\partial ^2 p}{\partial x ^2} \simeq \frac{{\textrm{d}}^2 p_{\text {w}}}{{\textrm{d}} x^2} \ \end{aligned}$$
(13)

which reads

$$\begin{aligned} p_{\text {base}}(x) \simeq p_{\text {w}}(x) \end{aligned}$$
(14)

from Eq. (8) provided \(\varepsilon ^2\ll 1\). The orders of magnitudes of the pressures are summarised as follows: \(O[p]=O[p_{\text {w}}]=P_{\text {ref}}\) and \(O[p_{\text {adj}}]=\varepsilon ^{2} P_{\text {ref}}\). Besides, \({\partial ^{} p_{\text {base}}}/{\partial y^{}} =0\) and Eq. (4b) yield

$$\begin{aligned} O\left[ \frac{\partial ^{} p}{\partial y^{}} \right] = O\left[ \frac{\partial ^{} p_{\text {adj}}}{\partial y^{}} \right] = \frac{1}{\varepsilon ^2}\frac{\mu V}{L^2} \ \end{aligned}$$

This fact characterises the present problem: although \(p_{\text {adj}}\) is small in comparison to \(p_{\text {w}}\), \({\partial ^{} p_{\text {adj}}}/{\partial y^{}}\) exhibits a comparable order of magnitude to \({{\textrm{d}}^{} p_{\text {w}}}/{{\textrm{d}} x^{}}\) under \(\varepsilon \lesssim 1\) and \(\varepsilon ^2\ll 1\).

Substitution of Eq. (13) into (12) identifies \(p_{\text {adj}}\) as

$$\begin{aligned} p_{\text {adj}}(x,y) = -\mu \frac{\partial ^{} }{\partial x^{}} \left[ -\frac{y(h-y)}{2\mu }\frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} +\frac{y\, U_{\text {r}}}{h+2\ell } \right] \ \end{aligned}$$
(15)

Eq. (15) shows that \(p_{\text {adj}}\) is the pressure adjustment due to the spatial change of the local Couette–Poiseuille flow induced by the gradient of \(p_{\text {w}}\) and the moving wall; the Couette component of the flow is slightly modified by the apparently increased gap width (\(h+2\ell\)).

By deleting \(p_{\text {w}}\) and \(p_{\text {adj}}\) from Eqs. (11, 12 and 15), a closed form of fourth-order differential equation for p(x, y) is shown in Appendix A. However, more feasible and equivalent lubrication model may be constructed as follows: first, \(p_{\text {w}}\) is solved from Eq.(11), and then, with \(p_{\text {adj}}(x, y)\) determined by Eq. (15), the pressure is eventually given by

$$\begin{aligned} p(x, y)=p_{\text {w}}(x)+p_{\text {adj}}(x, y) \ . \end{aligned}$$
(16)

For a system with independent slip lengths for the upper wall, \(\ell _{\textrm{t}}(x)\), and lower wall, \(\ell _{\textrm{b}}(x)\), the above lubrication model is generalised as below. The Reynolds lubrication equation is modified as

$$\begin{aligned}&\frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \!\left[ \frac{h^3}{12 \mu } \frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \right] + \frac{h^2}{2} \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \!\left[ \frac{\ell _{\textrm{p}}}{2 \mu } \frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \right] + h \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \!\left[ \frac{ \ell _{\textrm{b}}(h + \ell _{\textrm{p}})}{2 \mu }\frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \right] \nonumber \\&\quad = \frac{h^2}{2} \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{U_{\text {r}}}{h + \ell _{\textrm{c}}}\right] + h \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{\ell _{\textrm{b}}\,U_{\text {r}}}{h + \ell _{\textrm{c}}}+U_{\text {b}}\right] + V_{\text {r}}\ \end{aligned}$$
(17)

where

$$\begin{aligned} \ell _{\textrm{c}}=\ell _{\textrm{t}}+\ell _{\textrm{b}}\ , \qquad \ell _{\textrm{p}}=\frac{\ell _{\textrm{t}}-\ell _{\textrm{b}}}{h+\ell _{\textrm{c}}}h \ \end{aligned}$$
(18)

A further general form of Eq. (17) may be given by including the slip velocity components in the wall-normal direction (Aurelian et al. 2011). The adjusting component of the pressure is generalised as follows:

$$\begin{aligned} p_{\text {adj}}(x,y) = -\mu \frac{\partial ^{} }{\partial x^{}} \left[ -\frac{y(h+\ell _{\textrm{p}}-y)}{2\mu } \frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} + \frac{y\,U_{\text {r}}}{h+\ell _{\textrm{c}}} \right] \ \end{aligned}$$
(19)

The additional shift of the gap width \(\ell _{\textrm{p}}\) for the Poiseuille component in Eq.(19) characterises this setup of independent pair of slip lengths. These apparent shifts of the gap width (\(\ell _{\textrm{p}}\) and \(\ell _{\textrm{c}}\)) also appears in the three-dimensional version of the slip-wall lubrication model (see Appendix B).

Note that the effect of the slip boundary condition appears in Eq. (17) as additional terms (i.e. the second, third, and the fifth terms) to the original Reynolds lubrication equation with no-slip walls, indicating a modification of mass conservation at the \(\varepsilon ^0\)-order level. On the other hand, Eq. (19) retains essentially the same functional form (i.e. composed of the Poiseuille and Couette terms) as the case with the no-slip boundary condition.

Fig. 2
figure 2

Schematic of a corrugated plate above a moving flat plate, together with the computational mesh (body-conforming geometry) and boundary conditions. The gap width h(x) is given by Eq. (20)

Full size image

4 Validation

For a validation, the pressure distribution affected by slip boundary is calculated by the above lubrication model, and the result is compared with the fully resolved numerical result.

Here, we set out a problem of the flow induced by a curved object travelling at a constant speed, and different slip lengths, \(\ell _{\textrm{t}}(x)\) and \(\ell _{\textrm{b}}(x)\), are considered at the upper and lower boundaries, respectively. As schematically shown in Fig. 2, the lower flat wall is towed at the velocity \(U_0\) in the positive x direction, and a corrugated wall of sinusoidal geometry

$$\begin{aligned} h(x)=H_0\left[ 1+\delta \cos \big (kx\big ) \right] \end{aligned}$$
(20)

is fixed in space, i.e. \(V_{\text {r}}=0\). In the above equation, \(H_0\) is the average channel height, \(\delta\) is the non-dimensional parameter between 0 and 1, and the wave number k is set to \(2\pi /L_0\). The periodic boundary condition is applied in the x direction, and the slip lengths are given as \(\ell _{\textrm{b}}(x)=\gamma h(x)\) (\(\gamma\): a positive constant) and \(\ell _{\textrm{t}}=0\); only the upper wall is no-slip. Then, Eq. (17) is simplified as

$$\begin{aligned} \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \left( \frac{1}{12}+\frac{\gamma }{4(\gamma +1)}\right) \frac{h^3}{\mu } \frac{{\textrm{d}}^{} p_{\text {w}}}{{\textrm{d}} x^{}} \right] + \frac{1}{\gamma +1} \frac{h^2}{2} \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{U_0}{h} \right] =0 \ \end{aligned}$$
(21)

and the analytical solution is given as follows:

$$\begin{aligned} p_{\text {w}}(x)= \frac{6\mu U_0}{4\gamma +1} \frac{h(x) + H_0}{(2 + \delta ^2) (k H_0)^2} \frac{{\textrm{d}}^{} }{{\textrm{d}} x^{}} \left[ \frac{1}{h(x)} \right] \ \end{aligned}$$
(22)

With the above \(p_{\text {w}}\), the corresponding \(p_{\text {adj}}\) can be calculated from Eq. (19).

In the following, the aspect ratio of the corrugated channel is fixed at \(\varepsilon =H_0/L_0=0.1\). This value reasonably satisfies the condition \(\varepsilon ^2\ll 1\), and our previous study (Takeuchi and Gu 2019) showed that the lubrication model with the no-slip boundary condition (\(\ell _{\textrm{t}}=\ell _{\textrm{b}}=0\)) was found to reproduce the true pressure distribution for this aspect ratio of the corrugated channel.

For comparison, a direct numerical simulation (DNS), which solves the full Navier–Stokes equation, is carried out with a fully validated fourth-order finite difference method (Kajishima and Taira 2016). A structural body-fit mesh is prepared to conform the upper and lower walls and all the variables are defined on the collocated arrangement. The number of grid points are 200 and 20 in the x and y directions, respectively, and the number density of the grid points are increased near the upper and lower boundaries as well as in the narrowest gap region (i.e. around \(x=L_0/2\) or \(kx=\pi\)). For the DNS, the Reynolds number is set at \(\text {Re}=\rho U_0L_0/\mu =1\).

Figure 3 compares the pressure contours obtained by the slip-wall lubrication model (Eq. (16)) and the numerical simulation for \(\delta =\gamma =0.25\). Considering that the pressure obtained by the Reynolds lubrication equation is a function of only x (see Eq. (22)), the proposed slip-wall lubrication model reasonably reproduces the y-dependence of the pressure distribution.

Fig. 3
figure 3

Comparison of the pressures obtained by Eq. (16) and by a fully resolved numerical simulation (DNS) at steady state. The parameters are set at \(\varepsilon =H_0/L_0=0.10\) and \(\delta =\gamma =0.25\). The pressure is shown normalised by \(\mu U_0/L_0\ \)

Full size image

To see the effect of the corrugation amplitude and the slip length, \(\delta\) and \(\gamma\) are varied in the following range: \(\delta = 0.1, 0.25\) and \(\gamma =0.10, 0.25, 0.50\). For the values of \(\delta\), the maximum gradient of the surface profile is evaluated as \(H_0{\delta }k =2\pi \delta \varepsilon \fallingdotseq 0.63\times 10^{-1}\) and 0.16, respectively. Although the gradient at \(\delta =0.25\) is slightly large, the curvatures of the profiles for both \(\delta\) cases are sufficiently small: \(H_0{\delta }k^2=2\pi \delta \varepsilon ^2{H_0^{-1}}\fallingdotseq 0.63\times 10^{-2}H_0^{-1}\) and \(0.16\times 10^{-1}H_0^{-1}\), and we eliminate \({\partial ^{2} u}/{\partial x^{2}}\) as explained at Eq.(3).

Fig. 4
figure 4

Comparison of the pressure distributions along \(y=y_{\textrm{f}}{\mathop {=}\limits ^{\textrm{def}}}0.8H_0(1-\delta )\) obtained by the Reynolds lubrication equation (dashed line), the slip-wall lubrication model (solid lines) and by DNS (symbols) for different values of \(\delta\) and \(\gamma\). In the figure, “Re.Lubr.Model” represents the \(\varepsilon ^0\)-order slip-wall lubrication pressure, Eq. (22), and “Sw.Lubr.Model” means Eq. (16) with Eq. (22). The pressure value is normalised by \(\mu U_0/L_0\ \)

Full size image
Fig. 5
figure 5

Comparison of the maximum absolute differences between the pressure values obtained by DNS (indicated as \(p_{\textrm{DNS}}\)) and the models (i.e. \(p_{\text {w}}(x)\) and p(x, y)) for the \((\delta , \gamma )\) cases in Fig. 4. The pressures along the line \(y=y_{\textrm{f}}{\mathop {=}\limits ^{\textrm{def}}}0.8H_0(1-\delta )\) are taken

Full size image

The pressure profiles along the line of \(y=y_{\textrm{f}}{\mathop {=}\limits ^{\textrm{def}}}0.8H_0(1-\delta )\) (i.e. slightly below the lowest point of the upper boundary) are compared in Fig. 4. The symbol and solid line represent the results of the DNS and the present model (Eq. (16)), respectively. For all the \(\gamma\) and \(\delta\) cases (including the case of the larger amplitude, \(\delta =0.25\)), the proposed slip-wall lubrication model agrees well with the DNS result, and the importance of \(p_{\text {adj}}\) is clear by comparing with the profiles of the Reynolds lubrication solution, Eq. (22), represented by dashed line. Considering that the maximum pressures under the no-slip condition (i.e. \(\gamma =0\)) were found to be about \(10\mu U_0/L_0\) for \(\delta =0.10\) and \(25\mu U_0/L_0\) for \(\delta =0.25\) (Takeuchi and Gu 2019) for the same corrugated channel, the graph shows that the slip-wall condition significantly reduces the lubrication pressure. The comparison of the maximum absolute differences between the pressure values obtained by DNS and the models plotted in Fig. 5 show that Eq.(16) provides better prediction than \(p_{\text {w}}\).

The above result indicates that the proposed lubrication model well predicts the pressure distribution of the flow under the slip boundary condition in a channel of a smooth (non-circular/spherical) profile with sufficiently small \(\varepsilon ^2\).

5 Discussion

To study the effect of slip length on \(p_{\text {w}}\) and \(p_{\text {adj}}\) under a realistic condition, the cases with constant slip lengths are discussed. Here, the slip lengths at the top and bottom walls are set at \(\ell _{\textrm{t}}=0\) and \(\ell _{\textrm{b}}=\gamma H_0\), respectively. The other conditions remain the same as the previous section, including the geometry of the corrugation.

The pressure deviations for the present case with respect to the varying slip case (i.e. the previous section) are denoted as \(\Delta p_{\text {w}}\ (=p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}-p_{\text {w}}^{{\textrm{v}}.\ell _{\textrm{b}}})\) and \(\Delta p_{\text {adj}}\ (=p_{\text {adj}}^{{\textrm{c}}.\ell _{\textrm{b}}}-p_{\text {adj}}^{{\textrm{v}}.\ell _{\textrm{b}}})\), where the superscripts \({{\textrm{c}}.\ell _{\textrm{b}}}\) and \({{\textrm{v}}.\ell _{\textrm{b}}}\) denote the cases of constant and variable slip lengths, respectively, and \(p_{\text {w}}^{{\textrm{v}}.\ell _{\textrm{b}}}\) is identical to the \(p_{\text {w}}\) in Eq.(22). Assuming that the corrugation amplitude \(\delta\) and the slip factor \(\gamma\) are sufficiently small (i.e. \(0<\delta , \gamma \ll 1\)), the Taylor expansions of the RHSs of Eqs.(17) and (19) yield the following model:

$$\begin{aligned} \Delta p_{\text {w}}&= \frac{1}{\varepsilon ^2}\frac{\mu U_0}{L_0} \left[ \frac{3}{\pi }\gamma \delta \sin (kx) +\text {Res.} \right] \ \end{aligned}$$
(23a)
$$\begin{aligned} \Delta p_{\text {adj}}&= \frac{\mu U_0}{L_0} \left[ 2\pi \gamma \frac{y}{H_0}\frac{3y-2H_0}{H_0}\sin (kx) +\text {Res.} \right] \ \end{aligned}$$
(23b)

where \(\text {Res.}{\mathop {=}\limits ^{\textrm{def}}}O[\gamma ^2\delta ]+O[\gamma \delta ^2]\). Considering that \(p_{\text {w}}^{{\textrm{v}}.\ell _{\textrm{b}}}\) (and also \(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}\), as will be shown subsequently) is a similar curve to the major term of \(\Delta p_{\text {w}}\) (i.e. \(\sin (kx)\)) and has zeros at \(kx=n\pi \ (n=0,1,\cdots )\), Eq.(23a) implies \(|p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}|>|p_{\text {w}}^{{\textrm{v}}.\ell _{\textrm{b}}}|\). On the other hand, Eq.(23b) shows that \(\Delta p_{\text {adj}}\) is much smaller in magnitude and insensitive to \(\delta\), indicating that both adjustments (\(p_{\text {adj}}^{{\textrm{c}}.\ell _{\textrm{b}}}\) and \(p_{\text {adj}}^{{\textrm{v}}.\ell _{\textrm{b}}}\)) may be at the similar level in comparison to \(|p_{\text {w}}|\) or \(|\Delta p_{\text {w}}|\).

Fig. 6
figure 6

Comparison of the distributions of the pressures (\(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}\) and \(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}+p_{\text {adj}}^{{\textrm{c}}.\ell _{\textrm{b}}}\)) along \(y=y_{\textrm{f}}\) under constant slip lengths \(\ell _{\textrm{b}}=\gamma H_0\) (\(\gamma =0.10, 0.25, 0.50\)) for two different values of amplitude parameter \(\delta\). The pressure obtained by solving the one-dimensional Reynolds lubrication equation, Eq. (17), is represented as \(p_{\text {w}}\) and plotted with dashed line, and the pressure adjusted by Eq. (19) is plotted with solid line. The pressure value is normalised by \(\mu U_0/L_0\ \)

Full size image

The above prediction is investigated by comparing it numerically with the varying slip cases in Fig. 4. Here, \(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}\) is obtained by numerically solving the one-dimensional Reynolds lubrication equation, Eq. (17), with the constant slip boundary condition, and the adjusting pressure is calculated by substituting \(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}\) into Eq. (19). The parameters \(\delta\) and \(\gamma\) are varied in same ranges as in the previous section. Figure 6 compares the pressure distributions along \(y=y_{\textrm{f}}\). The dashed and solid lines represent \(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}\) and \(p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}+p_{\text {adj}}^{{\textrm{c}}.\ell _{\textrm{b}}}\), respectively. For each \((\delta , \gamma )\) case, \(|p_{\text {w}}^{{\textrm{c}}.\ell _{\textrm{b}}}|\) takes larger value than that of the same \((\delta , \gamma )\) case in Fig. 4, while the contributions of \(p_{\text {adj}}^{{\textrm{c}}.\ell _{\textrm{b}}}\) and \(p_{\text {adj}}^{{\textrm{v}}.\ell _{\textrm{b}}}\) are at similar levels for the same set of parameters. Although the values of \(\delta\) and \(\gamma\) may not be sufficiently small as assumed in the above, the pressure variation due to different slip lengths can be well explained by the model in Eq. (23).

6 Conclusion

To study the effect of the velocity slip at the solid wall on the lubrication in a relatively wide channel, a 2nd-order slip-wall lubrication model was developed.

For the moderately undulating surface profile with the aspect ratio \(\varepsilon\) under \(\varepsilon \lesssim 1\) and \(\varepsilon ^2\ll 1\), the effect of the velocity slip on the wall is considered, and the pressure was represented by a linear decomposition with two components: the component that obeys a Reynolds lubrication equation under the slip wall (\(p_{\text {w}}\sim \varepsilon ^0\)) and the corresponding higher order contribution (\(p_{\text {adj}}\sim \varepsilon ^2\)). The form of \(p_{\text {adj}}\) is composed of the longitudinal derivative of the local velocity of the Couette–Poiseuille flow driven by \(p_{\text {w}}\) and the tangential velocity of the walls, and this \(p_{\text {adj}}\) allows the pressure to distribute in both longitudinal and wall-normal directions.

In the equation of \(p_{\text {w}}\), the apparently increased gap widths and the additional terms to the Reynolds lubrication equation (under no-slip boundaries) represent the effect of slip length. Meanwhile, the effect of velocity slip in \(p_{\text {adj}}\) only appears as the apparent increases in gap widths for both the Poiseuille and Couette components; the form of the modification in the Poiseuille component is not trivial, which characterises the higher order correction of the pressure in the slip flow.

The validity of the slip-wall lubrication model was established by comparing the analytical predictions with the fully resolved numerical results for the pressure distribution in the region between a flat wall with varying slip length and a no-slip corrugated wall. For a wide range of slip lengths, the decrease in lubrication pressure due to velocity slip was significant, while the contribution of the higher order term \(p_{\text {adj}}\) markedly improved the pressure prediction. As a more realistic case, the pressure for the same geometry and constant slip length was investigated, and the trend of the pressure variation due to the change in slip characteristics was analytically studied and summarised as follows: the effect of constant or varying slip length mainly appears in \(p_{\text {w}}\), while the \(p_{\text {adj}}\) term is insensitive to the details of the slip characteristics.

The results show that the treatment of slip length in the proposed higher order slip-wall lubrication model was generalised to cover from the no-slip case to the slip case, and the applicability of the model to the regime that cannot be explained by the conventional thin-gap approximation (i.e. non-negligible gap regions with non-circular geometry) was established.