1 Introduction

The understanding of multi-phase flow at low flow rates in small confined geometries is crucial for many engineering applications ranging from hydrocarbon recovery, carbon sequestration, microfluidic devices and remediation of contaminated soil. The fluid dynamics depend on the complex interplay of inertial, capillary, viscous and gravitational forces (Méheust et al. 2002; Ferrari and Lunati 2013, 2014). Thus, marginal changes in fluid and rock properties as well as flow conditions can have a huge impact on displacement patterns (Avraam and Payatakes 1995).

In recent years, advancements in imaging techniques have improved the understanding of capillary-dominated flow substantially (Pak et al. 2015; Blois et al. 2015; Duxenneuner et al. 2014). However, numerical simulation tools are still indispensable for progress in theoretical understanding of the dynamic processes as well as for parameter optimisation (Zhou et al. 2017).

A variety of numerical methods exist that differ in their discretisation strategy and come with different challenges. We only provide a brief overview and refer to (Wörner 2012; Teschner et al. 2016) for a comprehensive discussion.

Smooth particle hydrodynamics (SPH) is a mesh-free method that discretizes partial differential equations considering particles that represent a spatial region (Fatehi et al. 2008). Properties of a particle (density, velocity, pressure) are computed using a smoothing kernel considering neighbouring particle properties as well that are within a specific length scale (smoothing length). Further, Tartakovsky and Meakin (2005) used SPH to mimic fluid dynamics by coarse-grained particles with specific interaction terms. SPH is mass conservative and inherently captures a sharp interface. Morris (2000) introduced the concept of modelling two-phase flows by including capillary effects in SPH. Kunz et al. (2016) have validated two phase SPH considering open boundaries for the formation of bubbles during gas injection. Lattice Boltzmann methods solve the Boltzmann equation for particle density in phase space on a lattice and reproduce fluid dynamics by specific collision terms (Zhang 2011) . The local nature of their formulation renders them very well suited for parallel computing. However, they generally require structured meshes and the link between spatio-temporal scales, physical parameters as well as as boundary conditions make extensions to include other physical phenomena cumbersome. In addition, density and viscosity contrasts pose a challenge.

Continuum methods directly solve the Navier–Stokes equations (NSE) through a conventional spatio-temporal discretisation. This renders them flexible with respect to mesh structures and inclusion of additional physics. In addition, density and viscosity contrasts generally do not pose a challenge. Continuum methods differ in the representation of the interface between the fluids. Lagrangian interface tracking methods such as moving mesh (MM) (Quan and Schmidt 2007), marker and cell (MAC) (Harlow et al. 1965) represent a sharp interface but struggle with topological changes such as break up and coalescence. Topological changes are well captured by Eulerian methods. The volume-of-fluid (VOF) method (Hirt and Nichols 1981) represents the two-phase system as a mixture and determines the two-phase properties based on the mixture parameter. The VOF method is simple and conserves mass on any type of mesh. However, the advection of the mixture parameter by conventional schemes lead to smearing of the interface. The level-set (LS) method (Sussman et al. 1994) tracks the distance to the interface by a smooth-signed distance function. The LS method represents a sharp interface but struggles to conserve mass. The phase-field (PF) method (Jacqmin 1999; Lim and Lam 2014) propagates the auxiliary phase-field function using the fourth-order Cahn–Hilliard’s equation. This diffuse interface method captures the contact line dynamics on the wall without developing stress singularity. Higher-order discretisation schemes are required to model the fourth-order term of Cahn–Hilliard’s equation which poses a challenge.

Though at different levels, all methods have in common that they are challenged by strong capillary forces. This stems from the multi-scale nature of the problem. The interface only spreads over a few molecules in distance and an explicit representation of the interface is out of reach. Further, capillary forces depend on the curvature of the interface and are, therefore, highly sensitive to even small errors. These inaccuracies lead to non-physical parasitic currents (PC) around the interface (Lafaurie et al. 1994) that potentially change the interface dynamics. In this paper, we investigate the VOF method due to its simplicity, mass conservative nature and ability to capture topological changes. In addition, the VOF method is available in many open-source and commercial software packages such as OpenFOAM (www.openfoam.com), Gerris (http://gfs.sourceforge.net), Ansys-Fluent (https://www.ansys.com) and others.

The VOF method represents the two-phase system by a mixture. Flow parameters are determined based on the volume fraction function, \(\alpha\) referred to as the colour function. The interface location is determined by steep gradients of the colour function. The capillary forces term is approximated as a body force.

Four implementations of open-source finite-volume VOF formulations are assessed in this manuscript: the continuum surface force (CSF) formulation of the interFoam solver of OpenFoam (version foam-extend 1.6, http://wikki.gridcore.se), the sharp surface force (SSF) and the filtered surface force (FSF) formulations of poreFoam (http://www.imperial.ac.uk/earth-science/research/research-groups/perm/research/pore-scale-modelling/software/direct-two-phase-flow-solver), a separately available solver for OpenFoam (version foam-extend 1.6) and the piecewise linear interface calculation (PLIC) formulation of Gerris (http://gfs.sourceforge.net) with a higher-order discretisation of the interface curvature through a height function. All the formulations differ in approximation of the capillary body force. SSF, FSF and PLIC have previously been benchmarked for a droplet and bubble relaxing in an equilibrium field (Raeini et al. 2012; Popinet 2009). PLIC was further validated for capillary waves and shape oscillations of an inviscid droplet during relaxation (Popinet 2009) and for droplet pinch-off in a T-shaped microchannel (Sivasamy et al. 2011). CSF was validated with experiments for capillary flows in microchannels consisting of integrated pillars (Saha et al. 2009). SSF and its close relatives (Lafaurie et al. 1994; Brackbill et al. 1992) have been used to study complicated flow phenomena in porous materials (Raeini et al. 2014; Ferrari and Lunati 2014) and microfluidic devices (Hoang et al. 2013).

Our contribution in this paper is to bridge the gap between static test cases and applications by introducing a dynamic test case with an analytic solution for spontaneous imbibition in a microchannel of Hele-Shaw cell symmetry considering partial slip on the wall. The imbibition occurs solely due to capillarity. We extend the Lucas–Washburn equation to arbitrary viscosity ratios and assess the performance of the different VOF formulations against this analytical solution. The numerical methods are validated for flows at different capillary numbers as well as different viscosity and density ratios. We quantify the magnitude of PC around the interface and discuss their impact on the flow dynamics.

The paper is structured as follows. Section 2 provides a detailed description of the four VOF formulations highlighting heuristic parameters. In Sect. 3 we develop the extension of the Lucas–Washburn equation to account for arbitrary viscosity ratios. Section 4 discusses the numerical set-up of the initial and boundary value problem. In Sect. 5, we present the assessment of the fourk VOF formulations against the test cases. Conclusions are given in Sect. 6.

2 Physical and numerical description of two-phase flows

The isothermal dynamics of two immiscible and incompressible fluids are governed by the Navier–Stokes Equations for each fluid phase. The NSE of the two fluid phases are coupled through a boundary condition at the interface between them. The interface dynamics are part of the solution and hence, a moving boundary problem has to be solved (Batchelor 2000). The VOF method (Hirt and Nichols 1981) simplifies the moving boundary problem by treating the two-phase fluid system as a mixture. The mixture parameter \(\alpha \in [0,1]\) referred to as a colour function represents the volume fraction of one of the phases in a control volume. The capillary forces at the interface are modelled through a body force.

The NSE for the VOF mixture are the mass conservation equation

$$\begin{aligned} \nabla \cdot \mathbf{U } = 0, \end{aligned}$$
(1)

and the momentum conservation equation

$$\begin{aligned} \rho \bigg (\frac{\partial \mathbf{U }}{\partial t} + \mathbf{U } \cdot \nabla \mathbf{U } \bigg ) = -\nabla p + \nabla \cdot \mu \bigg (\nabla \mathbf{U } + \nabla \mathbf{U }^T\bigg ) + {\mathbf{F}}_{\text {b}} + {\mathbf{F}}_{\text {cap}}, \end{aligned}$$
(2)

where \(\mathbf {U}\) denotes the velocity field, \(\rho\) the density, t the time, p the pressure, \(\mu\) the dynamic viscosity, \({\mathbf{F}}_{\text {b}}\) the external body force and \({\mathbf{F}}_{\text {cap}}\) the capillary body force.

The density (\(\rho\)) and the dynamic viscosity (\(\mu\)) of the mixture are given by

$$\begin{aligned} \rho&= \rho _w \alpha + \rho _n (1 - \alpha ), \end{aligned}$$
(3a)
$$\begin{aligned} \mu&= \mu _w \alpha + \mu _n (1 - \alpha ), \end{aligned}$$
(3b)

where the indices w and n denote the two fluids.

The capillary body forces are given by (Brackbill et al. 1992)

$$\begin{aligned} {\mathbf{F}}_{\text {cap}} = \sigma k {\mathbf{n}}_{\text {I}} \delta _{\text {I}}, \end{aligned}$$
(4)

where \(\sigma\) denotes the surface tension, k the interface curvature, \({\mathbf{n}}_{\text {I}}\) the unit normal to the interface and \(\delta _{\text {I}}\) the Dirac delta function that restricts the capillary forces to the interface. The system is closed with a transport equation for the colour function \(\alpha\). This equation is expressed in a conservative form with the help of Eq. (1) as

$$\begin{aligned} \frac{\partial \alpha }{\partial t} + \nabla \cdot (\mathbf{U } \alpha ) = 0. \end{aligned}$$
(5)

2.1 Variants of VOF formulations

The paper assesses the four VOF formulations CSF, SSF, FSF and PLIC. They differ in the discretisation of the interface curvature, the interface normal vector and the Dirac delta function for the capillary body forces of Eq. (4). PLIC further uses a different scheme for the advection equation of the colour function Eq. (5). This section discusses these formulations in detail and highlights any heuristic parameters. The explicit numbers of any heuristic parameters are given in the supplementary material.

2.1.1 Continuum surface force (CSF)

In CSF, the interface normal vector and the Dirac delta function in Eq. (4) are approximated by the gradient of the colour function. Here, we use the implementation of the interFoam solver of OpenFoam (version foam-extend 1.6). The capillary force vector is represented by its projection onto cell face normals to have a consistent discretization with the pressure gradient term while solving NSE (Francois et al. 2006). The discrete capillary force is given by

$$\begin{aligned} {\mathbf{F}}_{\text {cap}}^{\text {CSF}} = \sigma k \nabla \alpha . \end{aligned}$$
(6)

The interface curvature is computed from the gradient of the colour function as,

$$\begin{aligned} k = - \nabla \cdot {\mathbf{n}}_{\text {I}} = - \nabla \cdot \frac{\nabla \alpha }{|\nabla \alpha |}. \end{aligned}$$
(7)

Like other methods such as Lattice–Boltzmann, SPH and Level Set a drawback of VOF is the occurrence of non-physical currents, referred to as parasitic currents around the interface (Harvie et al. 2006). PC could potentially lead to abrupt changes in interfacial configurations and/or the general flow dynamics.

2.1.2 Sharp surface force (SSF)

The SSF has been developed based on CSF to reduce PC. The reduction is achieved by smoothing the colour function for calculating the curvature and sharpening the colour function for calculating the Dirac delta function in Eq. (4) (Raeini et al. 2012; Francois et al. 2006). Here, we use poreFoam solver (Raeini et al. 2012) and switch off the filtering coefficients (discussed in Sect. 2.1.3) to obtain SSF.

The smoothed colour function \(\alpha _{\text {s}}\) is obtained by mapping the cell-centred values of the colour function \(\alpha\) onto the cell faces and vice versa. In formal notation, the smoothed colour function is given by,

$$\begin{aligned} \alpha _{\text {s}} = \left\langle \left\langle \alpha \right\rangle _{c\rightarrow f}\right\rangle _{f\rightarrow c}, \end{aligned}$$
(8)

where the indices c and f denote the cell centre and face centre, respectively. The level of smoothing is controlled by the number of repeated applications of the mapping. We apply the smoothing once.

Numerical diffusion and inaccurate representation of the capillary forces lead to a smeared colour function. Since the capillary forces are approximated by the gradient of the colour function in Eq. (6), a smeared colour function implies that the capillary forces acts in domains where no interface is present. Raeini et al. (2012) have proposed a sharpening for the colour function to address this issue and restrict the region where the capillary forces act. The sharpened colour function \(\alpha _{\text {shp}}\) is given by (Raeini et al. 2012),

$$\begin{aligned} \alpha _{\text {shp}} = \frac{1}{1 - 2 C_{\text {shp}}}\big [{\text {min}}\big ({\text {max}}\big (\alpha , C_{\text {shp}}\big ), 1 - C_{\text {shp}}\big ) - C_{\text {shp}}\big ] \end{aligned}$$
(9)

where \(C_{\text {shp}}\in [0,0.5)\) denotes the heuristic sharpening coefficient. Values of \(C_{\text {shp}}\) \(\approx 0.5\) restrict the capillary forces to a narrow range of the colour function. While it appears that a large value is desirable, too large values induce instabilities. Purely heuristically, we set the sharpening coefficient to \(C_{\mathrm{shp}} = 0.2\).

The capillary body forces are given by,

$$\begin{aligned} {\mathbf{F}}_{\text {cap}}^{\text {SSF}} = - \sigma \nabla \cdot \bigg (\frac{\nabla \alpha _s}{|\nabla \alpha _s|}\bigg ) \nabla \alpha _{\text {shp}}. \end{aligned}$$
(10)

It has been shown that SSF reduces PC for static test cases such as droplet relaxing in an equilibrium field (Raeini et al. 2012). For dynamic cases such as droplet in a uniform velocity field at low \({\mathrm{Ca}}\), PC are generated parallel to the interface (Raeini et al. 2012).

2.1.3 Filtered surface force (FSF)

The FSF has been developed based on SSF to reduce PC under dynamic conditions. The reduction is achieved by dampening capillary-induced flows parallel to interface (Raeini et al. 2012). Here, we use the poreFoam solver.

To remove capillary-induced flows parallel to the interface, the total pressure p is expressed in terms of the dynamic pressure \(p_d\) and the capillary pressure \(p_c\). The capillary pressure is computed from the capillary forces through the boundary value problem

$$\begin{aligned} \nabla \cdot \nabla p_c = \nabla \cdot {\mathbf{F}}_{\text {cap}}^{\text {FSF}}, \end{aligned}$$
(11)

with a zero-gradient boundary condition for \(p_c\). The capillary forces parallel to the interface is dampened as

$$\begin{aligned} {\mathbf{F}}_{\text {cap,fi1}}= & {} \big (\delta _{\text {I}}\big ) \left( {\mathbf{F}}_{\text {cap,fi1}}^{\text {old}}+ C_{\text {fi1}} \big (\nabla p_c - (\nabla p_c \cdot {\mathbf{n}}_{\text {I}}){\mathbf{n}}_{\text {I}}\big )\right) , \end{aligned}$$
(12)

where \(\delta _{\text {I}}\) restricts the filtering to the sharpened interfacial region,

$$\begin{aligned} \delta _{\text {I}} = \bigg |\frac{\nabla \alpha _{\text {shp}}}{\nabla \alpha _{\text {shp}}+\epsilon }\bigg |. \end{aligned}$$
(13)

\(C_{\text {fi1}}\) in Eq. (12) is the filtering co-efficient set to 0.1 and \(\epsilon\) in Eq. (13) is \(10^{-12}\)/\(\root 3 \of {V_{\text {avg}}}\) (Raeini et al. 2012). \({\mathbf{F}}_{\text {cap,fi1}}^\text {old}\) represents the value of \({\mathbf{F}}_{\text {cap,fi1}}\) at the previous time step and the term \(\big (\nabla p_c - (\nabla p_c \cdot {\mathbf{n}}_{\text {I}}){\mathbf{n}}_{\text {I}}\big )\) represent the capillary term parallel to the interface. The filtered capillary forces is updated as

$$\begin{aligned} {\mathbf{F}}_{\text {cap,fi}}^{\text {FSF}} = {\mathbf{F}}_{\text {cap}}^{\text {SSF}} - {\mathbf{F}}_{\text {cap,fi1}}. \end{aligned}$$
(14)

Numerical error in computing the interface curvature results in computing inaccurate capillary forces. Hence, the zero net capillary forces constraint over a symmetric closed interface (\(\int {\mathbf{F}}_{\text {cap}} \cdot {\mathbf{S}}_s {\rm d}{\mathbf{S}}_s = 0\), \({\mathbf{S}}_s\) is the interfacial area) is violated. Therefore, the capillary momentum flux (\(\phi _{\text {cap}} = ({\mathbf{F}}_{\text {cap}}^{\text {FSF}} - \nabla p_c) {\mathbf{S}}_f\), \(\mathbf S _f\) is the surface area vector) below a small threshold is filtered,

$$\begin{aligned} \phi _{\text {cap,fi2}} = \phi _{\text {cap}} - \text {max}({\text {min}}(\phi _{\text {cap}}, \phi _{\text {cap,th}}), -\phi _{\text {cap,th}}). \end{aligned}$$
(15)

The threshold capillary momentum flux, \(\phi _{\text {cap,th}}\) is,

$$\begin{aligned} \phi _{\text {cap,th}} = C_{\text {fi2}} \left( {\mathbf{F}}_{\text {cap}}^{\text {FSF}}\right) _{\text {avg}} {\mathbf{S}}_f. \end{aligned}$$
(16)

\(C_{\text {fi2}}\) is the capillary flux-filtering coefficient, set to 0.005 (Raeini et al. 2012).

2.1.4 Piecewise linear interface calculation (PLIC)

PLIC constructs a sharp interface using line segments in the cells marked by the gradient of the colour function (cut cells) to geometrically advect the colour function with minimal diffusion (Popinet 2009; Youngs 1982). We use the PLIC formulation available for structured meshes in Gerris (Popinet 2003, 2009).

In 2D, the orientation of a line segment in cut cells is defined by,

$$\begin{aligned} r_x x + r_y y = c, \end{aligned}$$
(17)

where \(r_x, r_y\) are the interface normal components computed from the gradient of the colour function by Mixed-Young-Centred method (Aulisa et al. 2007). x, y are the spatial co-ordinates and c is a free parameter (Scardovelli and Zaleski 1999). For a given value of the colour function and computed interface normal, c is determined such that the mass of the fluids in the cut cells are conserved (Scardovelli and Zaleski 2000).

The interface curvature is computed using the height function method with finite differences (Afkhami and Bussmann 2008). For \(|r_y|> |r_x|\), a vertical height function f is computed over a \(3 \times 7\) stencil,

$$\begin{aligned} f_{i} = \sum _{j-3}^{j+3} \alpha _{i,j} \Delta _{\text {y}}, \end{aligned}$$
(18)

where \(\alpha _{i,j}\) represents the colour function in cell (i, j) and \(\Delta _\text {y}\) represents the cell size along the vertical direction. The case \(|r_x|> |r_y|\) follows accordingly by computing a horizontal height function. The interface curvature is computed from the height functions as

$$\begin{aligned} k = \frac{f_{xx}}{(1 + f_x^2)^{\frac{3}{2}}}. \end{aligned}$$
(19)

The derivatives \(f_x\) and \(f_{xx}\) are approximated by second-order central finite differences. In the boundary cells, the height functions are estimated in ghost cells (assuming linear projection of the contact line on the wall into the ghost cells) (Afkhami and Bussmann 2008). The capillary forces for PLIC is computed from Eq. (6). A smoothing kernel for the colour function is used to avoid jumps in the fluid properties (\(\rho , \mu\)) at the interface (Popinet 2009). We perform the smoothing twice.

Table 1 provides a brief summary of the discussed VOF formulations mentioning the advantages, disadvantages and heuristic parameters.

Table 1 Advantages, disadvantages and heuristic parameters for different VOF method formulations
Full size table

2.2 Boundary conditions on the wall

We use an equilibrium contact angle, \(\theta\) at the wall surface such that the interface normal is oriented as,

$$\begin{aligned} {\mathbf{n}}_{\text {I}} = {\mathbf{n}}_{\text {w}} \; {\cos} \; (\theta ) + {\mathbf{t}}_{\text {w}} \; \text {sin} \; (\theta ), \end{aligned}$$
(20)

where \({\mathbf{n}}_\text {w}\) is the unit normal to the wall and \({\mathbf{t}}_\text {w}\) is the unit tangent to the wall (Brackbill et al. 1992).

Displacing menisci on a no-slip boundary results in convergence issues. This is due to mesh dependent variable stresses developed on the boundary control-volumes leading to stress singularities (Afkhami et al. 2009; Huh and Scriven 1971). To overcome this numerical artefact, several approaches such as using a partial slip on the wall, lubricating films, dynamic contact angle or a combination of the abovementioned methods were proposed. We refer to Snoeijer and Andreotti (2013) and Sui et al. (2014) for a comprehensive review on moving contact line dynamics. We choose to use a partial “Navier” slip boundary condition for the velocity on the wall given by

$$\begin{aligned} U_{\text {w}} = \lambda \frac{\partial U}{\partial n}, \end{aligned}$$
(21)

where \(\lambda\) is the slip length (see Sect. 4.2) and n is the coordinate normal to the wall.

2.3 Discretization and numerical schemes

Foam-extend and Gerris use the finite-volume method for discretization. A collocated Eulerian grid arrangement is used with the field variables stored at the cell centres of a control volume.

In foam-extend, an implicit first-order Euler scheme is used for time discretization. The gradient terms are discretized by the second-order Gauss linear scheme. The advection term in the Navier–Stokes momentum equation is solved using limited linear differencing. A bounded solution for the colour function is ensured by the vanLeer advection scheme. To control the numerical diffusion of the interface while solving the advection equation of the colour function Eq. (5), an artificial compression velocity is added only at the interfacial region in a direction normal to the interface (Rusche 2003). The pressure-velocity coupling of NSE is achieved through a predictor–corrector step of Pressure Implicit with Splitting of Operators (PISO by Issa 1986).

Gerris (Popinet 2003, 2009) uses a second-order staggered time discretization. The advection term of the momentum equation is solved by a Godunov scheme (Bell et al. 1989). For the advection term of the mixture transport equation, a direction-split advection method with geometrical flux estimates is used (Gerlach et al. 2006). The pressure–velocity coupling of the NSE uses the time split projection method based on Hodge decomposition of the velocity field.

To ensure numerical stability for capillary problems, the time step is limited according to the Brackbill number (Brackbill et al. 1992) as

$$\begin{aligned} \Delta t_{\mathrm{BK}} = \sqrt{\frac{ \rho _{\text {avg}} (\Delta _x)^3}{\pi \sigma } }. \end{aligned}$$
(22)

3 Analytical solution for spontaneous imbibition in a rectangular channel

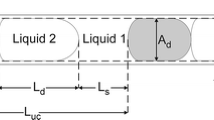
Spontaneous imbibition into a cylindrical capillary was first studied by Lucas (1918) and Washburn (1921). Balancing the forces in the absence of gravity, negligible inertia and assuming \(\mu _w \gg \mu _n\), they obtained that the position of the meniscus, \(x_\text {m}\) advances as \(x_{\text {m}} \propto \sqrt{t}\). The model was recently expanded to account for the viscosity of the defending gas phase in a long tube (Hultmark et al. 2011), for any viscosity ratio in a vertical capillary (Walls et al. 2016) and for arbitrary cross-sectioned microchannels (Berthier et al. 2015). Here, we consider horizontal displacement of the meniscus with a partial slip boundary in a Hele-Shaw cell (\(h \ll w\), see Fig. 1 for an illustration). We neglect gravity as the largest bond number considered is \({\mathrm{Bo}} = \Delta \rho g h^2 \sigma ^{-1} = 10^{-4}\).

Fig. 1
figure 1

Illustration of the problem set-up

Full size image

3.1 Derivation of extended Lucas–Washburn equation

We consider the geometry illustrated in Fig. 1. An overview of the entire derivation in detail is provided in the supplementary material. The velocity profile in a rectangular channel of length \(\ell\), width w and height h, where \(h\ll w\), with a partial slip boundary condition on the wall is approximately parabolic. The average velocity \(U_{\mathrm{avg}}\), according to Hagen–Poiseuille (Barthès-Biesel 2012), is given by

$$\begin{aligned} U_{\mathrm{avg}} = \frac{h^2 + 6h\lambda + 6\lambda ^2}{12 \mu }\frac{{\mathrm{d}}p}{{\mathrm{d}}x}. \end{aligned}$$
(23)

The pressure at the inlet and outlet boundaries of the channel are kept equal (see Sect. 4.1, Fig. 4). Therefore, the acting forces are the capillary forces \({F}_{\text {cap}}\) and the viscous forces \({F}_{\text {vis}}\). The capillary forces act over the circumference of the capillary at the meniscus defined by the product of the capillary pressure \((p_c = 2 \sigma {\text {cos}}(\theta )/h)\) and the area of the interface (wh)

$$\begin{aligned} {F}_{\text {cap}} = 2w \sigma {\text {cos}} \; (\theta ). \end{aligned}$$
(24)

Using Newton’s viscous law and Hele-Shaw’s principle (Batchelor 2000), the viscous forces is given by

$$\begin{aligned} {F}_{\text {vis}} = \frac{h}{2} \frac{{\mathrm{d}}p}{{\mathrm{d}}x} A, \end{aligned}$$
(25)

where \(A = 2wl\) denotes the surface area of the wall.

Substituting the pressure gradient \({\mathrm{d}}p/{\mathrm{d}}x\) from Eq. (23) in Eq. (25), the viscous forces is given by

$$\begin{aligned} {F}_{\text {vis}} = 12 {U}_{\mathrm{avg}}\frac{wh}{h^2 + 6h\lambda + 6\lambda ^2} \int _0^\ell \mu (x) \mathrm{d}\ell . \end{aligned}$$
(26)

Balancing the active forces within the system (\(F_{\text {cap}} = F_{\text {vis}}\)) we obtain,

$$\begin{aligned} \frac{(h^2 + 6h\lambda + 6\lambda ^2) \sigma \cos (\theta )}{6h} = {U}_{\text {avg}}[(\mu _w - \mu _n)x_{\text {m}} + \mu _n \ell ], \end{aligned}$$
(27)

where \(x_{\text {m}}\) denotes the position of the meniscus. As the fluids are incompressible and according to mass conservation (Eq. 1) the average velocity within the system (\(U_{\text {avg}}\)) is equal to the meniscus velocity (\(U_{\text {m}}\)). Therefore, \(U_{\text {avg}} = U_{\text {m}} = {\mathrm{d}}x_{\text {m}}/\mathrm{d}t\). Substituting \({\mathrm{d}}x_{\text {m}}/\mathrm{d}t\) for \(U_{\text {avg}}\) in the above expression and integrating both sides, we obtain an implicit equation for the location \(x_{\text {m}}\) of the meniscus, given by,

$$\begin{aligned} \frac{(h^2 + 6h\lambda + 6\lambda ^2) \sigma cos(\theta )}{6h} t = (\mu _w - \mu _n) \frac{x_{\text {m}}^2}{2} + \mu _n \ell x_{\text {m}} + C. \end{aligned}$$
(28)

Assuming \(x_{\text {m}} (t = 0) = 0\) we immediately get \(C = 0\). The meniscus velocity \(U_{\text {m}}\) is accordingly given by

$$\begin{aligned} U_{\text {m}}= & {} \frac{(h^2 + 6h\lambda + 6\lambda ^2) \sigma {\text {cos}}(\theta )}{6 h \mu _n \ell } \nonumber \\&\times \frac{1}{\sqrt{1 + 2\big (\frac{1}{M}-1\big )\frac{(h^2 + 6h\lambda + 6\lambda ^2) \sigma {\text {cos}}(\theta )t}{6 h \mu _n \ell ^2}}}, \end{aligned}$$
(29)

where M is the viscosity ratio (\(\mu _n\)/\(\mu _w\)). Note, that for \(M=1\), the meniscus velocity is constant in time (Eq. 30). Within a reference frame that moves at the fixed meniscus velocity, the velocity field within the capillary does not change with time. For \(M \ne 1\), the meniscus velocity changes with time and the velocity field within the capillary changes proportionally. We now proceed to express terms in dimensionless form. We take the meniscus velocity at \(t = 0\),

$$\begin{aligned} {U}_{\text {ref}} = \frac{(h^2 + 6h\lambda + 6\lambda ^2) \sigma {\text {cos}}(\theta )}{6 h \mu _n \ell }, \end{aligned}$$
(30)

and the time it takes to fill the channel at this velocity,

$$\begin{aligned} t_{\text {ref}} = \frac{\ell }{{U}_{\text {ref}}} = \frac{6 h \mu _n \ell ^2}{(h^2 + 6h\lambda + 6\lambda ^2) \sigma {\text {cos}} (\theta )}, \end{aligned}$$
(31)

as references. The dimensionless velocity is then given by,

$$\begin{aligned} {U}^{*} = \frac{{U}_{\text {m}}}{{U}_{\text {ref}}} = \frac{6 h {U}_{\text {m}} \mu _n \ell }{(h^2 + 6h\lambda + 6\lambda ^2) \sigma {\text {cos}}(\theta )}, \end{aligned}$$
(32)

and the dimensionless time by,

$$\begin{aligned} t^* = \frac{t}{t_{\text {ref}}} = \frac{(h^2 + 6h\lambda + 6\lambda ^2) \sigma {\text {cos}}(\theta )t}{6 h \mu _n \ell ^2}. \end{aligned}$$
(33)

We define the reference capillary number as,

$$\begin{aligned} Ca = \frac{ \mu _{n} {U}_{\text {ref}}}{\sigma } = \frac{(h^2 + 6h\lambda + 6\lambda ^2) {\text {cos}}(\theta )}{6 h \ell }, \end{aligned}$$
(34)

which, remarkably, is independent of viscosity and surface tension. Note, that the above definition of the capillary number applies exclusively for spontaneous imbibition in a (rectangular) capillary. Unlike forced imbibition scenarios where the imposed injection velocity serves as the reference velocity to determine the capillary number, spontaneous imbibition lacks a fixed injection velocity boundary condition. Hence, we choose the meniscus velocity at \(t=0\) given by Eq. 30 as the reference velocity to determine the capillary number.

In this study, we vary the capillary number by changing the channel length \(\ell\) while keeping the other length scales of the channel (\(h, \lambda\)) constant. Thus, small capillary numbers are achieved by long channels.

3.2 Model approximations

In the derivation of the extended Lucas–Washburn equation, we assume that the capillary and viscous forces are balanced at all times and a parabolic velocity profile along the length of the channel. These assumptions are not entirely met by the solution of the NSE. Here, we discuss briefly the expected error. Figure 2 shows a close-up of the flow field around the interface from a numerical solution with FSF. Details regarding the numerical set-up are given in Sect. 4. The curvature of the moving interface is constant in time resulting in a deviation of the parabolic flow profile in the vicinity (upstream and downstream) of the interface. The width \(\ell ^\prime\) of the region, where the velocity profile deviates from the parabolic shape for \(\mathrm{Ca} = 3.12 \times 10^{-3}\) and \(\mathrm{Ca} = 3.12 \times 10^{-4}\), is \(\ell '\approx 10 ~\upmu\)m. For \(\mathrm{Ca} = 3.12 \times 10^{-3}\), \(\ell ^\prime\)/\(\ell \approx 0.025\) and for \(\mathrm{Ca} = 3.12 \times 10^{-4}\), \(\ell ^\prime\)/\(\ell \approx 0.0025\). The flow field deviates smooth and continuously and hence we expect an error of less than 2.5% for \(\mathrm{Ca} = 3.12 \times 10^{-3}\) and less than 0.25% for \(\mathrm{Ca} = 3.12 \times 10^{-4}\).

Fig. 2
figure 2

Flow profile for \({\mathrm{Ca}} = 3.12 \times 10^{-3}\) (FSF, details given in Sect. 5.1.1). Markers 1 and 4 point to regions with a parabolic profile. Marker 2 points to the diverging flow profile upstream of the interface and Marker 3 points to the converging flow profile downstream of the interface. The length \(\ell ^\prime\) denotes the region where the flow profile is not parabolic

Full size image

The numerical simulations are started from no-flow boundary conditions and hence capillary and viscous forces are not instantaneously balanced at the beginning. The force balance allows us to estimate the time scale of the acceleration process by,

$$\begin{aligned} {F}_{\text {cap}} - {F}_{\text {vis}} = m \frac{{\mathrm{d}U}_{\text {m}}}{\mathrm{d}t}, \end{aligned}$$
(35)

where m denotes the cumulative mass of the fluids in the system. Solving this simple first-order ordinary differential equation for typical values used in this study (Table 2) yields an acceleration time scale of \(t_{\text {acc}}\approx 10^{-5}\,{\text {s}}\) and \(t_{\text {acc}}/t_{\text {ref}}\approx 10^{-3}\) for \({\mathrm{Ca}} = 3.12 \times 10^{-3}\). All numerical solutions match well with this approximation, Fig.  7.

4 Numerical set-up

In this section, we introduce the initial and boundary conditions used for spontaneous imbibition. A mesh dependence study is performed to find an optimal mesh resolution for the assessment. All essential files required to run the cases for all formulations are provided in the supplementary material.

Fig. 3
figure 3

Initial and boundary conditions used for spontaneous imbibition. The meniscus is initially relaxed with no flow boundary conditions at the inlet and outlet and then subjected to spontaneous imbibition

Full size image

4.1 Initial and boundary conditions

Figure 3 illustrates the initial and boundary conditions used for spontaneous imbibition. The meniscus is initially placed at a distance of 8 \(\upmu\)m from the inlet and is relaxed for \(2.5 \times 10^{-4}\,{\rm s}\) to make the numerical validation independent of capillary wave effects. During the relaxation stage, there is no inflow or outflow of the fluids across the boundaries and the interface reaches an equilibrium configuration based on the contact angle. Later, for spontaneous imbibition, we use a Dirichlet boundary condition for the pressure at both ends of the channel, \(p(0,t)=p(l,t)=p_0\). Figure 4 shows the pressure profile along the channel length for spontaneous imbibition considering fluids having different viscosities. Pressure at inlet and outlet boundaries are set to \(p_0 = 0\)Pa. Though the integrated pressure gradient over the entire channel length vanishes, a pressure gradient exists inside the channel due to capillarity. A zero-gradient Neumann boundary condition is applied for the velocity field at the inlet and outlet. Walls of the channel are fixed with a partial slip boundary condition (see Sects. 2.2 and 4.2) and an equilibrium contact angle. To save computational effort, a symmetric boundary condition is used along the length of the channel at a height of h/2.

Fig. 4
figure 4

Axial pressure profile for spontaneous imbibition. Pressure boundaries at inlet and outlet are set to Dirichlet with \(p_0 = 0\) Pa. Case: \(M=\frac{\mu _n}{\mu _w}\) = 0.1, Sect. 5.2.1. Formulation: PLIC, \(t^* = 1.15\)

Full size image

4.2 Mesh dependence

Table 2 provides the parameters used for mesh dependence analysis. The surface tension, the contact angle of the wetting phase with the wall and the height of the channel are kept constant for all the cases discussed in this paper.

Table 2 Parameters used for mesh resolution study
Full size table

We use a uniform and structured mesh to spatially discretise the domain for all formulations. We test the spontaneous imbibition with several levels of refinement, \(h/\Delta x = 8\) (\(\Delta x = 1.25~\upmu\)m), \(h/\Delta x = 16\) (\(\Delta x = 0.625~\upmu\)m) and \(h/\Delta x = 32\) (\(\Delta x = 0.3125~\upmu\)m). The average velocity \(U_{\text {avg}}\) within the channel represents the meniscus velocity, based on principles of continuity. The slip length (\(\lambda = 0.1~\upmu {\text {m}}\)) is chosen such that it is small enough compared to the channel height (2% of h) to avoid discrepancies with the Hagen–Poiseuille flow assumption used in the analytical solution. Figure 5 shows the meniscus velocity for different resolutions and at different \({\mathrm{Ca}}\) for all formulations with the analytical reference solution from Eq. (29) represented by dashed black lines. The convergence rate for successive refinements are also mentioned. The velocity data [(average (or) meniscus velocity and the maximum velocity] is output every two time steps during the simulation run. Even though the meniscus velocity is supposed to be constant (see PLIC for reference in Fig. 9) oscillations in the meniscus velocity are observed for CSF, SSF and FSF (Fig. 9). In quasi-steady state, these oscillations are periodic and uniform. Therefore, when the meniscus velocity oscillates, we determine the arithmetic average of the meniscus velocity in a period to obtain the meniscus velocity used in the plots of Fig. 5.

Fig. 5
figure 5

Mesh dependence study performed for all VOF formulations at different capillary numbers. Dashed black lines represent the analytic reference solution

Full size image

Figure 5 shows that CSF struggles to converge due to an inaccurate computation of the capillary forces and large magnitude of PC (see Sect. 5). An improvement in computing the capillary forces by SSF compared to CSF is seen to show better convergence and move the numerical solution towards the analytical solution. Compared to CSF and SSF, FSF and PLIC approximate the capillary forces better. At lower Ca \((<4\times 10^{-3})\), the solutions of SSF, FSF and PLIC converge (\(\lesssim 2\%\) with respect to the finest resolution) at \(h/\Delta x = 16\). All formulations at large Ca \((\approx 0.01)\) show a slower convergence rate, which indicate the requirement to either increase the slip length or resolve the mesh with a similar length scale as that of the slip length (Afkhami et al. 2009). Moreover, we see the numerical solution converging to values below the analytical reference solution which is potentially due to the parabolic flow assumption considered in the analytic solution where we expect around 8.5% discrepancy (\(\ell ^{'}/\ell \approx 0.085\), see Fig. 2). At \(Ca \le 3.12 \times 10^{-4}\), the impact of the parabolic flow assumption and stress singularities on the wall boundaries reduce. Hence, the numerical results converge towards the analytic solution.

Table 3 compares the time step size calculated by Eq. (22) and computation time for all the formulations performed on 4 Intel-Xeon processors (2.00 GHz frequency) for different resolutions.

Table 3 Time step size (\(\Delta t\)) in seconds and computation time in minutes for all formulations at different mesh resolutions
Full size table

Computation time of CSF is two times faster than SSF and FSF but produces the largest discrepancy in terms of the flow dynamics. Note that SSF and FSF are run with the poreFoam solver and for SSF, the filtering coefficients discussed in Sect. 2.1.3 are set to zero. The Gerris implementation of PLIC takes over 5 times longer compared to FSF but produces more accurate solutions.

Emphasising that the scope of this paper is to quantify PC at low Ca \(< 4 \times 10^{-3}\), observing convergence at a resolution of \(h/\Delta x = 16\) and taking into account the computation cost (Table 3) we choose to perform the rest of our analysis with a mesh resolution \(h/\Delta x = 16\) (\(\Delta x = 0.625\, \upmu\)m).

5 Benchmark cases

In this section, we assess the precision of the VOF formulations, CSF, SSF, FSF and PLIC (Sect. 2) for the capillary forces by comparing the numerical solution of the meniscus dynamics during spontaneous imbibition into a capillary with the analytic solution. We focus on flows at different \({\mathrm{Ca}}\) and quantify PC. We also study the resilience of the numerical solvers with respect to viscosity and density contrasts.

5.1 Flow at different capillary numbers

The focus of this study are flows at the brink where PC become dominant. The capillary numbers investigated are \({\mathrm{Ca}} = 3.12 \times 10^{-3}\) and \({\mathrm{Ca}} = 3.12 \times 10^{-4}\). We vary \({\mathrm{Ca}}\) by changing the length of the channel according to Eq. (34). Table 2 lists the parameters used for this case. Equation (29) provides the analytical solution. We terminate the simulations at 10 times the time taken to reach quasi-steady state for \({\mathrm{Ca}} = 3.12 \times 10^{-3}\) and at 15 times the time taken to reach quasi-steady state for \({\mathrm{Ca}} = 3.12 \times 10^{-4}\).

5.1.1 Case 1: \({\mathrm{ Ca}} = 3.12 \times 10^{-3}\)

The length of the channel is \(400 ~\upmu \text {m}\). Figure 6 shows a colour plot of the velocity magnitude for a section around the interface after reaching quasi-steady state. In a rectangular channel with Hagen–Poiseuille flow considering partial slip, the maximum velocity \(U_{\text {max}}\) occurs at the centre of the channel (slightly away from the upstream and downstream to vicinity of the meniscus) with a magnitude of (Equation 9 in Supplementary material),

$$\begin{aligned} U_{\text {max}} = 1.5 \times U_{\text {avg}} \frac{(2 \lambda + h)^2}{(h^2 + 6h\lambda + 6\lambda ^2)} = 1.47 U_{\text {avg}}. \end{aligned}$$
(36)

Dark red regions near the interface indicate PC with a magnitude greater than the maximum velocity of the analytical solution.

Fig. 6
figure 6

Velocity field close to the interface for \({\mathrm{Ca}} = 3.12 \times 10^{-3}\) at \(t^* \approx 0.027\). Black contour lines represent the interface with \(\alpha = 0.5\) for CSF, SSF and FSF. The red circle for CSF, SSF highlight PC at the interface. For SSF, PC are of the same order of magnitude as the physical velocity. The analytical solution yields \({U}_{\text {avg}} = 0.0312\) m/s and \({U}_{\text {max}} = 0.046\) m/s

Full size image

Figure 7 illustrates the meniscus velocity and the maximum velocity for all four formulations and the analytical solution.

Fig. 7
figure 7

Evolution of the velocities for \({\mathrm{Ca}} = 3.12 \times 10^{-3}\). Dashed black lines represent the analytical solution

Full size image

At quasi-steady state, the numerical solutions of the time-averaged meniscus velocity differ by \(8.25\%\) for CSF, \(5.4\%\) for SSF, \(3.4\%\) for FSF and \(2\%\) for PLIC from the analytic solution.

CSF shows the largest discrepancy due to inaccurate computation of the interface curvature and suffers from larger magnitude of PC at all times. The coarse representation of the capillary forces implies that more cells are affected by PC (marked by a red circle in Fig. 6). The PC increase viscous dissipation and decelerate the flow.

The solution of SSF is closer to the analytical reference (Fig. 7). Though PC occur, their magnitude has reduced compared to CSF. PC are of similar magnitude as the physical flow. They are continuously generated parallel to the interface (marked by a red circle in Fig. 6). The sharper representation of the capillary forces Eq. (10) restricts PC to fewer cells compared to CSF. The additional viscous dissipation from PC that occur close to the sharper interface explain the marginal rise in the amplitude of fluctuations of the meniscus velocity compared to CSF.

FSF and PLIC do not show any significant PC and the meniscus velocity is free from oscillations. Note that, based on the assumption of Hagen–Poiseuille flow for the analytical solution, we expect an error less than 2.5% as discussed in Sect. 3.2. The amount of filtering for FSF explain the remaining difference between the numerical and analytical solutions.

5.1.2 Case 2: \({\mathrm{ Ca}} = 3.12 \times 10^{-4}\)

The length of the channel is \(4000 ~\upmu {\text {m}}\). Figure 8 shows a colour plot of the velocity magnitude for a section around the interface at quasi-steady state. Dark red regions around the interface mark PC. An animation of the PC that occur for SSF and FSF are shown in the supplementary material.

Fig. 8
figure 8

Velocity field close to the interface for \({\mathrm{Ca}} = 3.12 \times 10^{-4}\) at \(t^* \approx 2.73 \times 10^{-4}\). The second figure for FSF shows the velocity field during a short burst at \(t^* \approx 3.53 \times 10^{-4}\). The analytical solution yields \({U}_{\text {avg}} = 0.00312\) m/s and \({U}_{\max } = 0.0046\) m/s

Full size image

Figure 9 shows the meniscus velocity and the maximum velocity for all formulations and the analytic solution.

Fig. 9
figure 9

Evolution of the velocities for \({\mathrm{Ca}} = 3.12 \times 10^{-4}\). Dashed black lines represent the analytical solution

Full size image

At quasi-steady state, the numerical solutions of the time-averaged meniscus velocity differ by 6.35% for CSF, 2.27% for SSF, 0.4% for FSF and 0.37% for PLIC from the analytical solution. The better match is due to the reduced impact of the Hagen–Poiseuille flow assumption on the analytic solution (Sect. 3.2), expecting an error less than 0.25%.

The magnitude of PC, however, has increased approximately three times for CSF, showcasing the importance of an accurate representation of the capillary forces to capture the flow dynamics at low \({\mathrm{Ca}}\). The number of interfacial cells affected by PC are also greater compared to the previous case and the amplitude of fluctuations of the meniscus velocity are within 1%.

For SSF, the magnitude of PC reduce approximately by a factor of two compared to CSF. However, PC occur at all times resulting in a fluctuating meniscus velocity with an amplitude of 3.3%.

For FSF, we see minimal PC generated at the interface at all times resulting in minor fluctuations of the meniscus velocity. Additionally, periodic bursts of PC temporarily decelerate the meniscus (represented by a dashed red circle in the inset of Fig. 9) having an amplitude of 2.6%. As the filtering removes these periodic bursts, the meniscus velocity returns back to the correct solution shortly after. For SSF, the bursts corresponding to maximum PC, are observed when the sharp colour function, \(\alpha _{\text {shp}}\) enters a new wall boundary cell. As we see in Fig. 9, the rise to and fall from maximum PC is gradual compared to FSF. Bursts corresponding to maximum PC for FSF are observed when the sharp colour function fills a wall boundary cell and commences to enter a new boundary cell. The bursts are sudden and filtering dampens these bursts much faster compared to SSF. These periodic bursts of PC for SSF and FSF are observed for the cases discussed in the next sections as well dealing with low capillary numbers.

PLIC shows a consistent velocity field with no significant PC around the interface at all times.

5.2 Effect of viscosity ratio

The displacement of the meniscus decelerate or accelerate during the imbibition process if the fluids viscosities differ. The length of the channel is \(400~\upmu\)m that corresponds to reference \({\mathrm{Ca}} = 3.12 \times 10^{-3}\) (Eq. 34). We obtain different viscosity ratios by fixing the viscosity of the non-wetting phase, \(\mu _{n} = 0.001\) kg/ms and by varying the viscosity of the wetting phase, \(\mu _{w}\) accordingly. Table 2 provides the other parameters for this case.

We define the reference velocity in Eq. (30) considering the viscosity of the non-wetting phase. Note, that the imbibition process starts with the wetting phase occupying 2% of the channels volume. Hence, the initial meniscus velocity differs from one. At the end of the imbibition process, the meniscus velocity depends only on the viscosity of the wetting phase. Therefore, as the wetting phase is close to imbibe the entire channel, the dimensionless meniscus velocity moves towards the viscosity ratio given by,

$$\begin{aligned} U^*_{\text {end}} = \frac{U_{\text {m}}}{U_\text {ref}} = \frac{\mu _n}{\mu _w}. \end{aligned}$$
(37)

We consider two cases, \(M = 0.1\) and \(M = 10\). We terminate the simulation when the wetting phase has imbibed half the length of the channel. The corresponding case with \(M = 1\) has been discussed in Sect. 5.1.1.

5.2.1 Case 1: \(M = 0.1\)

Figure 10 shows the evolution of the meniscus velocity and the maximum velocity for all formulations and the analytical solution.The inset shows a short time interval to highlight the fluctuations.

Fig. 10
figure 10

Evolution of velocities for \(M=0.1\). The dashed black lines represent the analytical solution

Full size image

The flow decelerates over time as the more viscous wetting phase \(\mu _w = 0.01\, \mathrm{kg/ms}\) invades the channel. All formulations qualitatively show a similar behaviour of the meniscus velocity. The numerical solutions of the meniscus velocity at the end of the inertial acceleration stage differ within 10% (for reference: 6.9% for PLIC) from the analytical solution which could potentially be due to the approximations used in the analytical solution, inaccurate computation of the interfacial curvature and due to PC for some formulations (see below). With time, as the flow decelerates, the discrepancy with respect to the analytical solution is seen to reduce.

Note, that for a later time when the meniscus velocity \({U}_{\text {avg}}^*\) reaches approximately 0.1 (not shown here, that is when the imbibition is about to end), the meniscus velocity is approximately equal to that discussed in Sect. 5.1.2.

As the flow decelerates, CSF and SSF show a gradual rise in the amplitude of fluctuations of the meniscus velocity towards the observations made in Sect. 5.1.2. This indicates that CSF and SSF are not sensitive to viscosity contrasts. Again, CSF shows the largest magnitude of PC at all times. For SSF, the magnitude of PC reduce approximately 1.5 times compared to CSF at \(t^* \approx 1.5\).

Periodic generation of PC for FSF results in a widely fluctuating meniscus velocity. The amplitude of fluctuations at \(t^* \approx 1.5\) is 6.3%. At a meniscus velocity 1.9 times (\({U}^* = 0.19\)) that discussed in Sect. 5.1.2, the amplitude of fluctuations of the meniscus velocity increase 2 times. This indicates that FSF is sensitive to viscosity contrasts.

PLIC shows only a minimal amount of PC that lead to marginal fluctuations of the meniscus velocity (at \(t^* = 1.5\), discrepancy with the analytical solution is within 1%)

5.2.2 Case 2: \(M = 10\)

Figure 11 shows the evolution of the meniscus velocity and the maximum velocity for all formulations and the analytical solution. The inset shows a short time interval to highlight the fluctuations.

Fig. 11
figure 11

Evolution of velocities for \(M=10\). The dashed black lines represent the analytical solution

Full size image

As the less viscous wetting phase \(\mu _w = 0.0001~\mathrm{kg/ms}\) invades the channel, the flow accelerates over time. At the end of the inertial acceleration stage, the numerical solutions of the meniscus velocity differ by 7.1% for CSF, 3.6% for SSF and 1.07% for FSF and PLIC from the analytic solution. This is primarily due to the coarser representation of the capillary forces for CSF and due to the expected discrepancy from the assumptions made for the analytical solution.

Again, CSF generates maximal PC at all times, whereas SSF shows periodic bursts of PC. The magnitude of PC for SSF at \(t^* = 0.15\) is approximately 1.12 times lower compared to CSF. These PC decelerate the meniscus due to additional viscous dissipation. At any given time, CSF and SSF predict more viscous non-wetting fluid in the channel than the analytical solution due to the retardation of the meniscus by PC. This results in a discrepancy of the viscous forces and hence a deterioration of the solutions of CSF and SSF over time. As the flow accelerates, the fluctuations of the meniscus velocity dampen.

The meniscus velocity for FSF and PLIC match closely with the analytical solution at initial stages. As the flow accelerates, the numerical solutions of FSF and PLIC lag behind the analytical solution. This could potentially be due to error we expect from the analytical assumption which leads to predict slightly larger volume of the more viscous non-wetting fluid in the channel compared to the analytical solution. FSF generates periodic PC though their magnitude is not as large compared to the previous case (\(M = 0.1\)). Hence, the impact of PC on the meniscus velocity is small. The periodic bursts of PC dampen as the flow accelerates. PLIC captures the flow dynamics accurately with no large PC observed around the interface.

5.3 Effect of density ratio

In this section, we investigate the sensitivity to density ratios of \(D=1000\) and \(D=10^{-3}\). As density neither occurs in Eq. (24) for the capillary forces nor in Eq. (26) for the viscous forces, we expect a quasi-steady displacement of the meniscus. However, based on the total mass of the fluids to be displaced in the capillary, the inertial acceleration time scales vary.

The channel length is \(4000~\upmu\)m corresponding to \({\mathrm{Ca}} = 3.12 \times 10^{-4}\) and the wetting phase initially occupies 0.2% of the channels length. Apart from the density of fluids, Table 2 provides the parameters for this case. The corresponding case for \(D = 1\) has been discussed in Sect. 5.1.2.

For PLIC, extremely small time steps (\(\Delta t = 0.08~t_{\mathrm{BK}}\), corresponding to a CFL \(\approx\) \(8\times 10^{-5}\) compared to a CFL \(\approx 9\times 10^{-4}\) at \(t_{\mathrm{BK}}\) for FSF) are required to validate \(D = 10^{-3}\) else resulted in an inconsistent flow field which made the validation infeasible. Hence, PLIC for \(D = 10^{-3}\) is omitted in the discussion.

5.3.1 Case 1: \(D = 1000\)

The specific fluid densities here are \(\rho _{n} = 1000\) kg/m\(^3\) and \(\rho _w = 1\) kg/m\(^3\). We terminate the simulation at 15 times the time it takes to reach quasi-steady state. Figure 12 shows the evolution of the meniscus velocity and the maximum velocity for all formulations (solid lines) and the analytical solution. The inset picture shows the difference in the inertial acceleration time scales for the two cases discussed. As the channel is initially filled by the denser non-wetting phase (99.8% of channel length), the total mass of fluids to be displaced is greater (compared to Sect. 5.3.2), and therefore, the inertial acceleration time scales last longer.

All the formulations show a similar behaviour during acceleration stage before PC for CSF, SSF and FSF induce fluctuations of the meniscus velocity at the end of the inertial flow regime. The amplitude of fluctuations of the meniscus velocity and the magnitude of PC for CSF and SSF are similar to the observations made for \(D = 1\).

PC of similar magnitude as the physical flow for FSF induce minimal fluctuations of the meniscus velocity. Compared to \(D = 1\), PC during periodic bursts have increased 1.22 times thereby increasing the amplitude of fluctuation of the meniscus velocity (amplitude = 3% compared to 2.6% for \(D = 1\)). Similar to Sect. 5.1.2, the maximum PC for SSF and FSF occur related to the sharp colour function entering a new cell along the wall boundary (similar observation for \(D=0.001\)).

PLIC captures the flow dynamics accurately at all sections of the channel.

5.3.2 Case 2: \(D = 0.001\)

Fluid densities considered for this case are \(\rho _n = 1\) kg/m\(^3\) and \(\rho _w = 1000\) kg/m\(^3\). The evolution of the velocity for CSF, SSF and FSF are represented by coloured dashed lines in Fig. 12. Due to lower density of the non-wetting phase occupying 99.8% of the channel length, the total mass of the fluids to be displaced in the system is less and quasi-steady state is reached instantaneously (inset picture of Fig. 12). We terminate the simulation at \(t^* = 9 \times 10^{-4}\). At quasi-steady state, the amplitude of fluctuations of the meniscus velocity for CSF, SSF and FSF are consistent with \(D=1000\). The range of PC for CSF have marginally increased compared to \(D = 1000\). For SSF and FSF, the range of PC are consistent with the observations for \(D = 1000\). This indicates that neither of CSF, SSF and FSF are sensitive to density contrasts.

Fig. 12
figure 12

Evolution of velocities for \(D = 1000\) (solid-coloured lines) and \(D = 0.001\) (dashed coloured lines). Dashed black lines represent the analytical solution

Full size image

6 Conclusion

We have presented spontaneous imbibition in a Hele-Shaw cell symmetry considering a partial slip wall boundary to validate the numerical precision of open-source finite-volume VOF formulations namely, CSF (solver: interFoam), Sharp Surface Force (solver: poreFoam), FSF (solver: poreFoam) and PLIC (solver: Gerris) for capillary numbers between \({\mathrm{Ca}} = 3.12 \times 10^{-4}\) to \({\mathrm{Ca}} = 3.12 \times 10^{-3}\). We extended the Lucas–Washburn equation for the meniscus velocity in a horizontal micro-channel for arbitrary viscosity ratios. We considered flows solely driven by capillarity to focus on quantifying parasitic currents at low \({\mathrm{Ca}}\). We also analysed the resilience of the numerical solvers at different density ratios.

Two important steps of the VOF method that impact the capillary forces are, advecting the colour function and computing the interface curvature.

Solving the colour functions advection equation numerically (CSF, SSF, FSF) results in numerical diffusion and a smeared interface. Geometric split advection technique (PLIC) avoids numerical diffusion and preserves the sharpness of the interface. Extending the concept of accurate geometric advection on unstructured meshes is an ongoing research work (Roenby et al. 2016; Maric et al. 2013).

The height function methodology (PLIC) to compute the interface curvature provides an accurate capillary forces with minimal PC compared to other formulations using Brackbill’s expression (CSF, SSF, FSF).

Along with an inaccurate computation of the interface curvature, PC were seen with CSF at all times increasing viscous dissipation thereby slowing the meniscus velocity. Though PC occur at all times, SSF reduced their magnitude twofold compared to CSF. FSF filtered PC around the interface. However, periodic bursts in the velocity field were seen that temporarily slowed down the meniscus. We observe that when the sharp interface (\(\alpha _\text {shp}\)) enters a new cell along the wall boundary resulted in maximum PC for SSF and FSF at low capillary flows. PLIC provided a consistent flow profile with no PC when the viscosity and density ratios were around one. At high viscosity ratios, minimal PC were seen with PLIC too. We observed that the PLIC solver struggled to model few cases with large density contrasts.

In conclusion, the PLIC formulation of Gerris in 2D is a viable numerical tool to model two-phase flows at low \(\mathrm {Ca}\) on structured grids. Even though SSF does not entirely eliminate PC, the smoothing and sharpening of the interface reduces PC substantially.

FSF reduces PC further but shows periodic bursts and requires additional heuristic parameters. The large magnitude of the periodic bursts of PC, raises concern that they can potentially alter the solution.