Introduction

Measurements of tree heights and diameters are essential in forest assessment and modeling. Tree heights are used for estimating timber volume, site index and other important variables related to forest growth and yield, succession and carbon budget models (Peng 2001). Considering that the diameter at breast height (dbh) can be more accurately obtained, and at lower cost than total tree height, only a subsample of heights is usually measured in the field. Height–diameter equations are then used to predict the heights of the remaining trees, thus reducing the cost of data acquisition. For these reasons, developing suitable height–diameter models may be considered one of the most important elements in forest design and monitoring.

The height–diameter relationship varies from stand to stand, and even within the same stand this relation is not constant over time (Curtis 1967). Therefore, a single height–diameter function without further predictor variables is not able to correctly describe all the possible relationships that may be found within a given forest. To reduce the level of variance, some basic relationships can be improved by taking into account stand variables that account for the dynamics of each stand. A generalized height–diameter function estimates the specific relationship between individual tree heights and diameters using stand variables such as basal area per hectare and quadratic mean diameter (see for example, Larsen and Hann 1987; López Sánchez et al. 2003; Temesgen and von Gadow 2004). The reason for using this approach is to avoid having to establish individual height–diameter relationships for every stand. In contrast in Germany so-called Einheitshöhenkurven have been routinely used for many decades (Lang 1938; Kramer 1964; von Laer 1964; Kennel 1972; Nagel 1991). In this approach, a height–diameter pair of a mean or dominant tree is used as predictor for the general height–diameter relationship. Hence, generalized height–diameter functions are used to estimate individual height–diameter relationships using additional predictor variables, while “Einheitshöhenkurven” are employed by applying additional measurements of a representative height–diameter pair.

In forest field inventories, height and diameter data are generally taken from trees growing in plots that are located in different stands. Often these plots are permanently marked, and the same trees are remeasured over time. Such clustered and longitudinal data are characterized by a lack of independence between observations, since data coming from the same sampling cluster and measurement occasion tend to resemble each other more than the average (Fox et al. 2001). This type of data can be also characterized as having a unit, cluster and occasion-specific heterogeneity (Brezger and Lang 2006), whereas in forest management a unit may refer to an ecoregion or forest district, and a cluster may refer to a sample plot. The lack of independence between observations results in biased estimates of the confidence intervals of the parameters if ordinary least squares regression techniques are used (Searle et al. 1992). To deal with this problem, the extension of ordinary regression to mixed model theory has been proposed in forest research (Gregoire 1987; Lappi 1991; Calama and Montero 2004; Mehtätalo 2004; Nothdurft et al. 2006). In mixed models, both fixed and random parameters are estimated simultaneously, providing consistent estimates of the fixed parameters and their standard errors. Furthermore, the inclusion of random parameters allows to model the variability detected for a given phenomenon among different locations, clusters and measurement occasions within a given population, after defining a common fixed functional structure (Castedo-Dorado et al. 2006). Mixed models also improve the predictive ability if it is possible to predict the value of the random parameters for a location and measurement occasion, which is not part of the dataset by using additional measurements as pre-information (Lappi 1997; Mehtätalo 2004). This particular method of predicting random effects by BLUPS (best linear unbiased predictors) is usually described as model calibration (Lappi 1997). Hence, applying mixed model methodology to generalized height–diameter functions allows for a prediction using both information in sync: predictors as mean quadratic diameter and additionally measured diameter–height pairs. The use of an arbitrary number of diameter–height pairs for calibration is an additional advantage. These measurements need not be from representative mean or dominant trees.

However, in many applications a theoretical problem remains since the random effects are usually assumed to be independently distributed. This assumption is violated if the data originating, for example, from large-scale inventories show spatial correlation patterns. Up to now, this topic has been rarely discussed in a forestry context (Brezger and Lang 2006; Augustin et al. 2009). An approach to model the spatial correlation of the random effects related to only one parameter of a height–diameter model via a geostatistical approach is presented by Nanos et al. (2004).

Spatial effects are usually a surrogate of the effects of other unobserved influential factors. But in many applications, the spatial effect is not only the result of factors that exist only locally, i.e. on cluster level but also the result of factors that show a strong spatial structure. Hence, the overall spatial trend can be separated into a spatially correlated (structured) and an uncorrelated (unstructured) effect (Brezger and Lang 2006). Subsequently, only the unstructured effect is modeled by (uncorrelated) random effects on cluster level. For the structured effect, two main approaches may be distinguished: (I) the structured spatial effect is modeled in the framework of so-called geoadditive models via a Gaussian Markov random field, i.e. spatially correlated random effects are estimated for the spatial units of the observations (Kammann and Wand 2003). (II) the structured spatial effect is modeled via 2-dimensional surface fitting by applying specific generalized additive models based on e.g. penalized regression splines with thin plate basis (Wahba 1990; Wood 2006). The second approach is particularly suited if the data locations are described by exact coordinates. The first approach can also be employed if the observations are assigned to adjacent geographic units like forest districts. Both approaches can be combined with the estimation of (uncorrelated) random effects to account for the unstructured spatial effect simultaneously. The resulting model types are still called either geoadditive models concerning approach I or generalized additive mixed models gamm concerning approach II (Lin and Zhang 1999; Fahrmeir and Lang 2001). However, the separation of both (structured and unstructured) spatial effects might easily lead to numerical problems using approach II, especially if the model for the 2-dimensional surface is rather complex (Wood 2006). If not only cross sectional but also longitudinal data should be modeled, the theory could be extended by modeling additionally a (nonlinear) time trend or even 3-dimensional space–time trends (Wood 2006; Augustin et al. 2009).

Further extensions are the implementation of nonlinear effects for additional covariates leading to the well-known generalized additive models gam (Hastie and Tibshirani 1990). If not only main effects but also interactions between nonlinear effects and categorical or continuous covariates are to be modeled, this specific type of a gam is called a varying coefficient model VCM (Hastie and Tibshirani 1993). In this model type the nonlinear effects are effect modifiers of the categorical or continuous covariates. If the interaction covariate is categorical, then this results in separate nonlinear effects for each level of the covariate. If the covariate is continuous, a special case of an interaction is modeled because one of the covariates enters the model still linearly. The natural extension to allow for an interaction term that is nonlinear with respect to several covariates is again based on 2- or multi-dimensional surface fitting (Wood 2006). In contrast to 2-dimensional surface fitting for describing structured spatial effects, usually tensor product splines are employed that allow for different degrees of smoothing (anisotropy) for the different dimensions (Wood 2006).

Both approaches (I) and (II) for describing structured spatial effects could be also combined with continuous or categorical covariates. In this case, a special type of a VCM with a spatially varying effect modifier results (Fotheringham et al. 2002). Hence, in this case not only the intercept is allowed to vary in space but also the coefficients of one or more covariates. All listed model classes are subsumed by Fahrmeir et al. (2007) under the class of structured additive regression models STAR.

The main objective of this paper is to predict tree height for a certain dbh with high accuracy using only a minimum set of information, i.e. only mean quadratic diameter and geographic coordinates that can be easily derived. No additional information should be used to allow for a very simple practical application, and no predictors should be used that are themselves resulting from extensive modeling processes and that include a prediction error. Hence, the main objective is prediction rather than quantification of stand and site effects. The effect of dg that changes with age and as a result of silviculture should account for the longitudinal development of the height–diameter relationship. The effect of the geographic coordinates subsumes the effects of all potential factors that are spatially correlated. This structured spatial effect can be employed in predictions even if no additional measurements are available. Finally, uncorrelated random effects subsume the effects of all spatially uncorrelated factors that appear only locally on plot level.

For this purpose, the well-known Näslund height–diameter function is parameterized within the generalized additive regression gam frame work (Hastie and Tibshirani 1990) applying the specific methodology of Wood (2006). A high flexibility of the model is needed, because only few predictor variables are used. The approach should additionally allow for a calibration of a mean population model if additional height–dbh measurements are available. As a result, we present a height–diameter model approach that is parameterized in the framework of methodologically well-founded STAR models (Fahrmeir et al. 2007) employing several of the initially stated model components.

Materials and methods

This section introduces the Estonian Permanent Forest Research Network that provides an extensive dataset for the study and explains the methods which were applied.

The Estonian Permanent Forest Research Network

During the past two decades, a permanent Forest Research Network database has been established in Estonia including measurements from different original data sources. The database was developed with the understanding that a long-term series of re-measured plots would provide a useful basis for forest growth modeling. All basic forest types, stand ages and stand densities should be represented. Tree coordinates should be assessed, and plot areas should be large enough to characterize stand structures (Kiviste et al. 2007).

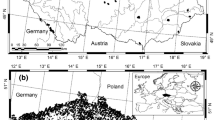
Trees have been measured since 1999 on the 16 × 16 km grid of the European ICP FORESTS Level 1 monitoring system, using circular plots with a radius of 15, 20 or 25 m to include at least 100 upper storey trees. Smaller trees (second storey and understorey trees) were measured in an inner circle with a radius of 8 or 10 m. For each tree, the coordinates, diameter at breast height (dbh) and possible faults were recorded. For a subset of “sample trees” (every 5th tree, biggest trees or rare species), the total tree height, height to crown base and the height to lowest dead branch were assessed. The Estonian Permanent Forest Research Network database currently includes a total of 680 field plots and measurements of close to 200,000 trees (Fig. 1). The field work has been carried out by the Department of Forest Management of the Estonian University of Life Sciences.

Fig. 1
figure 1

Map of the Estonian Permanent Forest Research Network that currently includes a total of 680 field plots, some circles represent clusters of 3–9 plots. Black dots are plots where Scots pine is the dominant species

Full size image

The map in Fig. 1 shows four concentrations of plots that represent previous research areas where traditional methods of assessment were used. The eastern-central cluster was established in a productive herb-rich forest region. Another more southerly cluster is represented by pure pine stands on fertile sandy soils. A third bigger group of plots is situated in northern Estonia on poor sandy soils, and a fourth group of plots was established on the island Hiiumaa. Altogether, 71,506 trees in 492 permanent sample plots have been re-measured once, and 12,841 trees in 97 plots were re-measured twice. A total of 198,909 measurement records of all tree species (including records of dead trees) is available. In this study, height–diameter measurements of 22,347 Scots pine trees were used (Fig. 2); 6,234 Pine trees from 90 plots have been re-measured twice, 13,900 Pine trees from 208 plots have been re-measured once, and 2,213 Pine trees from 104 plots have been measured only once. The country borders have been taken from polygones published by the Estonian Land Board.

Fig. 2
figure 2

Marginal and bivariate distributions of available diameter and height observations for Scots pine

Full size image

Choice of model

Underlining their importance in forest assessment and planning, a large number of stand-specific height–diameter equations have been published. According to Lei and Parresol (2001), the height–diameter relationship should be monotonically increasing and have a functional inflection point and an asymptote. A parameter-parsimonious model that meets these requirements is a widely used model which is known in Germany as the “Petterson function” (see for example, Kramer and Akça 1995) and in Scandinavia as the “Näslund function” (see for example, Kangas and Maltamo 2002):

$$ h_{ijk} = \left( \frac{{d_{ijk} }}{{\alpha + \beta d_{ijk} }} \right)^{\gamma} + 1.3 $$
(1)

where h ijk and d ijk are the total height (m) and breast height diameter (cm) of the kth tree on the ith plot at the jth measurement occasion, respectively; α, β and γ are empirical parameters. If mixed model approaches are applied, models are often linearized (Lappi 1997; Mehtätalo 2004; Kinnunen et al. 2007) as linear mixed model instead of nonlinear mixed model theory could be used. Additionally, in our application we need to linearize the model since we use generalized additive models where we have to specify a linear combination of (nonlinear) predictor effects. The Näslund function can be linearized by setting the exponent γ constant (in our case γ = 3, see Kramer and Akça 1995):

$$ y_{ijk} = {\frac{{d_{ijk} }}{{(h_{ijk} - 1.3)^{(1/3)} }}} = a + \beta d_{ijk} $$
(2)

In general terms, a basic linear mixed model can be written as (Lappi 1997):

$$ {\mathbf{y}} = {\mathbf{Xa}} + {\mathbf{Zb}} + {\mathbf{e}} $$
(3)

where the vector y of length n (number of observations) contains the measured values (in our case transformed), a is the vector of fixed population parameters of length p; the model matrix X of dimension n × p describes how y depends on a and contains the independent continuous variables and ones for the intercept and dummy variables for (potential) categorical variables; b is the vector of random parameters of length q; matrix Z of dimension n × q describes how y depends on b and e is the vector of random error terms.

In our case, we fit a two-level mixed model with random effects on stand and measurement occasion level for the quantification of the between-plot variability and the measurement occasion variability within plots, respectively. Therefore, Eq. 2 can be specified as a mixed model, as follows:

$$ y_{ijk} = \alpha + \beta d_{ijk} + a_{i} + b_{i} d_{ijk} + a_{ij} + b_{ij} d_{ijk} + \varepsilon_{ijk} $$
(2a)

where α is the fixed intercept, β is the fixed coefficient of dbh, both these terms provide an estimate of the (conditional) expectation value, i.e. the conditional population mean for a predefined dbh. a i is the random stand effect, i.e. the random standwise deviation of the intercept, b i is the random standwise deviation of the coefficient of dbh, a ij is the random measurement occasion effect within stand, i.e. the random intercept deviation of the measurement occasion within stand, b ij is the random measurement occasion deviation of the coefficient of dbh, and ε ijk is the random tree variation within stand and measurement occasion (residual error). It is assumed that the vectors of random effects on stand b i and measurement occasion level b ij are normally distributed with b i ~N(0, D 1) and b ij ~N(0, D 2) where D 1 and D 2 denote the variance–covariance matrices of the random effects on stand and measurement occasion level, respectively. For the vector of random error terms, it is assumed that it is normally distributed with e ~ N(0, R), where R denotes the variance–covariance matrix where the diagonal elements are equal to the variance of the residual error σ 2, and the nondiagonal elements are zero, if no within-group covariance and variance functions are modeled.

A generalized height–diameter model includes stand and/or site variables, such as the quadratic mean diameter (dg) to describe the original regression parameters as a function of those variables (Mehtätalo 2004). Our study attempts to relate the coefficients of Eq. 2 not only to the quadratic mean diameter but also to the plot geographic coordinates x and y. We solve the problem of spatially correlated random effects via the implementation of a structured spatial effect. The structured component of the overall spatial trend is quantified applying the specific methodology of Wood (2006) for 2-dimensional surface fitting. Additionally, the main effect of dg is modeled by a nonlinear effect using a penalized cubic regression spline (Eq. 2b). Standard software for parameterization of exactly this type of model is available within the statistic language and environment R (R Development Core Team 2007) employing the R-library mgcv (Wood 2006). A particular feature distinguishing the R-library mgcv from other methods for adapting generalized additive regression models (e.g. Hastie and Tibshirani 1990) is the implementation of multi-dimensional penalized regression splines for identifying and describing nonlinear multi-dimensional model effects. We fit the 2-dimensional surface via a penalized thin plate basis regression spline that is recommended by Wood (2006) for describing spatial trends. The main effect of dg and the 2-dimensional surface operate as modifier of the intercept α (Eq. 2). During model selection, we get further improvement when integrating varying coefficient terms that operate as modifier of the slope β, i.e. as modifier of the effect of the tree diameter (d ijk ). We integrated a 1-dimensional nonlinear modifier as a function of dg: f 3(dg ij ) and a 2-dimensional surface: f 4(north i ,east i ) that results in a spatially varying effect of tree diameter (Eq. 2b). The 1-dimensional effect was modeled as penalized cubic regression spline, and the 2-dimensional surface was modeled as penalized thin plate basis regression spline again. The extension of model 2a into a generalized additive mixed model gamm instead of a generalized linear mixed model glmm was necessary since the nonlinear model variants proved to be superior to their linear variants in the model selection processes. Models were compared using the Bayes information criterion (BIC) (Burnham and Anderson 2004; Schwarz 1978). Now, the model is defined as a generalized additive mixed model (Eq. 2b) including a 1-dimensional nonlinear effect of dg, a 2-dimensional surface for the structured spatial effect on the intercept α (Eq. 2), a varying coefficient term as a function of dg that modifies the effect of tree diameter d ijk and a 2-dimensional surface that operates as a spatially varying modifier of the effect of tree diameter d ijk . Unstructured (uncorrelated) spatial effects are modeled via (uncorrelated) random effects on plot and measurement occasion level (Eq. 2b).

$$ y_{ijk} = \alpha + f_{1} ({\text{dg}}_{ij} ) + f_{2} ({\text{north}}_{i} ,{\text{east}}_{i} ) + \beta d_{ijk} + f_{3} ({\text{dg}}_{ij} )d_{ijk} + f_{4} ({\text{north}}_{i} ,{\text{east}}_{i} )d_{ijk} + a_{i} + b_{i} d_{ijk} + a_{ij} + b_{ij} d_{ijk} + \varepsilon_{ijk} $$
(2b)

However, during the model building process it became evident that the proposed model structure could not be fitted directly due to numerical problems. Hence, the model was fitted in two steps. First, the fixed part of the model was fitted as a generalized additive model gam:

$$ y_{ijk} = \alpha + f_{1} ({\text{dg}}_{ij} ) + f_{2} ({\text{north}}_{i} ,{\text{east}}_{i} ) + \beta d_{ijk} + f_{3} ({\text{dg}}_{ij} )d_{ijk} + f_{4} ({\text{north}}_{i} ,{\text{east}}_{i} )d_{ijk} + \varepsilon_{ijk} $$
(2b1)

The estimated conditional expectation value \( \hat{y}_{ijk} \) was then integrated as ‘a priori information’ in a linear mixed model lme in a second step:

$$ y_{ijk} = \alpha_{0} \hat{y}_{ijk} + a_{i} + b_{i} d_{ijk} + a_{ij} + b_{ij} d_{ijk} + \varepsilon_{ijk} $$
(2b2)

where \( {\text{Var}}(\varepsilon_{ijk} ) = \sigma^{2} |\alpha_{0} \hat{y}_{ijk} |^{2\theta } \)

For ensuring centered random effects, a coefficient α 0 was also estimated. Hence, the estimated conditional expectation value \( \hat{y}_{ijk} \) enters the model as a predictor not just as an offset. To take heteroscedasticity into account, the variance can be modeled through a function involving either the predicted value or some explanatory variables (Davidian and Giltinan 1995; Pinheiro and Bates 2000). We used the power-of-the-mean function which is a well-known example of a variance function based on predicted values, where σ 2 is the residual variance, and θ is a parameter to be estimated (Eq. 2b2). The linear mixed model (Eq. 2b2) was parameterized employing the R-library nlme (Pinheiro et al. 2006).

Calibration

The linear mixed model, which is fitted in the second step, allows for a model calibration using prior information as in the case of Lappi and Methätalo. Different kinds of information of the predictors in the fixed part combined with additional local height measurements can be used to improve the prediction accuracy. Thus, the approach of a generalized height–diameter relationship that is fitted as a linear mixed model is superior to both approaches mentioned in the introduction: (a) generalized height curves that are not specified as mixed models and (b) “Einheitshöhenkurven”. In (a), no pre-information (height measurements) can be used to improve the prediction. In (b), no predictor variables can be used to improve the prediction and the estimation of the mean stand height and diameter from few measurements are assumed to be the “true” values. In our mixed model approach, the calibration of the height–diameter curve for a specific plot i, i.e. the prediction of random effects via BLUPS, is calculated by simple matrix algebra, using

$$ \hat{b}_{i} = \hat{D}Z^{T} (Z\hat{D}Z^{T} + \hat{R})^{ - 1} (y_{i} - \mu_{i} ) $$

where \( \hat{b}_{i} \) is a column vector of random effects to be estimated for plot i. In our case, it has 2 + 2 m i rows where m i denotes the number of measurement occasions of the i-th plot. \( \hat{D} \) denotes the variance–covariance matrix for the random effects. It is a block diagonal matrix, where the upper first block consists of D 1 , and the following m i blocks are filled with D 2 (Table 2); hence, it has dimension (2 + 2 m i ) × (2 + 2 m i ). The non-block-diagonal elements of Matrix D are zero as no cross-level correlations between the random effects on plot and measurement occasion level have been assumed. Matrix Z is the model matrix of the random effects of dimension (n i ) × (2 + 2 m i ), where n i denotes the number of single tree height measurements (observations) over all measurement occasions m i of plot i. \( \hat{R} \) is a diagonal matrix with dimension n i  × n i with the estimates of \( \sigma^{2} |\alpha_{0} \hat{y}_{ijk} |^{2\theta } \) in the diagonal and zero for the nondiagonal elements. y i is a vector that contains the (transformed) single tree height observations y ijk (Eq. 2) over all measurement occasions m i of plot i and has length n i . Vector μ i contains the related predicted values \( \alpha_{0} \hat{y}_{ijk} \) by employing only the fixed effect part of the model. Since we fit a 2-step model in our case, the \( \hat{y}_{ijk} \) are the predictions from the gam (Eq. 2b1) multiplied by the coefficient α 0 from the linear mixed model (Eq. 2b2). However, the fact that the estimates from the linear mixed model still have a minor bias calls for testing other equations as alternatives to the “Näslund function”.

Results

Generalized additive model

Of particular interest are the effects of the squared mean diameter (dg) and the geographic coordinates on the parameter estimates of Eq. 2b1 and the overall model accuracy. Statistical characteristics of the gam (Eq. 2b1) are presented in Table 1. Smooth terms in our case are presented by a combination of a linear term and a centered smooth term; hence, coefficients of parametric terms are estimated and displayed also.

Table 1 Statistical characteristics of the generalized additive model (Eq. 2b1)
Full size table

Effects of squared mean diameter (dg)

The effects of the dg on the original parameters α and β are definitely nonlinear since no straight line could be placed within the dashed lines that represent the two times pointwise standard error of the expectation value (Fig. 3). The original parameters α and β have no direct biological meaning. However, with decreasing parameters α and β the height–diameter curve generally shifts toward greater heights. Actually, the derived values of α increase with increasing dg. But concerning the resulting height–diameter curves (Fig. 4), this trend is over-compensated by the decreasing values of β (Fig. 3).

Fig. 3
figure 3

Effects of dg on the intercept (α; left) and slope (β; right) of the original Eq. 2 which are estimated as nonlinear effects (Eq. 2b1). Solid lines represent the predicted values (expectation values); dashed lines represent two times the standard error of the expectation value. The small lines along the x axis show the location of the sample plots concerning their values of dg

Full size image
Fig. 4
figure 4

Height–diameter curves predicted by employing Eq. 2b1 for different dg at geographic location north 58.5 and east 25.0

Full size image

The overall effect of the dg on the height–diameter curve is illustrated in Fig. 4. For a constant geographic location (northing 58.5, easting 25), the increase in dg results in larger heights for a predefined dbh. However, from a dg of 34 cm the height–diameter curve is assumed to be constant. This constraint was set during model parametrization since the derived (unconstraint) nonlinear effects resulted in an unfeasible set of curves for plots exceeding a dg of 34 cm up to the maximum dg within the database of 41.4 cm. Parameterizing unconstrained effects of dg resulted in a decrease in tree height for a given dbh for the entire diameter range. The crossing of height–diameter curves over time or with increasing dg is a natural consequence of different growth rates in different diameter and height classes that should not be constrained (Lappi 1997). However, in our investigation the entire curve moved toward lower heights, and this did not seem to be feasible. Only about 3% of the observed pine stands in our database have a dg of more than 34 cm. Thus, the decrease in the height–diameter curve with increasing dg in the area of large dg’s might be due to confounding effects and an unbalanced data structure. For example, site index is often correlated with stand age, and thus patterns like “old stands grow mostly on poor sites” confound the original correlation. The results show that the database needs to be extended for large dg’s that cover the whole range of sites in Estonia.

Geographical effects (structured spatial effects)

The influence of the geographical location within Estonia on the original parameters α and β (Eq. 2b1) is shown in the two maps in Fig. 5. The maps do not present the statistical effects of the geographical location, but isohetes of parameter values for a dg set constant to 20 cm; plot locations are shown as black dots on the maps. Two cross sections permit a more detailed analysis of the spatial effect on the height–diameter relations. The northern section cuts across the northern part of Hiiumaa in the west over Rapla and Roosna-Alliku to Tudulinna in the eastern part of Estonia. The southern section runs from Kuressaare on the island Saaremaa in the west across over Pärnu and Viljandi to Tartu in the eastern part of the country. The two cross sections are shown as dashed lines in Fig. 5.

Fig. 5
figure 5

Influence of the geographical location within Estonia on the values of the intercept (α) and the slope (β) of the original Eq. 2 that are estimated as nonlinear effects (Eq. 2b1). The maps present the isohetes of the parameter values for a constant dg of 20 cm; the graphs below the maps show the parameter values for different easting values of the northern and southern crosscuts. Larger white dots with black edge mark the positions for that exemplary height–diameter curves are predicted (Fig. 6)

Full size image

The changes in the parameter values predicted by the gam for different easting values are shown in the lower part of Fig. 5, separately for the northern and the southern cross section. For a comparison of parameter values between different geographic locations, the predicted values are supplemented by estimations of the two times pointwise standard errors again. The interpretation of the map features and the gam results allows three conclusions:

  • both parameters show a considerable variability within Estonia, which underlines the need for two 2-dimensional surface estimators that vary α and β simultaneously.

  • the parameters are negatively correlated as the spatial distributions are similar but inverted;

  • the variable width of the confidence intervals in Fig. 5 reflects the different sample densities; as expected, it is rather narrow in the south-central part where the highest concentration of research plots is found.

In view of the complexity of the model, the question could be raised whether the estimates are plausible. An informal way to evaluate the plausibility is to generate a set of diameter–height curves for locations located on the cross sections of Fig. 5 and to ask local experts whether a specific height curve is plausible in a particular location (Fig. 6).

Fig. 6
figure 6

Predicted height–diameter relationships on locations located on the northern cross sections (left) and southern cross section (right) of Fig. 5. Solid lines were initialized with a dg of 30 cm and dashed lines with a dg of 15 cm

Full size image

These results confirm empirical observations and local experience. Local experts could confirm the validity of the relationships for extreme sites in the northwest and southeast of the country. The poor sites in the northwest are characterized by shallow soils on limestone, known as “Loo” (Arcostaphylos/Calamagrostis/Sesleria) sites in Estonia. The fertile sites in the southeastern part of the country are known as “Jänesekapsa” (Oxalis-Rhodococcum) sites (Lõhmus 2004). A more formal procedure of evaluating the results is to calculate diagnostic plots as boxplots of residuals (observation-prediction) over classes of predicted heights. Since our model uses coordinates as predictors, a specific validation concerns the model predictions for different regions of Estonia. In doing so, the most important criterion is the average deviance between observations and predictions which should be approximately zero. However, when comparing the residual boxplots for cross sections of one degree longitude and latitude width (Gauss-Krüger), respectively, through Estonia and comparing combinations with a high number of observations only, in most cases a slight positive bias is obvious (Figs. 7, 8). Focussing on these combinations, it is also obvious, however, that none of them shows a serious bias.

Fig. 7
figure 7

Residuals (gam, Eq. 2b1) over predicted tree height classes on three east-westerly cross sections through Estonia. Cross section ‘north: 57.5’ comprises all tree heights with a northing coordinate of less or equal to 58. Cross section ‘north: 58.5’ refers to northing coordinates within [58,0001-59] and cross section ‘north: 59.5’ to northing coordinates of more than 59. The table gives the number of observations that belong to a certain height and coordinate class combination. The bias of the class is given in brackets

Full size image
Fig. 8
figure 8

Residuals (gam, Eq. 2b1) over predicted tree height classes on six cross sections that run from south to north through Estonia. Cross section ‘east: 23’ comprises all trees heights with an easting coordinate of less or equal to 23.5 and greater than 22.5, cross section ‘east: 24’ comprises all trees heights with an easting coordinate of less or equal to 24.5 and greater 23.5 and so on. The table gives the number of observations that belong to a certain height and coordinate class combination. The bias of the class is given in brackets

Full size image

When calculating the residual plots for different individual tree diameter and dg classes for the whole area of Estonia (Fig. 9), the slight bias is still obvious but smaller compared to the bias within classes of predicted heights in the different cross sections.

Fig. 9
figure 9

Residuals of the gam (Eq. 2b1) over diameter and dg classes for Estonia

Full size image

Mixed model

The coefficient α 0 of the fixed effect is approximately 1 and an additional (fixed) intercept was not significant, indicating that the prediction from the gam is an unbiased estimation for the expectation value of transformed heights (Eq. 2b2). All random effects are significantly different from zero (Table 2). The variation in the random effects on plot level is much higher than on measurement occasion level within plots. Thus, the variance of the intercepts on the measurement occasion level a ij is only about 10% of the variance of the plot level intercepts a i (Table 2). The variance of the random coefficients b ij is only about 3% of the variance of the plot level coefficients b i (Table 2). This result implies that the height–diameter curves within stands vary over time to a much lesser extent compared with the variation in the mean stand curves around the mean curve of Estonia. This data pattern is of considerable interest in forest management planning, since from only one measurement occasion the prediction accuracy for other points in time for the same plot can be significantly improved. However, the partition of the overall variation is only valid for short periods, since the observed time series cover on average only 6.8 years. Additionally, the number of remeasurements is relatively low since 90 plots have been measured three times, 208 plots have been measured two times, and 104 plots have been measured only once. During model selection, it became clear that the variance–covariance matrix on the measurement occasion level D2 can be parameterized as a diagonal positive-definite matrix, and the covariance need not to be estimated (Table 2). No cross-level correlations between the random effects on plot and measurement occasion level have been assumed. The positive parameter of the variance function indicates a slight heteroscedasticity while the variance is increasing with increasing height. The bias of the linear mixed model is considerably reduced when comparing it with the gam results (from 0.156 to 0.084 m), and the residual standard error decreases from 1.92 to 1.37 m.

Table 2 Statistical characteristics of the linear mixed model (Eq. 2b2)
Full size table

Discussion and conclusions

The presented model for Scots pine provides a first comprehensive basis for tree height estimation from measured diameters for the whole area of Estonia, based on the extensive database of the Estonian forest growth experiments. Like Mehtätalo (2004), we use dg instead of age (Lappi 1997; Eerikäinen 2003) to describe the longitudinal development of the height–diameter curves. Since the height–diameter relationship is modeled as a function of dg, the model can be used as a surrogate for a real height growth model also. This would require a combination with a diameter growth model. The advantage of this often-used approach is that tree height increments are not required for model parameterization. The linear mixed model used in our analysis shows some similarity with the approaches presented by Lappi (1997) and Mehtätalo (2004). However, there some differences. Firstly, Lappi and Mehtätalo use a reparameterized logarithmic height–diameter relationship (Korf-Function) where the parameters have some biological meaning and a somewhat lower correlation than the Näslund function. However, the Näslund function was already applied successfully in linear mixed models (Kangas and Maltamo 2002; Kinnunen et al. 2007). Lappi and Mehtätalo present generalized models that include different sets of predictor variables to describe the trends of the original parameters. They also include a mean tree diameter, as we have done, but additionally basal area. Mehtätalo (2004) also uses the north coordinate and a categorical variable to differentiate the site nutrient supply. The different sets of predictors should account for differences in the availability of information. However, their model variants that are predictor parsimonious are considerably less (spatially) flexible compared with our approach since the model effects are simple linear relationships. It can be assumed that their variants with several predictors are more flexible especially if the predictors are itself predictions from regionalization processes. But our model combines a high flexibility with parsimonious input information. In the future, additional predictors might be used in our model also, especially in view of improving the biological interpretability. However, it can be assumed due to unobserved influencing factors and limited regionalization processes that spatial trends still will be present in many databases. Hence, our methodology of estimating 2-dimensional surfaces for structured spatial trends will still be required for optimum estimation.

The approach by Nanos et al. (2004) shows a high spatial flexibility also. But their procedure does not separate between a structured (correlated) spatial effect and an unstructured (uncorrelated) spatial effect like we do. Our 2-step approach is a result of numerical problems, but theoretically the procedure employs a simultaneous estimation of 2-dimensional surfaces and (uncorrelated) random effects. In contrast, the 2-step approach employed by Nanos et al. (2004) is the result of the underlying methodology: The random effects of a nonlinear mixed model are predicted in a second step by applying geostatistical methods. Hence, several methodological aspects have to be discussed: (I) Is the geostatistical model flexible enough to account for the unstructured spatial trend also? In our model, this unstructured spatial trend is quantified by uncorrelated random effects. (II) In the geostatistical approach, the preceding (first step) estimation of random effects is employed without considering spatial correlation. Additionally, only one parameter is assumed to vary randomly, and it is not clear in which way the geostatistical approach could be extended to models with random variation of several parameters since the random effects are usually correlated. In our approach, this correlation is accounted for, because the two 2-dimensional surfaces are estimated simultaneously. (III) In practical applications, the approach of Nanos et al. (2004) employs two different models depending on whether height–diameter measurements are available or not. If prior information is available, the random effects are predicted via the mixed nonlinear model; otherwise, the random effects are estimated via the geostatistical approach. In our case, the fixed part of the model (Eq. 2b1) is already spatially explicit and is employed even if prior information is not available. If prior information is available, the calibration is based on the same model but the random part is employed also.

Because of the more complex specification of the 2-dimensional trend function within a gam, we had to apply a 2-step procedure by first fitting the gam and then using the prediction as ‘a priori information’ in a linear mixed model. This procedure might not be ideal, and further approaches like geoadditive models that estimate the structured spatial trend via a Gaussian Markov random field should be tested. However, the quantification of the spatial pattern of the height–diameter curve is a considerable advantage of the model and accounts already for the structured spatial effects. Additionally, further studies are required concerning the temporal autocorrelation of the random effects of different measurement occasions from the same plot. Until now, only a subsample of the database includes remeasurements, and the observed time series are rather short.

We recommend that the already excellent Forest Research Network database will be extended in the future or complemented with the dataset of the Estonian National Forest Inventory, especially with the aim of capturing areas with large dg’s and regions of Estonia that are sparsely covered with sample plots. A such extended database would possibly improve our model, e.g. removal of the unconstraint decrease of the height–diameter curve for dg larger 34 cm. As an alternative monotonicity constraints could be explicitly integrated in the model (Brezger and Steiner 2003).

If the spatial distribution of sample plots will be more regular, further investigation into the choice of the basis dimension of the 2-dimensional trend function could be conducted. Wood (2006) recommends to test informally by increasing the maximum basis dimension, if the chosen dimension is sufficient to represent the underlying data structure reasonably well. An indication for inadequate model flexibility would be an estimated basis dimension near the defined maximum. Given sufficient flexibility (i.e. the basis dimension is large enough), the degree of smoothing is almost exclusively governed by a “penalizing term”, which is controlled by a smoothing parameter. To determine the optimal smoothing parameter, extended generalized cross-validation techniques are applied which result in minimizing a generalized cross-validation score (GCV score; Wood 2006).

First attempts of increasing the basis dimension of the 2-dimensional smooth function resulted in a reduced bias. Increasing the dimension considerably from 29 to 225 resulted in a decrease of the overall height bias from 0.156 to 0.106 m. Further enlargement of the dimension had almost no effect on the bias reduction. However, this part of model selection needs to be supplemented by extensive cross-validation, especially due to the unbalanced spatial distribution of the experimental plots.