Introduction

Diameter and height of trees are some of the basic attributes in forest inventories. Because diameter at breast height (DBH) can be measured more easily and accurately than tree height, for a forest inventory, DBH is measured for all trees sampled, but height is measured only for a small number of trees. The measurements are then used in graphical or statistical models to describe the relationships between the two variables. Modeling the relationships between these variables allows for height estimations, which is an important variable for estimating the volume of single trees and the stand, developing single-tree increment models, acquiring information on stand structure and biomass, and estimating carbon sequestration without spending time and effort on height measurements (Curtis 1967; Parresol 1992; Van Laar and Akça 1997; Von Gadow and Hui 1999; Calama and Montero 2004; VanderSchaaf 2014; Ciceu et al 2020; Yang and Burkhart 2020).

The relationships between the DBH and total height of trees vary from stand to stand. The relationships may also differ depending on the changes in the stand over time. Trees of different ages and growing at different sites and densities have different height‒diameter (H‒D) relationships (Curtis 1967; Castedo et al. 2005). Because stand structures are not homogeneous in forest ecosystems, it is very difficult to explain H‒D relations with a single model. Therefore, generalized H‒D models (Lappi 1997; Mısır 2010; Özçelik and Çapar 2014; Ercanli 2015; Ercanli and Eyuboglu 2019) should be developed for each stand to reduce the variability in H‒D relationships (i.e., the change from stand to stand and change over time in the same stand) (Calama and Montero 2004; Özçelik and Çapar 2014). Including stand characteristics as independent variables in H‒D models may help to reduce this variability (Curtis 1967; López-Sánchez et al 2003; Sharma and Zhang 2004; Temesgen and Von Gadow 2004; Castedo et al. 2006).

Turkiye has several quite different climatic and topographical regions. Because tree species can often grow over large areas with quite different ecological conditions, it is of great importance to account for these differences in H‒D models aimed to provide a basis for ecologically based, functional planning studies.

Ecologically based models provide more reliable predictions for single trees and stands than do commonly used models that do not include ecological factors in the modeling stage (Klos et al 2007). Planning and management strategies made with reliable forecasts will obviously provide more acurate results. Ecological classification of natural environments is critical for revealing and focusing on the potential of natural resources such as forests to ensure the best use of these resources (Atalay 2014). Ecological classifications are based on various factors, such as climate, soil, topography, bedrock, and vegetation. The ecological subregions (ecoregions) set up by the classification form the basis for the development of ecoregion-based H‒D models. Because studies have revealed that growth rates differ among ecological regions, ecoregion-based studies are important for reliable prediction of growth-related characteristics (Pillsbury et al 1995; Huang 1999; Huang et al 2000; Álvarez González et al 2005; Özçelik et al 2014; Seki and Sakici 2022).

Mixed-effects models can offer an important perspective on the inclusion of sampling unit differences in models. Mixed-effects models are increasingly prominent in H‒D modeling due to their ability to incorporate tree H‒D variability from different subjects (e.g., forest type/sites, species, sample plots, clusters, and ecoregions in this study) (Chenge 2021). The introduction to the model of random parameters that are specific for each groups of sampling units enables the modeling of the variability determined for a given situation at different sites or locations after defining a common fixed functional structure (Lindstrom and Bates 1990).

In various studies that have developed ecoregion-based H‒D models (e.g., Huang et al 2000; Castedo et al. 2005; Seki and Sakici 2022), ecological differences were tested by using the dummy variable (indicator variable for ecoregions to indicate the absence or presence of some categorical effect) method. Calama and Montero (2004) and Adame et al (2008) also used a mixed-effects modeling approach with a dummy variable in testing ecological and regional differences. Wang et al (2008) used an empirical comparison of the two modeling approaches to dominant height modeling. Fu et al (2012) and Zeng (2015) investigated differences in aboveground biomass in terms of ecological region and origin, using a dummy variables and mixed-effects modeling approaches and tested the differences. They stated that the mixed-effects modeling approach was superior to the dummy variable method in terms of providing flexible estimations. Therefore, this method is important in testing ecoregional differences.

In this study, the effect of ecoregional differences on H‒D relationships was investigated using nonlinear mixed-effects modeling for Scots pine (Pinus sylvestris L.) stands in Turkiye. Scots pine stands have different characteristics in Turkiye depending on the climate, topography, soil, and bedrock. The border areas of the Kastamonu and Sinop regions, which are the subject of the present study, are very large, and the Scots pine stands in these regions grow in quite different conditions. Although Kastamonu and Sinop are important distribution areas of Scots pine stands, their H‒D relations have not been studied. To reveal the ecoregional differences affecting the H‒D relationships in the study area, we used the ecological classification developed by Atalay (2014) and developed ecoregion-based H‒D models.

Materials and methods

Study area

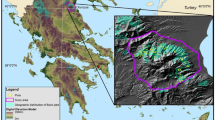
In the Kastamonu and Sinop regions of northwest Turkiye forested areas cover approximately 65% of the study area, and Scots pine stands are spread over an area of approximately 50,772 ha, which has varying ecological characteristics, stand densities, and ages (Fig. 1). According to data from the General Directorate of Meteorology, the average annual precipitation for Kastamonu and Sinop Province is 525.3 and 727.8 mm in 1991‒2020 period, respectively (URL-1, https://kastamonuobm.ogm.gov.tr/Sayfalar/Kurulusumuz/GenelBilgiler.aspx [accessed on 25.11.2021]; URL-2, https://www.mgm.gov.tr/veridegerlendirme/il-ve-ilceler-istatistik.aspx?k=H&m=KASTAMONU [accessed on 02.04.2024]).

Fig. 1
figure 1

Distribution of pure Scots pine stands and sample plots by ecoregion in the study area in Turkiye

Full size image

Ecoregions

According to Atalay (2014), the Kastamonu and Sinop regions are in the Black Sea Climate Region, which is divided into five subregions: Ecoregion 1 (E1), Humid Mild Broad Leaved Forest Subregion; Ecoregion 2 (E2), Black Sea Coastral Mountains Humid Cold Coniferous Forest Subregion; Ecoregion 3 (E3), Subhumid Cold Coniferous Forest Subregion of Backward Black Sea Plateau and Mountains; Ecoregion 4 (E4), Dry Forest Shrub Subregion of Backward Black Sea Region; Ecoregion 5 (E5), Mountain Grass Subregion.

Scots pine stands are concentrated in ecoregions E1, E2 and E3, ranked from highest to lowest distribution: E3 (36,286 ha), E1 (6646 ha), E2 (6323 ha). Scots pine stands in E4 and E5 are quite small. For these reasons, we studied the pure, productive Scots pine stands in E1, E2, and E3, where approximately 97% of the Scots pine stands are found.

Field measurements

Pure Scots pine stands in the study area were identified with the help of forest management plans and digital maps. The data were obtained from 292 sample plots randomly selected from Scots pine stands in managed forests; 68 of the plots were in E1, 73 in E2, and 151 in E3. The distribution of the sample plots in the study area and ecoregions is shown in Fig. 1.

The data used in the development of the models were obtained from temporary sample plots and sample trees. The size of sample plots were 800, 600 or 400 m2 in size for stands with 11%–40%, 41%–70% and more than 70% of crown closure, respectively. All trees with DBH of 8 cm and above in the sample plots were numbered. The diameters of all trees in the sample plots were then measured. Stand age was determined by counting the annual rings in increment cores from five or six representative trees. The heights of 9–10 trees with different diameters in each sample plot were also measured.

For developing an ecoregion-based H‒D model, the H‒D data (for 2831 sample trees) were randomly divided into model development data (2107, ~ 75%) and validation data (724, ~ 25%) for testing the developed models. Descriptive statistics of the data sets are shown in Table 1, and the H‒D distributions of these sample trees are shown in Fig. 2.

Table 1 Descriptive statistics for data sets for diameter (D) and height (H) of Scots pine trees in three ecoregions in Turkiye. N = number of sample trees
Full size table
Fig. 2
figure 2

Height and DBH for Scots pine trees used in model and validation data sets for the three ecoregions

Full size image

Data analyses

Regression modeling

When the H‒D data were represented graphically for ecoregions, H‒D relationships had nonlinear trends (Fig. 2); growth in height with respect to diameter increased rapidly at younger ages and slowed later (Lei and Parresol 2001).

The H‒D models were developed in two stages. In the first stage, 10 generalized H‒D equations, which are frequently used in the literature, were selected, and the model parameters were estimated using nonlinear regression analysis (Table 2). The nls function in the R version 4.0.5 (R Core Team 2021) was used to develop the base models. Different starting values for the parameters were used to find a global minimum.

Table 2 Model forms used for the development of H‒D models
Full size table

In the second stage, the nonlinear mixed-effects modeling approach was applied to the H‒D model that yielded the best results in terms of statistical criteria and parameter significance. A general expression for the nonlinear mixed-effects model can be written in vector form as follows (Lindstrom and Bates 1990; Pinheiro and Bates 1998):

$$y_{i} = f\left( {\phi_{i} ,x_{{\text{i}}} } \right) + e_{i} \;\;\;\;\;\;\;\;e_{i} \sim N\left( {0,R_{i} } \right)$$
(1)

where, yi is the (ni \(\times\) 1) vector of the observations from the ith sampling unit, f is a nonlinear function,\(\phi_{i}\) is a (r \(\times\) 1) parameter vector (where r is the number of parameters in the model), xi is the (ni \(\times\) 1) predictor vector of the observations from the ith sampling unit, ei is a (ni \(\times\) 1) vector of the residual terms and Ri is a (ni \(\times\) ni) positive variance–covariance matrix for the error term. The parameter vector \(\phi_{i}\) can then be broken down into fixed and random components. The fixed component is common to the population (i.e., all sample units), and the random part varies from unit to unit:

$$\phi_{i} = A_{i} \beta + B_{i} u_{i} \;\;\;\;\;\;u_{i} \sim N\left( {0,D} \right)$$
(2)

where, \(\beta\) is the (p \(\times\) 1) vector of fixed population parameters (where p is the number oxed parameters in the model), ui is the (q \(\times\) 1) vector of random effects associated with the ith unit (where q is the number of rand ps ithe model), which is assumed to follow a multivariate normal distribution with mean 0 and variance–covariance matrix and Ai and Bi are design matrices of size (r \(\times \hspace{0.17em}\)p) and (r \(\times\) q) for the fixed and random effects specific to each unit, respectively. Elements of these design matrices are usually 0 or 1, or the value of the covariates associated with the fixed or random effects. Details on nonlinear mixed effects modelling for H‒D relationships are provided by Calama and Montero (2004) and Castedo et al. (2006).

The ecological conditions in the three ecoregions could have an important effect on the H‒D relationships. Smaller differences in H‒D relationships are expected for trees within a given ecoregion because the growth trends of trees within the same ecoregion are likely more similar than for trees across multiple ecoregions covering larger areas. The difference in H‒D relations among ecoregions can be explained by nonlinear mixed-effects modeling. Kearsley et al (2017) assessed site-level variability by introducing site as random effects in a nonlinear mixed-effects model. Consequently, the nonlinear mixed-effects modeling approach is suitable to account for differences between groups and can reduce predicted bias (Timilsina and Staudhammer 2013; Lin et al 2022). Because nonlinear mixed-effects models allow for both fixed and random effects parameters, we tested the random effect by applying different combinations of random effects to the model parameters. In the nonlinear mixed-effects model, fixed-effects parameters were common for all ecoregions, while random-effects parameters were specific for each ecoregion (Pinheiro and Bates 2000). A key question when fitting mixed-effects models is selection of the parameters considered as fixed effects and those considered in defining random effects. Pinheiro and Bates (1998) suggest that all parameters in the model should first be considered mixed if convergence is possible. The best nonlinear mixed-effects model fit was selected based on the Akaike information criterion \(\left(\text{AIC}=-2\text{LL}+2p\right)\) and Bayesian information criterion \(\left(\text{BIC}=-2\text{LL}+p\text{log} N\right)\), N is the number of observations, LL is the log likelihood of the ftted model, p is the number of model parameters. These criteria were used to check whether random effects were significant (Timilsina and Staudhammer 2013). The R package nlme was used to develop the nonlinear mixed-effects models fit by maximum likelihood (Pinheiro et al. 2021; R Core Team 2021).

Testing ecoregional differences

The nonlinear sum of extra squares test, also known as the F-test, was used to determine whether there were differences between ecoregions in terms of H‒D relationships (Pillsbury et al 1995; Neter et al 1996):

$$F = \frac{{\left( {{\text{SSE}}_{{\text{R}}} - {\text{SSE}}_{{\text{F}}} } \right)/\left( {{\text{df}}_{{\text{R}}} - {\text{df}}_{{\text{F}}} } \right)}}{{\left( {{\text{SSE}}_{{\text{F}}} /{\text{df}}_{{\text{F}}} } \right)}}$$
(3)

where, \({\text{SSE}}_{\text{R}}\) and \({\text{SSE}}_{\text{F}}\) are the sum of squares of the error for the reduced and the full H‒D models, respectively, and \({\text{df}}_{\text{R}}\) and \({\text{df}}_{\text{F}}\) are the degrees of freedom for the reduced and the full H‒D models, respectively.

For the implementation of the F-test, the full and the reduced model structures were needed. While the model structure that uses the same parameter values for all ecoregions is called the reduced model, the model structure that uses different parameter values for each ecoregion is called the full model (Pillsbury et al 1995). Saunders and Wagner (2008), on the other hand, used log-likelihood ratio tests (LRT) for testing full and reduced models. Full model structures are usually presented using dummy variables. In a regression analysis, dummy variables are independent variables that take the value of either 0 or 1 to indicate the absence or the presence of some categorical effect. The dummy variables method is also frequently used in forestry (Fu et al 2012). However, in the present study, we used a new approach to develop the ecoregion-based generalized H‒D model and to test for ecoregional differences by using a nonlinear mixed-effects modeling approach to reveal the full model structures. We estimated the fixed parameters and variance components in the nonlinear mixed-effects model. Random effects for ecoregions can be calculated the R functions random.effects or nlmeStruct to obtain the full model structure to be used to test the differences between ecoregions (Pinheiro and Bates 2000; Mehtätalo 2013). In addition, ecoregional H‒D differences were also tested with the dummy variable model method, and the model results were compared with those of the nonlinear mixed-effects model. To obtain the full model structure using dummy variables, model parameter were assumed to vary according to ecoregions as explained by:

$$\alpha + \alpha_{{1}} Z_{{1}} + \alpha_{{2}} Z_{{2}}$$
(4)

where α refers to model parameters, αi refers to associated parameters and Zi refers to dummy variables. These variables are Z1 = 1 and Z2 = 0 for ecoregion E1; Z1 = 0 and Z2 = 1 for E2; Z1 = 0 and Z2 = 0 for E3. Additionally, the full model form for the best model is given in the Results section.

The F distribution was used to interpret the F-value for detecting ecological differences. We concluded that there were statistical differences between ecoregions when the P-value was less than 0.05 (Pillsbury et al 1995). If there are differences between ecoregions, the full model structures should be used instead of reduced models.

Evaluation and validation of the models

The model fitting quality of the H‒D models was compared with statistical evaluations. First, the parameter estimates of the models were made. The base models were evaluated generally on the basis of four statistical criteria, the AIC (described above), coefficient of determination (R2), root mean square error (RMSE), mean absolute bias (MAB) (Eqs. 5–7):

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {h_{i} - \hat{h}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {h_{i} - \overline{h}_{i} } \right)^{2} }}$$
(5)
$${\text{RMSE }} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {h_{i} - \hat{h}_{i} } \right)^{2} }}{n - p}}$$
(6)
$${\text{MAB }} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {\hat{h}_{i} - h_{i} } \right|}}{n}$$
(7)

where, \({h}_{i},\) \({\widehat{h}}_{i}\), \({\overline{h} }_{i}\) are the measured, estimated and average values of the dependent variable, respectively, n is the number of observations, and p is the number of model parameters.

Based on the statistical criteria provided by the above equations, the models with the highest coefficient of determination (R2) and the lowest error values (MAB, RMSE, AIC) were determined. The relative ranking suggested by Poudel and Cao (2013) was used to decide on the best model.

The best model was applied to validation data set to evaluate accuracy of the model, and a paired samples t-test was used to determine any significant differences between observed and predicted heights. We used this test for the evaluation because the group variances were homogeneous (with a significance level of α = 0.05) and the sample size of the groups was large enough and data were normally distributed. Additionally, the assumption of homoscedasticity and the normality of the residuals was checked by plotting the predicted height values versus the residuals.

Results

As a result of the significance of the parameters and relative ranking according to various statistical criteria, equations HD5, HD6, and HD9 were not included in the relative ranking because they had statistically insignificant parameter values. Although the parameters of the HD8 model were significant, this model was not included in the relative ranking because it had very low fit statistics. The equation that modeled the data set most successfully was the HD10 model (Richards 1959) modified by Sharma and Parton (2007), which had a relative ranking of 1.00. The R2 value for the HD10 model was 0.950, the RMSE was 1.227, the MAB was 0.913, and the AIC was 6854.870. The second place model was HD4 (Krumland and Wensel 1988), with a relative ranking of 1.08. The last model in terms of relative ranking of 6.00 was the HD1 model (Meyer 1940) (Tables 3 and 4).

Table 3 Parameter estimation values and statistical criteria for H‒D models
Full size table
Table 4 Relative ranking of H‒D models according to statistical criteria. The parameters of the HD8 model were significant, but the model was not included in the relative ranking because it has very low fit statistics
Full size table

The HD10 model, in which all parameters were significant and which had the best statistical criteria, was chosen for the development of a nonlinear mixed-effects H‒D model. In this context, various alternatives were tested for deciding on the combinations of fixed and random effects parameters for the model when using a nonlinear mixed-effects modeling approach. AIC and BIC were used to select the most appropriate combination.

All combinations of parameters a, b, c, d and e were tried in order to decide on the combinations of fixed and random effects parameters, and the combinations that reached the solution and had statistically significant parameter estimation values were subjected to relative ranking. As a result of the evaluations based on the AIC and BIC, the d parameter was better than the other combinations as a random effects parameter. The c and b random effects parameter options took second and third place, respectivelly. As a result, the nonlinear mixed-effects model structure of the HD10 model took the following form (Eq. 8):

$$H_{ij} = 1.3 + \left( {ah_{0i}^{b} } \right)\left\{ {1 - \exp \left[ { - c\left( {\frac{{N_{i} }}{{G_{i} }}} \right)^{{d + u_{1} }} DBH_{ij} } \right]} \right\}^{e} + \varepsilon_{ij}$$
(8)

where Hij, is height, DBHij is diameter at breast height, and εij is the error estimated by the model for the ith tree observation in the jth sample unit; a, b, c, d, and e are the fixed parameters of the model; and u1 is the random effects parameter with the variance (\({\sigma }_{{u}_{1}}^{2}\)) of the model related to the ecoregions; other abbreviations and symbols are the same as in Table 2. Parameter estimates for the nonlinear mixed-effects model are given in Table 5.

Table 5 Parameter estimates for the nonlinear mixed-effects HD10 model. R2, AIC and BIC criteria were given for the model. \({\sigma }_{{u}_{1}}^{2}\): variance of the random parameter. \({\sigma }^{2}\): residual variance
Full size table

To investigate whether there were significant differences between ecoregions in terms of H‒D relationships for pure Scots pine stands in the Kastamonu and Sinop regions, we estimated parameter d for three different ecoregions using the nlmeStruct and random.effects functions. The full model structure to be used to test the differences was obtained. As a result of the analysis, parameter d was 0.2163 for E1, 0.2494 for E2, and 0.2450 for E3. Other parameters had the same values for all three ecoregions.

After developing the nonlinear mixed-effects H‒D models and estimating the d parameters for ecoregions, we calculated the F-values to test for differences between ecoregions (Table 6). E1 differed significantly from other ecoregions in terms of H‒D relationships (P < 0.001), but E2 and E3 did not differ significantly. According to the results, there was a significant difference between ecoregions in general, and therefore, it was appropriate to use an ecoregion-based nonlinear mixed-effects H‒D model with different parameters for each ecoregion.

Table 6 F-test results calculated for HD10 model. The sum of squares of the error (SSE), df, F, and P for Reduced Model and Full Model are given to test the differences between ecoregions
Full size table

Based on the results, the ecoregion-based form of the HD10 model could be written as follows:

Ecoregion 1

$$H = 1.3 + \left( {0.9544h_{0}^{1.0173} } \right)\left\{ {1 - \exp \left[ { - 0.0191\left( \frac{N}{G} \right)^{0.2163} {\text{DBH}}} \right]} \right\}^{0.3133}$$
(9)

Ecoregion 2

$$H = 1.3 + \left( {0.9544h_{0}^{1.0173} } \right)\left\{ {1 - \exp \left[ { - 0.0191\left( \frac{N}{G} \right)^{0.2494} {\text{DBH}}} \right]} \right\}^{0.3133}$$
(10)

Ecoregion 3

$$H = 1.3 + \left( {0.9544h_{0}^{1.0173} } \right)\left\{ {1 - \exp \left[ { - 0.0191\left( \frac{N}{G} \right)^{0.2450} {\text{DBH}}} \right]} \right\}^{0.3133}$$
(11)

To evaluate the results, tree heights in the validation data set for a specific ecoregion were calculated with the help of the reduced H‒D model and the ecoregion-based nonlinear mixed-effects H‒D model for three ecoregions; error percentages were also calculated (Table 7).

Table 7 Prediction bias of inappropriate use of H‒D models. The reduced model refers to the base HD10 model. Full E1, Full E2 and Full E3 refers to Eq. 9, Eq. 10 and Eq. 11, respectively
Full size table

The HD10 model was used to predict heights of trees for the independent data group reserved for model control. The observed and predicted height values of the trees in validation data sets were compared using a paired samples t-test because the group variances were homogeneous (Levene’s test with F = 0.480, P = 0.489) and the sample size of the groups were large enough and normally distributed (Kolmogorov–Smirnov with P > 0.05). Consequently, we determined that the observed and predicted height values were not significantly different (paired sample t-test with t = –0.431, P = 0.667).

The assumption of homogeneous variance was examined visually by plotting residuals (the differences between observed and predicted heights) versus predicted height values obtained with nonlinear mixed-effects models (Eqs. 9–11), using the validation data (Fig. 3). These models also had an approximately homogeneous variance over the full range of the predicted height values, as well as no systematic pattern in the variation of the residuals. It was also understood that the height values observed and predicted by the HD10 model were close to each other. Another way to evaluate the nonlinear mixed-effects models is to look at the graphics of the normal probability plots of the residuals. The normal probability plots of the residuals do not indicate any serious violation of the assumption of normality for the nonlinear mixed-effects models (Fig. 4).

Fig. 3
figure 3

Plots of predicted vs. observed heights (top) and predicted heights vs. residuals (low) for ecoregions. In the data interval, there is no systematic pattern in the variability of residuals

Full size image
Fig. 4
figure 4

Plots of residuals for nonlinear mixed-effects model

Full size image

Parameter estimates of the dummy variable model, which is another preferred method for revealing ecoregional differences, are given in Table 8. For HD10, only parameter d was assumed to vary between ecoregions because it was found to represent the variation between subjects. The fit statistics for the ecoregion-based nonlinear mixed-effects model and dummy variable model are also given in Table 9. The fit statistics of the two models can be seen to be quite close to each other. Using the dummy variable approach, the full model of the H‒D equation can be written as:

$$H = 1.3 + \left( {ah_{0}^{b} } \right)\left\{ {1 - \exp \left[ { - c\left( \frac{N}{G} \right)^{{\left( {d + d_{1} Z_{1} + d_{2} Z_{2} } \right)}} {\text{DBH}}} \right]} \right\}^{{\text{e}}}$$
(12)
Table 8 Parameter estimates for the dummy variable model (HD10)
Full size table
Table 9 Fit statistics for the ecoregion-based nonlinear mixed-effects model and dummy variables model
Full size table

For the validation data set, the observed height values and the height values predicted from nonlinear mixed-effecs model and dummy variable model were examined (Fig. 5). In Fig. 5, the height values predicted from these two models are very close to the observed height values.

Fig. 5
figure 5

Observed heights and predicted heights from models according to ecoregions

Full size image

Discussion

The 10 H‒D models in which all of the parameters were statistically significant were evaluated based on R2, RMSE, MAB, and AIC, and the model that achieved the most satisfactory results was Richards (1959) modified by Sharma and Parton (2007) with a relative ranking of 1.00. The independent variables of the model (HD10), DBH, dominant height, number of trees, and basal area, explained 95% of the variance in H‒D relationships.

A nonlinear mixed-effects modeling approach was applied to the HD10 model to construct full model to test ecoregional differences in H‒D relationships. The fact that parameter d in the ecoregion-based nonlinear mixed-effects H‒D model had a random effect reveal the effects of the N (tree/ha) and G (m2/ha) in stand characteristics on the H‒D relationships. N and G are an indicator of the stand density. Stand density is an obvious factor affecting the H‒D relationship in a stand (Zeide and VanderSchaaf 2002); that is, trees of the same diameter are usually taller in denser stands (Corral-Rivas et al 2014). Thus, stand density had a significant effect on H‒D relationships. The main reason for ecoregional differences was not only stand density, but also a combination of climatic, edaphic and topographic factors.

The F-test results revealed that ecoregions E2 and E3 were similar, while E1 was different (Table 6). The signifcant differences are understandable, because E1 is coastal and E2 and E3 are inland ecoregions. Based on this result, the two similar ecoregions can be combined as one or the models for E2 and E3 can be used reliably for height predictions for trees in these ecoregions.

Statistical tests showed that there were significant differences in H‒D relationships between ecoregions. As stated by Atalay (2014), differences in physiographic, edaphic and climatic features cause differences in H‒D between ecoregions. Similar results were also obtained in studies by Huang (1999), Huang et al (2000), Zhang et al (2002), Calama and Montero (2004), Peng et al (2004), Brooks and Wiant (2005), Özçelik et al (2014) and Seki and Sakici (2022), and ecological differences were revealed with the dummy variable approach. Calama and Montero (2004) and Adame et al (2008) also used the mixed-effects modeling approach with a dummy variable in testing regional differences. While the first found significant differences in H‒D relationships, the second did not.

In this study, a nonlinear mixed-effects approach was used to develop ecoregion-based H‒D models. The model fits developed with this approach were satisfactory. At the same time, ecoregion-based H‒D models were also fitted using the dummy variable modeling approach. The prediction results for the two modeling approaches were quite similar. Overall, negligible differences were observed between ecoregion-based nonlinear mixed-effects and dummy variables models, which was expected because in the case of the large sample size, the results of the two modelling approaches did not differ significantly (Fu et al 2012; Zeng 2015; Magalhães 2017). For this reason, both approaches will provide similar results in revealing ecoregional differences. Additionally, Wang et al (2008) found that in terms of height growth description, the dummy modeling approach was preferred, but in terms of height prediction, the mixed-effects modeling approach was more appropriate. Fu et al (2012) stated that, generally speaking, the mixed-effects models is more flexible and applicable. Based on these results, we find it appropriate to propose the mixed-effects modeling for developing ecoregion-based H‒D models.

Improper application of an H‒D model in these ecoregions may cause prediction errors (Pillsbury et al 1995; Huang et al 2000; Peng et al 2004). Table 7 shows that the error percentages (as absolute values) in the height estimations made using the reduced model were 1.85% for E1, 1.16% for E2, and 0.57% for E3. The reduced H‒D model overestimated E1 and underestimated E2 and E3. The lowest value in terms of estimation error was seen in E3. If the models developed for E1, E2, and E3 are used in the relevant ecoregion, the error percentage values (as absolute values) are 0.86, 0.72, and 0.46%, respectively. It can be seen that the amount of error increases when the models developed for each ecoregion are used in different ecoregions. Heights of trees in E1 were estimated using models for other ecoregions, and error percentages (absolute) were calculated as 2.29% for the model for E2 and 2.10% for the model for E3. Estimating height without considering ecological differences can lead to biased results (Huang et al 2000; Zhang et al 2002; Peng et al 2004), especially for models that are associated with a high number of errors as a result of their use in unsuitable ecological regions.

Ecological factors have a significant effect on both H‒D and growth models, so including them in the models contributes significantly to their predictive ability and reduces estimation errors. However, including the factors in the models makes the model structure complex and is not practical for practitioners; thus, it may be more appropriate to consider the ecological classifications created by accounting for various ecological factors in further H‒D and growth modeling studies. The Kastamonu and Sinop provinces cover large areas, and therefore, the Scots pine stands in our study developed in quite different ecological conditions. Hence, the models were developed based on an ecological classification.

Conclusion

The models fitted for the study provided reliable estimates for the regions and species from which the data were obtained. In addition, the use of ecoregion-based H‒D models in the appropriate ecoregions was very important for achieving reliable predictions with small prediction errors.

In developing ecoregion-based models that are sensitive to ecological differences, it may be preferable to use one of the mixed-effects modeling approaches and dummy variable approaches. The evaluations in this study revealed that these two approaches gave similar results to each other. However, the study revealed that developing full model structures that allow testing ecoregional differences with a mixed-effect modeling approach is a more practical option.