Introduction

Ionospheric modeling is an important issue in many real-time GNSS applications. Reliable and fast knowledge about ionospheric variations becomes increasingly important. GNSS users of single-frequency receivers and satellite navigation systems need accurate corrections to remove signal degradation caused by the ionosphere. Ionospheric modeling using signal-processing techniques is the subject of discussion in the present contribution. Long-term ionospheric prediction is in progress for future work.

Variations of the ionosphere can be classified as regular and irregular. Regular variations occur more or less in cycles and therefore can be modeled in advance with reasonable accuracy. Irregular variations, which are mainly due to abnormal solar behavior such as sudden changes in solar radiation, cannot be predicted in advance. Examples of regular variations are diurnal, annual, and solar cycle variations (Jain et al. 1996). Possible modulations of the diurnal signal with other frequencies are also identified as regular variations. In this case, the amplitude of the daily signal changes from one season to another. A mathematical foundation is developed to detect and model such occurrences.

Since the existence of the ionosphere is due to solar radiation, the relative location of the earth with respect to the sun is responsible for a large part of the ionospheric variations. The daily earth rotation changes the solar zenith angle, which describes a large part of the daily ionospheric variations. The principal diurnal (24 h) component of the daily signal and its higher harmonics (24/n hours, n > 1) are due to the day–night variation of the ionosphere and hence of the total electron contents (TEC) values.

The solar zenith angle has also an annual period. Seasonal variations are the result of the earth’s revolution as the sun moves from one hemisphere to the other. Therefore, regular daily variations of the ionosphere contain a seasonal signature. Parts of these variations are known as anomalies. For example, the ionization density of the layers is greatest during the summer. The F2 layer, however, does not follow this pattern; its ionization is greatest in winter and least in summer. As a result, operating frequencies for F2 layer propagation are higher in the winter than in the summer. This is known as winter anomaly (Jones et al. 1959).

There exist other anomalies that can be related to the regular modulated variations of the ionosphere. The semiannual anomaly is caused because NmF2 is greater at equinoxes than at either solstice (Torr and Torr 1973). The evening anomaly explains that midlatitude summer NmF2 attains its highest values several hours beyond midday (Papagiannis and Mullaney 1971). This is in connection with the daytime double maxima (Pi et al. 1993), which explains that twin peaks in the ionospheric TEC at middle and lower latitudes are due to substorm signatures in both auroral electrojet and ring current variations. There exists another double maxima phenomenon on the latitude profile near the maximum ionospheric effect (latitude profile at zero longitude in the sun-fixed frame) that is due to equatorial anomaly (Anderson 1973; Oliveira and Walter 2005).

Sunspots are partly responsible for variations in the ionization level of the ionosphere. A regular solar cycle variation of sunspot activity has a minimum and maximum level and occurs approximately every 11 years. The sunspot distribution at the solar surface is not homogeneous. Solar rotation with an approximate period of 27 days is also reflected in sunspot numbers (Le Mouël et al. 2007). The number of sunspots at any given time continually changes as some disappear and new ones emerge.

Because the TEC values show cyclic variations for their regular part, they can be modeled by a series of periodic functions such as sinusoidal functions. We apply the least-squares harmonic estimation (LS-HE), developed by Amiri-Simkooei (2007), to the TEC values derived from ionospheric models. Modulated and multivariate formulations of the LS-HE will be developed. The formulation used is aimed to detect, elaborate, and hence, model parts of the regular modulated variations of the ionosphere. The time series in our analysis consists of 12 years of bihourly TEC values provided by IGS analysis centers.

We first introduce a mathematical foundation for the harmonic estimation where multivariate time series and/or modulated signals are involved. Compared with previous studies, (Zhao et al. 2007; Unnikrishana et al. 2002), we consider a more advanced model that includes not only the pure sinusoidal signals but also a few modulated ones. Then, the numerical results based on the application of the proposed method to the TEC time series are presented. We aim to find the principal pure and modulated frequencies present in the TEC time series. Based on the new model and the preliminary results obtained, a few observations regarding the modulated part of the TEC behavior are presented. Finally, we summarize and conclude the study.

Least-squares harmonic estimation (LS-HE)

The least-squares harmonic estimation (LS-HE) was introduced and applied to GPS position time series by Amiri-Simkooei (2007) and Amiri-Simkooei et al. (2007). The method improves the functional part of the model by identifying and including harmonic functions to the model. Consider the following linear model of observation equations,

$$ E(y) = Ax,D(y) = Q_{y} $$
(1)

where A is the m × n design matrix, Q y is the m × m covariance matrix of the m-vector of observables y, x is the n-vector of unknown parameters, and E and D are the expectation and dispersion (or covariance) operators, respectively. The linear model needs to be improved by identifying some periodic patterns in the series. Such periodic patterns are expressed as a series of sinusoidal signals in LS-HE.

The harmonic estimation (HE) is used to find any potential periodicities in the non-equally spaced TEC time series provided by different analysis centers. There are periodic components to the solar variations, the principal one being the 11-year sunspot cycles, also called the solar cycle. The TEC values exhibit this period. Other significant signals that are supposed to be detectable by HE are the diurnal and annual signals, along with their higher-order harmonics. In this section, we introduce different aspects of the LS-HE.

To increase the detection power of the signals, we derive the formulation of the harmonic estimation for a multivariate linear model. The goal is to detect common-mode signals that are assumed to be present in different TEC time series. It is then applied to a set of TEC time series given at different latitudes. Another aspect of HE is the use of modulated sinusoidal signals rather than the pure sine functions to express parts of the regular variations of the ionosphere. This leads us to the modulated LS-HE.

As a generalized form of the Fourier spectral analysis, LS-HE is limited neither to evenly spaced data nor to integer frequencies. As a special case, in the sequel, our formulation will be considerably simplified for a zero-mean stationary random process. If, in addition, the noise of the random process is only white, we may write Q y  = I, which further simplifies the formulations. The simplified formulations will be provided for these special cases.

Univariate harmonic estimation

The harmonic estimation (HE) is used to identify unmodeled periodic effects in the functional model. The simplest structure of the series may take into account an individual trigonometric term \( y(t) = a_{k}^{1} \cos \omega_{k} t + a_{k}^{2} \sin \omega_{k} t, \) which is a sinusoidal wave with an initial phase. One then has to extend the functional part Ax of the model to

$$ E(y) = Ax + A_{k} x_{k} , \, D(y) = Q_{y} $$
(2)

where the matrix A k consists of two columns corresponding to frequency ω k of the sinusoidal function

$$ A_{k} = \left[ {\begin{array}{*{20}c} {\cos \omega_{k} t_{1} } & {\sin \omega_{k} t_{1} } \\ {\cos \omega_{k} t_{2} } & {\sin \omega_{k} t_{2} } \\ \vdots & \vdots \\ {\cos \omega_{k} t_{m} } & {\sin \omega_{k} t_{m} } \\ \end{array} } \right],\quad x_{k} = \left[ {\begin{array}{*{20}c} {a_{k}^{1} } \\ {a_{k}^{2} } \\ \end{array} } \right] $$
(3)

with \( a_{k}^{1} ,a_{k}^{2} \) and ω k being unknown real numbers. The unknown frequency ω k in (2) is identified using HE. For this purpose, the following null and alternative hypotheses are put forward: H 0: E(y) = Ax versus H a : E(y) = Ax + A k x k . This means that under the null hypothesis the periodic effect is absent, while under the alternative hypothesis it is present. The identification of the frequency ω k is completed through the following maximization problem (Amiri-Simkooei et al. 2007):

$$ \omega_{k} = \arg \mathop {\max }\limits_{{\omega_{j} }} P(\omega_{j} ) $$
(4)

where

$$ P(\omega_{j} ) = \hat{e}_{0}^{T} Q_{y}^{ - 1} A_{j} (A_{j}^{T} Q_{y}^{ - 1} P_{A}^{ \bot } A_{j} )^{ - 1} A_{j}^{T} Q_{y}^{ - 1} \hat{e}_{0} $$
(5)

with \( \hat{e}_{0} = P_{A}^{ \bot } y \) the least-squares residuals and \( P_{A}^{ \bot } = I - A(A^{T} Q_{y}^{ - 1} A)A^{T} Q_{y}^{ - 1} \) an orthogonal projector (both are given under the null hypothesis). The matrix A j has the same structure as A k in (3) in which ω j replaces ω k ; the one that maximizes P(ω j ) is set to be A k . Analytical evaluation of this maximization problem is complicated due to the existence of many local maxima. One may apply the global optimization methods such as those presented in Xu (2002). In practice, it is more convenient to be satisfied with numerical evaluation of the maximization, which provides us with the full spectrum. A plot of the spectral values P(ω j ) versus a set of discrete values for ω j is used to investigate the contribution of different frequencies in the construction of the original time series y. We, therefore, compute the spectral values P(ω j ) for discrete frequencies ω j , sampled according to Amiri-Simkooei and Tiberius (2007) and take the one that maximizes P(ω j ). This is considered to be ω k from which the matrix A k is constructed using (3).

After the detection of ω k , one has to test H 0 against H a to see whether the spectrum at this frequency is indeed significant. The following test statistic is used:

$$ T_{2} = \hat{e}_{0}^{T} Q_{y}^{ - 1} A_{k} (A_{k}^{T} Q_{y}^{ - 1} P_{A}^{ \bot } A_{k} )^{ - 1} A_{k}^{T} Q_{y}^{ - 1} \hat{e}_{0} $$
(6)

If Q y is known, this test statistic has a central chi-square distribution with two degrees of freedom under H 0, i.e., T 2 ~ χ2(2,0) (Teunissen 2000). If the covariance matrix is of the form Q y  = σ2 Q, with σ2 denoting the unknown variance of unit weight, the test statistic as well as its distribution will be modified (Amiri-Simkooei 2007). If the null hypothesis is rejected, we may perform the same procedure for finding yet other frequencies.

In the study by Vaníček (1971), Lomb (1976), Scargle (1982, 1989, 1997), and Kay (1999), some forms of Fourier transform and power spectrum methods applicable for unevenly spaced data series are presented. With LS-HE presented in this contribution, we may in addition include the following terms in the analysis: 1) the linear trend A x, as a deterministic part of the model, and the covariance matrix Q y , as a stochastic part of the model. Also, multivariate and modulated LS-HE are presented, which are the unique features of this method.

For a zero-mean stationary random process, the preceding formulation of the spectral values P(ω j ) can be simplified. In this case, we have A = 0 and hence \( P_{A}^{ \bot } = I \). Further simplification is possible in case that the random process contains only white noise (Q y  = I). Equation (5) then simplifies to

$$ P(\omega_{j} ) = \hat{e}_{0}^{T} A_{j} (A_{j}^{T} A_{j} )^{ - 1} A_{j}^{T} \hat{e}_{0} $$
(7)

This spectrum is identical to the least-squares spectral analysis (LSSA) method developed by Vaníček (1971), Lomb (1976), and Scargle (1982). For some applications of LSSA, we may refer to the study by (Craymer 1998; Abbasi 1999; Asgari and Harmel 2005).

Multivariate harmonic estimation

If in a linear model, there exist several (r) time series, i.e., observation vectors with identical design matrix A and covariance matrix Q y , the model is referred to as a multivariate linear model (Amiri-Simkooei 2007; 2009). We may for instance think of the TEC time series at different latitudes. For a multivariate model, equation (1) is generalized to

$$ {\text{E}}({\text{vec}}(Y)) = (I_{r} \otimes A){\text{vec}}(X) + (I_{r} \otimes A_{k} ){\text{vec}}(X_{k} ) $$
(8)

with the multivariate covariance matrix

$$ {\text{D}}({\text{vec}}(Y)) = \Upsigma \otimes Q $$
(9)

where vec is the vector operator and ⊗ is the Kronecker product, which is an operation on two matrices of arbitrary size resulting in a block matrix. For the properties of the vector operator and the Kronecker product, we refer to the study by Magnus (1988) and Amiri-Simkooei (2007). The structure introduced in I r  ⊗ A k indicates that there exists a common periodic signal in all of the series, which needs to be detected using the harmonic estimation method. The amplitude and phase of the common sinusoidal signal are allowed to vary among different series. The m × r matrix Y = [y 1 y 2…y r ] collects observations from the r series, as do the n × r matrices X = [x 1 x 2…x r ] and X k  = [x 1k x 2k …x rk ] for the unknowns. In general, the full structure of the r × r matrix Σ and some unknowns of the m × m matrix Q can be estimated using a multivariate analysis method (see Amiri-Simkooei 2009).

For obtaining the power spectrum of the multivariate model, one needs to substitute the terms in (2) from the multivariate model as follows: \( I \otimes A \to A \), \( I \otimes A_{j} \to A_{j} \), \( \Upsigma \otimes Q \to Q_{y} \), \( {\text{vec}}(\hat{E}) \to \hat{e} \). One then obtains

$$ \omega_{k} = \arg \mathop {\max }\limits_{{\omega_{j} }} P(\omega_{j} ) $$
(10)

where

$$ P(\omega_{j} ) = tr(\hat{E}^{T} Q_{{}}^{ - 1} A_{j} (A_{j}^{T} Q_{{}}^{ - 1} P_{A}^{ \bot } A_{j} )^{ - 1} A_{j}^{T} Q_{{}}^{ - 1} \hat{E}\Upsigma^{ - 1} ) $$
(11)

with \( \hat{E} = P_{A}^{ \bot } Y, \) the least-squares residuals of r groups and \( P_{A}^{ \bot } = I - A(A^{T} Q^{ - 1} A)^{ - 1} A^{T} Q^{ - 1} , \) the orthogonal projector of the univariate model. The power spectrum given in (11) is referred to as multivariate power spectrum, which simultaneously uses all time series and takes into account the cross-correlation through Σ and time correlation through Q in an optimal least-squares sense. We estimate Σ as \( \hat{\Upsigma } = \hat{E}^{T} Q^{ - 1} \hat{E}/(m - n) \) (Amiri-Simkooei 2009). To test the significance of the detected signal, the following test statistic

$$ T = {\text{tr}}(\hat{E}^{T} Q^{ - 1} A_{k} (A_{k}^{T} Q^{ - 1} P_{A}^{ \bot } A_{k} )^{ - 1} A_{k}^{T} Q^{ - 1} \hat{E}\Upsigma^{ - 1} ) $$
(12)

is used, which under the null hypothesis is distributed as a central chi-square distribution with 2r degrees of freedom, i.e., \( T \sim \chi^{2} (2r,0) \) provided that both Σ and Q are known and that the original observables are normally distributed.

A special case of the multivariate model occurs when the time series y i are zero-mean series, which gives A = 0, and therefore, \( P_{A}^{ \bot } = I \). Further simplification is achieved by choosing \( \Upsigma = {\text{diag}}(\sigma_{11} ,\sigma_{22} , \ldots ,\sigma_{rr} ) \) when the series are uncorrelated, and taking Q = I m when the noise of the series is white. In this case, the power spectrum simplifies to

$$ P(\omega_{j} ) = \sum\limits_{i = 1}^{r} {\hat{e}_{i}^{T} A_{j} (A_{j}^{T} A_{j} )^{ - 1} A_{j}^{T} \hat{e}_{i} /\sigma_{ii} } , $$
(13)

which is the weighted stacked power spectrum of the individual power spectra. This power spectrum has been used in the study by Amiri-Simkooei et al. (2007) and Ray et al. (2008) for the detection of the common-mode signals in multivariate GPS position time series. Note that the aforementioned assumptions are hardly valid, as the GPS position time series are spatially and temporally correlated. This also holds for the time series of TEC provided by the analysis centers.

Modulated harmonic estimation

In its basic form, amplitude modulation consists of the signal \( y(t) = A(t)\sin (\omega t + \varphi ) \), in which the amplitude A(t) of the signal is a function of time. When A(t) is also a sinusoidal wave, amplitude modulation produces a signal with power concentrated at the carrier frequency and in two adjacent sidebands, which is called double-sideband amplitude modulation. Therefore, the modulated signal has three components, the original wave and two sinusoidal waves whose frequencies are slightly above and below the original frequency.

To understand how the harmonic estimation method works for such modulated signals, consider that the amplitude modulation is created by forming the following product: \( y(t) = (A + M\sin (\omega_{1} t + \varphi_{1} ))\sin (\omega_{2} t + \varphi_{2} ) \). This can, for instance, be due to the diurnal signal with frequency ω2 modulated with the annual signal with frequency ω1, i.e., the amplitude of the diurnal signal changes periodically over one year.

One can show that the frequency spectrum of this expression consists of 3 components at frequencies ω2, ω2 + ω1, and ω2 − ω1. These two sinusoidal components at the sum and difference frequencies of the modulator and original signal are called sidebands of the original signal. The choice A = 0 eliminates the carrier component, but leaves the sidebands. The modulated part of y(t), namely \( y(t) = M\sin (\omega_{1} t + \varphi_{1} )\sin (\omega_{2} t + \varphi_{2} ), \) can be trigonometrically manipulated into the following equivalent form:

$$ y = B_{k} \sin (\omega_{k}^{s} t + \varphi_{2} + \varphi_{1} ) + B_{k} \sin (\omega_{k}^{d} t + \varphi_{2} - \varphi_{1} ) $$
(14)

or

$$ y = b_{k}^{1} \cos \omega_{k}^{s} t + b_{k}^{2} \sin \omega_{k}^{s} t + b_{k}^{3} \cos \omega_{k}^{d} t + b_{k}^{4} \sin \omega_{k}^{d} t $$
(15)

where \( \omega_{k}^{s} = \omega_{2} + \omega_{1} \) and \( \omega_{k}^{d} = \omega_{2} - \omega_{1} \). The amplitudes of the trigonometric terms have the following relation: \( B_{k} = \sqrt {(b_{k}^{1} )^{2} + (b_{k}^{2} )^{2} } = \sqrt {(b_{k}^{3} )^{2} + (b_{k}^{4} )^{2} } \). This relation indicates that there exist only 3 independent unknown coefficients in (15). In the subsequent analysis, it is assumed that all coefficients in (15) are unknown. This is allowed since overparameterization in the functional model in general does not introduce biases provided that the observations contain respective information that allow estimation of all parameters and that the remaining redundancy is large enough to obtain sufficiently precise estimates for the parameters. This holds for time series analysis as we usually have m ≫ n in (1).

For the modulated signal, the extended functional part of the model E(y) = Ax + A k x k has the following form for A k :

$$ A_{k} = \left[ {\begin{array}{*{20}c} {\cos \omega_{k}^{s} t_{1} } & {\sin \omega_{k}^{s} t_{1} } \\ {\cos \omega_{k}^{s} t_{2} } & {\sin \omega_{k}^{s} t_{2} } \\ \vdots & \vdots \\ {\cos \omega_{k}^{s} t_{m} } & {\sin \omega_{k}^{s} t_{m} } \\ \end{array} \, \begin{array}{*{20}c} {\cos \omega_{k}^{d} t_{1} } & {\sin \omega_{k}^{d} t_{1} } \\ {\cos \omega_{k}^{d} t_{2} } & {\sin \omega_{k}^{d} t_{2} } \\ \vdots & \vdots \\ {\cos \omega_{k}^{d} t_{m} } & {\sin \omega_{k}^{d} t_{m} } \\ \end{array} } \right],\quad x_{k} = \left[ {\begin{array}{*{20}c} {b_{k}^{1} } \\ \begin{gathered} b_{k}^{2} \hfill \\ b_{k}^{3} \hfill \\ b_{k}^{4} \hfill \\ \end{gathered} \\ \end{array} } \right] $$
(16)

Having A j based on the preceding equation (replace ω k with ω j ), equation (5) can be used to obtain the modulated spectrum. Also, in case of r time series, equation (11) can be used to obtain the multivariate modulated spectrum. For the modulated spectrum, the test statistics in (6) and (12), with A k taken from (16), has now a central chi-square distribution with 4 and 4r degrees of freedom, respectively, i.e., \( T_{2} \sim \chi^{2} (4,0) \) and \( T_{2} \sim \chi^{2} (4r,0) \).

Finally, a practical comment on the implementation of the modulated harmonic estimation is in order. Because the search space is two dimensional over ω1 and ω2, the method could be time-consuming. This indicates that for a given ω1, a full search for the ω2 is required. Since the number of candidates to be searched for either of the frequencies is large, two-dimensional searches become inefficient. It is, therefore, suggested to hold one of the frequencies to an expected value, which for instance is given from the univariate harmonic analysis and search for the other frequency. As example, ω2 can be equated to the suspected diurnal frequency or its higher harmonics in order to find the modulation with other frequencies such as the annual signal.

Results and discussions

The data used in this study are the global TEC time series provided by the international GNSS service (IGS) product centers. The data can be downloaded from ftp://cddis.gsfc.nasa.gov/gps/products/ionex/. The daily files include 12 bihourly VTEC maps starting at 1:00 UT, or more recent containing 13 maps starting at 0:00 UT. Such bihourly maps are expressed in an earth-fixed frame. The geographic longitude and latitude, respectively, range from −180° to 180° (5° resolution) and from −87.5° to 87.5° (2.5° resolution).

Different data sets were extracted and analyzed from these analysis centers. The results presented in this study use data from the JPL analysis center, due to the relative completeness of its data sets. The latitude cross section with the fixed longitude λ = 0° (Greenwich meridian) will be analyzed. The TEC values were extracted on the equator and on every latitude increments of ±5°, from −80° to +80°. This makes 33 bihourly time series of TEC values. The series are non-equally spaced and cover 12 years from 1998 to 2009. The temporal and spatial variations of ionosphere are of particular interest in this study and will be explored with the methodology developed in the previous section.

Harmonic analysis

The least-squares harmonic estimation (LS-HE) method developed in the previous section is now applied. The numerical search for the discrete frequencies is applied to (5) and (11) for the univariate, multivariate, and modulated spectra. The step size used for the sampled periods T j  = 2π/ω j is small at high frequencies and gets larger at lower frequencies. The following recursive relation (Amiri-Simkooei and Tiberius 2007) is used, \( T_{j + 1} = T_{j} \left( {1 + \alpha T_{j} /T} \right),\, \) \( \alpha = 0.1,\quad j = 1,2, \ldots \) and a starting frequency of \( \omega_{1} = 2\pi /T_{1} ,{\text{ with }}T_{1} = 4\, \)hours (Nyquist frequency). The letter T is being the total time span of 12 years. For this time series, the lowest frequency checked in the analysis is ω min = 2π/T, i.e., one cycle over the total time span.

Regular periodic signals

The method is applied to the multivariate TEC time series, consisting of 33 separate series, to obtain the least-squares spectrum of the series and to interpret the results. Common-mode signals can be detected using the multivariate analysis. The periods with dominant spectral values are started from 4 h to one day (Figure 1). The spectrum shows a periodic pattern with periods of 24 h/n, n = 1,…,6; the spectral peaks are at harmonics of 1–6 cycles per day. Higher harmonics could likely be seen if the sampling rate was higher than 2 h. To explain these signals, we recall the theory of Fourier series expansion of periodic functions. Let the function f(x) be a periodic function with period of T [i.e., f(x) = f(x + T)]. This function can be written as an infinite sum of sine and cosine functions on the interval [− T/2, T/2]. The results presented are in fact an interesting example of Fourier decomposition of a periodic function of T = 24 h into a ‘truncated’ sum of simple oscillating functions sines and cosines.

Fig. 1
figure 1

Multivariate least-squares power spectrum of 33 bihourly TEC time series covering latitudes ranging from −80 to 80 degrees and period 2001–2007. The vertical dashed lines indicate diurnal and annual signals along with their higher harmonics

Full size image

Seasonal variations of the TEC values are also of particular interest. A periodic pattern with periods of 365.25/n days, n = 1,…,4 is the most obvious one. This is another example of the Fourier decomposition of another periodic pattern (T = 365.25 days) into a truncated sum of sines and cosines. The well-known annual cycle results from the changing of the solar zenith angle and hence solar radiation, through one year. The first harmonics (183 days) known as semiannual signal is due to seasonal variation of F2 region (Mansillaa et al. 2005). Total F2 ionization is actually lower in the local summer months than in the winter (Seeber 2003), which is known as the winter anomaly.

There are signals with solar cycle variation. Quasiperiodicities near the solar rotation period of 27-days appear in the time series of the TEC. A cluster of periods close to the 27-day period, along with their first harmonics, can be seen in the spectrum. This indicates irregularities at this solar cycle period as the number of sunspots at any given time are not constant.

Modulated periodic signals

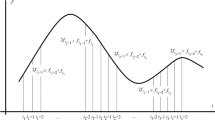
The regular signals with the periods mentioned above are not the only signals in the TEC time series. A zoom-in of the diurnal signal in Fig. 1 is shown in Fig. 2-a. Close to the diurnal signal itself a series of peaks with periods of \( 1 \pm j\varepsilon = 1 \pm j/365.25 = 1 \pm 0.0027j \) days (j = 1, 2, …) are clearly seen in the spectrum. Each pair of plus and minus signals corresponds to the diurnal signal modulated with the annual signal and its higher harmonics (1 year/j, j = 1, 2, …).

Fig. 2
figure 2

Zoom-in of multivariate least-squares spectrum of TEC time series. Harmonics \( i, \, i = 1, 2, \ldots \) of diurnal signals are modulated to harmonics \( j,\,{{ j}} = 1,2, \ldots \) of annual signal as \( \omega_{ijM} = 2\pi i(1 \pm j/365.25i) \). Modulated diurnal signal (a), semidiurnal signal (b), tri-diurnal signal (c), and quad-diurnal signal (d)

Full size image

A similar situation holds true for the higher harmonics of the diurnal signals (frames b, c, and d in Fig. 2). A close inspection indicates that they are also modulated with the annual signal and its higher harmonics. In other words, if the frequencies of the diurnal and annual signal harmonics are ω i  =  2πi and ω j  =  2πj/365.5, (i, j = 1, 2, …), respectively, the frequency of the modulated signals are then \( \omega_{ijM} = 2\pi i(1 \pm j/365.25i) \). This is clearly seen for the semi-, tri-, and quad-diurnal signals in frames b, c, and d in Fig. 2, respectively.

The above-mentioned results can also be verified through an investigation into the modulated power spectrum. To see this, the multivariate spectrum of (11), with A j from the modulated model of (16), is calculated. For this spectrum, the original diurnal frequency \( \omega_{2} = 2\pi \) is kept fixed, and the goal is to detect its modulated signal(s) with frequency of ω 1 (therefore, the search is done over ω 1). Figure 3-a shows that the modulated signals to the diurnal signal are the annual signal and its higher frequencies (1 year/j, j = 1, 2, 3, 4). The same situation holds for the semi-, tri-, and quad-diurnal signals (frame b, semidiurnal signal only).

Fig. 3
figure 3

Multivariate least-squares spectrum of diurnal (a) and semidiurnal (b) signals modulated with annual (j = 1), semiannual (j = 2), tri-annual (j = 3), and quad-annual (j = 4) signals

Full size image

Model identification

A realistic functional model should therefore include the diurnal signal and its higher harmonics, (\( i = 1,2,3,4 \)), modulated to the annual signal and its higher harmonics (\( j = 1,2,3,4 \)). Because each of the modulated signals introduces 4 columns, there are \( 4 \times 4 \times 4 = 64 \) additional columns into the A matrix.

The results presented above show that an appropriate model that can present the long-term regular variations of the ionosphere is composed of a series of harmonic functions and modulated harmonic functions

$$ y(t) = y_{1} (t) + y_{2} (t) $$
(17)

where

$$ y_{1} (t) = \sum\limits_{k = 1}^{p} {a_{k}^{1} \cos \omega_{k} t + a_{k}^{2} \sin \omega_{k} t} $$
(18)

represents the regular harmonic terms, and

$$ y_{2} (t) = \sum\limits_{k = 1}^{q} {b_{k}^{1} \cos \omega_{k}^{s} t + b_{k}^{2} \sin \omega_{k}^{s} t + b_{k}^{3} \cos \omega_{k}^{d} t + b_{k}^{4} \sin \omega_{k}^{d} t} $$
(19)

represents the regular modulated harmonic terms (\( \omega_{k}^{s} = \omega_{2} + \omega_{1} \) and \( \omega_{k}^{d} = \omega_{2} - \omega_{1} \)). In this study, both p and q are set to 4. The model expressed in (17) containing the y 1(t) and y 2(t) terms can be used to evaluate several regular variations of the ionosphere. The best known examples are the seasonal anomaly (winter anomaly), semiannual anomaly, evening anomaly, and equatorial anomaly. Evaluation of these observations and phenomena using TEC time series analysis, based on the combined effects of y 1(t) and y 2(t), will be in progress. In the next subsection, some preliminary results on the modulated regular signal will be provided using the second part y 2(t) in (17) only. The average values of such variations become zero over one full day. They could therefore be considered as anomaly or disturbance of the purely harmonic variations, which change over different seasons.

Modulated regular ionospheric variations

This section presents the modulated regular variation of TEC values. The time series of the TEC have been detrended using a linear regression model and a series of harmonic functions to remove the diurnal and annual variations along with their higher harmonics (18). The detrended series are then input to a least-squares fit using the modulated model (19).

Diurnal signals modulated with annual signals

The diurnal signal frequencies are modulated with the annual signal frequencies for the time series of TEC at the equator (\( \omega_{ijM} = 2\pi i(1 \pm j/365.25i) \)). Figure 4 shows the diurnal and semidiurnal signals modulated with the annual and semiannual signals. Among them, the diurnal signal modulated with the semiannual signal shows the largest variations of ±10 TECU at high solar variations for the year 2001. At low solar variations in 2006, it could reach up to ±4 TECU (results not included). Indicated in the plot is also the superposition of the total modulated signal, which can reach ±15 TECU.

Fig. 4
figure 4

Diurnal/semidiurnal signal modulated with annual (frame a/b) and semiannual (frame c/d) signals for 2001. Superposition of diurnal and semidiurnal signals modulated with annual/semiannual signals (frames on right; a + b/c + d), superposition of diurnal/semidiurnal signal modulated with annual and semiannual signals (frames on bottom; a + c/b + d), and superposition of all four signals (frames at corner; a + b+c + d). Vertical lines indicate equinoxes and solstices

Full size image

For signals modulated with the annual frequency, the diurnal signal shows maximum variations in February and August and minimum in May and November, while the semidiurnal signal shows maximum variations in solstices and minimum in equinoxes. For signals modulated with the semiannual frequency, both diurnal and semidiurnal signals show their maximum variations in the equinoxes and solstices.

Superposition of all four signals (a + b+c + d) indicates that the maximum variations occur in March equinox and the June and December solstices, while the minimum variations belong to the September equinox. The largest values occur in March equinox and June solstice, and the smallest values belong to the December solstice.

Variations of modulated signal

Superposition of total diurnal signal, including its higher harmonics up to i = 4, modulated with the annual signal, including its higher harmonics up to j = 4, is investigated now. Since the series have been detrended using the regular diurnal and annual signals, the modulated signal changes around zero, with the average over one day being zero. The changes in the modulated signal are shown for one full year and different latitudes. See Fig. 5 for the high solar activities in 2001 and Fig. 6 for the low activities in 2006.

Fig. 5
figure 5

Map of diurnal variation of TEC in 2001 using modulated formula (19) at different geographical latitudes. The northern hemisphere is left, and the southern hemisphere is right. White horizontal lines indicate the equinoxes and solstices

Full size image
Fig. 6
figure 6

Map of diurnal variation of TEC in 2006 using modulated formula (19) at different geographical latitudes

Full size image

At all latitudes, the largest variations happen in July when the maximum +15 TECU is at around 6 local time, and the minimum of −15 TECU is around 14 local time. This holds also approximately in January. A reverse situation holds in April and November, where the minimum occurs in the morning and the maximum in the afternoon. The fact that the cross section of the daily signal experiences two peaks (two maxima and two minima over one year) highlights the effect of the diurnal signal modulated with the semiannual signal.

The following observations can also be established: (1) Close to the equinoxes in May and September the lowest daily variations can be observed, (2) TEC variations at different latitudes exhibit similar pattern, though they are different in the details, (3) At very high latitudes such as \( \phi = 75^{ \circ } \), the range of variations reduces by a factor of 2 (±7 TECU for the high solar period in 2001), (4) Some of the maxima and minima variations are around the equinoxes and solstices, while some are halfway between equinox and solstice, and (5) Similar plots to Figs. 5 and 6, but versus latitudes and not shown here, indicate that most of the largest variations are at lower and middle latitude adjacent the equator, in agreement with the equatorial anomaly, which states that at low latitudes in midday and evening hours the NmF2 is greater at about 15° north and south of the geomagnetic equator than at the equator itself.

Summary and conclusions

Based on the least-squares harmonic estimation (LS-HE), we attempted to model regular modulated variations of the ionosphere. For this purpose, a mathematical foundation for the multivariate and modulated LS-HE was developed. The method was applied to the time series of total electron contents (TEC) at different latitudes provided by the JPL analysis center. Multivariate and modulated least-squares spectra were estimated for the series to detect and hence model the regular and modulated dominant frequencies of the periodic patterns.

As expected, two significant periodic patterns were the diurnal and annual signals with the periods of 24/n hours and 365.25/n days (n = 1, 2,…), along with their higher harmonics. The spectra showed a cluster of periods around 27 days. These clustered periods indicate irregularities at this solar cycle period. A zoom-in of the spectrum for the diurnal signal and/or its higher harmonics showed a series of peaks with periods close to these signals. This indicated that the daily signal harmonics of \( \omega_{i} = 2\pi i,\quad i = 1, 2, \ldots \) were modulated with the annual signal harmonics of \( \omega_{j} = 2\pi j/365.25,\quad j = 1, 2, \ldots \), as \( \omega_{ijM} = 2\pi i(1 \pm j/365.25i), \) which are called regular modulated frequencies. It was shown that the largest variations belong to diurnal signal modulated to the semiannual signal. The maximum ranges of the total modulated daily signal are ±15 TECU and ±6 TECU at high and low solar activity periods, respectively.

A model consisting of a linear trend plus regular sinusoidal functions along with modulated sinusoidal ones is capable of studying long-term variations of the ionosphere. Future applications of the proposed method will consider studying different anomalies such as the winter anomaly, semiannual anomaly, evening anomaly, and equatorial anomaly of the ionosphere. Long-term prediction of the regular ionospheric variations could also be another application of the proposed method, which is considered in future work.