Curvature- and fluid-stress-driven tissue growth in a tissue-engineering scaffold pore

Abstract

Cell proliferation within a fluid-filled porous tissue-engineering scaffold depends on a sensitive choice of pore geometry and flow rates: regions of high curvature encourage cell proliferation, while a critical flow rate is required to promote growth for certain cell types. When the flow rate is too slow, the nutrient supply is limited; when it is too fast, cells may be damaged by the high fluid shear stress. As a result, determining appropriate tissue-engineering-construct geometries and operating regimes poses a significant challenge that cannot be addressed by experimentation alone. In this paper, we present a mathematical theory for the fluid flow within a pore of a tissue-engineering scaffold, which is coupled to the growth of cells on the pore walls. We exploit the slenderness of a pore that is typical in such a scenario, to derive a reduced model that enables a comprehensive analysis of the system to be performed. We derive analytical solutions in a particular case of a nearly piecewise constant growth law and compare these with numerical solutions of the reduced model. Qualitative comparisons of tissue morphologies predicted by our model, with those observed experimentally, are also made. We demonstrate how the simplified system may be used to make predictions on the design of a tissue-engineering scaffold and the appropriate operating regime that ensures a desired level of tissue growth.

1 Introduction and motivation

In vitro tissue engineering aims to create functional tissue and organ samples external to the body to replace damaged or diseased tissues and organs needed in multiple clinical therapies (Rose and Oreffo 2002; Martin et al. 2004). By using autologous cell sources, often seeded within a porous scaffold that acts as a template for the developing tissue, tissue-engineered products have many advantages over traditional approaches such as donor tissue and organ transplantation that can elicit an adverse immune response. The development of the growing tissue construct—the combination of scaffold, cells and extracellular matrix (ECM) with biological cues—often occurs within a bioreactor. In perfusion-bioreactor systems, a flow of culture medium (nutrient-rich fluid) is driven through the porous scaffold. This serves two purposes. Firstly, the flow imposes fluid mechanical forces (shear stress, pressure) on mechanosensitive cells found in, for example, bone, cartilage, muscle, liver and blood vessels (Mullender et al. 2004). The mechanical environment that cells experience affects their differentiation, proliferation, orientation, gene expression and a host of other activities: the mechanical stimuli are integrated into the cellular response via a process known as mechanotransduction. For example, fluid shear stress has been shown to enhance extracellular matrix formation in vitro (Bakker et al. 2004; Klein-Nulend et al. 1995; You et al. 2000), and stimulation by hydrostatic pressure promotes stem cell differentiation down the chondrogenic lineage to form cartilaginous tissues (Elder and Athanasiou 2009). Additionally, fluid flows are employed to ensure adequate solute delivery to the cells within the porous scaffold. A variety of dynamic flow-perfusion bioreactors have been developed, including direct and free-flow perfusion systems, and the rotary cell culture system (RCCS) (see Martin et al. (2004) and references therein). By selecting an appropriate bioreactor system, tissue engineers aim to provide the optimum stimulatory environment for in vitro tissue growth to engineer a tissue construct that remains functional for significant periods of time.

In addition to the selection of perfusion bioreactor, the scaffold properties are of central importance to the tissue engineering approach. Scaffolds with a highly porous, interconnected structure encourage cell penetration, vascularization of the construct from the surrounding tissue (when implanted in vivo) and efficient mass transfer of nutrients and waste products. The scaffold material must be compatible with the host material so that it does not elicit an adverse immune response upon implantation (Salgado et al. 2004). The scaffold plays the role of the extracellular matrix (ECM) in tissues and defines its mechanical properties (e.g. the collagen and elastin fibres present in ECM, or the calcium hydroxyapatite that lends bone tissue its rigidity). One challenge is to select the appropriate material properties for the scaffold (porous, poroelastic, viscoelastic, etc.) to ensure that the cells experience the appropriate mechanical environment when the construct is subjected to an applied load. Another challenge is to ensure that the scaffold is sufficiently porous without compromising its mechanical integrity. Additionally, the rates of scaffold degradation (e.g. due to hydrolysis) must be matched to the rate of nascent tissue growth in vivo so that once the construct is in vivo, the artificial scaffold is replaced by native ECM and the mechanical integrity of the construct is maintained. Finally, both topographical and biochemical characteristics of the porous scaffold have been exploited to enhance cell–scaffold adherence, and to direct cell movement or differentiation (Weiss 1945; Salgado et al. 2004): for example, scaffolds can deliver growth factors or DNA (Sipe 2002), or contain specific cellular recognition molecules (Freed and Vunjak-Novakovic 1998). For a comprehensive discussion of scaffolds for tissue engineering applications see Atala et al. (1997), Hutmacher (2006), Hollister (2005) and references therein.

The motivation for this work is the experimental observation that tissue growth is strongly affected by the geometrical features of the pores in an artificial 3D tissue scaffold (Rumpler et al. 2008), which has formed the focus of many recent studies (see, for example, Bidan et al. 2013; Werner et al. 2017; Lo et al. 2016; Kommareddy et al. 2010, among many others). For example, Bidan et al. (2013) emphasized how geometric constraints may guide tissue formation in vitro and showed that optimizing scaffold architectures may improve tissue formation independently of the scaffold material used. Furthermore, Werner et al. (2017) systematically investigated the influence of 3D surface curvature on cell and nucleus morphology and the subsequent effect on the migratory and differentiation behaviour of human mesenchymal stem cells. Key to successful tissue engineering is the coordination of the various cellular cues to enhance tissue growth. Mechanistic mathematical modelling has an important role to play in this regard, elucidating mechanisms and providing quantitative information about the cellular microenvironment (e.g. the shear-stress field) that is not straightforward (or even possible) to measure experimentally. Mathematical models may be validated against measurable experimental data, such as perfusion flow rate or bioreactor outlet nutrient concentration, and then exploited to reveal details of the mechanical and biochemical fields within the scaffold and bioreactor system. The quantitative models can be used to predict the outcome of a particular experimental scenario (limiting the need for numerous and expensive bioreactor experiments, potentially saving time and resources) and to optimize tissue-engineering protocols.

There has been a large body of work using mathematical models to understand the relationship between flow, associated transport and tissue growth in perfusion-bioreactor systems with a porous scaffold. Numerous macroscale continuum models for bioactive porous media have been proposed for artificial tissue growth, with many accounting for the influence of fluid shear stress on tissue growth (see O’Dea et al. (2012) and references therein). Multiphase models account for multiple phases explicitly (e.g. fluid, scaffold, cells, etc.). The governing equations are derived from conservation of mass and momentum for each phase, and appropriate constitutive laws are specified to capture the interactions between the phases, enabling a wide variety of biological systems to be modelled (O’Dea et al. 2010; Pearson et al. 2014). An alternative approach is to include the effect of cell growth on the fluid flow implicitly, by prescribing the scaffold porosity to be a function of cell density, which satisfies a conservation-of-mass equation (Coletti et al. 2006; Pohlmeyer and Cummings 2013; Pohlmeyer et al. 2013; Shakeel et al. 2013). Fluid flow through the porous scaffold is then governed by Darcy’s law. In these macroscale approaches, constitutive assumptions relate microscale processes, such as cell growth, to macroscale parameters. Alternatively, homogenization techniques have been proposed to capture the precise relationship between macroscopic parameters in continuum models, such as porosity, and pore-scale growth and flow processes (Shipley et al. 2009; Penta et al. 2014; O’Dea et al. 2015). As an alternative to continuum models, network models have been proposed for artificial tissue growth, particularly where the scaffold biomaterial contains relatively few pores (Krause et al. 2017a, b). These continuum and network approaches complement computational and algorithmic approaches employed to model various aspects of tissue engineering; see Geris (2013) for a comprehensive review.

The above studies consider tissue growth on the scale of the tissue construct. Although there are studies that have mapped the shear stress at the pore scale for realistic flows through a perfusion bioreactor (see, e.g. Raimondi et al. 2005), to the best of our knowledge, no mathematical studies have considered the interplay between fluid shear stresses and pore curvature on cell growth at the scale of an individual pore. In this paper, we will focus on the combined roles of fluid shear stress and topographical cues, in particular pore curvature, on tissue growth within a single pore of a scaffold. The paper is laid out as follows: in Sect. 2, we introduce a mathematical model for flow through a pore of a tissue-engineering scaffold. The governing equations describing the flow of nutrient-rich solution and tissue growth are presented in Sects. 2.1 and 2.2, respectively. The model is analyzed in Sect. 3 by using an asymptotic approach exploiting the small aspect ratio of the pore. Asymptotic and numerical techniques are used to obtain solutions for the tissue growth in Sect. 4. We also discuss which initial internal pore morphology gives more tissue growth in Sect. 4.4. Finally, we conclude in Sect. 5 with a discussion of our model and results in the context of pores within a real tissue-engineering scaffold.

2 A mathematical model for flow within a scaffold pore

We consider a single scaffold pore lined with cells, through which nutrient-rich culture medium flows. Over time, the cells proliferate and the pore will constrict as the tissue layer lining it thickens. We consider the dynamics of the system on the timescale of cell proliferation, as the cells lining the pore wall grow on a much longer timescale than that associated with the transport of fluid through the pore (see values presented in Table 1 later). Thus, the pore wall may be considered stationary when considering the fluid flow, a quasi-static assumption.

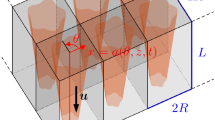
The fluid–cell-layer interface is of length ${\hat{L}}$ and has typical radius ${\hat{R}}$. (Hats will be used throughout to distinguish dimensional quantities from their dimensionless equivalents.) We define the aspect ratio $\epsilon =\hat{R}/{\hat{L}}\ll 1$. We will explore how modifications in fluid–cell-layer interface geometry influence the resulting tissue growth. We will assume that the initial cell layer is sufficiently thin that its internal configuration reflects the underlying substrate geometry, which we assume to be approximately circular with small azimuthal and axial variation. We consider the regime in which the fluid–cell-layer interface remains nearly circularly cylindrical so that deviations of the circumference geometry from circular are small (see Fig. 1).

Nutrient is assumed to be present in excess so that no significant depletion occurs over the length of the pore. In many applications, the flux of fluid is held constant to ensure a continued supply of nutrient (Pearson et al. 2014; Shakeel et al. 2013); we assume this throughout. Specifically, we prescribe the inlet flux $\hat{Q}_i$ and the downstream pressure $\hat{P}_{\mathrm{d}}$. The nutrient-rich culture medium is modelled as an incompressible Newtonian viscous fluid of (dynamic) viscosity ${\hat{\mu }}$ and density $\hat{\rho }$.

We work in cylindrical coordinates $(\hat{r},\theta ,\hat{z})$, where $\hat{z}$ is aligned with the pore axis, and ${\varvec{e}}_{i}$ correspond to the unit vectors in the i direction. The fluid–cell-layer interface is described by $\hat{r}=\hat{a}(\theta ,\hat{z},\hat{t})$, and the initial configuration $\hat{r}=\hat{a}(\theta ,\hat{z},0)$ is prescribed.

Fig. 1

Schematic diagram of a possible geometry of a tissue-lined pore within a tissue-engineering construct

2.1 Fluid dynamics

The fluid flow has velocity $\hat{{\varvec{u}}}=\hat{u}{\varvec{e}}_{\hat{r}} +\hat{v}{\varvec{e}}_{\theta }+\hat{w}{\varvec{e}}_{\hat{z}}$ and pressure $\hat{p}$. Neglecting flow inertia within the pore (Chung et al. 2007; Lemon et al. 2006), we assume the flow is governed by the Stokes equations. We introduce the following scalings:

$$\begin{aligned}&\hat{{\varvec{u}}}=\displaystyle \frac{\hat{Q}_i}{\pi \hat{R}^2}{\varvec{u}}=\displaystyle \frac{\hat{Q}_i}{\pi {\hat{R}}^2} (\epsilon u, \epsilon v, w), \quad \hat{p}=\displaystyle \frac{{\hat{\mu }} {\hat{L}} \hat{Q}_i}{\pi {\hat{R}}^4}p+{\hat{P}}_{\text {d}}, \nonumber \\&(\hat{r},\hat{a},\hat{z})={\hat{L}}(\epsilon r,\epsilon a, z). \end{aligned}$$

(1)

The dimensionless governing flow equations are then

$$\begin{aligned}&\displaystyle \frac{1}{\epsilon ^2} \frac{\partial p}{\partial r}=\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial u}{\partial r}\right) +\frac{1}{r^2}\frac{\partial ^2 u}{\partial {\theta }^2}+\epsilon ^2 \frac{\partial ^2 u}{\partial {z}^2}-\frac{u}{r^2} -\frac{2}{r^2}\frac{\partial v}{\partial \theta }, \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \frac{1}{\epsilon ^2 r} \frac{\partial p}{\partial \theta }=\frac{1}{r}\frac{\partial }{\partial r}\left( r\frac{\partial v}{\partial r}\right) +\frac{1}{r^2}\frac{\partial ^2 v}{\partial {\theta }^2}+\epsilon ^2 \frac{\partial ^2 v}{\partial {z}^2}-\frac{v}{r^2} +\frac{2}{r^2}\frac{\partial u}{\partial \theta }, \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \frac{\partial p}{\partial z}=\frac{1}{r} \frac{\partial }{\partial r}\left( r\frac{\partial w}{\partial r}\right) +\frac{1}{r^2} \frac{\partial ^2 w}{\partial {\theta }^2}+\epsilon ^2\frac{\partial ^2 w}{\partial {z}^2}, \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle \frac{1}{r}\frac{\partial }{\partial r} \bigl (ru \bigr ) +\frac{1}{r}\frac{\partial v}{\partial \theta } +\frac{\partial w}{\partial z}=0, \end{aligned}$$

(5)

holding in the flow domain $0\le r\le a(\theta ,z,t)$, $0\le z \le 1$. These equations must be solved subject to the following boundary conditions:

$$\begin{aligned} u=v=w=0&\text{ on } r=a(\theta ,z,t)\text{, } \end{aligned}$$

(6)

enforcing no slip and no penetration at the fluid–cell-layer interface, and the symmetry conditions

$$\begin{aligned} u=v=\frac{\partial w}{\partial r}=0&\text{ at } r=0\text{. } \end{aligned}$$

(7)

We assume that the (dimensionless) pressure drop across the length of the pore is given by $\zeta (t)$, which will increase monotonically to sustain the constant flux as the pore constricts under cell growth. The system is thus closed by applying the boundary conditions

$$\begin{aligned} p|_{z=0}=\zeta (t), \quad p|_{z=1}=0, \end{aligned}$$

(8)

and enforcing constant fluid influx,

$$\begin{aligned} \int _0^{2\pi }\int _0^a w{(r,\theta ,0,t)}r\,\mathrm {d}r \mathrm {d}\theta =\pi . \end{aligned}$$

(9)

Note that setting $\zeta (t)=1$ in (8), and dropping the condition (9), describes the alternative scenario in which the pressure drop is constant.

Table 1 Dimensional and dimensionless parameters and approximate values (from Rumpler et al. 2008; Shipley and Waters 2011)

2.2 Tissue growth

For the cell proliferation (tissue growth) within the pore, we prescribe a phenomenological law based on experimental observations. Specifically, cells proliferate more quickly when exposed to higher shear stresses at their surface (mechanotransduction) and in regions where the underlying substrate has higher curvature (see, for example, O’Dea et al. (2010) and references therein; and Rumpler et al. (2008)). In the original dimensional variables, we propose

$$\begin{aligned} \frac{\partial \hat{a}}{ \partial \hat{t}}=-{\hat{\lambda }} \hat{\kappa } f(\hat{\sigma }_{\hat{\mathrm{s}}}). \end{aligned}$$

(10)

Here, $\hat{\kappa }=\hat{\varvec{\nabla }}\mathbf {\cdot }{\varvec{n}}$ is the mean curvature, with $\hat{\varvec{\nabla }}$ the dimensional gradient operator and ${\varvec{n}}$ the unit normal to the fluid–cell-layer interface (in the direction pointing into the fluid), given by

$$\begin{aligned} {\varvec{n}}&= \frac{\hat{\varvec{\nabla }}{(\hat{r}-\hat{a})}}{\vert \hat{\varvec{\nabla }}{(\hat{r}-\hat{a})}\vert }. \end{aligned}$$

(11)

The characteristic growth rate (m$^2$ s$^{-1}$) is given by $\hat{\lambda }$, and the function f captures the specific dependence of tissue growth on the total fluid shear stress at the fluid–cell-layer interface, $\hat{\sigma }_{{\hat{s}}}$. We will explore physically realistic expressions for f in Sect. 4 and discuss the limitations of the growth law (10) in Sect. 5.

Without the shear stress dependence ($f(\hat{\sigma }_{\hat{\mathrm{s}}})=\text{ constant }$), (10) is precisely the growth law considered by Rumpler et al. (2008). Note also that, for cylindrical pores, $\kappa =1/a$ and (10) then implies that the rate of change of tissue volume depends only on shear stress, i.e.

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm d \hat{t}}\left( \pi (\hat{a}^2\vert _{\hat{t}=0}-\hat{a}^2)\right) =2\pi f(\hat{\sigma }_{\hat{s}}). \end{aligned}$$

(12)

At the fluid–cell-layer surface, the stress vector $\hat{{\varvec{\tau }}}$ is given by

$$\begin{aligned} \hat{{\varvec{\tau }}}=\hat{\varvec{\sigma }}\cdot {\varvec{n}}, \end{aligned}$$

(13)

where

$$\begin{aligned} \hat{\varvec{\sigma }}=-{\hat{p}}{\varvec{I}}+{\hat{\mu }} \left( \hat{\varvec{\nabla }} {\varvec{\hat{u}}}+\left( \hat{\varvec{\nabla }}{\varvec{{\hat{u}}}}\right) ^T\right) \end{aligned}$$

(14)

is the Cauchy stress tensor for the fluid, where ${\varvec{I}}$ is the identity matrix. The magnitude of the stress vector in the normal direction is given by

$$\begin{aligned} {\hat{\sigma }}_{ \mathrm n}=\hat{{\varvec{\tau }}}\cdot {\varvec{n}}. \end{aligned}$$

(15)

The total shear stress at the fluid–cell-layer interface, $\hat{\sigma }_{{\hat{\mathrm{s}}}}$, is then given by

$$\begin{aligned} \hat{\sigma }_{\hat{\mathrm{s}}}=\sqrt{\hat{{\varvec{\tau }}}\cdot \hat{{\varvec{\tau }}}-{\hat{\sigma }}^2_{ \mathrm n}}. \end{aligned}$$

(16)

Using the non-dimensionalization presented in (1) together with the additional scales

$$\begin{aligned} \hat{t} = \frac{{\hat{R}}^2}{{\hat{\lambda }}}t,\quad \hat{\kappa } = \frac{1}{{\hat{R}}}\kappa ,\quad \hat{\sigma }_{\hat{\mathrm{s}}}=\frac{{\hat{\mu }} \hat{Q}_i}{\pi {\hat{R}}^3}\sigma _{\mathrm{s}}, \end{aligned}$$

(17)

gives the dimensionless growth law

$$\begin{aligned} \frac{\partial a}{ \partial t}=- \kappa f(\sigma _{\mathrm{s}}). \end{aligned}$$

(18)

The unit normal to the fluid–cell-layer interface, using (11), is given in dimensionless form by

$$\begin{aligned} {\varvec{n}}=\frac{1}{\sqrt{1+\displaystyle \frac{1}{r^2}\left( \frac{\partial a}{\partial \theta }\right) ^2+\epsilon ^2\left( \frac{\partial a}{\partial z}\right) ^2}}\left( {\varvec{e}}_r -\frac{1}{r}\frac{\partial a}{\partial \theta }{\varvec{e}}_{\theta } -\epsilon \frac{\partial a}{\partial z} {\varvec{e}}_z\right) . \end{aligned}$$

(19)

3 Model analysis

3.1 Asymptotic ansätze

The full system outlined in Sect. 2 can be solved numerically for a specified growth function f. However, this would be computationally costly, limiting the parameter ranges that can be explored and affording only limited insight into the effects of model parameters. We therefore take an alternative asymptotic approach, exploiting the smallness of the typical pore aspect ratio, $\epsilon ={\hat{R}}/{\hat{L}}\ll 1$. This enables us to make analytical progress, leading to a more tractable model, which can be solved cheaply to provide insights into the dynamics of the system.

In addition to the assumption of small pore aspect ratio, we assume that the initial cell layer is sufficiently thin that its internal configuration reflects the underlying substrate geometry, which we assume to be approximately circular with small azimuthal and axial variation. This motivates relegation of spatial variations in the fluid–cell-layer interface to first (axial) and second (azimuthal and axial) order in the aspect ratio. Below we find that the leading-order fluid velocity is unidirectional and independent of the axial coordinate z. As a result, the leading-order shear stress at the fluid–cell-layer interface is independent of z. We make the quasi-static assumption of slow tissue growth compared with the timescale of nutrient transport through the scaffold, and the further assumption that there is a plentiful supply of nutrient so that all parts of the growing tissue experience the same concentration. As a result, the cell layer grows in a spatially uniform manner with time to leading order in the pore aspect ratio. Continuing the analysis to higher order in the aspect ratio, we determine the dependence of the tissue growth on the axial and azimuthal coordinates at first and second order in the pore aspect ratio, respectively.

We therefore assume that the fluid–cell-layer interface may be expressed as

$$\begin{aligned} a(\theta ,z,t)=a_0(t)+\epsilon a_1 (z,t)+\epsilon ^2 a_2(\theta ,z,t)+O(\epsilon ^3).\nonumber \\ \end{aligned}$$

(20)

We further assume that $a_2$ is of the form

$$\begin{aligned} a_2(\theta ,z,t)=\varLambda _2 (z,t) \cos n\theta + \varUpsilon _2 (z,t), \end{aligned}$$

(21)

where $\varLambda _2(z,t)$ and $\varUpsilon _2(z,t)$ are functions to be determined and n is an integer. This form corresponds to periodic perturbations of the pore from a circular cross section that has n lobes. While this ansatz clearly imposes constraints on the type of tissue growth we study, we will find that this strikes a balance between allowing us to make substantial analytical progress while retaining a suitable level of generality to the form of the cross-sectional profile.

We assume that the initial fluid–cell-layer interface shape $a(\theta ,z,0)$ is given, then determine its subsequent evolution via Eq. (18).

In the following section, we pose asymptotic expansions of the form

$$\begin{aligned} u=u_0+\epsilon u_1+\epsilon ^2 u_2 +\cdots , \end{aligned}$$

(22)

and similarly for v, w, p, $\zeta$, $\sigma _{\mathrm{s}}$ and $\kappa$, and systematically examine the system at each order to determine reduced equations.

3.2 Asymptotic analysis for the flow

3.2.1 Leading-order analysis

For the fluid–cell-layer interface configuration (20), the flow will be independent of $\theta$ to leading order in $\epsilon$. Substituting the asymptotic expansions (22) into Eqs. (2)–(5) and conditions (6)–(9) and retaining leading-order terms give a system of equations for the leading-order velocities, $u_0$, $v_0$ and $w_0$, pressure $p_0$, and $\zeta _0$ (the leading-order pressure at the pore inlet, determined as part of the solution in our specified-flux scenario):

$$\begin{aligned}&u_0=0, \quad v_0=0, \quad w_0=\displaystyle \frac{\zeta _0}{4}(a_0^2-r^2),\nonumber \\&p_0=\displaystyle \zeta _0(1-z), \quad \zeta _0=\displaystyle \frac{8}{a_0^4}. \end{aligned}$$

(23)

3.2.2 First-order analysis

At $O(\epsilon )$, based on the ansatz (20), we seek a $\theta$-independent solution to the governing equations, finding

$$\begin{aligned} u_1= & {} \frac{\partial a_1}{\partial z}\frac{\zeta _0}{4a_0}\ r \left( a_0^2-r^2\right) , \quad v_1=0, \quad w_1 = \frac{a_1\zeta _0}{2a_0} \left( 2r^2-a_0^2\right) , \end{aligned}$$

(24)

$$\begin{aligned} p_1= & {} -\frac{4\zeta _0}{a_0}\int _z^1 a_1(\tilde{z},t)\,\mathrm {d}\tilde{z}, \quad \zeta _1 = -\frac{4\zeta _0}{a_0}\int _0^1a_1(z,t)\,\mathrm {d}z. \end{aligned}$$

(25)

3.2.3 Second-order analysis

Considering Eq. (4) at $O(\epsilon ^2)$ motivates seeking a solution $w_2$ of the form

$$\begin{aligned} w_2&=\left[ \frac{\varLambda _2}{2} a_0^{1-n} r^n\cos n\theta +\tilde{w}_2 (r,z,t)\right] \zeta _0. \end{aligned}$$

(26)

Using (4) and (6), we find

$$\begin{aligned} \zeta _0\tilde{w}_2 = \frac{1}{4}\frac{\partial p_2}{\partial z} \left( r^2-a_0^2\right) + \left( -\frac{7}{4}a_1^2+\frac{a_0\varUpsilon _2}{2}\right) \zeta _0. \end{aligned}$$

(27)

Imposing the boundary conditions (6)–(8) and the flux condition (9) gives, after some manipulation,

$$\begin{aligned} \frac{a_0^4}{4} p_2= & {} \bigg [3a_0^2 \int _z^1a^2_1(z',t)\,\mathrm {d}z'-a_0^3\int _z^1\varUpsilon _2(z',t)\,\mathrm {d}z'\nonumber \\&+\frac{1}{4}\int _z^1 a^4_1(z',t)\,\mathrm {d}z'\bigg ]\zeta _0, \end{aligned}$$

(28)

$$\begin{aligned} \zeta _2= & {} \frac{4}{a_0^4} \bigg [3a_0^2 \int _0^1a^2_1(z',t)\,\mathrm {d}z'-a_0^3 \int _0^1\varUpsilon _2(z',t)\,\mathrm {d}z'\nonumber \\&+\frac{1}{4} \int _0^1a^4_1(z',t)\,\mathrm {d}z'\bigg ]\zeta _0, \end{aligned}$$

(29)

and the axial velocity is given by

$$\begin{aligned} w_2= & {} \Bigg [\frac{\varLambda _2}{2} a_0^{1-n} r^n\cos n\theta + \frac{1}{a_0^4}\left( -3a_0^2a_1^2+a_0^3\varUpsilon _2\right. \nonumber \\&\left. -\frac{a_1^4}{4}\right) (r^2-a_0^2)-\frac{7}{4}a_1^2+\frac{a_0\varUpsilon _2}{2}\Bigg ]\zeta _0. \end{aligned}$$

(30)

Note that $u_2$ and $v_2$ may also be determined, but are not required in the analysis that follows.

3.2.4 Summary

The flow within the pore defined by

$$\begin{aligned} r= & {} a_0(t)+\epsilon a_1(z,t) +\epsilon ^2 ( \varLambda _2 (z,t) \cos n\theta + \varUpsilon _2(z,t)) \nonumber \\&+ O(\epsilon ^3), \quad 0\le z \le 1{,} \end{aligned}$$

(31)

and driven by constant flux, is

$$\begin{aligned} {\varvec{u}}= & {} (\epsilon u,\epsilon v, w)=(\epsilon ^2 u_1+O(\epsilon ^3), O(\epsilon ^3), w_0+\epsilon w_1\nonumber \\&+\epsilon ^2 w_2+ O(\epsilon ^3)), \end{aligned}$$

(32)

where $w_0$, $u_1$, $w_1$ and $w_2$ are given by (23), (24) and (30). The corresponding pressure drop between $z=0$ and $z=1$ is $\zeta =\zeta _0+\epsilon \zeta _1+\epsilon ^2\zeta _2+\cdots$, where $\zeta _0$, $\zeta _1$, $\zeta _2$ are given by (23), (25) and (29), respectively.

3.3 Asymptotic analysis for the tissue growth

Equation (19) yields the asymptotic expansion of the unit normal,

$$\begin{aligned} {\varvec{n}}&=\left[ {\varvec{e}}_r - \epsilon ^2 \frac{a_{2\theta }}{r}{\varvec{e}}_{\theta } -\epsilon ^2 a_{1z} {\varvec{e}}_z \right] _{r=a_0} +O(\epsilon ^3). \end{aligned}$$

(33)

Substituting (17), (32) and (33) into (16), we obtain the dimensionless shear stress at the fluid–cell-layer interface as

$$\begin{aligned} \sigma _{\mathrm{s}}(\theta ,z,t)= & {} \sigma _\mathrm{s0}(t)+\epsilon \sigma _{\mathrm{s1}}(z,t) +\epsilon ^2 (\sigma _{\mathrm{s2a}}(z,t) \cos n\theta \nonumber \\&+\,\, \sigma _\mathrm{s2b}(z,t))+O(\epsilon ^3), \end{aligned}$$

(34)

where

$$\begin{aligned} \sigma _\mathrm{s0}= & {} \frac{a_0}{2}\zeta _0,\quad \sigma _\mathrm{s1}=2a_1\zeta _0,\quad \sigma _\mathrm{s2a}=\frac{n\varLambda _2 \zeta _0}{2}, \nonumber \\ \sigma _\mathrm{s2b}= & {} \frac{1}{a_0^3} \left( -6a_0^2a_1^2+2a_0^3\varUpsilon _2-\frac{a_1^4}{2}\right) \zeta _0. \end{aligned}$$

(35)

The dimensionless mean curvature is given by

$$\begin{aligned} \kappa&=\kappa _0(t)+\epsilon ^2 \kappa _{2}(z,t) \cos n\theta +O(\epsilon ^3), \end{aligned}$$

(36)

where

We integrate the growth-law Eq. (18), to yield an explicit expression for the fluid–cell-layer interface shape,

$$\begin{aligned} a(\theta , z, t)=a(\theta ,z,0)-\int _0^t \kappa (\theta ,z,t') f(\sigma _\mathrm{s}(\theta ,z,t'))\,\mathrm {d}t'. \end{aligned}$$

(38)

Substituting our asymptotic expansions for a, $\sigma _\mathrm{s}$ and $\kappa$, Eqs. (20), (34) and (36), respectively, into (38), give

$$\begin{aligned}&{a_0}(t)= a_0(0)-\int _0^t \kappa _0(\tau ) f(\sigma _\mathrm{s0}(\tau ))\,\mathrm {d}\tau , \end{aligned}$$

(39)

$$\begin{aligned}&a_1(z,t)=a_1(z,0)-\int _0^t\kappa _0(\tau ) \sigma _\mathrm{s1}(z,\tau )f'(\sigma _\mathrm{s0}(\tau ))\,\mathrm {d}\tau , \end{aligned}$$

(40)

$$\begin{aligned}&{\varLambda _2}(z,t)=\varLambda _2(z,0)\nonumber \\&\quad - \int _0^t \bigl [ \kappa _2(z,\tau ) f(\sigma _\mathrm{s0}(\tau ))+\kappa _0(\tau ) \sigma _\mathrm{s2a}(z,\tau )f'(\sigma _\mathrm{s0}(\tau ))\bigr ]\,\mathrm {d}\tau , \end{aligned}$$

(41)

$$\begin{aligned}&{\varUpsilon _2}(z,t)=\varUpsilon _2(z,0)\nonumber \\&\quad -\int _0^t\kappa _0(\tau ) \left[ \sigma _\mathrm{s2b}(z,\tau )f'(\sigma _\mathrm{s0}(\tau ))+\frac{\sigma ^2_\mathrm{s1}(z,\tau )}{2}f''(\sigma _\mathrm{s0}(\tau ))\right] \,\mathrm {d}\tau .\nonumber \\ \end{aligned}$$

(42)

Here, primes denote differentiation with respect to the argument and arise due to a Taylor expansion of f, while $\sigma _\mathrm{s0}$, $\sigma _\mathrm{s1}$, $\sigma _\mathrm{s2a}$, $\sigma _\mathrm{s2b}$, $\kappa _0$ and $\kappa _2$ are given by (35) and (37).

4 Results

In this section, we present simulations of the model (39)–(42) for a physically realistic growth law. Specifically, we choose f (see Eq. (18)) to be of the form:

$$\begin{aligned} f(x)&=F_1+(F_2-F_1)\left[ \frac{1+\mathrm{tanh}(m(x-\sigma _1))}{2} \right] \nonumber \\&\quad -F_2\left[ \frac{1+\mathrm{tanh}(m(x-\sigma _2))}{2}\right] , \end{aligned}$$

(43)

where $F_1<F_2$, $\sigma _1<\sigma _2$ and $m\gg 1$. Based on the shear-stress scaling in (17), $\sigma _1$ and $\sigma _2$ will typically be order-one quantities (Rumpler et al. 2008). For large values of m, this corresponds to a function that has three regions in which it is approximately constant, connected by rapid but smooth transition regions (see Fig. 2). Similar constitutive laws have been considered elsewhere (see, for example, Krause et al. 2017a, b; Pearson et al. 2014). This captures low growth at small shear stresses ($f\approx F_1$ for $\sigma <\sigma _1$), enhanced growth at intermediate shear stress ($f \approx F_2>F_1$ for $\sigma _1<\sigma <\sigma _2$), and the adverse impact of high shear stress on growth ($f \approx 0$ for $\sigma >\sigma _2$). We note that our analysis readily generalizes for nonzero growth, or even negative growth (capturing cell death and degradation), for high stresses, but we do not consider this here. We note that as m becomes large, gradients in f become large (order m). However, our Taylor series expansion in (39)–(42) remains valid, since the window over which the gradient is large is only of width 1 / m. Thus, our asymptotic expansion in $\epsilon$ holds, irrespective of the size of m.

Fig. 2

Growth function f defined in (43) that appears in the growth law (18), with $F_1=1$, $F_2=3$, $\sigma _1=7$, $\sigma _2=15$ for different values of m

From Eqs. (23) and (35), $\sigma _\mathrm{s0}=4/a_0^3$ and since the initial leading-order term for the fluid–cell-layer interface position $a_0(0)$ is prescribed, the leading-order shear stress, $\sigma _\mathrm{s0}$, is known initially. Therefore, in order to observe the transition between the different growth regimes, we investigate two possible scenarios for $\sigma _1$ and $\sigma _2$:

• Case (i): $\sigma _1$ and $\sigma _2$ are chosen such that $\sigma _\mathrm{s0}(0)<\sigma _1<\sigma _2$.

• Case (ii): $\sigma _1<\sigma _\mathrm{s0}(0)<\sigma _2$.

In Case (i), tissue growth begins in the first (low growth-rate) phase at a rate $F_1$. The tissue growth leads to pore shrinkage, hence (with the imposed constant fluid flux), increased shear stress. The growth rate thus transitions into the second phase, where growth occurs at a higher rate $F_2$, before finally transitioning into the third phase, where growth ceases. In Case (ii), tissue growth starts in the second phase (at a rate $F_2$) and, as shear stress increases, moves into the third phase, where growth stops. Note that for most of our simulations, we choose the values $F_1=1$, $F_2=3$, $\sigma _1=7$ and $\sigma _2=15$ for the growth function f given by (43). How the choice of these parameters affects model results is discussed further below.

Our model contains two dimensionless geometrical parameters: the pore aspect ratio, $\epsilon$, and the azimuthal wavenumber n that appears in the perturbation $a_2$ in Eq. (21). The pore aspect ratio, $\epsilon$, is unknown for the experiments of Rumpler et al. (2008) and varies between scaffolds: here, we set $\epsilon =0.2$ for most of our simulations to highlight more clearly the effects of pore shape on the tissue growth in the $\theta$ direction. This appears to be a reasonable choice, based on the qualitative comparison made in Fig. 7 later. We consider a range of positive integer values for n to gain insight into the role it plays in the total amount of tissue growth and final patterns obtained.

4.1 Case (i): $\sigma _\mathrm{s0}(0)<\sigma _1<\sigma _2$

While the system (39)–(42) may be readily solved numerically for any suitably smooth differentiable function f, we begin by considering the specific functional form of f, given by (43), when $m\rightarrow \infty$. This corresponds to the case where the tissue growth rates undergo jump discontinuities at critical values of the shear stress. We can then solve the system analytically for the three separate constant-growth-rate regions corresponding to $\sigma _\mathrm{s}<\sigma _1$ (when $f=F_1$), $\sigma _1<\sigma _\mathrm{s}<\sigma _2$ (when $f=F_2$), and $\sigma _\mathrm{s}>\sigma _2$ (when $f=0$). Finally, we connect these regions to determine the full solution. This analytical approach provides physical insight into the parametric dependence of the system growth.

From equations (23) and (35), $\sigma _\mathrm{s0}=4/a_0^3$; therefore, (37), (39) and (43) give

$$\begin{aligned} a_0(t)=\sqrt{a_0^2(0)-2 F_1t} \quad \text{ for } \quad 0\le t<t^*_{01}, \end{aligned}$$

(44)

when $\sigma _\mathrm{s0}(0)< \sigma _1$. Here, $t_{01}^*$ is the time at which $\sigma _\mathrm{s0}=\sigma _{1}$, determined by $a_0(t_{01}^*)=({4}/{\sigma _1})^{1/3}$, and so may be explicitly written as

$$\begin{aligned} t_{01}^*=\frac{a_0^2(0)-(4/\sigma _1)^{2/3}}{2 F_1}. \end{aligned}$$

(45)

At this time, the cell growth transitions into the second phase, where $\sigma _1\le \sigma _\mathrm{s0}<\sigma _2$. Equation (39) then gives

$$\begin{aligned} a_0(t)=\sqrt{a_0^2(0)-2 (F_1-F_2)t_{01}^*-2 F_2t} \quad \text{ for }\quad t_{01}^*\le t<t_{02}^*,\nonumber \\ \end{aligned}$$

(46)

where $a_0(t_{02}^*)=({4}/{\sigma _2})^{1/3}$ and

$$\begin{aligned} t_{02}^*=\frac{a_0^2(0)-2 (F_1-F_2)t_{01}^*-(4/\sigma _2)^{2/3}}{2 F_2}. \end{aligned}$$

(47)

Equation (47) provides an explicit prediction for the time at which tissue growth stops and its dependence on the model parameters $\sigma _1$, $\sigma _2$, $F_1$ and $F_2$ in the limit $m\rightarrow \infty$. We note that, when we substitute for $t_{01}^*$ using (45), there is a rather complex dependence on each of the parameters that appears in our tissue-growth ansatz, (43). However, importantly, order-one changes in any of these parameters will lead to order-one changes in the time taken for the tissue growth. This highlights the need to determine the value of these parameters for a given experimental scenario if this model is to form a predictive tool. We emphasize that in the subsequent examples, the values taken for these parameters are illustrative, but give qualitatively similar behaviour to results in the literature. Repeating the previous procedure for $t\ge t^*_{02}$, we obtain the leading-order fluid–cell-layer interface position:

$$\begin{aligned} a_0(t)=\left\{ \begin{array}{l@{}l@{}l} \sqrt{a_0^2(0)-2 F_1t}&{} \,\,\text{ if }&{} 0\le t<t_{01}^*,\\ \sqrt{a_0^2(0)-2 (F_1-F_2)t_{01}^*-2 F_2t}&{} \,\, \text{ if }&{} t_{01}^*\le t<t_{02}^*,\\ \left( 4/\sigma _2\right) ^{1/3} &{} \,\,\text{ if }&{} t \ge t_{02}^*. \end{array} \right. \nonumber \\ \end{aligned}$$

(48)

We thus see that, to leading order, the position of the fluid–cell-layer interface is $(4/\sigma _2)^{1/3}$. This means that, for a given underlying pore structure, the total amount of tissue grown is independent of $F_1$, $F_2$ and $\sigma _1$. These additional parameters only control the rate at which the final state is approached. Note that when substituting the functional form of f defined in (43) in Eqs. (40) and (42) we find that $a_1$ and $\varUpsilon _2$ do not depend on time and therefore retain their initial values throughout, i.e. $a_1(z,t)=a_1(z,0)$ and $\varLambda _2(z,t)=\varLambda _2(z,0)$. (This is because the integrals in (40) and (42) involve first and higher derivatives of the growth function f, which are thus zero.) This allows for the possibility of axial variations in the equilibrium fluid–cell-layer interface.

Following a similar process to that used above to determine $a_0$, $\varLambda _2(z,t)$ may be found from (35), (37), (41) and (43) as

$$\begin{aligned}&\varLambda _2(z,t)\nonumber \\&=\left\{ \begin{array}{lll} \varLambda _2(z,0) \big [1-2 F_1t/a_0^2(0) \big ]^{n^2/2}&{} \text{ if }&{} 0\le t<t_{01}^*,\\ \varLambda _2(z,0) \big [1-(2 (F_1-F_2)t_{01}^*-2 F_2t)/a_0^2(0)\big ]^{n^2/2}&{} \text{ if }&{} t_{01}^*\le t<t_{02}^*,\\ \varLambda _2(z,0) \big [1-(2 (F_1-F_2)t_{01}^*-2 F_2t_{02}^*)/a_0^2(0)\big ]^{n^2/2}&{} \text{ if }&{} t \ge t_{02}^*. \end{array} \right. \nonumber \\ \end{aligned}$$

(49)

Thus, the evolving cross-sectional profile of the tissue structure is given by

$$\begin{aligned} a(\theta ,z,t)= & {} a_0(t)+\epsilon a_1(z,0)\nonumber \\&+\,\epsilon ^2\big (\varLambda _2(z,t)\cos (n\theta )+\varUpsilon _2(z,0)\big ), \end{aligned}$$

(50)

where $a_0(t)$ and $\varLambda _2(z,t)$ are given by (48) and (49), respectively. Note that if the nutrient solution is supplied under conditions of specified pressure drop rather than specified flux (so that $\zeta (t)=1$), then an identical analysis holds, except with

$$\begin{aligned} t_{01}^*=\frac{a_0^2(0)-4\sigma _1^2}{2 F_1}, \quad t_{02}^*=\frac{a_0^2(0)-2 (F_1-F_2)t_{01}^*-4\sigma _2^2}{2 F_2}. \nonumber \\ \end{aligned}$$

(51)

Fig. 3

Solutions to (39) and (41) for $a_0$ and $\varLambda _2$ in the expression (20) for the fluid–cell-layer interface, for Case (i), Sect. 4.1. Here, $\epsilon =0.2$, $n=4$; the initial conditions are as in (52) with $a_0(0)=0.9$, $a_1(z,0)=-z-0.5$, $\varLambda _2(z,0)=-z+2$, $\varUpsilon _2(z,0)=-z+2$ and growth function f given in (43) with $F_1=1$, $F_2=3$, $\sigma _1=7$, $\sigma _2=15$. The black graphs in a show the numerical solution for $a_0$ for several different values of m, while the analytical solution ($m\rightarrow \infty$) is given by the red dashed graphs (see (48)). b$\varLambda _2(z,t)$ at several different times, where black and red graphs are numerical (for $m=1000$) and analytical ($m\rightarrow \infty$) solutions, respectively. Here, $t_\mathrm{f}=0.25$ is chosen to be sufficiently large that the system has reached an approximate steady state and tissue growth stops

We now compare the above (rather general) analytical solution with numerical simulations to the system (39)–(42) in the appropriate parameter regimes in the following analysis. We relax our assumption of $m\rightarrow \infty$ in the expression for the growth function f given in (43) and consider finite values of m so that the tissue growth transitions smoothly between the three growth rate regions as shear stress increases. We first consider an initial fluid–cell-layer interface that is cylindrical to leading order, but for which higher-order corrections are all chosen to be linearly decreasing along the pore axis (see (31)):

$$\begin{aligned} a_0(0)= & {} 0.9, \end{aligned}$$

(52a)

$$\begin{aligned} a_1(z,0)= & {} -z-0.5, \end{aligned}$$

(52b)

$$\begin{aligned} \varLambda _2(z,0)= & {} -z+2, \end{aligned}$$

(52c)

$$\begin{aligned} \varUpsilon _2(z,0)= & {} -z+2. \end{aligned}$$

(52d)

We choose $\sigma _1$ such that the initial leading-order shear stress $\sigma _\mathrm{s0}(0)<\sigma _1$, and so, as the fluid–cell-layer grows, with attendant increase in shear stress, we sweep through all three regions of the growth function f, given by (43).

In the simulation illustrated in Fig. 3, the wavenumber $n=4$ is used in the azimuthal perturbation to the fluid–cell-layer interfacial profile (see (21)) and the initial fluid–cell-layer interface configuration is given by Eqs. (52). The black curves in Fig. 3a show the numerical solution to (39) for the leading-order fluid–cell-layer interface $a_0(t)$ versus time t, for several different values of m, while the red graph shows the analytical solution (see (48)). Our results here confirm that as the value of m increases, the numerical solution to (39) converges to the analytical solution for $a_0$ in (48). Furthermore, Fig. 3b confirms that when $m\gg 1$ ($m=1000$ is used here), the numerical solution to (41) for $\varLambda _2$ is almost identical to the analytical solution in (49). Therefore, for the remainder of the paper, we use the analytical solutions ($m \rightarrow \infty$) to (39)–(42) for both Case (i) and (ii).

Fig. 4

Analytical solution to (39)–(42) ($m\rightarrow \infty$) as obtained in (44)–(50) for Case (i), Sect. 4.1$\sigma _\mathrm{s0}(0)<\sigma _1<\sigma _2$: a–d are profiles for $a_0$, $a_1$, $\varLambda _2$ and $\varUpsilon _2$, respectively, for the fluid–cell-layer interface (20), with $\epsilon =0.2$, $n=4$ and initial conditions (52), with $a_0(0)=0.9$, $a_1(z,0)=-z-0.5$, $\varLambda _2(z,0)=-z+2$ and $\varUpsilon _2(z,0)=-z+2$; e, f are shear stresses at leading and $\epsilon$ orders, $\sigma _\mathrm{s0}(t)$ and $\sigma _\mathrm{s1}(t)$ (see (23) and (35)), respectively, and g, h are the fluid–cell-layer interfacial cross sections at initial and final times ($t_\mathrm{f}=0.25$, chosen to be sufficiently large that the system has reached an approximate steady state and tissue growth stops), respectively, for the growth function f given in (43) with $F_1=1$, $F_2=3$, $\sigma _1=7$, $\sigma _2=15$ and $m\rightarrow \infty$. Here, $(x,y)=(r \sin \theta ,r \cos \theta ).$ The red dashed lines in a, e correspond to the transition times and the values of $\sigma _1$, $\sigma _2$, respectively

Figure 4 illustrates the analytical results to (39)–(42) ($m\rightarrow \infty$) as obtained in (44)–(50) for the initial fluid–cell-layer interface configuration in (52). (The results of Fig. 4a, c were already shown in Fig. 3, but we now discuss them in more detail.) The leading-order radius of the fluid–cell-layer interface, $a_0(t)$, decreases approximately linearly with t (Fig. 4a), which is consistent with a Taylor expansion of (44) for small time. The leading-order shear stress, $\sigma _\mathrm{s0}$, also increases approximately linearly, until it surpasses the value $\sigma _1$ and we enter the regime of maximal tissue growth rate ($\sigma _1\le \sigma _\mathrm{s0}<\sigma _2$) (Fig. 4e). The fluid–cell-layer interfacial radius then decreases rapidly so that the shear stress also rapidly increases further, until finally it exceeds $\sigma _2$ and the growth is halted (see the solution for $a_0(t)$ in Fig. 4a).

Since the function f, given by (43), is piecewise constant for our chosen limit $m\rightarrow \infty$, $a_1$ and $\varUpsilon _2$ do not vary in time, as discussed in our analytical work above (see Fig. 4b, d). The evolution of $\varLambda _2(z,t)$ is shown in Fig. 4c (see (49)): this function retains its linear dependence on the axial coordinate z, while approaching zero smoothly as time progresses. The evolution of the leading- and second-order shear-stress components, $\sigma _\mathrm{s0}$ and $\sigma _\mathrm{s1}$, is shown in Fig. 4e, f, which are obtained from (23) and (35).

The overall picture may be visualized by considering the fluid–cell-layer interfacial profile at several different cross sections along the scaffold, both initially, and when the system has reached equilibrium (Fig. 4g, h, respectively). As observed, the tissue will grow so that ultimately the tube is circular in cross section, but the radius may vary along the axis at $O(\epsilon )$ due to the initial choices of $a_1$ and $\varUpsilon _2$.

We next consider an initial configuration in which the initial profiles for $a_1$, $\varUpsilon$ and $\varLambda$ all increase rather than decrease with distance along the pore axis (the direction of flow):

$$\begin{aligned} a_0(0)= & {} 0.9, \end{aligned}$$

(53a)

$$\begin{aligned} a_1(z,0)= & {} z-0.5, \end{aligned}$$

(53b)

$$\begin{aligned} \varLambda _2(z,0)= & {} z-2, \end{aligned}$$

(53c)

$$\begin{aligned} \varUpsilon _2(z,0)= & {} z-2. \end{aligned}$$

(53d)

As in the previous example, during the tissue growth, the shear stress attains values in all three regions of the domain of the growth function f, taking the tissue growth through regimes of moderate, fast, and ultimately cessation of growth. The final fluid–cell-layer interfacial profile is again circular in cross section, though with radius that varies along the length of the pore. The evolution towards this final configuration is shown in Fig. 5.

Fig. 5

Analytical solution to (39)–(42) ($m\rightarrow \infty$) as obtained in (44)–(50) for Case (i), Sect. 4.1$\sigma _\mathrm{s0}(0)<\sigma _1<\sigma _2$: a–d are profiles for $a_0$, $a_1$, $\varLambda _2$ and $\varUpsilon _2$, respectively, in the fluid–cell-layer interface (20), with $\epsilon =0.2$, $n=4$ and initial conditions (53) with $a_0(0)=0.9$, $a_1(z,0)=z-0.5$, $\varLambda _2(z,0)=z-2$ and $\varUpsilon _2(z,0)=z-2$; e, f are shear stresses at leading and $\epsilon$ orders, $\sigma _\mathrm{s0}(t)$ and $\sigma _\mathrm{s1}(t)$ (see (23) and (35)) respectively, and g, h are fluid–cell-layer interface cross sections at initial and final times ($t_\mathrm{f}=0.25$, chosen to be sufficiently large that the system has reached an approximate steady state and tissue growth stops), respectively, for the growth function f given in (43) with $F_1=1$, $F_2=3$, $\sigma _1=7$, $\sigma _2=15$ and $m\rightarrow \infty$. Here, $(x,y)=(r \sin \theta ,r \cos \theta )$. The red dashed lines in figures a, e correspond to the transition times and the values of $\sigma _1$, $\sigma _2$, respectively

4.2 Case (ii) $\sigma _1<\sigma _\mathrm{s0}(0)<\sigma _2$

When $\sigma _1<\sigma _\mathrm{s0}(0)<\sigma _2$, cell growth begins in the second of the three regions of the domain of the growth function f illustrated in Fig. 2 (fast initial growth). As in Sect. 4.1, we examine the case $m\rightarrow \infty$ in which analytical progress is possible. Substituting (23), (35), (37) and (43) into (39)–(42) and following a similar approach to that of Sect. 4.1 gives

$$\begin{aligned} a_0(t)=\left\{ \begin{array}{lll} \sqrt{a_0^2(0)-2 F_2t}&{} \,\, \text{ if }&{} 0 \le t<t_0^*,\\ \left( 4/\sigma _2\right) ^{1/3} &{} \,\, \text{ if }&{} t \ge t_0^*, \end{array} \right. \end{aligned}$$

(54)

and

$$\begin{aligned} \varLambda _2(z,t)=\left\{ \begin{array}{lll} \varLambda _2(z,0) \big [1-2 F_2t/a_0^2(0) \big ]^{n^2/2}&{} \text{ if }&{} 0\le t<t_0^*,\\ \varLambda _2(z,0) \big [1-2 F_2t_0^*/a_0^2(0)\big ]^{n^2/2}&{} \text{ if }&{} t\ge t_0^*, \end{array} \right. \nonumber \\ \end{aligned}$$

(55)

where

$$\begin{aligned} t_0^*=\frac{a_0^2(0)-(4/\sigma _2)^{2/3}}{2 F_2}. \end{aligned}$$

(56)

Note that $a_1$ and $\varUpsilon _2$ again do not depend on time, i.e. $a_1(z,t)=a_1(z,0)$ and $\varLambda _2(z,t)=\varLambda _2(z,0)$, as discussed earlier in Sect. 4.1. As in Case (i), the position of the fluid–cell-layer interface is given, to leading order, by $(4/\sigma _2)^{1/3}$, (54). Hence, for a given underlying pore structure, the leading-order amount of tissue grown will be independent of $F_1$, $F_2$ and $\sigma _1$. Equation (56) provides a prediction for the time at which tissue growth stops in this regime and its dependence on the model parameters in the limit $m\rightarrow \infty$. Since this scenario is simpler than Case (i), the dependence of the time taken for the tissue to complete growth is less complex. In particular, in this case the time to cessation of growth is independent of $\sigma _1$ and $F_1$, and depends on $F_2$ in an inversely proportional fashion. Nevertheless, as outlined in Case (i) in Sect. 4.1, there is a clear need to determine the values for $\sigma _2$ and $F_2$ if this model is to form a reliable predictive tool.

Fig. 6

Analytical solution to (39)–(42) ($m\rightarrow \infty$) as obtained in (44)–(50) for Case (ii), Sect. 4.2, $\sigma _1<\sigma _\mathrm{s0}<\sigma _2$: a–d are profiles for $a_0$, $a_1$, $\varLambda _2$ and $\varUpsilon _2$, respectively, in the fluid–cell-layer interface (20), with $\epsilon =0.2$, $n=4$ and initial conditions (52) with $a_0(0)=0.8$, $a_1(z,0)=-z-0.5$, $\varLambda _2(z,0)=-z+2$ and $\varUpsilon _2(z,0)=-z+2$; e, f are shear stresses at leading and $\epsilon$ orders, $\sigma _\mathrm{s0}(t)$ and $\sigma _\mathrm{s1}(t)$ (see (23) and (35)), respectively, and g, h are fluid–cell-layer interface cross sections at initial and final times ($t_\mathrm{f}=0.25$, chosen to be sufficiently large that the system has reached an approximate steady state and tissue growth stops), respectively, for the growth function f given in (43) with $F_1=1$, $F_2=3$, $\sigma _1=7$, $\sigma _2=15$ and $m\rightarrow \infty$. Here, $(x,y)=(r \sin \theta ,r \cos \theta ).$ The red dashed lines in figures a, e correspond to the transition time and the value of $\sigma _2$, respectively

In Fig. 6, we consider an initial configuration identical to that used in Fig. 4, given by Eq. (52), except that the leading-order fluid–cell-layer interfacial radius is slightly smaller, $a_0=0.8$. This ensures that the initial leading-order shear stress $\sigma _\mathrm{s0}(0)$ is sufficiently large to lie within the second region of the domain of the growth function f in (43) for identical values of $\sigma _1$, $\sigma _2$, $F_1$ and $F_2$. The tissue growth here is initially faster than in the previous cases: the fluid–cell-layer interfacial profile shrinks rapidly and we quickly transit to region three of the domain of the growth function, in which growth is suppressed.

Note that, similar to what was shown in Fig. 3, excellent agreement was again obtained between the numerical solutions of the system (39)–(42) (for $m=1000$) and the analytical asymptotic prediction (54) and (55) for the leading-order fluid–cell-layer interfacial radius $a_0$ as a function of time and the perturbation function $\varLambda _2(z,t)$ versus z at several different times (results not shown here).

4.3 Comparison with experimental results

Figure 7 shows a direct comparison between experimental results visualized under a confocal laser scanning microscope by Rumpler et al. (2008), and analytical solutions of our model for several different values of the polygonal cross section n (the wavenumber in the azimuthal perturbation to the initial fluid–cell-layer interfacial profile (see (21)). The results show that our model gives a reasonable qualitative agreement with the experimental results, illustrating the tendency of the fluid–cell-layer interface to become ultimately circular, independent of the underlying pore geometry. Note that here the experimental tissue grown (in Fig. 7a–c) is shown after 21 days, while in our simulation the dimensionless time at which the tissue growth is observed to stop is $t_\mathrm{f}=0.25$ (see Figs. 4–6), which corresponds to a dimensional time of 20.5 days using the time scale identified in Table 1. Furthermore, as shown in Fig. 7 (and as expected from the form of the growth law), more tissue grows at the corners of the scaffold structure so that the fluid–cell-layer interface subsequently becomes more circular. This behaviour leads to the formation of a final round fluid–cell-layer interface, regardless of the original shape (at least for the parameters chosen here).

Fig. 7

a–c New tissue formed in three-dimensional matrix channels visualized under a confocal laser scanning microscope by Rumpler et al. (2008). d–f Upstream side ($z=0$) of the fluid–cell-layer interfacial cross section at initial and final times ($t_\mathrm{f}=0.25$, chosen to be suitably large such that the system has reached an approximate steady state) for $n=3$, $n=4$ and $n=6$, respectively, with $\epsilon =0.2$ and for the initial conditions in (52) with $a_0(0)=0.9$, $a_1(z,0)=z-0.5$, $\varLambda _2(z,0)=z-2$ and $\varUpsilon _2(z,0)=z-2$, the growth function f given in (43) with $F_1=1$, $F_2=3$, $\sigma _1=7$, $\sigma _2=15$ and $m\rightarrow \infty$. Here, $(x,y)=(r \sin \theta ,r \cos \theta )$

4.4 Optimization and parameter sensitivity

A question of interest to tissue engineers is the optimal scaffold configuration, in terms of internal pore morphology (pore size and shape) that maximizes net tissue yield over the course of an experiment. To answer this question, we first identify a metric for tissue growth. The total volume V(t) of tissue grown within the pore by time t is given by

$$\begin{aligned} V(t)=\int _0^1\int _0^{2\pi } \frac{1}{2} \left( a^2(z,\theta , 0)-a^2(z,\theta , t)\right) \,\mathrm {d}\theta \,\mathrm {d}z. \end{aligned}$$

(57)

To gain insight into the influence of the pore shape on the tissue growth, we first consider the dependence of V(t) on the value of n, the number of azimuthal modes in the internal fluid–cell-layer configuration within the pore, in Fig. 8a. These results indicate that introducing regions of high curvature in the fluid–cell-layer interfacial structure enables tissue to be formed more quickly in the structure over the intermediate growth period. During the initial growth phase, V(t) is an increasing function of n: for $t=0.025$, for example, the volume of tissue with $n=6$ is approximately double that with $n=2$. However, as t increases, the volumes for all n values equalize, and the final amount of tissue growth is largely independent of the number of lobes, n. Thus, we may conclude that if the rate of tissue growth is a primary objective, then increasing the number of lobes in the tissue-engineering construct is advantageous. However, if the concern is only with the final volume of tissue grown, then the pore shape is less important.

Fig. 8

Total volume of tissue, V(t) (defined in (57)) versus time, for fluid–cell-layer interfacial profile (20), with the initial fluid–cell-interface configuration given in (52), $a_0(0)=0.9$, $a_1(z,0)=-z-0.5$, $\varLambda _2(z,0)=-z+2$, $\varUpsilon _2(z,0)=-z+2$ and for a several different values of the polygonal cross section n (the wavenumber in the azimuthal perturbation to the fluid–cell-layer interfacial profile (see (21)); b fluid–cell-layer interfacial aspect ratio $\epsilon$; c$F_1$ and $F_2$ (see (43)); and d shear stresses $\sigma _1$ and $\sigma _2$ (see (43)). In (a), $\epsilon =0.5$; in (b), $n=4$ and the growth function f is as given in Fig. 2 with $F_1=1$, $F_2=3$, $\sigma _1=7$ and $\sigma _2=15$. In (c) and (d), $\epsilon =0.5$ and $n=4$. In all cases $m\rightarrow \infty$

In order to further study the model’s parameter sensitivity, we also investigate how our results depend on $\epsilon$, the fluid–cell-layer interfacial aspect ratio. A graph showing the total amount of tissue grown within the pore, V(t), as a function of $\epsilon$, is shown in Fig. 8b. Here, our results show that the final amount of tissue grown increases with $\epsilon$ (though only by about 10% over the model’s range of validity). The variation of total tissue grown with $\epsilon$ manifests itself through $\varLambda _2$, given by (49) and (55) for cases (i) and (ii), respectively.

The temporal dependence of tissue growth on the parameters $F_1$ and $F_2$, and $\sigma _1$ and $\sigma _2$ is shown in Fig. 8c, d, respectively. The final position of the fluid–cell-layer interface was seen to be given to leading order by $(4/\sigma _2)^{1/3}$ (Eqs. (48) and (54) for Cases (i) and (ii), respectively). This indicates that for a given underlying pore structure, the total amount of tissue grown is independent of $F_1$, $F_2$ and $\sigma _1$ to leading order, which is confirmed in Fig. 8c, d.

5 Conclusions

We have presented a simplified mathematical model for the growth of tissue in a tissue-engineering scaffold to gain insight into the effect of pore morphology on the tissue growth. The flow of nutrient to the cells was captured by the Stokes equations, while the cell proliferation was modelled by a law that accounted for the effects of the underlying fluid–cell-layer interface curvature, and fluid shear stress at the growing tissue surface, on the rate of tissue growth. Exploiting the geometrical features of a typical scaffold, namely a structure composed of a series of pores that are nearly cylindrical, allowed us to proceed via an asymptotic approach that led to a reduced system of four simple differential equations for the tissue growth. The resulting equations were analyzed numerically and analytically for a typical growth law, and an analytic expression was obtained when the growth law was piecewise constant. The analytic solution was shown to agree with the numerics, supporting its use for rapid testing and analysis of the system in comparisons with experimental data from Rumpler et al. (2008).

The number of azimuthal modes in the initial fluid-cell-layer interface profile, n (which we take as a proxy for the shape of the underlying scaffold pore), was found to have a minimal effect on the final amount of tissue grown. These results suggest that focusing effort into engineering the pore geometry may be beneficial if the rate of tissue growth is a principal concern, but if maximizing the final volume of tissue that can be grown is the main objective, then the details of the shape of the (nearly cylindrical) pore within the scaffold are not important. In contrast, the total amount of tissue grown depends on $\epsilon$, the fluid–cell-layer interface aspect ratio, with the amount of final tissue grown increasing with increasing $\epsilon$.

The results of this work, once calibrated against available data, offer a simple framework for testing the behaviour of different scaffold pore geometries without the need for many complex experiments to be conducted. The model should ultimately allow for the prediction of regimes in which tissue growth may be enhanced, offering improvements and additional insight into the current operating strategies used. To compare our theoretical results with experiments requires an estimate of ${\hat{\lambda }}$, the growth-rate parameter in Eq. (10), for the dataset under consideration. This parameter depends on many experimental details, including cell type, the physical characteristics of the tissue-engineering scaffold and the concentration of the nutrient in the culture fluid. In principle, $\hat{\lambda }$ could be measured or estimated directly from a suitable experimental dataset, as we did for the data of Rumpler et al. (2008). Here, ${\hat{\lambda }}$ was estimated by extracting the gradient of the projected tissue area versus time graph in Fig. 4(b) of Rumpler et al. (2008). The time taken for the tissue to form and the total amount of tissue grown were inherently linked to the parameters in our tissue-growth ansatz. For this model to form a reliable predictive tool, the parameters that appear in the growth ansatz need to be determined experimentally. While this is possible in principle by examining temporal data, in this paper we had access only to final-time snapshots. A close collaboration between experimentalists would be necessary to pin down these parameters more accurately, and represents a future research direction.

The model presented in this paper has the advantage of simplicity, but obviously fails to capture many details of the real experimental system, which may be important in some scenarios. For example, throughout this study, the nutrient is assumed to be present in excess so that cells always have sufficient nutrient to proliferate, and no significant nutrient depletion occurs over the length of the pore. If nutrient is present in low concentration, this may not be true. In such cases, our model could be generalized to capture the effect of nutrient concentration gradients (Sanaei and Cummings 2017, 2018). While significant gradients in nutrient concentration are unlikely to arise at the single-pore scale, they could certainly be present over the scale of an entire scaffold, consisting of many pores. One could consider scaling-up our model to describe an entire scaffold, with the nutrient flux varying in both time and spatial location within the scaffold. The growth parameter $\hat{\lambda }$ [see (10)] would then be considered a function of the local nutrient concentration, again informed by available data.

Furthermore, our growth model is empirical, based purely on experimental observations of how a tissue interface grows within pores of differing curvatures. Though these observations were validated across a range of different pores (Rumpler et al. 2008), one could argue that a more complete model is needed, which accounts for the details at the cell scale and the underlying mechanisms that drive cells to proliferate. Much remains to be done in terms of building such a detailed predictive model, which could offer improved insight into how the structural details of an underlying scaffold impact tissue engineering outcomes. Nonetheless, we believe that this model, which is characterized through a simple yet descriptive growth law that may be connected to data through the growth parameter $\hat{\lambda }$ and can be solved with minimal computational effort, offers some utility in addressing scaffold design questions.