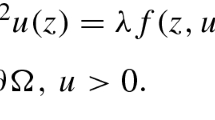Nonlinear Robin problems with a reaction of arbitrary growth

Abstract

We consider Robin problems driven by a nonhomogeneous differential operator involving a reaction that has zeros and no global growth restriction. Using variational methods together with truncation and perturbation techniques as well as Morse theory, we prove multiplicity theorems with precise sign information for all the solutions.

1 Introduction

Let ${\varOmega }\subseteq {\mathbb {R}}^N$ be a bounded domain with a $C^2$-boundary $\partial {\varOmega }$. In this paper, we deal with the following nonlinear Robin problem

$$\begin{aligned} \begin{aligned} -{{\mathrm{div}}}a(\nabla u)&= f(x,u) \quad \text {in } {\varOmega },\\ \frac{\partial u}{\partial n_a}&= -\beta (x) |u|^{p-2}u \quad \text {on } \partial {\varOmega }, \end{aligned} \end{aligned}$$

(1.1)

where $a: {\mathbb {R}}^N\rightarrow {\mathbb {R}}^N$ is assumed to be continuous, strictly monotone and satisfies certain regularity and growth conditions which are listed in hypotheses H(a) below. These hypotheses are general enough to incorporate various differential operators of interest such as the p-Laplacian ($1<p<\infty$). However, we stress that the differential operator here is not $(p-1)$-homogeneous, and this is a source of difficulties in the analysis of problem (1.1), in particular in the search for nodal (sign changing) solutions. By $\frac{\partial u}{\partial n_a}$, we denote the generalized normal derivative defined by

$$\begin{aligned} \frac{\partial u}{\partial n_a}=\left( a(\nabla u),n\right) _{{\mathbb {R}}^N} \end{aligned}$$

with n(x) being the outward unit normal at $x\in \partial {\varOmega }$. We further assume that the reaction $f:{\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function; that is, $x\mapsto f(x,s)$ is measurable for all $s\in {\mathbb {R}}$ and $s\mapsto f(x,s)$ is continuous for a.a. $x\in {\varOmega }$. The interesting feature of our work is the fact that we do not impose any global growth condition on $f(x,\cdot )$. Instead, we assume that $f(x,\cdot )$ admits x-dependent zeros of constant sign. In the context of Dirichlet equations driven by the p-Laplacian, reactions with zeros but having subcritical global growth were considered by Bartsch et al. [4] and Iturriaga et al. [11]. In both papers, the zeros are supposed to be x independent, that is, constant functions. For Neumann equations involving the p-Laplacian, subcritical nonlinearities with constant zeros have been studied by Aizicovici et al. [2]. Other works dealing with Robin equations driven by the p-Laplacian are those of Zhang et al. [28] and Zhang and Xue [29], but with stronger hypotheses on the reaction. Finally, we mention the papers of Duchateau [7], Lê [13] and Papageorgiou and Rădulescu [20] dealing with different types of eigenvalue problems for the Robin p-Laplacian.

The aim of this work is to prove multiplicity theorems for problem (1.1) providing complete sign information of the solutions obtained. We use variational methods based on critical point theory combined with suitable truncation and perturbation techniques along with Morse theory to show that problem (1.1) has at least three nontrivial solutions whereby two of them have constant sign (one positive, the other negative) and the third one is nodal. To the best of our knowledge, for Robin problems, only Papageorgiou and Rădulescu [20] and Winkert [26] obtained nodal solutions for a different class of parametric Robin equations driven by the p-Laplacian being a $(p-1)$-homogeneous differential operator.

In the next section, for the reader’s convenience, we review the main mathematical tools that we will use in the sequel.

2 Mathematical background

Let X be a Banach space with norm $\Vert \cdot \Vert _X$ and denote by $X^*$ its dual space equipped with the dual norm $\Vert \cdot \Vert _{X^*}$, that is

$$\begin{aligned} \Vert \xi \Vert _{X^*}=\sup \left\{ \langle \xi , v \rangle _{(X^*,X)} : v \in X, \Vert v\Vert _X\le 1\right\} , \end{aligned}$$

where $\langle \cdot ,\cdot \rangle _{(X^*,X)}$ stands for the duality paring of $(X^*,X)$.

Definition 2.1

The functional ${\varphi }\in C^1(X)$ fulfills the Palais–Smale condition (the PS-condition for short) if the following holds: Every sequence $(u_n)_{n \ge 1} \subseteq X$ such that $({\varphi }(u_n))_{n \ge 1}$ is bounded in ${\mathbb {R}}$ and ${\varphi }'(u_n) \rightarrow 0$ in $X^*$ as $n \rightarrow \infty$ admits a strongly convergent subsequence.

This is a compactness-type condition on the functional ${\varphi }$ which compensates the fact that the ambient space X need not to be locally compact (X is in general infinite dimensional). The PS-condition leads to a deformation theorem which in turn generates the minimax theory for the critical values of ${\varphi }$. One of the main results in this theory is the so-called mountain pass theorem due to Ambrosetti and Rabinowitz [3].

Theorem 2.2

Let $\varphi \in C^1(X)$ be a functional satisfying the PS-condition and let $u_1,u_2 \in X, \Vert u_2-u_1\Vert _X> \rho >0$,

$$\begin{aligned} \max \{\varphi (u_1),\varphi (u_2)\}<\inf \, \{\varphi (u): \Vert u-u_1\Vert _X=\rho \}=:m_\rho \end{aligned}$$

and $c=\inf _{\gamma \in {\varGamma }}\,\max _{0 \le t \le 1} \varphi (\gamma (t))$ with ${\varGamma }=\{\gamma \in C\left([0,1],X\right): \gamma (0)=u_1, \gamma (1)=u_2\}$. Then, $c \ge m_\rho$ with c being a critical value of $\varphi$.

By $L^{p}({\varOmega }) \; \left( \text {or } L^{p}\left( {\varOmega };{\mathbb {R}}^N\right) \right)$ and $W^{1,p}({{\varOmega }})$, we denote the usual Lebesgue and Sobolev spaces with their norms $\Vert \cdot \Vert _{p}$ and $\Vert \cdot \Vert _{1,p}$, which is given by

$$\begin{aligned} \Vert u\Vert _{1,p}= \left( \Vert \nabla u\Vert ^p_{p} +\Vert u\Vert ^p_{p}\right) ^{\frac{1}{p}} \quad \text {for all }u \in W^{1,p}({\varOmega }). \end{aligned}$$

The norm of ${\mathbb {R}}^N$ is denoted by $|\cdot |$, and $(\cdot ,\cdot )_{{\mathbb {R}}^N}$ stands for the inner product in ${\mathbb {R}}^N$. In addition to the Sobolev space $W^{1,p}({\varOmega })$, we will also use the ordered Banach space $C^1(\overline{{\varOmega }})$ with norm $\Vert \cdot \Vert _{C^1({\overline{{\varOmega }}})}$ and its positive cone

$$\begin{aligned} C^1(\overline{{\varOmega }})_+=\left\{ u \in C^1(\overline{{\varOmega }}): u(x) \ge 0 \quad \text {for all } x \in \overline{{\varOmega }}\right\} , \end{aligned}$$

which has a nonempty interior given by

$$\begin{aligned} {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) =\left\{ u \in C^1({\overline{{\varOmega }}})_+: u(x)>0 \quad \text {for all } x \in {\overline{{\varOmega }}}\right\} . \end{aligned}$$

On $\partial {\varOmega }$, we use the $(N-1)$-dimensional Hausdorff (surface) measure denoted by $\sigma (\cdot )$. Then, we can define the Lebesgue spaces $L^{s}(\partial {\varOmega })$ with $1 \le s \le \infty$ and norm $\Vert \cdot \Vert _{s,\partial {\varOmega }}$. It is known that there exists a unique linear continuous map $\gamma _0:W^{1,p}({{\varOmega }}) \rightarrow L^{p}(\partial {\varOmega })$, known as the trace map, such that $\gamma _0(u) =u\big |_{\partial {\varOmega }}$ for all $u \in W^{1,p}({{\varOmega }}) \cap C({\overline{{\varOmega }}})$. In fact, the mapping $\gamma _0$ is compact and

$$\begin{aligned} {{\mathrm{im}}}\gamma _0=W^ {\frac{1}{p'},p}(\partial {\varOmega }), \qquad \ker \gamma _0=W^{1,p}_0({{\varOmega }}) \end{aligned}$$

with $\frac{1}{p}+\frac{1}{p'}=1$. From now on, for the sake of notational simplicity, we drop the use of the trace map $\gamma _0$. It is understood that all restrictions of the Sobolev functions $u \in W^{1,p}({{\varOmega }})$ on the boundary $\partial {\varOmega }$ are defined in the sense of traces.

Next, we introduce our hypotheses on the map $a(\cdot )$. To this end, let $\omega \in C^1(0,+\infty )$ and assume that it satisfies

$$\begin{aligned} 0 < \hat{c} \le \frac{t \omega '(t)}{\omega (t)} \le c_0 \quad \text {and} \quad c_1 t^{p-1} \le \omega (t) \le c_2 (1+t^{p-1}) \end{aligned}$$

(2.1)

for all $t>0$ and with some constants $c_1,c_2>0$. The hypotheses on $a: {\mathbb {R}}^N \rightarrow {\mathbb {R}}^N$ read as follows.

• H(a): $a(\xi )=a_0\left(|\xi |\right)\xi$ for all $\xi \in {\mathbb {R}}^N$ with $a_0(t)>0$ for all $t>0$ and

  • (i) $a_0 \in C^1(0,\infty ), t\mapsto ta_0(t)$ is strictly increasing on $(0,\infty ), \lim _{t \rightarrow 0^+} t a_0(t)=0$, and $\displaystyle \lim _{t \rightarrow 0^+} \frac{t a_0'(t)}{a_0(t)}=c>-1$;

  • (ii) $\displaystyle \left|\nabla a(\xi )\right| \le c_3 \frac{\omega \left(|\xi |\right)}{|\xi |}$ for all $\xi \in {\mathbb {R}}^N {\setminus } \{0\}$ and some $c_3>0$;

  • (iii) $\displaystyle \left(\nabla a(\xi ) y , y \right)_{{\mathbb {R}}^N}\ge \frac{\omega \left(|\xi |\right)}{|\xi |} |y|^2$ for all $\xi \in {\mathbb {R}}^N {\setminus }\{0\}$ and all $y \in {\mathbb {R}}^N$.

  • (iv) if $G_0(t)=\int ^t_0 a_0(s)s \mathrm{d}s$, then

    $$\begin{aligned} pG_0(t)-a_0(t)t^2 \ge 0 \quad \text {for all }t\ge 0 \end{aligned}$$

    and there exist $1<\theta <\varsigma \le p$ and $\tilde{c},c^*>0$ such that

    $$\begin{aligned} t \rightarrow G_0 \left(t^{\frac{1}{\varsigma }} \right) \text { is convex on } {\mathbb {R}}_+=[0,+\infty ) \end{aligned}$$

    and

    $$\begin{aligned} \lim _{t \rightarrow 0^+} \frac{\varsigma G_0(t)}{t^\varsigma }=c^*, \qquad a_0(t)t^2-\theta G_0(t) \ge \tilde{c} t^p \quad \text {for all }t>0. \end{aligned}$$

Remark 2.3

These conditions on $a(\cdot )$ are motivated by the nonlinear regularity theory of Lieberman [14] and the nonlinear maximum principles of Pucci and Serrin [23]. The above hypotheses imply that $G_0(\cdot )$ is strictly convex and strictly increasing. Let $G(\xi )=G_0(|\xi |)$ for all $\xi \in {\mathbb {R}}^N$. Then, we have

$$\begin{aligned} \nabla G(\xi )=G_0'(|\xi |) \frac{\xi }{|\xi |}=a_0(|\xi |)\xi =a(\xi ) \quad \text {for all } \xi \in {\mathbb {R}}^N {\setminus } \{0\}. \end{aligned}$$

Hence, $G(\cdot )$ is the primitive of $a(\cdot )$ and of course $\xi \mapsto G(\xi )$ is convex with $G(0)=0$. It follows that

$$\begin{aligned} G(\xi ) \le (a(\xi ),\xi )_{{\mathbb {R}}^N} \quad \text {for all }\xi \in {\mathbb {R}}^N. \end{aligned}$$

(2.2)

The next lemma is a straightforward consequence of the above hypotheses and summarizes the main properties of the map $a(\cdot )$.

Lemma 2.4

If hypotheses H(a)(i), (ii), (iii) hold, then

• (i) the map $\xi \rightarrow a(\xi )$ is continuous, maximal monotone and strictly monotone;

• (ii) $\left|a(\xi )\right| \le c_4 \left(1+\left|\xi \right|^{p-1}\right)$   for all $\xi \in {\mathbb {R}}^N$ and some $c_4>0$;

• (iii) $\left( a(\xi ) , \xi \right)_{{\mathbb {R}}^N} \ge \frac{c_1}{p-1}\left|\xi \right|^p$   for all $\xi \in {\mathbb {R}}^N$.

This lemma together with (2.1) and (2.2) leads to the following growth estimates for the primitive $G(\cdot )$.

Corollary 2.5

If hypotheses H(a) (i), (ii), (iii) hold, then

$$\begin{aligned} \frac{c_1}{p(p-1)}|\xi |^p \le G(\xi ) \le c_5\left(1+\left|\xi \right|^{p}\right) \quad \text {for all } \xi \in {\mathbb {R}}^N \text { and some } c_5>0. \end{aligned}$$

Example 2.6

The following maps $a:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^N$ satisfy hypotheses H(a).

• (i) Let $1<p<\infty$, and let $a(\xi )=|\xi |^{p-2}\xi$. Then, $a(\cdot )$ represents the well-known p-Laplace differential operator defined by

  $$\begin{aligned} {\varDelta }_p u={{\mathrm{div}}}\left(|\nabla u|^{p-2} \nabla u\right) \quad \text {for all } u \in W^{1,p}({\varOmega }). \end{aligned}$$

• (ii) Let $1<q<p<\infty$ and let $a(\xi )=|\xi |^{p-2}\xi +|\xi |^{q-2}\xi$. Then, $a(\cdot )$ becomes the (p, q)-differential operator defined by

  $$\begin{aligned} {\varDelta }_p u+{\varDelta }_q u={{\mathrm{div}}}\left(|\nabla u|^{p-2} \nabla u\right)+{{\mathrm{div}}}\left(|\nabla u|^{q-2} \nabla u\right) \end{aligned}$$

  for all $u \in W^{1,p}({\varOmega })$. Such differential operators arise in various physical applications (see Papageorgiou and Smyrlis [21], Papageorgiou and Winkert [22] and the references therein).

• (iii) Let $1<p<\infty$ and let $a(\xi )=\left(1+|\xi |^2\right)^{\frac{p-2}{2}}\xi$. In this case, $a(\cdot )$ corresponds to the generalized p-mean curvature differential operator which is defined by

  $$\begin{aligned} {{\mathrm{div}}}\left[ \left(1+|\nabla u|^2\right)^{\frac{p-2}{2}} \nabla u \right] \quad \text {for all } u \in W^{1,p}({\varOmega }). \end{aligned}$$

• (iv) For $1<p<\infty$ let $a(\xi )=|\xi |^{p-2}\xi \left[ 1+\frac{1}{1+|\xi |^p} \right]$. In this case, the primitive $G_0(\cdot )$ is

  $$\begin{aligned} G_0(t)=\frac{1}{p}t^p+\frac{1}{p}\ln \left( 1+t^p\right) \quad \text {for all } t \ge 0 \end{aligned}$$

  and the corresponding differential operator is

  $$\begin{aligned} {\varDelta }_p u+{{\mathrm{div}}}\left( \frac{|\nabla u|^{p-2}\nabla u}{1+|\nabla u|^p} \right) \quad \text {for all } u \in W^{1,p}({\varOmega }), \end{aligned}$$

  which arises in plasticity theory (see Fuchs and Gongbao [8]).

Our hypotheses on the boundary weight function $\beta (\cdot )$ are the following.

H($\beta$)::

$\beta \in C^{0,\alpha }(\partial {\varOmega })$ with $0<\alpha <1$ and $\beta (x) \ge 0$ for all $x\in \partial {\varOmega }$.

Let $f_0 : {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a Carathéodory function satisfying a subcritical growth with respect to $s\in {\mathbb {R}}$, that is

$$\begin{aligned} |f_0(x,s)| \le \tilde{a}(x)\left( 1+|s|^{r-1}\right) \quad \text { for a.a. } x \in {\varOmega }\text { and all } s \in {\mathbb {R}}, \end{aligned}$$

with $\tilde{a} \in L^\infty ({\varOmega })_+$, and $1<r<p^*$, where $p^*$ is the critical exponent of p given by

$$\begin{aligned} p^*= {\left\{ \begin{array}{ll} \frac{Np}{N-p} \quad &{} \text { if } p <N, \\ +\infty &{} \text { if } p \ge N. \end{array}\right. } \end{aligned}$$

Let $F_0(x,s)=\int ^s_0f_0(x,t)dt$, and let $\varphi _0: W^{1,p}({\varOmega }) \rightarrow {\mathbb {R}}$ be the $C^1$-functional defined by

$$\begin{aligned} \varphi _0(u)=\int _{{\varOmega }}G(\nabla u)\mathrm{d}x +\frac{1}{p}\int _{\partial {\varOmega }} \beta (x) |u|^p\mathrm{d}\sigma -\int _{\varOmega }F_0(x,u) \mathrm{d}x. \end{aligned}$$

The next result can be proved exactly as in Papageorgiou and Rădulescu [20] and Winkert [24] based on the regularity results of Lieberman [14].

Theorem 2.7

If $u_0 \in W^{1,p}({\varOmega })$ is a local $C^1(\overline{{\varOmega }})$-minimizer of $\varphi _0$; i.e., there exists $\rho _0>0$ such that

$$\begin{aligned} \varphi _0(u_0) \le \varphi _0(u_0+h) \quad \text {for all } h \in C^1(\overline{{\varOmega }}) \text { with } \Vert h\Vert _{C^1(\overline{{\varOmega }})} \le \rho _0, \end{aligned}$$

then, $u_0 \in C^{1,\gamma }(\overline{{\varOmega }})$ for some $\gamma \in (0,1)$ and $u_0$ is also a local $W^{1,p}({\varOmega })$-minimizer of $\varphi _0$; i.e., there exists $\rho _1>0$ such that

$$\begin{aligned} \varphi _0(u_0) \le \varphi _0(u_0+h) \quad \text {for all } h \in W^{1,p}({\varOmega }) \text { with } \Vert h\Vert _{W^{1,p}({\varOmega })} \le \rho _1. \end{aligned}$$

As already mentioned, our approach involves the usage of critical groups (Morse theory). So, let us recall the definition of critical groups. Given ${\varphi }\in C^1(X)$ and $c\in {\mathbb {R}}$, we consider the following sets

For every topological pair $(Y_1,Y_2)$ with $Y_2 \subseteq Y_1 \subseteq X$ and every integer $k \ge 0$, we denote by $H_k(Y_1,Y_2)$ the $k \overset{th}{=}$-relative singular homology group with integer coefficients. If $u \in K^c_{\varphi }$ is isolated, then the critical groups of ${\varphi }$ at u are defined by

$$\begin{aligned} C_k(\varphi ,u)=H_k\left(\varphi ^c \cap U, \varphi ^c \cap U {\setminus } \{u\}\right) \quad \text {for all integers } k \ge 0, \end{aligned}$$

where U is a neighborhood of u such that $K_\varphi \cap \varphi ^c \cap U=\{u\}$. The excision property of singular homology theory implies that the definition of critical groups above is independent of the particular choice of the neighborhood U.

If ${\varphi }\in C^1(X)$ satisfies the PS-condition and $\inf {\varphi }(K_{\varphi })>-\infty$, then the critical groups of ${\varphi }$ at infinity are defined by

$$\begin{aligned} C_k({\varphi },\infty )=H_k(X,{\varphi }^c) \quad \text {for all } k \ge 0, \end{aligned}$$

where $c<\inf {\varphi }(K_{\varphi })$. The second deformation theorem (see, e.g., Gasiński and Papageorgiou [9, p. 628]) implies that this definition is independent of the level c.

Assuming that $K_{\varphi }$ is finite, we define

$$\begin{aligned}&M(t,u)=\sum _{k \ge 0} {{\mathrm{rank}}}C_k(\varphi ,u)t^k \quad \text {for all }t \in {\mathbb {R}}\text { and all }u \in K_\varphi ,\\&P(t,\infty )=\sum _{k \ge 0} {{\mathrm{rank}}}C_k(\varphi ,\infty )t^k \quad \text {for all }t \in {\mathbb {R}}. \end{aligned}$$

Then, the Morse relation says

$$\begin{aligned} \sum _{u \in K_\varphi }M(t,u)=P(t,\infty )+(1+t)Q(t) \quad \text {for all } t\in {\mathbb {R}}, \end{aligned}$$

(2.3)

where $Q(t)=\sum _{k \ge 0} \beta _k t^k$ is a formal series in $t \in {\mathbb {R}}$ with nonnegative integer coefficients $\beta _k$.

In what follows, we denote by $A: W^{1,p}({{\varOmega }}) \rightarrow \left(W^{1,p}({{\varOmega }}) \right)^*$ the nonlinear map defined by

$$\begin{aligned} \left\langle A(u),v \right\rangle =\int _{{\varOmega }}\left(a(\nabla u),\nabla v \right)_{{\mathbb {R}}^N}\mathrm{d}x \quad \text {for all }u,v \in W^{1,p}({{\varOmega }}). \end{aligned}$$

By means of Lemma 2.4, we can easily see that A is semicontinuous and maximal monotone.

Since our hypotheses on the reaction $f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ involve the spectrum of the Robin p-Laplacian, let us recall some basic features of this spectrum. We refer to Lê [13] and Papageorgiou and Rădulescu [20] (see also Motreanu and Winkert [18] for the Robin-Fučík-spectrum of the p-Laplacian) for more details. We consider the following nonlinear eigenvalue problem

$$\begin{aligned} \begin{aligned} -{\varDelta }_\mu u&= \hat{\lambda } |u|^{\mu -2}u \quad&\text {in } {\varOmega },\\ \frac{\partial u}{\partial n_\mu }&= -\beta (x) |u|^{\mu -2}u&\text {on } \partial {\varOmega }, \end{aligned} \end{aligned}$$

(2.4)

where $\beta$ fulfills H($\beta$), $\mu \in (1,p)$, and $\frac{\partial u}{\partial n_\mu }=|\nabla u|^{\mu -2} \frac{\partial u}{\partial n}$ for all $u \in W^{1,\mu }({{\varOmega }})$. We say that $\hat{\lambda } \in {\mathbb {R}}$ is an eigenvalue of the negative Robin $\mu$-Laplacian, henceforth denoted by $-{\varDelta }^R_\mu$, if problem (2.4) admits a nontrivial solution $\hat{u}\in W^{1,\mu }({{\varOmega }})$ known as an eigenfunction corresponding to $\hat{\lambda }$. We know that there exists a smallest eigenvalue denoted by $\hat{\lambda }_1(\mu ,\beta )$ which has the following properties:

• $\hat{\lambda }_{1}(\mu ,\beta ) \ge 0$ and $\hat{\lambda }_{1}(\mu ,\beta ) > 0$ if $\beta \ne 0$;

• $\hat{\lambda }_{1}(\mu ,\beta )$ is isolated in the spectrum $\hat{\sigma }(\mu ,\beta )$ of $-{\varDelta }^R_\mu$;

• $\hat{\lambda }_{1}(\mu ,\beta )$ is simple, that is, if $\hat{u}, \hat{v}$ are eigenfunctions corresponding to $\hat{\lambda }_{1}(\mu ,\beta )$, then $\hat{u}=\xi \hat{v}$ for some $\xi \ne 0$;

• 

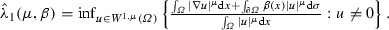  (2.5)

The infimum in (2.5) is realized on the corresponding one-dimensional eigenspace. Owing to (2.5), it is clear that the elements of this eigenspace do not change sign. In what follows, we denote by $\hat{u}_1(\mu ,\beta )$ the positive $L^\mu$-normalized (that is, $\Vert \hat{u}_1(\mu ,\beta )\Vert _\mu =1$) eigenfunction corresponding to the eigenvalue $\hat{\lambda }_1(\mu ,\beta )$. The nonlinear regularity theory (see Lieberman [14]) implies $\hat{u}_1(\mu ,\beta ) \in C^1({\overline{{\varOmega }}})_+ {\setminus } \{0\}$. Moreover, by virtue of the nonlinear maximum principle (see Pucci and Serrin [23]), we obtain $\hat{u}_1(\mu ,\beta ) \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$.

It is easy to check that the spectrum $\hat{\sigma }(\mu ,\beta )$ of $-{\varDelta }^R_\mu$ is closed, and so the second eigenvalue is well defined by

$$\begin{aligned}&\hat{\lambda }_{2}(\mu ,\beta )=\inf \left[ \hat{\lambda } \in \hat{\sigma }(\mu ,\beta ): \hat{\lambda }>\hat{\lambda }_{1}(\mu ,\beta ) \right] . \end{aligned}$$

Now, let $\partial B^{L^\mu }_1=\{u \in L^{\mu }({\varOmega }): \Vert u\Vert _{\mu }=1\}, S_\mu =W^{1,\mu }({{\varOmega }}) \cap \partial B_1^{L^\mu }$, and $\xi (u)=\Vert \nabla u\Vert _{\mu }^\mu +\int _{\partial {\varOmega }} \beta (x)|u|^\mu d\sigma$ for all $u \in W^{1,\mu }({{\varOmega }})$. Then, due to Papageorgiou and Rădulescu [20], we have the following variational characterization of $\hat{\lambda }_{2}(\mu ,\beta )$.

Proposition 2.8

There holds

$$\begin{aligned} \hat{\lambda }_{2}(\mu ,\beta )= \inf _{\hat{\gamma } \in \hat{{\varGamma }}(\mu ,\beta )} \max _{-1 \le t \le 1} \xi (\hat{\gamma }(t)), \end{aligned}$$

where $\hat{{\varGamma }}(\mu ,\beta )=\{ \hat{\gamma } \in C\left([-1,1],S_\mu \right): \hat{\gamma }(-1)=-\hat{u}_1(\mu ,\beta ), \hat{\gamma }(1)=\hat{u}_1(\mu ,\beta ) \}$.

Moreover, owing to the Ljusternik–Schnirelman theory, there exists a whole sequence $\left(\hat{\lambda }_k(\mu ,\beta ) \right)_{k\ge 1}$ of eigenvalues such that $\hat{\lambda }_k(\mu ,\beta ) \rightarrow + \infty$ as $k \rightarrow +\infty$. However, we do not know whether this sequence exhausts $\hat{\sigma }(\mu ,\beta )$. This is true if $p=2$ (linear eigenvalue problem) or if $N=1$ (ordinary differential equation).

Finally, let us fix our notation. Given $s\in {\mathbb {R}}$, we set $s^{\pm }=\max \{\pm s,0\}$. Then, for $u \in W^{1,p}({{\varOmega }})$, we define $u^{\pm }(\cdot )=u(\cdot )^{\pm }$. Recall that

$$\begin{aligned} u^{\pm } \in W^{1,p}({\varOmega }), \quad |u|=u^++u^-, \quad u=u^+-u^-. \end{aligned}$$

By $|\cdot |_N$, we denote the Lebesgue measure on ${\mathbb {R}}^N$. Furthermore, for $u,v \in W^{1,p}({{\varOmega }})$ and $v \le u$, we define by [v, u] the ordered interval given by

$$\begin{aligned}{}[v,u]=\left\{ y \in W^{1,p}({{\varOmega }}): v(x) \le y(x) \le u(x) \text { a.e. in } {\varOmega }\right\} . \end{aligned}$$

3 Solutions of constant sign

In this section, we are going to prove the existence of constant sign solutions for problem (1.1). To this end, we suppose the following assumptions on the function $f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$.

H$_1$::

$f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function such that $f(x,0)=0$ for a.a. $x\in {\varOmega }$ and

• (i) for every $\rho >0$, there exists $a_\rho \in L^\infty ({\varOmega })_+$ such that

  $$\begin{aligned} |f(x,s)| \le a_\rho (x) \quad \text {for a.a. }x \in {\varOmega }\text { and all }|s| \le \rho ; \end{aligned}$$

• (ii) there exist functions $w_{\pm } \in W^{1,p}({{\varOmega }}) \cap C({\overline{{\varOmega }}})$ and constants $c_\pm \in {\mathbb {R}}$ such that

  $$\begin{aligned}&w_-(x) \le c_-<0<c_+\le w_+(x) \quad \text {for all }x\in {\overline{{\varOmega }}};\\&f(x,w_+(x))\le 0 \le f(x,w_-(x)) \quad \text {for a.a. }x \in {\varOmega };\\&A(w_-) \le 0 \le A(w_+) \quad \text {in } \left(W^{1,p}({{\varOmega }})\right)^*; \end{aligned}$$

• (iii) if $\varsigma \in (1,p]$ and $c^*>0$ are as in hypothesis H(a) (iv), then there exists $\eta \in L^{\infty }({\varOmega })$ such that

  $$\begin{aligned}&\eta (x) \ge c^* \hat{\lambda }_1(\mu ,\hat{\beta }) \text { a.e. in } {\varOmega }, \,\, \eta \ne c^* \hat{\lambda }_1(\mu ,\hat{\beta }), \,\, \hat{\beta }=\frac{1}{c^*} \beta ;\\&\liminf _{s \rightarrow 0} \frac{f(x,s)}{|s|^{\varsigma -2}s} \ge \eta (x) \quad \text {uniformly for a.a. }x \in {\varOmega }; \end{aligned}$$

• (iv) if ${M}_{*}=\max \left\{ \left\Vert {w}_{+}\right\Vert_{\infty }, \left\Vert{w}_{-}\right\Vert_{\infty } \right\}$, then there exists $\xi _{*}>0$ such that

  $$\begin{aligned} f(x,s)s+\xi _* |s|^p \ge 0 \quad \text {for a.a. }x \in {\varOmega }\text { and all }|s| \le M_*. \end{aligned}$$

Remark 3.1

In the above hypotheses, we do not employ any global growth condition on $f(x,\cdot )$. In fact, the particular structure of $f(x,\cdot )$ beyond $w_\pm (x)$ is irrelevant. Note that hypothesis H$_1$(ii) is automatically satisfied if we can find $c_-<0<c_+$ such that

$$\begin{aligned} f(x,c_+) \le 0 \le f(x,c_{-}) \quad \text {for a.a. }x\in {\varOmega }. \end{aligned}$$

Hypotheses H$_1$(ii),(iii) imply that $f(x,\cdot )$ exhibits an oscillatory behavior near zero and the last inequality in H$_1$(ii) means that

$$\begin{aligned} \left\langle A\left(w_-\right),h\right\rangle \le 0 \le \left\langle A\left(w_+\right),h\right\rangle \quad \text {for all } h \in W^{1,p}({{\varOmega }}) \text { with }h \ge 0. \end{aligned}$$

By means of H$_1$(iii), we see that $f(x,\cdot )$ is either $(\varsigma -1)$-superlinear or $(\varsigma -1)$-linear near zero. Finally, hypothesis H$_1$(iv) is a perturbed sign condition.

The following function fulfills these hypotheses

$$\begin{aligned} f(s)= {\left\{ \begin{array}{ll} \xi \left( |s|^{q-2}s-|s|^{p-2}s \right) &{} \text {if }|s|\le 1,\\ e^{|s|}-e &{} \text {if }|s|>1, \end{array}\right. } \end{aligned}$$

with $\xi >c^* \hat{\lambda }_1(\varsigma ,\hat{\beta })$ and $1<q<p$.

Proposition 3.2

Let hypotheses H(a), H($\beta$) and H$_1$ be satisfied. Then, problem (1.1) admits at least two nontrivial constant sign solutions

$$\begin{aligned} u_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) \quad \text {and} \quad v_0 \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) . \end{aligned}$$

Proof

We begin with the positive constant sign solution. To this end, let $\hat{f}_+ : {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a truncation perturbation defined by

$$\begin{aligned} \hat{f}_+(x,s)= {\left\{ \begin{array}{ll} 0 &{} \text {if } s<0,\\ f(x,s)+s^{p-1} &{} \text {if }0 \le s \le w_+(x),\\ f(x,w_+(x))+w_+(x)^{p-1} &{} \text {if }s>w_+(x), \end{array}\right. } \end{aligned}$$

(3.1)

which is a Carathéodory function. We set $\hat{F}_+(x,s)=\int ^s_0 \hat{f}_+(x,t)\mathrm{d}t$ and consider the $C^1$-functional $\hat{{\varphi }}_+:W^{1,p}({{\varOmega }}) \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \hat{{\varphi }}_+(u)=\int _{{\varOmega }}G(\nabla u)\mathrm{d}x+\frac{1}{p} \Vert u\Vert ^p_{p}+\frac{1}{p}\int _{\partial {\varOmega }} \beta (x) \left(u^+\right)^p \mathrm{d}\sigma -\int _{{\varOmega }}\hat{F}_+(x,u)\mathrm{d}x. \end{aligned}$$

Note that $\hat{{\varphi }}_+$ is coercive due to Corollary 2.5, hypothesis H($\beta$) and the truncation defined in (3.1). Moreover, by the Sobolev embedding theorem and the compactness of the trace operator, we see that $\hat{{\varphi }}_+$ is sequentially weakly lower semicontinuous. Therefore, the Weierstrass theorem implies the existence of $u_0 \in W^{1,p}({{\varOmega }})$ such that

$$\begin{aligned} \hat{{\varphi }}_+(u_0)=\inf \left[\hat{{\varphi }}_+(u): u \in W^{1,p}({{\varOmega }}) \right]. \end{aligned}$$

(3.2)

Given $\varepsilon >0$, by virtue of hypotheses H(a)(iv) and H$_1$(iii), there exists $\delta =\delta (\varepsilon ) \in \left( 0, \min \{1,c_+\} \right)$ such that

$$\begin{aligned} G(\xi ) \le \frac{c^*+\varepsilon }{\varsigma } |\xi |^{\varsigma } \quad \text {for all }|\xi |\le \delta \end{aligned}$$

(3.3)

and

$$\begin{aligned} f(x,s) \ge \left(\eta (x)-\varepsilon \right)s^{\varsigma -1} \quad \text {for a.a. } x\in {\varOmega }\text { and all } s \in [0,\delta ]. \end{aligned}$$

(3.4)

If $F(x,s)=\int ^s_0 f(x,t)\mathrm{d}t$, then (3.4) gives

$$\begin{aligned} F(x,s) \ge \frac{1}{\varsigma }\left(\eta (x)-\varepsilon \right)s^{\varsigma } \quad \text {for a.a. } x\in {\varOmega }\text { and all } s \in [0,\delta ]. \end{aligned}$$

(3.5)

Let $t\in (0,1)$ be small such that $t \hat{u}_1(\varsigma ,\hat{\beta })(x) \in (0,\delta ]$ for all $x \in {\overline{{\varOmega }}}$. Recall that $\hat{\beta }=\frac{1}{c^*}\beta$ and that $\hat{u}_1(\varsigma , \hat{\beta } ) \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$. Then, due to (3.1), (3.3), (3.5) and $\varsigma <p$, we obtain

$$\begin{aligned} \hat{{\varphi }}_+\left(t \hat{u}_1(\varsigma ,\hat{\beta }) \right)&=\int _{{\varOmega }}G \left( \nabla \left( t \hat{u}_1(\varsigma ,\hat{\beta }) \right) \right) \mathrm{d}x+\frac{1}{p}\int _{\partial {\varOmega }} \beta (x)\left(t \hat{u}_1(\varsigma ,\hat{\beta })\right)^p\mathrm{d} \sigma \nonumber \\&\quad -\int _{{\varOmega }}F \left(x,t \hat{u}_1(\varsigma ,\hat{\beta })\right)\mathrm{d}x\nonumber \\&\le \frac{c^*+\varepsilon }{\varsigma } t^\varsigma \left\Vert\nabla \hat{u}_1(\varsigma ,\hat{\beta }) \right\Vert^\varsigma _{\varsigma }+\frac{t^\varsigma }{\varsigma } \int _{\partial {\varOmega }} \beta (x) \hat{u}_1(\varsigma ,\hat{\beta })^\varsigma \mathrm{d} \sigma \nonumber \\&\quad -\frac{t^\varsigma }{\varsigma } \int _{{\varOmega }}\left( \eta (x)-\varepsilon \right) \hat{u}_1(\varsigma ,\hat{\beta })^\varsigma \mathrm{d}x\nonumber \\&=\frac{t^\varsigma }{\varsigma } \left[ \int _{{\varOmega }}\left(c^*\hat{\lambda }_1(\varsigma ,\hat{\beta })-\eta (x)\right) \hat{u}_1(\varsigma ,\hat{\beta })\mathrm{d}x+\left(\hat{\lambda }_1(\varsigma ,\hat{\beta })+1\right)\varepsilon \right] .\nonumber \\ \end{aligned}$$

(3.6)

Note that by hypothesis H$_1$(iii) and since $\hat{u}_1(\varsigma ,\hat{\beta })\in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$, we have

$$\begin{aligned} \hat{\mu }=\int _{{\varOmega }}\left(\eta (x)-c^*\hat{\lambda }_1(\varsigma ,\hat{\beta })\right) \hat{u}_1(\varsigma ,\hat{\beta })\mathrm{d}x>0. \end{aligned}$$

Therefore, if we choose $\varepsilon \in \left(0,\frac{\hat{\mu }}{\hat{\lambda }_1(\varsigma ,\hat{\beta })+1} \right)$, it follows

$$\begin{aligned} \hat{{\varphi }}_+\left(t \hat{u}_1(\varsigma ,\hat{\beta }) \right)<0, \end{aligned}$$

that means, $\hat{{\varphi }}_+\left(u_0 \right)<0=\hat{{\varphi }}_+\left(0\right)$, and thus, $u_0 \ne 0$. By means of (3.2), there holds $\hat{{\varphi }}_+'\left(u_0 \right)=0$ which results in

$$\begin{aligned} \left\langle A(u_0),h\right\rangle +\int _{{\varOmega }}|u_0|^{p-2}u_0h\mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) \left(u_0^+ \right)^{p-1} h \mathrm{d}\sigma =\int _{{\varOmega }}\hat{f}_+(x,u_0)h\mathrm{d}x \end{aligned}$$

(3.7)

for all $h \in W^{1,p}({{\varOmega }})$. Taking $h=-u_0^- \in W^{1,p}({{\varOmega }})$ in (3.7) and applying Lemma 2.4(iii) combined with the truncation in (3.1) gives

$$\begin{aligned} \frac{{c}_{1}}{p-1} {\left\| {\nabla u}_{0}^{-}\right\| }_{p}^{p}+{\left\| u_{0}^{-}\right\| }^{p}_{p} \le 0. \end{aligned}$$

Hence, $u_0\ge 0$ and $u_0 \ne 0$. Now we choose $h=\left(u_0-w_+\right)^+ \in W^{1,p}({{\varOmega }})$ in (3.7). Then, because of hypotheses H$_1$(ii) and H($\beta$) along with (3.1), one has

$$\begin{aligned}&\left\langle A(u_0),\left(u_0-w_+\right)^+\right\rangle +\int _{{\varOmega }}u_0^{p-1}\left(u_0-w_+\right)^+\mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) u_0^{p-1} \left(u_0-w_+\right)^+ d\sigma \\&\quad =\int _{{\varOmega }}\left(f(x,w_+)+w_+^{p-1}\right) \left(u_0-w_+\right)^+\mathrm{d}x\\&\quad \le \left\langle A(w_+),\left(u_0-w_+\right)^+\right\rangle +\int _{{\varOmega }}w_+^{p-1}\left(u_0-w_+\right)^+\mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) w_+^{p-1} \left(u_0-w_+\right)^+ \mathrm{d}\sigma . \end{aligned}$$

Therefore,

$$\begin{aligned} \left\langle A(u_0)-A(w_+),\left(u_0-w_+\right)^+\right\rangle +\int _{{\varOmega }}\left( u_0^{p-1}-w_+^{p-1}\right) \left(u_0-w_+\right)^+ \mathrm{d}x \le 0, \end{aligned}$$

which implies $\left| \left\{ u_0>w_+\right\} \right|_N=0$ meaning $u_0 \le w_+$. In summary, we have proved that $u_0 \in [0,w_+], u_0 \ne 0$. Then, by virtue of (3.1), Eq. (3.7) becomes

$$\begin{aligned} \left\langle A(u_0),h\right\rangle +\int _{\partial {\varOmega }} \beta (x) u_0^{p-1} h \mathrm{d}\sigma =\int _{{\varOmega }}f(x,u_0)h\mathrm{d}x \quad \text {for all } h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

(3.8)

Applying the nonlinear Green’s identity (see, e.g., Gasiński and Papageorgiou [9, p. 210]) yields

$$\begin{aligned} \left\langle A(u_0), h \right\rangle = \left\langle -{{\mathrm{div}}}a\left(\nabla u_0 \right),h\right\rangle + \left\langle \frac{\partial u}{\partial n_a},h \right\rangle _{\partial {\varOmega }}, \end{aligned}$$

(3.9)

where $\langle \cdot , \cdot \rangle _{\partial {\varOmega }}$ denotes the duality brackets for the pair $\left( W^{-\frac{1}{p'},p'}(\partial {\varOmega }),W^{\frac{1}{p'},p}(\partial {\varOmega })\right)$. From the representation theorem for the elements of $W^{-1,p'}(\partial {\varOmega })=\left( W^{1,p}_0({{\varOmega }}) \right)^*$ (see, e.g., Gasiński and Papageorgiou [9, p. 211]) and Lemma 2.4, we get

$$\begin{aligned} {{\mathrm{div}}}a(\nabla u_0) \in W^{-1,p'}({\varOmega })=\left( W^{1,p}_0({{\varOmega }}) \right)^*. \end{aligned}$$

From (3.8) and (3.9) as well as the fact that $h \big |_{\partial {\varOmega }}=0$ for all $h \in W^{1,p}_0({{\varOmega }})$, it follows

$$\begin{aligned} \left\langle -{{\mathrm{div}}}a\left(\nabla u_0 \right),h\right\rangle =\int _{{\varOmega }}f(x,u_0)h\mathrm{d}x \quad \text {for all }h \in W^{1,p}_0({{\varOmega }}), \end{aligned}$$

which implies

$$\begin{aligned} -{{\mathrm{div}}}a(\nabla u_0)=f(x,u_0) \quad \text {a.e. in }{\varOmega }. \end{aligned}$$

Hence, (3.8) and (3.9) imply

$$\begin{aligned} \left\langle \frac{\partial u}{\partial n_a}+\beta (x)u_0^{p-1},h \right\rangle _{\partial {\varOmega }}=0 \quad \text {for all }h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

(3.10)

Recall that $\gamma _0 \left( W^{1,p}({{\varOmega }}) \right)=W^{\frac{1}{p'},p}(\partial {\varOmega })$ (see, e.g., Gasiński and Papageorgiou [9, p. 209]). So, from (3.10), we may infer that

$$\begin{aligned} \frac{\partial u}{\partial n_a}+\beta (x)u_0^{p-1}=0 \quad \text {on } \partial {\varOmega }. \end{aligned}$$

From Winkert [25], we get $u_0 \in L^{\infty }({\varOmega })$ and the regularity results of Lieberman [14, p. 320] ensure that $u_0 \in C^1({\overline{{\varOmega }}})_+ {\setminus } \{0\}$.

Now, let $\xi _*>0$ be as in hypothesis H$_1$(iv). Then,

$$\begin{aligned} -{{\mathrm{div}}}a(\nabla u_0)+\xi _* u_0^{p-1}=f(x,u_0)+\xi _*u_0^{p-1} \ge 0 \quad \text {for a.a. }x \in {\varOmega }, \end{aligned}$$

which gives

$$\begin{aligned} {{\mathrm{div}}}a(\nabla u_0(x))\le \xi _* u_0^{p-1} \quad \text {for a.a. }x \in {\varOmega }. \end{aligned}$$

(3.11)

Let $\vartheta (t)=a_0(t)t$ for all $t>0$. Then, (2.2) and hypothesis H(a)(iii) lead to the following one-dimensional estimate

$$\begin{aligned} \vartheta '(t)t=a_0'(t)t^2+a_0(t)t\ge c_1 t^{p-1} \quad \text {for all }t>0, \end{aligned}$$

which, by integration of parts and hypothesis H(a)(iv), implies

$$\begin{aligned} \int ^t_0 \vartheta '(s)sds&=\vartheta (t)t -\int ^t_0 \vartheta (s)\mathrm{d}s\nonumber \\&= a_0(t)t^2-G_0(t)\nonumber \\&\ge \tilde{c} t^p \quad \text {for all }t>0. \end{aligned}$$

(3.12)

Because of (3.11) and (3.12), we may apply the strong maximum principle of Pucci and Serrin [23, p. 111] which yields

$$\begin{aligned} u(x)>0 \quad \text {for all }x \in {\varOmega }. \end{aligned}$$

Taking into account the boundary point theorem of Pucci and Serrin [23, p. 120], we conclude that $u_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$.

In order to prove the existence of a negative solution, we introduce the Carathéodory function

$$\begin{aligned} \hat{f}_-(x,s)= {\left\{ \begin{array}{ll} f(x,w_-(x))+|w_-(x)|^{p-2} w_-(x) &{} \text {if } s<w_-(x),\\ f(x,s)+|s|^{p-2}s &{} \text {if }w_-(x) \le s \le 0,\\ 0&{} \text {if }s>0. \end{array}\right. } \end{aligned}$$

Then, we set $\hat{F}_-(x,s)=\int ^s_0 \hat{f}_-(x,t)dt$ and consider the $C^1$-functional $\hat{{\varphi }}_-:W^{1,p}({{\varOmega }}) \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \hat{{\varphi }}_-(u)=\int _{{\varOmega }}G(\nabla u)\mathrm{d}x+\frac{1}{p} \Vert u\Vert ^p_{p}-\frac{1}{p}\int _{\partial {\varOmega }} \beta (x) \left(u^-\right)^p \mathrm{d}\sigma -\int _{{\varOmega }}\hat{F}_-(x,u)\mathrm{d}x. \end{aligned}$$

Working as above with $\hat{f}_-$ and $\hat{{\varphi }}_-$, we produce a negative solution $v_0$ of (1.1) such that

$$\begin{aligned} v_0 \in [w_-,0]\cap \left( -{{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) \right). \end{aligned}$$

$\square$

In fact, we can produce extremal constant sign solutions for problem (1.1), that is the smallest positive solution and the greatest negative solution. For this purpose, we introduce the following solution sets

Proposition 3.2 implies directly that

Given $\varepsilon >0$ and $r \in \left(p,p^*\right)$, by virtue of hypotheses H$_1$(i),(iii), there exists $c_6=c_6(\varepsilon ,r)>0$ such that

$$\begin{aligned} f(x,s)s \ge \left(\eta (x)-\varepsilon \right)|s|^\varsigma -c_6|s|^r \quad \text {for a.a. }x \in {\varOmega }\quad \text {and all}\quad |s|\le \rho , \end{aligned}$$

(3.13)

where $\rho =\max \{\Vert w_+\Vert _\infty ,\Vert w_-\Vert _\infty \}$.

We consider the subsequent auxiliary Robin problem

$$\begin{aligned} \begin{aligned} -{{\mathrm{div}}}a(\nabla u)&= \left(\eta (x)-\varepsilon \right)|u|^{\varsigma -2}u-c_6|u|^{r-2}u\quad&\text {in } {\varOmega },\\ \frac{\partial u}{\partial n_a}&= -\beta |u|^{p-2}u&\text {on } \partial {\varOmega }. \end{aligned} \end{aligned}$$

(3.14)

Proposition 3.3

If hypotheses H(a) and H($\beta$) are satisfied, then problem (3.14) has a unique positive solution $\overline{u} \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$, and since (3.14) is odd, $\overline{v}=-\overline{u} \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ is the unique negative solution of (3.14).

Proof

First, we establish the existence of a positive solution. To this end, let $\psi _+: W^{1,p}({{\varOmega }}) \rightarrow {\mathbb {R}}$ be the $C^1$-functional defined by

$$\begin{aligned} {\psi }_{+}(u)&= \int _{{\varOmega }}G(\nabla u)\mathrm{d}x+\frac{1}{p}{\Vert u^{-}\Vert }^{p}_{p}+\frac{1}{p}{\int }_{\partial {\varOmega }} \beta (x) \left( u^+\right) ^{p}\mathrm{d} \sigma \\&\quad -\frac{1}{\varsigma } \int _{{\varOmega }}\left( \eta (x)-\varepsilon \right) \left( u^{+}\right) ^{\varsigma } \mathrm{d}x+\frac{c_6}{r} \left\| u^+\right\| ^r_{r}. \end{aligned}$$

Since $r>p$ and due to Corollary 2.5, we obtain

$$\begin{aligned} \psi _{+}(u)&\quad \ge \frac{c_1}{p(p-1)} \left\| \nabla u^+\right\| ^p_{p}+\frac{c_6}{r} \left\| u^{+}\right\| ^r_r+\frac{c_1}{p(p-1)} \left\| \nabla u^-\right\| ^p_p+\frac{1}{p} \left\| u^-\right\| ^p_p\\&\qquad -\frac{1}{\varsigma } \int _{{\varOmega }}\left( \eta (x)-\varepsilon \right) \left( u^+\right) ^\varsigma \mathrm{d}x\\&\quad \ge c_7 \left[ \left\| u^+\right\| ^p_{1,p}+\left\| u^-\right\| ^p_{1,p} \right] -c_8 \left( \Vert u\Vert ^\varsigma _{1,p}+1\right) \\&\quad = c_7 \Vert u\Vert ^p_{1,p}-c_8 \Vert u\Vert ^\varsigma _{1,p}-c_8 \end{aligned}$$

for some $c_7, c_8>0$. Recall that $\varsigma <p$ we see that $\psi _+$ is coercive. Since $\psi _+$ is sequentially weakly lower semicontinuous as well, we find $\overline{u} \in W^{1,p}({{\varOmega }})$ such that

$$\begin{aligned} \psi _+(\overline{u})=\inf \left[\psi _+(u): u \in W^{1,p}({{\varOmega }})\right]. \end{aligned}$$

(3.15)

Reasoning as in the proof of Proposition 3.2 along with hypothesis H(a)(iv) and the assumptions on $\eta (\cdot )$ (see H$_1$(iii)) we get, for $t\in (0,1)$ sufficiently small,

$$\begin{aligned} \psi _+\left(t \hat{u}_1(\varsigma , \hat{\beta }) \right)<0. \end{aligned}$$

Therefore, $\psi _+(\overline{u})<0=\psi _+(0)$; thus, $\overline{u} \ne 0$. Because $\overline{u}$ is a critical point of $\psi _+$, it holds $\psi _+'(\overline{u})=0$ which gives

$$\begin{aligned}&\left\langle A(\overline{u}),h\right\rangle -\int _{{\varOmega }}\left( \overline{u}^-\right)^{p-1}h \mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) \left(\overline{u}^+\right)^{p-1}h \mathrm{d} \sigma \nonumber \\&\quad = \int _{{\varOmega }}\left(\eta (x)-\varepsilon \right) \left(\overline{u}^+\right)^{\varsigma -1}h \mathrm{d}x-c_6 \int _{{\varOmega }}\left( \overline{u}^+\right)^{r-1} h \mathrm{d}x \quad \text {for all } h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

(3.16)

We choose $h=-\overline{u}^- \in W^{1,p}({{\varOmega }})$ in (3.16) and apply Lemma 2.4(iii) to get

$$\begin{aligned} \frac{c_1}{p-1} \left\Vert\nabla \overline{u}^-\right\Vert^p_p+\left\Vert\overline{u}^-\right\Vert^p_p \le 0, \end{aligned}$$

which gives $\overline{u} \ge 0, \overline{u} \ne 0$. Then, (3.16) becomes

$$\begin{aligned}&\left\langle A(\overline{u}),h\right\rangle +\int _{\partial {\varOmega }} \beta (x) \overline{u}^{p-1}h d \sigma \\&\quad = \int _{{\varOmega }}\left(\eta (x)-\varepsilon \right) \overline{u}^{\varsigma -1}h dx-c_6 \int _{{\varOmega }}\overline{u}^{r-1} h dx \quad \text {for all } h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

As in the proof of Proposition 3.2, using the nonlinear Green’s identity, we see from the equation above that $\overline{u}$ is a positive solution of the auxiliary problem given in (3.14). Note that $\overline{u} \in L^{\infty }({\varOmega })$ (see, e.g., Winkert and Zacher [27]). Then, the nonlinear regularity theory (see Lieberman [14]) and the nonlinear maxmium principle (see Pucci and Serrin [23]) imply $\overline{u} \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$.

In order to finish the proof, we have to show the uniqueness of $\overline{u}$. To this end, we consider the integral functional ${\varUpsilon }: L^1({\varOmega }) \rightarrow {\mathbb {R}}\cup \{\infty \}$ defined by

$$\begin{aligned} {\varUpsilon }(u)= {\left\{ \begin{array}{ll} \displaystyle \int _{\varOmega }G\left( \nabla u^{\frac{1}{\varsigma }}\right) \mathrm{d}x +\frac{1}{p} \int _{\partial {\varOmega }} \beta (x)|u|^{\frac{p}{\varsigma }}d\sigma \quad &{} \text {if } u \ge 0, u^{\frac{1}{\varsigma }} \in W^{1,p}({\varOmega }),\\ +\infty &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Let $u_1, u_2$ be in the domain of ${\varUpsilon }$; i.e., $u_1, u_2 \in {{\mathrm{dom}}}({\varUpsilon })=\left\{ u \in L^{1}({\varOmega }): {\varUpsilon }(u)<+\infty \right\}$, and let further $u=((1-t)u_1+t u_2)^{\frac{1}{\varsigma }}$ with $t \in [0,1]$. Applying Lemma 1 of Díaz and Saá [5], there holds

$$\begin{aligned} |\nabla u(x)| \le \left[ (1-t) \left| \nabla u_1(x)^{\frac{1}{\varsigma }}\right| ^\varsigma + t \left| \nabla u_2(x)^{\frac{1}{\varsigma }}\right| ^\varsigma \right] ^{\frac{1}{\varsigma }} \quad \text {a.e. in }{\varOmega }. \end{aligned}$$

Recall that $G_0$ is increasing. Therefore, due to hypothesis H(a)(iv), it follows

$$\begin{aligned}&G_0\left( \left| \nabla u(x)\right| \right) \\&\quad \le G_0 \left( \left( (1-t) \left| \nabla u_1(x)^{\frac{1}{\varsigma }}\right| ^\varsigma + t \left| \nabla u_2(x)^{\frac{1}{\varsigma }}\right| ^\varsigma \right) ^{\frac{1}{\varsigma }} \right) \\&\quad \le (1-t) G_0 \left( \left| \nabla u_1(x)^{\frac{1}{\varsigma }}\right| \right) + t G_0 \left( \left| \nabla u_2(x)^{\frac{1}{\varsigma }}\right| \right) \quad \text {a.e. in }{\varOmega }. \end{aligned}$$

Since $G(\xi )=G_0(|\xi |)$ for all $\xi \in {\mathbb {R}}^N$, we obtain

$$\begin{aligned} G(\nabla u(x)) \le (1-t) G\left( \nabla u_1(x)^{\frac{1}{\varsigma }}\right) +t G\left( \nabla u_2(x)^{\frac{1}{\varsigma }}\right) \quad \text {a.e. in }{\varOmega }, \end{aligned}$$

which implies that ${\varUpsilon }$ is convex. By means of Fatou’s lemma, we easily verify that ${\varUpsilon }$ is lower semicontinuous as well.

Now, let $\overline{y}$ be another positive solution of (3.14) and recall that $\overline{u}, \overline{y} \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$. Then, for every $h \in C^1({\overline{{\varOmega }}})$ and for |t| small enough, we have $\overline{u}^\varsigma +th, \overline{y}^\varsigma +th \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$. Hence, ${\varUpsilon }$ is Gateaux differentiable at $\overline{u}^\varsigma$ and $\overline{y}^\varsigma$ in the direction h. Moreover, the chain rule and the nonlinear Green’s identity give

$$\begin{aligned}&{\varUpsilon }'\left( \overline{u}^\varsigma \right) (h)=\frac{1}{\varsigma }\int _{\varOmega }\frac{-{{\mathrm{div}}}a(\nabla \overline{u})}{\overline{u}^{\varsigma -1}}h dx , \end{aligned}$$

(3.17)

$$\begin{aligned}&{\varUpsilon }'\left( \overline{y}^\varsigma \right) (h)=\frac{1}{\varsigma }\int _{\varOmega }\frac{-{{\mathrm{div}}}a(\nabla \overline{y})}{\overline{y}^{\varsigma -1}}h dx , \end{aligned}$$

(3.18)

for all $h \in W^{1,p}({{\varOmega }})$ (recall that $C^1({\overline{{\varOmega }}})$ is dense in $W^{1,p}({{\varOmega }})$). Note that ${\varUpsilon }'$ is monotone because of the convexity of ${\varUpsilon }$. Then, owing to (3.17) and (3.18), we obtain

$$\begin{aligned} 0&\le \left\langle {\varUpsilon }'\left( \overline{u}^\varsigma \right) -{\varUpsilon }' \left( \overline{y}^\varsigma \right) ,\overline{u}^\varsigma -\overline{y}^\varsigma \right\rangle _{L^1({\varOmega })}\\&= \frac{1}{\varsigma }\int _{\varOmega }\left( \frac{-{{\mathrm{div}}}a(\nabla \overline{u})}{\overline{u}^{\varsigma -1}}+\frac{{{\mathrm{div}}}a(\nabla \overline{y})}{\overline{y}^{\varsigma -1}} \right) \left( \overline{u}^\varsigma -\overline{y}^\varsigma \right) \mathrm{d}x\\&= \frac{1}{\varsigma }\int _{\varOmega }\left( \frac{(\eta (x)-\varepsilon )\overline{u}^{\varsigma -1}-c_6\overline{u}^{r-1} }{\overline{u}^{\varsigma -1}}- \frac{(\eta (x)-\varepsilon )\overline{y}^{\varsigma -1}-c_6\overline{y}^{r-1}}{\overline{y}^{\varsigma -1}} \right) \left( \overline{u}^\varsigma -\overline{y}^\varsigma \right) \mathrm{d}x\\&= \frac{c_6}{\varsigma } \int _{\varOmega }\left( \overline{y}^{r-\varsigma }-\overline{u}^{r-\varsigma } \right) \left( \overline{u}^\varsigma -\overline{y}^\varsigma \right) \mathrm{d}x\\&\le 0, \end{aligned}$$

since $r>\varsigma$. Thus, $\overline{u}=\overline{v} \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ is the unique positive solution of (3.14).

The fact that problem (3.14) is odd implies that $\overline{v}=-\overline{u}\in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ is the unique negative solution of (3.14). $\square$

Proposition 3.4

Let hypotheses H(a), H$(\beta$) and H$_1$ be satisfied. Then, there holds

Proof

Let and introduce the Carathédory function $k: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} k(x,s)= {\left\{ \begin{array}{ll} 0 &{} \text {if } s<0,\\ \left( \eta (x)-\varepsilon \right) s^{\varsigma -1}-c_6 s^{r-1}+s^p &{} \text {if }0 \le s \le u(x),\\ \left(\eta (x)-\varepsilon \right)u(x)^{\varsigma -1}-c_6 u(x)^{r-1}+u(x)^p &{} \text {if }s>u(x). \end{array}\right. } \end{aligned}$$

(3.19)

Setting $K(x,s)=\int ^s_0 k(x,t)dt$, we consider the $C^1$-functional $\hat{\psi }: W^{1,p}({{\varOmega }}) \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} \hat{\psi }(u)=\int _{{\varOmega }}G(\nabla u) dx+\frac{1}{p}\Vert u\Vert ^p_p+\frac{1}{p}\int _{\partial {\varOmega }} \beta (x) \left(u^+\right)^p d\sigma -\int _{{\varOmega }}K(x,u)dx. \end{aligned}$$

By means of the truncation defined in (3.19) and Corollary 2.5, it follows that $\hat{\psi }$ is coercive. Since $\hat{\psi }$ is also sequentially weakly lower semicontinuous, we find an element $\overline{u}_* \in W^{1,p}({{\varOmega }})$ such that

$$\begin{aligned} \hat{\psi }(\overline{u}_*)=\inf \left[\hat{\psi }(u): u \in W^{1,p}({{\varOmega }}) \right]. \end{aligned}$$

(3.20)

Recall that $u \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$, so we can choose $t\in (0,1)$ small enough such that $t \hat{u}_1(\varsigma ,\hat{\beta }) \le u$. Then, as in the proof of Proposition 3.2, we may show that $\hat{\psi }(t\hat{u}_1(\varsigma ,\hat{\beta })<0$ meaning that $\hat{\psi }(\overline{u}_*)<0=\hat{\psi }(0)$. Hence, $\overline{u}_* \ne 0$.

Because of $\hat{\psi }'(\overline{u}_*)=0$, we have

$$\begin{aligned}&\left\langle A(\overline{u}_*),h\right\rangle +\int _{{\varOmega }}\left|\overline{u}_*\right|^{p-2}\overline{u}_*h\mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) \left(\overline{u}_*^+\right)^{p-1}h \mathrm{d} \sigma \nonumber \\&\quad =\int _{{\varOmega }}k\left(x,\overline{u}_*\right)h\mathrm{d}x \quad \text {for all }h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

(3.21)

If $h=-\overline{u}_*^- \in W^{1,p}({{\varOmega }})$ in (3.21), then, by reason of Lemma 2.4(iii) and (3.19), it follows

$$\begin{aligned} \frac{c_1}{p-1}\left\Vert\nabla \overline{u}_* \right\Vert^p_p+\left\Vert\overline{u}_* \right\Vert^p_p \le 0, \end{aligned}$$

therefore, $\overline{u}_* \ge 0, \overline{u}_* \ne 0$. On the other side, if we choose $h= \left(\overline{u}_*-u\right)^+ \in W^{1,p}({{\varOmega }})$ in (3.21), we obtain

$$\begin{aligned}&\left\langle A(\overline{u}_*),\left(\overline{u}_*-u\right)^+\right\rangle +\int _{{\varOmega }}\overline{u}_*^{p-1} \left(\overline{u}_*-u\right)^+\mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) \overline{u}_*^{p-1} \left(\overline{u}_*-u\right)^+ \mathrm{d} \sigma \\&\quad =\int _{{\varOmega }}\left[\left(\eta (x)-\varepsilon \right)u^ {\varsigma -1}-c_6 u^{r-1}+u^{p-1}\right]\left(\overline{u}_*-u\right)^+\mathrm{d}x\\&\quad \le \left\langle A(u),\left(\overline{u}_*-u\right)^+\right\rangle +\int _{{\varOmega }}u^{p-1} \left(\overline{u}_*-u\right)^+ \mathrm{d}x+\int _{\partial {\varOmega }} \beta (x) u^{p-1}\left(\overline{u}_*-u\right)^+ \mathrm{d} \sigma , \end{aligned}$$

where we used the definition of the truncation in (3.19) and the fact that (see (3.13)). Finally, we derive

$$\begin{aligned} \left\langle A(\overline{u}_*)-A(u),\left(\overline{u}_*-u\right)^+\right\rangle +\int _{{\varOmega }}\left(\overline{u}_*^{p-1} -u^{p-1}\right) \left(\overline{u}_*-u\right)^+dx \le 0, \end{aligned}$$

which gives $\left|\left\{ \overline{u}_*> u \right\} \right|_N=0$, hence $\overline{u}_*\le u$. We have proved that

$$\begin{aligned} \overline{u}_* \in [0,u], \,\, \overline{u}_* \ne 0. \end{aligned}$$

(3.22)

Then, by virtue of (3.19), Eq. (3.21) becomes

$$\begin{aligned}&\left\langle A(\overline{u}_*),h\right\rangle +\int _{\partial {\varOmega }} \beta (x) \overline{u}_*^{p-1}h \mathrm{d} \sigma =\int _{{\varOmega }}\left[\left(\eta (x)-\varepsilon \right)\overline{u}_*^{\varsigma -1}-c_6\overline{u}_*^{r-1} \right]h\mathrm{d}x \end{aligned}$$

for all $h \in W^{1,p}({{\varOmega }})$. Hence, $\overline{u}_*$ is a nontrivial positive solution of problem (3.14). Taking into account Proposition 3.3, we infer that $\overline{u}_*=\overline{u} \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$. Because of (3.22), it follows

Following the same ideas, we can prove that $v \le \overline{v}$ for all . $\square$

Now we are in the position to prove the existence of extremal constant sign solutions of problem (1.1).

Proposition 3.5

If hypotheses H(a), H($\beta$) and H$_1$ hold, then problem (1.1) has a smallest positive solution $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ and a greatest negative solution $v_* \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$.

Proof

Owing to Dunford and Schwartz [6, p. 336], we find a sequence such that

Recall that $u_n \in [0,w_+] \cap {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ and

(3.23)

Since $u_n \in L^{\infty }({\varOmega })$, we may apply the regularity results of Lieberman; that is, there exist $\gamma >0$ and $c_9>0$ such that

$$\begin{aligned} u_n \in C^{1,\gamma }({\overline{{\varOmega }}}) \quad \text {and} \quad \Vert u_n\Vert _{C^{1,\gamma }({\overline{{\varOmega }}})} \le c_9 \quad \text {for all }n \ge 1. \end{aligned}$$

Exploiting the compact embedding of $C^{1,\gamma }({\overline{{\varOmega }}})$ into $C^{1}({\overline{{\varOmega }}})$ and passing to a suitable subsequence if necessary, we have

$$\begin{aligned} u_n \rightarrow u_* \quad \text {in } C^{1}({\overline{{\varOmega }}}) \quad \text {as}\quad n \rightarrow \infty . \end{aligned}$$

(3.24)

Combining (3.9) and (3.23) yields

$$\begin{aligned} \langle A(u_n),h\rangle -\left\langle \frac{\partial u_n}{\partial n_a},h\right\rangle _{\partial {\varOmega }}=\int _{{\varOmega }}f(x,u_n)hdx \quad \text {for all } h \in W^{1,p}({{\varOmega }}) \end{aligned}$$

which implies, again due to (3.23),

$$\begin{aligned} \langle A(u_n),h\rangle +\int _{\partial {\varOmega }} \beta (x) u_n^{p-1} h d\sigma =\int _{{\varOmega }}f(x,u_n)h\mathrm{d}x \quad \text {for all } h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

Passing to the limit as $n\rightarrow \infty$ and using (3.24), we obtain

$$\begin{aligned} \langle A(u_*),h\rangle +\int _{\partial {\varOmega }} \beta (x) u_*^{p-1} h d\sigma =\int _{{\varOmega }}f(x,u_*)h\mathrm{d}x \quad \text {for all } h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

Therefore, $u_*$ is a solution of (1.1), and by Proposition 3.4, we know that $\overline{u} \le u_n$ for all $n \ge 1$ which ensures that

$$\begin{aligned} \overline{u} \le u_*. \end{aligned}$$

In summary, we have and .

Similarly, we prove that such that . $\square$

4 Nodal solutions

By applying the extremal constant sign solutions obtained in the previous section, we can now generate nodal (sign changing) solutions of problem (1.1). To do this, we strengthen the condition on $f(x,\cdot )$ near zero and consider two different cases. In the first one, we suppose that $f(x,\cdot )$ is $(\varsigma -1)$-superlinear near zero, and in the second case, we assume that $f(x,\cdot )$ is $(\varsigma -1)$-linear near zero. The proofs of the two cases differ.

In the first case, the hypotheses on $f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ are the following.

H$_2$::

$f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function such that $f(x,0)=0$ for a.a. $x\in {\varOmega }$, hypotheses H$_2$(i),(ii),(iv) are the same as the corresponding hypotheses H$_1$(i),(ii),(iv) and

• (iii) if $F(x,s)=\int ^s_0 f(x,t)\mathrm{d}t$, then there exist $\delta _0 \in \left(0,\min \left\{ \pm c_{\pm },1 \right\} \right)$ and $q\in (1, \theta )$ such that

  $$\begin{aligned} c_{10} |s|^q \le f(x,s)s \le q F(x,s), \end{aligned}$$

  for a.a. $x\in {\varOmega }$, for all $|s| \le \delta _0$, and for some $c_{10}>0$.

We first introduce the following truncation functions $e: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ and $d: \partial {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$.

$$\begin{aligned} e(x,s)= {\left\{ \begin{array}{ll} f(x,w_-)+|w_-(x)|^{p-2}w_-(x) &{} \text {if } s<w_-(x),\\ f(x,s)+|s|^{p-2}s &{} \text {if }w_-(x) \le s \le w_+(x),\\ f(x,w_+)+w_+(x)^{p-1} &{} \text {if }s>w_+(x), \end{array}\right. } \end{aligned}$$

(4.1)

and

$$\begin{aligned} d(x,s)= {\left\{ \begin{array}{ll} \beta (x) |w_-(x)|^{p-2}w_-(x) &{} \text {if } s<w_-(x),\\ \beta (x)|s|^{p-2}s &{} \text {if }w_-(x) \le s \le w_+(x),\\ \beta (x) w_+(x)^{p-1} &{} \text {if }s>w_+(x). \end{array}\right. } \end{aligned}$$

(4.2)

Setting $E(x,s)=\int ^s_0 e(x,t)dt$ and $D(x,s)=\int ^s_0 d(x,t)dt$, we define the $C^1$-functional ${\varphi }: W^{1,p}({{\varOmega }})\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} {\varphi }(u)=\int _{{\varOmega }}G(\nabla u)\mathrm{d}x +\frac{1}{p}\Vert u\Vert ^p_p+\int _{\partial {\varOmega }} D(x,u)\mathrm{d}\sigma -\int _{{\varOmega }}E(x,u)\mathrm{d}x. \end{aligned}$$

In the first step, we have to compute the critical groups of ${\varphi }$ at the origin. Note that a similar computation under stronger hypotheses and for $G(\xi )=\frac{1}{\xi } |\xi |^p$ for all $\xi \in {\mathbb {R}}^N$ was done by Moroz [16] ($p=2$) and Jiu-Su [12] ($1<p<\infty$). In both works, the ambient space is $W^{1,p}_0({{\varOmega }})$.

Proposition 4.1

Let hypotheses H(a), H($\beta$) and H$_2$ be satisfied, and suppose that $K_{\varphi }$ is finite. Then,

$$\begin{aligned} C_k({\varphi },0)=0 \quad \text {for all } k\ge 0. \end{aligned}$$

Proof

Regarding hypotheses H$_2$(i),(iii) and (4.1), there exist $c_{11}>0$ and $r>p$ such that

$$\begin{aligned} E(x,s)\ge \frac{c_{10}}{q} |s|^q-c_{11}|s|^r \quad \text {for a.a. }x\in {\varOmega }\text { and all } s \in {\mathbb {R}}. \end{aligned}$$

(4.3)

Moreover, hypotheses H(a)(iv) and Corollary 2.5 imply

$$\begin{aligned} G(\xi )\le c_{12}\left(|\xi |^\varsigma +|\xi |^p\right)\quad \text {for all }\xi \in {\mathbb {R}}^N \text { and some }c_{12}>0. \end{aligned}$$

(4.4)

Let $u\in W^{1,p}({{\varOmega }})$ and $t\in (0,1)$. Then, due to (4.2), (4.3) and (4.4), it follows

$$\begin{aligned} {\varphi }(tu)&= \int _{{\varOmega }}G(\nabla (tu))dx +\frac{t^p}{p}\Vert u\Vert ^p_p+\int _{\partial {\varOmega }} D(x,tu)d\sigma -\int _{{\varOmega }}E(x,tu)dx\nonumber \\&\le c_{12}\left(t^\varsigma \Vert \nabla u\Vert ^\varsigma _\varsigma +t^p\Vert \nabla u\Vert ^p_p\right)+\frac{t^p}{p}\Vert u\Vert ^p_p+\frac{t^p}{p}c_{13}\Vert u\Vert ^p_{p,\partial {\varOmega }}\nonumber \\&\quad +c_{11}t^r\Vert u\Vert ^r_r-\frac{c_{10}}{q}t^q\Vert u\Vert ^q_q \end{aligned}$$

(4.5)

for some $c_{13}>0$. Since $q<\varsigma <p<r$, with view to (4.5), we can find $t^*=t^*(u)\in (0,1)$ small enough such that

$$\begin{aligned} {\varphi }(tu)<0 \quad \text {for all } t\in \left(0,t^*\right). \end{aligned}$$

(4.6)

Let $u \in W^{1,p}({{\varOmega }})$ with $0<\Vert u\Vert _{1,p}\le 1$ and ${\varphi }(u)=0$. Then, owing to $d(x,s)s \ge \varsigma D(x,s)$ on $\partial {\varOmega }\times {\mathbb {R}}$, we obtain

$$\begin{aligned} \frac{d}{\mathrm{d}t} {\varphi }(tu) \bigg |_{t=1}&= \left\langle {\varphi }'(u),u\right\rangle \nonumber \\&= \int _{{\varOmega }}\left(a(\nabla u),\nabla u \right)_{{\mathbb {R}}^N}\mathrm{d}x + \Vert u\Vert ^p_p+\int _{\partial {\varOmega }} d(x,u)ud\sigma -\int _{{\varOmega }}e(x,u)u\mathrm{d}x\nonumber \\&\ge \int _{{\varOmega }}\left[\left(a(\nabla u),\nabla u \right)_{{\mathbb {R}}^N} - \theta G(\nabla u) \right]\mathrm{d}x+\left( 1-\frac{\theta }{p}\right) \Vert u\Vert ^p_p\nonumber \\&\quad +(\theta -q)\int _{{\varOmega }}E(x,u)\mathrm{d}x+\int _{{\varOmega }}\left[ qE(x,u)-e(x,u)u\right]\mathrm{d}x. \end{aligned}$$

(4.7)

Hypotheses H$_2$(i),(iii) and (4.1) imply

$$\begin{aligned} qE(x,s)-e(x,s)s\ge -c_{14}|s|^r \quad \text {for a.a } x\in {\varOmega }\text { and all }s\in {\mathbb {R}}, \end{aligned}$$

(4.8)

where $c_{14}$ is a positive constant. Applying (4.3), (4.8) and hypotheses H(a)(iv) in (4.7), we obtain, as $\varsigma >q$,

$$\begin{aligned} \frac{d}{\mathrm{d}t} {\varphi }(tu) \bigg |_{t=1}\ge \tilde{c}\Vert \nabla u\Vert ^p_p +\left( 1-\frac{\varsigma }{p}\right) \Vert u\Vert ^p_p-c_{15}\Vert u\Vert ^r_r \end{aligned}$$

for some $c_{15}>0$. Therefore,

$$\begin{aligned} \frac{d}{\mathrm{d}t} {\varphi }(tu) \bigg |_{t=1}\ge c_{16}\Vert u\Vert ^p_{1,p} -c_{17}\Vert u\Vert ^r_{1,p} \quad \text {for some }c_{16},c_{17}>0. \end{aligned}$$

(4.9)

From (4.9) and since $r>p$, we can find $\rho \in (0,1)$ small enough such that

$$\begin{aligned} \frac{d}{\mathrm{d}t} {\varphi }(tu) \bigg |_{t=1}>0 \quad \text {for all }u\in W^{1,p}({{\varOmega }}) \text { with }0<\Vert u\Vert _{1,p}\le \rho ,\,\, {\varphi }(u)=0. \end{aligned}$$

(4.10)

Fixing $u\in W^{1,p}({{\varOmega }})$ with $0<\Vert u\Vert _{1,p}\le \rho$ and ${\varphi }(u)=0$, we claim that

$$\begin{aligned} {\varphi }(tu)\le 0 \quad \text {for all }t\in [0,1]. \end{aligned}$$

(4.11)

We argue indirectly and suppose we can find $t_0 \in (0,1)$ such that ${\varphi }(t_0u)>0$. Since ${\varphi }(u)=0$ and ${\varphi }$ is continuous, by Bolzano’s theorem, we have

$$\begin{aligned} t_*=\min \left\{ t\in [t_0,1]: {\varphi }(tu)=0 \right\} >t_0>0. \end{aligned}$$

Then,

$$\begin{aligned} {\varphi }(tu)>0 \quad \text {for all }t\in [t_0,t_*). \end{aligned}$$

(4.12)

We set $v=t_*u$. Then, $0<\Vert v\Vert _{1,p}\le \Vert u\Vert _{1,p}\le \rho$ and ${\varphi }(v)=0$. So, from (4.10), it follows

$$\begin{aligned} \frac{d}{\mathrm{d}t} {\varphi }(tv) \bigg |_{t=1}>0. \end{aligned}$$

(4.13)

Note that, because of (4.12),

$$\begin{aligned} {\varphi }(v)={\varphi }(t_*u)=0<{\varphi }(tu) \quad \text {for all }t\in [t_0,t_*), \end{aligned}$$

which implies

$$\begin{aligned} \frac{d}{\mathrm{d}t} {\varphi }(tv) \bigg |_{t=1}=t_* \frac{d}{\mathrm{d}t}{\varphi }(tu)\bigg |_{t=t_*}=t_* \lim _{t\rightarrow t_*^-} \frac{{\varphi }(tu)}{t-t_*}\le 0. \end{aligned}$$

(4.14)

Comparing (4.13) and (4.14), we reach a contradiction. This proves (4.11).

Let $\rho \in (0,1)$ be small such that $K_{\varphi }\cap \overline{B}_\rho =\{0\}$. We consider the deformation $h: [0,1] \times \left({\varphi }^0 \cap \overline{B}_\rho \right)\rightarrow {\varphi }^0 \cap \overline{B}_\rho$ defined by

$$\begin{aligned} h(t,u)=(1-t)u. \end{aligned}$$

By reason of (4.10) and (4.11), we see that this deformation is well defined and that ${\varphi }^0 \cap \overline{B}_\rho$ is contractible in itself.

Let $u \in \overline{B}_\rho$ with ${\varphi }(u)>0$. We are going to show that there exists an unique $t(u)\in (0,1)$ such that

$$\begin{aligned} {\varphi }(t(u)u)=0. \end{aligned}$$

(4.15)

Taking into account (4.6) along with Bolzano’s theorem, we verify that such a $t(u)\in (0,1)$ exists. We only need to show its uniqueness. Arguing by contradiction, suppose that there exist

$$\begin{aligned} 0<t_1=t(u)_1<t_2=t(u)_2<1 \quad \text {such that} \quad {\varphi }(t_1u)={\varphi }(t_2u)=0. \end{aligned}$$

Relation (4.11) gives

$$\begin{aligned} {\varphi }(tt_2u)\le 0 \quad \text {for all }t\in [0,1], \end{aligned}$$

which implies that

$$\begin{aligned} \frac{t_1}{t_2}\in (0,1) \text { is a maximizer of } t \rightarrow {\varphi }(tt_2u) \quad \text {on }[0,1]. \end{aligned}$$

We conclude that

$$\begin{aligned} \frac{t_1}{t_2} \frac{d}{\mathrm{d}t} {\varphi }(tt_2u) \bigg |_{t=\frac{t_1}{t_2}}=\frac{d}{\mathrm{d}t} {\varphi }(tt_1u)\bigg |_{t=1}=0, \end{aligned}$$

which contradicts (4.10). This proves the uniqueness of $t(u)\in (0,1)$ satisfying (4.15). We have

$$\begin{aligned} {\varphi }(tu)<0 \quad \text {for all } t \in (0,t(u)) \quad \text {and}\quad {\varphi }(tu)>0 \quad \text {for all }t \in (t(u),1]. \end{aligned}$$

Consider the function $E_1: \overline{B}_\rho {\setminus }\{0\} \rightarrow (0,1]$ defined by

it is easy to check that $E_1$ is continuous. Let $E_2: \overline{B}_\rho {\setminus }\{0\} \rightarrow \left({\varphi }^0\cap \overline{B}_\rho \right) {\setminus }\{0\}$ be defined by

Evidently, $E_2$ is continuous and

$$\begin{aligned} E_2\bigg |_{\left({\varphi }^0\cap \overline{B}_\rho \right) {\setminus }\{0\}}={{\mathrm{id}}}\bigg |_{\left({\varphi }^0\cap \overline{B}_\rho \right) {\setminus }\{0\}}. \end{aligned}$$

We conclude that $\left({\varphi }^0\cap \overline{B}_\rho \right) {\setminus }\{0\}$ is a retract of $\overline{B}_\rho {\setminus }\{0\}$ and the latter is contractible. It follows that $\left({\varphi }^0\cap \overline{B}_\rho \right) {\setminus }\{0\}$ is contractible in itself. Moreover, we have seen before that ${\varphi }^0\cap \overline{B}_\rho$ is contractible in itself. Then, from Granas and Dugundji [10, p. 389], we have

$$\begin{aligned} H_k \left( {\varphi }^0\cap \overline{B}_\rho , \left({\varphi }^0\cap \overline{B}_\rho \right) {\setminus }\{0\} \right)=0 \quad \text {for all }k \ge 0, \end{aligned}$$

which implies

$$\begin{aligned} C_k({\varphi },0)=0 \quad \text {for all } k \ge 0. \end{aligned}$$

$\square$

Using this proposition, we can prove the existence of a nodal solution of (1.1). In what follows, we denote by $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ and $v_* \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ the two extremal constant sign solutions of (1.1) obtained in Proposition 3.5.

Proposition 4.2

Let H(a), H($\beta$), and H$_2$ be satisfied. Then, problem (1.1) admits a nodal solution $y_0 \in [v_*,u_*] \cap C^1({\overline{{\varOmega }}})$.

Proof

We introduce the Carathéodory functions $\eta : {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}, \gamma : \partial {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \eta (x,s)= {\left\{ \begin{array}{ll} f(x,v_*(x))+|v_*(x)|^{p-2}v_*(x) &{} \text {if } s<v_*(x),\\ f(x,s)+|s|^{p-2}s &{} \text {if } v_*(x) \le s \le u_*(x),\\ f(x,u_*(x))+u_*(x)^{p-1} &{} \text {if } s>u_*(x), \end{array}\right. } \end{aligned}$$

(4.16)

and

$$\begin{aligned} \gamma (x,s)= {\left\{ \begin{array}{ll} \beta (x)|v_*(x)|^{p-2}v_*(x) &{} \text {if } s<v_*(x),\\ \beta (x)|s|^{p-2}s &{} \text {if } v_*(x) \le s \le u_*(x),\\ \beta (x)u_*(x)^{p-1} &{} \text {if } s>u_*(x). \end{array}\right. } \end{aligned}$$

(4.17)

Let $H(x,s)=\int ^s_0 \eta (x,t)dt, {\varGamma }(x,s)=\int ^s_0 \gamma (x,t)\mathrm{d}t$ and let $\psi : W^{1,p}({{\varOmega }}) \rightarrow {\mathbb {R}}$ be the $C^1$-functional given by

$$\begin{aligned} \psi (u)=\int _{{\varOmega }}G(\nabla u)\mathrm{d}x+\frac{1}{p} \Vert u\Vert ^p_p+\int _{\partial {\varOmega }} {\varGamma }(x,u) \mathrm{d}\sigma -\int _{{\varOmega }}H(x,u)\mathrm{d}x. \end{aligned}$$

Additionally, we consider the positive and negative truncations of $\eta (x,\cdot )$ and $\gamma (x,\cdot )$, that is,

$$\begin{aligned} \eta _{\pm }(x,s)=\eta \left( x, \pm s^{\pm }\right) \quad \text {and} \quad \gamma _{\pm }(x,s)=\gamma \left(x,\pm s^\pm \right). \end{aligned}$$

We set $H_\pm (x,s)=\int ^s_0 \eta _\pm (x,t)dt, {\varGamma }_\pm (x,s)=\int ^s_0 \gamma _\pm (x,t)dt$ and consider the $C^1$-functionals $\psi _\pm : W^{1,p}({{\varOmega }}) \rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \psi _\pm (u)=\int _{{\varOmega }}G(\nabla u)\mathrm{d}x+\frac{1}{p} \Vert u\Vert ^p_p+\int _{\partial {\varOmega }} {\varGamma }_\pm (x,u) \mathrm{d}\sigma -\int _{{\varOmega }}H_\pm (x,u)\mathrm{d}x. \end{aligned}$$

Claim 1

$K_\psi \subseteq [v_*,u_*], \, K_{\psi _+}=\left\{ 0, u_* \right\} , \, K_{\psi _-}=\left\{ v_*,0\right\}$

Let $u \in K_\psi$, that is, $\psi '(u)=0$ which results in

$$\begin{aligned} \langle A(u),h\rangle +\int _{{\varOmega }}|u|^{p-2}uh\mathrm{d}x+\int _{\partial {\varOmega }} \gamma (x,u)h\mathrm{d}\sigma =\int _{{\varOmega }}\eta (x,u)h\mathrm{d}x \end{aligned}$$

(4.18)

for all $h \in W^{1,p}({{\varOmega }})$. Choosing $h=\left(u-u_*\right)^+\in W^{1,p}({{\varOmega }})$ in (4.18) and applying (4.16), (4.17) gives

$$\begin{aligned}&\langle A(u),\left(u-u_*\right)^+ \rangle +\int _{{\varOmega }}u^{p-1}\left(u-u_*\right)^+ \mathrm{d} x+\int _{\partial {\varOmega }} \beta (x) u_*^{p-1} \left(u-u_*\right)^+ \mathrm{d}\sigma \\&\quad =\int _{{\varOmega }}\left[f(x,u_*)+u_*^{p-1} \right]\left(u-u_*\right)^+\mathrm{d}x\\&\quad = \langle A(u_*),\left(u-u_*\right)^+\rangle + \int _{{\varOmega }}u_*^{p-1} \left(u-u_*\right)^+ \mathrm{d}x +\int _{\partial {\varOmega }} \beta (x) u_*^{p-1} \left(u-u_*\right)^+ \mathrm{d} \sigma , \end{aligned}$$

which implies

$$\begin{aligned}&\langle A(u)-A(u_*),\left(u-u_*\right)^+ \rangle +\int _{{\varOmega }}\left(u^{p-1}-u_*^{p-1}\right)\left(u-u_*\right)^+ \mathrm{d}x=0. \end{aligned}$$

Therefore, $\left|\left\{ u>u_*\right\} \right|_N=0$, hence, $u \le u_*$. Similarly, if we choose $h=\left(v_*-u\right)^+ \in W^{1,p}({{\varOmega }})$, then we obtain $v_* \le u$. Thus, $u \in [v_*,u_*]$ meaning $K_\psi \subseteq [v_*,u_*]$. In the same way, we can show that

$$\begin{aligned} K_{\psi _+} \subseteq [0,u_*] \quad \text {and} \quad K_{\psi _-} \subseteq [v_*,0]. \end{aligned}$$

But the extremality of $u_*$ and $v_*$ implies

$$\begin{aligned} K_{\psi _+} = \{0,u_*\} \quad \text {and} \quad K_{\psi _-} = \{v_*,0\}. \end{aligned}$$

This proves Claim 1.

By virtue of Claim 1, we may assume that $K_\psi$ is finite. Otherwise, due to (4.16) and (4.17), we already have infinity nodal solutions and so we are done.

Claim 2

$u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ and $v_* \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ are local minimizers of $\psi$.

It is clear that $\psi _+$ is coercive due to the presence of the truncations. Since it is also sequentially weakly lower semicontinuous, we find $\overline{u}_* \in W^{1,p}({{\varOmega }})$ such that

$$\begin{aligned} \psi _+\left(\overline{u}_* \right)= \inf \left[\psi _+(u): u \in W^{1,p}({{\varOmega }}) \right]. \end{aligned}$$

(4.19)

As before (see the proof of Proposition 3.2), for $|t|\in (0,1)$ small enough such that at least

$$\begin{aligned} t \hat{u}_1(\varsigma ,\hat{\beta }) \in [v_*,u_*], \,\, |t| \hat{u}_1(\varsigma ,\hat{\beta }) \le \delta _0 \quad \text {for all }x \in {\overline{{\varOmega }}}\end{aligned}$$

(recall that $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ and $v_* \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$, hence such a $|t|\in (-1,1)$ can be found) and using hypothesis H$_2$(iii), we obtain

$$\begin{aligned} \psi _+ \left(t\hat{u}_1(\varsigma ,\hat{\beta }) \right)<0. \end{aligned}$$

Therefore, $\psi _+(\overline{u}_*)<0=\psi _+(0)$, and thus, $\overline{u}_* \ne 0$. Since $\overline{u}_*$ is a global minimizer of $\psi _+$ (see (4.19)), there holds $\overline{u}_* \in K_{\psi _+} {\setminus }\{0\}$, which implies, due to Claim 1, that $\overline{u}_*=u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$.

As $\psi \big |_{C^1({\overline{{\varOmega }}})_+}=\psi _+\big |_{C^1({\overline{{\varOmega }}})_+}$, it follows that $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ is a local $C^1({\overline{{\varOmega }}})$-minimizer of $\psi$. Invoking Theorem 2.7, we infer that $u_*$ is a local $W^{1,p}({{\varOmega }})$-minimizer of $\psi$.

The second assertion can be shown in the same way, using $\psi _-$ instead of $\psi _+$. This proves Claim 2.

Without any loss of generality, we may assume that $\psi _+(v_*) \le \psi _+(u_*)$ (the analysis is similar if the opposite inequality holds). Since $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ is a local $W^{1,p}({{\varOmega }})$-minimizer of $\psi$ (see Claim 2), there exists $\rho \in (0,1)$ such that

$$\begin{aligned} \psi (v_*) \le \psi (u_*)<\inf \left[\psi (u): \Vert u-u_*\Vert _{1,p}=\rho \right]=m_\rho , \quad \Vert v_*-u_*\Vert _{1,p}>\rho \end{aligned}$$

(4.20)

(see Aizicovici et al. [1, Proof of Proposition 29]). Recall that the functional is coercive; hence, it satisfies the PS-condition. This fact along with (4.20) permits the use of the mountain pass theorem stated in Theorem 2.2. This yields $y_0 \in W^{1,p}({{\varOmega }})$ such that

$$\begin{aligned} y_0 \in K_\psi \quad \text {and} \quad m_\rho \le \psi (y_0). \end{aligned}$$

(4.21)

Then, by means of Claim 1, we have $y_0 \in [v_*,u_*]$. From this and (4.20), (4.21), it follows that $y_0 \ne u_*, y_0 \ne v_*$ and $y_0$ is a solution of (1.1) (see the definition of the truncations in (4.16), (4.17)). Moreover, the nonlinear regularity theory implies that $y_0 \in [v_*,u_*]\cap C^1({\overline{{\varOmega }}})$. Since $y_0$ is a critical point of $\psi$ of mountain pass type, we have

$$\begin{aligned} C_1(\psi ,y_0) \ne 0 \end{aligned}$$

(4.22)

(see, e.g., Motreanu et al. [17, p. 176]).

We consider now the homotopy $\hat{h}(t,u)$ defined by

$$\begin{aligned} \hat{h}(t,u)=(1-t)\psi (u)+t{\varphi }(u) \quad \text {for all } (t,u) \in [0,1]\times W^{1,p}({{\varOmega }}). \end{aligned}$$

Suppose we could find sequences $(t_n)_{n\ge 1} \subseteq [0,1]$ and $(u_n)_{n \ge 1} \subseteq W^{1,p}({{\varOmega }})$ such that

$$\begin{aligned} t_n \rightarrow t\in [0,1], \quad u_n \rightarrow 0 \quad \text {in }W^{1,p}({{\varOmega }}), \quad \text {and} \quad \hat{h}'_u(t_n,u_n)=0 \,\,\, \text {for all }n \ge 1. \end{aligned}$$

(4.23)

This gives

$$\begin{aligned}&\langle A(u_n),h\rangle +\int _{{\varOmega }}|u_n|^{p-2}u_nh\mathrm{d}x+(1-t_n)\int _{\partial {\varOmega }} \gamma (x,u_n)h\mathrm{d}\sigma +t_n\int _{\partial {\varOmega }} d(x,u_n)h \mathrm{d}\sigma \\&\quad =(1-t_n) \int _{{\varOmega }}\eta (x,u_n) h\mathrm{d}x+t_n \int _{{\varOmega }}e(x,u_n)h\mathrm{d}x \quad \text {for all } h \in W^{1,p}({{\varOmega }}). \end{aligned}$$

As before, we can show that $u_n \in [w_-,w_+]$ for all $n \ge 1$ and via the nonlinear Green’s identity (see the proof of Proposition 3.2) we obtain

$$\begin{aligned} \begin{aligned} -{{\mathrm{div}}}a(\nabla u_n)+|u_n|^{p-2}u_n&= (1-t_n) \eta (x,u_n)+t_ne(x,u_n)\quad&\text {in } {\varOmega },\\ \frac{\partial u}{\partial n_a}&= -(1-t_n)\gamma (x,u_n)-t_nd(x,u_n)&\text {on } \partial {\varOmega }. \end{aligned} \end{aligned}$$

The regularity results of Lieberman [14, p. 320] imply the existence of $\lambda \in (0,1)$ and $c_{18}>0$ such that

$$\begin{aligned} u_n \in C^{1,\lambda }({\overline{{\varOmega }}}) \quad \text {and} \quad \Vert u_n\Vert _{C^{1,\lambda }({\overline{{\varOmega }}})} \le c_{18} \quad \text {for all }n \ge 1. \end{aligned}$$

(4.24)

The compact embedding of $C^{1,\lambda }({\overline{{\varOmega }}})$ into $C^1({\overline{{\varOmega }}})$ along with (4.23) and (4.24) yields

$$\begin{aligned} u_n \rightarrow 0 \quad \text {in } C^1({\overline{{\varOmega }}}) \quad \text {as } \quad n \rightarrow \infty . \end{aligned}$$

Hence, $u_n \in [v_*,u_*]$ for all $n \ge n_0\ge 1$, and because of Claim 1, it follows $(u_n)_{n \ge n_0} \subseteq K_\psi$ which contradicts the fact that $K_\psi$ is finite. Therefore, (4.23) cannot happen, and then, the homotopy invariance of critical groups (see Motreanu et al. [17]) implies that

$$\begin{aligned} C_k(\psi ,0)=C_k({\varphi },0) \quad \text {for all } k \ge 0. \end{aligned}$$

Using this together with Proposition 4.1, there holds

$$\begin{aligned} C_k(\psi ,0)=0 \quad \text {for all } k \ge 0. \end{aligned}$$

(4.25)

Comparing (4.22) and (4.25), we see that $y_0 \ne 0$. Hence, $y_0 \in [v_*,u_*] \cap C^1({\overline{{\varOmega }}})$ is nodal. $\square$

Now we can state the first multiplicity result for problem (1.1)

Theorem 4.3

Let hypotheses H(a), H($\beta$) and H$_2$ be satisfied. Then, problem (1.1) has at least three nontrivial solutions

$$\begin{aligned} u_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad v_0 \in -{{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad \text {and} \quad y_0 \in [v_0,u_0] \cap C^1({\overline{{\varOmega }}}) \text { nodal}. \end{aligned}$$

Remark 4.4

An interesting question was posed by the referee, namely whether we can describe the nodal regions of the solution $y_0$. It seems to us that in this generality this cannot be done. However, for more particular reaction terms and differential operators maybe more information can be provided for the nodal solution. This is an interesting open problem worth pursuing further.

In Theorem 4.3, hypothesis H$_2$(iii) dictates the presence of a concave nonlinearity near zero (recall that $1<q<\theta <\varsigma \le p$). Next, we examine what happens if $f(x,\cdot )$ is $(\varsigma -1)$-linear near zero. For example, suppose that $a(\xi )=|\xi |^{p-2}\xi$ for all $\xi \in {\mathbb {R}}^N$ with $1<p<\infty$; that is, the differential operator is the p-Laplacian. Then, $c_1=p-1$, and we can take $\varsigma =p$ (see hypothesis H(a)(iv)). In this case, the reaction $f(x,\cdot )$ will be $(p-1)$-linear near zero, and so the geometry near the origin changes from the previous case.

H$_3$::

$f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function such that $f(x,0)=0$ for a.a. $x\in {\varOmega }$, hypotheses H$_3$(i),(ii),(iv) are the same as the corresponding hypotheses H$_1$(i),(ii),(iv) and

• (iii) there exists constants $c_{19}, c_{20}>0$ such that

  $$\begin{aligned} c^* \hat{\lambda }_2(\varsigma ,\hat{\beta })<c_{19} \end{aligned}$$

  and

  $$\begin{aligned} c_{19}\le \liminf _{s \rightarrow 0} \frac{f(x,s)}{|s|^{\varsigma -2}s} \le \limsup _{s \rightarrow 0} \frac{f(x,s)}{|s|^{\varsigma -2}s} \le c_{20} \end{aligned}$$

  uniformly for a.a. $x\in {\varOmega }$.

Remark 4.5

Note that Proposition 4.1 is no longer true under hypothesis H$_3$ because the geometry near the origin is now different and so the approach changes. The idea in the current case is to use Proposition 2.8 instead.

Theorem 4.6

If hypotheses H(a), H($\beta$) and H$_3$ hold, then problem (1.1) has at least three nontrivial solutions

$$\begin{aligned} u_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad v_0 \in -{{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad \text {and} \quad y_0 \in [v_0,u_0] \cap C^1({\overline{{\varOmega }}}) \text { nodal}. \end{aligned}$$

Proof

Evidently, the results of Sect. 3 remain valid, and so we can find extremal constant sign solutions $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ and $v_* \in -{{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$ of (1.1). Then, as in the proof of Proposition 4.2, defining the $C^1$-functionals $\psi$ and $\psi _\pm$, the mountain pass theorem (see Theorem 2.2) implies the existence of a solution $y_0 \in [v_*,u_*]\cap C^1({\overline{{\varOmega }}})$ of problem (1.1). We need to show that $y_0 \ne 0$. From the mountain pass theorem, it follows

$$\begin{aligned} m_\rho \le \psi (y_0)=\inf _{\gamma \in {\varGamma }} \max _{0\le t \le 1} \psi (\gamma (t)), \end{aligned}$$

(4.26)

where ${\varGamma }=\left\{ \gamma \in C\left([0,1],W^{1,p}({{\varOmega }})) \right): \gamma (0)=v_*, \gamma (1)=u_* \right\}$. According to (4.26), in order to establish the nontriviality of $y_0$, it suffices to produce a path $\gamma _* \in {\varGamma }$ such that $\psi \big |_{\gamma _*}<0$. For this purpose, we introduce the following Banach $C^1$-manifolds

$$\begin{aligned} S_\varsigma =W^{1,p}({{\varOmega }})\cap \partial B_1^{L^\varsigma } \quad \text {and} \quad S_\varsigma ^c=S_\varsigma \cap C^1({\overline{{\varOmega }}}). \end{aligned}$$

Recall that $B_1^{L^\varsigma }=\left\{ u \in L^{\varsigma }({\varOmega }): \Vert u\Vert _\varsigma =1\right\}$ and note that $S_\varsigma ^c$ is dense in $S_\varsigma$. We consider the subsequent sets of paths

$$\begin{aligned} \hat{{\varGamma }}(\varsigma ,\hat{\beta })&=\left\{ \hat{\gamma } \in C \left([-1,1],S_\varsigma \right): \hat{\gamma }(-1)=\hat{u}_1(\varsigma ,\hat{\beta }), \,\, \hat{\gamma }(1)=\hat{u}_1(\varsigma ,\hat{\beta })\right\} , \\ \hat{{\varGamma }}_c(\varsigma ,\hat{\beta })&=\left\{ \hat{\gamma } \in C \left([-1,1],S_\varsigma ^c \right): \hat{\gamma }(-1)=\hat{u}_1(\varsigma ,\hat{\beta }), \,\, \hat{\gamma }(1)=\hat{u}_1(\varsigma ,\hat{\beta })\right\} \end{aligned}$$

Claim

$\hat{{\varGamma }}_c(\varsigma ,\hat{\beta })$ is dense in $\hat{{\varGamma }}(\varsigma ,\hat{\beta })$.

Let $\hat{\gamma } \in \hat{{\varGamma }}(\varsigma ,\hat{\beta })$ and $\varepsilon \in (0,1)$. Consider the multifunction $T_\varepsilon : [-1,1] \rightarrow 2^{C^1({\overline{{\varOmega }}})}$ defined by

$$\begin{aligned} T_\varepsilon (t)= {\left\{ \begin{array}{ll} \left\{ u \in C^1({\overline{{\varOmega }}}): \left\Vert u- \hat{\gamma }(t) \right\Vert_{1,p}<\varepsilon \right\} &{} \text {if } -1<t<1,\\ \left\{ \pm \hat{u}_1(\varsigma ,\hat{\beta }) \right\} &{} \text {if }t=\pm 1, \end{array}\right. } \end{aligned}$$

we easily verify that $T_\varepsilon$ has nonempty and convex values. Moreover, $T_\varepsilon (t)$ is open for all $t\in (-1,1)$, while $T_\varepsilon (\pm 1)$ are singletons. In addition, the continuity of $\hat{\gamma }$ implies that the multifunction $T_\varepsilon$ is lower semicontinuous (see Papageorgiou and Kyritsi [19, p. 458]). Therefore, we can apply Theorem 3.1 of Michael [15] to obtain a continuous path $\hat{\gamma }_\varepsilon : [-1,1] \rightarrow C^1({\overline{{\varOmega }}})$ such that

$$\begin{aligned} \hat{\gamma }_\varepsilon (t) \in T_\varepsilon (t) \quad \text {for all } t \in [-1,1]. \end{aligned}$$

Now, let $\varepsilon _n=\frac{1}{n}, n\ge 1$, and let $\left(\hat{\gamma }_n=\hat{\gamma }_{\varepsilon _n} \right)_{n \ge 1} \subseteq C \left([-1,1],C^1({\overline{{\varOmega }}}) \right)$ be as above. We have

$$\begin{aligned}&\left\Vert\hat{\gamma }_n(t)-\hat{\gamma }(t) \right\Vert_{1,p}<\frac{1}{n} \quad \text {for all } t\in (-1,1),\nonumber \\&\hat{\gamma }_n(\pm 1)=\pm \hat{u}_1(\varsigma ,\hat{\beta })\quad \text {for all } n \ge 1. \end{aligned}$$

(4.27)

Since $\hat{\gamma }(t) \in \partial B_1^{L^\varsigma }$ for all $t \in [-1,1]$, we may assume, due to (4.27), that $\left\Vert\hat{\gamma }_n(t)\right\Vert_\varsigma \ne 0$ for all $t\in [-1,1]$ and all $n \ge 1$. We set

$$\begin{aligned} \hat{\gamma }^0_n(t)=\frac{\hat{\gamma }_n(t)}{\left\Vert\hat{\gamma }_n(t)\right\Vert_\varsigma } \quad \text {for all }t\in [-1,1] \text { and all }n \ge 1. \end{aligned}$$

(4.28)

Clearly, $\hat{\gamma }^0_n \in C([-1,1],S^c_\varsigma )$ and $\hat{\gamma }^0_n(\pm 1)=\pm \hat{u}_1(\varsigma ,\hat{\beta })$. Moreover, due to (4.27) and (4.28), we obtain

$$\begin{aligned} \left\Vert\hat{\gamma }^0_n(t)-\hat{\gamma }(t) \right\Vert_{1,p}&\le \left\Vert\hat{\gamma }^0_n(t)-\hat{\gamma }_n(t) \right\Vert_{1,p} + \left\Vert\hat{\gamma }_n(t)-\hat{\gamma }(t) \right\Vert_{1,p}\\&\le \frac{\left|1-\left\Vert\hat{\gamma }_n(t) \right\Vert_\varsigma \right|}{\left\Vert\hat{\gamma }_n(t) \right\Vert_\varsigma } \left\Vert\hat{\gamma }_n(t) \right\Vert_{1,p} +\frac{1}{n} \quad \text {for all }t\in [-1,1] \quad \text {and all }n\ge 1. \end{aligned}$$

Note that, because $\hat{\gamma }(t) \in S_\varsigma$ for all $t \in [-1,1]$, (4.27), and the embedding $W^{1,p}({{\varOmega }}) \hookrightarrow L^{\varsigma }({\varOmega })$,

$$\begin{aligned} \max _{-1\le t \le 1} \left|1-\left\Vert\hat{\gamma }_n(t) \right\Vert_\varsigma \right|&=\max _{-1\le t \le 1} \left|\left\Vert\hat{\gamma }(t) \right\Vert_{\varsigma }-\left\Vert\hat{\gamma }_n(t) \right\Vert_\varsigma \right|\\&\le \max _{-1\le t \le 1} \left\Vert\hat{\gamma }(t)-\hat{\gamma }_n(t) \right\Vert_\varsigma \\&\le c_{21} \max _{-1\le t \le 1} \left\Vert\hat{\gamma }(t)-\hat{\gamma }_n(t) \right\Vert_{1,p}\\&\le \frac{c_{21}}{n} \end{aligned}$$

for some $c_{21}>0$ and for all $n \ge 1$. Therefore, $\hat{{\varGamma }}_c(\varsigma ,\hat{\beta })$ is dense in $\hat{{\varGamma }}(\varsigma ,\hat{\beta })$. This proves the Claim.

The Claim combined with Proposition 2.8 imply, for given $\delta >0$, the existence of $\hat{\gamma }_0 \in \hat{{\varGamma }}_c(\varsigma ,\hat{\beta })$ such that

$$\begin{aligned} \max _{-1\le t \le 1} \xi \left( \hat{\gamma }_0(t)\right) \le \hat{\lambda }_2(\varsigma ,\hat{\beta })+\delta . \end{aligned}$$

(4.29)

Recall that $\xi (u)=\Vert \nabla u\Vert ^p_p+\int _{\partial {\varOmega }} \hat{\beta }(x) |u|^p d\sigma$ for all $u \in W^{1,p}({{\varOmega }})$. Given $\varepsilon \in \left(0,c_{19}-c^* \hat{\lambda }_1(\varsigma ,\hat{\beta }) \right)$, owing to hypotheses H(a)(iv) and H$_3$(iii), we can find $\hat{\delta }=\hat{\delta }(\varepsilon ) \in (0,\delta )$ such that

$$\begin{aligned} F(x,s)&\ge \frac{c_{19}-\varepsilon }{\varsigma }|s|^\varsigma \quad \text {for a.a. }x\in {\varOmega }\quad \text {and all }|s|\le \hat{\delta }, \end{aligned}$$

(4.30)

$$\begin{aligned} G(\xi )&\le \frac{c^*+\varepsilon }{\varsigma }|\xi |^\varsigma \quad \text {for all }|\xi |\le \hat{\delta }. \end{aligned}$$

(4.31)

Since $\hat{\gamma }_0 \in \hat{{\varGamma }}_c(\varsigma ,\hat{\beta })$ and $u_* \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , v_* \in - {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$, we find $\lambda \in (0,1)$ small enough such that, for all $t\in [-1,1]$,

$$\begin{aligned} \lambda \hat{\gamma }_0(t) \in [v_*,u_*] \quad \text {and} \quad \lambda \left|\hat{\gamma }_0(t)(x)\right|, \lambda \left| \nabla \hat{\gamma }_0(t)(x) \right| \le \hat{\delta } \quad \text {for all }x\in {\overline{{\varOmega }}}. \end{aligned}$$

(4.32)

Now, applying (4.16), (4.17), (4.29), (4.30), (4.31), (4.32) and using the fact that $\left\Vert\hat{\gamma }_0(t)\right\Vert_\varsigma =1$ and $\varsigma <p$, we get

$$\begin{aligned} \psi \left(\lambda \hat{\gamma }_0(t) \right)= & {} \int _{{\varOmega }}G \left(\lambda \nabla \hat{\gamma }_0(t) \right)dx+\frac{\lambda ^p}{p} \int _{\partial {\varOmega }} \beta (x) \left|\hat{\gamma }_0(t) \right|^pd\sigma - \int _{{\varOmega }}F \left(x,\lambda \hat{\gamma }_0(t) \right)dx\nonumber \\\le & {} \frac{c^*+\varepsilon }{\varsigma } \lambda ^\varsigma \left\Vert\nabla \hat{\gamma }_0(t) \right\Vert^p_p + \frac{\lambda ^\varsigma }{\varsigma } c^* \int _{\partial {\varOmega }} \hat{\beta }(x) \left|\hat{\gamma }_0(t) \right|^pd\sigma -\frac{\lambda ^\varsigma }{\varsigma }(c_{19}-\varepsilon )\nonumber \\= & {} \frac{\lambda ^\varsigma }{\varsigma } \left[c^* \xi \left(\hat{\gamma }_0(t)\right)+\varepsilon \left( \left\Vert\nabla \hat{\gamma }_0(t) \right\Vert^p_p +1 \right)-c_{19} \right]\nonumber \\\le & {} \frac{\lambda ^\varsigma }{\varsigma }\left[c^* \hat{\lambda }_2(\varsigma ,\hat{\beta })+c^*\delta +\varepsilon c_{22}-c_{19} \right] \end{aligned}$$

(4.33)

for some $c_{22}>0$ and for all $t \in [-1,1]$. Since $c_{19}>c^* \hat{\lambda }_2(\varsigma ,\hat{\beta })$, choosing $\varepsilon >0$ and $\delta >0$ small enough, from (4.33), it follows

$$\begin{aligned} \psi \left(\lambda \hat{\gamma }_0(t) \right)<0 \quad \text {for all } t \in [-1,1]. \end{aligned}$$

We easily see that $\hat{\gamma }:=\lambda \hat{\gamma }_0$ is a continuous path in $W^{1,p}({{\varOmega }})$ which connects $-\lambda \hat{u}_1(\varsigma ,\hat{\beta })$ and $\lambda \hat{u}_1(\varsigma ,\hat{\beta })$ satisfying

$$\begin{aligned} \psi \big |_{\hat{\gamma }}<0. \end{aligned}$$

(4.34)

Next, we have to construct a continuous path in $W^{1,p}({{\varOmega }})$ connecting $\lambda \hat{u}_1(\varsigma ,\hat{\beta })$ and $u_*$. For this purpose, let

$$\begin{aligned} \mu =\psi _+(u_*)=\inf \left[\psi _+(u): u \in W^{1,p}({{\varOmega }}) \right]<0=\psi _+(0) \end{aligned}$$

(4.35)

(see the proof of Proposition 4.2). The second deformation theorem (see, e.g., Gasiński and Papageorgiou [9, p. 628]) implies the existence of a deformation $h: [0,1] \times \left( \psi _+^0 {\setminus } K^0_{\psi _+} \right) \rightarrow \psi ^0_+$ such that

$$\begin{aligned}&h(0,u)=u \quad \text {for all } u \in \psi _+^0 {\setminus } K^0_{\psi _+}, \end{aligned}$$

(4.36)

$$\begin{aligned}&h \left(1, \psi _+^0 {\setminus } K^0_{\psi _+} \right) \subseteq \psi _+^\mu , \end{aligned}$$

(4.37)

and

$$\begin{aligned}&\psi _+ (h(t,u)) \le \psi _+(h(s,u)) \end{aligned}$$

(4.38)

for all $s,t \in [0,1]$ with $0\le s\le t \le 1$ and all $u \in \psi _+^0 {\setminus } K^0_{\psi _+}$.

Recall, owing to Claim 1 in the proof of Proposition 4.2, that $K_{\psi _+}=\left\{ 0,u_*\right\}$. Therefore, due to (4.34) and (4.35),

$$\begin{aligned} \psi _+^\mu = \{u_*\} \end{aligned}$$

(4.39)

and

$$\begin{aligned} \psi _+\left(\lambda \hat{u}_1 (\varsigma ,\hat{\beta } )\right)=\psi \left(\lambda \hat{u}_1(\varsigma ,\hat{\beta }) \right)=\psi \left(\hat{\gamma }(1)\right)<0. \end{aligned}$$

Therefore, $\lambda \hat{u}_1 (\varsigma ,\hat{\beta } ) \in \psi ^0_+ {\setminus } K^0_{\psi _+}=\psi ^0_+ {\setminus } \{0\}$. This means we can define

$$\begin{aligned} \hat{\gamma }_+(t)=h \left(t,\lambda \hat{u}_1(\varsigma ,\hat{\beta }) \right)^+ \quad \text {for all } t \in [0,1]. \end{aligned}$$

(4.40)

Then, by virtue of (4.34), (4.36), (4.37), (4.38), and (4.39), it follows

$$\begin{aligned}&\hat{\gamma }_+(0)=h \left( 0, \lambda \hat{u}_1 (\varsigma ,\hat{\beta } )\right)^+=\lambda \hat{u}_1 (\varsigma ,\hat{\beta } )\\&\hat{\gamma }_+(1)=h \left( 1, \lambda \hat{u}_1 (\varsigma ,\hat{\beta } ) \right)^+=u_*,\\&\psi \left(\hat{\gamma }_+(t) \right)=\psi _+\left( \hat{\gamma }_+(t) \right) \le \psi _+ \left(\lambda \hat{u}_1 (\varsigma ,\hat{\beta } ) \right)=\psi \left(\lambda \hat{u}_1 (\varsigma ,\hat{\beta } ) \right)<0. \end{aligned}$$

Hence, $\hat{\gamma }_+$ is a continuous path connecting $\lambda \hat{u}_1 (\varsigma ,\hat{\beta } )$ and $u_*$ fulfilling

$$\begin{aligned} \psi \big |_{\hat{\gamma }_+}<0. \end{aligned}$$

(4.41)

In a similar fashion, using the functional $\psi _-$ instead of $\psi _+$, we may construct a continuous path $\hat{\gamma }_-$ in $W^{1,p}({{\varOmega }})$ which connects $-\lambda \hat{u}_1 (\varsigma ,\hat{\beta } )$ and $v_*$ satisfying

$$\begin{aligned} \psi \big |_{\hat{\gamma }_-}<0. \end{aligned}$$

(4.42)

The union of the curves $\hat{\gamma }_-, \hat{\gamma }$, and $\hat{\gamma }_+$ forms a continuous path $\gamma _* \in {\varGamma }$ such that, because of (4.34), (4.41), and (4.42),

$$\begin{aligned} \psi \big |_{\gamma _*}<0. \end{aligned}$$

This implies that $y_0 \in [v_*,u_*] \cap C^1({\overline{{\varOmega }}})$ is a nodal solution of (1.1). $\square$

In order to prove the existence of a second nodal solution of (1.1), we will consider the special case when $a(\xi )=\xi$ is the Laplacian and the reaction $f(x,\cdot )$ is linear near zero and differentiable. To be more precise, the problem under consideration is given by

$$\begin{aligned} \begin{aligned} -{\varDelta }u&= f(x,u)\quad&\text {in } {\varOmega },\\ \frac{\partial u}{\partial n}&= -\beta (x) u&\text {on } \partial {\varOmega }. \end{aligned} \end{aligned}$$

(4.43)

The reason that we consider the above special case of problem (1.1) is because we will use tools from Morse theory, in particular critical groups. As it is well known, the strongest and more definitive results on critical groups can be produced in the context of Hilbert spaces and for $C^2$-functionals. In fact, in problem (4.43) we could have used a general strongly elliptic second-order differential operator but for simplicity in the exposition we have decided to proceed with the Laplacian. For the general problem (1.1), additional nodal solutions can be produced if we introduce symmetry structure in the problem something that we wanted to avoid in this paper.

The new hypotheses on $f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ read as follows.

H$_4$::

$f: {\varOmega }\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a measurable function such that $f(x,\cdot ) \in C^1({\mathbb {R}}), f(x,0)=0$ for a.a. $x\in {\varOmega }$ and

• (i) for every $\rho >0$, there exists $a_\rho \in L^{\infty }({\varOmega })_+$ such that

  $$\begin{aligned} |f'_s(x,s)| \le a_\rho (x) \quad \text {for a.a. }x\in {\varOmega }\text { and all } |s| \le \rho ; \end{aligned}$$

• (ii) there exist functions $w_\pm \in H^1({\varOmega }) \cap C({\overline{{\varOmega }}})$ and constants $c_\pm \in {\mathbb {R}}$ such that

  $$\begin{aligned}&w_-(x) \le c_-<0<c_+\le w_+(x) \quad \text {for all }x\in {\overline{{\varOmega }}};\\&f(x,w_+(x))\le 0 \le f(x,w_-(x)) \quad \text {for a.a. }x \in {\varOmega };\\&A(w_-) \le 0 \le A(w_+) \quad \text {in } \left(H^1({\varOmega })\right)^*; \end{aligned}$$

• (iii) there exist constants $c_{23}, c_{24}>0$ and $m \ge 2$ such that

  $$\begin{aligned}&\hat{\lambda }_m(2,\beta ) < c_{23}\le c_{24}< \hat{\lambda }_{m+1}(2,\beta ), \end{aligned}$$

  and

  $$\begin{aligned}&c_{23} \le f'_s(x,0)=\lim _{s\rightarrow 0} \frac{f(x,s)}{s} \le c_{24} \end{aligned}$$

  uniformly for a.a. $x\in {\varOmega }$.

Remark 4.7

Note that in this case, using the mean value theorem, we see that if ${M}_{*}=\max \left\{ {\left\| {w}_{+} \right\| }_{\infty },{\left\| {w}_{-} \right\| }_{\infty } \right\}$, then there exists $\xi _*>0$ such that $s \mapsto f(x,s)+\xi _*s$ is nondecreasing on $[-M_*,M_*]$ for a.a. $x\in {\varOmega }$.

Theorem 4.8

Let hypotheses H($\beta$) and H$_4$ be satisfied. Then, problem (4.43) admits at least four nontrivial solutions

$$\begin{aligned} u_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad v_0 \in -{{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad \text {and} \quad y_0, \hat{y} \in {{\mathrm{int}}}_{C^1({\overline{{\varOmega }}})}[v_0,u_0] \text { nodal}. \end{aligned}$$

Proof

Because of Theorem 4.6, we already have three nontrivial solutions

$$\begin{aligned} u_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad v_0 \in -{{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right) , \quad \text {and} \quad y_0 \in [v_0,u_0] \cap C^1({\overline{{\varOmega }}}) \text { nodal}. \end{aligned}$$

In addition, by virtue of Proposition 3.5, we may assume that $u_0$ and $v_0$ are extremal constant sign solutions of (4.43).

Let $\xi _*>0$ be as postulated in Remark 4.7. Since $y_0 \le u_0$, we obtain

$$\begin{aligned} -{\varDelta }u_0+\xi _* u_0&=f(x,u_0)+\xi _* u_0 \ge f(x,y_0)+\xi _* y_0= -{\varDelta }y_0+\xi _* y_0 \quad \text {a.e. in } {\varOmega }. \end{aligned}$$

This implies

$$\begin{aligned} {\varDelta }(u_0-y_0) \le \xi _* (u_0-y_0) \quad \text {a.e. in } {\varOmega }, \end{aligned}$$

which, in view of Pucci and Serrin [23], results in $u_0-y_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$. Similarly, we can show that $y_0-v_0 \in {{\mathrm{int}}}\left( C^1_0(\overline{{\varOmega }})_+\right)$. Therefore,

$$\begin{aligned} y_0 \in {{\mathrm{int}}}_{C^1({\overline{{\varOmega }}})}[v_0,u_0]. \end{aligned}$$

(4.44)

Using the notation from the proof of Proposition 4.2, we know that $u_0$ and $v_0$ are local minimizers of the functional $\psi$, hence

$$\begin{aligned} C_k(\psi ,u_0)=C_k(\psi ,v_0)=\delta _{k,0} {\mathbb {Z}}\quad \text {for all }k \ge 0. \end{aligned}$$

(4.45)

Additionally, the proof of Theorem 4.6 had shown that $y_0$ is a critical point of $\psi$ of mountain pass type. Thus, from Motreanu et al. [17, p. 177] and since (4.44), we have

$$\begin{aligned} C_k(\psi ,y_0)= \delta _{k,1} {\mathbb {Z}}\quad \text {for all } k \ge 0. \end{aligned}$$

(4.46)

Note that $u=0$ is a nondegenerate critical point of $\psi$ of Morse index

$$\begin{aligned} d_m=\dim \bigoplus _{i=1}^m E\left( \hat{\lambda }_i(2,\beta ) \right) \ge 2 \end{aligned}$$

with $E\left( \hat{\lambda }_i(2,\beta ) \right)$ being the eigenspace corresponding to the eigenvalue $\hat{\lambda }_i(2,\beta )$. Hence,

$$\begin{aligned} C_k(\psi ,0)= \delta _{k,d_m} {\mathbb {Z}}\quad \text {for all } k \ge 0. \end{aligned}$$

(4.47)

Finally, since $\psi$ is coercive, it follows that

$$\begin{aligned} C_k(\psi ,\infty )= \delta _{k,0} {\mathbb {Z}}\quad \text {for all } k \ge 0. \end{aligned}$$

(4.48)

Supposing $K_\psi = \{0, u_0, v_0, y_0\}$, from (4.45), (4.46), (4.47), (4.48) and the Morse relation with $t=-1$ (see (2.3)), we obtain

$$\begin{aligned} (-1)^{d_m}+2(-1)^0+(-1)^1=(-1)^0, \end{aligned}$$

which implies $(-1)^{d_m}=0$, a contradiction. Thus, there exists $\hat{y} \in K_{\psi } \subseteq [v_0,u_0]$ with $\hat{y} \not \in \{0, u_0, v_0, y_0\}$. Hence, $\hat{y}$ is a second nodal solution of (4.43). Similarly, as done for $y_0$, we can show that $\hat{y} \in {{\mathrm{int}}}_{C^1({\overline{{\varOmega }}})}[v_0,u_0]$. $\square$