Euclidean Distance Degree and Mixed Volume

Abstract

We initiate a study of the Euclidean distance degree in the context of sparse polynomials. Specifically, we consider a hypersurface $f=0$ defined by a polynomial f that is general given its support, such that the support contains the origin. We show that the Euclidean distance degree of $f=0$ equals the mixed volume of the Newton polytopes of the associated Lagrange multiplier equations. We discuss the implication of our result for computational complexity and give a formula for the Euclidean distance degree when the Newton polytope is a rectangular parallelepiped.

1 Introduction

Let $X\subset {\mathbb R}^n$ be a real algebraic variety. For a point $u\in {\mathbb R}^n\smallsetminus X$, consider the following problem:

$$\begin{aligned} \text {compute the critical points of } d_X:X\rightarrow {\mathbb R}, \; x\mapsto \Vert u-x\Vert , \end{aligned}$$

(1)

where $\Vert u-x\Vert = \sqrt{(u-x)^T(u-x)}$ is the Euclidean distance on ${\mathbb R}^n$.

Seidenberg [26] observed that if X is nonempty, then it contains a solution to (1). He used this observation in an algorithm for deciding if X is empty. Hauenstein [14] pointed out that solving (1) provides a point on each connected component of X. So the solutions to (1) are also useful in learning the number and position of the connected components of the variety. From the point of view of optimization, problem (1) is a relaxation of the optimization problem of finding a point $x\in X$ that minimizes the Euclidean distance to u. A prominent example of this is low-rank matrix approximation, which can be solved by computing the singular value decomposition. In general, computing the critical points of the Euclidean distance between X and u is a difficult task in nonlinear algebra.

We consider problem (1) when $X\subset {\mathbb R}^n$ is a real algebraic hypersurface in ${\mathbb R}^n$ defined by a single real polynomial,

$$\begin{aligned} X = {{\mathcal V}_{{\mathbb R}}(f)} := \{x\in {\mathbb R}^n \mid f(x)=0\}, \text { where } f(x) = f(x_1,\ldots ,x_n) \in {\mathbb R}[x_1,\ldots ,x_n]. \end{aligned}$$

The critical points of the distance function $d_X$ from (1) are called ED-critical points. They can be found by solving the associated Lagrange multiplier equations. This is a system of polynomial equations defined as follows.

Let us write ${\partial _i}$ for the operator of partial differentiation with respect to the variable $x_i$, so that $\partial _i f:= \frac{\partial f}{\partial x_i}$, and also write ${\nabla f(x)} = (\partial _1 f(x),\ldots , \partial _n f(x))$ for the vector of partial derivatives of f (its gradient). The Lagrange multiplier equations are the following system of $n{+}1$ polynomial equations in the $n{+}1$ variables $(\lambda ,x_1,\ldots ,x_n)$.

$$\begin{aligned} {{\mathcal L}_{f,u}(\lambda ,x)}\ :=\ \begin{bmatrix} f(x) \\ \nabla f(x) - \lambda (u-x)\end{bmatrix}\ =\ 0\,, \end{aligned}$$

(2)

where $\lambda$ is an auxiliary variable (the Lagrange multiplier).

We consider the number of complex solutions to ${\mathcal L}_{f,u}(\lambda ,x)=0$. For general u, this number is called the Euclidean distance degree (EDD) [9] of the hypersurface $f=0$:

$$\begin{aligned} {{\,\mathrm{\mathrm{EDD}}\,}}(f)\ :=\ \text { number of solutions to } {\mathcal L}_{f,u}(\lambda ,x)=0 \text { in } \mathbb C^{n+1} \text { for general } u. \end{aligned}$$

(3)

Here, “general” means for all u in the complement of a proper algebraic subvariety of ${\mathbb R}^n$. In the following, when referring to ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$ we will simply speak of the EDD of f.

Figure 1 shows the solutions to ${\mathcal L}_{f,u}(\lambda ,x)=0$ for a biquadratic polynomial f.

Fig. 1

The curve $X={\mathcal V}_{{\mathbb R}}(x_1^2 x_2^2 - 3x_1^2 - 3x_2^2+5)\subset {\mathbb R}^2$ is in blue and $u=(0.025, 0.2)$ is in green. The 12 red points are the critical points of the distance function $d_X$; that is, they are the x-values of the solutions to ${\mathcal L}_{f,u}(\lambda ,x)=0$. In this example, the Euclidean distance degree of X is 12, so all complex solutions are in fact real (Color figure online)

Determining the Euclidean distance degree is of interest in applied algebraic geometry, but also in related areas, because, as we will discuss in Sect. 3, our results on the EDD of f have implications for the computational complexity of solving problem (1).

There is a subtle point about ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$. The definition in (3) does not need us to assume that ${\mathcal V}_{{\mathbb R}}(f)$ is a hypersurface in $\mathbb R^n$. In fact, ${\mathcal V}_{{\mathbb R}}(f)$ can even be empty. Rather, ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$ is a property of the complex hypersurface ${X_{\mathbb C}:={\mathcal V}_{\mathbb C}(f)}$. We will therefore drop the assumption of ${\mathcal V}_{{\mathbb R}}(f)$ being a real hypersurface in the following. Nevertheless, the reader should keep in mind that for the applications discussed at the beginning of this paper the assumption is needed. We will come back to those applications only in Sects. 3.2 and 3.3.

In the foundational paper [9], the Euclidean distance degree of f was related to the polar classes of $X_{\mathbb C}$, and there are other formulas involving characteristic classes [1] or Euler characteristic [23] of $X_{\mathbb C}$. In this paper, we give a new formula for the Euclidean distance degree ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$.

Our main result is Theorem 1 in the next section. We show that, if f is sufficiently general given its support $\mathcal A$ with $0\in \mathcal A$, then ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$ is equal to the mixed volume of the Newton polytopes of ${\mathcal L}_{f,u}(\lambda ,x)$. This opens new paths to compute Euclidean distance degree using tools from convex geometry. We demonstrate this in Sect. 6 and compute the EDD of a general hypersurface whose Newton polytope is a rectangular parallelepiped. We think it is an interesting problem to relate our mixed volume formula to other formulas involving topological invariants.

Our proof strategy relies on Bernstein’s Other Theorem (Proposition 1). This result gives an effective method for proving that the number of solutions to a system of polynomial equations can be expressed as a mixed volume. We hope our work sparks a new line of research that exploits this approach in other applications, not just EDD.

2 Statement of Main Results

We give a new formula for the Euclidean distance degree that takes into account the monomials in f. In Sect. 6 we work this out in the special case when this Newton polytope is a rectangular parallelepiped.

Before stating our main results, we have to introduce notation: A vector $a=(a_1,\dotsc ,a_n)$ of nonnegative integers is the exponent of a monomial ${x^a}:= x_1^{a_1}\cdots x_n^{a_n}$, and a polynomial $f\in \mathbb C[x_1,\dotsc ,x_n]$ is a linear combination of monomials. The set ${\mathcal A}$ of exponents of monomials that appear in f is its support. The Newton polytope of f is the convex hull of its support. Given polytopes $Q_1,\dotsc ,Q_m$ in ${\mathbb R}^m$, we write ${{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m)$ for their mixed volume. This was defined by Minkowski; its definition and properties are explained in [12, Sect. IV.3], and we revisit them in Sect. 6. Our main result expresses the ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$ in terms of mixed volume.

We denote by $P,P_1,\ldots ,P_n$ the Newton polytopes of the Lagrange multiplier equations ${\mathcal L}_{f,u}(\lambda ,x)$ from (2). That is, P is the Newton polytope of f, and $P_i$ is the Newton polytope of $\partial _i f-\lambda (u_i-x_i)$. Observe that $P,P_1,\dotsc ,P_n$ are polytopes in ${\mathbb R}^{n+1}$, because ${\mathcal L}_{f,u}(\lambda ,x)$ has $n+1$ variables $\lambda ,x_1,\ldots ,x_n$.

We state our first main result. The proof is given in Sect. 4.

Theorem 1

If f is a polynomial whose support ${\mathcal A}$ contains 0, then

$$\begin{aligned} {{\,\mathrm{\mathrm{EDD}}\,}}(f)\ \le \ {{\,\mathrm{\mathrm{MV}}\,}}(P,P_1,\dotsc ,P_n)\,, \end{aligned}$$

where P is the Newton polytope of f and $P_i$ is the Newton polytope of $\partial _i f-\lambda (u_i-x_i)$ for $1\le i\le n$. There is a dense open subset U of polynomials with support ${\mathcal A}$ such that when $f\in U$ this inequality is an equality and for $u\in {\mathbb C}^n$ general, all solutions to ${\mathcal L}_{f,u}$ occur without multiplicity.

The important point of this theorem is that polynomial systems of the form ${\mathcal L}_{f,u}$ form a proper subvariety of the set of all polynomial systems with the same support—its dimension is approximately $\frac{1}{n}$th of the dimension of the ambient space. We also remark that the assumption $0\in {\mathcal A}$ is essential to our proof, and it ensures that ${\mathcal V}(f)$ is smooth at 0.

In the following, we refer to polynomials $f\in U$ as general given the support ${\mathcal A}$.

Since $P,P_1,\dotsc ,P_n$ are the Newton polytopes of the entries in ${\mathcal L}_{f,u}$, Bernstein’s theorem [4] implies the inequality in Theorem 1 (commonly known as the BKK bound; see also [10]). Our proof of Theorem 1 appeals to a theorem of Bernstein which gives conditions that imply equality in the BKK bound. These conditions require the facial systems to be empty.

Our next main result is an application of Theorem 1. We compute ${{\,\mathrm{\mathrm{EDD}}\,}}(f)$ when the Newton polytope of f is the rectangular parallelepiped

$$\begin{aligned} {B(a)} := [0,a_1]\times \cdots \times [0,a_n], \end{aligned}$$

(4)

where ${a}:=(a_1,\dotsc ,a_n)$ is a list of positive integers. For each $1\le k \le n$, let

$$\begin{aligned} {e_k(a)}\ :=\ \sum _{1\le i_1<\cdots < i_k\le n} a_{i_1}\cdots a_{i_k} \end{aligned}$$

be the k-th elementary symmetric polynomial in n variables evaluated at a. The next theorem is our second main result.

Theorem 2

Let $a=(a_1,\dotsc ,a_n)$. If $f\in {\mathbb R}[x_1,\dotsc ,x_n]$ has Newton polytope B(a), then

$$\begin{aligned} {{\,\mathrm{\mathrm{EDD}}\,}}(f)\ \le \ \sum _{k=1}^n k!\, e_k(a)\,. \end{aligned}$$

There is a dense open subset U of the space of polynomials with Newton polytope B(a) such that for $f\in U$, this inequality is an equality.

There is a conceptual change when passing from Theorem 1 to Theorem 2. Theorem 1 is formulated in terms of the support of f, whereas Theorem 2 concerns its Newton polytope. This is because the equality in Theorem 2 needs the Newton polytope of the partial derivative $\partial _i f$ to be $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_n)$ for each $1\le i\le n$.

When $n=2$, a polynomial f with Newton polytope the $2\times 2$ square B(2, 2) is a biquadratic, and the bound of Theorem 2 becomes $2!\cdot 2\cdot 2 + 1!\cdot (2+2)\ =\ 12\,$, which was the number of critical points found for the biquadratic curve in Fig. 1.

Remark 1

Observe that for $1\le i_1<\cdots <i_k\le n$, if we project B(a) onto the coordinate subspace indexed by $i_1,\dotsc ,i_k$, we obtain $B(a_{i_1},\dotsc , a_{i_k})$. Thus, the product $a_{i_1}\cdots a_{i_k}$ is the k-dimensional Euclidean volume of this projection and $k!\,a_{i_1}\cdots a_{i_k}$ is the normalized volume of this projection. On the other hand, $e_k(a)=\sum _{1\le i_1< \cdots <i_k\le n}a_{i_1}\cdots a_{i_k}$. This observation implies an appealing interpretation of the formula of Theorem 2: It is the sum of the normalized volumes of all coordinate projections of the rectangular parallelepiped B(a).$\diamond$

Remark 2

Experiments with HomotopyContinuation.jl [7] suggest that a similar formula involving mixed volumes should hold for general complete intersections. That is, for $X=\{x\in {\mathbb R}^n \mid f_1(x) = \cdots = f_k(x)=0\}$ such that $\dim X = n-k$ and $f_1,\dotsc ,f_k$ are general given their Newton polytopes. The Lagrange multiplier Eq. (2) become $f_1(x)=\cdots =f_k(x)=0$ and $J\lambda -(u-x)=0$, where $\lambda = (\lambda _1,\ldots ,\lambda _k)$ is now a vector of variables, and $J=(\nabla f_1,\dotsc ,\nabla f_k)$ is the $n\times k$ Jacobian matrix.

We leave this general case of $k>1$ for further research.$\diamond$

2.1 Outline

In Sect. 3, we explain implications of Theorem 1 for computational complexity in the context of using the polyhedral homotopy for solving the Lagrange multiplier equations ${\mathcal L}_{f,u}=0$ for problem (1). In Sect. 4, we explain Bernstein’s conditions and give a proof of Theorem 1. The proof relies on a lemma asserting that the facial systems of ${\mathcal L}_{f,u}$ are empty. Section 5 is devoted to proving this lemma. The arguments that are used in this proof are explained on an example at the end of Sect. 4. We conclude in Sect. 6 with a proof of Theorem 2.

3 Implications for Computational Complexity

We discuss the implications of Theorem 1 for the computational complexity of computing critical points of the Euclidean distance (1).

3.1 Polyhedral Homotopy is Optimal for EDD

Polynomial homotopy continuation is an algorithmic framework for numerically solving polynomial equations which builds upon the following basic idea: Consider the system of m polynomials $F(x)=(f_1(x),\ldots , f_m(x))= 0$ in variables $x=(x_1,\ldots ,x_m)$. The approach to solve $F(x)=0$ is to generate another system G(x) (the start system) whose zeros are known. Then, F(x) and G(x) are joined by a homotopy, which is a system H(x, t) of polynomials in $m{+}1$ variables with $H(x,1)=G(x)$ and $H(x,0)=F(x)$. Differentiating $H(x,t)=0$ with respect to t leads to an ordinary differential equation called Davidenko equation. The ODE is solved by standard numerical continuation methods with initial values the zeros of G(x). This process is usually called path-tracking and continuation. For details, see [27].

One instance of this framework is the polyhedral homotopy of Huber and Sturmfels [16]. It provides a start system G(x) for polynomial homotopy continuation and a homotopy H(x, t) such that the following holds: Let $Q_1,\ldots ,Q_m$ be the Newton polytopes of F(x). Then, for all $t\in (0,1]$ the system of polynomials H(x, t) has ${{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\ldots ,Q_m)$ isolated zeros (at $t=0$ this can fail, because the input $F(x)=H(x,0)$ may have fewer than ${{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\ldots ,Q_m)$ isolated zeroes). Polyhedral homotopy is implemented in many polynomial homotopy continuation software packages; for instance in HomotopyContinuation.jl [7], HOM4PS [19], PHCPack [29].

Theorem 1 implies that the polyhedral homotopy is optimal for computing ED-critical points in the following sense: If we assume that the continuation of zeroes has unit cost, then the complexity of solving a system of polynomial equations $F(x)=0$ by polynomial homotopy continuation is determined by the number of paths that have to be tracked. This number is at least as large as the number of solutions to $F(x)=0$ that are computed. We say that a homotopy is optimal if the following three properties hold: (1) the start system G(x) has as many zeros as the input F(x); (2) all continuation paths end in a zero of F(x); and (3) for every zero of F(x), there is a continuation path which converges to it. In an optimal homotopy, no continuation paths have to be sorted out. That is, the number of paths which need to be tracked is optimal.

We now have the following consequence of Theorem 1, as ${\mathcal L}_{f,u}=0$ has ${{\,\mathrm{\mathrm{MV}}\,}}(P,P_1,\dotsc ,P_n)$ isolated solutions.

Corollary 1

If f is general given its support ${\mathcal A}$ with $0\in {\mathcal A}$, polyhedral homotopy is optimal for solving ${\mathcal L}_{f,u}=0$.

Corollary 1 is an instance of a structured problem for which we have an optimal homotopy available.

In our definition of optimal homotopy, we ignored the computational complexity of path-tracking in polyhedral homotopy. We want to emphasize that this is an important part of contemporary research. We refer to Malajovich’s work [20] [21] [22].

3.2 Computing Real Points on Real Algebraic Sets

Hauenstein [14] observed that solving the Lagrange multiplier equations ${\mathcal L}_{f,u}=0$ gives at least one point on each connected component of the real algebraic set $X={\mathcal V}_{{\mathbb R}}{(f)}$. Indeed, every real solution to ${\mathcal L}_{f,u}=0$ corresponds to a critical point of the distance function from (1). Every connected component of X contains at least one such critical point.

Corollary 1 shows that polyhedral homotopy provides an optimal start system for Hauenstein’s approach. Specifically, Corollary 1 implies that when using polyhedral homotopy in the algorithm in [14, Sect. 2.1], one does not need to distinguish between the sets $E_1$ (= continuation paths which converge to a solution to ${\mathcal L}_{f,u}=0$) and E (= continuation paths which diverge). This reduces the complexity of Hauenstein’s algorithm, who puts his work in the context of complexity in real algebraic geometry [2, 3, 24, 26].

3.3 Certification of ED-Critical Points

We consider a posteriori certification for polynomial homotopy continuation: Zeros are certified after and not during the (inexact) numerical continuation. Implementations using exact arithmetic [15, 18] or interval arithmetic [6, 18, 25] are available. In particular, box interval arithmetic in $\mathbb C^n$ is powerful in combination with our results. We explain this.

Box interval arithmetic in the complex numbers is arithmetic with complex intervals that are of the form $\{x+{\sqrt{-1}}y \mid x_1\le x\le x_2, \, y_1\le y\le y_2\}$ for $x_1,x_2,y_1,y_2\in \mathbb R$. Box interval arithmetic in $\mathbb C^n$ uses products of such intervals. By Theorem 1, if f is general given its support and $u\in {\mathbb C}^n$ is general, then ${\mathcal L}_{f,u}$ has exactly ${{\,\mathrm{\mathrm{MV}}\,}}(P,P_1,\dotsc ,P_n)$ solutions. Therefore, if we compute ${{\,\mathrm{\mathrm{MV}}\,}}(P,P_1,\dotsc ,P_n)$ numerical approximations to solutions, and then certify that each corresponds to a true zero, and if we can certify that those true zeros are pairwise distinct, we have provably obtained all zeros of ${\mathcal L}_{f,u}$. Furthermore, if we compute box intervals in $\mathbb C^{n+1}$ which provably contain the zeros of ${\mathcal L}_{f,u}$, then we can use those intervals to certify whether a zero is real (see [6][Lemma 4.8]) or whether it is not real (by checking whether the intervals intersect the real line; this is a property of box intervals).

If it is possible to classify reality for all zeros, we can take a set of intervals $\{r_1,\ldots ,r_k\}$ of ${\mathbb R}^n$ which contain the real critical points of the distance function $d_X$ from (1). The $r_j$ are obtained from the coordinate projection $(\lambda ,x)\mapsto x$ of the intervals containing the real zeros of ${\mathcal L}_{f,u}$. Setting $d_j:=\{d_X(s)\mid s\in r_j\}$ gives a set of intervals $\{d_1,\ldots ,d_k\}$ of ${\mathbb R}$. If there exists $d_i$ such that $d_i\cap d_j =\emptyset$ and $\min d_i < \min d_j$ for all $i\ne j$, then this is a proof that the minimal value of $d_X$ is contained in $d_i$ and that the minimizer for $d_X$ is contained in $r_i$.

4 Bernstein’s Theorem

The relation between number of solutions to a polynomial system and mixed volume is given by Bernstein’s theorem [4].

Let $g_1,\dotsc ,g_m\in {\mathbb C}[x_1,\dotsc ,x_m]$ be m polynomials with Newton polytopes $Q_1,\dotsc ,Q_m$. Let $({\mathbb C}^\times )^m$ be the complex torus of m-tuples of nonzero complex numbers and $\#{\mathcal V}_{{\mathbb C}^\times }(g_1,\dotsc ,g_m)$ be the number of isolated solutions to $g_1=\cdots =g_m=0$ in $({\mathbb C}^\times )^m$, counted by their algebraic multiplicities. Bernstein’s theorem [4] asserts that

$$\begin{aligned} \#{\mathcal V}_{{\mathbb C}^\times }(g_1,\dotsc ,g_m)\ \le \ {{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m)\,, \end{aligned}$$

(5)

and the inequality becomes an equality when each $g_i$ is general given its support. The restriction of the domain to $({\mathbb C}^\times )^m$ is because Bernstein’s theorem concerns Laurent polynomials, in which the exponents in a monomial are allowed to be negative.

An important special case of Bernstein’s theorem was proven earlier by Kushnirenko. Suppose that the polynomials $g_1,\dotsc ,g_m$ all have the same Newton polytope. This means that $Q_1=\cdots =Q_m$. We write Q for this single polytope. Then, the mixed volume in (5) becomes ${{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m) = m! {{\,\mathrm{\mathrm{Vol}}\,}}(Q)$, where ${{\,\mathrm{\mathrm{Vol}}\,}}(Q)$ is the m-dimensional Euclidean volume of Q. Kushnirenko’s theorem [17] states that if $g_1,\dotsc ,g_m$ are general polynomials with Newton polytope Q, then

$$\begin{aligned} \#{\mathcal V}_{{\mathbb C}^\times }(g_1,\dotsc ,g_m)\ =\ m! {{\,\mathrm{\mathrm{Vol}}\,}}(Q)\,. \end{aligned}$$

That the mixed volume becomes the normalized Euclidean volume when the polytopes are equal is one of three properties which characterize mixed volume, the others being symmetry and multiadditivity. This is explained in [12][Sect. IV.3] and recalled in Sect. 6.

Inequality (5) is called the BKK bound [5]. The key step in proving it is what we call Bernstein’s Other Theorem. This a posteriori gives the condition under which inequality (5) is strict (equivalently, when it is an equality). We explain that.

Let $g\in {\mathbb C}[x_1,\dotsc ,x_m]$ be a polynomial with support ${\mathcal A}\subset {\mathbb Z}^m$, so that

$$\begin{aligned} g\ =\ \sum _{a\in {\mathcal A}} c_a x^a\ \qquad (c_a\in {\mathbb C})\,. \end{aligned}$$

For $w\in {\mathbb Z}^m$, define $h_w({\mathcal A})$ to be the minimum value of the linear function $x\mapsto w\cdot x$ on the set ${\mathcal A}$ and write ${\mathcal A}_w$ for the subset of ${\mathcal A}$ on which this minimum occurs. This is the face of ${\mathcal A}$ exposed by w. We write

$$\begin{aligned} {g_w}\ :=\ \sum _{a\in {\mathcal A}_w} c_a z^a\,, \end{aligned}$$

(6)

for the restriction of g to ${\mathcal A}_w$. For $w\in {\mathbb Z}^{m}$ and a system $G=(g_1,\dotsc ,g_m)$ of m polynomials, the facial system is ${G_w}:=((g_1)_{w},\dotsc ,(g_m)_{w})$.

We state Bernstein’s Other Theorem [4][Theorem B].

Proposition 1

Let $G=(g_1,\dotsc ,g_m)$ be a system of Laurent polynomials in variables $x_1,\dotsc ,x_m$. For each $1\le i \le m$, let ${\mathcal A}_i$ be the support of $g_i$ and $Q_i={{\,\mathrm{\mathrm{conv}}\,}}({\mathcal A}_i)$ its Newton polytope. Then

$$\begin{aligned} \#{\mathcal V}_{{\mathbb C}^\times }(g_1,\dotsc ,g_m)\ <\ {{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m) \end{aligned}$$

if and only if there is $0\ne w\in {\mathbb Z}^{m}$ such that the facial system $G_w$ has a solution in $({\mathbb C}^\times )^{m}$. Otherwise, $\#{\mathcal V}_{{\mathbb C}^\times }(g_1,\dotsc ,g_m)$ is equal to ${{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m)$

While this statement is similar to Bernstein’s formulation, we use its contrapositive, that the number of solutions equals the mixed volume when no facial system has a solution. We use Bernstein’s Other Theorem when $G = {\mathcal L}_{f,u}$ and $m=n{+}1$. For this, we must show that for a general polynomial f with support ${\mathcal A}\subset {\mathbb N}^n$, all the solutions to ${\mathcal L}_{f,u}=0$ lie in $({\mathbb C}^\times )^{n+1}$ and no facial system $({\mathcal L}_{f,u})_w=0$ for $0\ne w\in {\mathbb Z}^{n+1}$ has a solution in $({\mathbb C}^\times )^{n+1}$. The latter is given by the next theorem which is proved in Sect. 5.

Theorem 3

Suppose that f is general given its support ${\mathcal A}$, that $0\in {\mathcal A}$, and that $u\in {\mathbb C}^n$ is general. For any nonzero $w\in {\mathbb Z}^{n+1}$, the facial system $({\mathcal L}_{f,u})_w$ has no solutions in $({\mathbb C}^\times )^{n+1}$.

Using this theorem we can now prove Theorem 1.

Proof

(Proof of Theorem 1) Suppose that a polynomial $f(x) \in {\mathbb C}[x_1,\dotsc ,x_n]$ is general given its support ${\mathcal A}$ and that $0\in {\mathcal A}$. We may also suppose that $u\in {\mathbb C}^n\smallsetminus {\mathcal V}_{{\mathbb C}}(f)$ is general. By Theorem 3, no facial system $({\mathcal L}_{f,u})_w$ has a solution. By Bernstein’s Other Theorem, the Lagrange multiplier equations ${\mathcal L}_{f,u}=0$ have ${{\,\mathrm{\mathrm{MV}}\,}}(P,P_1,\dotsc ,P_n)$ solutions in $({\mathbb C}^\times )^{n+1}$. It remains to show that there are no other solutions to the Lagrange multiplier equations.

For this, we use standard dimension arguments, such as [13][Theorem 11.12], and freely invoke the generality of f. Consider the incidence variety

$$\begin{aligned} {{\mathcal S}_f}\ :=\ \{(u,\lambda ,x)\in {\mathbb C}^n_u\times {\mathbb C}_\lambda \times {\mathbb C}^n_x \mid {\mathcal L}_{f,u}(\lambda ,x)=0\}\,, \end{aligned}$$

which is an affine variety. As $f=0$ is an equation in ${\mathcal L}_{f,u}=0$, this is a subvariety of ${\mathbb C}^n_u\times {\mathbb C}_\lambda \times X_{\mathbb C}$, where $X_{\mathbb C}$ is the complex hypersurface $X_{\mathbb C}={\mathcal V}_{\mathbb C}(f)$.

Write $\pi$ for the projection of ${\mathcal S}_f$ to $X_{\mathbb C}$ and let $x\in X_{\mathbb C}$. The fiber $\pi ^{-1}(x)$ over x is

$$\begin{aligned} \{ (u,\lambda )\in {\mathbb C}^n_u\times {\mathbb C}_\lambda \mid \nabla f(x)=\lambda (u-x)\}\,. \end{aligned}$$

Let $(u,\lambda )\in \pi ^{-1}(f)$. As f is general, $X_{\mathbb C}$ is smooth, so that $\nabla f(x)\ne 0$ and we see that $\lambda \ne 0$ and $u\ne x$. Thus $u = x + \tfrac{1}{\lambda }\nabla f(x)$. This identifies the fiber $\pi ^{-1}(x)$ with ${\mathbb C}^\times _\lambda$, proving that ${\mathcal S}_f\rightarrow X_{\mathbb C}$ is a ${\mathbb C}^\times$-bundle and thus is irreducible of dimension n.

The projection of ${\mathcal S}_f$ to ${\mathbb C}^n_u$ is dominant, and therefore, Bertini’s theorem implies that the general fiber is zero-dimensional and smooth. That is, for $u\in {\mathbb C}^n_u$ general, ${\mathcal L}_{f,u}=0$ has finitely many solutions and each has multiplicity 1.

Let ${Z}\subset X_{\mathbb C}$ be the set of points of $X_{\mathbb C}$ that do not lie in $({\mathbb C}^\times )^n$ and hence lie on some coordinate plane. As f is irreducible and $f(0)\ne 0$, we see that Z has dimension $n{-}2$, and its inverse image $\pi ^{-1}(Z)$ in ${\mathcal S}_f$ has dimension $n{-}1$. The image W of $\pi ^{-1}(Z)$ under the projection to ${\mathbb C}^n_u$ consists of those points $u\in {\mathbb C}^n_u$ which have a solution $(x,\lambda )$ to ${\mathcal L}_{f,u}(\lambda ,x)=0$ with $x\not \in ({\mathbb C}^\times )^n$. Since W has dimension at most $n{-}1$, this shows that for general u all solutions to ${\mathcal L}_{f,u}(\lambda ,x)=0$ lie in $({\mathbb C}^\times )^{n+1}$ (we already showed that $\lambda \ne 0$).

This completes the proof of Theorem 1. $\square$

4.1 Application of Bernstein’s Other Theorem

To illustrate Theorem 3, let us consider two facial systems of the Lagrange multiplier equations in an example.

Let ${\partial _i{\mathcal A}}$ be the support of $\partial _i f$. It depends upon the support ${\mathcal A}$ of f and the index i in the following way. Let ${\mathbf{e}_i}:=(0,\ldots ,0,1,0,\ldots ,0)$ be the ith standard basis vector (1 is in position i). To obtain $\partial _i{\mathcal A}$ from ${\mathcal A}\subset {\mathbb N}^n$, first remove all points $a\in {\mathcal A}$ with $a_i=0$, then shift the remaining points by $-\mathbf{e}_i$. The support of $\partial _i f-\lambda (u_i-x_i)$ is obtained by adding $\mathbf{e}_{0}$ and $\mathbf{e}_i+\mathbf{e}_{0}$ to ${\partial _i{\mathcal A}}$. (As usual, we identify ${\mathbb N}^n$ with $\{0\}\times {\mathbb N}^n\subset {\mathbb N}^{n+1}$.) Throughout the paper, we associate to $\lambda$ the exponent with index 0.

Consider the polynomial in two variables,

$$\begin{aligned} f\ =\ c_{00}+c_{10}x_1+c_{01}x_2+c_{11}x_1x_2 + c_{21}x_1^2x_2\,. \end{aligned}$$

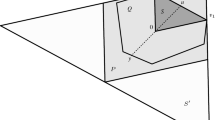
Its support is ${{\mathcal A}} = \{(0,0), (0,1), (1,1), (2,1), (1,0)\}$ and its Newton polytope is $P={{\,\mathrm{\mathrm{conv}}\,}}({\mathcal A})$, which is a trapezoid. Figure 2 shows the Newton polytope P along with the Newton polytopes of $\partial _1 f-\lambda (u_1-x_1)$ and $\partial _2 f-\lambda (u_2-x_2)$. These are polytopes in ${\mathbb R}^3$; we plot the exponents of the Lagrange multiplier $\lambda$ in the (third) vertical direction in Fig. 2.

Fig. 2

The three Newton polytopes of ${\mathcal L}_{f,u}$ for $f=c_{00}+c_{10}x_1+c_{01}x_2+c_{11}x_1x_2 + c_{21}x_1^2x_2$

The faces exposed by $w=(0,1,0)$ are shown in red in Fig. 3.

Fig. 3

The faces ${\mathcal A}_w$, $({\mathcal A}_1)_w$ and $({\mathcal A}_2)_w$ for $w=(0,1,0)$ are shown in red (Color figure online)

The corresponding facial system is

$$\begin{aligned} ({\mathcal L}_{f,u})_w\ =\ \begin{bmatrix} c_{00}+c_{10}x_1\\ c_{10}-\lambda (u_1-x_1)\\ c_{01}+c_{11}x_1+c_{21}x_1^2-\lambda u_2 \end{bmatrix}\ . \end{aligned}$$

Let us solve $({\mathcal L}_{f,u})_w=0$. We solve the first equation for $x_1$ and then substitute that into the second equation and solve it for $\lambda$ to obtain

$$\begin{aligned} x_1\ =\ -\frac{c_{00}}{c_{10}}\qquad \text{ and }\qquad \lambda \ =\ \frac{c_{10}}{u_1-x_1}\ =\ \frac{c_{10}^2}{c_{10}u_1 + c_{00}}\ . \end{aligned}$$

Substituting these into the third equation and clearing denominators gives the equation

$$\begin{aligned} 0\ =\ (c_{10}u_1 + c_{00})(c_{10}^3 - c_{11} c_{10} c_{00} + c_{00}^2 c_{21}) \ -\ c_{10}^4 u_2 \end{aligned}$$

which does not hold for f, u general. The proof of Theorem 3 is divided into three cases and one involves such triangular systems, which are independent of some of the variables.

The faces exposed by $w=(0,-1,1)$ are shown in red in Fig. 4.

Fig. 4

The faces ${\mathcal A}_w$, $({\mathcal A}_1)_w$ and $({\mathcal A}_2)_w$ for $w=(0,-1,1)$ are shown in red (Color figure online)

The corresponding facial system is

$$\begin{aligned} ({\mathcal L}_{f,u})_w \ =\ \begin{bmatrix} c_{01}x_2+c_{11}x_1x_2+c_{21}x_1^2x_2\\ c_{11}x_2+2c_{21}x_1x_2\\ c_{01}+c_{11}x_1+c_{21}x_1^2-\lambda x_2 \end{bmatrix} \ =\ \begin{bmatrix} f_w \\ \partial _1 (f_w) \\ \partial _2 (f_w) -\lambda x_2 \end{bmatrix}\ . \end{aligned}$$

Observe that $h_w(\mathcal A)=-1$ and that we have

$$\begin{aligned} h_w(\mathcal A)\cdot f_w\ =\ -f_w{\ }&=\ w_1\cdot x_1\cdot \partial _1 (f_w) + w_2\cdot x_2\cdot \partial _2 (f_w)) \nonumber \\&=\ 0\cdot x_1\cdot (\partial _1 (f_w)) + (-1)\cdot x_2\cdot (\partial _2 (f_w))\ =\ x_2\partial _2 f\,. \end{aligned}$$

(7)

This is an instance of Euler’s formula for quasihomogeneous polynomials (Lemma 2). If $(\lambda ,x)$ is a solution to $({\mathcal L}_{f,u})_w=0$, then the third equation becomes $\partial _2 f = \lambda x_2$. Substituting this into (7) gives $0 = -f_w = \lambda x_2^2$, which has no solutions in $(\mathbb C^\times )^3$. One of the cases in the proof of Theorem 3 exploits Euler’s formula in a similar way.

$\diamond$

5 The Facial Systems of the Lagrange Multiplier Equations are Empty

Before giving a proof of Theorem 3, we present two lemmas to help understand the support of f and its interaction with derivatives of f and then make some observations about the facial system $({\mathcal L}_{f,u})_w$.

Let $f\in {\mathbb C}[x_1,\dotsc ,x_m]$ be a polynomial with support ${{\mathcal A}}\subset {\mathbb N}^{n}$, which is the set of the exponents of monomials of f. We assume that $0\in {\mathcal A}$. As before we write ${\partial _i{\mathcal A}}\subset {\mathbb N}^{n}$ for the support of the partial derivative $\partial _i f$. For $w\in {\mathbb Z}^n$, the linear function $x\mapsto w\cdot x$ takes minimum values on ${\mathcal A}$ and on $\partial _i{\mathcal A}$, which we denote by

$$\begin{aligned} {h^*}\ =\ h_w({\mathcal A})\ :=\ \min _{a\in {\mathcal A}} w\cdot a \qquad \text {and}\qquad {h^*_i}\ =\ h_w(\partial _i{\mathcal A})\ :=\ \min _{a\in \partial _i {\mathcal A}} w\cdot a\,. \end{aligned}$$

(8)

(We suppress the dependence on w.) Since $0\in {\mathcal A}$, we have $h^*\le 0$. Also, if $h^*=0$ and if there is some $a\in {\mathcal A}$ with $a_i>0$, then $w_i\ge 0$.

Recall that the subsets of ${\mathcal A}$ and $\partial _i{\mathcal A}$ where the linear function $x\mapsto w\cdot x$ is minimized are their faces exposed by w,

$$\begin{aligned} {\mathcal A}_w\ :=\ \{a\in {\mathcal A}\mid w\cdot a = h^*\} \quad \text {and}\quad {(\partial _i{\mathcal A})_w}\ :=\ \{a\in \partial _i{\mathcal A}\mid w\cdot a = h^*_i\}\,. \end{aligned}$$

(9)

The proof below of Lemma 1 shows that $\partial _i({\mathcal A}_w)\subset (\partial _i{\mathcal A})_w$ with equality when $\emptyset \ne \partial _i({\mathcal A}_w)$. As in (6) we denote by $f_w$ the restriction of f to ${\mathcal A}_w$, and similarly, $(\partial _i f)_w$ denotes the restriction of the partial derivative $\partial _i f$ to $(\partial _i {\mathcal A})_w$. The ith partial derivative of $f_w$ is $\partial _i(f_w)$ and its support is denoted $\partial _i({\mathcal A}_w)$. The proof below of Lemma 1 shows that $\partial _i ({\mathcal A}_w) \subseteq (\partial _i {\mathcal A})_w$ with equality when $\emptyset \ne \partial _i ({\mathcal A}_w)$.

Our proof of Theorem 3 uses the following two results.

Lemma 1

For each $1\le i\le n$ and $w \in \mathbb Z^n$, we have $h^*_i\ge h^*-w_i$. If $\partial _i (f_w) \ne 0$, then $\partial _i(f_w) = (\partial _i f)_w$ and $h_i^* = h^* - w_i$.

Proof

Fix $1\le i\le n$. Let $a\in \partial _i{\mathcal A}$. Then $a+\mathbf{e}_i\in {\mathcal A}$ and so $h^*\le w\cdot (a+\mathbf{e}_i)=w\cdot a +w_i$. Thus $w\cdot a\ge h^*-w_i$. Taking the minimum over $a\in \partial _i{\mathcal A}$ gives $h^*_i \ge h^*-w_i$.

Suppose now that $\emptyset \ne \partial _i({\mathcal A}_w)$. Let $a\in \partial _i({\mathcal A}_w)$. Then $a+\mathbf{e}_i\in {\mathcal A}_w$ and $h^*=w\cdot (a+\mathbf{e}_i)=w\cdot a + w_i$. But then $h^*-w_i=w\cdot a\ge h^*_i$, which implies that $h_i^* = h^* - w_i$. It also implies that $w\cdot a=h^*_i$. Since ${\mathcal A}_w\subset {\mathcal A}$, we have that $a\in \partial _i{\mathcal A}$. As $w\cdot a=h^*_i$, we conclude that $a\in (\partial _i{\mathcal A})_w$. This proves the inclusion $\partial _i({\mathcal A}_w)\subset (\partial _i{\mathcal A})_w$.

For the other inclusion, suppose that $\partial _i({\mathcal A}_w)\ne \emptyset$. As we showed, $h_i^* = h^* - w_i$. Let $a\in (\partial _i{\mathcal A})_w$. Then $w\cdot a= h^*_i$ and as $a\in \partial _i{\mathcal A}$, we have $a+\mathbf{e}_i\in {\mathcal A}$. But then $w\cdot (a+\mathbf{e}_i)=h^*_i+w_i=h^*$, so that $a+\mathbf{e}_i\in {\mathcal A}_w$. We conclude that $a\in \partial _i({\mathcal A}_w)$.

To complete the proof, observe that $\partial _i (f_w) \ne 0$ is equivalent to $\partial _i({\mathcal A}_w)\ne \emptyset$, and that $\partial _i(f_w)$ and $(\partial _i f)_w$ are subsums of $\partial _i f$ over terms corresponding to $\partial _i({\mathcal A}_w)$ and to $(\partial _i{\mathcal A})_w$, respectively. $\square$

The restriction $f_w$ of f to the face of ${\mathcal A}$ exposed by w is quasihomogeneous with respect to the weight w, and thus, it satisfies a weighted version of Euler’s formula.

Lemma 2

(Euler’s formula for quasihomogeneous polynomials) For $w\in {\mathbb Z}^n$, we have

$$\begin{aligned} h^*\cdot f_w\ =\ \sum _{i=1}^n w_i x_i \partial _i (f_w)\,. \end{aligned}$$

Proof

For a monomial $x^a$ with $a\in {\mathbb Z}^n$ and $1\le i\le n$, we have that $x_i\partial _i x^a= a_i x^a$. Thus

$$\begin{aligned} \sum _{i=1}^n w_i x_i \partial _i x^a\ =\ \sum _{i=1}^n w_i a_i \ x^a\ =\ (w\cdot a) x^a\,. \end{aligned}$$

The statement follows because for $a\in {\mathcal A}_w$ (the support of $f_w$), $w\cdot a= h^*$. $\square$

Our proof of Theorem 3 investigates facial systems $({\mathcal L}_{f,u})_w$ for $0\ne w\in {\mathbb Z}^{n+1}$ with the aim of showing that for f general given its support ${\mathcal A}$, no facial system has a solution. Recall from (2) that the Lagrange multiplier equations for the Euclidean distance problem are

$$\begin{aligned} {\mathcal L}_{f,u}(\lambda ,x_1,\ldots ,x_n)\ =\ \begin{bmatrix} f(x_1,\ldots ,x_n)\\ \partial _1 f - \lambda (u_1-x_1)\\ \vdots \\ \partial _n f - \lambda (u_n-x_n) \end{bmatrix}\ =\ 0\,. \end{aligned}$$

Fix $0\ne w=(v,w_1,\ldots ,w_{n})\in {\mathbb Z}^{n+1}$. The initial coordinate of w is $v\in {\mathbb Z}$. It has index 0 and corresponds to the variable $\lambda$.

The first entry of the facial system $({\mathcal L}_{f,u})_{w}$ is $f_{w}$. The shape of the remaining entries depends on w as follows. Recall from (8) that we have set $h^* := \min \{w\cdot a\mid a\in {\mathcal A}\}$ and $h^*_i := \min \{w\cdot a\mid a\in \partial _i {\mathcal A}\}$. As v and $v+w_i$ are the weights of the monomials $\lambda u_i$ and $\lambda x_i$, respectively, there are seven possibilities for each of these remaining entries,

$$\begin{aligned} \left( \partial _i f - \lambda (u_i-x_i)\right) _{w}\ =\ \left\{ \begin{array}{ll} (\partial _i f)_{w}&{} \text { if } h^*_i< \min \{v, v + w_i\}\,, \\ (\partial _i f)_{w} - \lambda (u_i-x_i)&{} \text { if } h^*_i = v \text { and } w_i = 0\,, \\ (\partial _i f)_{w} - \lambda u_i&{} \text { if } h^*_i = v \text { and } w_i> 0\,, \\ (\partial _i f)_{w} + \lambda x_i&{} \text { if } h^*_i = v + w_i \text { and } w_i< 0\,, \\ - \lambda (u_i-x_i)&{} \text { if }h^*_i> v \text { and } w_i = 0\, , \\ - \lambda u_i&{} \text { if }h^*_i> v \text { and } w_i> 0\, , \\ \lambda x_i&{} \text { if }h^*_i > v + w_i \text { and } w_i < 0\, . \end{array}\right. \end{aligned}$$

(10)

Note that if one of the polynomials $f_w$ or $\left( \partial _i f - \lambda (u_i-x_i)\right) _{w}$ is a monomial, then $({\mathcal L}_{f,u})_w$ has no solutions in $({\mathbb C}^\times )^{n+1}$.

For a subset ${\mathcal I}\subset \{1,\dotsc ,n\}$ and a vector $u\in {\mathbb C}^n$, let ${u_{\mathcal I}}:=\{ u_i\mid i\in {\mathcal I}\}$ be the components of u indexed by $i\in {\mathcal I}$. We similarly write $w_{\mathcal I}$ for $w\in {\mathbb Z}^n$ and $x_{\mathcal I}$ for variables $x\in {\mathbb C}^n$ and write ${\mathbb C}^{\mathcal I}$ for the corresponding subspace of ${\mathbb C}^n$.

We recall Theorem 3, before we give a proof.

Theorem 4

Suppose that f is general given its support ${\mathcal A}$, that $0\in {\mathcal A}$, and that $u\in {\mathbb R}^n$ is general. For any nonzero $w\in {\mathbb Z}^{n+1}$, the facial system $({\mathcal L}_{f,u})_w$ has no solutions in $({\mathbb C}^\times )^{n+1}$.

Proof

Let $0\ne w=(v,w_1,\ldots ,w_n)\in {\mathbb Z}^{n+1}$. As before, v corresponds to the variable $\lambda$ and $w_i$ to $x_i$. We argue by cases that depend upon w and ${\mathcal A}$, showing that in each case, for a general polynomial f with support ${\mathcal A}$, the facial system has no solutions in $({\mathbb C}^\times )^{n+1}$. Note that the last two possibilities in (10) do not occur as they give monomials. As f has support ${\mathcal A}$, if $\partial _i (f_w)=0$, then ${\mathcal A}_w\subset \{a\in {\mathbb N}^n\mid a_i=0\}$.

We distinguish three cases.

Case 1 (the constant case): Suppose that $\partial _i f_{w} = 0$ for all $1\le i\le n$. Then $f_w$ is the constant term of f. Since $0\in {\mathcal A}$, this is nonvanishing for f general and the facial system $({\mathcal L}_{f,u})_w$ has no solutions.

For the next two cases, we may assume that there is a partition ${{\mathcal I}} \sqcup {{\mathcal J}} =\{1,\ldots ,n\}$ with ${\mathcal I}$ nonempty such that $\partial _i f_{w} \ne 0$ for $i\in {\mathcal I}$ and $\partial _j f_{w} = 0$ for $j\in {\mathcal J}$. By Lemma 1, we have

$$\begin{aligned} h_i^*\ =\ h^* - w_i \ \text {for all}\ i\in {\mathcal I}\,. \end{aligned}$$

(11)

As $j\in {\mathcal J}$ implies that $\partial _j f_{w} = 0$, we see that if $a\in {\mathcal A}_w$, then $a_{\mathcal J}=0$. This implies that $f_w$ is a polynomial in only the variables $x_{\mathcal I}$, that is, $f_w\in {\mathbb C}[x_{\mathcal I}]$.

Case 2 (triangular systems): Suppose that for $i\in {\mathcal I}$, $w_i\ge 0$, that is, $w_{{\mathcal I}}\ge 0$. We claim that this implies $w_{{\mathcal I}} = 0$. To see this, let $a\in {\mathcal A}_w$. As we observed, $a_{\mathcal J}=0$. We have

$$\begin{aligned} 0\ \ge h^*\ =\ w\cdot a\ =\ w_{{\mathcal I}} \cdot a_{{\mathcal I}}\ \ge \ 0\,. \end{aligned}$$

Thus $h^* = w_{{\mathcal I}} \cdot a_{{\mathcal I}} = 0$, which implies that $0\in {\mathcal A}_w$. Let $i\in {\mathcal I}$. Since $\partial _i f_{w} \ne 0$, there exists some $a\in {\mathcal A}_w$ with $a_i>0$. Since $w_{{\mathcal I}} \cdot a_{{\mathcal I}} = 0$ for all $a\in {\mathcal A}_w$, we conclude that $w_i=0$.

Let $i\in {\mathcal I}$. By Lemma 1, we have $h_i^* = h^* - w_i$, so that $h^*_i = h^*=0$, and we also have $(\partial _i f)_{w} = \partial _i f_{w}$. As $w_i=0$, the possibilities from (10) become

$$\begin{aligned} \left( \partial _i f - \lambda (u_i-x_i)\right) _{w}\ =\ {\left\{ \begin{array}{ll} \partial _i f_{w}&{} \text { if } v > 0\,, \\ \partial _i f_{w} - \lambda (u_i-x_i)&{} \text { if } v = 0\,, \\ - \lambda (u_i-x_i)&{} \text { if } v< 0\,. \end{array}\right. } \end{aligned}$$

We consider three subcases of $v<0$, $v>0$, and $v=0$ in turn. Suppose first that $v<0$ and that $(\lambda ,x)\in ({\mathbb C}^\times )^{n+1}$ is a solution to $({\mathcal L}_{f,u})_w$. As $\lambda \ne 0$ and we have $\lambda (u_i-x_i)=0$ for all $i\in {\mathcal I}$, we conclude that $x_{{\mathcal I}} = u_{{\mathcal I}}$. Since $f_w\in {\mathbb C}[x_{\mathcal I}]$ is a general polynomial with support ${\mathcal A}_w$ and u is general, we do not have $f_w(u_{{\mathcal I}})=0$. Thus $({\mathcal L}_{f,u})_{w}$ has no solutions when $v<0$.

Suppose next that $v>0$. Then, the subsystem of $({\mathcal L}_{f,u})_w=0$ involving $f_w$ and the equations indexed by ${\mathcal I}$ is

$$\begin{aligned} f_w\ =\ \partial _i (f_w)\ =\ 0\,,\qquad \text{ for } i\in {\mathcal I}\,. \end{aligned}$$

(12)

As $f_w\in {\mathbb C}[x_{\mathcal I}]$, the system of Eq. (12) implies that the hypersurface ${\mathcal V}_{({\mathbb C}^\times )^{\mathcal I}}(f_w)\subset ({\mathbb C}^\times )^{\mathcal I}$ is singular. However, since $f_w$ is general, this hypersurface must be smooth. Thus $({\mathcal L}_{f,u})_w$ has no solutions when $v>0$.

The third subcase of $v=0$ is more involved. When $v=0$, the subsystem of $({\mathcal L}_{f,u})_w$ consisting of $f_w$ and the equations indexed by ${\mathcal I}$ is

$$\begin{aligned} f_w\ =\ \partial _i (f_w)-\lambda (u_i-x_i)\ =\ 0 \qquad \text{ for } i\in {\mathcal I}\,. \end{aligned}$$

(13)

As $f_w\in {\mathbb C}[x_{\mathcal I}]$ and $0\in {\mathcal A}_w$, this is the system $({\mathcal L}_{f,u})_w$ in ${\mathbb C}_\lambda \times {\mathbb C}^{\mathcal I}$ for the critical points of Euclidean distance from $u_{\mathcal I}\in {\mathbb C}^{\mathcal I}$ to the hypersurface ${\mathcal V}_{{\mathbb C}^{\mathcal I}}(f_w)\subset {\mathbb C}^{\mathcal I}$. Thus $({\mathcal L}_{f,u})_w$ is triangular; to solve it, we first solve (13) and then consider the equations in $({\mathcal L}_{f,u})_w$ indexed by ${\mathcal J}$.

Since $\partial _j f_w=0$ for $j\in {\mathcal J}$, the remaining equations are independent of $u_{\mathcal I}$ and $f_w$. We will see that they are also triangular.

Since $h^*=0$, if $a\in {\mathcal A}\smallsetminus {\mathcal A}_w$, then $w\cdot a>0$. Let $j\in {\mathcal J}$. We earlier observed that if $a\in {\mathcal A}_w$ then $a_j=0$ and we defined $h^*_j$ to be the minimum $\min \{ w\cdot a\mid a\in \partial _j{\mathcal A}\}$. Since if $a\in \partial _j{\mathcal A}$, then $a+\mathbf{e}_j\in {\mathcal A}$, we have that $a+\mathbf{e}_j\in {\mathcal A}\smallsetminus {\mathcal A}_w$. We arrive at $w\cdot (a+\mathbf{e}_j)>0$, which implies that $w\cdot a>-w_j$. Taking the minimum over $a\in \partial _j{\mathcal A}$ implies that $h^*_j>-w_j$.

Consider now the members of the facial system $({\mathcal L}_{f,u})_w$ indexed by $j\in {\mathcal J}$. Since $v=0$ and $h^*_j>-w_j$, the second and fourth possibilities for $(\partial _jf-\lambda (u_j-x_j))_w$ in (10) do not occur. Recall that the last two possibilities also do not occur. As $v=0$, we have three cases

$$\begin{aligned} \left( \partial _j f - \lambda (u_j-x_j)\right) _w\ = \ {\left\{ \begin{array}{ll} (\partial _j f)_w&{} \text { if } h^*_j < \min \{0, w_j\}\,,\\ (\partial _j f)_w - \lambda u_j&{} \text { if } h^*_j = 0 \text { and } w_j> 0\,, \\ - \lambda (u_j-x_j)&{} \text { if }h^*_j > 0 \text { and } w_j = 0\, . \end{array}\right. } \end{aligned}$$

(14)

If the first case holds for some $j\in {\mathcal J}$, then as $h^*_j>-w_j$, we have $w_j>0$. Since $w_j\ge 0$ in the other cases, we have $w_j\ge 0$ for all $j\in {\mathcal J}$. As we showed earlier that $w_{\mathcal I}=0$, we have $w\ge 0$. But then as $\partial _j{\mathcal A}\subset {\mathbb N}^n$, we have $h^*_j\ge 0$ for all $j\in {\mathcal J}$. In particular, the first case in (14)—in which $h^*_j<0$—does not occur. Thus the only possibilities for the jth component of $({\mathcal L}_{f,u})_w$ are the second or the third cases in (14), so that $w_{\mathcal J}\ge 0$.

Let us further partition ${\mathcal J}$ according to the vanishing of $w_j$,

$$\begin{aligned} {\mathcal K}\ :=\ \{k\in {\mathcal J}\mid w_k=0\} \qquad \text{ and }\qquad {\mathcal M}\ :=\ \{m\in {\mathcal J}\mid w_m>0\}\,. \end{aligned}$$

Every component of $w_{\mathcal M}$ is positive and $w_{\mathcal I}=w_{\mathcal K}=0$. Moreover, the second entry in (14) shows that $h^*_m=0$ for all $m\in {\mathcal M}$. We conclude from this that no variable in $x_{\mathcal M}$ occurs in $(\partial _m f)_w$, for any $m\in {\mathcal M}$.

Let us now consider solving $({\mathcal L}_{f,u})_w$, using triangularity. Let $(\lambda ,x_{\mathcal I})$ be a solution to subsystem (13) for critical points of the Euclidean distance from $u_{\mathcal I}$ to ${\mathcal V}_{{\mathbb C}^{\mathcal I}}(f_w)$ in ${\mathbb C}^{\mathcal I}$. We may assume that $\lambda \ne 0$ as $f_w$ is general. Then the subsystem corresponding to ${\mathcal K}$ gives $x_k=u_k$ for $k\in {\mathcal K}$. Let $m\in {\mathcal M}$. Since $(\partial _m f)_w$ only involves $x_{\mathcal I}$ and $x_{\mathcal K}$, substituting these values into $(\partial _m f)_w$ gives a constant, which cannot be equal to $\lambda u_m$ for general $u_m\in {\mathbb C}$. As $w\ne 0$, we cannot have ${\mathcal M}=\emptyset$, so this last case occurs. Thus $({\mathcal L}_{f,u})_w$ has no solutions when $v=0$.

Case 3 (using the Euler formula): Let us now consider the case where there is some index $i\in {\mathcal I}$ with $w_i<0$ and suppose that the facial system $({\mathcal L}_{f,u})_w$ has a solution. Let $i\in {\mathcal I}$ be such an index with $w_i<0$. As the facial system has a solution, the last possibility in (10) for $(\partial _i f-\lambda (u_i-x_i))_w$ does not occur. Thus either first or the fourth possibility occurs. Hence, $h_i^*\le w_i+v<v$, as $w_i<0$. By (11), we have $h^*=h^*_i+w_i\le 2w_i+v < v$.

For any $i\in {\mathcal I}$, we have $h^*_i=h^*-w_i<v-w_i$, by (11). Thus if $w_i\ge 0$, then $h^*_i<v$. As we obtained the same inequality when $w_i<0$, we conclude that for all $i\in {\mathcal I}$ we have $h_i^*<v$. Thus only the first or the fourth possibility in (10) occurs for $i\in {\mathcal I}$. That is,

$$\begin{aligned} (\partial _i f - \lambda (u_i-x_i))_{w} = {\left\{ \begin{array}{ll} \partial _i f_{w} &{} \text { if } h^* - w_i< \min \{v, w_i + v\} \,, \\ \partial _i f_{w} + \lambda x_i&{} \text { if } h^* = 2w_i + v \text{ and } w_i<0\,. \end{array}\right. } \end{aligned}$$

(15)

These cases further partition ${\mathcal I}$ into sets ${\mathcal K}$ and ${\mathcal M}$, where

$$\begin{aligned} {{\mathcal K}}{\ }&:=\ \{k\in {\mathcal I}\mid h^* - w_k< \min \{v, w_k + v\} \}\,\; \text{ and }\\ {{\mathcal M}}\&:=\ \{m\in {\mathcal I}\mid h^* = 2w_m + v \text{ and } w_m<0\}\, . \end{aligned}$$

For $k\in {\mathcal K}$ the corresponding equation in $({\mathcal L}_{f,u})_w=0$ is $\partial _k f_w=0$ and for $m\in {\mathcal M}$ it is $\partial _m f_{w} + \lambda x_m=0$. If ${\mathcal M}=\emptyset$, then ${\mathcal K}={\mathcal I}$ and the subsystem of $({\mathcal L}_{f,u})_w$ consisting of $f_w$ and the equations indexed by ${\mathcal I}$ is (12), which has no solutions as we already observed.

Now suppose that ${\mathcal M}\ne \emptyset$. Define ${w^*}:=\min \{w_i\mid i\in {\mathcal I}\}$. Then $w^*<0$. Moreover, by (15) we have that if $m\in {\mathcal M}$, then $w_m=\frac{1}{2}(h^*-v)$. Thus, $w_m=w^*$ for every $m\in {\mathcal M}$. Suppose that $(\lambda ,x)$ is a solution to $({\mathcal L}_{f,u})_w$. For $k\in {\mathcal K}$, we have $\partial _k f_w(x)=0$ and for $m\in {\mathcal M}$, we have that $\partial _m f_{w}(x)=-\lambda x_m$. Then by Lemma 2, we get

$$\begin{aligned} 0\ =\ h^* f_w(x)\ =\ \sum _{i\in {\mathcal I}} w_i \, x_i \, \partial _i (f_w)(x)\ =\ -\lambda w^*\sum _{m\in {\mathcal M}} x_m^2 \ . \end{aligned}$$

The last equality uses that ${\mathcal I}={\mathcal K}\sqcup {\mathcal M}$. Since $\lambda \ne 0$ and $w^*\ne 0$, we have $\sum _{m\in {\mathcal M}} x_m^2= 0$. Let Q be this quadratic form. Then the point $x_{\mathcal I}$ lies on both hypersurfaces ${\mathcal V}(f_w)$ and ${\mathcal V}(Q)$. Since $\partial _k f_w(x_{\mathcal I})=\partial _k Q=0$ for $k\in {\mathcal K}$ and $2\partial _m f_w(x_{\mathcal I})=\lambda \partial _m Q$ for $m\in {\mathcal M}$, we see that the two hypersurfaces meet nontransversely at $x_{\mathcal I}$. But this contradicts $f_w$ being general. Thus, there are no solutions to $({\mathcal L}_{f,u})_{w}=0$ in this last case.

This completes the proof of Theorem 3. $\square$

6 The Euclidean Distance Degree of a Rectangular Parallelepiped

Let $a=(a_1,\dotsc ,a_n)$ be a vector of nonnegative integers and recall from (4) the definition of the rectangular parallelepiped:

$$\begin{aligned} B(a)\ =\ [0,a_1]\times \cdots \times [0,a_n]\ \subset \ {\mathbb R}^n\,. \end{aligned}$$

We consider the Euclidean distance degree of a general polynomial whose Newton polytope is B(a), with the goal of proving Theorem 2. We consider polytopes in ${\mathbb R}^n$, such as B(a), as polytopes in ${\mathbb R}^{n+1}$, using the identification of ${\mathbb R}^n$ with $\{0\}\times {\mathbb R}^n\subset {\mathbb R}^{n+1}$.

Recall that ${\mathbf{e}_i}:=(0,\dotsc ,1,\dotsc ,0)$ is the ith standard unit vector in ${\mathbb R}^n$ (the unique 1 is in the ith position). The 0-th unit vector $\mathbf{e}_0$ corresponds to the variable $\lambda$. Let f be a general polynomial with Newton polytope B(a). Then the Newton polytope of the partial derivative $\partial _i f$ is $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_n)$.

For each $1\le i\le n$, let ${P_i(a)}{\subset {\mathbb R}^{n+1}}$ be the convex hull of $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_n)$ and the two points $\mathbf{e}_0$ and $\mathbf{e}_0+\mathbf{e}_i$. Then $P_i(a)$ is the Newton polytope of $\partial _i f - \lambda (u_i-x_i)$. Consequently, $B(a),P_1(a),\dotsc ,P_n(a)$ are the Newton polytopes of the Lagrange multiplier Eq. (2).

Recall that for each $1\le k\le n$, $e_k(a)$ is the elementary symmetric polynomial of degree k evaluated at a. It is the sum of all square-free monomials in $a_1,\dotsc ,a_n$. Let us write

$$\begin{aligned} {E(a)}\ := \sum _{k=1}^n k! \,e_k(a)\,. \end{aligned}$$

(16)

The main result in this section is the following mixed volume computation. It and Theorem 1 together imply Theorem 2.

Theorem 5

With these definitions, ${{\,\mathrm{\mathrm{MV}}\,}}(B(a),P_1(a),\dotsc ,P_n(a)) = E(a)$.

Our proof of Theorem 5 occupies Sect. 6.3, and it depends upon lemmas and definitions collected in Sects. 6.1 and 6.2. One technical lemma from Sect. 6.2 is proven in Sect. 6.4.

6.1 Mixed Volumes

Let m be a positive integer. The Minkowski sum of two polytopes P, Q in ${\mathbb R}^m$ is the sum of all pairs of points, one from each of P and Q,

$$\begin{aligned} {P+Q}\ :=\ \{p+q\mid p\in P\ \text{ and } \ q\in Q\}\,. \end{aligned}$$

Let m be a positive integer. As explained in [12][Sect. IV.3], mixed volume is a nonnegative function ${{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m)$ of polytopes $Q_1,\dotsc ,Q_m$ in ${\mathbb R}^m$ that is characterized by three properties:

Normalization. If $Q_1=\cdots =Q_m=Q$, and ${{\,\mathrm{\mathrm{Vol}}\,}}(Q)$ is the Euclidean volume of Q, then

$$\begin{aligned} {{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m)\ =\ m!{{\,\mathrm{\mathrm{Vol}}\,}}(Q)\,. \end{aligned}$$

Symmetry. If $\sigma$ is a permutation of $\{1,\dotsc ,m\}$, then

$$\begin{aligned} {{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_m)\ =\ {{\,\mathrm{\mathrm{MV}}\,}}(Q_{\sigma (1)},\dotsc ,Q_{\sigma (m)})\,. \end{aligned}$$

Multiadditivity. If $Q'_1$ is another polytope in ${\mathbb R}^m$, then

$$\begin{aligned} {{\,\mathrm{\mathrm{MV}}\,}}(Q_1{+}Q'_1,Q_2,\dotsc ,Q_m)\ {=}\ {{\,\mathrm{\mathrm{MV}}\,}}(Q_1,Q_2,\dotsc ,Q_m)\ {+}\ {{\,\mathrm{\mathrm{MV}}\,}}(Q'_1,Q_2,\dotsc ,Q_m)\,. \end{aligned}$$

Mixed volume decomposes as a product when the polytopes possess a certain triangularity (see [28][Lem. 6] or [11][Thm. 1.10]). We use a special case. For a positive integer b, write $[0,b\,\mathbf{e}_i]$ for the interval of length b along the ith axis in ${\mathbb R}^{m}$. For each $1\le j\le m$, let ${\pi _j}:{\mathbb R}^{m}\rightarrow {\mathbb R}^{m-1}$ be the projection along the coordinate direction j.

Lemma 3

Let $Q_1,\dotsc ,Q_{m-1}\subset {\mathbb R}^m$ be polytopes, b be a positive integer, and $1\le j\le m$. Then

$$\begin{aligned} {{\,\mathrm{\mathrm{MV}}\,}}(Q_1,\dotsc ,Q_{m-1},[0,b\,\mathbf{e}_j])\ =\ b\,{{\,\mathrm{\mathrm{MV}}\,}}(\pi _j(Q_1),\dotsc ,\pi _j(Q_{m-1}))\,. \end{aligned}$$

Proof

We paraphrase the proof in [11], which is bijective and algebraic. Consider a system $g_1,\dotsc ,g_m$ of general polynomials with Newton polytopes $Q_1,{\dotsc },Q_{m-1},[0,b\,\mathbf{e}_j]$, respectively. As $g_m$ is a univariate polynomial of degree b in $x_j$, $g_m(x_j)=0$ has b solutions. For each solution $x^*_j$, if we substitute $x_j=x^*_j$ in $g_1,\dotsc ,g_{m-1}$, then we obtain general polynomials with Newton polytopes $\pi _j(Q_1),\dotsc ,\pi _j(Q_{m-1})$. Thus, there are ${{\,\mathrm{\mathrm{MV}}\,}}(\pi _j(Q_1),\dotsc ,\pi _j(Q_{m-1}))$ solutions to our original system for each of the b solutions to $g_m(x_j)=0$. $\square$

6.2 Pyramids

Let $1\le m\le n$ and $a=(a_1,\dotsc ,a_m)$ be a vector of positive integers. The small rectangular parallelepiped is ${B(a)}:=[0,a_1]\times \cdots \times [0,a_m]$. It is the Minkowski sum of intervals:

$$\begin{aligned} B(a)\ =\ [0,a_1\mathbf{e}_1]+\cdots +[0,a_k\mathbf{e}_m]\,. \end{aligned}$$

Its Euclidean volume is $a_1\cdots a_m$, the product of its side lengths. This is embedded in ${\mathbb R}^{m+1}$ as $\{0\}\times B(a)$.

As before, ${P_i(a)}$ is the convex hull of $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_m)$ and $\mathbf{e}_0+[0,\mathbf{e}_i]$. Define ${{{\,\mathrm{\mathrm{Pyr}}\,}}(a)}$ to be the pyramid with base the rectangular parallelepiped B(a) and apex $\mathbf{e}_0$, this is the convex hull of B(a) and $\mathbf{e}_0$. For each $j=1,\ldots ,m$ we have the projection $\pi _j:\mathbb R^{m}\rightarrow \mathbb R^{m-1}$ along the jth coordinate, so that $\pi _j(a)=(a_1,\dotsc ,a_{j-1}\,,\,a_{j+1},\dotsc ,a_m)$. We then have that $\pi _j(B(a))=B(\pi _j(a))$. The following is immediate from the definitions.

Lemma 4

Let $a=(a_1,\dotsc ,a_m)$ and $1\le i,j\le m$. Then we have

$$\begin{aligned} \pi _j(P_i(a)) =\ \left\{ \begin{array}{rcl} P_i(\pi _j(a)) &{}\ &{}\text{ if } \; i\ne j\\ {{\,\mathrm{\mathrm{Pyr}}\,}}(\pi _j(a)) &{}\ &{}\text{ if } \; i = j \end{array}\right. . \end{aligned}$$

We now have the following lemma. Recall definition (16) of E(a).

Lemma 5

We have ${{\,\mathrm{\mathrm{MV}}\,}}({{\,\mathrm{\mathrm{Pyr}}\,}}(a),P_1(a),\dotsc ,P_m(a))\ =\ 1 + E(a)$.

We prove this in Sect. 6.4.

6.3 Proof of Theorem 5

Since B(a) is the Minkowski sum of the intervals $[0,a_i\mathbf{e}_i]$ for $1\le i\le n$, multiadditivity and Lemma 3 give

$$\begin{aligned} {{\,\mathrm{\mathrm{MV}}\,}}(B(a),P_1(a),\dotsc ,P_n(a))&=\ \sum _{j=1}^n {{\,\mathrm{\mathrm{MV}}\,}}([0,a_j\mathbf{e}_j], P_1(a),\dotsc ,P_n(a))\\&=\ \sum _{j=1}^n a_j {{\,\mathrm{\mathrm{MV}}\,}}( \pi _j(P_1(a)),\dotsc ,\pi _j(P_n(a)))\,. \nonumber \end{aligned}$$

(17)

By Lemma 4, the jth term is

$$\begin{aligned} a_j {{\,\mathrm{\mathrm{MV}}\,}}( P_1(\pi _j(a)),\dotsc ,P_{j-1}(\pi _j(a))\,,\, {{\,\mathrm{\mathrm{Pyr}}\,}}(\pi _j(a))\,,\, P_{j+1}(\pi _j(a)),\dotsc ,P_n(\pi _j(a)))\,. \end{aligned}$$

Applying symmetry and Lemma 5 with $m=n{-}1$, this is $a_j(1+E(\pi _j(a)))$, where $E(\bullet )$ is defined in (16). Thus, the mixed volume (17) is

$$\begin{aligned} e_1(a)\ +\ \sum _{k=1}^{n-1} k!\ \sum _{j=1}^n a_j e_k(\pi _j(a)) \ = E(a)\,. \end{aligned}$$

The equality in this formula follows from the identity,

$$\begin{aligned} \sum _{j=1}^n a_j e_k(\pi _j(a))\ =\ \sum _{j=1}^n a_j e_k(a_1,\dotsc ,a_{j-1}\,,\, a_{j+1},\dotsc , a_n)\ =\ (k{+}1) e_{k+1}(a)\,. \end{aligned}$$

This finishes the proof of Theorem 5. $\square$

6.4 Proof of Lemma 5

We use Bernstein’s theorem to show that a general polynomial system with support ${{\,\mathrm{\mathrm{Pyr}}\,}}(a),P_1(a),\dotsc ,P_m(a)$ has $1+E(a)$ solutions in the torus $({\mathbb C}^\times )^{m+1}$, where $a=(a_1,\dotsc ,a_m)$ is a vector of positive integers.

A general polynomial with Newton polytope ${{\,\mathrm{\mathrm{Pyr}}\,}}(a)$ has the form $c\lambda +f$, where f has Newton polytope B(a) and $c\ne 0$. Here, $\lambda$ is a variable with exponent $\mathbf{e}_0$. Dividing by c, we may assume that the polynomial is monic in $\lambda$. Similarly, as $P_i(a)$ is the convex hull of $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_m)$ and $\mathbf{e}_0+[0,\mathbf{e}_i]$, a general polynomial with support $P_i(a)$ may be assumed to have the form $\lambda \ell _i(x_i) + f_i(x)$, where $f_i$ has Newton polytope $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_m)$ and ${\ell _i(x_i)}:=c_i+x_i$ is a linear polynomial in $x_i$ with $c_i\ne 0$.

We may therefore assume that a general system of polynomials with the given support has the form

$$\begin{aligned} \lambda -f\,,\ \, \lambda \ell _1(x_1)+f_1\,,\ \dotsc \,,\ \lambda \ell _m(x_m)+f_m\,, \end{aligned}$$

(18)

where f is a general polynomial with Newton polytope B(a) and for each $1\le i\le m$, $f_i$ is a general polynomial with Newton polytope $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_m)$. We show that $1+ E(a)$ is the number of common zeros in $({\mathbb C}^\times )^{n+1}$ of the polynomials in (18).

Using the first polynomial to eliminate $\lambda$ from the rest shows that solving system (18) is equivalent to solving the system

$$\begin{aligned} F\ :\ f_1+\ell _1(x_1)f\,,\ \dotsc \,,\ f_m + \ell _m(x_m) f\,, \end{aligned}$$

(19)

which is in the variables $x_1,\dotsc ,x_m$, as $z\mapsto (f(z),z)$ is a bijection between the solutions z to (19) and the solutions to (18). We show that the number of common zeroes to (19) is $1+E(a)$, when $f,f_1,\dotsc ,f_m$ are general given their Newton polytopes.

Unlike system (18), the system F is not general given its support. Nevertheless, we will show that no facial system has any solutions. Then, by Bernstein’s Other Theorem, its number of solutions is the corresponding mixed volume, which we now compute.

Since $B(a_1,\dotsc ,a_i{-}1,\dotsc ,a_m)\subset B(a)$, the Newton polytope of $f_i+\ell _i(x_i)f$ is $B(a)+[0,\mathbf{e}_i]$. Thus the mixed volume we seek is

$$\begin{aligned} {{\,\mathrm{\mathrm{MV}}\,}}(B(a)+[0,\mathbf{e}_1],\dotsc ,B(a)+[0,\mathbf{e}_m])\ =\ \sum _{{\mathcal I}\subset \{1,\dotsc ,m\}} |{\mathcal I}|! \prod _{i\in {\mathcal I}} a_i\ =\ 1 + E(a)\,. \end{aligned}$$

To see this, first observe that the second equality is the definition of E(a). For the first equality, consider expanding the mixed volume using multilinearity. This will have summands indexed by subsets ${\mathcal I}$ of $\{1,\dotsc ,m\}$ where in the summand indexed by ${\mathcal I}$, we choose B(a) in the positions in ${\mathcal I}$ and $[0,\mathbf{e}_j]$ when $j\not \in {\mathcal I}$. A repeated application of Lemma 3 shows that this summand is ${{\,\mathrm{\mathrm{MV}}\,}}(B(a_{\mathcal I}),\dotsc ,B(a_{\mathcal I}))$, as projecting a from the coordinates $j\not \in {\mathcal I}$ gives $a_{\mathcal I}$. This term is $|{\mathcal I}|!\prod _{i\in {\mathcal I}} a_i$, by the normalization property of mixed volume.

We now show that no facial system of (19) has any solutions. Since each Newton polytope is a rectangular parallelepiped $B(a)+[0,\mathbf{e}_j]$, its proper faces are exposed by nonzero vectors $w\in \{-1,0,1\}^m$, and each exposes a different face.

Let $w\in \{-1,0,1\}^m$ and suppose that $w\ne 0$. We first consider the face of B(a) exposed by w. This is a rectangular parallelepiped whose ith coordinate is

$$\begin{aligned} 0 \text{ if } \ w_i=1\,,\qquad [0,a_i] \text{ if } \ w_i=0\,,\qquad \text{ and }\qquad a_i \text{ if } \ w_i=-1\,. \end{aligned}$$

In the same manner as (9), we define ${B(a)_w}:= \{b^*\in B(a) \mid w\cdot b^* = \min _{b\in B(a)} w\cdot b\}$, and we similarly define $(B(a)+[0,\mathbf{e}_j])_w$ for each $j=1,\ldots ,m$. Then,

$$\begin{aligned} B(a)_w\ =\ \sum _{i:w_i=1}\{0\} \ +\ \sum _{i:w_i=0}[0,a_i\mathbf{e}_i] \ +\ \sum _{i:w_i=-1}\{a_i\mathbf{e}_i\} \ , \end{aligned}$$

(20)

and we have

$$(B(a)+[0,\mathbf{e}_j])_w = {\left\{ \begin{array}{ll} B(a)_w, &{}\text { if } w_j = 1,\\ B(a)_w+ [0,\mathbf{e}_j], &{}\text { if } w_j = 0,\\ B(a)_w+ \mathbf{e}_j, &{}\text { if } w_j = -1. \end{array}\right. } $$

As $\ell _j=c_j+x_j$, we also have

$$\ell _j(x_j)_w = {\left\{ \begin{array}{ll} c_j, &{}\text { if } w_j = 1,\\ \ell _j(x_j), &{}\text { if } w_j = 0,\\ x_j, &{}\text { if } w_j = -1. \end{array}\right. } $$

The Newton polytope of $f_i$ has ith coordinate the interval $[0,(a_i{-}1)]$ and for $j\ne i$ its jth coordinate is the interval $[0,a_j]$. The Newton polytope of $\ell _i\cdot f$ differs in that its ith coordinate is the interval $[0,(a_i{+}1)]$. We get

$$\begin{aligned} (f_i+\ell _if)_w\ =\ \left\{ \begin{array}{rcl} (f_i)_w+c_i \cdot f_w&{}\ &{}\text{ if } w_i=1\\ (f_i)_w+\ell _i \cdot f_w&{}\ &{}\text{ if } w_i=0\\ x_i\cdot f_w&{}\ &{}\text{ if } w_i=-1 \end{array}\right. , \end{aligned}$$

(21)

and for $f_i$ general $(f_i)_w\ne 0$ when $w_i\ne 1$.

Let $\alpha$ be the number of coordinates of w equal to 0, $\beta$ be the number of coordinates equal to 1 and set ${\gamma }:=n-\alpha -\beta$, which is the number of coordinates of w equal to $-1$. The faces of $(B(a)+[0,\mathbf{e}_j])_w$ exposed by w have dimension $\alpha$, by (20), so the facial system $F_w$ of (19) is effectively in $\alpha$ variables. Suppose first that $\gamma >0$. Since on $({\mathbb C}^\times )^n$ each variable $x_i$ is nonzero, by (21) the facial system $F_w$ is equivalent to

$$\begin{aligned} f_w\,,\ \{(f_i)_w\mid w_i\ne -1\}\,. \end{aligned}$$

As these are nonzero and general given their support, and there are $\alpha +\beta +1>\alpha$ of them, we see that $F_w$ has no solutions.

If $\gamma =0$, then $\beta >0$. Consider the subfamily $\widehat{F}$ of systems of form (19) where $f=0$, but the $f_i$ remain general. Then the facial system $F_w$ is equivalent to the system $\{(f_i)_w\mid w_i\ne -1\}$ of $\alpha +\beta >\alpha$ polynomials which are nonzero and general given their support, so that $\widehat{F}_w$ has no solutions.

As the condition that $F_w$ has no solutions is an open condition in the space of all systems (18), this implies that for a general system (18) with corresponding system F (19), no facial system $F_w$ has a solution. This completes the proof of the lemma. $\square$