Introduction

Environmental studies typically involve surveying large areas. The collected data are used to estimate population parameters such as density or abundance. A common survey design used in environmental studies is two-stage sampling (Fattorini and Pisani 2004). In conventional two-stage sampling, an initial sample of primary units is selected, from which a sample of secondary units is selected. Stratified sampling can be considered a form of two-stage sampling where every primary unit is selected. Primary units are usually large spatial units defined according to some habitat characteristic. Secondary units are usually smaller spatial units such as plots or quadrats in vegetation surveys, tows or grabs in fisheries, and, in animal surveys, stations of trap or faecal-count lines for recording animal-signs.

Various methods for allocation of second-stage effort among primary units have been suggested. Adaptive and sequential designs for second-stage effort allocation can improve survey efficiency (e.g., Francis 1984; Jolly and Hampton 1990; Manly et al. 2002; Manly 2004). These designs require the primary units or strata to be revisited. Allocation of final survey effort among primary units is decided once the result of an initial survey within the primary units is complete. These designs have been used predominantly in fisheries applications, e.g., Smith and Lundy (2006) used an adaptive allocation in a stratified design to survey sea scallops (Placopecten magellanicus). Designs where additional sampling effort is allocated without a repeat visit to the site have been considered by Salehi M. and Seber (1997) and Christman (2003). In Salehi M. and Seber’s two-stage adaptive cluster sampling, selected primary units are surveyed using adaptive cluster sampling. They describe two schemes, one where the clusters are allowed to overflow across the edges of primary sample unit and the other where they cannot. In Christman’s adaptive two-stage design, one secondary sample unit is selected initially from each primary unit stratum sampling.

More recently, a two-stage sequential sampling design has been proposed (Salehi M. and Smith 2005). In this sampling design, the population is partitioned into M primary units of size N i units. In the first stage, a selection of m primary units are selected from the M units. In the second stage, an initial simple random sample of size n i1 is taken from each of the selected primary units. If any of the units in the initial sample from primary unit i meet a condition, C, and say y ij  > c, then a fixed number of n i2 additional units from that primary unit are selected.

The motivation for this design is sampling rare and clustered populations. Adaptive cluster sampling (Thompson 1990) is a useful design for these types of populations and it has been used in a range of applications from surveying waterfowl (Smith et al. 1995) and fish larvae (Lo et al. 1997) to forest trees (Acharya et al. 2000) and herbaceous plants (Philippi 2005). See Smith et al. (2004) and Philippi (2005) for a review of these, and other, applications. However, there are some limitations to adaptive cluster sampling (Salehi M. and Smith 2005), probably the most important being the need to measure, in some way, edge units. Edge units are those surrounding a spatially-contiguous network of survey units that all meet the adaptive sampling condition. Edge units need to be measured to identify the “edge” of the network. In doing so there is a cost because, regardless of the measure used, it will take some effort, but the information from edge units is not used in the sample-estimator. The two-stage sequential sampling design can be an efficient alternative design for such rare and clustered populations (Salehi M. and Smith 2005).

The “sequential” aspect of two-stage sequential sampling means that the number of secondary sample units chosen within each selected primary unit is either n i1 or n i1 + n i2. This unequal allocation of effort among selected primary sampling units, where primary units with high values are over-sampled compared with other primary units, is consistent with the approach recommended by Kalton and Anderson (1986) for sampling rare populations with stratified sampling.

A drawback of the two-stage sequential sampling is that there is limited flexibility in how much, or how little, a selected primary sample unit is sampled because the number of additional units in the sequential sampling is fixed as n i2. We propose a modification to two-stage sequential sampling where, rather than using a fixed number of additional secondary sample units, the number of additional units is g i × λ. units where g i is the number of sampled units in the ith primary unit that satisfy the condition C and λ is some multiplier. We call this design adaptive two-stage sequential sampling.

In this paper, we examine the gains in efficiency from using adaptive two-stage sequential sampling compared with two-stage sequential sampling, and discuss how best to design such a survey.

Adaptive two-stage sequential sampling notation and estimator

We begin the introduction of the proposed design with some notation. Suppose we have a total population of N units partitioned into M primary units, (PSU) of size N i units (i = 1, 2,…, M). Let the unit (i, j) denote the jth unit in the ith primary unit with an associated measurement or count y ij . Let \( T = \sum\nolimits_{j = 1}^{N_i } {y_{ij} } \) be the sum of the y values in the ith primary unit, and let \( T = \sum\nolimits_{i = 1}^M {T_i } \) be the total for the whole population.

In the first stage of the sampling, we choose a sample of m from the M primary units without replacement by some design with inclusion probability π i for primary unit i. At the second stage, we take an initial simple random sample of n i1 units without replacement from primary unit i (i = 1, 2,…, m) so that \( n = \sum\nolimits_{i = 1}^m {n_{i1} } \) is the total initial sample size. Let C be the condition that, if satisfied for g i units in the sample set from primary unit i, results in g i  · λ number of additional units being selected at random from the remaining units in primary unit i, where λ is a predetermined value. As a result, n i2 = g i  · λ is the number of adaptively added units in the ith PSU and \( n_2 = \sum\nolimits_{i = 1}^m {n_{i2} } \) is the number of adaptively added units in the final sample, and is a random variable. Let l i and \(l^{\prime}_{i}\) be, respectively, the number of units satisfying and not satisfying the condition C in the final sample set from primary unit i. Note that when m = M, we have a stratified adaptive allocation sampling scheme.

We use Murthy’s estimator (1957) to devise unbiased estimators for this design. The estimator for the sum of the y values of the ith primary unit is:

$$ \hat T_i = N_i \left[ {\frac{{g_i }}{{n_{i1} }}\bar y_{ic} + \frac{{n_{i1} - g_i }}{{n_{i1} }}\bar y_{i\bar c} } \right], $$

where \( \bar y_{ic} \) and \( \bar y_{i\bar c} \) are, respectively, the mean of units satisfying and not satisfying the condition C in the final sample set from primary unit i. Derivations of this estimator are provided in the Appendix.

The estimator for the sample variance of the ith primary unit is:

$$ \begin{aligned} \text{v} \hat{\text{a}}\text{r}(\hat T_i ) & = N_i \left\{ {\frac{{g_i }}{{n_{i1} }}\left[ {\frac{{\left( {N_i - 1} \right)\left( {g_i - 1} \right)}}{{n_{i1} - 1}} + \left( {\frac{{\left( {N_i - n_{i1} } \right)\frac{{g_i }}{{n_{i1} }}}}{{n_{i1} - 1}} - N_i \left( {1 - \frac{{g_i }}{{n_{i1} }}} \right)} \right)\frac{{l_i - 1}}{{l_i }}} \right]s_{ic}^2 } \right. \\ & \quad + \frac{{g_i }}{{n_{i1} }}\left( {1 - \frac{{g_i }}{{n_{i1} }}} \right)\frac{{N_i - n_{i1} }}{{n_{i1} - 1}}\left( {\bar y_{ic} - \bar y_{i\bar c} } \right)^2 \\ & \quad \left. { + \left( {1 - \frac{{g_i }}{{n_{i1} }}} \right)\left[ {\frac{{\left( {N_i - 1} \right)\left( {n_{i1} g_i - 1} \right)}}{{n_{i1} - 1}} + \left( {\frac{{\left( {N_i - n_{i1} } \right)\left( {1 - \frac{{g_i }}{{n_{i1} }}} \right)}}{{n_{i1} - 1}} - N_i \frac{{g_i }}{{n_{i1} }}} \right)\frac{{l'_i - 1}}{{l'_i }}} \right]s_{i\bar c}^2 } \right\}, \\ \end{aligned} $$

where s 2 ic is the variance of the l i units satisfying the condition C in the final sample set from primary unit i,

$$ s_{ic}^2 = \frac{1}{{l_i - 1}}\sum\limits_{j = 1}^{l_i } {\left( {y_{ij} - \bar y_{ic} } \right)} ^2 , $$

and \( s_{i\bar c}^2 \) is the variance of the \(l^{\prime}_{i}\) units not satisfying the condition C in the final sample set from primary unit i,

$$ s_{i\bar c}^2 = \frac{1}{{l'_i - 1}}\sum\limits_{j = 1}^{l'_i } {\left( {y_{ij} - \bar y_{i\bar c} } \right)} ^2 . $$

Derivations of the variance estimator are given by Salehi M. et al. (unpublished data). Code in the R language (R Core Development Team 2004) for calculating these rather daunting estimators is available from one the authors, M.S.M.

Simulation study

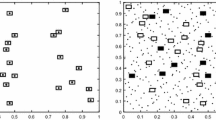
A simulation study was conducted to compare adaptive two-stage sequential sampling with ordinary two-stage sampling and with two-stage sequential sampling. The data were from a population count of blue-winged teal (Anas discors) from helicopter surveys, December 1992, in central Florida (Smith et al. 1995; Salehi M. and Smith 2005). The population is extremely clustered (Fig. 1).

Fig. 1
figure 1

Numbers of blue-winged teal (Anas discors) as given by Smith et al. (1995). The population is partitioned into eight primary units. Within each primary unit there are 25 secondary units

Full size image

Primary sample units were selected in the first stage using simple random sampling. Sampling of each selected PSU was then conducted using three different two-stage designs: ordinary two-stage sampling (TS), two-stage sequential sampling (TSS), and adaptive two-stage sequential sampling (ATSS). Secondary sample units were chosen from each selected primary unit using simple random sampling (without replacement). For comparison, the same selected PSU were used for each of the three designs. This simulation was repeated r = 10,000 times. After each simulation, a simple random sample (SRS) was drawn, disregarding the structure of the data into primary units, for comparison.

The teal population was partitioned into M = 8 PSU. We used m = 2, 4, 6, 8 and n i1 = 1, 2, 3,…,10. Two levels for the condition C were used: c = 1 for the condition y ij  ≥ 1 and c  = 10 for y ij  ≥ 10.

For two-stage sequential sampling selection, n i2 = 1, 2,…, 20, and for adaptive two-stage sequential sampling selection λ = 0.25, 0.5, 0.75, 1, 1.25, 2, 2.5, 3, 3.5, 4,…, 20. The maximum size of the final sample with a primary unit was 25 so not all combinations of sample design would be used in a simulation run. For example, consider a simulation with n i1 = 2. If both units satisfied the condition then the maximum value that λ could be for the simulation is 11.5, meaning all 23 remaining units would be selected. The estimate, \( \hat T_k \) was calculated for each sample.

We compared sample designs using the respective sample variances,

$$ \text{var} (\hat T) = \frac{1}{{r - 1}}\sum\limits_{k = 1}^r {\left( {\hat T_k - \bar T} \right)^2 } . $$

Relative efficiency of one sample design to another was defined as the ratio of the two sample variances.

Using the same number of selected PSU, sample designs were compared using matched final sample sizes. For two-stage sequential sampling, and for the adaptive version, the final sample size υTSS for a given design was calculated as the average of the final observed sample sizes over the r = 10,000 simulations,

$$ \upsilon _{\text{TSS}} = \frac{1}{r}\sum\limits_{k = 1}^r {\upsilon _k } . $$

For ordinary two-stage sampling, final sample size is fixed, υ TS = m · n 1. The size of the second stage sample, n 1, for ordinary two-stage sampling was calculated from the final sample size of the sequential designs, n 1 = υ TSS/m rounding n 1 to the nearest whole number. For simple random sampling, the size of the sample was the same as υ TSS.

Results

The two-stage sequential sampling designs were more efficient than simple random sampling, except when sample sizes were very small, e.g., when only two PSU were selected with only one sample unit selected from each. In all but these cases, the relative efficiency of the sequential two-stage designs compared with simple random sampling, \( \text{var} (\hat T_{\text{SRS}} )/\text{var} (\hat T_{\text{TSS}} ) \)and \( \text{var} (\hat T_{\text{SRS}} )/\text{var} (\hat T_{\text{ATSS}} ) \) was greater than 1 (Fig. 2). In Fig. 2 we display a selection of results, but the trends are consistent over all design combinations.

Fig. 2
figure 2

Relative efficiency of two-stage sampling (dashed line), two-stage sequential sampling (solid line) and adaptive two-stage sequential sampling (dotted line) compared with simple random sampling. Sample sizes were matched using the same number of selected PSU, m = 2, 4, 6, 8; N = 200. For the two sequential designs shown, the size of the initial second stage sample within each selected PSU was n 1 = 4. If any of the selected secondary sample units met the condition c = 1 (graphs on left) or c = 10 (graphs on right), additional units were selected. For ordinary two-stage sampling, the size of the secondary sample was estimated from the final sample size of the sequential designs. Simple random sampling ignored the PSU design structure

Full size image

The sequential designs lead to an improvement in relative efficiency over ordinary two-stage sampling (Fig. 2). For a given number of selected PSU, the gain in relative efficiency of the sequential two-stage designs over ordinary two-stage sampling increased as more effort was allocated to the sequential addition of extra units in the second stage. Each graph in Fig. 2 is for a fixed number of selected PSU and, for the sequential designs, for a fixed initial second stage sample size. Increasing final sample sizes (moving right on the horizontal axis) are results from simulations with increasing number of additional units in the second stage.

The other trend seen in the graphs is the effect on relative efficiency of changing the condition. When c = 1, if any selected sample unit had teal present, selection of additional units within the PSU was initiated. When c = 10, additional units were selected only when high-count initial units were selected. The effect of the higher threshold is that selection of additional units is initiated less frequently then with the lower threshold, and for the same design combination sample sizes are smaller. Comparison for a given final sample size of the sequential two-stage design results for c = 1 with c = 10 shows improved relative efficiency with the higher threshold. For ease of comparison, information from the graphs in Fig. 2 from the same range in the horizontal axes is superimposed in Fig. 3.

Fig. 3
figure 3

Relative efficiency of two-stage sequential sampling for c = 1 (dark solid line) and c = 10 (light solid line) and adaptive two-stage sequential sampling for c = 1 (dark dotted line) and c = 10 (light dotted line). Two-stage sequential sampling is compared with simple random sampling with matched sample sizes and the same number of selected PSU, m = 2, 4, 6, 8. For the two-stage designs, the initial second stage sample within each selected PSU was n 1 = 4

Full size image

The adaptive allocation of additional units in the second stage of sampling led to a small increase in relative efficiency. ATSS was generally more efficient than TSS for the same final sample size. Direct comparison is difficult between the two designs because there are multiple design combinations that will give the same final sample size. For example, with m = 4, two-stage sequential sampling with n i1 = 4, n i2 = 4 resulted in an average final sample size of 21. That same sample size was produced from adaptive two-stage sequential sampling with n i1 = 4, λ = 3 and with n i1 = 2, λ = 16. The design with the highest relative efficiency (r.e.) in this set was ATSS with n i1 = 2 (r.e. = 2.13), followed by ATSS with n i1 = 4 (r.e. = 1.12) and then TSS with n i1 = 4 (r.e. = 1.07). The graphical displays in Figs. 2 and 3 illustrate comparative efficiency for the same initial second-stage sample, and reflect the more conservative comparison.

This study also allowed comparison of ordinary two-stage sampling compared with simple random sampling. For this waterfowl dataset, while generally two-stage sampling was more efficient than simple random sampling the gain was small—the average relatively efficiency over all the sample design combinations was 1.1 and the maximum relative efficiency was only 1.5. In contrast, the average relative efficiency of the two sequential two-stage sampling designs was 1.5 with maximum relative efficiency of 3.6.

Discussion

Two-stage sequential sampling is an efficient design and, in this study, was generally more efficient than ordinary two-stage sampling. The sequential design can be enhanced by adaptive allocation of the additional units in the second stage. Direct comparison of TSS and ATSS is difficult because many design combinations can lead to the same final sample size, but in the conservative comparison with the same number of primary units, and the same sized initial second-stage sample, ATSS was marginally more efficient than TSS.

One of the reasons for the improved efficiency of TSS and ATSS over ordinary TS is that the variable allocation of the second stage effort assists in survey effort being directed to the higher-abundance PSU. In TSS, a fixed amount of extra effort is allocated to higher-abundance PSU. In ATSS, the amount of extra effort allocated to higher-abundance PSU is directly related to the actual PSU abundance. The marginal gain in efficiency of ATSS over TSS is because the design is more flexible and adaptable in how much extra effort can be directed to these higher-abundance PSU. Higher-abundance PSU are often associated with higher variance (higher standard deviation) for rare and clustered populations. Therefore, ATSS comes closer to the optimal allocation (Neyman 1934) than TSS when m = M.

The study gives some insight into how to design a two-stage sequential sample. The observed gain in relative efficiency of TSS and ATSS compared with TS was highest for designs where there was considerable additional second stage survey effort. For the same final sample size and same number of selected PSU, it was preferable to put less effort into the initial survey within each PSU and have more effort available for sequentially selecting additional units, compared with designs with large within-PSU initial sample sizes and few additional units. Of course, in a sequential survey, the total survey effort will not be known prior to sampling, but as a general rule, in designing a two-stage sequential sample (TSS or ATSS) one should aim for small initial sample size within the PSU and budget for allocation of additional effort.

Another design consideration is the choice of the condition. In this study, for the same final sample size, the higher threshold condition resulted in higher efficiency than the lower threshold. Again, given that the total survey effort will not be known prior to sampling the general rule should be to use a higher threshold rather than a lower threshold. Extremes in threshold should be avoided: a threshold of c ≥ 0 would result in every selected unit initiating selection of additional units, and c ≥ x where x was an excessively large number would mean there was no selection of additional units. These recommendations are consistent with advice for adaptive cluster sampling (e.g., Brown 2003; Smith et al. 2004).

In this study, ordinary two-stage sampling was never greater than 1.5 times more efficient than simple random sampling whereas this gain in efficiency was the average for the two-stage sequential designs. The sequential designs do introduce extra complexity in the survey method; in particular the size of the sample within each PSU is not defined prior to sampling, which makes planning of surveys difficult. However, to counterbalance this, the use of a sequential design, especially ATSS, will be more efficient.