Spatially Clustered Survey Designs

Abstract

Direct observation, through surveys, underpins nearly all aspects of environmental sciences. Survey design theory has evolved to make sure that sampling is as efficient as possible whilst remaining robust and fit-for-purpose. However, these methods frequently focus on theoretical aspects and often increase the logistical difficulty of performing the survey. Usually, the survey design process will place individual sampling locations one-by-one throughout the sampling area (e.g. random sampling). A consequence of these approaches is that there is usually a large cost in travel time between locations. This can be a huge problem for surveys that are large in spatial scale or are in inhospitable environments where travel is difficult and/or costly. Our solution is to constrain the sampling process so that the sample consists of spatially clustered observations, with all sites within a cluster lying within a predefined distance. The spatial clustering is achieved by a two-stage sampling process: first cluster centres are sampled and then sites within clusters are sampled. A novelty of our approach is that these clusters are allowed to overlap and we present the necessary calculations required to adjust the specified inclusion probabilities so that they are respected in the clustered sample. The process is illustrated with a real and on-going large-scale ecological survey. We also present simulation results to assess the methods performance. Spatially clustered survey design provides a formal statistical framework for grouping sample sites in space whilst maintaining multiple levels of spatial-balance. These designs reduce the logistical burden placed on field workers by decreasing total travel time and logistical overheads.Supplementary materials accompanying this paper appear on-line.

1 Introduction

In the environmental sciences, there is no substitute for direct field observations. Observations play a pivotal role in underpinning scientific inference and as a base for natural resource management decisions. To obtain field observations, scientists must physically visit locations where observations are made. This provides a logistical challenge: transporting people and equipment to where they are needed. When designing a field program, these logistical considerations need to be considered and be balanced with scientific and statistical considerations.

A fundamental statistical consideration for any field sampling task is that the samples provide information about the population of interest. Statistical practice shows that a method to ensure this link is to use random sampling of spatial locations (e.g. Thompson 2012; Smith et al. 2017; Tillé and Wilhelm 2017). However, naive random sampling of the designated survey area can be inefficient, as it can place too few samples in locations where the sampling variation is likely to be large (and too many where it is likely to be small) (e.g. Godambe and Joshi 1965; Thompson 2012). Placing more samples in areas where there is greater variation is achieved by sampling with uneven inclusion probabilities; sites that are likely to have high variance are assigned higher inclusion probabilities and site selection uses these assigned inclusion probabilities in the random sampling, e.g. Poisson sampling (see Thompson 2012). In the context of wildlife monitoring, this usually involves upweighting the inclusion probabilities where abundance could be high as variance typically increases with the mean (e.g. Taylor 1961). Additionally, random sampling—with or without uneven inclusion probabilities—can be made even more efficient if the sample locations are well spread throughout the space surveys (Stevens and Olsen 2004; Grafström et al. 2012; Robertson et al. 2013, 2017; Grafström et al. 2012) and should be beneficial to any survey design process.

However, neither random sampling nor spatially balanced sampling consider the extensive travel logistics that are sometimes inherent with fieldwork. Spatially balanced designs, by construction, implicitly aim to increase overall travel requirements by spreading the sampling locations. This necessitates a high logistical cost in obtaining the samples for the given design. One approach to reducing logistical overhead is to create a design that specifies a ‘cluster’ of sampling locations that are within a distance that is easily travelled. This allows field researchers to set up a base and perform multiple samples from that base. We note that spatially clustered designs are not a new idea, see Thompson (e.g. 2012, Chapter 12), Stehman and Selkowitz (2010) and Van Wilgenburg et al. (2020). All these approaches discretise space into non-overlapping regions and perform two-stage sampling of regions and then sites within each sampled region. In this work, we present an alternative method in which we: (1) allow for clustered designs that adhere to an arbitrarily defined inclusion probability map, (2) remove the unnecessary non-overlapping constraint and allow clusters to overlap so that clusters form non-disjoint spatial regions, (3) are scalable in both the number of clusters and the number of sites within each cluster, and (4) allow spatial balance between clusters and within clusters. Similar strategies, with technical differences and end goals, have been used before for sampling tools that are deployed simultaneously and/or capture multiple observations within one deployment (such as marine video recorders, or transect samples Langlois et al. 2020; Foster et al. 2020, respectively).

To illustrate the design problem, we use an example of surveying for koalas (Phascolarctos cinereus) throughout its entire range in eastern Australia (see Fig. 1); a study area of $\sim$2.3 million km$^2$. This is a vast area and without clustering, sample locations may be substantially separated from its nearest neighbour. These distances can mean that a large portion of valuable field time and human energy is devoted to travel, packing and unpacking. The end result of increased logistical effort is that less time is spent sampling, and ultimately less samples will be taken (or a greater budget needed).

Fig. 1

Inclusion probabilities for surveying koalas. The raster is a $\sim 250\times 250$ m grid. The western and northern extents were chosen to comfortably encompass the known distribution of koalas

In this work, we develop a method that will simultaneously produce spatial clusters of sampling sites whose inclusion probabilities conform to those specified. We propose to do this by developing a two-step sampling procedure: first sample clusters and then sample locations within clusters. A key concern is defining the inclusion probabilities in both steps so that the user-specified inclusion probabilities are respected. The methods are made available in the R-package MBHdesign (Foster 2021) and from the package’s github repository https://github.com/Scott-Foster/MBHdesign.

2 A Method to Cluster Samples

A fundamental part of the design process is specifying the the inclusion probabilities. These specify the probability that any cells within the raster grid is chosen in the sample. In this work, we assume that the inclusion probabilities are given, but we acknowledge that they should be the result of a well considered process with consultation of relevant experts. The specified inclusion probabilities are notated here as $\varvec{\pi }^{(s)}=(\pi _1^{(s)},\ldots ,\pi _N^{(s)})^\top$ where $\pi _i^{(s)}$ is the ith cell of a raster grid. The inclusion probabilities will usually be spatially smooth but they need not be. Also, the inclusion probabilities are scaled so that $\sum _{i=1}^N\pi _i^{(s)}=nm$, where n is the number of clusters and m is the number of sites within a cluster (constant for all clusters).

The design task tackled in this work is to sample n clusters of m sites so that the set of sites conforms to the specified inclusion probabilities ($\varvec{\pi }^{(s)}$). A cluster is defined as all cells that are within distance r of its central cell, and we note that individual cells will be within distance r of multiple cluster centres as the clusters are not disjoint. The clusters can be identified by their central cell as no two clusters will have the same central cell.

Our method for generating spatial clusters consists of two parts. The first step is to choose a set of n cells that will be cluster centres. The second step, conditional on already sampling the cluster centres, is to choose m cells within each cluster. This is similar to a standard two-stage sampling process (e.g. Thompson 2012; Van Wilgenburg et al. 2020) with the additional complexity of non-disjoint clusters.

For spatially clustered sampling we need further constructs calculated from the specified inclusion probabilities ($\varvec{\pi }^{(s)}$), which are now described and summarised in Table 1. These extra constructs are needed irrespective of the type of randomisation algorithm used. We highlight that individual cells can be chosen as a member of multiple clusters and this flexibility motivates the need for a set of working inclusion probabilities, labelled $\varvec{\pi }^{(w)}$. The working probabilities are interim probabilities and are necessary to ensure that each site is selected with the specified inclusion probabilities, regardless of cluster choice. The working inclusion probabilities can be quite different to the specified inclusion probabilities due to local unevenness of specified inclusion probabilities and edge effects, which occur when some clusters consist of more cells than others. These ideas parallel those in Foster et al. (2020), except that there are more severe constraints there. The technical details for calculating working inclusion probabilities from the specified inclusion probabilities are deferred to Sect. 2.1.

Table 1 Summary of the different types of inclusion probabilities and their nomenclature

For two-staged cluster sampling, we need to define the probability of choosing clusters. A natural definition is the sum of the working inclusion probabilities within its neighbourhood:

$$\begin{aligned} {\bar{\pi }}_i&\triangleq \sum _{i'\in {\mathcal {N}}(i)}\pi _{i'}^{(w)} \end{aligned}$$

(1)

where ${\mathcal {N}}(i)$ is the set of all raster cells within the cluster centred at location i (its neighbourhood). We call $\bar{\varvec{\pi }}$ the cluster inclusion probabilities (see Table 1). The first stage of sampling randomly chooses n of these clusters with probability $\bar{\varvec{\pi }}$. Whilst any randomisation could be used, including simple random sampling, we use the spatially balanced BAS algorithm (Robertson et al. 2013) with adjustment from Robertson et al. (2017).

Once a cluster has been chosen to be in the sample (the ith cluster say), the second stage of the sampling process is to choose m sites from ${\mathcal {N}}(i)$. This can be done by sampling with the conditional probabilities

$$\begin{aligned} \pi _{i'|i}^{(w)}&\triangleq \frac{\pi _{i'}^{(w)}}{{\bar{\pi }}_i} \end{aligned}$$

(2)

for any $i'\in {\mathcal {N}}(i)$. Once again we recommend spatially balanced sampling, but any randomisation could be used.

The final type of probability needed for two-stage cluster sampling are the observed inclusion probabilities. These are the inclusion probabilities that the process of sampling clusters and sites within clusters will produce. The working inclusion probabilities should be chosen so that the observed inclusion probabilities equal the specified inclusion probabilities. The probability of sampling grid cell i from any one of the overlapping clusters that i is a member of is

$$\begin{aligned} \pi _i^{(o)}&=\sum _{i'\in {\mathcal {N}}(i)}{\bar{\pi }}_{i'}\left( 1-\left( 1-\frac{\pi _i^{(w)}}{{\bar{\pi }}_{i'}}\right) ^m\right) . \end{aligned}$$

(3)

With these observed inclusion probabilities, the two-stage sampling process can be seen to possess some desirable features. Firstly, when $m=1$ the observed inclusion probabilities are a known multiple of the working probabilities $\pi _i^{(o)}=\left| {\mathcal {N}}(i)\right| \pi _i^{(w)}$, which means that cluster sampling reduces to non-clustered sampling but with edges adjusted for. Secondly, when the cluster radius r is very small (so that ${\mathcal {N}}(i)$ is a single cell), the clustered sampling approach again reduces to its non-clustered counterpart.

2.1 Calculating Working Inclusion Probabilities

The working inclusion probabilities are dependent upon the specified inclusion probabilities and the geometry of the sampling area (see Table 1 for a summary of the types of inclusion probabilities). The working inclusion probabilities, $\pi _i^{(w)}$, should be chosen so that the observed inclusion probabilities, $\pi _i^{(o)}$, equal (or approximate closely) the specified inclusion probabilities. However, the observed inclusion probabilities are a nonlinear function of the working probabilities, and direct algebraic manipulation will not yield a simple expression for the working probabilities in terms of the specified probabilities. Here, we propose a numerical method which iteratively linearises and then solves a simplified set of equations. The algorithm proceeds by:

• 1. Calculate starting values for $\pi _i^{(w)}$. We have found that $\nicefrac {\pi _i^{(s)}}{m\left| {\mathcal {N}}(i)\right| }$ is a useful starting value. This is formed by using the approximation $(1-\nicefrac {\pi _i^{(w)}}{{\bar{\pi }}_{i'}})^m\approx 1-m\nicefrac {\pi _i^{(w)}}{{\bar{\pi }}_{i'}}$ in (3).

• 2. We aim to minimise the difference between the observed and specified inclusion probabilities and define an objective function $Q(\pi _i^{(w)})\triangleq \left( \pi _i^{(o)} - \pi _i^{(s)}\right) ^2$. We note that the minimum of $Q(\pi _i^{(w)})$ may be a small value that is larger than zero due to particular local properties of the specified inclusion probabilities (e.g. irregular boundaries and non-smooth inclusion probabilities). The objective function is minimised iteratively using Newton–Raphson updates of the form

  $$\begin{aligned} {\pi _{i}^{(w)*}}&=\pi _i^{(w)}-\alpha \frac{Q\left( \pi _i^{(w)}\right) }{Q'\left( \pi _i^{(w)}\right) }, \end{aligned}$$

  where $Q'(\pi _i^{(w)})$ is the derivative of $Q(\pi _i^{(w)})$ with respect to $\pi _i^{(w)}$ only and $\alpha \in (0,1]$ is a dampening factor to avoid potentially large and erroneous steps. We choose $\alpha =1-\exp (-k/5)$ so as to progressively be less restrictive as the iterative process progresses through iterations (k). To avoid the complexities of co-dependence between $\pi _i^{(w)}$ and $\pi _{i'}^{(w)}$ ($i\ne i'$), we consider $\pi _i^{(o)}$ and subsequently $Q(\pi _i^{(w)})$ as though it is only a function of $\pi _i^{(w)}$ within each iteration. This means that ${\bar{\pi }}_i$ is considered a function of only $\pi _i^{(w)}$. The local sum, ${\bar{\pi }}_i$, is updated only as a consequence of updating the full set of $\pi _i^{(w)}$. This approach simplifies computation substantially as each $\pi _i^{(w)}$ can be updated sequentially. With this approach the derivative is $Q'(\pi _i^{(w)})=2\left( \pi _i^{(o)} - \pi _i^{(s)}\right) \sum _{i'\in {\mathcal {N}}(i)}\left( 1+(m-1)\left( 1-\nicefrac {\pi _i^{(w)}}{{\bar{\pi }}_i}\right) ^m\right)$.

• 3. After calculating the updates for each iteration, they are assessed to see if $Q(\pi _i^{(w)})$ improves. The update is not taken for any raster cells where improvement is not made. The updates are also checked to ensure that the updated working probabilities are within [0, 1]. Any that are not are arbitrarily moved towards the offending boundary by 10% of the distance to that boundary. It is our experience that this safe-guard is rarely needed.

• 4. The iterative process continues until convergence to a pre-specified tolerance. We use the criterion that $f\left( |\pi _i^{(o)} - \pi _i^{(s)}|\right) <\epsilon$ where $f(\cdot )$ is the 99.9th percentile of the cell-wise values, and $\epsilon$ is defined to be 0.01% of the median (nonzero) specified inclusion probability $\pi _i^{(s)}$. We acknowledge that this convergence criterion allows the possibility that the occasional working inclusion probability is outside the tolerance by an unknown amount. This is allowed as some patterns in the specified inclusion probability surface cannot be completely accommodated, for example situations where a single cell with nonzero inclusion probability is far removed from other nonzero cells.

2.2 Design-Based Estimators

Data that arise from the implementation of a spatially clustered designs can be analysed using either model-based or design-based analyses. Model-based estimation is flexible and the exact form will depend on the research goals and the particular attributes of the data. For design-based estimation of a population mean from a design with a single stage of randomisation, the Horvitz-Thompson (HT) estimator is well known and unbiased (Horvitz and Thompson 1952; Thompson 2012). For two-stage designs, like our proposal, the extension of the HT estimator is the same as that for the sites, ignoring the clusters. This is due to the construction that each cell is chosen with the specified inclusion probabilities. We recommend that the HT estimator is calculated using the observed inclusion probabilities, as calculated in (3), rather than the specified inclusion probabilities. This is solely because there might be some very minor discrepancies when the working inclusion probabilities are calculated. In practice, we expect there to be no, or very little, observable difference from this choice.

Variance for estimators from a spatially clustered design is likely be higher than the corresponding non-clustered design, due to the extra level of randomisation. Variance of an estimate for a single-stage spatially balanced design can be performed using a nearest neighbour variance estimate (Stevens and Olsen 2003). We envisage that this estimator may be appropriate for spatially clustered designs too, but note that the nearest neighbours will usually be in the same cluster. Hence, it may only represent within cluster variance and not the between-cluster variance.

3 Example: Survey Design for Koalas

The koala (Phascolarctos cinereus) is an iconic Australian marsupial. It feeds on the foliage of predominantly eucalypt trees. As such, it is strongly associated with particular habitats and the koala’s success is likely to fluctuate with the fates of these habitats. The species is divided into two distinct populations for conservation and management purposes, split at the border of New South Wales and Victoria. The northern population was recently up-listed to endangered as a result of ongoing pressures across their range (Threatened Species Scientific Committee 2021), including the acute affects of the devastating 2019–2020 ‘Black Summer’ bushfires. Despite this endangered status, understanding of national koala populations is limited due to their wide distribution, remote locations and the difficulty in spotting individual koalas. This presents a challenge for policy makers and natural resource managers as decisions must be made without access to consistent and broad-scale data on population status and trends for the species. To address this, the Australian Government has funded a national scale monitoring program which is currently being implemented. The entire distribution of the species is to be surveyed, including the listed northern and unlisted southern populations. The sampling area was chosen to cover the known range of the koala.

The design process starts with defining the specified inclusion probabilities for drawing the sampling locations ($\pi _i^{(s)}$, see Table 1). For this survey, the inclusion probabilities were specified by first identifying a small number of environmental covariates that are thought to produce substantial variation in koala abundance. The covariates, identified in an expert workshop, were: presence of feed trees, soil moisture and maximum summer temperature. Briefly, koalas are strongly dependent on feed trees for habitat and food, prefer sites that are not too dry and are not very hot. These locations are mostly located in the south and east of the study area. When combined, these covariates generate the set of inclusion probabilities in Fig. 1 and are defined over a 250 m raster grid. These probabilities are uneven, with: $\sim$34 million cells within the sampling area, $\sim$15 million cells with a nonzero inclusion probability, the smallest nonzero probability is $\sim 2.75\times 10^{-14}$, the largest is $\sim 2.63\times 10^{-4}$, and the median nonzero inclusion probability is $\sim 1.43\times 10^{-4}$. Whilst there is definite spatial patterning in the inclusion probabilities, due to the general spatial smoothness of the covariates, there are also some abrupt spatial changes, due to a number of reasons: natural geographical features (e.g. mountain ranges, peninsulas and islands) and anthropogenic usage.

To generate the clustered survey design ($m=10$, $n=200$ and $r=21$km), the working inclusion probabilities must first be calculated ($\pi _i^{(w)}$, see Table 1). This is performed using the methods described in Sect. 2.1 and the various types of inclusion probabilities are presented in Figs. 1 and 2. The observed inclusion probabilities, Fig. 2a match the specified inclusion probabilities well (Fig. 1), as the direct comparison in Figs. 3a, b show—agreement is within <0.01% of the specified inclusion probabilities for almost all cells.

Fig. 2

a Observed $\pi _i^{(o)}$, b working $\pi _i^{(w)}$ and c cluster ${\bar{\pi }}_i$ inclusion probabilities for the koala survey design. See Sect. 2.1 for details about how these probabilities are calculated and Table 1 for a summary of the types of inclusion probabilities

In spite of this general excellent agreement between specified and observed inclusion probabilities (Fig. 3, there remains some patterning to the disagreement). We stress that this patterning is on a much smaller scale than most of the inclusion probabilities (maximum of just $\sim$0.015% of specified inclusion probabilities). However, there is spatial patterning, with areas of high variability in $\varvec{\pi }^{(s)}$ corresponding to higher relative error (observed probabilities higher than specified), see Fig. 3a. This is often seen in areas that border onto zero inclusion probability.

Fig. 3

Comparison of specified and observed inclusion probabilities for the koala design. a Spatial map of per cent relative error ($100(\pi _i^{(o)}-\pi _i^{(s)}) / \pi _i^{(s)}$). Note that the colour scale has been truncated at ±99.9% of the nonzero relative errors. b distribution of per cent relative error

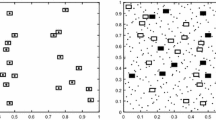
The design is presented in Fig. 4a. It exhibits all the attributes that have been specified. Notably, that the sample locations are grouped together in clusters with a known maximum radius. A closer inspection of an area shows that the sites follow the inclusion probabilities, at least as far as most of the sites are located within cells with high inclusion probability, but a few are located where there is low inclusion probability, see Fig. 4b.

Fig. 4

An example of a spatially balanced clustered design for Koalas. a The first 100 clusters (of $n=200$) of $m=10$ sites throughout the entire study area. The black points are the sampling sites and the red box is the boundary of an arbitrarily chosen example area. b The example area with heterogeneous inclusion probabilities. In both plots, the underlying spatial layer is the inclusion probabilities from Fig. 1

4 Simulation

To check that the design process performs the task specified, a simulation study was undertaken. This study consisted of generating $B=10$ million designs, each with $n=20$ clusters of $m=10$ sites and of $r=21$km radius. The specified inclusion probabilities are taken from the national koala survey (Fig. 1), but have been aggregated to a 1 km grid and we only consider the state of Victoria (see Fig. 5). The reason for subsetting and coarsening the survey area is purely computational – it would take too long to generate sufficient designs for the entire region. Further, Victoria is expected to be challenging as it has an irregular coastline and the inclusion probabilities are very uneven and patchy. An empirical version of the observed inclusion probabilities is obtained by calculating the proportion of designs in which each cell is included in the survey design.

The results of the simulation study are presented in Fig. 5. If the design method is working well, the empirical estimate of the observed inclusion probability should match the specified inclusion probabilities. For this match to occur, the calculation of the working inclusion probabilities has to have been successful and that the sampling process respects these probabilities needs to have been successful. From Fig. 5, it is clear that there is general agreement between the empirical observed probabilities and the specified inclusion probabilities. However, there are departures, Fig. 5c, with the departures being distributed around perfect agreement. The departures could be due to a number of sources, such as:

• 1. Simulation error will contribute to all discrepancies and we think the most likely source of all error. Given the number of cells in the map and the low inclusion probabilities, it is very difficult to estimate each and every cell with enough frequency to reduce error. We note that the pattern of variation is consistent with multinomial sampling—increasing variance with specified inclusion probability. We also note that the spatially clustered designs have less variation than BAS and two-stage designs, whilst more than SRS (same simulation setup, Fig. A.1).

• 2. Non-exact match between the specified and observed probabilities, as calculated using the methods in Sect. 2.1. It is expected that this source of variation is small (Fig. 3).

• 3. Local features/pathologies in the inclusion probability surface that make spatially balanced sampling difficult. For example, one cell of high inclusion probability in a cluster of very low (or zero) inclusion probability cells.

• 4. Mismatch between drawing from a discrete grid rather than a continuous field (BAS Robertson et al. 2013, was designed originally for continuums).

• 5. Deficiencies in the BAS method (Robertson et al. 2013), even after the adjustment from Robertson et al. (2017).

Fig. 5

Results of simulation study over $B=10$ million designs. a Specified inclusion probabilities for Victoria, b The corresponding empirical observed inclusion probabilities from the simulation study. c Empirical observed versus specified inclusion probabilities. If the two sets agree, then all points will lay on the $y=x$ line (red)

To compare the performance of the spatially clustered designs to other approaches, we also generated 10,000 designs of each of: (1) simple random sampling without replacement (SRS), (2) BAS, and (3) a two-stage approach (similar to Stehman and Selkowitz 2010; Thompson 2012; Van Wilgenburg et al. 2020). The two-stage sample was performed by first randomly sampling n disjoint clusters without replacement, using the inclusion probability defined as the sum of its member cells. Cells were then randomly chosen without replacement based on their specified inclusion probabilities within each cluster. For choosing clusters, the aggregated inclusion probabilities were scaled to sum to n, and for choosing cells within each chosen cluster, the inclusion probabilities were scaled to sum to m. For each design type, we calculated: (1) the Horvitz-Thompson (HT) estimate of population total (labelled ${\hat{\mu }}_T$, Horvitz and Thompson 1952), (2) the local-neighbour variance estimate (labelled ${\hat{\sigma }}_{nn}$Stevens and Olsen 2003), and (3) a measure of spatial balance, based on Voronoi polygons (labelled $\zeta$, Stevens and Olsen 2004). The surface that the designs are sampling is a log-linear function of the inclusion probabilities and spatially coloured random noise.

The simulation study suggests that the HT estimators for all design types agree (Table 2), to within measured uncertainty. The HT estimates’ standard deviations show that BAS is the most precise design type, followed by SRS and the spatially clustered, and with the two-stage design relatively imprecise. The nearest neighbour variance estimate underestimated true variation for all designs, but particularly so for the spatially clustered approach. It appears that it essentially measured within cluster variation only, which is expected as it was not designed for non-clustered surveys.

The spatial balance is best for the single-staged BAS design, which was followed by the SRS design. The spatially clustered design is more evenly spread than the two-staged SRS approach, but both are much less well spread than the single-staged approaches. This is not surprising and is desirable given the motivation for these design types.

5 Summary and Discussion

In this work, we have introduced a method that produces spatially clustered survey designs. These designs can ease the logistical burden introduced by spatially balanced designs over larger areas. The method succeeds in this by allowing for arbitrarily specified inclusion probability layers, which is enabled by having potentially overlapping clusters. This sets the spatial clustering process apart from previous clustered sampling methods that first discretise space into disjoint areas and then perform standard two-stage sampling.

The design method, described in Sect. 2, was illustrated by generating a design for koalas throughout its entire distribution, Sect. 3. This illustration showed the process of calculating working inclusion probabilities ($\pi _i^{(w)}$), from which the cluster inclusion probabilities (${\bar{\pi }}_i$) were calculated. See Table 1 for a description of the different sets of inclusion probabilities. The design is then a two-step randomisation using spatially balanced methods (Robertson et al. 2013) at each step. The accuracy of the process was assessed using simulation (Sect. 4), where it was shown that there is agreement between the empirical and specified inclusion probabilities. The simulation also showed the cost in statistical efficiency in clustering: clustered designs are less efficient than single-stage designs.

Table 2 Summary of the simulation study using different design types for HT estimate of the sum (${\hat{\mu }}_T$), the local variance estimate (presented as its square root, standard deviation ${\hat{\sigma }}_{nn}$) and the spatial balance metric ($\zeta$)

The clustered designs are more computationally demanding than their non-clustered counterparts. Most of this computational cost comes from calculating the working inclusion probabilities. For the designs in the simulation study, Sect. 4, the calculation of the working inclusion probabilities ($\sim 1$ km grid) took just over 1 min on a laptop with 8 cores, 32Gb RAM and a clock speed of 3GHz. On the same machine, a clustered design then took just over half a second. The design for the national koala survey is a much more demanding task, which we performed on a computer cluster with 64 cores and 256Gb of memory. That task took approximately a day and a half to perform. Overall, the computational requirements will increase with: (1) the resolution of the inclusion probability raster, (2) the complexity/irregularity of the study area, (3) the unevenness of the inclusion probabilities, (4) the radius of the clusters, and lastly (5) the size of the design (n and m). Our experience has shown that the size of the raster grid, especially in relation to the cluster radius (r) are the biggest factors in determining computation time.

The clustered design approaches a non-clustered design when one of the conditions are met: $m\rightarrow 1$, $r\rightarrow |A|$ and/or $r\rightarrow 0$, where A is the sampling area. In the first case, the working inclusion probabilities reduce to be identical to the specified inclusion probabilities. In the second case, each of the spatial domains for each of the n clusters overlap and so the design is the same as combining a number of spatially balanced designs of the same region. When $n=2$, this is similar, but not identical, to the approach for extending a survey studied in van Dam-Bates et al. (2018), who showed via simulation that spatial-balance was compromised but still superior to random sampling. When the clusters become very small ($r\rightarrow 0$), the clustered design reduces to repeated sampling of an unclustered design. Whilst these cases are the limits of the design space, they are reassuring in that they provide evidence that the proposed designs are embedded within standard and well-used methods.

These clustered designs are superior, when they are needed, as they enable more data to be collected using a given set of resources. However, we warn against utilising these designs for all situations. In particular, when the cluster radius r is small compared to the dependence in the observations, then there will be a reduction in the total information available. In a model-based analysis, this is exhibited by the necessity to allow for non-independent errors that are possibly/probably spatially structured. We stress that any model-based design, with uneven inclusion probabilities, should include terms to account for the design process (e.g Gelman et al. 2013). Typically these terms will either be the covariates that contribute to the inclusion probabilities, or the inclusion probabilities themselves. With such a model, the design is conditionally ignorable (e.g. Gelman et al. 2013), meaning that inferences are not dependent on the design itself.

Whilst we have outlined some possibilities for performing a design-based analysis (Sect. 2.2), our preference is for performing a model-based analysis. Such an analysis allows for a more nuanced understanding of the processes leading to the estimate, such as a distribution map or an understanding of relationships with environmental gradients, which can be valuable (Dumelle et al. 2022), even more valuable than the overall estimate itself. Also, model-based analyses can have smaller estimates of uncertainty (Dumelle et al. 2022) implying that they make the most efficient use of the data, but do so with extra assumptions about the processes underlying the data and their collection. Of particular interest is that spatially clustered designs share beneficial attributes with good designs for model-based estimates, such as a good spread of points but with a number of points in close proximity (Zimmerman 2006). We note that design-based surveys automatically avoid many common issues with model-based design (Williams and Brown 2019), such as ignorability (e.g. Gelman et al. 2013), or at least the design-based randomisation process informs how the design is conditionally ignorable—just add the inclusion probabilities as a covariate in the model. Further, the randomisation approach allows for easy re-use of the data, which makes data collections more powerful into the years and decades to come (Foster et al. 2021).

In a similar fashion to other spatially balanced designs, the clustered design can also be used to produce an ‘master-sample’ of clusters and sites (Larsen et al. 2008; van Dam-Bates et al. 2018). The extra clusters in the master-sample can be used if clusters of the original sample are not available to be sampled, or if the survey is to be extended in the future. However, the extra sites (within a cluster) should only be utilised if individual sites are not available for sampling. The reason for this is that the working probabilities, in (1), are dependent on m, which should therefore remain constant if the specified inclusion probabilities are to be obtained. To create a clustered master-sample one must simply sample more clusters and sites within clusters. Care should be taken though, that the working inclusion probabilities are calculated using the number of samples per cluster (m) that is planned and not the number of sites in each cluster’s master-sample. For the koala example, we generated a master-sample for each cluster of $20>m=10$ sites.