Uncertainty from sampling, in the context of fitness for purpose

Abstract

Sampling is an integral part of nearly all chemical measurement and often makes a substantial or even a dominant contribution to the uncertainty of the measurement result. In contrast with analysis, however, the uncertainty contribution from sampling has usually been ignored. Indeed, far less is known about sampling uncertainty, although in some application sectors it is known to exceed the analytical uncertainty, especially when raw materials (natural or industrial) are under test. In 1995 the authors of this paper proposed a framework of concepts and procedures for studying, quantifying, and controlling the uncertainty arising from the sampling that normally precedes analysis. Many of the ideas were based on analogy with well-established procedures and considerations relating to quality of analytical measurement, ideas such as validation of the sampling protocol, sampling quality control and fitness for purpose. Since that time many of these ideas have been explored experimentally and found to be effective. This paper is a summary of progress to date.

The context of sampling uncertainty

Chemical analysis is nearly always preceded by sampling. We extract a small amount of material (the sample) to determine the composition of a much larger body (the target). This sample should ideally have exactly the same composition as the target, but never does. The discrepancy gives rise to uncertainty from sampling. It is axiomatic that the end-user of analytical results needs to know the uncertainty in the estimated composition of the target to make an informed decision. The only appropriate uncertainty for this purpose is the combined uncertainty from sampling and analysis [1–4]. It is also clear that the level of this combined uncertainty has financial implications for the end-user. The proper context of uncertainty from sampling is therefore fitness for purpose, defined by the level of uncertainty in the result of the analysis that best suits the application.

In most sectors requiring chemical analysis, protocols for sampling have been carefully developed and documented. These protocols are regarded as best practice, and therefore thought to be fit for purpose. Until recently, and in most application sectors, the uncertainty from sampling has been ignored. Sampling protocols are seldom validated in a manner comparable with analytical methods. The end-users, to their detriment, have no information on sampling uncertainty and therefore no means of estimating the combined uncertainty of measurement. Applied geochemical analysis has been exceptional in this regard. In that application sector the interactions between the uncertainties of sampling and analysis, numbers of samples taken and, at least informally, consequence costs have been taken into account since the 1960s (see, for example, Garrett [5, 6]). This sector-specific awareness was subsequently developed into a general conceptual framework and tool-kit for handling sampling uncertainty, applicable to most sectors requiring chemical measurement [7].

Let us consider an example, the determination of nitrate in lettuce. The grower and distributor need to decide whether the crop is fit to eat, by ensuring that the concentration of nitrate does not exceed the recommended maximum level. The decision, based on the result (and its uncertainty) of a measurement involving sampling and analysis, is made according to the agreed procedure illustrated in Fig. 1. An incorrect estimation of the uncertainty of the result could give rise to an incorrect decision, for example, to reject a crop that was acceptable for consumption or to distribute a crop that was unfit. Both of these incorrect decisions have adverse financial or social implications, called “consequence costs”.

Fig. 1

Schematic interpretation of results against an upper rejection limit. A and C show results with analytical uncertainty alone; B and D show combined uncertainty (analytical plus sampling uncertainty), which demands a different interpretation

There is a protocol for taking a sample from a field of lettuce [8], and following this gives rise to an uncertainty u _sam . There is also a recommended procedure for the analysis of the sample and this gives rise to the uncertainty of analysis, u _an . The result has a combined standard uncertainty of $u = {\sqrt {u^{2}_{{sam}} + u^{2}_{{an}} } },$ which applies to the result that the customer uses to make a decision. Clearly it is the value of u rather than u _an that should be taken into account in making the decision of whether to accept or reject the crop. In this particular example, u _sam is often large enough to provide an important, or even the dominant, contribution to u, so it cannot safely be ignored in the decision-making process. In a study of this lettuce problem [9], for a mean nitrate level of 3,150 ppm, the experimenters found values of u _sam  = 319 and u _an  = 168 ppm (“ppm” indicates a mass fraction × 10⁶). The combined standard uncertainty estimate (assuming no bias) is therefore 361 ppm for the recommended procedures, clearly dominated by sampling variation.

We also need to achieve the best division of resources between sampling and analysis. The value of u, for a fixed total expenditure, is minimized when u _sam  ≈ u _an , unless the costs of sampling and analysis differ greatly. For example, if u _sam  = 3u _an , a more cost-efficient outcome would nearly always be obtained if more were spent on sampling and less on analysis. In the lettuce example, the implication is that the sampling variance should be reduced as in this case fitness for purpose requires a lower combined uncertainty.

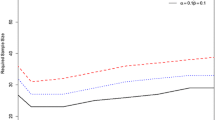
So what exactly is fitness for purpose? Decision theory [10] can supply the answer to this question. We see that the proportion of incorrect decisions, and therefore the long-term average of the consequence costs, increases with an increasing uncertainty of the result. A naïve consideration suggests that analysts should aim for the smallest possible uncertainty, and that is what they have done traditionally. However, the cost of analysis is inversely related to the uncertainty: reducing the uncertainty demands rapidly escalating costs. At some point there must be a minimum expectation of total (measurement plus consequence) cost (Fig. 2), and that provides a rational definition of the uncertainty that is fit for purpose [11, 12]. In the lettuce study the expectation of loss using the recommended protocols was £874. A minimum expectation of £395 was predicted to occur when the combined standard uncertainty was 184 ppm (Fig. 3). In a subsequent experiment, this level of uncertainty was closely approached by reducing the sampling variance by taking a greater number of increments (40 rather than 10 heads of lettuce).

Fig. 2

Schematic expectation of loss (cost) as a function of uncertainty, showing the minimal loss at fit-for-purpose uncertainty u _f . A Cost of measurement. B Expectation of cost of incorrect decisions. C Total expectation of loss

Fig. 3

Expectation of loss versus uncertainty for the lettuce study, showing the experimental point (filled circle), the estimated function (multiplication symbol), and the optimal condition defining fitness for purpose (open circle)

The concepts of uncertainty from sampling

To a large extent, ideas about sampling uncertainty are analogous with those relating to analytical uncertainty. We can consider the existence of sampling bias and sampling precision by extending familiar definitions. It is also convenient to distinguish between rational and empirical sampling protocols. We can extend the idea of precision by defining, in an obvious way, repeatability and reproducibility conditions for replicated sampling. We can entertain the possibilities of utilising, in sampling practice, the analogues of method validation, internal quality control, proficiency tests, collaborative trials, and reference materials [7]. All of these ideas have been explored with at least some success. However, we must recognize the existence of three important differences from analytical practice. The first such arises because of heterogeneity of the target.

When we speak of analytical uncertainty, we are thinking in terms of the combination of a specific method and a specific type of material presented in a controlled state, for example a finely ground powder. There may be some residual heterogeneity in the prepared sample but its contribution to the combined uncertainty will usually be negligible. For a given concentration of the analyte we can reasonably expect the same analytical uncertainty to be applicable to every measurement result. This is not necessarily the case with sampling: in many instances the greater part of uncertainty from sampling is derived from the heterogeneity of the target material and the degree of heterogeneity may vary from target to target and will be outside the control of the sampler.

The implications are manifold. First, when we speak of the validation of the sampling protocol, the uncertainty estimate can refer to ‘typical’ targets only, that is, an estimate protected against the statistical influence of unusually heterogeneous targets. In this context a judicious use of robust analysis of variance [13, 14] can be valuable. Second, internal quality control needs to be carried out in order to detect the occurrence of such atypically heterogeneous targets and, if possible, adjust the estimate of combined uncertainty accordingly. Third, we must be aware that when a sampling protocol thus validated is used on an atypical target, the measurement result may not be fit for purpose (in the decision theory sense), even though the sampling has been carried out strictly according to the sampling protocol.

The second difference between concepts common to sampling and analysis is that the status of bias is disputed in sampling. Gy and his followers [15, 16] contend that sampling bias is nonexistent—if the sampling is carried out ‘correctly’ (that is, according to the protocol) there is no bias. This conceptual position regards all sampling protocols as analogous to empirical analytical methods, where the method defines both the analyte and the measurand. This position has a convenient corollary: no bias contribution to sampling uncertainty needs to be estimated. However, it is easy to see a number of ways in which sampling bias can arise, for example misapplication of the protocol, failing to recognize the boundaries of the target, contamination of the sample, etcetera and, in principle these potential biases should be investigated. Unfortunately, the estimation of sampling bias may present considerable practical difficulties, so its contribution to uncertainty from sampling is often inaccessible and deliberately ignored. In practice, however, even an incomplete estimate of sampling uncertainty (that is, based only on accessible precision estimates) is better than no estimate.

A third difference between sampling and analysis needs to be mentioned here. Sampling variation can be studied only by making analytical measurements. This complication has to be circumvented by carefully designed experiment.

Randomisation

In studies of sampling uncertainty, randomisation (or an effective approximation to it) is of paramount importance. To define a random sample, if we divide the target conceptually into a large number of compartments of equal mass, each compartment must have an equal chance of being selected to contribute to the sample. An important property of randomization is that only a random sample is guaranteed to be unbiased. This means that the mean composition of a large number n of samples will tend towards the composition of the target as n increases. It is also possible (but not guaranteed) for samples collected on a systematic basis to be unbiased, for example where the increments of a composite sample are taken at the intersections of a rectangular grid. Bias could arise in that situation when there is a ‘hotspot’ of high analyte concentration that does not fall on any grid intersection, because of its size, shape or orientation.

Full randomization would often be impracticably costly, so systematic schemes are often used instead. It is a matter of professional judgement or experience whether this compromise is satisfactory. Of course, there may be situations in which part of the target is completely inaccessible to sampling, for example, peanuts at the bottom of a hold of a ship. Strictly speaking, no inference about the average composition of the shipment can be made without the extra assumption that the accessible part of the target is representative of the whole.

Randomisation is also important in the study of sampling precision. To obtain a valid estimate of the variance of sampling, the protocol has to be replicated in a randomized fashion, otherwise there is a strong likelihood of underestimating the variance. Methods for randomizing the application of a protocol to the target must vary with the nature of the target—here we must rely on the ingenuity of the sampler. Some suggestions are shown in Figs. 4, 5, and 6. When sampling lettuce from a field by collecting specimens at several points along the legs of a ‘W’-shaped walk, a suitable duplicate could be taken by performing a walk along a second ‘W’ with a randomly different orientation (Fig. 4). When sampling the topsoil of a field conceptually divided into ‘strata’ (Fig. 5) two increments could be taken from each stratum at random positions and used to prepare duplicate composite samples. When sampling from a conveyor belt, increments could be taken from the belt at times indicated by two independent series of random numbers to be combined to give the duplicate composite samples (Fig. 6).

Fig. 4

A field sampled twice with increments taken on a W-shaped walk, showing how the protocol might be randomly repeated

Fig. 5

A field divided into strata, with duplicate increments taken at random in each stratum

Fig. 6

Duplicated samples taken at random from a conveyor belt

Sampling bias

Sampling bias is conceptually the difference between the composition of the target and the mean composition of a large number of samples. The problem, familiar from its analogue in analysis, resides in independently determining the average composition of the target [17]. The analytical analogues of the tools available are (a) the reference material and (b) the reference method. Reference materials can be produced by mixing pure constituents, but are more usually certified after analysis of a test material by a reference method such as IDMS, or from the consensus of a certification trial among expert laboratories.

In sampling, experimental reference targets have been made by mixing [18]. The main problems are those of long-term stability and the cost of maintaining a necessarily very large mass of material. The reference target would have to be large enough to ensure that a large number of successive sampling events could not materially affect the composition or appearance of the target. This raises the awkward fact that, to be useful, the target would need to be ‘typical’, but a target much larger than normal may not be typical. These problems are formidable and, in many instances, prohibitive.

The alternative approach, the reference sampling method, requires neither long-term stability nor unduly large targets, and is thus widely applicable. Moreover, it can be readily applied to a succession of targets so as to obtain a typical outcome. Simply, the reference sampling protocol is applied once to a target, followed by the protocol under validation, giving rise to a pair of analytical results. The procedure is applied to a sequence of typical targets, and the mean difference between corresponding pairs of results, if significantly different from zero, is an estimate of the bias. If the successive targets have a wide range of analyte concentrations, the bias could be alternatively considered as a function of concentration (Fig. 7). In principle, some of the bias could stem from the technique of a particular sampler, so ideally we would like to use the mean result of a number of samplers each using the reference and candidate methods. Indeed, significant between-sampler variation has been reported under some conditions (as shown in the section on sampling collaborative trials). However, this refinement is unlikely to be widely practicable. We should note also that implicit in this approach is the availability of a plausibly unbiased reference method, which may or may not be realistic. The ‘paired sample’ method has been applied to sampling topsoil in public gardens for the measurement of toxic metals [19].

Fig. 7

Two possible outcomes of a paired-sampling test for sampling bias, showing experimental data (points), estimated relationship (solid line) and hypothetical line of zero bias (dashed line). a A translational (constant) bias. b A rotational (proportional) bias. (Other outcomes are possible.)

The contribution of potential sampling bias to measurement uncertainty can also be incorporated by the use of inter-organisational sampling trials, as will be discussed in the section covering sampling precision.

Sampling precision

The most complete information about the precision of a sampling protocol can be obtained from the sampling collaborative trial (CTS). By analogy with the analytical collaborative trial (more strictly, the ‘interlaboratory method performance study’) the CTS should involve: (a) a number (n ≥ 8) of experienced samplers (b) a number (m ≥ 5) of typical targets, preferably with an appropriate range of analyte concentrations. However, it is preferable for the number of targets to exceed the minimum five by a substantial margin, to allow for a proportion of atypical targets. The nested design is shown in Fig. 8. Because of the special circumstances of sampling, the samplers have to be supervised to some extent to ensure that the repeat samples are extracted in a random fashion. In addition, the best estimates of sampling precision are obtained if the analysis is carried out under repeatability conditions with suitably high analytical precision.

Fig. 8

Design of a sampling collaborative trial (only one target shown)

The mean squares found by hierarchical analysis of variance are: (a) between-sampler; (b) within-sampler/between-sample; and (c) between-analysis. Tests for a variance ratio significantly greater than unity can then be applied and standard deviations of sampling repeatability $\hat{\sigma }_{{rS}}$ and, where justified, sampling reproducibility $\hat{\sigma }_{{RS}}$ can be calculated. A few CTSs have now been carried out on an experimental basis (for trace elements in soil [20–22], various analytes in wheat and raw coffee beans [23]). In some instances a significant between-sampler effect has been found. This shows that caution must be used in equating sampling uncertainty with repeatability (single-sampler) precision in circumstances where sampler bias is perforce assumed to be negligible.

Example: Nickel in raw coffee beans

Duplicate samples from a shipment of about 11 ton in 185 sacks were collected by eight samplers. For each sample, five of the sacks were selected at random and a 100-g increment taken in accordance with established practice. The increments were combined and powdered to form the laboratory sample. The duplicated results are shown in Table 1 and Fig. 9. The nested analysis of variance (Table 2) shows a significant variation between samples but not between samplers. The estimated precisions are quantified by the standard deviations $\hat{\sigma }_{{sam}} {\left( { = \hat{\sigma }_{{rS}} } \right)} = 0.51$ and $\hat{\sigma }_{{an}} = 0.51.$

Table 1 Results (ppm = mass fraction × 10⁶) of the duplicate analysis of duplicate samples of coffee beans collected by eight samplers

Fig. 9

Results from a sampling collaborative trial for the determination of nickel in a shipment of coffee

Table 2 Hierarchical analysis of variance: (a) between samplers; (b) between samples/within sampler; (c) between results/within samples, applied to the data in Table 1

Sampling collaborative trials are expensive and logistically difficult to carry out: the samplers have to travel to the targets, and each one has to perform duplicate sampling in an overall random fashion. Proprietors of the targets are often unwilling to allow the disruption and delay incurred. In some instances sampling precision is regarded as proprietary information unsuitable for publication. CTSs are therefore currently unlikely to be used apart from purposes of research. However, it is evident that a body of statistics from a wider range of such studies would be an invaluable asset for the analytical community. As yet the evidence is completely inadequate to demonstrate whether generalizations, comparable with Horwitz’s [24] in the analytical field, might be applicable to sampling precision.¹ It would be very useful to know whether σ _RS or $\sigma _{{RS}} /c$ generally showed a tendency to be dependent on the concentration c of the analyte or the test material, and whether the ratio $\hat{\sigma }_{{rS}} /\hat{\sigma }_{{RS}}$ was predictable and independent of analyte, test material, and method.

Validation within a single organization

Validation of a sampling protocol on the scale required by a CTS would seldom be practicable for routine purposes. The alternative approach, using a single sampler, is usually more suitable for single organizations. The most obvious experimental design is the ‘duplicate method’ shown in Fig. 10. Ideally all of the analysis should be done under repeatability conditions or, if that is impossible, with a small between-run standard deviation. The multiple targets ensure that the influence of atypical targets can be recognized and downweighted. If all of the targets have a similar content of the analyte, a two-level hierarchical analysis of variance provides estimates of the sampling standard deviation $\hat{\sigma }_{{rS}}$ if it is significantly large in comparison with the analytical standard deviation. (An estimate of the between-target standard deviation is also obtained, but that is not relevant in the present context.) The sampling uncertainty can be quantified as $\hat{\sigma }_{{rS}} ,$ but we must remember that this is true only if the sampling is unbiased. Bearing in mind the difficulties of establishing the presence of a sampling bias, this estimate will often be the best available and it is clearly better than assuming a zero sampling uncertainty. A number of such studies have been reported [25, 26].

Fig. 10

Balanced design of an experiment to validate a sampling protocol for precision

Example: Aluminium in animal feed
Each target was a separate batch of the feedstuff. Nine successive targets were sampled in duplicate and each sample analysed in duplicate. The raw results are shown in Table 3 and Fig. 11, and the analysis of variance in Table 4. There is a significant sampling variation and the standard deviations of sampling and analysis are of comparable magnitude at about 8 % relative to the concentration.

Table 3 Data set for validation of sampling protocol, Al in animal feed (ppm)

Fig. 11

Results from a nested duplication exercise to validate the sampling protocol for aluminium in animal feed

Table 4 Hierarchical analysis of variance applied to data in Table 3, to determine $\hat{\sigma }_{{sam}} = 7.18$ and $\hat{\sigma }_{{an}} = 6.48$

Other experimental designs and statistical models are possible. The analysis of variance can be conducted on results from an unbalanced design (Fig. 12), which is somewhat more economical as it requires less analysis. However, conducting robust analysis of variance with this design needs special software. In some applications, the concentration of the analyte may vary widely between targets. This condition results in heteroscedasticity, that is, the sampling precision depends on the concentration of the analyte or other factors. An alternative model, such as a constant relative standard deviation, might be appropriate here. That could be executed simply by log-transforming the data before the analysis of variance.

Fig. 12

Unbalanced design of an experiment to validate a sampling protocol for precision

These are all empirical approaches to the estimation of uncertainty from sampling. The alternative modelling approach can also be employed using either cause-and-effect models [27–29], or sampling theory in the instance or particulate materials [30], as discussed below in more detail.

Sampling quality control

We need initially to validate an intended sampling protocol to confirm that the uncertainty generated can meet fitness-for-purpose requirements. For routine use of the method, we also need to know that conditions affecting sampling uncertainty have not changed since validation time. In particular, we need to know that the uncertainty has not been affected by the incidence of an atypically heterogeneous target. That circumstance could make a particular measurement result unfit for purpose even if the sampling is carried out in accordance with the validated protocol. This continual checking comprises sampling quality control. However, this cannot be carried out in the simple manner used for analytical IQC, which makes use (among other techniques) of one or more control materials (incorrectly called ‘check samples’), which are analysed among the test materials in every run of analysis. Accessing the analogous sampling control target for every test target is clearly impracticable.

The alternative is randomly to duplicate the sampling of each target and compare the two results. A design is shown in Fig. 13. In this design, the difference between the two results should be a random variable from a distribution with zero mean and a standard deviation of $\sigma = {\sqrt {2{\left( {\sigma ^{2}_{{sam}} + \sigma ^{2}_{{an}} } \right)}} }.$ (If there is a bias, either in sampling or analysis, its effects will not be apparent in the difference between the two results.) The result can be plotted on a Shewhart chart with control lines at 0, ±2σ, and ±3σ, with the usual rules of interpretation applying. Alternatively a zone chart could be used [31].

Fig. 13

Design for routine sampling quality control

If σ _sam  > 2σ _an , sampling variation will dominate the control chart and normal variations in the analytical results will have little influence on it. An out-of-control condition would almost always indicate a sampling problem. If σ _sam  < σ _an /2, the control chart will reflect analytical variation mostly and only gross problems with sampling will be demonstrated. That behaviour of the control chart is acceptable, however, because under this latter condition, sampling precision will make only a minor contribution to the combined uncertainty. In the intermediate condition (σ _sam  ≈ σ _an ) an out-of-control condition could signify either a sampling problem or an analytical problem.

This procedure is simple but increases the measurement cost somewhat. The cost is unlikely to be doubled, however, because the overhead costs (travel to the target, setting up, calibrating and checking the analytical system etcetera) will be common to both measurements. A few accounts of SQC in practice have been reported [32] but none using a control chart, although there seems to be no special difficulty.

Example: Aluminium in animal feed

The validation statistics (Tables 3, 4) were used to set up a control chart for combined analytical and sampling precision, as described above. A further 21 successive targets were sampled in duplicate and each sample analysed once. (Each target was a separate batch of feed.) The differences between corresponding pairs of results were plotted on the chart with the outcome shown in Fig. 14. No sampling episode was found to be out of control.

Fig. 14

Routine internal quality control chart for combined analytical and sampling variation for the determination of aluminium in animal feed. The training set (in Table 3) comprises the first nine observations. No observation is shown to be out of bounds

The Split Absolute Difference (SAD) procedure, a design that does not require duplicate sampling, is available in instances where the sample is a composite of a number of increments. In this design the increments, in the total number specified in the protocol or rounded up to an even number, are consigned at random into two equal subsets or ‘splits’. The design is illustrated in Fig. 15. The two splits are prepared and analysed separately. The mean of the two results has a standard deviation of ${\sqrt {\sigma ^{2}_{{sam}} + {\sigma ^{2}_{{an}} } \mathord{\left/ {\vphantom {{\sigma ^{2}_{{an}} } 2}} \right. \kern-\nulldelimiterspace} 2} }.$ This is the same precision obtained when a normal sized composite is analysed in duplicate, so the mean result is usable for routine purposes. The difference between the results found for the two splits has a zero expectation and a standard deviation of $\sigma _{{SAD}} = {\sqrt {4\sigma ^{2}_{{sam}} + 2\sigma ^{2}_{{an}} } }.$ It is therefore possible to set up a one-sided Shewhart chart with control lines at 0, 2σ _SAD , and 3σ _SAD (or an equivalent zone chart), again with the standard interpretation (Fig. 16). Clearly the SAD method is more sensitive to sampling variation (in comparison with analytical variation) than the simple design. So far, the use of the SAD method has been reported only by the originators, although many examples show that it is practicable [33, 34] (Fig. 16).

Fig. 15

Design for the SAD method of quality control for sampling. Increments are assigned to the two splits at random

Fig. 16

Example of results by the SAD method of sampling quality control. The target was bottled water and the analyte Mg (mg L⁻¹). The first 15 rounds were used as the training set. Round 19 shows an outlying result

Sampling proficiency tests

The sampling proficiency test (SPT) is the counterpart of the analytical proficiency test. The purpose is therefore to enable samplers to detect unsuspected problems in their protocols or in the manner in which they put them into action. The basic format of an SPT is for each participating sampler to visit in succession a single target and take an independent sample using a protocol of their choice. Independence implies that the samplers see neither each other in action nor the residual signs of previous sampling activity. There are two options for the subsequent chemical analysis. If the samples are analysed together (that is, under randomized repeatability conditions) by using a high-accuracy method, we can attribute any differences between the results to sampling error alone. In contrast, if each sample is analysed in a different laboratory with unspecified accuracy, the variation among the results will represent the entire measurement process comprising sampling plus analysis. Which option is preferable depends on circumstances.

Either way, a result x _i needs to be converted into a score. The authors prefer the z-score, z _i  = (x _i  − x _A )/σ _p , based upon that recommended for analytical proficiency tests [35]. The assigned value x _A could be a consensus of the participants’ results, if that seemed appropriate, but as the number of samplers participating is likely to be small (i.e., less than 20), the consensus will have an uncomfortably large standard error. A separate result, determined by a more careful sampling conducted by the test organizer, if possible, is therefore preferred. For an example of how this could be achieved, if the samplers had restricted access to the target in situ, the test organizer could sample the target material much more effectively at a later time when the material is on a conveyor belt. The standard deviation for proficiency σ _p is best equated with the uncertainty regarded as fit for purpose. However, there are several differences between sampling and analytical PTs that need to be addressed in the scoring system. The scoring must therefore take into account the heterogeneity if the sampling target, and the contribution from the analytical uncertainty, both of which should not obscure the contribution from the sampling itself.

Several sampling proficiency tests have been carried out on a ‘proof-of-concept’ basis, and the idea found to be feasible [36, 37]. They are obviously costly to execute, but not as costly as a collaborative trial. Whether they will find use on a scale comparable with that of analytical proficiency tests remains to be seen.

The role of sampling theory

Sampling theory can be used, in favourable instances, to predict sampling uncertainty from basic principles [30]. The statistical properties of a random sample of given mass can be stated formally from the properties of the target material, such as the frequency distribution of the grain sizes, the shape of the grains, and the distribution of the analyte concentrations in grains of different sizes. However, this formal statement is often difficult to convert to a serviceable equation, except in restricted range of applications, for example, where the target material is a manufactured product with predictable physical and chemical constitution, for example a particulate material with a narrow range of grain sizes.

One problem with this application of sampling theory is that the determinants of the sampling uncertainty interact in their effects: for example, grains of different sizes may have distinct chemical compositions, and a single size range may contain grains of different compositions. Another is that the analyte in a real target might be mainly confined to different spatial or temporal bulk parts of the target. All of this implies that we would require a considerable amount of information about the target material, and the effort needed to obtain this information would far exceed the task of estimating the uncertainty empirically, that is, from a randomized replicated experiment. In addition, cautious users would want any estimate of uncertainty derived from sampling theory to be validated by a practical experiment. Discrepancies between the results of the two approaches are often found in practice [38]. Finally, targets tend to differ among themselves unpredictably, and it is the unusual targets rather than the predicable ones that are of particular consequence–theory does not help us with sampling quality control.

It seems therefore that the primary role of sampling theory is in designing sampling protocols ab initio to meet predetermined fitness-for-purpose criteria. A resulting protocol would then have to be experimentally validated to see if it actually met the criterion. Theory can also be used to estimate uncertainty when the properties of the target are highly predictable, for instance in certain fields of industrial production or when, for any reason, the empirical approach is impossible. Finally, theory can also indicate how to modify an existing protocol to achieve a desirable change in the sampling uncertainty that it gives rise to, for instance in calculating the mass of the sample (or the number of increments) required to give fitness for purpose. In some applications this has been shown to work well [9], in others less so [39].

Conclusions

The end-users of chemical measurements need a combined uncertainty of measurement (sampling plus analytical) to make correct decisions about the target. They need to compare the combined uncertainty obtained with that regarded as fit for purpose. They also need to compare sampling and analytical uncertainties with each other to ensure that resources are partitioned optimally between sampling and analysis.

Apart from the difficult issue of sampling bias, it seems perfectly feasible to obtain reliable estimates of the uncertainty from sampling, by using simple empirical techniques of protocol validation, and to ensure continuing fitness for purpose by using sampling quality control. The consideration of sampling bias has raised some so-far unanswered questions, but it seems better to proceed with what we have at the moment than to do nothing until the bias question is resolved. All of these issues are covered in a new guide to uncertainty from sampling, to be published in 2007, sponsored by Eurachem, Eurolab, and CITAC [40].

Taking sampling uncertainty into proper account will certainly raise some weighty issues for analytical practitioners, samplers, and end-users of the results of chemical measurements alike.

• There are questions of interpretation of results in the presence of unexpectedly high uncertainty, which regulatory bodies and enforcement agencies will have to consider.

• There is the extra financial burden of estimating the uncertainty from sampling, which end-users will ultimately have to bear, although this cost may in many instances be offset, or even obviated, by better distribution of resources between sampling and analysis or by adjusting the combined uncertainty closer to fitness for purpose.

• A far closer collaboration between samplers and analysts is called for and the question of ‘who is in overall charge’ will have to be resolved.

Finally, it is clear at the moment that the subject is still woefully short of hard information. We need much more quantitative empirical knowledge to make theory workable. If progress is to be made, funding bodies must be willing to pay more for basic studies of sampling uncertainty and commercial organizations will have to allow greater access to their materials and information.