1 Introduction

The double electron–electron resonance (DEER) or pulsed electron double resonance (PELDOR) technique is nowadays increasingly used as a complementary tool to X-ray structure analysis, nuclear magnetic resonance (NMR) spectroscopy and cryogenic electron microscopy. It provides structural information on biological systems and materials of increasing complexity by distance distribution analysis in the nanometer range. Originally introduced by Milov et al. [1, 2] and later extended to a dead time-free four-pulse sequence [3, 4], DEER separates pairwise couplings between electron spins from other electron spin interactions. In an approach similar to the spin–echo double resonance (SEDOR) experiment in NMR spectroscopy [5], the interactions are observed in the time domain. The optimal range for the application of DEER is 1.5–8 nm, but by deuteration of the solvent [6] and the protein [7] the distance range can be extended up to 16 nm [8] in favorable cases.

In cases where double resonance, double-quantum [9] or solid-echo based [10] experiments are sufficient, experimental strategies usually aim for the preparation of systems with no more than two electron spins in the distance range of interest. But many systems, in particular biomolecules, cannot be prepared in a way where the isolated spin pair approximation holds. This leads to multi-spin contributions [11,12,13] which complicate interpretation of the data in terms of a distance distribution. Even in cases where the isolated spin pair approximation is not violated, full structural information on the system may not be obtainable if multiple conformations are populated [14]. To tackle this problem we recently introduced the triple electron resonance (TRIER) experiment [15] for systems with more than two paramagnetic centers. TRIER requires the selective excitation of three distinct subsets of spins with sufficiently high probability. In systems that contain only one type of spin label, this is best done with shaped and frequency modulated pulses, which have become accessible in the past few years through fast arbitrary waveform generators (AWGs). In combination with a local oscillator and sufficiently broadband digitizers, AWGs provide access to bandwidths up to 0.8 GHz for observed and up to 2.5 GHz for pumped spins [16] and have been implemented in spectrometers operating from 0.33 to 6.8 T [17,18,19,20,21] magnetic field. Besides enhancing the excitation bandwidth, frequency-swept pulses can allow for more precise control of spin systems through adiabatic passage [22] even in the presence of a strongly varying resonator profile through the principle of offset-independent adiabaticity [17, 23]. Thanks to the excitation of larger spin fractions, signal intensity can be increased [18, 19] and this in turn makes it possible to conduct new correlation experiments [15, 24,25,26]. Two overview articles on state-of-the-art EPR with frequency-swept pulses have recently been published [16, 27].

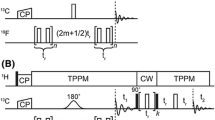
TRIER itself can be seen as an extension of the one-dimensional DEER experiment to a two-dimensional experiment (Fig. 1a) correlating dipolar frequencies that stem from the same molecule. In our initial work on TRIER [15] we obtained correlation spectra for several model compounds. Here, we demonstrate that we are able to obtain two-dimensional distance correlation maps and apply TRIER to protein samples of current interest. Best results are achieved by optimizing processing parameters with the help of the spectrum, which acts as quality control and helps to avoid processing artifacts. The two-dimensional time traces are then subjected to two-dimensional approximate Pake transform (2D-APT), which yields two dimensional distance correlation maps. TRIER acts exclusively as a correlation experiment and is intended to complement, not to replace DEER. To set experimental and processing parameters some knowledge about the distances in the molecule is required. We show that this information can come from DEER data and, for known systems, from simulations.

Fig. 1
figure 1

a The pulse sequence of the TRIER experiment. The times \(t_1\) and \(t_2\) are varied and provide the two indirect dimensions. The three colors (gray, blue and orange) represent the different excitation frequency ranges of the pulses. Experimental inversion profiles of the individual pulses are given in b. The nitroxide spectrum is shown in the back in light gray (color figure online)

Full size image

This paper is structured as follows: in Sect. 2, we discuss pulse shapes that we investigated for their application and further development of the pulse sequence. In Sect. 3, we describe how we process the two-dimensional time-domain data and how we obtain distance correlation maps through two-dimensional approximate Pake transformation. This is followed by a description of our experimental setup in Sect. 4 and the sample preparation and characterization in Sect. 5. Finally, results from three model compounds of different geometries and two proteins are shown in Sect. 6. This work finishes with a summary and outlook in Sect. 7. We also provide Supplementary Information (SI) which contains an in-depth characterization of the proteins, a comprehensive summary of the measurements and data processing and details on the synthesis of one of the model compounds.

2 Improvements of the TRIER Pulse Sequence

We investigated different types of pulses and their effect on sensitivity and modulation depth, as well as a modification of inter-pulse delays. The TRIER experiment correlates inter spin distances of molecules that contain three electron spins. A detailed discussion on the TRIER sequence itself and all pathways that can lead to a modulation of the echo can be found in [15].

2.1 Investigated Pulse Types

The TRIER experiment (Fig. 1a) requires pulses with three different excitation windows: One for the detection subsequence (gray) and two for the pump pulses (blue and orange). As sensitivity is a challenge in TRIER, it is essential that excitation profiles possess steep edges and no ripples in and outside of the excitation band, so that they cover most of the spectrum without overlap of the excitation bands intended for exciting different subsets of spins (Fig. 1b). In our initial work on TRIER [15] we used linearly frequency-swept pulses (chirp pulses) [17] with smoothed edges for the detection sequence and asymmetric hyperbolic secant (HS) pulses [28, 29] for pumping. Meanwhile we have also tested Gaussian [30, 31] and Gaussian cascade (GC) [32,33,34] pulses and compared their excitation windows and the resulting sensitivity and modulation depth. While frequency-swept pulses such as chirps and HS pulses allow for highly-efficient inversion due to adiabatic passage [22, 35], they require slightly more complex pulse schemes for proper refocusing [35] and can suffer from loss of magnetization due to transverse interference effects [16, 25].

With respect to the narrower banded (\(\sim\) 25 MHz) observer pulses, the poor quality of the excitation windows of GC and HS pulses (Fig. S10), especially for \(\pi /2\)-pulses, and the resulting low sensitivity made these two pulse types unsuitable for the detection subsequence. Gaussian and chirp pulses on the other hand both showed well defined excitation profiles and comparable modulation depths (Fig. S11), and could both be used for TRIER.

Pump pulses on the other hand require excitation bandwidths of around 60 MHz. Here, the Gaussian and chirp pulses cannot compete with the steep edges of the excitation profiles of asymmetric HS or GC pulses. Although HS and GC both show good excitation profiles, HS pulses provide deeper modulation depths (Fig. S11).

2.2 Modification of Timings in the Pulse Sequence

In the initial description of TRIER, we used identical lengths for the delays \(\tau _1\) and \(\tau _3\). This leads to an overlap of the TRIER echo with an echo that is created by the \(\pi /2\) and the second observer inversion pulse. Instead of adding an additional step to the already complex phase cycle [15] we opted for increasing \(\tau _3\) of the TRIER echo, which separates the two echoes. This strategy is similar to the one we used in five-pulse DEER [36] and for dynamical decoupling with multipulse sequences [37].

3 Data Processing

Compared to our introduction of TRIER [15], we improved data processing and added several more steps that allow us to obtain spectra with strongly improved resolution and distance correlation maps. In brief, we use the spectrum to find parameters for the Lorentz-to-Gauss transformation (see below) that give a good balance between reduced line width and the addition of noise [15]. The Lorentz-to-Gauss transformed time traces are then used to obtain distance correlation maps through 2D-APT. We provide an overview of the data processing in form of a flowchart in the SI in Sect. 2.1.

3.1 Background Correction and Lorentz-to-Gauss Transformation

After the acquisition of echo transients for all time pairs \(t_1\), \(t_2\), each time trace was multiplied with a Gaussian that was fitted to the echo. The product was then integrated—this corresponds to an observer bandwidth-matched filter and strongly improves the quality of the integration [38]. The integrated echo signals at all time pairs \(t_1\), \(t_2\) now constitute a two-dimensional data set. All echoes that are not modulated along both indirect dimensions [15] (this also includes all DEER signals) are removed by background correction. As the background also contains contributions that stem from time-modulated DEER signals, a simultaneous fit along both dimensions is not feasible. Instead, the exponentially decaying background decay is removed sequentially: First, the fit along one dimension is subtracted from the signal, second, the background along the other dimension is fitted and subtracted. Best results were usually obtained when the dimension with the deeper modulation depth was corrected first.

After background removal, a Savitzky–Golay filter of high order [39, 40] is applied to the background corrected signal. The smoothed, two-dimensional time traces are then subjected to a Lorentz-to-Gauss transformation in both dimensions [15]. This is a crucial step and changes the line shape from Lorentzian to Gaussian, which reduces overlap and removes peak-like features in the spectra that stem from overlap. But, at the same time, Lorentz-to-Gauss transformation decreases the signal-to-noise ratio and it is important to find a balance between line width and noise before computing distance correlation maps.

3.2 The TRIER Spectrum

TRIER spectra are expected to be reflection symmetric about the axes and the diagonals, but background correction and non-equivalent modulation depths introduce a (sometimes strong) asymmetry into the data. Hence, after two-dimensional Fourier transform (2D-FT), with the superscript T denoting the transpose, the matrix \(\mathbf A\) of the asymmetric spectrum \({A}(\omega _1,\omega _2)\) is symmetrized through geometric averaging

$$\begin{aligned} \mathbf{S } = \sqrt{\mathbf{AA }^{\mathrm{T}}} \end{aligned}$$
(1)

which is superior to arithmetic averaging and gives better artifact suppression. If at this point the signal-to-noise ratio in the spectrum is not satisfying, the quality of it can be improved by a procedure that can be described as “covariance filtering”. For this the symmetric covariance matrix \(\mathbf{C }\), based on the covariance map \({C}(\omega _2,\omega _2^\prime )\), needs to be obtained by mapping sets of one-dimensional spectra of one dimensions [41, 42], which are averaged over a time \(t_1^{\mathrm{max}}\) along the other indirect dimension. A detailed discussion of covariance filtering and how to obtain the covariance matrix can be found in the SI in Sect. 2.2. Then, the spectrum is multiplied with the covariance matrix:

$$\begin{aligned} {\mathbf{S}}^{\prime } = \mathbf{SC }. \end{aligned}$$
(2)

This resembles the use of matched filters and not only increases the signal-to-noise ratio, but also removes spurious frequencies that stem from imperfect background correction.

The parameters of the Lorentz-to-Gauss transformation are manually adjusted until a good balance between added noise and reduced line width is achieved. As it is easier to see and verify the results from Lorentz-to-Gauss transformation in the spectrum, it has proven to be more efficient to use the spectrum for the optimization than the distance map. This optimization works quite well, since for narrow distributions the data is dominated by a single frequency perpendicular to the unique axis (horn of the Pake pattern). For broad distributions optimization works just as well because the Pake pattern is washed out. Covariance filtering is not applied in processing that leads to distance correlation maps (see Fig. S3), but is merely used to improve the quality of the spectrum, since it is a frequency-domain filter.

3.3 Two-Dimensional Approximate Pake Transformation

The next step involves a transformation of the signal to the distance domain. For this the time-domain signal after optimized Lorentz-to-Gauss transformation is used. In the analysis of DEER data, one way to obtain distance distributions is through approximate Pake transformation (APT) [43], which is very fast and can be extended to a two-dimensional data set. The linear TRIER signal \({V}_{\mathrm{lin}}(t_1,t_2)\) is the product of a discrete distribution of combinations of dipolar frequencies \({P}(\omega _1,\omega _2)\) and the kernel basis \({V}(\omega _1,t_1,\omega _2,t_2)\):

$$\begin{aligned} {V}_{\mathrm{lin}}(t_1,t_2) = \iint {P}(\omega _1,\omega _2) {V}(\omega _1,t_1,\omega _2,t_2) \mathop {}\!{\mathrm{d}}\omega _1 \mathop {}\!{\mathrm{d}}\omega _2. \end{aligned}$$
(3)

To obtain \({P}(\omega _1,\omega _2)\), Eq. (3) must be inverted by an integral transformation which would require a memory-straining four-dimensional kernel function \({K}(\omega _1,t_1,\omega _2,t_2)\). But by recognizing and exploiting the separability of the problem, the basis in matrix form \({\varvec{V}}_{4\varvec{D}}\) factorizes into

$$\begin{aligned} {\varvec{V}}_{4\varvec{D}} = {\varvec{V}}_{2\varvec{D}} \otimes {\varvec{V}}_{2\varvec{D}}, \end{aligned}$$
(4)

where the basis function \(V_{2D}\) is given by

$$\begin{aligned} {V}_{2D}(\omega ,t) =\int _{0}^{\pi /2}\cos [(3\cos ^2(\theta )-1) \omega t] \sin (\theta )\mathop {}\!{\mathrm{d}}\theta \end{aligned}$$
(5)

assuming the angles \(\theta\) between the spin–spin vectors and the magnetic field are uncorrelated. This approximation is similar to neglect of orientation selection, which is often permissible for spin labels in proteins. For our rigid model compounds, the approximation is still reasonable, because of free rotation around the triple bonds in the linker backbone and of the non-zero angle between the label arms. If this assumption holds, the kernel factorizes as

$$\begin{aligned} {\varvec{K}}_{4{\varvec{D}}} = {\varvec{K}}_{2{\varvec{D}}}\otimes {\varvec{K}}_{2{\varvec{D}}}. \end{aligned}$$
(6)

This significantly reduces the memory requirements for data processing. The kernel function is derived analytically

$$\begin{aligned} {K}(\omega _1,t_1,\omega _2,t_2) = {c}(\omega _1,\omega _2){V}(\omega _1,t_1,\omega _2,t_2)f(t_1,t_2) \end{aligned}$$
(7)

and should ideally fulfill the orthogonality condition

$$\begin{aligned} \iint V(\omega _1,t_1,\omega _2,t_2)K(\omega _1',t_1,\omega _2',t_2) \mathop {}\!{\mathrm{d}}t_1\mathop {}\!{\mathrm{d}}t_2 =\delta (\omega _1-\omega _1')\delta (\omega _2-\omega _2'). \end{aligned}$$
(8)

Here, \(f(t_1,t_2) = t_1t_2\) is set in relation to a Bessel transformation [43] and the normalization function \({c}(\omega _1,\omega _2)\) is given by

$$\begin{aligned} {c}(\omega _1,\omega _2) =\iint \left( V(\omega _1,t_1)V(\omega _{2},t_{2})\right) ^2 t_1 t_2 \; \mathop {}\!\mathrm {d}t_1 \mathop {}\!\mathrm {d}t_2. \end{aligned}$$
(9)

The kernel is approximate in the sense that Eq. (8) cannot be exactly fulfilled. The quality of the approximation can be quantified by the condition number of \({K}(\omega _1,t_1,\omega _2,t_2)\) which is the ratio between the maximum and minimum singular value of \({K}(\omega _1,t_1,\omega _2,t_2)\). Inversion of Eq. (3) yields the discrete frequency distribution

$$\begin{aligned} P^{(0)}(\omega _1,\omega _2) = \iint \frac{1}{c(\omega _1,\omega _2)}V(\omega _1,t_1)S(t_1,t_2)V(\omega _2,t_2) t_1 t_2 \mathop {}\!\mathrm {d}t_1\mathop {}\!\mathrm {d}t_2 \end{aligned}$$
(10)

which is related to the true frequency distribution \({P}(\omega _1,\omega _2)\) through

$$\begin{aligned} {D}(\omega _1,\omega _1',\omega _2,\omega _2'){P}(\omega _1',\omega _2')={P}^\text {(0)}(\omega _1,\omega _2). \end{aligned}$$
(11)

\({D}(\omega _1,\omega _1',\omega _2,\omega _2')\) is the cross talk matrix, and accounts for the erroneous admixture of other frequency components at a given frequency [43]. Again, the four-dimensional matrix \({D}(\omega _1,\omega _1',\omega _2,\omega _2')\) can be obtained from its two-dimensional analogs

$$\begin{aligned} {d}(\omega _i,\omega _i') = \frac{1}{\int V(\omega _i,t_i)^2t_i\mathop {}\!\mathrm {d}t_i}\int V(\omega _i,t_i)V(\omega _i',t_i)\mathop {}\!\mathrm {d}t_i \end{aligned}$$
(12)

where \(i = 1,2\), through

$$\begin{aligned} {D}(\omega _1,\omega _1',\omega _2,\omega _2') = \frac{1}{{c}(\omega _1,\omega _2)}d(\omega _1,\omega _1')\otimes {d}(\omega _2,\omega _2'). \end{aligned}$$
(13)

Computationally, the true frequency distribution can be obtained by solving the linear matrix problem

$$\begin{aligned} \mathbf{p } = \mathbf{D }{\setminus }{\mathbf {p}}^{{\mathbf {(0)}}}, \end{aligned}$$
(14)

where \(\mathbf p\) and \(\mathbf {p^{(0)}}\) and are the vectorized forms of the matrix representations \(\mathbf{P }\) and \(\mathbf {P^{(0)}}\) of \(P(\omega _1,\omega _2)\) and \(P^{(0)}(\omega _1,\omega _2)\), respectively. This step would require the construction of a four-dimensional cross talk matrix \(\mathbf D\). However, by exploiting the relation

$$\begin{aligned} (\mathbf{A }\otimes \mathbf{B }) \mathbf x = \mathbf{C } \rightarrow \mathbf x = (\mathbf{A }{\setminus} \mathbf{C })/\mathbf{B }^{\mathrm{T}} \end{aligned}$$
(15)

the linear problem can be expressed with the two dimensional cross talk matrices \(\mathbf d\)

$$\begin{aligned} \mathbf P = (\mathbf d {\setminus} \mathbf {P^{(0)}})/\mathbf {d}^{\mathrm{T}}. \end{aligned}$$
(16)

Such crosstalk correction amplifies noise contributions to an extent that increases with increasing condition number of \(K(\omega _1,t_1,\omega _2,t_2)\). This is a consequence of the underlying problem being ill-posed [44,45,46]. After computation of the crosstalk-corrected frequency distribution, the distance correlation map \(P(r_1,r_2)\) can be computed by mapping the frequencies in both dimensions to distances according to the relation

$$\begin{aligned} r(\omega ) = \left( \frac{2\pi \omega _0}{\omega }\right) ^{1/3}, \end{aligned}$$
(17)

where \(\omega _0/2\pi = 52.04\,\) MHz is the dipolar frequency at 1 nm for an electron with \(g = g_\mathrm {e}\).

While the \(\omega _1,\omega _2\) coordinates are linearly spaced, the ordinates created in this manner in the distance domain are spaced proportionally to \(r^{-3}\), which increases the noise at short distances dramatically [43]. This effect can be reduced by distance domain smoothing (DDS), which filters the distance distribution by convolution with a Gaussian function of a certain width \(\sigma\), which will be referred to as DDS-parameter. This filter is constructed according to

$$\begin{aligned} F(\omega _1,\omega _2,r_1,r_2) = \exp \left[ \frac{r(\omega _1)-r_1}{\sigma }\frac{r(\omega _2)-r_2}{\sigma }\right] \end{aligned}$$
(18)

and the smoothed distance correlation map is obtained through

$$\begin{aligned} P^\prime (r_1,r_2)= \frac{\iint F(\omega _1,\omega _2,r_1,r_2)P(r_1,r_2)\mathop {}\!\mathrm {d}\omega _1\mathop {}\!\mathrm {d}\omega _2}{\iint F(\omega _1,\omega _2,r_1,r_2)\mathop {}\!\mathrm {d}\omega _1\mathop {}\!\mathrm {d}\omega _2}, \end{aligned}$$
(19)

where \(\omega _1\) and \(\omega _2\) correspond to the dipolar frequencies of the distances \(r_1\) and \(r_2\). The selection of the DDS parameter is important. When chosen too large, peaks in the distributions are artificially broadened, and when chosen too small, broad peaks are artificially split into many narrow peaks. Loosely speaking, the effect of \(\sigma\) is similar to a regularization parameter [44,45,46]. Usually, good distributions are obtained with values in the range \(0.5~{\text {nm}}> \sigma > 0.01~{\text {nm}}\).

To keep a constant integral the maps were normalized according to [43]:

$$\begin{aligned} P^{\prime \prime }(r_1,r_2) = \frac{P^\prime (r_1,r_2)}{r_1^4r_2^4}. \end{aligned}$$
(20)

Just like the spectrum, the such obtained distance correlation maps suffer from the asymmetry of the TRIER signal as well, and are hence symmetrized to yield the final distance correlation map

$$\begin{aligned} \mathbf{M } = \sqrt{ {\mathbf {P}}^{\prime \prime }{\mathbf {P}}^{{\prime \prime }\mathrm{T}} }. \end{aligned}$$
(21)

3.4 Comment on 2D Tikhonov Regularization

Tikhonov regularization has become the most widely applied approach to computing distance distributions from DEER data [44, 46,47,48]. Therein, a regularization parameter \(\alpha\) is fixed according to the L-curve method [45, 49], which finds a balance between under- and over smoothing. We tried to extend the currently existing one-dimensional Tikhonov regularization to the two-dimensional problem at hand. However, as previously reported for other applications [48, 50, 51], the selection of a single regularization parameter for a two-dimensional distribution led to wrong results. Note also that determination of the regularization parameter \(\alpha\) from the L-curve is not necessarily optimal for DEER as has been found recently [52].

4 Materials and Methods

4.1 EPR Spectrometer

All experiments were performed at 50 K on a home-built high-power EPR spectrometer with arbitrary waveform excitation capability [16, 35, 53] at Q-band frequencies around 34 GHz. Pulse sequences were generated by an AWG with built-in sequencer (Agilent/Keysight M8190A operated at a sampling rate of 8 GSa/s) and up-converted to Q band by a 33 GHz local oscillator. The same local oscillator was used to down-convert signals to frequencies around 1.5 GHz, with subsequent acquisition with a 2 GSa/s digitizer (SP Devices ADQ412) via subsampling. The pulses, which were amplified by a 200 W traveling wavetube amplifier (Applied Systems Engineering TWT 187 Ka), were fed into an overcoupled home-built pent loop-gap resonator for 1.6 mm tubes with a loaded quality factor \(Q_{\mathrm {L}} = 100\) described in [54]. The spectrometer was controlled by home-written MATLAB scripts. The magnetic field was always chosen such that the nitroxide spectrum was centered around the maximum of the resonator response mode, providing reasonable microwave field amplitudes for all excitation frequencies. The spectrometer was operated continuously between 4 hours and 9 days and we did not encounter instabilities of temperature or microwave frequency and phase. With respect to stability, new-generation spectrometers with a fixed-frequency microwave local oscillator, a fast AWG, and a robust very broadband resonator may be favorable compared to spectrometers with a frequency-controllable Gunn diode.

4.2 DEER Measurements

Four-pulse DEER dipolar spectra were measured with the standard pulse sequence \((\pi /2)_{\nu _{\mathrm {obs}}}- \tau _1- (\pi )_{\nu _{\mathrm {obs}}}- t'- (\pi )_{\nu _{\mathrm {pump}}}- (\tau _1+\tau _2-t')- (\pi )_{\nu _{\mathrm {obs}}}- \tau _2-\)echo [4]. Observer frequencies \(\nu _{{\mathrm {obs}}}\) were between 34 and 34.5 GHz and \(\nu _{\mathrm {obs}} - \nu _{\mathrm {pump}} = 0.1\) GHz. The observer was set to the maximum of the field-swept echo-detected EPR spectrum of the nitroxide and to the center of the resonator dip. All pulses had a length of 16 ns. The value of the delay \(\tau _1\) was 680 ns. A phase cycle \([+(+x)-(-x)]\) was applied to the \(\pi /2\) observer pulse to cancel receiver offset. The dipolar modulation time \(t = t' - \tau _1\) was varied between \(-\,120\) ns and 4480 ns using an interpulse delay \(\tau _2 = 4500\) ns. The data were background corrected and Fourier transformed in DeerAnalysis2016. The “ghost suppression” feature of DeerAnalysis was used to reduce contributions of combination frequencies.

4.3 TRIER Measurements

With the information from DEER, timings of the TRIER sequence were adapted to suit each sample optimally. Hence, only a general description of the pulses and timings is provided here. Detailed sample specific experimental conditions can be found in Sect. 3 of the SI.

Over the width of the nitroxide spectrum the amplitude response of the resonator varies significantly. By measuring the resonator profile beforehand, all pulses were compensated for this frequency dependence, which provided a constant adiabaticity over the entire excitation range of each pulse [16, 17].

4.3.1 Observer Subsequence

We used chirp pulses for the detection subsequence (gray in Fig. 1). While Gaussian pulses have the advantage that all the pulses can have the same pulse length, chirps require the last refocusing pulse to be half the length of the previous pulses. Only this ensures proper refocusing of the echo [35]. The amplitudes of all pulses were optimized separately for maximum echo integral. The \(\pi /2\) and the first two \(\pi\) pulses had a length of 100 ns. The third \(\pi\) pulse had a length of 50 ns. All chirps had a bandwidth of 25 MHz and tails were smoothed with a quarter sine of variable length \(t_{\mathrm {rise}}\) that was optimized to provide smooth excitation profiles.

The center frequency of the observer pulses was approximately \(-\,50\) MHz from the maximum of the spectrum. The interpulse delays were set to \(\tau _1 = 400\) ns and \(\tau _3 = 900\) ns. With the information obtained from the DEER spectra, \(\tau _2\) was set sample specific and fell in the range of 2500–3900 ns. A phase cycle \([+(+x)-(-x)]\) was applied to the \(\pi /2\) and \([+(+x)+(+y)+(-x)+(-y)]\) to the second and third observer pulses.

4.3.2 Pump Pulses

For the pump pulses (blue and orange in Fig. 1), asymmetric HS pulses with a length of 100 ns and a bandwidth of 60 MHz were used. The center frequency of the first pump pulse was approximately − 100 MHz from the center frequency of the observer pulses and the sweep was performed from low to high frequencies. The initial delay of the first pump pulse was 200 ns after the beginning of the second observer pulse and in consecutive experiments it was stepped with a sample-dependent increment that was chosen such that it fulfilled the Nyquist criterion for all distances visible in the DEER data.

The second pump pulse was positioned such that its center frequency was approximately + 100 MHz from the center frequency of the observer pulses. In contrast to the first pump pulse, the second pump pulse was swept in the opposite direction, from high to low frequencies. The initial delay between the end of the pump pulse and the beginning of the last observer pulse was 200 ns. In consecutive experiments, the second pump pulse was moved towards the third observer pulse with the same increment as the first pump pulse.

While the order of both HS pulses was 6 for the first half of the pulse, it was set to a lower value (usually between 1 and 4) for the second half to provide a steeper excitation profile in the frequency domain. The apodization parameter was 10 for both sides of the pulses. The pulse amplitudes were optimized to provide a clean echo, which, after incorporation of the resonator profile, resulted in critical adiabaticities [35] of about \(Q_{\mathrm {crit}} \approx 8\).

5 Sample Preparation

We measured TRIER experiments with three triradical model compounds and two triply-labeled proteins. All samples were measured in clear fused quartz capillaries (Wilmad LabGlass) with an outer diameter of 1.6 mm.

5.1 Model Compounds

The model compounds were identical to the ones used previously [15]. All triradicals were dissolved in perdeuterated o-terphenyl-d\(_{14}\) (dOTP) that was synthesized according to a published standard procedure [55] and kindly provided by Herbert Zimmermann. The chemical structures are depicted in Fig. 2.

Fig. 2
figure 2

Triradicals that were used for measuring TRIER spectra. For triradicals of equilateral, isosceles and scalene geometry we used T\(_{\mathbf{equilateral }}\), T\(_{\mathbf{isosceles} }\) and T\(_{\mathbf{scalene }}\), respectively

Full size image

The triradical T\(_{\mathbf{equilateral} }\) is of equilateral geometry and we used a concentration of 120 \(\upmu\)M in dOTP. The synthesis of T\(_{\mathbf{equilateral }}\) is described in [11]. As a triradical, where the nitroxides are arranged in isosceles geometry, we used T\(_{\mathbf{isosceles }}\) of which a detailed synthesis is given in [11]. The sample had a concentration of 240 \(\upmu\)M in dOTP. In T\(_{\mathbf{scalene }}\) the nitroxides form a scalene triangle. For T\(_{\mathbf{scalene }}\) we used a concentration of 100 \(\upmu\)M in dOTP.

The synthesis of T\(_{\mathbf{scalene }}\) is described in Sect. 5.2.

Just prior to measurement, probes were melted with a heat gun set to 90 \(^{\circ }\)C and shock frozen by quick immersion in liquid nitrogen to provide a homogeneous glassy solid.

5.2 Synthesis of Model Compound with Scalene Geometry

The synthesis of T\(_{\mathbf{scalene }}\) is shown in Fig. 3.

Fig. 3
figure 3

Synthesis of T\(_{\mathbf{scalene }}\)

Full size image

The scaffold was built up and the three isoindoline moieties were connected through Sonogashira–Hagihara cross coupling reactions. The last step was the oxidation of the isoindoline moieties to N-oxylisoindoline moieties. The attempt to attach a spacer unit similar to the building block 3, however, already coupled with the isoindolineimide moiety instead of having the alkyne protecting group CH\({_2}\)OH, failed due to the low reactivity of bromoisoindoline for the cross coupling with alkynes and the incompatibility of the imide moiety with primary amines. A detailed discussion of the synthesis can be found in Sect. 5 of the SI.

5.3 RRM1 of PTBP1 and Rpo4/7 as Protein Model Systems

5.3.1 Protein Expression and Purification

Two soluble proteins that are well-characterized by X-ray structure analysis [56, 57], NMR [58] and EPR spectroscopy [59,60,61] served as application model systems for TRIER: the heat-stable complex of subunits Rpo4 and Rpo7 (also known as F and E, respectively) of the archeal RNA polymerase of M. jannaschii [57, 62] and the isolated RNA recognition motif 1 (RRM1) of the alternative splicing regulator polypyrimidine-tract binding protein 1 (PTBP1) [59, 60]. The labeling sites for the Rpo4/7 complex (Rpo4: C36, G63C; Rpo7: V49C) were selected from a larger set of sites reported in [61], where all pairwise distances from DEER experiments have been measured.

The three labeling positions in RRM1 (T71C/L80C/T109C) were chosen to lie in solvent exposed surfaces of \(\alpha\)-helical regions.

The two subunits, Rpo4 and Rpo7, of the Rpo4/7 complex were individually over-expressed in Escherichia coli (E. coli) following the established protocols [61, 62]. A more detailed description of the purification of both constructs can be found in the SI in Sect. 1.

RRM1, encoding an N-terminal chitin binding domain as affinity tag, was over-expressed in E. coli and afterwards purified by affinity and size-exclusion chromatography following previously published protocols [59, 60].

Protein concentrations were determined with a NanoDrop Spectrophotometer ND-1000 (Witec AG) using the theoretical calculated extinction coefficients [63] of \(\epsilon = 29.34\) L mmol\(^{-1}\) cm\(^{-1}\) for Rpo4/7 and \(\epsilon = 4.47\) L mmol\(^{-1}\) cm\(^{-1}\) for RRM1.

5.3.2 Site-Directed Spin Labeling and Sample Preparation

Rpo4/7 was spin labeled after complex formation of the two subunits with tenfold molar excess of MTSSL ((1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl)methanethiosulfonate, Toronto Research Chemicals) over cysteine at a protein concentration of 10 \(\upmu\)M. Unreacted spin label was washed out by repeated concentration and re-dilution in a 10 kDa MWCO centrifugal concentrator (Vivaspin-500, 10 kDa MWCO, Sigma-Aldrich). Removal of the free label and spin label attachment was checked by CW EPR spectroscopy.

The final protein sample was lyophilised, resuspended in a D\(_2\)O/d\(_8\)-glycerol mixture (1:1 by volume) and transferred into the sample tube.

The triple cysteine version of RRM1 (T71C/L80C/T109C) was diluted to a concentration of 40 \(\upmu\)M and site-directed spin labeling (SDSL) was performed with tenfold molar excess of MTSSL. After incubation over night at room temperature, unattached spin label was removed by PD10 desalting columns (GE Healthcare LifeScience) and RRM1 was concentrated to 180 \(\upmu\)M. Spin label attachment was proven by continuous-wave EPR (CW EPR) spectroscopy at X-band (9.5 GHz) at room temperature (see SI for detailed description). Finally, RRM1 was diluted 1:1 with d\(_8\)-glycerol (Sigma Aldrich) and 10 \(\upmu\)L of the solution was transferred into to the quartz capillary.

6 Experimental Results and Discussion

A summary of the timings and pulse parameters that were used for each sample can be found in the SI in Sect. 3. Before measuring TRIER spectra we acquired DEER traces. Based on the DEER data we selected appropriate TRIER timings, such as the time steps \(\Delta t_1, \Delta t_2\) and the maximum observation time \(\max (t_1), \max (t_2)\) in the two indirect dimensions. Challenges presented itself for samples that contained very short and rather long distances. This situation requires long time traces that are sampled with a short time step, which requires prolonged measurement times. For the model compounds measurement times were between 24–72 h and for the protein samples up to around 200 h. We expect to reduce measurement time in the future by introducing non-uniform sampling to TRIER.

After acquisition of the time traces, we usually first optimized our data-processing (background correction and Lorentz-to-Gauss transformation) until peaks were well separated in the frequency domain. Only then the 2D-APT algorithm was run. As it is easier to see the results from the Lorentz-to-Gauss transformation in the spectrum, this has proven to be more efficient than immediately optimizing the distance map. Distance correlation maps usually show more details (such as shoulders) than the spectra and offer the advantage of more intuitive units. All of our two dimensional TRIER plots (spectra and distance correlation maps) feature projections plots. For display, the DEER distance distributions were superimposed onto the sum projections of the TRIER distance correlation maps after normalization to their maximum amplitude.

In powdered solids the dipole-dipole coupling usually leads to the characteristic Pake doublet. However, our projections do not show fully resolved Pake patterns. This is due to our processing which emphasized the peaks of the Pake patterns (see Sect. 3.2). It can also be seen in Fig. 6 of Ref. [11] that the angular backbone geometry compared to the straight one leads to a broadened distance distribution already in a biradical and that no classical Pake pattern is observed for this geometry.

Many of the TRIER distance projection plots appear to resolve distances better than the DEER distance distributions they are compared to. Note that all DEER data was measured up to the time where the dipolar oscillations had fully decayed and a significant section of clean background was present. Hence, the seemingly narrower distributions in TRIER are a result of the data processing and distance distributions in TRIER sum projections are not as reliable as the ones obtained from DEER.

6.1 Comments on the Interpretation of TRIER Spectra and Distance Correlation Maps

If all three spin labels are of the same type, the TRIER spectrum is expected to be symmetric with respect to the axes and each quadrant contains the complete correlation pattern. When describing the spectra, we, therefore, limit our discussion to the first quadrant. We start each of our discussions with the spectrum and then move on to the distance correlation map.

The TRIER experiment correlates distances between spin labels that are in the same molecule. Ideally, the two-dimensional background correction removes any signals that are not modulated along both dimensions (this includes all DEER signals, see discussion on TRIER pathways in [15]). Combination frequencies as they arise from the multi-spin contribution in DEER (ghost peaks), have no equivalent in TRIER with three spin labels, as this would require one pump pulse to excite two spins, and at the same time the other pump pulse has to excite one spin as well. This is not possible with only three unpaired electrons. Ghost peaks can appear in molecules that contain four or more electron spins, but the discussion of this is beyond the scope of this paper.

We also want to point out that the peaks on the diagonal in the spectra and the distance correlation maps are usually not autocorrelation peaks. They are in fact cross-correlation peaks between two distances that just happen to have the same length. If the TRIER experiment is set up correctly, autocorrelation peaks, where a distance is correlated with itself, are not or only weakly present as they can only arise if the excitation bands of the pump pulses overlap. When measuring a triradical, the intensity of auto-correlation peaks was negligible compared to the intensity of the cross peaks [15]. However, pulse overlap in combination with a background correction that does not completely remove DEER signals, can lead to the appearance of diagonal peaks, even for diradicals (where no TRIER peaks are present). Therefore, we investigated a mixture of diradicals: the distance correlation map showed two peaks along the diagonal that corresponded to the autocorrelation, but no off-diagonal peaks were observed (data not shown). In combination with DEER data this still allows to discriminate between a mixture of diradicals and a triradical.

On the processing side, we observed a general trend of the 2D-APT in combination with our background correction to create artifact diagonal peaks for the longest distance that is present. This problem needs to be addressed in future work.

6.2 Equilateral Geometry

In T\(_{\mathbf{equilateral }}\) all three distances between the nitroxides are equal if bending of the spacer is neglected and are, according to structure simulations with Chem3D (PerkinElmer Informatics), expected to be \(r^{\text {sim}} = 4.2\,\) nm. This corresponds to a dipolar frequency of \(\omega ^{\text {sim}} /2\pi = 0.70\,\) MHz. Since only one distance is present, only one correlation peak is expected per quadrant in the TRIER spectrum (Fig. 4a) at (0.7 MHz/0.7 MHz).

Fig. 4
figure 4

Experimental a TRIER spectrum and b distance correlation map of T\(_{\mathbf{equilateral }}\). The trinitroxide is of equilateral geometry and, therefore, only one correlation peak is present in each quadrant of the spectrum and of the distance correlation map. The TRIER projections in b are shown in blue and the DEER distance distribution in orange (color figure online)

Full size image

The experimentally observed dipolar frequency \(\omega ^{\text {exp}} /2\pi = 0.6\,\) MHz is slightly smaller than the expected \(\omega ^{\text {sim}}\). Compared to the previously recorded spectrum [15], we were able to reduce the line width with the improved processing algorithm. With 2D-APT a distance correlation map can be obtained that shows, as expected, only one correlation peak at (4.1 nm/4.1 nm).

6.3 Isosceles Geometry

In T\(_{\mathbf{isosceles }}\) the nitroxides form an isosceles triangle and two different distances \(r_{\mathrm {A}}^{\mathrm {ref}} = 3.9\) nm and \(r_{\mathrm {B}}^{\mathrm {ref}} = r_{\mathrm {C}}^{\mathrm {ref}}= 3.2\,\) nm are present [15]. This corresponds to the dipolar frequencies \(\omega _{\mathrm {A}}^{\mathrm {ref}}/2\pi = 0.88\,\) MHz and \(\omega _{\mathrm {B}}^{\mathrm {ref}}/2\pi = \omega _{\mathrm {C}}^{\mathrm {ref}}/2\pi = 1.59\,\) MHz. A total of three correlation peaks can be expected: Two peaks represent the correlations between \(r_{\mathrm {A}}\) and \(r_{\mathrm {B}}\) and are expected at (\(\omega _{\mathrm {A}}/\omega _{\mathrm {B}}\)) and (\(\omega _{\mathrm {B}}/\omega _{\mathrm {A}}\)). As \(r_{\mathrm {B}}\) and \(r_{\mathrm {C}}\) have the same length, these peaks coincide with the correlation of \(r_{\mathrm {A}}\) and \(r_{\mathrm {C}}\), which gives rise to peaks at (\(\omega _{\mathrm {A}}/\omega _{\mathrm {C}}\)) (\(\omega _{\mathrm {C}}/\omega _{\mathrm {A}}\)). The third correlation peak is expected to fall on the diagonal, since (\(\omega _{\mathrm {B}}/\omega _{\mathrm {C}}\)) and (\(\omega _{\mathrm {C}}/\omega _{\mathrm {B}}\)) connect two distances with the same length.

The experimentally observed dipolar frequencies in Fig. 5 are \(\omega _{\mathrm {A}}^{\mathrm {exp}}/2\pi = 0.9\,\) MHz and \(\omega _{\mathrm {B}}^{\mathrm {exp}}/2\pi = \omega _{\mathrm {C}}^{\mathrm {exp}}/2\pi = 1.4\,\) MHz, and match the expected frequencies quite well. Though the difference between \(\omega _{\mathrm {A}}\) on the one hand and \(\omega _{\mathrm {B}}\), \(\omega _{\mathrm {C}}\) on the other hand is rather small, all peaks are resolved. A closer look at the spectrum appears to reveal a peak at (0.9 MHz/0.9 MHz) or (\(\omega _{\mathrm {A}}/\omega _{\mathrm {A}}\)). This is an artifact that stems from overlap between the peaks at (0.9 MHz/1.4 MHz) and (1.4 MHz/0.9 MHz), and could be reduced by a stronger Lorentz-to-Gauss transformation, which would decrease the signal-to-noise ratio [15]. Overlap of the off-diagonal peaks also explains the stronger intensity of the diagonal peak at (1.4 MHz/1.4 MHz). Compared to the previously published spectrum of T\(_{\mathbf{isosceles }}\) in [15], the improved data processing enabled us to well resolve the three peaks and remove most of the artifact at \((\omega _{\mathrm {A}}/\omega _{\mathrm {A}})\).

Fig. 5
figure 5

Experimental a TRIER spectrum and b distance correlation map of T\(_{\mathbf{isosceles }}\). The trinitroxide is of isosceles geometry which leads to three correlation peaks. The TRIER projections in b are shown in blue and the DEER distance distribution in orange (color figure online)

Full size image

For the distance correlation map, three peaks are expected as well: Two peaks that are mirrored along the diagonal at (\(r_{\mathrm {A}}/r_{\mathrm {B}}\)),(\(r_{\mathrm {A}}/r_{\mathrm {C}}\)) and (\(r_{\mathrm {B}}/r_{\mathrm {A}}\)), (\(r_{\mathrm {C}}/r_{\mathrm {A}}\)) and a peak at (\(r_{\mathrm {B}}/r_{\mathrm {C}}\)), (\(r_{\mathrm {C}}/r_{\mathrm {B}}\)). As predicted, the distance correlation map (Fig. 5b) shows three peaks at (3.20 nm/3.75 nm), (3.75 nm/3.20 nm) and (3.15 nm/3.15 nm), which fits the expected distances. For reasons currently unknown to us, the diagonal peak appears at a slightly shorter distance than one would expect from the off-diagonal peaks.

According to the discussion about the absence of autocorrelation peaks (Sect. 6.2) and under the assumption that all distances have similarly wide distribution, all peaks in the distance correlation map are expected to have the same intensity as they all correspond to two correlation peaks each. The intensities of the peaks in the projection plot fit the DEER data (Fig. 6 in SI) and reveal the double presence of the shorter distance.

6.4 Scalene Geometry

In T\(_{\mathbf{scalene }}\) the nitroxides compose a scalene triangle, resulting in three different distances and a total of six expected correlation peaks. According to geometric structure simulation with Chem3D, the distances are about \(r^{\mathrm {sim}}_{1} = 1.9\) nm, \(r^{\mathrm {sim}}_{2} = 2.2\) nm and \(r^{\mathrm {sim}}_{3} = 3.4\) nm, with their respective dipolar frequencies being \(\omega _{\mathrm {A}}^{\mathrm {sim}}/2\pi = 7.5\,\)MHz, \(\omega _{\mathrm {B}}^{\mathrm {sim}}/2\pi = 4.9\) MHz and \(\omega _{\mathrm {C}}^{\mathrm {sim}}/2\pi = 1.3\) MHz. In this system, the short distances highlight one of the current challenges of TRIER: To be properly recorded, the high frequencies require a smaller time step in both indirect dimensions which strongly impacts acquisition time. This is particularly problematic in combination with long distances (low frequencies), which in turn require long time traces. Detection of the contribution from the short distances is additionally complicated by the fact that the width of the Pake pattern scales with \(r^{-3}\) and thus the amplitude scales with \(r^3\) [64]. In particular, detection of correlations between two short distances requires a very-high signal-to-noise ratio. In such a situation, Lorentz-to-Gauss transform has to be applied carefully: though it can separate the correlation peaks at small frequencies, the increase of noise in the spectrum can lead to correlation peaks from the short distances dropping beneath the noise level.

Using improved data processing we were able to improve the quality of the TRIER spectrum of T\(_{\mathbf{scalene }}\) compared to the previously published one [15], where the spectrum had a strong cross shape, lacking all correlations between \(\omega _{\mathrm {A}}\) and \(\omega _{\mathrm {B}}\). From the projection plots in Fig. 6a, we obtained the experimental dipolar frequencies \(\omega _{\mathrm {A}}^{\mathrm {exp}}/2\pi = 8.1\,\) MHz, \(\omega _{\mathrm {B}}^{\mathrm {exp}}/2\pi = 4.0\,\) MHz and \(\omega _{\mathrm {C}}^{\mathrm {exp}}/2\pi = 1.7\,\) MHz. The discrepancy between the simulated values and the observed dipolar frequencies is attributed to the inaccuracy of the simulation in combination with the \(r^{-3}\) dependency of the dipolar frequency, which lets small changes in the distance have a big impact on the frequency. The spectrum shows the correlation of \(r_{\mathrm {A}}\) with \(r_{\mathrm {B}}\) at (8.2 MHz/4.1 MHz) and (4.1 MHz/8.2 MHz). The correlation of \(r_{\mathrm {A}}\) with \(r_{\mathrm {C}}\) is revealed through the peaks at (8.2 MHz/1.7 MHz) and (1.7 MHz/8.2 MHz) and the connection between \(r_{\mathrm {B}}\) and \(r_{\mathrm {C}}\) is revealed in the slightly broader peaks at (1.7 MHz/4.0 MHz) and (4.0 MHz/1.7 MHz). The spectrum also shows an additional peak at (1.5 MHz/1.5 MHz) which we assign to imperfect background correction.

Fig. 6
figure 6

Experimental a TRIER spectrum and b distance correlation map of T\(_{\mathbf{scalene }}\). The TRIER projections in b are shown in blue and the DEER distance distribution in orange. The trinitroxide is of scalene geometry and has six correlation peaks. The diagonal peaks at (1.2 MHz/1.2 MHz) in a and (3.3 nm/3.3 nm) in b come from imperfect background correction in combination with the 2D APT algorithm (color figure online)

Full size image

The distance correlation map (Fig. 6b) reveals the scalene geometry of T\(_{\mathbf{scalene }}\) more clearly: Correlation of \(r_{\mathrm {A}}\) with \(r_{\mathrm {B}}\) can be seen from the peak at (2.1 nm/2.3 nm), (2.3 nm/2.1 nm) and with \(r_{\mathrm {C}}\) at (2.1 nm/3.3 nm), (3.2 nm/2.1 nm). The correlation peak of \(r_{\mathrm {B}}\) with \(r_{\mathrm {C}}\) is at (2.3 nm/3.3 nm), (3.2 nm/2.3 nm). All correlation peaks involving \(r_{\mathrm {B}}\) show a shoulder that was not visible in the spectrum, but is in agreement with DEER data (orange in Fig. 6b). The peaks on the diagonal at (2.1 nm/2.1 nm), (2.3 nm/2.3 nm) appear to arise from overlap of the neighboring off-diagonal peaks The artifact at (3.2 nm/3.2 nm) corresponds to the strong peaks that are visible in the spectrum at (1.5 MHz/1.5 MHz) and arises from imperfect background correction.

6.5 Rpo4/7

After obtaining distance correlation maps with model compounds, we extended our scope to systems that are more typical for the main current application field of DEER. With the open-source toolbox MMM (Multiscale Modeling of Macromolecules) [65] we simulated interspin distances for the mutant of the Rpo4/7 complex (see Fig. 7a). The chosen set of mutation positions consists of two overlapping distance distributions in the range of 2.8–3.3 nm (\(r_{\mathrm {A}}\), red and \(r_{\mathrm {B}}\), blue) and 4.2–4.4 nm (\(r_{\mathrm {C}}\), yellow). With this we expect the dipolar frequencies to be approximately \(\omega ^{\mathrm {sim}}_{\mathrm {A}} /2\pi = \omega ^{\mathrm {sim}}_{\mathrm {B}} /2\pi = 1.8\,\) MHz and \(\omega ^{\mathrm {sim}}_{\mathrm {C}} /2\pi = 0.4\,\) MHz, resembling the situation of T\(_{\mathbf{isosceles }}\) (Sect. 6.3). However, \(r_{\mathrm {B}}\) shows a strong shoulder at \(r^{\text {shoulder}}_{\mathrm {B}} = 3.3\,\) nm (\(\omega _{\mathrm {B}}^{\text {shoulder}} /2\pi = 1.4\,\) MHz) that does not overlap with \(r_{\mathrm {A} }\) and additional peaks or a splitting of the peaks can be expected. Indeed, the spectrum (Fig.  7a) shows a strong peak at (1.8 MHz/1.8 MHz) which corresponds to the correlation of the two shorter distances \(r_{\mathrm {A}}\) and \(r_{\mathrm {B}}\). The broad peak at (1.8 MHz/1.8 MHz) appears to have shoulders at around (1.8 MHz/1.2 MHz) and (1.2 MHz/1.8 MHz), which fit the expected correlation of the shoulder of \(r^{\text {shoulder}}_{\mathrm {B}}\) with \(r_{\mathrm {A}}\). The two coinciding correlations of \(r_{\mathrm {A}}\) with \(r_{\mathrm {C}}\) and \(r_{\mathrm {B}}\) with \(r_{\mathrm {C}}\) can be discerned at (0.5 MHz/1.8 MHz) and (1.8 MHz/0.5 MHz). A small shoulder appears to be visible at (0.5 MHz/1.2 MHz) and (1.2 MHz/0.5 MHz).

Interpretation of the correlation pattern is simplified in the distance-correlation map (Fig. 7b). A broad feature is at (3.0 nm/3.0 nm) which corresponds to the correlation of \(r_{\mathrm {A}}\) with \(r_{\mathrm {B}}\). Correlation of \(r_{\mathrm {B}}^{\text {shoulder}}\) with \(r_{\mathrm {A}}\) cannot be discerned as a peak. The peaks at (4.6 nm/3 nm) and (3 nm/4.6 nm) stem from correlation of \(r_{\mathrm {A}}\) with \(r_{\mathrm {C}}\) as well as \(r_{\mathrm {B}}\) with \(r_{\mathrm {C}}\) The correlation of \(r_{\mathrm {B}}^{\text {shoulder}}\) with \(r_{\mathrm {C}}\) is clearly visible at (4.7 nm/3.5 nm) and (3.5 nm/4.7 nm). The peak at (4.7 nm/4.7 nm) is an artifact from 2D-APT (Sect. 6.1).

Fig. 7
figure 7

a MMM simulation of the interspin distances based on the PDB structure 1GO3, experimental b TRIER spectrum and c distance correlation map of Rpo4/7. The TRIER projections in c are shown in blue and the DEER distance distribution in orange (color figure online)

Full size image

6.6 RRM1 of PTBP1

MMM simulations (Fig. 8a) for the RRM1 domain show three distinct distance distributions with maxima \(r_{\mathrm {A}}^{\mathrm {sim}} = 2\) nm (\(\omega _{\mathrm {A}}^{\mathrm {sim}} /2\pi = 7.0\,\)MHz, orange), \(r_{\mathrm {B}}^{\mathrm {sim}} = 2.3\,\)nm (\(\omega _{\mathrm {B}}^{\mathrm {sim}} /2\pi = 4.3\,\) MHz, blue) and \(r_{\mathrm {C}}^{\mathrm {sim}} = 3.5\,\) nm (\(\omega _{\mathrm {C}}^{\mathrm {sim}} /2\pi = 1.2\,\) MHz, yellow). The TRIER spectrum (Fig.  8b) shows correlation peaks at (1.5 MHz/4.5 MHz), (4.5 MHz/1.5 MHz) and at (4.5 MHz/4.5 MHz). All of the peaks show some splitting, as the two shorter distances do not fully overlap. Hence, RRM1 is similar to T\(_{\mathbf{scalene }}\), but with a larger difference between the short and the long distances. The peak like feature at (1.5 MHz/1.5 MHz) is an artifact from background correction.

Fig. 8
figure 8

a MMM simulation of the interspin distances based on the PDB structure 2N3O, experimental b TRIER spectrum and c distance correlation map of the RRM1 domain of PTBP1. The TRIER projections in c are shown in blue and the DEER distance distribution in orange (color figure online)

Full size image

The distance correlation map (Fig. 8c) shows the expected picture: The strong feature between 2–2.5 nm is in agreement with the correlation pattern of the two partially overlapping distributions \(r_{\mathrm {A}}\) and \(r_{\mathrm {B}}\). The correlation peaks of \(r_{\mathrm {A}}\) with \(r_{\mathrm {C}}\) are visible at (2 nm/3.5 nm) and (3.5 nm/2 nm) and between \(r_{\mathrm {B}}\) and \(r_{\mathrm {C}}\) at (2.7 nm/3.5 nm) and (3.5 nm/2.7 nm). The peak at (3.5 nm/3.5 nm) once again is an artifact from imperfect background correction.

7 Conclusion

Improvements in the TRIER pulse sequence and, in particular, in data processing enabled us to obtain much better resolved spectra of trinitroxide model compounds than in the original paper on TRIER [15]. Using two-dimensional APT we are now able to obtain the first two-dimensional distance correlation maps from the TRIER time-domain data. We showed that such correlation maps can not only be obtained for well-defined model compounds, but also for biological, relevant systems that are currently under investigation.

Nonetheless, application of TRIER in structural biology as a routine approach still poses significant challenges: proper setting of experimental (such as the time step and trace lengths) and processing parameters (Lorentz-to-Gauss transformation) require previous knowledge about what distances are to be expected. This information can generally be obtained through DEER measurements and, in our case, could also be predicted by MMM simulations. We recommend to use TRIER as a complement to DEER rather than a stand-alone technique. In systems that contain a distribution of distances that reach from short to long, the required experimental parameters can lead to long acquisition times up to 200 h for proteins even on a new generation AWG-based high-power Q-band spectrometer. A third problem arises from the fact that the amplitude of the Pake patterns scales with \(r^3\), meaning that correlation peaks with a short distance have a reduced intensity. This effect is particularly strong for correlations of two short distances, which can make them hard to detect and require long measurement times. One more issue is that in some cases the current implementation of background correction and data processing produces an artifact autocorrelation peak for the longest distance, which can lead to misinterpretation of the TRIER data.

We envision TRIER as an extension to DEER, where it can be useful in several cases: It can be used to distinguish between a mixture of two diradicals and a triradical. Only in the latter case we observe a TRIER signal with off-diagonal peaks. In the second scenario, TRIER can also be used to accurately probe the distance in a triradical, where the spin labels form an equilateral triangle. In such a case the DEER distance distribution suffers from sum and difference combination frequencies (ghost distances, [13]), which, at the cost of longer measurement times, are not present in the distance correlation maps.

In a third scenario, TRIER can aid interpretation of DEER distance distributions for macromolecules that exist in more than one conformation. In this case, distance correlation maps can be used to assign DEER distances that belong to the same molecule.

In follow-up work we expect to improve our experimental parameters to speed up the acquisition process, for example through non-uniform sampling. For data processing, we plan to implement stable regularization algorithms, such as gradient projection [66, 67], which is better suited for larger-scale problems. This should provide better resolved distance correlation maps and reduce the impact of artifact diagonal peaks at long distances. Future investigations will also involve compounds with different types of spin labels (such as nitroxide, gadolinium, copper and trityl). In this case, each spin label type can be assigned a role (observer, first pump, second pump). Since the spectra are well separated, complete elimination of overlap should be possible, which would increase the intensity of the echo and hence sensitivity. Not only would this allow larger fractions of spins to be excited, but also with better excitation selectivity, the contribution from pathways that lead to modulation in only one dimension could be reduced and the modulation depth for TRIER increased. On top of this, working with a combination of different spin labels has the benefit that it reduces the number of peaks in the spectrum which in turn facilitates assignment and interpretation, especially in cases where two or more conformations are present.