On the dynamic response of bi-directional functionally graded nanobeams under moving harmonic load accounting for surface effect

Abstract

This paper presents an investigation of the dynamic behavior of bi-directionally functionally graded (BDFG) micro/nanobeams excited by a moving harmonic load. The formulation is established in the context of the surface elasticity theory and the modified couple stress theory to incorporate the effects of surface energy and microstructure, respectively. Based on the generalized elasticity theory and the parabolic shear deformation beam theory, the nonclassical governing equations of the problem are obtained using Lagrange’s equation accounting for the physical neutral plane concept. The material properties of the beam smoothly change along both the axial and thickness directions according to power-law distribution, accounting for the gradation of the material length scale parameter and the surface parameters, i.e., residual surface stress, two surface elastic constants, and surface mass density. Using trigonometric Ritz method (TRM), the trial functions denoting transverse, axial deflections, and rotation of the cross sections of the beam are expressed in sinusoidal form. Then, with the aid of Lagrange’s equation, the system of equations of motion are derived. Finally, Newmark method is employed to find the dynamic responses of BDFG subjected to a moving harmonic load. To validate the present formulation and solution method, some comparisons of the obtained fundamental frequency and dynamic response with those available in the literature are performed. A parametric study is performed to extensively explore the impact of the key parameters such as the gradient indices in both directions, moving speed, and excitation frequency of the acting load on the dynamic response of BDFG nanobeams. The obtained results can serve as a guideline for assessing the multi-functional and optimal design of micro/nanobeams acted upon by a moving load.

1 Introduction

Functionally graded materials (FGMs) are composite materials with nonhomogeneous microstructures. FGMs are composed of two or more different materials with specific gradients leading to a desired continuous variation of the material properties in specific spatial direction(s). In comparison with the traditional composites, FGMs can provide many advantages such as higher strength, higher stiffness, lower stress intensity factor, higher thermal resistance, higher corrosion resistance, and elimination of residual stresses and interlaminar shear stress, [1, 2]. Due to their unique characteristics, FGMs are speedily used as structural elements in various engineering fields such as nuclear, aerospace, automotive, marine industry, biomedical, and optical engineering, [3]. As a consequence, a very huge number of studies has been performed using analytical, semi-analytical, and numerical techniques to investigate the static and dynamic problems of FGM structures, whose material properties are graded in only one direction, i.e., transversely functionally graded in the thickness direction (TFG), or axially functionally graded in the length direction (AFG), (see Refs. [4,5,6]).

In the last decades, the design and analysis of nanomaterials and nanostructures have been extensively increased because of their superior mechanical, thermal, and electrical properties. Nanostructures such as nanorods, nanobeams, nanoplates, and nanoshells have recently been used in many applications in micro/nanoscale devices such as sensors and actuators. For modelling of micro/nanoscale structures, the size effect on their mechanical and physical properties should be considered. Since the classical continuum mechanics is size-independent, it cannot capture the effect of small size [7,8,9,10,11,12]. In this regard, the molecular dynamic approaches and size-dependent continuum mechanics are employed to include the small-scale effect in micro- and nanostructures [13, 14]. Numerical simulations based on the molecular dynamic approaches are, however, generally complex and computationally expensive, especially for complicated structures with a huge number of atoms, and thus the nonclassical size-dependent continuum mechanics is extensively used. Several different nonclassical continuum mechanics theories including additional material length scale parameter(s) have been developed and employed to model the size-dependent phenomenon in miniaturized systems, such as the strain gradient theory “SGT” ([15, 16]), couple stress theory “CST” ([17,18,19]), nonlocal continuum elasticity theory “NET” ([20]), modified strain gradient theory “MSGT” ([9]), nonlocal strain gradient theory ([21]), modified couple stress theory “MCST” ([22]), and surface elasticity theory “SET” ([23, 24]). Critical reviews on modelling of micro/nanostructures based on the different nonclassical continuum mechanics theories have been presented by [25, 26]. The main difficulty encountered in the nonclassical continuum theories is the determination of the microstructural material-dependent length scale parameters. The MCST proposed by [22] has the advantage of involving only one additional microstructure-dependent length scale parameter for isotropic materials. Here, the MCST will be employed to capture the microstructure effect on the predicted response.

Structures and components in advanced machines such as aerospace shuttles and craft require advanced composites whose properties vary continuously in more than one direction to satisfy the requirements of temperature and stress distributions in two or more directions [27]. By the rapid advancement in nanomechanics, the static and dynamic characteristics of bi-directional functionally graded (BDFG) micro/nanosized beams have been modelled and investigated based on the differential nonlocal elasticity theory “DNET” ([6, 28,29,30,31,32,33,34]), MCST ([35,36,37,38,39,40,41,42]), and the differential nonlocal strain gradient theory “DNSGT” ([43,44,45]).

One of the most important characteristics of nanoscale structures is their extremely increasing ratio of surface area-to-bulk volume. As a result, the energy associated with the surface atoms is different from that of the bulk. Unlike in classical continuum mechanics, the surface energy cannot be neglected as it contributes significantly to the total energy. This is because the effects of the surface residual stress (surface tension) and surface elasticity are of the most important size-dependent effects in the analysis of the mechanical behavior of the nanoscale structures [46]. Gurtin and Murdoch ([23, 24]) proposed a surface elasticity theory to approximate the contribution of surface energy by assuming an elastic body with elastic surface layers of zero thickness that is perfectly bonded to the surface of the bulk continuum. The Gurtin and Murdoch surface elasticity theory (GM-SET) has been successfully employed in conjunction with the other nonclassical continuum theories in the analysis of homogeneous and one-dimensional FG structures, i.e., GM-SET combined with the DNET ([47,48,49]), GM-SET combined with the SGT ([50]), GM-SET combined with the DNSGT ([51]), GM-SET combined with the MCST ([52,53,54,55,56,57,58,59,60,61,62,63,64]), and GM-SET combined with the MCST in the framework of DNET ([65, 66]). Based on these studies, it has been shown that incorporating the influence of surface energy may show a stiffness-hardening or stiffness-softening of the studied nanostructures depending on whether the signs of the surface elastic constants are positive or negative.

Considering the surface effect on BDFG nanobeams, only few models have been recently developed. Lal and Dangi [67] adopted the differential nonlocal elasticity theory together with GM-SET to investigate the vibration response of BDFG Timoshenko nanobeam using the differential quadrature method (DQM). Power law was used to express the gradation of the material properties of the bulk continuum in the thickness and length directions, whereas the surface elastic constants were assumed to vary in thickness direction only, and the nonlocal parameter was assumed to be spatially-independent. Shanab and Attia [68,69,70] studied the bending, buckling, and vibration characteristics of uniform and tapered BDFG Euler–Bernoulli and Timoshenko micro/nanobeams in the framework of the MCST and GM-SET. Unlike [67], all the material properties of the bulk and surface continuums were assumed to vary in both the thickness and length directions via power law.

Furthermore, analysis of structures’ response under moving mass and moving load is very important for many practice engineering applications, such as bridges, tunnels, and rail. The vibration problems of a homogenous beam subjected to moving loads were extensively studied by [71,72,73,74,75]. The dynamic performance of one-directional FGM beams undergoing a moving load was studied based on the material gradation in the thickness direction by [76,77,78,79,80,81,82] or the material gradation in the length direction by [83,84,85]. Taking the features of BDFG into account, Şimşek [86] investigated the free and forced vibration responses of BDFG Timoshenko beams acted upon by moving loads using Ritz and the implicit time integration methods. Exponential functions were adopted to express the material variation in both thickness and length directions. Utilizing finite element method (FEM) and Newmark method, the vibration of a BDFG Timoshenko beam under a moving load was investigated by [87] assuming that the material properties were varied in both thickness and length directions via power law functions. Yang et al. [88] studied the vibration characteristics of a tapered BDFG Timoshenko beam subjected to a moving harmonic force employing the meshfree boundary-domain integral equation in conjunction with 2D elasticity theory. The exponential distribution was assumed for the variation of Young’s modulus and mass density in transverse and axial directions. Employing Ritz method and Gram-Schmidt orthogonalization procedure, [89] studied the free and forced vibrations of functionally graded graphene nanoplatelet-reinforced beams due to multiple moving loads based on third-order shear deformation beam theory. Recently, [90] utilized FEM with the aid of Newmark method to explore the dynamic response of a sandwich Timoshenko beam with BDFG face layers under a moving load. Power law functions were adopted to express the material properties of the skin layers. This work was extended by [91] to explore the effect of a partial Pasternak support on the dynamic response of BDFG sandwich beams under a moving mass using a quasi-3D theory. Based on the third-order shear deformation theory, the influences of Coriolis and centrifugal forces on the dynamic response of an inclined BDFG sandwich beam were considered by [92]. For the double-BDFG porous Timoshenko beam system subjected to moving load, its vibration performance was studied by [93] adopting Ritz and Newmark methods. Based on Timoshenko beam theory, [94] utilized Ritz method with the aid of Newmark method to explore the free and dynamic responses of a sandwich beam with TFG face layers under harmonic moving loads with elastic foundation for different boundary conditions. Using Chebyshev collocation method, and based on the third-order shear deformation theory, the free vibration of TFG beam and sandwich plates resting on an elastic foundation was investigated by [95] and [96], respectively. Recently, [97] utilized the Gram–Schmidt procedure to generate the shape functions for the Ritz method, and then the Newmark method was used to explore the dynamic response of TFG sandwich plates under multiple moving loads.

To capture the scale phenomena of micro/nanoscale beams acted upon by moving loads, [98, 99] adopted the DNET to study the dynamic response of simply supported TFG Euler–Bernoulli nanobeams subjected to a constant moving load. Based on DNET, the influences of surface energy and viscoelastic foundation on the steady-state response of Euler–Bernoulli nanobeam in a thermal environment and subjected to a moving concentrated load were examined by [100] using the multiple scales method. In [101], the forced vibration response of TFG nanobeams resting on Winkler–Pasternak foundation and under a uniform harmonic dynamic load was investigated employing a higher-order shear deformation beam theory in the context of DNET. In the context of MCST, [102] used the FEM and Wilson-theta method to study the forced vibration of nonuniform BDFG microbeams resting on a linear elastic foundation and acted upon by a moving harmonic load/mass. The influence of various models of the material gradation was presented. In the framework of parabolic shear deformation theory (PSDPT), [103] employed the MCST to study the vibration response of BDFG porous microbeams excited by a moving harmonic load using FEM. For even and uneven porosity distributions, power law functions were adopted to model the material variation in both thickness and length directions. The authors [104] adopted the MCST to explore the effects of thermal rise and moving load on the vibration response of a BDFG microbeam using FEM. Temperature-dependent material properties were assumed with a power law distribution in both the thickness and length directions. In the framework of NSGT, the dynamic performance of TFG nanobeams under a moving load was studied by [105, 106].

Based on the above-mentioned review, it is observed that the dynamic performance of BDFG nanobeams is still limited. The main objective of the present study is to develop an integrated microstructure-surface energy-based model for the dynamic response of BDFG nanobeams under a moving harmonic load based on a higher-order shear deformation beam theory, for the first time. Effects of microstructure and surface energy are captured via the MCST and GM-SET, respectively. The material properties of the bulk and surface continuums of the nanobeam are varying gradually along both the thickness and length directions according to power law functions. Based on the generalized elasticity theory, the formulation accounts for the physical neutral axis concept. Employing Lagrange’s equation, the nonclassical equations of motion and boundary conditions are derived. Ritz method in conjunction with Newmark method is used to obtain the dynamic deflection of a BDFG nanobeam under moving load. Both the present formulation and solution procedure are verified by comparing the predicted results with previous studies. By a parametric study, the effects of gradient indices in both thickness and length directions, velocity of moving load, excitation frequency, microstructure, and surface energy on the dynamic response of simply supported BDFG nanobeams are explored in detail.

2 Theory and formulation

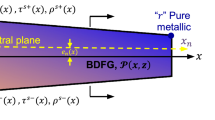
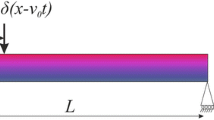
Consider a straight uniform BDFG microbeam with length $L$, width $b$, and thickness $h$, as demonstrated in Fig. 1, in a Cartesian coordinate system ($x$, $y$, $z$) that denotes the geometrical neutral plane (midplane). The beam is excited by a moving load with a constant velocity $v$. The BDFG beam is composed of a mixture of ceramic and metallic constituents, where the lowermost ($x$ = 0, $z$ = $-h/2$) and uppermost ($x$ = $L$, $z$ = $h/2$) surfaces of the nanobeam are pure metal “m” and pure ceramic “c”, respectively. The effective material properties describing the bulk and surface continuums of BDFG can be expressed via power law in both axial and transverse directions, such that [40, 41, 102]:

$$\left\{\begin{array}{c}{E}^{B}\left(x,z\right)\\ \nu \left(x,z\right)\\ {\rho }^{B}\left(x,z\right)\end{array}\right\}=\left\{\begin{array}{c}{E}_{m}^{B}\\ {\nu }_{m}\\ {\rho }_{m}^{B}\end{array}\right\}+\left\{\begin{array}{c}{E}_{c}^{B}-{E}_{m}^{B}\\ {\nu }_{c}-{\nu }_{m}\\ {\rho }_{c}^{B}-{\rho }_{m}^{B}\end{array}\right\}\left[{\left(\frac{x}{L}\right)}^{{k}_{x}}{\left(\frac{1}{2}+\frac{z}{h}\right)}^{{k}_{z}}\right],$$

(1)

$$l\left(x,z\right)={l}_{m}+\left({l}_{c}-{l}_{m}\right)\left[{\left(\frac{x}{L}\right)}^{{k}_{x}}{\left(\frac{1}{2}+\frac{z}{h}\right)}^{{k}_{z}}\right],$$

(2)

$$\left\{\begin{array}{c}{\tau }^{s}\left(x,z\right)\\ {\lambda }^{s}\left(x,z\right)\\ {\upmu }^{s}\left(x,z\right)\\ {\rho }^{s}\left(x,z\right)\end{array}\right\}=\left\{\begin{array}{c}{\tau }_{m}^{s}\\ {\lambda }_{m}^{s}\\ {\upmu }_{m}^{s}\\ {\rho }_{m}^{s}\end{array}\right\}+\left\{\begin{array}{c}{\tau }_{c}^{s}-{\tau }_{m}^{s}\\ {\lambda }_{c}^{s}-{\lambda }_{m}^{s}\\ {\upmu }_{c}^{s}-{\upmu }_{m}^{s}\\ {\rho }_{c}^{s}-{\rho }_{m}^{s}\end{array}\right\}\left[{\left(\frac{x}{L}\right)}^{{k}_{x}}{\left(\frac{1}{2}+\frac{z}{h}\right)}^{{k}_{z}}\right]$$

(3)

where the superscripts “$s$” and “$B$” refer, respectively, to the surface and bulk continuums of the beam. ${E}^{B}$, $\nu$, and ${\rho }^{B}$ are, respectively, Young’s modulus, Poisson’s ratio, and the mass density of the bulk continuum, $l$ represents the material length-scale parameter describing the microstructure effect on the bulk continuum, and ${\tau }^{s}$, ${\lambda }^{s}$, ${\upmu }^{s}$, and ${\rho }^{s}$ are the surface residual stress, elastic parameters, and surface mass density of the surface continuum. ${k}_{x}$ and ${k}_{z}$ are the gradient indices in the axial and transverse directions, respectively. The classical Lamé’s parameters of the bulk continuum are given by

Fig. 1

Illustration of a BDFG nanobeam with surface layers exposed to a moving load

$${\lambda }^{B}\left(x,z\right)=\frac{{E}^{B}\left(x,z\right) \nu \left(x,z\right)}{\left(1+\nu \left(x,z\right)\right)\left(1-2\nu \left(x,z\right)\right)}\quad \mathrm{and}\quad {\upmu }^{B}\left(x,{z}_{m}\right)=\frac{{E}^{B}\left(x,z\right)}{2\left(1+\nu \left(x,z\right)\right)}.$$

(4)

Ignoring the Poisson’s effect yields $\left[{\lambda }^{B}\left(x,z\right)+2{\upmu }^{B}\left(x,z\right)\right]\equiv {E}^{B}\left(x,z\right)$ as adopted by [43, 44, 103].

In Eqs. (1–3), the axially (AFG) and transversely (TFG) functionally graded distributions can be recovered by setting ${k}_{z}=0$ and ${k}_{x}=0$, respectively. An homogeneous beam made of pure metal constituent is obtained when ${k}_{x}={k}_{z}=0$.

Due to the nonsymmetric distribution of the material properties of the BDFG beam about its midplane, the geometrical neutral plane (GNP) does not coincide with the physical neutral plane (PNP), as demonstrated in Fig. 1. The deviation between the positions of GNP and PNP is given by [40, 41, 68, 69]

$$\large {e}_{n}\left(x\right)=\frac{{\int }_{-h/2}^{h/2}{\int }_{-b/2}^{b/2}z \left[{\lambda }^{B}\left(x,z\right)+2{\upmu }^{B}\left(x,z\right)\right] dydz}{{\int }_{-h/2}^{h/2}{\int }_{-b/2}^{b/2}\left[{\lambda }^{B}\left(x,z\right)+2{\upmu }^{B}\left(x,z\right)\right] dydz}, {z}_{n}\left(x\right)=z-{e}_{n}(x).$$

(5)

Unlike the TFG beam, the position of the physical neutral axis “${e}_{n}$” in a BDFG beam depends on the $x$-coordinate. For simplicity, Cartesian coordinates are used to approximate the ${z}_{n}$-coordinate instead of the curvilinear coordinates.

2.1 Kinematics and constitutive relations

In this study, a general shear deformation theory is used to express the kinematics of the BDFG nanobeam, in which the displacement field is given by

$$\begin{array}{l}{u}_{x}\left(x,z,t\right) =u\left(x\right)+f({z}_{n})\frac{\partial w\left(x,t\right)}{\partial x}+R\left({z}_{n}\right)\phi \left(x,t\right),\\ {u}_{y}\left(x,z,t\right)=0,\\ {u}_{z}\left(x,z,t\right)=w\left(x,t\right)\end{array}$$

(6)

where $u$ and $w$ are the displacement components of the midplane along, respectively, $x$ and $z$ directions, and $\phi$ is the transverse shear strain, and $t$ denotes time. Accounting for the physical neutral plane concept, the shear-strain function $R\left({z}_{n}\right)=R\left(z\right)-{r}_{n}(x)$, where

$${r}_{n}\left(x\right)= \frac{{\int }_{-h/2}^{h/2}{\int }_{-b/2}^{b/2}R\left(z\right) \left[{\lambda }^{B}\left(x,z\right)+2{\upmu }^{B}\left(x,z\right)\right] dydz}{{\int }_{-h/2}^{h/2}{\int }_{-b/2}^{b/2}\left[{\lambda }^{B}\left(x,z\right)+2{\upmu }^{B}\left(x,z\right)\right] dydz}.$$

(7)

Various beam theories can be satisfied by appropriate section of the functions $f({z}_{n})$ and $R\left({z}_{n}\right)$. Adopting the third-order parabolic shear deformable beam theory (PSDBT), [107],

$$f\left({z}_{n}\right)=-{z}_{n}\left(x\right) \mathrm{and} R\left({z}_{n}\right)=z\left(1-\frac{4{z}^{2}}{3{h}^{2}}\right)-{r}_{n}(x).$$

(8)

In the framework of generalized elasticity theory in combination with the modified couple stress theory, [22], the infinitesimal Green strain tensor ${\varvec{\varepsilon}}$, classical Cauchy stress tensor ${{\varvec{\sigma}}}^{B}$, symmetric curvature tensor ${\varvec{\chi}}$, and the deviatoric part of the couple stress tensor ${\varvec{m}}$ are given by [55, 65]:

$${\varvec{\varepsilon}}=\frac{1}{2}\left[\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^{T}\right],$$

(9.1)

$${{\varvec{\sigma}}}^{B}={\lambda }^{B}\left(x,z\right) \mathrm{tr}\left({\varvec{\varepsilon}}\right)I+2{\upmu }^{B}\left(x,z\right)\boldsymbol{ }{\varvec{\varepsilon}},$$

(9.2)

$${\varvec{\chi}}=\frac{1}{2}\left[\nabla {\varvec{\uptheta}}+{\left(\nabla {\varvec{\uptheta}}\right)}^{T}\right], {\varvec{\uptheta}}=\frac{1}{2}\mathrm{curl}\left(\mathbf{u}\right),$$

(10.1)

$${\varvec{m}}=\left[2{l}^{2}\left(x,z\right) {\upmu }^{B}\left(x,z\right)\right]{\varvec{\chi}}$$

(10.2)

where $\mathbf{u}$ and ${\varvec{\uptheta}}$ represent the displacement field and rotation field vectors, respectively. $l$ denotes the material length scale parameter (MLSP) of the material, which captures the size-dependent effect of the material microstructure. Here, the gradation of the MLSP in both thickness and length directions of the BDFG beam is considered, as depicted in Eq. (2).

Based on the Gurtin–Murdoch surface elasticity theory, the surface layer of a bulk material is assumed to be of zero thickness and fulfills different constitutive equations involving the surface parameters, i.e., residual surface stress ${\tau }^{s}$ and the surface elastic constants ${\lambda }^{s}$ and ${\upmu }^{s}$, [23, 24]. According to this theory, the in-plane (${{\varvec{\sigma}}}^{s}$) and out-of-plane (${\sigma }_{n\alpha }^{s}$) components of the surface stress tensor are given by Gurtin and Murdoch [23, 24] as follows, respectively:

$${{\varvec{\sigma}}}^{s\pm }=2\left[{\upmu }^{s\pm }\left(x,z\right)-{\tau }^{s\pm }\left(x,z\right)\right]{{\varvec{\varepsilon}}}^{\pm }+\left[{\tau }^{s\pm }\left(x,z\right)+\left[{\lambda }^{s\pm }\left(x,z\right)+{\tau }^{s\pm }\left(x,z\right)\right]\mathrm{tr}\left({{\varvec{\varepsilon}}}^{\pm }\right)\right] I+{\tau }^{s\pm }\left(x,z\right){\nabla }^{s}{\mathbf{u}}^{\pm },$$

(11.1)

$${\sigma }_{n\alpha }^{s\pm }={\tau }^{s\pm }\left(x,z\right){u}_{n,\alpha }^{\pm } , \alpha =\mathrm{1,2},$$

(11.2)

In Eqs. (11), signs (+) and (−) stand for the upper and lower surface layers of the BDFG beam, respectively. ${n}_{i}$ denotes the components of the outward unit normal vector $\mathbf{n}$ to the beam lateral surface.

The nonzero components of the Green strain and the symmetric curvature tensor in accordance with Eqs. (6), (8), (9.1), and (10.1) can be obtained as

$$\begin{gathered} \varepsilon _{{xx}} = \frac{{\partial u_{x} }}{{\partial x}} = \frac{{\partial u}}{{\partial x}} - z_{n} \left( x \right)\frac{{\partial ^{2} w}}{{\partial ^{2} x}} + R\left( {z_{n} } \right)\frac{{\partial \phi }}{{\partial x}} - z_{{n,x}} \frac{{\partial w}}{{\partial x}} - r_{{n,x}} \phi, \hfill \\ \gamma _{{xz}} = \gamma _{{zx}} = 2\varepsilon _{{xz}} = \frac{{\partial R\left( {z_{n} } \right)}}{{\partial z}}\phi, \hfill \\ \end{gathered}$$

(12)

$$\begin{gathered} \chi _{{xy}} = \chi _{{yx}} = \frac{1}{2}\left( {\frac{1}{2}\frac{{\partial R\left( {z_{n} } \right)}}{{\partial z}}\frac{{\partial \phi }}{{\partial x}} + \frac{1}{2}\frac{{\partial ^{2} R\left( {z_{n} } \right)}}{{\partial z\partial x}}\phi - \frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right), \hfill \\ \chi _{{yz}} = \chi _{{zy}} = \frac{1}{4}\frac{{\partial ^{2} R\left( {z_{n} } \right)}}{{\partial z^{2} }}\phi \hfill \\ \end{gathered}$$

(13)

where subscript $x$ represents the derivative w.r.to $x$. It should be mentioned that the derivative $\frac{{\partial }^{2}R\left({z}_{n}\right)}{\partial z\partial x}$ will be zero.

In light of Eqs. (9.2) and (10.2), the nonzero components of the classical Cauchy stress tensors and the deviatoric part of the couple stress tensor are [40, 41]

$$\begin{gathered}{\sigma }_{xx}^{B}={\mathbb{E}}^{B}\left(x,z\right){\varepsilon }_{xx};\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\mathbb{E}}^{B}\left(x,z\right)=\left[{\lambda }^{B}\left(x,z\right)+2{\upmu }^{B}\left(x,z\right)\right],\\ {\sigma }_{xz}^{B}={\upmu }^{B}\left(x,z\right)\frac{\partial R\left({z}_{n}\right)}{\partial z} \phi ,\end{gathered}$$

(14)

$$\begin{gathered}{m}_{yx}={m}_{xy}=2\left[{l}^{2}\left(x,z\right) {\upmu }^{B}\left(x,z\right)\right] {\chi }_{xy},\\ {m}_{zy}={m}_{yz}=2\left[{l}^{2}\left(x,z\right) {\upmu }^{B}\left(x,z\right)\right] {\chi }_{zy}.\end{gathered}$$

(15)

Besides, the nonzero components of the surface stresses in the BDFG nanobeam based on PSDBT can be obtained by substituting Eqs. (6) and (12) into Eq. (11), such that

$$\begin{array}{l}{\sigma }_{xx}^{s}={\tau }^{s\pm }\left(x,z\right)+{\mathbb{E}}^{s}\left(x,z\right){\varepsilon }_{xx} , {\mathbb{E}}^{s}\left(x,z\right)={\lambda }^{s\pm }\left(x,z\right)+2{\upmu }^{s\pm }\left(x,z\right),\\ {\sigma }_{xs}^{s}=\left[2{\upmu }^{s\pm }\left(x,z\right){\varepsilon }_{xz}-{\tau }^{s\pm }\left(x,z\right)\frac{\partial w}{\partial x}\right]{n}_{y} \equiv {\sigma }_{xz}^{s} {n}_{y},\\ {\sigma }_{sx}^{s}=\left[2{\upmu }^{s\pm }\left(x,z\right){\varepsilon }_{zx}-{\tau }^{s\pm }\left(x,z\right)\frac{\partial {u}_{x}}{\partial z}\right]{n}_{y}\equiv {\sigma }_{zx}^{s} {n}_{y},\\ {\sigma }_{nx}^{s}={\tau }_{s}{u}_{n,x}^{s}\equiv \left[{\tau }^{s\pm }\left(x,z\right)\frac{\partial w}{\partial x}\right]{n}_{z}\end{array}$$

(16)

where ${n}_{y}$ and ${n}_{z}$ denote the components of the unit outward normal vector $\mathbf{n}$ to the beam lateral surface in the $y$ and $z$ directions, respectively, i.e., with $\theta$ the angle between the $y$-axis and the normal vector $\mathbf{n}$, then ${n}_{y}$ and ${n}_{y}$ are given by, respectively, $\mathrm{cos}\theta$ and $\mathrm{sin}\theta$. The subscript “$s$” represents the direction of the unit tangent vector $\mathbf{s}$ on the boundary of the beam. ${\sigma }_{xz}^{s}$ represents the in-plane shear stress component on the two lateral surfaces (parallel to the $xz$ plane) of a beam with a uniform rectangular cross section. When $\theta =0$, the values of ${\sigma }_{zx}^{s}$ and ${\sigma }_{xz}^{s}$, equal those of ${\sigma }_{sx}^{s}$ and ${\sigma }_{xs}^{s}$, respectively. It is important to emphasize the fact that the in-plane shear stress tensor defined by Eq. (11.1) in not symmetric, and thus ${\sigma }_{xz}^{s}$ and ${\sigma }_{zx}^{s}$ are not equal [53]. Many authors employed the Gurtin–Murdoch surface elasticity theory claiming a symmetric in-plane shear stress tensor in their variational models.

2.2 Variational formulation

In the context of the generalized elasticity theory in combination with the surface elasticity theory and modified couple stress theory, the total strain energy (${\mathbb{U}}$) of an isotropic elastic BDFG deformed nanobeam can be written as follows [55, 65]:

$${\mathbb{U}}=\frac{1}{2}{\int }_{0}^{L}\left[{\int }_{A}\left[{\sigma }_{ij}^{B}{\varepsilon }_{ij}+{m}_{ij}{\chi }_{ij}\right]dA+{\oint }_{\partial A}\left[{\sigma }_{ij}^{s} {\varepsilon }_{ij}\right]dS\right]dx$$

(17)

where $A$ and $\partial A$ are, respectively, the cross-sectional area and the boundary of the beam. Substitution of Eqs. (14–16) into Eq. (17) yields

$$\begin{aligned} {\mathbb{U}} & = \frac{1}{2}\int _{0}^{L} \left\{ {\int _{A} \left( {\sigma _{{xx}}^{B} \varepsilon _{{xx}} + 2\sigma _{{xz}}^{B} \varepsilon _{{xz}} + 2m_{{xy}} \chi _{{xy}} + 2m_{{yz}} \chi _{{yz}} } \right)dA} \right. \\ & \quad \left. { + \oint_{{\partial A}} \left( {\sigma _{{xx}}^{s} \varepsilon _{{xx}} + \sigma _{{xs}}^{s} \varepsilon _{{xs}} + \sigma _{{sx}}^{s} \varepsilon _{{sx}} + 2\sigma _{{nx}}^{s} \varepsilon _{{nx}} } \right)} \right\}dx \\ \end{aligned}$$

(18)

with

$$\begin{aligned}{\varepsilon }_{sx}&={\varepsilon }_{xs}=\frac{1}{2}\left(\frac{\partial {u}_{z}}{\partial x}+\frac{\partial {u}_{x}}{\partial z}\right){n}_{y}\equiv \frac{1}{2}\left[-\frac{\partial R\left({z}_{n}\right)}{\partial {z}_{n}}\phi \right]{n}_{y}\equiv {\varepsilon }_{zx}{n}_{y},\\ {\varepsilon }_{nx}&={\varepsilon }_{xn}=\frac{1}{2}\left(\frac{\partial {u}_{z}}{\partial x}\right){n}_{z}=\frac{1}{2}\left(\frac{\partial w}{\partial x}\right){n}_{z},\end{aligned}$$

(19)

Substituting Eqs. (14–16) and (19) into Eq. (18) and with some mathematical manipulations, the total strain energy of the BDFG nanobeam including the microstructure and surface energy effects can be obtained in terms of the displacement field as follows:

$$\begin{gathered} \mathbb{U} = \frac{1}{2}\int_{0}^{L} {\left\{ {\left[ {A_{{xx}} \left( {\frac{{\partial u}}{{\partial x}}} \right)^{2} - 2B_{{xx}} \frac{{\partial u}}{{\partial x}}\frac{{\partial ^{2} w}}{{\partial ^{2} x}} + \left[ {D_{{xx}} + A_{{xz}} } \right]\left( {\frac{{\partial ^{2} w}}{{\partial x^{2} }}} \right)^{2} + 2E_{{xx}} \frac{{\partial u}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}}} \right.} \right.} \hfill \\ \left. { - 2\left[ {F_{{xx}} + \frac{1}{2}D_{{xz}} } \right]\frac{{\partial ^{2} w}}{{\partial ^{2} x}}\frac{{\partial \phi }}{{\partial x}} + \left[ {H_{{xx}} + \frac{1}{4}B_{{xz}} } \right]\left( {\frac{{\partial \phi }}{{\partial x}}} \right)^{2} } \right] \hfill \\ + 2z_{{n,x}} \left\{ {A_{{xx}}^{B} \left[ { - ~\frac{{\partial u}}{{\partial x}}\frac{{\partial w}}{{\partial x}} + \frac{1}{2}z_{{n,x}} \left( {\frac{{\partial w}}{{\partial x}}} \right)^{2} + r_{{n,x}} \frac{{\partial w}}{{\partial x}}\phi } \right] - E_{{xx}}^{B} \frac{{\partial \phi }}{{\partial x}}\frac{{\partial w}}{{\partial x}}} \right\} \hfill \\ + 2r_{{n,x}} \left\{ {A_{{xx}}^{B} \left[ { - ~\frac{{\partial u}}{{\partial x}}\phi + \frac{1}{2}r_{{n,x}} \phi ^{2} } \right] - E_{{xx}}^{B} \frac{{\partial \phi }}{{\partial x}}\phi } \right\} + \left[ {B_{{xz}} + \frac{1}{4}E_{{xz}} } \right]\phi ^{2} \hfill \\ \left. { + \left[ {C_{0}^{s} \frac{{\partial u}}{{\partial x}} - C_{1}^{s} \frac{{\partial ^{2} w}}{{\partial ^{2} x}} + C_{2}^{s} \frac{{\partial \phi }}{{\partial x}}} \right] + C_{n}^{s} \left( {\frac{{\partial w}}{{\partial x}}} \right)^{2} } \right\}dx \hfill \\ \end{gathered}$$

(20)

in which

$$\left\{ {\begin{array}{*{20}c} {A_{{xx}} (x)} \\ {B_{{xx}} (x)} \\ {D_{{xx}} (x)} \\ {E_{{xx}} (x)} \\ {F_{{xx}} (x)} \\ {H_{{xx}} (x)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {A_{{xx}}^{B} (x)} \\ {B_{{xx}}^{B} (x)} \\ {D_{{xx}}^{B} (x)} \\ {E_{{xx}}^{B} (x)} \\ {F_{{xx}}^{B} (x)} \\ {H_{{xx}}^{B} (x)} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {A_{{xx}}^{s} (x)} \\ {B_{{xx}}^{s} (x)} \\ {D_{{xx}}^{s} (x)} \\ {E_{{xx}}^{s} (x)} \\ {F_{{xx}}^{s} (x)} \\ {H_{{xx}}^{s} (x)} ,\\ \end{array} } \right\},$$

(21.1)

$${\mathcal{B}}_{xz}\left(x\right)={B}_{xz}^{B}\left(x\right)+{B}_{m}^{s}\left(x\right)-\frac{1}{2}{B}_{t}^{s}\left(x\right)$$

(21.2)

with

$$\left\{\begin{array}{c}{A}_{xx}^{B}(x)\\ {B}_{xx}^{B}(x)\\ {D}_{xx}^{B}(x)\\ {E}_{xx}^{B}(x)\\ {F}_{xx}^{B}(x)\\ {H}_{xx}^{B}(x)\end{array}\right\}={\int }_{-b/2}^{b/2}{\int }_{-h/2}^{h/2}{\mathbb{E}}^{B}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n} \\ {z}_{n}^{2}\\ R\left({z}_{n}\right)\\ {z}_{n}R\left({z}_{n}\right)\\ {R}^{2}\left({z}_{n}\right)\end{array}\right\}dzdy,$$

(22.1)

$$\begin{array}{c}\left\{\begin{array}{c}{A}_{xx}^{s}(x)\\ {B}_{xx}^{s}(x)\\ {D}_{xx}^{s}(x)\\ {E}_{xx}^{s}(x)\\ {F}_{xx}^{s}(x)\\ {H}_{xx}^{s}(x)\end{array}\right\}={\oint }_{\partial A}{\mathbb{E}}^{s}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n} \\ {z}_{n}^{2}\\ R\left({z}_{n}\right)\\ {z}_{n}R\left({z}_{n}\right)\\ {R}^{2}\left({z}_{n}\right)\end{array}\right\}dS,\end{array}$$

(22.2)

$${B}_{xz}^{B}\left(x\right)={\int }_{-b/2}^{b/2}{\int }_{-h/2}^{h/2}{\upmu }^{B}\left(x,z\right){\left(\frac{\partial R\left({z}_{n}\right)}{\partial {z}_{n}}\right)}^{2}dzdy,$$

(22.3)

$$\left\{\begin{array}{c}{A}_{xz}(x)\\ {B}_{xz}(x)\\ {D}_{xz}(x)\\ {E}_{xz}(x)\end{array}\right\}={\int }_{-b/2}^{b/2}{\int }_{-h/2}^{h/2}\left[{l}^{2}\left(x,z\right) {\upmu }^{B}\left(x,z\right)\right]\left\{\begin{array}{c}1\\ {\left(\frac{\partial R\left({z}_{n}\right)}{\partial {z}_{n}}\right)}^{2}\\ \frac{\partial R\left({z}_{n}\right)}{\partial {z}_{n}}\\ {\left(\frac{{\partial }^{2}R\left({z}_{n}\right)}{\partial {{z}_{n}}^{2}}\right)}^{2}\end{array}\right\}dzdy,$$

(22.4)

$$\left\{\begin{array}{c}\begin{array}{c}{\mathcal{C}}_{0}^{s}\\ {\mathcal{C}}_{1}^{s}\end{array}\\ {\mathcal{C}}_{2}^{s}\\ {\mathcal{C}}_{n}^{s}\end{array}\right\}={\oint }_{\partial A}{\tau }^{s}\left(x,z\right)\left\{\begin{array}{c}\begin{array}{c}1\\ {z}_{n}\end{array}\\ R\left({z}_{n}\right)\\ {n}_{z}^{2}\end{array}\right\}dS,$$

(22.5)

$$\left\{\begin{array}{c}{B}_{m}^{s}\\ {B}_{t}^{s}\end{array}\right\}={\oint }_{\partial A}\left\{\begin{array}{c}{\upmu }^{s}\left(x,z\right)\\ {\tau }^{s}\left(x,z\right)\end{array}\right\}{\left(\frac{\partial R\left({z}_{n}\right)}{\partial {z}_{n}}\right)}^{2}{n}_{y}^{2} dS.$$

(22.6)

It is worth noting that the stiffnesses ${B}_{xx}^{B}(x)$ disappear in case of neutral axis analysis.

The kinetic energy of the BDFG nanobeams accounting for the surface effects can be expressed as

$$\begin{aligned} {\mathbb{T}} & \equiv \frac{1}{2}\int _{0}^{L} \int _{A} \rho ^{B} \left( {x,z } \right)\left[ {\left( {\frac{{\partial u_{x} }}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{{\partial t}}} \right)^{2} } \right]dAdx + \frac{1}{2}\int _{0}^{L} {\oint }_{{\partial A}} \rho ^{s} \left( {x,z } \right)\left[ {\left( {\frac{{\partial u_{x} }}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{{\partial t}}} \right)^{2} } \right]dsdx \\ & = \frac{1}{2}\int _{0}^{L} \left[ {\left( {{\text{I}}_{A} \frac{{\partial u}}{{\partial t}} - {\text{I}}_{B} \frac{{\partial ^{2} w}}{{\partial x\partial t}} + {\text{I}}_{E} \frac{{\partial \phi }}{{\partial t}}} \right)\frac{{\partial u}}{{\partial t}} + {\text{I}}_{A} \left( {\frac{{\partial w}}{{\partial t}}} \right)\frac{{\partial w}}{{\partial t}}} \right. \\ &\left. \quad - \left( {{\text{I}}_{B} \frac{{\partial u}}{{\partial t}} - {\text{I}}_{D} \frac{{\partial ^{2} w}}{{\partial x\partial t}} + {\text{I}}_{F} \frac{{\partial \phi }}{{\partial t}}} \right)\frac{{\partial ^{2} w}}{{\partial x\partial t}} + \left( {{\text{I}}_{E} \frac{{\partial u}}{{\partial t}} - {\text{I}}_{F} \frac{{\partial ^{2} w}}{{\partial x\partial t}} + {\text{I}}_{H} \frac{{\partial \phi }}{{\partial t}}} \right)\frac{{\partial \phi }}{{\partial t}} \right]dx \\ \end{aligned}$$

(23)

in which the mass moments of inertia, incorporating the mass density of the bulk and surface continuums, are

$$\left\{\begin{array}{c}{\mathrm{I}}_{A}(x)\\ {\mathrm{I}}_{B}(x)\\ {\mathrm{I}}_{D}(x)\\ {\mathrm{I}}_{E}(x)\\ {\mathrm{I}}_{F}(x)\\ {\mathrm{I}}_{H}(x)\end{array}\right\}={\int }_{-b/2}^{b/2}{\int }_{-h/2}^{h/2}{\rho }^{B}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n} \\ {z}_{n}^{2}\\ R\left({z}_{n}\right)\\ {z}_{n}R\left({z}_{n}\right)\\ {R}^{2}\left({z}_{n}\right)\end{array}\right\}dzdy+{\oint }_{\partial A}{\rho }^{s}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n} \\ {z}_{n}^{2}\\ R\left({z}_{n}\right)\\ {z}_{n}R\left({z}_{n}\right)\\ {R}^{2}\left({z}_{n}\right)\end{array}\right\}dS.$$

(24)

A general form for the virtual work done by the forces applied on the current beam in the context of the modified couple stress theory and surface elasticity theory can be expressed as [53, 65]:

$$\delta {\mathbb{W}}={\int }_{\Omega }\left(\mathbf{f}\bullet \delta {\varvec{u}}+{\mathbf{f}}_{c}\bullet \delta {\varvec{\uptheta}}\right)d\Omega +{\oint }_{\partial A}\left(\overline{\mathbf{t}}\boldsymbol{ }.\delta \mathbf{u}+\overline{\mathbf{s}}\boldsymbol{ }.\delta {\varvec{\uptheta}}\right)dS$$

(25)

where $\mathbf{f}$ and ${\mathbf{f}}_{c}$ are, respectively, the body force resultant and body couple resultant, both per unit volume, $\overline{\mathbf{t} }$ and $\overline{\mathbf{s} }$ are, respectively, the traction resultant and surface couple resultant, both per unit area. In the absence of an applied compressive force, assuming the externally applied harmonic load moves with a constant speed ignoring its inertial effect, and employing zero initial conditions, the virtual work can be obtained as

$$\delta {\mathbb{W}}={\int }_{0}^{L}\left\{{f}_{u}\delta u+\left[P\left(t\right)w({x}_{Q},t)\updelta \left(x-vt\right)+q+\frac{\partial }{\partial x}\left({f}_{c}-\frac{1}{2}{f}_{c}{a}_{c}(x) \right)\right]\delta w-\left(\frac{1}{2}{f}_{c}{a}_{c}(x) \right)\delta \frac{\partial w}{\partial x}+\left(\frac{1}{2}{f}_{c}{a}_{c}(x) \right)\delta \phi \right\}dx+{\left\{\overline{N }\delta u+\left[\overline{V }-\left({f}_{c}-\frac{1}{2}{f}_{c}{a}_{c}(x) \right)\right]\delta w-\left({\overline{M} }_{c}+{\overline{M} }_{nc}\right)\delta \frac{\partial w}{\partial x}-{\overline{M} }_{c}\delta \phi \right\}_{0}^{L}}$$

(26)

where $v$ is the velocity of the moving harmonic load, $\updelta$ represents the Dirac-delta function, ${f}_{u}$ and $q$ are, respectively, the distributed loads in $x$- and $z$-directions per unit length along the $x$-axis, ${f}_{c}$ is the $y$-component of the body couple per unit length along the $x$-axis. $\overline{N }$, $\overline{V }$, ${\overline{M} }_{c}$, and ${\overline{M} }_{nc}$ are, respectively, the applied axial force and lateral force, classical external bending moment, and the nonclassical external bending moment due to the couple stress exerted at the two ends of the beam, and ${a}_{c}$ is defined as

$${a}_{c}(x)={\int }_{-b/2}^{b/2}{\int }_{-h/2}^{h/2}\frac{\partial R\left({z}_{n}\right)}{\partial {z}_{n}} dzdy.$$

(27)

The applied external moving harmonic load is given by

$$P\left(t\right)={P}_{0}\mathrm{sin}\left(\Omega t\right)$$

(28)

in which ${P}_{0}$ and $\Omega$ are, respectively, the amplitude and frequency of the applied moving load. The location of the moving load at any instant, measured from the left end of the beam, is defined as

$${x}_{Q}\left(t\right)=vt, {0<x}_{Q}<L, 0<t<L/v.$$

(29)

Finally, the total energy of the BDFG nanobeam is given as

$$\Pi ={\mathbb{T}}-\left({\mathbb{U}}+{\mathbb{W}}\right).$$

(30)

3 Solution procedure

In this Section, the Lagrange’s equations are used to obtain the system of equations of motion. For this purpose, trigonometric Ritz method (TRM) is applied first. The displacement functions $w\left( {x,t} \right)\;u\left( {x,t} \right)$, and $\phi \left( {x,t} \right)$ are approximated by series of trigonometric functions that satisfy the geometric simply supported boundary conditions as follows:

$$\left\{ {\begin{array}{*{20}c} {w\left( {x,t} \right)} \\ {u\left( {x,t} \right)} \\ {\phi \left( {x,t} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\sum\limits_{r = 1}^{M} {A_{r} \left( t \right)\theta_{wr} \left( x \right)} } \\ {\sum\limits_{r = 1}^{M} {B_{r} \left( t \right)\theta_{ur} \left( x \right)} } \\ {\sum\limits_{r = 1}^{M} {C_{r} \left( t \right)\theta_{\phi r} \left( x \right)} } \\ \end{array} } \right\}$$

(31)

where $A_{r} \left( t \right),\;B_{r} \left( t \right)$, and $C_{r} \left( t \right)$ are the unknown time-dependent coefficients to be determined. The admissible trigonometric functions are defined as follows:

$$\begin{array}{*{20}c} {\theta_{{{{wr}}}} \left( x \right) = \sin \left( {\frac{r\pi x}{L}} \right)}, \\ {\theta_{{{{ur}}}} \left( x \right) = \theta_{\phi r} \left( x \right) = \frac{{d\theta_{{{{wr}}}} }}{dx}}, \\ \end{array}$$

(32)

Substituting Eqs. (31, 32) into Eq. (30), and then using Lagrange’s equations given by Eq. (33)

$$\frac{d}{dt}\left( {\frac{\partial \Pi }{{\partial \dot{q}_{k} }}} \right) - \frac{\partial \Pi }{{\partial q_{k} }} = 0, k = 1,2,3, \ldots , 3M$$

(33)

in which

$$q_{k} = \left\{ {\begin{array}{*{20}l} {A_{k} \left( t \right),\;k = 1,2, \ldots M} \hfill \\ {B_{k} \left( t \right),\;k = M + 1, \ldots 2M} \hfill \\ {C_{k} \left( t \right),\;k = 2M + 1, \ldots 3M} \hfill \\ \end{array} } \right.$$

(34)

Applying the Lagrange equations yields the following system of equations of motion:

$$\left[ {\mathbb{K}} \right]\left\{ {q_{k} \left( t \right)} \right\} + \left[ {\mathbb{M}} \right]\left\{ {\ddot{q}_{k} \left( t \right)} \right\} = \left\{ {F^{t} } \right\} - \left\{ {F^{SE} } \right\}$$

(35)

where the elements of the stiffness matrix $\left[ {\mathbb{K}} \right]$ and the mass matrix $\left[ {\mathbb{M}} \right]$ are, respectively, defined as

$$\left\{ {\begin{array}{*{20}l} {{\mathbb{K}}_{11} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{12} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{13} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{21} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{22} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{23} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{31} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{32} \left( {r,k} \right)} \hfill \\ {{\mathbb{K}}_{33} \left( {r,k} \right)} \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\left[ {D_{xx} + A_{xz} } \right]\theta_{wr}^{^{\prime\prime}} \theta_{wk}^{^{\prime\prime}} + \left( {{\mathcal{C}}_{n}^{s} + z_{0,x}^{2} A_{xx}^{B} } \right)\theta_{wr}^{^{\prime}} \theta_{wk}^{^{\prime}} } \hfill \\ { - B_{xx} \theta_{ur}^{^{\prime}} \theta_{wk}^{^{\prime\prime}} - z_{0,x} A_{xx}^{B} \theta_{ur}^{^{\prime}} \theta_{wk}^{^{\prime}} } \hfill \\ { - \left[ {F_{xx} + \frac{1}{2}D_{xz} } \right]\theta_{\phi r}^{^{\prime}} \theta_{wk}^{^{\prime\prime}} + z_{0,x} r_{0,x} A_{xx}^{B} \theta_{\phi r} \theta_{wk}^{^{\prime}} + z_{0,x} E_{xx}^{B} \theta_{\phi r}^{^{\prime}} \theta_{wk}^{^{\prime}} } \hfill \\ { - B_{xx} \theta_{wr}^{^{\prime\prime}} \theta_{uk}^{^{\prime}} - z_{0,x} A_{xx}^{B} \theta_{wr}^{^{\prime}} \theta_{uk}^{^{\prime}} } \hfill \\ {A_{xx} \theta_{ur}^{^{\prime}} \theta_{uk}^{^{\prime}} } \hfill \\ {E_{xx} \theta_{\phi r}^{^{\prime}} \theta_{uk}^{^{\prime}} - r_{0,x} A_{xx}^{B} \theta_{\phi r} \theta_{uk}^{^{\prime}} } \hfill \\ { - \left[ {F_{xx} + \frac{1}{2}D_{xz} } \right]\theta_{wr}^{^{\prime\prime}} \theta_{\phi k}^{^{\prime}} + z_{0,x} r_{0,x} A_{xx}^{B} \theta_{wr}^{^{\prime}} \theta_{\phi k} - z_{0,x} E_{xx}^{B} \theta_{wr}^{^{\prime}} \theta_{\phi k}^{^{\prime}} } \hfill \\ {E_{xx} \theta_{ur}^{^{\prime}} \theta_{\phi k}^{^{\prime}} - r_{0,x} A_{xx}^{B} \theta_{ur}^{^{\prime}} \theta_{\phi k} } \hfill \\ {\left[ {H_{xx} + \frac{1}{4}B_{xz} } \right]\theta_{\phi r}^{^{\prime}} \theta_{\phi k}^{^{\prime}} + \left[ {B_{xz} + \frac{1}{4}E_{xz} + r_{0,x} A_{xx}^{B} } \right]\theta_{\phi r} \theta_{\phi k} - r_{0,x} E_{xx}^{B} \left( {\theta_{\phi r}^{^{\prime}} \theta_{\phi k} + \theta_{\phi r} \theta_{\phi k}^{^{\prime}} } \right)} \hfill \\ \end{array} } \right\}dx,$$

(36)

$$\left\{ {\begin{array}{*{20}l} {{\mathbb{M}}_{11} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{12} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{13} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{21} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{22} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{23} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{31} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{32} \left( {r,k} \right)} \hfill \\ {{\mathbb{M}}_{33} \left( {r,k} \right)} \hfill \\ \end{array} } \right\} = \int_{0}^{L} {\left\{ {\begin{array}{*{20}l} {I_{A} \theta_{{{{wr}}}} \theta_{{{{wk}}}} + I_{D} \theta_{{{{wr}}}}^{^{\prime}} \theta_{{{{wk}}}}^{^{\prime}} } \hfill \\ { - I_{B} \theta_{{{{ur}}}} \theta_{{{{wk}}}}^{^{\prime}} } \hfill \\ { - I_{F} \theta_{\phi r} \theta_{{{{wk}}}}^{^{\prime}} } \hfill \\ { - I_{B} \theta_{{{{wr}}}}^{^{\prime}} \theta_{{{{uk}}}} } \hfill \\ {I_{A} \theta_{{{{ur}}}} \theta_{{{{uk}}}} } \hfill \\ {I_{E} \theta_{\phi r} \theta_{{{{uk}}}} } \hfill \\ { - I_{F} \theta_{{{{wr}}}}^{^{\prime}} \theta_{\phi k} } \hfill \\ {I_{E} \theta_{{{{ur}}}} \theta_{\phi k} } \hfill \\ {I_{H} \theta_{\phi r} \theta_{\phi k} } \hfill \\ \end{array} } \right\}} dx,$$

(37)

Due to the presence of the three terms $\left[ {{\mathcal{C}}_{0}^{s} \frac{\partial u}{{\partial x}} - {\mathcal{C}}_{1}^{s} \frac{{\partial^{2} w}}{{\partial^{2} x}} + {\mathcal{C}}_{2}^{s} \frac{\partial \phi }{{\partial x}}} \right]$ in the total strain energy, Eq. (20), an internal right-hand side is obtained when applying the Lagrange equations. These terms are nonzero when including the effect of the surface residual stress of the BDFG nanobeam, i.e., when ${\tau }^{s}\ne$ 0 and ${k}_{z}\ne$ 0 as seen from Eq. (22.5). So, these terms act as self-excitation loading and cause deformation of the nanostructure at no external load [63].

The force vector $\left\{{F}^{SE}\right\}$ represents a self-excitation force resulting from the surface energy contribution, i.e.,

$$\left\{{F}^{SE}\right\}=0.5{\int }_{0}^{L}\left\{\begin{array}{c}-{\mathcal{C}}_{1}^{s}{\uptheta }_{wr}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\\ {\mathcal{C}}_{0}^{s}{\uptheta }_{ur}^{\mathrm{^{\prime}}}\\ {\mathcal{C}}_{2}^{s}{\uptheta }_{\phi r}^{\mathrm{^{\prime}}}\end{array}\right\}dx,$$

(38)

and the force vector’s $\left\{{F}^{t}\right\}$ components due to the external moving harmonic load are given by

$$\left\{ {F^{t} } \right\} = \left\{ {\begin{array}{*{20}c} {\left[ {P_{0} \sin \left( {\Omega t} \right)\theta_{wr} \left( {x_{Q} } \right)} \right]_{k \times 1} } \\ {\varvec0_{k \times 1} } \\ {\varvec0_{k \times 1} } \\ \end{array} } \right\},\;k = 1,2, \ldots M.$$

(39)

The system of equations of motion, Eq. (35), is solved by using the implicit time integration Newmark method ([108, 109]). After obtaining the time-dependent coefficients {${A}_{r}\left(t\right)$, ${B}_{r}\left(t\right)$, ${C}_{r}\left(t\right)$}, the displacements, velocities, and accelerations of the beam at the considered point and time are determined for any time $t$ between $0<t<L/v$.

For better numerical analysis of the forced vibration, the following nondimensional quantities are introduced:

$$\overline{w }\left(x,t\right)=\frac{w\left(x,t\right)}{{D}_{0}}, \quad{\overline{\omega }}_{1}={\omega }_{1}{L}^{2}\sqrt{{\rho }_{c}bh/{E}_{c}I} ,\quad \overline{v }=\frac{v}{{V}_{c}}, \quad{V}_{c}=\frac{L{\omega }_{1}}{\pi },\quad \tau =\frac{t}{L/v}$$

(40)

where $\overline{w }\left(x,t\right)$ represents the normalized dynamic deflections of the BDFG beam, ${D}_{0}$ is the deflection of a pure metal beam under a point load ${P}_{0}$ at mid-span $( {D}_{0} ={P}_{0} {L}^{3}/48{E}_{m} I),$ $I=b{h}^{3}/12$. ${\omega }_{1}$ is the dimensionless fundamental frequency of free vibration analysis. $\overline{v }$ indicates the dimensionless velocity of the external load, where ${V}_{c}$ is the critical velocity (the velocity at which the maximum magnitudes of the maximum deflections occur). τ denotes the dimensionless time, and $0<\tau <1.$ It is worth mentioning that, when $\tau$ is larger than one, the load leaves away from the BDFG microbeam. In addition, for the Newmark procedure, 2000-time increments are adopted for each dynamic response.

4 Validation studies

This Section is devoted to study the accuracy and convergence of the developed model and solution procedure by comparing the obtained results with those in the previous works. In the first example, a simply supported transversely functionally graded (TFG) beam composed of a mixture of metal (SUS304 steel) and ceramic (Al₂O₃) is considered. Young’s modulus is taken as ${E}_{m}$ = 210 GPa and ${E}_{c}$ = 390 GPa, and mass density of ${\rho }_{m}^{B}$ = 7800 kg/m³ and ${\rho }_{c}^{B}$ = 3960 kg/m³, for the metal and ceramic materials, respectively. The beam has width, thickness, and length of 0.4 m, 0.9 m, and 20 m, respectively. Table 1 compares the predicted maximum dynamic magnification factors, i.e., peak values of the maximum normalized deflections $\left({\overline{w} }_{p}\right)$ and the corresponding absolute velocities $\left({v}_{p}\right)$ of the simply supported TFG SUS304/Al₂O₃ beam with the results reported by Simsek and Kocatürk [76] and Nguyen et al. [87], for Euler–Bernoulli beam theory (EBT) and Timoshenko beam theory (TBT), respectively, at ${\Omega }_{f}=0$. In the same example, the variation of the maximum normalized deflection at the center of a simply supported TFG beam with the power-law exponent ${k}_{z}$ for ${\Omega }_{f}$ = 40 and 80 rad/s is also predicted and compared with by [76], as shown in Fig. 2. It is depicted that the present results well agree with the published one for the dynamic response of a TFG beam based on the classical formulation.

Table 1 Comparison of the peak values of maximum normalized dynamic deflection ${\overline{w} }_{p}$ and corresponding absolute velocity ${v}_{p}$ of simply supported TFG SUS304/Al₂O₃ beam

Fig. 2

Comparison of the variation of the dimensionless maximum dynamic deflection at the center of the beam with the gradient index of simply supported TFG SUS304/Al₂O₃ beam for (a) ${\Omega }_{f}=40$ (b) ${\Omega }_{f}=80$ rad/s

In the second example, the dynamic response of the simply supported BDFG microbeam predicted by the present model and that obtained by Zhang and Liu [103] is compared. The material properties of SUS304/Al₂O₃ mentioned above are used with a constant material length scale parameter of ${l}_{m}$ = ${l}_{c}$ = $0.5h$. The beam dimensions are $b$ =1 μm, $h$ =10 μm, and $L$ = $20h$. Based on the MCST, the dimensionless central deflections are plotted in Fig. 3 at a dimensionless moving velocity of $\overline{v }=0.1$. Under these conditions, the maximum dynamic magnification factors, i.e., peak values of the maximum normalized deflections $\left({\overline{w} }_{p}\right)$, and the corresponding dimensionless velocities $\left({\overline{v} }_{p}\right)$ are obtained and compared as provided in Table 2. A very good agreement between the present results with those of [103] is observed from Fig. 3 and Table 2.

Fig. 3

Comparison of the dimensionless dynamic deflection at the center of a simply supported BDFG SUS304/Al₂O₃ microbeam based on MCST ($\overline{v }=0.1$, ${l}_{m}$ = ${l}_{c}$ = $0.5h$)

Table 2 Comparison of the peak values of maximum normalized dynamic deflection ${\overline{w} }_{p}$ and corresponding dimensionless velocity ${\overline{v} }_{p}$ for a simply supported BDFG SUS304/Al₂O₃ microbeam based on MCST

Finally, the third validation example compares the predicted dimensionless fundamental frequency (${\overline{\omega }}_{1}$) of the present PSDBT simply supported BDFG with that reported by Shafiei et al. [110], as illustrated in Fig. 4. In this example, Young’s modulus, Poisson ratio, and mass density are, respectively, ${E}_{m}$ = 201.04 GPa, ${\nu }_{m}$ = 0.3262, and ${\rho }_{m}^{B}$ = 8166 kg/m³ for the metal material, and ${E}_{c}$ = 349.55 GPa,${\nu }_{c}$ = 0.24, and ${\rho }_{c}^{B}$ = 3800 kg/m³ for the ceramic material. The geometrical parameters of the microbeam are $h$ = $15\,{\upmu} {\mathrm{m}}$, $b$ = $h$, and $L$ = $100 h,$ and the material length scale parameter is taken as ${l}_{m}$ = ${l}_{c}$ = $0.25h$. It is observed from Fig. 4 that there is a good agreement between the present model for the free vibration response of BDFG microbeams. Considering the comparison presented in Figs. 2, 3, and 4 and Tables 1 and 2, it can be concluded that the developed model and solution procedure can accurately predict the dynamic response of BDFG beams subjected to a moving load.

Fig. 4

Comparison of the dimensionless fundamental frequency of a simply supported BDFG microbeam based on MCST (${l}_{m}$ = ${l}_{c}$ = $0.25h$)

5 Results and discussion

In this Section, numerical results are presented to investigate the effect of the gradient indices in length and thickness directions, velocity of the moving load, and excitation frequency on the dynamic response of simply supported BDFG nanobeams exposed to a moving load. The influences of microstructure and surface energy are considered. Unlike most of the existing models, the present model accounts for the exact location of the physical neutral axis, and the gradation of Poisson’s ratio, material length scale parameter, residual surface stress, two surface elastic constants, and surface mass density. The BDFG beam is made of a mixture of aluminum (metal) and silicon (Si) materials. Young’s modulus, Poisson’s ratio, and the bulk mass density of the metallic constituent are, respectively, ${E}_{m}$ = 90 GPa, ${\nu }_{m}$ = 0.23, and ${\rho }_{m}^{B}$ = 2700 kg/m³, and of the ceramic constituent are ${E}_{c}$ = 210 GPa,${\nu }_{c}$ = 0.24, and ${\rho }_{c}^{B}$ = 2331 kg/m³, respectively, [111]. The surface residual stress ${\tau }_{m}^{s}$ = 0.5689 N/m, surface elastic constants ${\upmu }_{m}^{s}$ = ‒5.4251 N/m, ${\lambda }_{m}^{s}$ = 3.4939 N/m, and the surface mass density ${\rho }_{m}^{s}$ = 5.461 kg/m² for the metallic constituent, while the corresponding values of the surface parameters for the ceramic constituent are ${\tau }_{c}^{s}$ = 0.6056 N/m, ${\upmu }_{c}^{s}$ = ‒2.7779 N/m, ${\lambda }_{c}^{s}$ = ‒4.4039 N/m, and ${\rho }_{c}^{s}$ = 3.1688 kg/m², respectively, [70]. Since the value of the material length scale parameter (MLSP) differs from a material to another, it is not reasonable to assume a constant MLSP in FGMs. Unfortunately, there is no available experimental data for the MLSP of Al/Si FGM, and therefore, the ratio of MLSP of silicon to that of aluminum (${l}_{c}$/${l}_{m}$) is assumed [38, 66, 112]. The dimensions of the nanobeam are taken as h = 10 nm, b = h, and L = 20 h. Also, the MLSP of the metal and ceramic phases is taken as ${l}_{m}$ = 2 $h$/3 and ${l}_{c}$ = 3 ${l}_{m}$/4. All the above-mentioned material and geometrical parameters are kept unchanged throughout the forthcoming results, except other values are determined. Figure 5 shows the dependency of the distances indicating the location of the physical neutral axis (${e}_{n}$ and ${r}_{n}$) on the thickness and length gradient indices of the nanobeam.

Fig. 5

Variation of the distances ${e}_{n}$ and ${r}_{n}$ between the physical neutral and the midplane surfaces at different gradient indices

The influence of the thickness and length gradient indices on the variation of the maximum normalized dynamic deflection (dynamic magnification factor) at the center of the simply supported BDFG Al/Si nanobeam versus the dimensionless velocity of the moving load is illustrated in Figs. 6 and 7, respectively. To clearly explore the nonclassical effects due to the small-scale size, the present results are predicted based on the classical “CL” formulation when l = 0 and ${\tau }^{s}$ = ${\upmu }^{s}$ = ${\lambda }^{s}$ = ${\rho }^{s}$ = 0, couple stress “CS” formulation in the absence of the surface effect (${\tau }^{s}$ = ${\upmu }^{s}$ = ${\lambda }^{s}$ = ${\rho }^{s}$ = 0), surface energy “SE” formulation when the couple stress (microstructure) effect is ignored (l = 0), and full-nonclassical “CSSE” formulation which incorporates the simultaneous effects of microstructure and the surface energy.

Fig. 6

Variation of the maximum normalized dynamic deflection ${\overline{w} }_{max}(L/2,t)$ for a BDFG beam with velocity at different values of ${k}_{z}$ (${k}_{x}\,=\,$ 0.5)

Fig. 7

Variation of the maximum normalized dynamic deflection ${\overline{w} }_{max} (L/2,t)$ for a BDFG beam with velocity at different values of ${k}_{x}$ (${k}_{z}\,=\,$ 0.5)

From Figs. 6 and 7, it is depicted that the maximum normalized dynamic deflection in the entire time history both increases and decreases, it then increases to reach the peak value when the moving load velocity reaches a certain value, and then after the maximum normalized dynamic deflection gradually decreases as the moving load velocity increases [113]. The velocity at which the maximum normalized dynamic deflection attains its peak value is referred to as the critical velocity of the BDFG beam [114]. At lower moving load velocities, the repeated increase and decrease of the maximum normalized dynamic deflection is due to the beam oscillations. Regardless of the velocity and the gradient indices, incorporating the nonclassical effects significantly reduces the predicted maximum normalized dynamic deflection. The highest maximum normalized dynamic deflection is associated with the classical elasticity-based formulation, followed with SE, CS, and CSSE formulations, which is due to the stiffness-hardening effect because of the couple stress and surface energy. A stiffer nanobeam resists a moving load better than a soft one. Generally, the trends of the maximum normalized dynamic deflection-dimensionless moving velocity curves are independent of the gradient indices and the nonclassical formulations.

Peak values of the maximum normalized dynamic deflections (${\overline{w} }_{p}$) and their corresponding absolute and dimensionless critical velocities (${v}_{p}$ and ${\overline{v} }_{p}$, respectively) are provided in Table 3 at various values of the gradient indices of the BDFG nanobeam and different formulations. It can also be discerned from Table 3 and Figs. 6 and 7 that increasing the gradation indices in thickness or length direction, k_z or k_x, respectively, shows a considerable increase in the maximum normalized dynamic deflections, which is observed for CL, CS, SE, and CSSE formulations. This is due to the fact that increasing k_z and/or k_x increases the volume fraction of metal constituent, and thus the effective rigidity of the beam decreases. Additionally, the influence of the gradient index in the length direction $\left({k}_{x}\right)$ on the dynamic response is much larger than that in the thickness direction $\left({k}_{z}\right)$. It is also depicted that the influence of the gradient indices is more pronounced when their values are low. Keeping k_x = 0.5, increasing k_z from 0.0 to 1, shows an increase in ${\overline{w} }_{p}$ by about 30.66, 17.78, 23.31, and 15.72%, and a decrease in ${v}_{p}$ by 14.32, 10.06, 12.60, and 9.98% for CL, CS, SE, and CSSE formulations, respectively, while increasing k_z from 2 to 10 under the same conditions results in increasing ${\overline{w} }_{p}$ by about 16.13, 11.74, 11.37, and 10.15% and reducing ${v}_{p}$ by 7.47, 6.56, 5.71, and 5.62% for CL, CS, SE, and CSSE formulations, respectively. On the other hand, increasing k_x from 0.0 to 1, while keeping k_z = 0.5, increases ${\overline{w} }_{p}$ by 30.49, 16.311, 23.39, and 14.59% and reduces ${v}_{p}$ by 16.32, 10.17, 9.43, and 10.88%, while increasing k_x from 2 to 10 under the same conditions increases ${\overline{w} }_{p}$ by 16.36, 12.63, 10.97, and 10.73% and reduces ${v}_{p}$ by 7.12, 5.39, 5.08, and 5.52% for CL, CS, SE, and CSSE formulations, respectively.

Table 3 Comparisons of the peaks of maximum normalized deflection at mid-span ${\overline{w} }_{p}$ of the simply supported BDFG nanobeam and corresponding velocities at different gradation indices using various formulations

Furthermore, the results presented in Table 3 and Figs. 6 and 7 reveal that there is a considerable influence of the nonclassical microstructure and surface energy on the dynamic response of BDFG nanobeams. For the BDFG nanobeam under investigation, the highest and lowest nonclassical effects are associated with the CSSE and SE formulations, respectively. The maximum normalized dynamic deflections predicted using CS, SE, and CSSE formulations are, respectively, 0.395, 0.751, and 0.35 times that predicted using CL formulation when k_x = 0.5 and k_z = 1, and are, respectively, 0.382, 0.742, 0.338 when k_x = 1 and k_z = 0.5. Employing classical elasticity-based formulation yields a considerable underestimation of the critical velocity ${v}_{p}$. However, the impact of surface energy and couple stress on the dynamic response increases by increasing the bi-directional gradient indices. Also, the effect of the thickness gradient index on the contribution of surface energy and/or couple stress is slightly larger than that of the length gradient index.

For examining the mutual effect of the thickness and length gradient indices on the dynamic response of a BDFG nanobeam under moving load in more detail, the maximum normalized dynamic deflection ${\overline{w} }_{max}$ as a function of the gradation indices k_x and k_z is shown in Figs. 8, 9, and10 for three different dimensionless moving load velocities, $\overline{v }\,=\,0.1$, 0.6, and 0.8, respectively. It is seen that as the gradient indices k_x and/or k_z increase, ${\overline{w} }_{max}$ increases, regardless of the velocity of moving load and the formulation type. When k_x = k_z = 0, the beam is made of purely ceramic “silicon”, and thus the beam attains its lowest dynamic deflection, while the highest dynamic deflection is reached when k_x = k_z = 10 as the beam is almost pure metal. Based on the results in Figs. 6, 7, 8, 9, and 10, it can be extracted that the dynamic response of a BDFG nanobeam can be controlled by the selection of the gradient indices.

Fig. 8

Variation of the maximum normalized dynamic deflection at mid-span with gradient indices at $\overline{v }=0.1$(a) CL (b) CS (c) SE, and (d) CSSE formulation

Fig. 9

Variation of the maximum normalized dynamic deflection at mid-span with gradient indices at $\overline{v }=0.6$ (a) CL (b) CS (c) SE, and (d) CSSE formulation

Fig. 10

Variation of the maximum normalized dynamic deflection at mid-span with gradient indices at $\overline{v }=0.8$ (a) CL (b) CS (c) SE, and (d) CSSE formulation

The influences of the bi-directional gradient indices k_z and k_x on the time history of the normalized dynamic deflection at the nanobeam center $\overline{w }(L/2,t)$ are depicted in Figs. 11 and 12, respectively, for three different values of the moving load dimensionless velocity $\overline{v }$ as well as different formulations. Table 4 records the numerical values of the dimensionless central deflection of a simply supported BDFG nanobeam for different values of the gradation indices and dimensionless velocities of the acting moving load. It is found that the gradient indices, moving load velocity, and the employed formulation have a significant role in the dynamic behavior of BDFG nanobeams. The gradation indices have a considerable influence on the amplitude of dynamic deflection, but they slightly affect the curve shapes of the time histories, regardless of the adopted formulation. It is indicated that the moving load velocity has a significant impact on the dynamic deflection response, and low velocities of the travelling load increase the number of vibration cycles of a BDFG nanobeam, which is attributed to the low ratio of the moving load velocity to the critical velocity.

Fig. 11

Variation of the dimensionless deflection at mid-span over time for a BDFG beam based on different models and different ${k}_{z}$ (${k}_{x}=$ 0.5) for (a) $\overline{v }=0.1$, (b) $\overline{v }=0.4$, and (c) $\overline{v }=0.8$

Fig. 12

Variation of the dimensionless deflection at mid-span over time for a BDFG beam based on different models and different ${k}_{x}$ (${k}_{z}=$ 0.5) for (a) $\overline{v }=0.1$, (b) $\overline{v }=0.4$, and (c) $\overline{v }=0.8$

Table 4 Comparisons of the maximum dimensionless deflection at mid-span ${\overline{w} }_{max}(L/2,t)$ of the simply supported BDFG nanobeam at different gradation indices and dimensionless velocities of moving load using various formulations

Figure 13 demonstrates the variations of the normalized dynamic deflection at the center of a simply supported BDFG nanobeam versus the dimensionless velocity of acting moving load and dimensionless time for ${k}_{x}$ = ${k}_{z}$ = 1. Various formulations are presented to show the influence of microstructure and surface energy on the predicted dynamic deflection. It is observed that the inclusion of couple stress and/or surface energy considerably decreases the predicted dynamic deflection during the time interval regardless of the moving load velocity. Employing CSSE formulation gives the smallest normalized dynamic deflection, whereas the classical formulation gives the largest one. For the different formulations, it is depicted that a faster moving load, i.e., higher moving velocity, takes less traveling time, and thus the BDFG nanobeam exhibits low fluctuations, and these fluctuations are almost not obvious the dimensionless velocity approaches 0.6.

Fig. 13

Variation of the maximum normalized dynamic deflections at the center of the beam versus time at different velocities of the moving load at ${k}_{z}\,=1, {k}_{x}\,=1$

The relation between the maximum normalized dynamic deflection at the mid-span of a BDFG nanobeam and the dimensionless velocity of moving load is shown in Fig. 14 at different values of the excitation frequency ratio, i.e., ${r}_{\Omega } = {\Omega }_{f}/{\omega }_{1}$, of 0.1, 0.2, and 0.4. The gradation indices are fixed at ${k}_{x}$=${k}_{z}$=1. For the classical and nonclassical formulations, it is obvious that while the dimensionless velocity increases, the trends of the dynamic deflection versus the dimensionless time are not influenced for different values of the excitation frequency ratio. Also, as the excitation frequency ratio increases, the peak value of the maximum normalized dynamic deflection and its corresponding dimensionless velocity are remarkably increased. Figure 15 presents the variation of the maximum normalized dynamic deflection with the excitation frequency for different gradient indices of a BDFG nanobeam employing various formulations. The dimensionless moving velocity is kept constant at $\overline{v }$= 0.2. It is noticed that the maximum dynamic deflection reaches its peak value at some value of the excitation frequency, which is the fundamental frequency of the BDFG nanobeam. It is noted that the fundamental frequency of the BDFG nanobeam reduces by increasing the gradation indices ${k}_{x}$ and ${k}_{z}$. On the other hand, increasing the gradation indices yields a remarkable increase in the predicted peak values of the deflection curves, for both classical and nonclassical formulations. Inclusion of the microstructure and/or surface energy effects significantly reduces the maximum dynamic deflection and increases the fundamental frequency.

Fig. 14

Variation of the maximum normalized dynamic deflections at the center of the beam versus dimensionless velocity of the moving load at different excitation frequencies and ${k}_{z}=1, {k}_{x}=1$ (${r}_{\Omega }={\Omega }_{\mathrm{f}}/{\omega }_{1}$)

Fig.15

Variation of maximum normalized deflection at mid-span versus the excitation frequency (moving load frequency) at different values of the gradient indices ($\overline{v }$ = 0.2)

The required time for the moving load to reach the right end of the nanobeam, i.e., ${x}_{p}=L$, is ${t}^{*}=\pi /\left(\overline{v}{\omega }_{1}\right),$ and the corresponding load becomes $P\left({t}^{*}\right)={P}_{0}\mathrm{sin}\left(\pi {r}_{\Omega }/\overline{v }\right)$, where ${r}_{\Omega }/\overline{v }$ represents the dimensionless time taken by the moving load to move across the entire nanobeam, Zhang and Liu [103]. In this regard, consider a BDFG nanobeam with ${k}_{x}$ = 1 and ${k}_{z}$ = 1 and subjected to a moving load with a dimensionless moving velocity of $\overline{v }$ = 0.2. The time-history of the normalized dynamic deflection at the mid-span of the nanobeam is provided in Figs. 16 and 17 for, respectively, ${r}_{\Omega }$ ≤ 0.2 and ${r}_{\Omega }$ ≥ 0.2. When ${r}_{\Omega }$ ≤ 0.2, it is depicted from Fig. 16 that lower values of the excitation frequency ratios lead to lower values of the amplitudes of the dynamic deflections at the mid-span of the BDFG nanobeam. On the other hand, when ${r}_{\Omega }$ > 0.2, the resonance phenomenon is observed when the fundamental frequency of the considered BDFG nanobeam equals the excitation frequency of the applied moving load, i.e., ${r}_{\Omega }={\Omega }_{f}/{\omega }_{1}=1$. Therefore, the normalized mid-span dynamic deflection reaches it largest value in the resonance case. As the excitation frequency ratio increases more than 1, i.e., the fundamental frequency of the beam is lower than the excitation frequency of moving load, the periodic load decreases, and consequently, the amplitude of the dynamic deflection significantly decreases. When the excitation frequency ratio approaches 3, the periodic load is about zero, and thus, the dynamic deflection is almost vanishing.

Fig. 16

Variation of the maximum normalized dynamic deflections at the center of the beam versus time at different frequencies of the moving load at ${k}_{z}=1, {k}_{x}=1$ (${r}_{\Omega }={\Omega }_{f}/{\omega }_{1}$ ≤ 0.2, $\overline{v }$ = 0.2)

Fig. 17

Variation of the maximum normalized dynamic deflections at the center of the beam versus time at different frequencies of the moving load at ${k}_{z}=1, {k}_{x}=1$ (${r}_{\Omega }={\Omega }_{f}/{\omega }_{1}$ ≥ 0.2, $\overline{v }$ = 0.2)

6 Conclusions

In the present work, the dynamic response of bi-directional FG nanobeams acted upon by a moving concentrated harmonic load is investigated. A new nonclassical beam model is developed in the framework of higher-order shear deformation beam theory in conjunction with the modified couple stress theory and the Gurtin–Murdoch surface elasticity theory. The proposed model accounts for the bi-directional gradation of the material length scale parameter to capture the microstructure effect as well as the bi-directional gradation of the surface residual stress, two surface lamé constants, and the surface mass density to include the surface energy effect. Introducing the physical neutral plane concept, the equations of motion are derived using Lagrange’s equations. In the solution procedure, the trigonometric Ritz method is employed, and the dynamic response in the time domain is obtained by Newmark method. An extensive numerical parametric study is performed to examine the influence of some key parameters such as the gradation indices in thickness and length directions, moving load velocity, and the excitation frequency on the dynamic response of a simply supported BDFG nanobeam using the four different formulations. Some important conclusions can be summarized as follows:

• The dynamic deflection employing the nonclassical formulations is considerably smaller than that predicted by the classical formulation, regardless of the gradient indices, due to the stiffening induced by surface energy.

• The normalized dynamic deflection and the maximum deflection are significantly increased as the gradation indices increase, whereas the corresponding velocity is considerably decreased.

• Incorporating the nonclassical surface energy and/or microstructure effects reduces the influence of the gradient indices.

• The influence of the gradient index in thickness direction on the dynamic response is slightly lower than that in the length direction.

• As the velocity of moving load increases, the predicted normalized maximum dynamic deflection increases first and then decreases as the velocity becomes larger than its critical value.

• Increasing the velocity of the applied moving load reduces the number of the dynamic vibration cycles, whereas the number of the vibration cycles is almost unaffected by the gradient indices and the nonclassical contribution.

• The predicted dimensionless mid-span deflection of a BDFG nanobeam value is increased as the excitation frequency increases and reaches its peak value as the fundamental frequency of a BDFG nanobeam equals the excitation frequency.