1 Introduction

Since the pioneering work conducted by Griffith and Taylor (1921), a vast number of experimental and theoretical studies have been dedicated to understanding failure phenomena. It is widely recognized from previous studies that crack surfaces are generated when the crack evolution condition is satisfied and that the evolution of brittle fracture requires a portion of stored strain energy. Specifically, when an instantaneous energy release rate \({\mathcal {G}}^*\) is equal to or larger than the critical value (\({\mathcal {G}}^* \ge {\mathcal {G}}_\textrm{c}\)) inherent in the material, the crack begins to propagate. Meanwhile, in the case of ductile materials such as aluminum or steel, since plastic deformation accompanied by hardening occurs before crack initiation, another portion of energy must be dissipated by the inelastic (plastic) deformation. Accordingly, the critical value \({\mathcal {G}}_\textrm{c}\) of elastoplastic materials is known to be larger than that of brittle materials; see, e.g., Irwin (1957) and Orowan (1949) for more detailed discussions.

Based on the experimental and theoretical developments, numerical simulations using, for example, the finite element method (FEM) have been conducted to predict the crack propagations or understand the mechanisms and physics of fracture phenomena. In general, techniques within the FE framework to represent crack propagations are classified into two major groups. One of them is a collection of techniques that incorporate discontinuous displacement fields into FE approximations: the node-releasing FEM (Ngo and Scordelis 1967; Ingraffea and Saouma 1985), the partition of unity FEM (PU-FEM) (Melenk and Babuška 1996; Babuška and Melenk 1997, the embedded FEM (Jirásek 2000), the generalized or extended FEM (GFEM and X-FEM) (Strouboulis et al. 2000, 2001; Moës et al. 1999; Dolbow et al. 2000), the manifold method (MM) (Shi 1992), the finite cover method (FCM) (Terada et al. 2003; Kurumatani and Terada 2005). The other group pursues constitutive modeling to replace the discrete expression of fracture with the strain-softening behavior within each finite element: the Gurson–Tvergaard–Needleman (GTN) model (Gurson 1977; Tvergaard and Needleman 1984), the Lemaitre model (Lemaitre 1985) and the microplane damage model (Bažant and Prat 1988). This class of modeling, known as the so-called “local approach”, often encounters numerical instability problems typically caused by the ill-posedness of partial differential equations (Bažant et al. 1984). To circumvent these problems, several numerical techniques have been proposed, such as non-local integral algorithms (Kruch 1992; Bazant and Pijaudier-Cabot 1988) and gradient-enhanced approximations (Peerlings et al. 1996a, b).

Independent of the main family of continuum damage models but having an equivalent concept to the gradient-enhanced approaches, the “crack phase-field model (PF model)” has recently received attention. This model originates from the pioneering work of Francfort and Marigo (1998), in which brittle fracture behavior is formulated as a minimization problem of the corresponding potential energy based on Griffith’s theory. The geometry representation of discrete crack surfaces is subsequently regularized by adopting a so-called phase-field approximation (Mumford and Shah 1989; Ambrosio and Tortorelli 1990; Bourdin et al. 2000). See review papers Ambati et al. (2015a); Wu et al. (2020) for the history of developments and applications of PF models. When limited to ductile fracture, Alessi et al. (2014, 2015) proposed a variational elastoplastic gradient damage model by introducing a “plastic-damage coupled dissipation potential” to realize plasticity-dependent damage. Also, Ambati et al. (2015b, 2016) proposed a characteristic degradation function depending on both the phase-field variable and the accumulated plastic strain to realize plasticity-dependent damage. At almost the same time, Miehe et al. (2015, 2016) introduced pseudo-plastic strain energy density to represent the contribution of plastic deformation to the driving force of damage evolution. A comparative review, including the investigations of the above models, was done by Alessi et al. (2018a). More recently, as an alternative concept, Dittmann et al. (2018) and Yin and Kaliske (2020) have proposed different functions of fracture toughness that degrade with the accumulation of plastic strain. This concept can be phenomenologically regarded as fatigue damage models (Alessi et al. 2018b; Carrara et al. 2020; Ulloa et al. 2021), although only the monocycle failure is considered. With these ideas in mind, Han et al. (2022) proposed a model incorporating both the plastic driving force and degrading fracture toughness for ductile fracture simulations.

In this study, we take a cue from previous PF models (Dittmann et al. 2018; Yin and Kaliske 2020; Han et al. 2022) and propose a gradient damage model introducing a degradation of damage hardening modulus. Specifically, the damage hardening modulus is degraded by both the accumulated plastic strain and negative hydrostatic pressure, so damage occurs in the region with large plastic deformation or volume expansion. Under the assumption of plastic incompressibility, this approach is equivalent to introducing the effect of stress triaxiality into damage evolution. Thanks to this characteristic feature, the proposed model is capable of realizing the breaking elongation and the transitional behavior from unstable to stable crack propagations, as well as the corresponding load–displacement curves for advanced high strength steel sheets with different tensile strengths. Also, the model successfully reproduces and predicts the crack initiation positions in notched specimens with different notch radii. The results are in close agreement with the experimental results recently obtained by Omiya et al. (2022).

The structure of this paper is as follows: the formulation of the proposed model is presented in Sect. 2. Also, the specific function form for degrading the damage hardening modulus is suggested. Section 3 presents the spatial discretization within the IGA (Cottrell et al. 2009) framework. In Sect. 4, two parameter studies are carried out to confirm the basic performance of the proposed model. Section 5 presents a series of numerical simulations of the tensile loading experiments carried out on single notched specimens (Omiya et al. 2022). Finally, in Sect. 6, we summarize the implications of the research outcomes and describe our outlook for future studies.

2 Gradient damage model for ductile fracture

We propose a gradient damage model introducing a degradation of damage hardening modulus by the accumulated plastic strain and negative hydrostatic pressure. This section is devoted to deriving the governing equations of the proposed model.

2.1 Constitutive work density functional

Let us consider an arbitrary continuum body in the finite deformation framework having its initial configuration \({\mathcal {B}}_0\subset {\mathbb {R}}^s\) and current configuration \({\mathcal {B}}_t\subset {\mathbb {R}}^s\) with dimension \(s\in \left\{ 2,3\right\} \). Similarly, their boundaries are denoted by \(\partial {\mathcal {B}}_0\subset {\mathbb {R}}^{s}\) and \(\partial {\mathcal {B}}_t\subset {\mathbb {R}}^{s}\), respectively. At time \(t\in {\mathcal {T}}=\left[ 0,T\right] \), points denoted by \({\varvec{X}}\in {\mathcal {B}}_0\) are mapped onto \({\varvec{x}}\in {\mathcal {B}}_t\) by the motion \({\varvec{x}}={\varvec{\varphi }}\left( {\varvec{X}},t\right) :{\mathcal {B}}_0 \times {\mathcal {T}}\rightarrow {\mathbb {R}}^s\).

To represent the energy state of the body, we define the following constitutive work density functional:

$$\begin{aligned} \begin{aligned} \Psi := \underbrace{\Psi ^\textrm{e}\left( {\varvec{F}},{\varvec{F}}^\textrm{p}, d\right) }_{\text {stored energy}}+ \underbrace{\Psi ^\textrm{p}\left( \alpha \right) +\Psi ^\textrm{f}\left( {\varvec{F}}^\textrm{e},\alpha ,d, \nabla d \right) }_{\text {accumulated dissipation}}. \end{aligned} \end{aligned}$$
(1)

Here, \(\Psi ^\textrm{e}\), \(\Psi ^\textrm{p}\), and \(\Psi ^\textrm{f}\) are the elastic strain energy density, the pseudo-plastic strain energy density (for convenience, which is referred to simply as “plastic strain energy density” hereafter), and the crack surface generation energy density, respectively. Also, \({\varvec{F}}:=\partial {\varvec{x}}/\partial {\varvec{X}}\) is the deformation gradient, which is decomposed into the elastic and plastic parts, \({\varvec{F}}^\textrm{e}\) and \({\varvec{F}}^\textrm{p}\), so that \({\varvec{F}}={\varvec{F}}^\textrm{e}\cdot {\varvec{F}}^\textrm{p}\). Also, \(\alpha :{\mathcal {B}}_0 \times {\mathcal {T}}\rightarrow {\mathbb {R}}\) is the accumulated plastic strain adopted as a hardening variable in this study. Furthermore, \(d:{\mathcal {B}}_0 \times {\mathcal {T}}\rightarrow {\mathbb {R}}\) is the damage variable, and its spatial gradient is denoted by \(\nabla d\). Intact and fully broken states correspond to \(d=0\) and \(d=1\), respectively. Also, the damage variable is considered irreversible: \({\dot{d}}\ge 0\). In this paper, \(\nabla \) and \(\nabla _x\) denote the spatial gradient operator referring to the initial and current configurations, \({\mathcal {B}}_0\) and \({\mathcal {B}}_t\), respectively. In what follows, the specific function forms of these energy density functionals are provided in turn.

First, following Ambati et al. (2016), we employ the Neo-Hookean constitutive law for the undamaged state, whose elastic strain energy density \(\Psi ^\textrm{e}_0\) is given as

$$\begin{aligned} \begin{aligned} \Psi ^\textrm{e}_0:&= \Psi ^\textrm{e}_{0, \textrm{vol}}+\Psi ^\textrm{e}_{0, \textrm{dev}}\\&=\dfrac{\kappa }{2}\left( \dfrac{{J^\textrm{e}}^2-1}{2}-\text {ln}J^\textrm{e}\right) +\dfrac{\mu }{2}\left( I_{\bar{{{\varvec{C}}}}^\textrm{e}}-3\right) . \end{aligned} \end{aligned}$$
(2)

Here, \(\Psi ^\textrm{e}_{0,\textrm{vol}}\) and \(\Psi ^\textrm{e}_{0,\textrm{dev}}\) are the volumetric and deviatoric components, and \(\mu \) and \(\kappa \) are the shear and bulk moduli of elasticity, respectively. Also, \(J^\textrm{e}\) denotes the Jacobian of the elastic deformation gradient \({\varvec{F}}^\textrm{e}={\varvec{F}}\cdot {{\varvec{F}}^{\textrm{p}}}^{-1}\). Assuming plastic incompressibility, namely \(\det \left[ {\varvec{F}}^\textrm{p}\right] =1\), the identity \(J^\textrm{e}=\det \left[ {\varvec{F}}^\textrm{e}\right] =\det \left[ {\varvec{F}}\right] =J\) is ensured for the deformation gradient \({\varvec{F}}\). Also, \(I_{\bar{{{\varvec{C}}}}^\textrm{e}}\) is the first invariant of the second-order tensor \(\bar{{{\varvec{C}}}}^\textrm{e}={J^\textrm{e}}^{-2/3}{{\varvec{C}}}^\textrm{e}\) with \({{\varvec{C}}}^\textrm{e}={{\varvec{F}}^\textrm{e}}^\textrm{T}\cdot {\varvec{F}}^\textrm{e}\) being the elastic right Cauchy-Green tensor. To describe the degradation of material stiffness by the damage variable d, the volumetric-deviatoric split (Amor et al. 2009) of the elastic strain energy function is employed as

$$\begin{aligned} \begin{aligned} \Psi ^\textrm{e}&= {\left\{ \begin{array}{ll} g\left( d \right) \underbrace{\left( \Psi ^\textrm{e}_{0,\textrm{dev}}+\Psi ^\textrm{e}_{0,\textrm{vol}}\right) }_{\Psi ^{\textrm{e}+}_{0}} +\underbrace{0}_{\Psi ^{\textrm{e}-}_{0}} &{}\ \text {for}\ J^\textrm{e}\ge 1\\ g\left( d \right) \underbrace{\Psi ^\textrm{e}_{0,\textrm{dev}}}_{\Psi ^{\textrm{e}+}_{0}} +\underbrace{\Psi ^\textrm{e}_{0,\textrm{vol}}}_{\Psi ^{\textrm{e}-}_{0}} &{}\ \text {for}\ J^\textrm{e}< 1 \end{array}\right. } , \end{aligned} \end{aligned}$$
(3)

where \(g\left( d\right) =\left( 1-d\right) ^2\) is a degradation function, and \(\Psi ^{\textrm{e}+}_{0}\) & \(\Psi ^{\textrm{e}-}_{0}\) are the damage driving component and the remaining component that does not contribute to damage evolution, respectively.

Second, we define the plastic strain energy density (energy storage due to hardening) as follows:

$$\begin{aligned} \begin{aligned} \Psi ^\textrm{p}:=\int ^{\alpha }_0 r^\textrm{p}\left( {\hat{\alpha }}\right) d{\hat{\alpha }}, \end{aligned} \end{aligned}$$
(4)

where \(r^\textrm{p}\left( {\alpha }\right) \) is the hardening function at each material point: its specific function form will be given in Sects. 4 and 5. Here, following the setting in \(J_2\) plasticity, we admit

$$\begin{aligned} \begin{aligned}&\dot{\alpha }=\sqrt{\dfrac{2}{3}}\Vert {\varvec{D}}^\textrm{p}\Vert =\sqrt{\dfrac{2}{3}}\Vert {\varvec{L}}^\textrm{p}_\text {sym}\Vert \ge 0, \end{aligned} \end{aligned}$$
(5)

where \({\varvec{L}}^\textrm{p}=\dot{{\varvec{F}}}^\textrm{p}\cdot {{\varvec{F}}^\textrm{p}}^{-1}\) and \({\varvec{D}}^\textrm{p}={\varvec{L}}^\textrm{p}_\text {sym}\) denote the rate of plastic deformation tensor and its symmetric part. Using Eq. (4), the plastic dissipation rate yields

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\textrm{p}=\dot{\Psi }^\textrm{p}=r^\textrm{p}\dot{\alpha }. \end{aligned}\end{aligned}$$
(6)

Finally, let us define the energy density of crack surface generation (stored energy associated with damage) as follows:

$$\begin{aligned} \begin{aligned}&\Psi ^\textrm{f}:=\int ^t_0 \dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{{l_\textrm{f}}} \left( d{\dot{d}} + l_\textrm{f}^2 \nabla d\cdot {\nabla {\dot{d}}}\right) {\textsf{d}}{\textsf{t}}, \end{aligned} \end{aligned}$$
(7)

where \(l_\textrm{f}\) is the crack length scale parameter. Also, \(H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) \) denotes the damage hardening modulus, which is sometimes called “damage hardening material parameter” in the literature in the form of “\({H^*}/{{l_\textrm{f}}}\)”. It should be noted that since the value of \(H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) \) is path-dependent, Eq. (7) is defined by a time-integral form. The specific form of \({H^*}\) is presented at the end of this section based on the physical justification. Accordingly, the damage dissipation rate is given as

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\textrm{f}=\dot{\Psi }^\textrm{f}=\dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{l_\textrm{f}} \left( d{\dot{d}} + l_\textrm{f}^2 \nabla d\cdot {\nabla {\dot{d}}}\right) . \end{aligned} \end{aligned}$$
(8)

Remark 1

Plasticity-induced degrading fracture toughness. Similar setups for the energy density of crack surface generation, Eq. (7), are seen in the literature regarding crack phase-field modeling. In some studies describing ductile fracture (Dittmann et al. 2018; Yin and Kaliske 2020), the part corresponding to Eq. (7) is defined as follows:

$$\begin{aligned} \begin{aligned}&\Psi ^\textrm{f}=\dfrac{G_\textrm{c}^*}{{l_\textrm{f}}} \left( d^2 + l_\textrm{f}^2\Vert \nabla d\Vert ^2\right) , \end{aligned} \end{aligned}$$
(9)

in which \(G_\textrm{c}^*\) is degraded by the accumulated plastic strain and may be referred to as “degrading fracture toughness” as in Yin and Kaliske (2020). While this setting can reproduce ductile fracture to some extent, it has a flaw with respect to dissipation; that is, the value of \(\Psi ^\textrm{f}\) vanishes for \(d\rightarrow 1\).

Remark 2

Fatigue degradation function/History-dependent fracture toughness. In some studies describing fatigue fracture (Alessi et al. 2018b; Carrara et al. 2020; Ulloa et al. 2021), the part corresponding to Eq. (7) is defined as

$$\begin{aligned} \begin{aligned}&\Psi ^\textrm{f}=\int ^t_0 f\left( \theta \right) \dfrac{G_\textrm{c}}{{l_\textrm{f}}} \left( d{\dot{d}} + l_\textrm{f}^2 \nabla d\cdot {\nabla {\dot{d}}}\right) {\textsf{d}}{\textsf{t}}, \end{aligned}\end{aligned}$$
(10)

in which \(f\left( \theta \right) \) denotes the fatigue degradation function that is determined by fatigue variable \(\theta \). Here, one may argue that the term \(f\left( \theta \right) G_\textrm{c}\) can be regarded as the history-dependent fracture toughness. Although this setting is reasonable in terms of dissipation, it is not able to lead to a sharp-interface limit; that is, \(G_\textrm{c}\Gamma _{l_\textrm{f}}\approx G_\textrm{c}\Gamma \), for \(l_\textrm{f}\rightarrow 0\). Therefore, along with Remark 1, it is safe to regard the proposed model not as a crack phase-field model but as a gradient damage model.

Remark 3

Irreversibility of damage evolution. Irreversibility of damage evolution is imposed by the explicit condition \({\dot{d}}\ge 0\). Another way is to let Eq. (8) take an infinite value for non-admissible rates as

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\textrm{f}= {\left\{ \begin{array}{ll} \dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{l_\textrm{f}} \left( d{\dot{d}} + l_\textrm{f}^2 \nabla d\cdot {\nabla {\dot{d}}}\right) &{}\text {for}\quad {\dot{d}}\ge 0\\ +\infty &{}\text {for}\quad {\dot{d}}<0 \end{array}\right. } \end{aligned} \end{aligned}$$
(11)

2.2 Governing equations in strong form

To derive the governing equations in strong form, we consider the following energy balance equation:

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {B}}_0}\dot{\Psi }\textsf {dV} -\int _{{\mathcal {B}}_0}{\varvec{B}}\cdot \dot{{\varvec{\varphi }}}\textsf {dV} -\int _{\partial {\mathcal {B}}_0^{{\varvec{T}}}}{\varvec{T}}\cdot \dot{{\varvec{\varphi }}}\textsf {dA}=0, \end{aligned} \end{aligned}$$
(12)

where \({\varvec{B}}\) and \({\varvec{T}}\) are the body and traction forces in the initial configuration, respectively. Taking into account of Eqs. (3), (6), and (8), (12) is expanded as

$$\begin{aligned} \begin{aligned}&-\int _{{\mathcal {B}}_0}\left( \nabla \cdot {\varvec{P}}+{\varvec{B}}\right) \cdot \dot{{\varvec{\varphi }}}\textsf {dV}+\int _{\partial {\mathcal {B}}_0^{{\varvec{T}}}}\left( {\varvec{P}}\cdot {\varvec{N}}-{\varvec{T}}\right) \cdot \dot{{\varvec{\varphi }}}\textsf {dA}\\&-\int _{{\mathcal {B}}_0}\sqrt{\dfrac{3}{2}}\left( \Vert {\varvec{M}}^\textrm{p}_\textrm{dev}\Vert -\sqrt{\dfrac{2}{3}}r^\textrm{p}\right) \dot{\alpha }\textsf {dV}\\&-\int _{{\mathcal {B}}_0}\left( -\dfrac{\partial \Psi ^\textrm{e}}{\partial d}- \dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{l_\textrm{f}}\left( d - l_\textrm{f}^2 \Delta d\right) \right) {\dot{d}}\textsf {dV}\\&+\int _{\partial {\mathcal {B}}_0}H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) l_\textrm{f}\nabla d\cdot {\varvec{N}} {\dot{d}}\textsf {dA} =0 \end{aligned}\end{aligned}$$
(13)

along with Eq. (5) as well as some relevant relations

$$\begin{aligned}&{\varvec{P}}={\varvec{F}}\cdot {\varvec{S}}= {\varvec{F}}\cdot {{\varvec{F}}^\textrm{p}}^{-1}\cdot \left( 2\dfrac{\partial \Psi ^{\textrm{e}}}{\partial {\varvec{C}}^\textrm{e}}\right) \cdot {{\varvec{F}}^\textrm{p}}^{-\textrm{T}}\end{aligned}$$
(14)
$$\begin{aligned}&{\varvec{M}}^{\textrm{p}}={{\varvec{C}}^\textrm{e}}\cdot \left( 2\dfrac{\partial \Psi ^{\textrm{e}}}{\partial {\varvec{C}}^\textrm{e}}\right) \end{aligned}$$
(15)
$$\begin{aligned}&{\varvec{M}}^{\textrm{p}}:{\varvec{D}}^\textrm{p}={\varvec{M}}^{\textrm{p}}_\textrm{dev}:{\varvec{D}}^\textrm{p}, \end{aligned}$$
(16)

where \({\varvec{N}}\), \({\varvec{P}}\), \({\varvec{S}}\), and \({\varvec{M}}^\textrm{p}\) denote the outward unit normal vector on the boundary referring to the initial configuration, the first and second Piola-Kirchhoff stress tensors, and the Mandel stress tensor, respectively. On the other hand, the first-order stability condition for any possible admissible functions \(\left\{ \tilde{ {\varvec{\varphi }}},\tilde{\alpha }, {\tilde{d}}\right\} \) can be written in a similar form as

$$\begin{aligned} \begin{aligned}&-\int _{{\mathcal {B}}_0}\left( \nabla \cdot {\varvec{P}}+{\varvec{B}}\right) \cdot \tilde{{\varvec{\varphi }}}\textsf {dV}+\int _{\partial {\mathcal {B}}_0^{{\varvec{T}}}}\left( {\varvec{P}}\cdot {\varvec{N}}-{\varvec{T}}\right) \cdot \tilde{{\varvec{\varphi }}}\textsf {dA}\\&-\int _{{\mathcal {B}}_0}\sqrt{\dfrac{3}{2}}\left( \Vert {\varvec{M}}^\textrm{p}_\textrm{dev}\Vert -\sqrt{\dfrac{2}{3}}r^\textrm{p}\right) \tilde{\alpha }\textsf {dV}\\&-\int _{{\mathcal {B}}_0}\left( -\dfrac{\partial \Psi ^\textrm{e}}{\partial d}- \dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{l_\textrm{f}}\left( d - l_\textrm{f}^2 \Delta d\right) \right) {\tilde{d}}\textsf {dV}\\&+\int _{\partial {\mathcal {B}}_0}H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) l_\textrm{f}\nabla d\cdot {\varvec{N}} {\tilde{d}}\textsf {dA}\ge 0. \end{aligned} \end{aligned}$$
(17)

From Eq. (13), the local equilibrium equation for the mechanical field is derived as follows:

$$\begin{aligned} \begin{aligned}&\nabla \cdot {\varvec{P}}+{\varvec{B}}={\varvec{0}}\quad \text {in}\ {\mathcal {B}}_0\\&\quad \text {Neumann condition}\quad {\varvec{P}}\cdot {\varvec{N}}={\varvec{T}}\quad \text {on}\ \partial {\mathcal {B}}^{T}_0. \end{aligned} \end{aligned}$$
(18)

Meanwhile, from Eqs. (13) and (17) as well as the above prescribed irreversible conditions, the threshold functions (yield functions) for plasticity and damage with loading/unloading conditions are derived as

$$\begin{aligned} \begin{aligned}&\Phi ^\textrm{p}=\Vert {\varvec{M}}^\textrm{p}_\textrm{dev}\Vert -\sqrt{\dfrac{2}{3}}r^\textrm{p}\le 0, \quad \dot{\alpha }\ge 0,\quad \Phi ^\textrm{p}\dot{\alpha }=0\quad \text {in}\ {\mathcal {B}}_0 \end{aligned} \end{aligned}$$
(19)

and

$$\begin{aligned} \begin{aligned}&\Phi ^\textrm{f}=-\dfrac{\partial g\left( d\right) }{\partial d}\Psi ^{\textrm{e}+}_0- \dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{l_\textrm{f}}\left( d - l_\textrm{f}^2 \Delta d\right) \le 0\\&\quad {\dot{d}}\ge 0,\quad \Phi ^\textrm{f}{\dot{d}}=0\quad \text {in}\ {\mathcal {B}}_0\\&\quad \text {Neumann condition}\quad \nabla d\cdot {\varvec{N}}=0\quad \text {on}\ \partial {\mathcal {B}}^{T}_0. \end{aligned} \end{aligned}$$
(20)

In this study, Eqs. (18) and (20) are spatially discretized, while Eq. (19) is calculated locally at material points.

Remark 4

Dissipation. Taking Eqs. (6) and (8) into account, the total dissipation rate density yields

$$\begin{aligned} \begin{aligned} {\mathcal {D}}&={\mathcal {D}}^\textrm{p}+{\mathcal {D}}^\textrm{f}=\dot{\Psi }^\textrm{p}+\dot{\Psi }^\textrm{f}\\&=r^\textrm{p}\dot{\alpha }+\dfrac{H^*\left( {\varvec{F}}^\textrm{e},\alpha \right) }{l_\textrm{f}}\left( d{\dot{d}} + l_\textrm{f}^2 \nabla d\cdot {\nabla {\dot{d}}}\right) \end{aligned} \end{aligned}$$
(21)

from \(\int ^t_0{\mathcal {D}}{\textsf{d}}{\textsf{t}}=\Psi -\Psi ^\textrm{e}=\Psi ^\textrm{p}+\Psi ^\textrm{f}\). Then, one soon notices Eq. (21) takes a zero or positive value as

$$\begin{aligned} \ \begin{aligned} {\mathcal {D}}&={\varvec{M}}^\textrm{p}:{\varvec{D}}^\textrm{p}-\dfrac{\partial \Psi ^\textrm{e}}{\partial d}{\dot{d}}\ge 0 \end{aligned} \end{aligned}$$
(22)

by virtue of Eqs. (19) and (20).

Fig. 1
figure 1

Micro-mechanisms of ductile fracture and its numerical approximation (Han et al. 2022)

Full size image

2.3 Proposal of damage hardening modulus

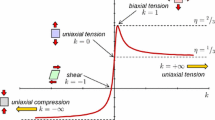
An elastoplastic material is supposed to undergo plastic deformation before crack initiation. Micro-cracks and/or voids are generated under the large deformation region, and their coalescences lead to macro-scale crack propagations. From the macroscopic and phenomenological viewpoints, this can be interpreted as the deterioration of material properties according to the amount of deformation, as illustrated in Fig. 1.

To reflect the above physical background regarding ductile fracture in the current damage modeling, the damage hardening modulus can be degraded depending on the amount of plastic deformation. Since the second term in Eq. (20) becomes smaller, this approach promotes the damage evolution in the region having large plastic deformation. Note that the degradation of damage hardening modulus is conceptionally equivalent to the degrading fracture toughness in crack phase-field modeling. For instance, Dittmann et al. (2018) and Yin and Kaliske (2020) allowed the fracture toughness to decrease with the accumulation of plastic strain; see also the extension by Han et al. (2022). While these previous studies have made it possible to successfully represent ductile fracture in elastoplastic materials to some extent, there is still some concern regarding the assumption that the damaged region only depends on plastic deformation. That is, the simulated fracture behavior can not be consistent with the actual phenomena, since the afore-mentioned micro-crack and/or voids can also be generated by the volume expansion of the material. Thus, the effect of negative hydrostatic pressure relevant to volume expansion should be considered in addition to the effect of plastic deformation.

In this context, we propose a damage hardening modulus as a function of both the accumulation of plastic strain and the negative hydrostatic pressure, which is assumed to degrade from the initial value to nearly zero. Specifically, the following exponential function is used to express the damage hardening modulus:

$$\begin{aligned} \begin{aligned} H^*\left( {\varvec{F}}^\textrm{e},\alpha \right)&= H^*\left( \tau ^*_{\textrm{p}},\alpha ^*\right) \\&=H_{\infty }+\left( H_{0}-H_{\infty }\right) \exp \left( -\beta _{\textrm{G}1}\tau ^*_{\textrm{p}}-\beta _{\textrm{G}2}\alpha ^*\right) , \end{aligned} \end{aligned}$$
(23)

where \(H_{0}\) and \(H_{\infty }\) are the initial and critical moduli, respectively. Here, \(\tau ^*\) and \(\alpha ^*\) are the values determined with the volumetric component of the Kirchhoff stress and the accumulated plastic strain that are defined, respectively, as

$$\begin{aligned} \begin{aligned}&\tau ^*_{\textrm{p}}=\left<\dfrac{1}{3}\textrm{tr}\left[ {\varvec{\tau }}\right] -\tau _{\textrm{p},\textrm{cr}}\right> \quad \text {and}\quad \alpha ^*=\left<\alpha -\alpha _{\textrm{cr}}\right>, \end{aligned} \end{aligned}$$
(24)

where \(\left<\bullet \right>\) is the Macaulay bracket \(\langle \bullet \rangle =\left( \bullet +|\bullet |\right) /2\), and \(\tau _{\textrm{p},\textrm{cr}}\) and \(\alpha _{\textrm{cr}}\) are thresholds to control the initiation of the degradation of the damage hardening modulus. Also, the material parameters, \(\beta _{\textrm{G}1}\) and \(\beta _{\textrm{G}2}\), in Eq. (23), which are associated with the volume expansion and plastic deformation, respectively, are supposed to be determined by calibrations.

It should be noted that the degradation of the damage hardening modulus by negative hydrostatic pressure can be interpreted as a promotion of damage due to the volume expansion because of the plastic incompressibility, while the degradation of the damage hardening modulus due to accumulated plastic strain can be interpreted as a promotion of damage due to the shear deformation. Viewed from another perspective, since the hardening variable \(\alpha \) is determined by the amount of equivalent stress in the yield function, the proposed degradation function in Eq. (23) realizes the stress triaxiality-induced damage evolution.

Remark 5

Another plasticity-induced damage modeling. For plasticity-induced damage modeling, one might introduce a “plasticity-damage coupling dissipation term”, which results in the emergence of “plastic damage driving force” in the damage evolution equation in Eq. (20); see Alessi et al. (2014, 2015) and Miehe et al. (2015, 2016). Although this type of modeling has virtue in terms of its variational structure, it is not easy to reflect the effects other than plastic deformation in damage evolution. For instance, if we want to consider volume expansion-induced damage, as in this study, we probably need to define a special degradation function or dissipation potential to secure the effect of volume expansion, which might bring about the complexity of the formulation. In contrast, the proposed model is expected to easily include effects other than plastic deformation into damage evolution without compromising the variational structure.

3 Weak forms and spatial discretization

3.1 Governing equations in weak form

Weak forms for the mechanical field corresponding to Eq. (18) and that for the damage field corresponding to Eq. (20) are given as, respectively,

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {B}}_0} {\varvec{P}} : \nabla \delta {\varvec{u}} \textsf {dV} \!-\!\int _{{\mathcal {B}}_0}\! {\varvec{B}} \cdot \delta {\varvec{u}} \textsf {dV} \!-\! \int _{\partial {\mathcal {B}}^{{\varvec{T}}}_{0}} \!{\varvec{T}} \cdot \delta {\varvec{u}}\textsf {dA}\!=\!0 \end{aligned} \end{aligned}$$
(25)

and

$$\begin{aligned} \begin{aligned} \int _{{\mathcal {B}}_0}&\left( \dfrac{\partial g\left( d\right) }{\partial d}\Psi ^{\textrm{e}+}_0\delta d+\dfrac{H^*}{l_\textrm{f}}d\delta d +H^*l_\textrm{f}\nabla d \cdot \nabla \delta d\right) \!\textsf {dV}\\&\qquad =0, \end{aligned} \end{aligned}$$
(26)

where \(\delta {\varvec{u}}\) and \(\delta d\) are the virtual displacement and virtual damage variable, respectively. The spatial counterparts of these weak forms are obtained by the push-forward operations as

$$\begin{aligned} \begin{aligned}&\int _{{\mathcal {B}}_t} \dfrac{1}{J}\underbrace{{\varvec{\tau }}}_{{\varvec{F}}\cdot {\varvec{S}}\cdot {\varvec{F}}^\textrm{T}}: \nabla _{{\varvec{x}}}\delta {\varvec{u}} \textsf {dv} -\int _{{\mathcal {B}}_t} {\varvec{b}}\cdot \delta {\varvec{u}} \textsf {dv}\\&\qquad -\int _{\partial {\mathcal {B}}^{{\varvec{T}}}_{t}} {\varvec{t}} \cdot \delta {\varvec{u}}\textsf {da}=0 \end{aligned}\nonumber \\ \end{aligned}$$
(27)

and

$$\begin{aligned} \begin{aligned} \int _{{\mathcal {B}}_t} \dfrac{1}{J}&\left( \dfrac{\partial g\left( d\right) }{\partial d}\Psi ^{\textrm{e}+}_0\delta d +\dfrac{H^*}{l_\textrm{f}}d\delta d \right. \\&\left. \qquad +H^*l_\textrm{f}\left( \nabla _{{\varvec{x}}}d\cdot {\varvec{F}}\right) \cdot \left( \nabla _{{\varvec{x}}}\delta d\cdot {\varvec{F}}\right) \right) \textsf {dv}=0. \end{aligned} \end{aligned}$$
(28)

Here, \({\varvec{b}}\) and \({\varvec{t}}\) are the body and traction forces in the current configuration and are given, respectively, as

$$\begin{aligned} \begin{aligned} {\varvec{b}} = \dfrac{{\varvec{B}}}{J} \quad \text{ and } \quad {\varvec{t}} = \dfrac{{\varvec{T}}}{J\sqrt{{\varvec{N}} \cdot {\varvec{C}}^{-1}\cdot {\varvec{N}}}}. \end{aligned} \end{aligned}$$
(29)

3.2 Spatial discretization

The global variables and their variations are approximated in a general manner by using second-order NURBS basis functions \(\mathfrak {R}\) as

$$\begin{aligned} \begin{aligned}&{\varvec{u}}\approx {\varvec{u}}^h = \sum _{I=1}^{n_\text {node}} \mathfrak {R}^{I}{\varvec{u}}^{I},\quad \delta {\varvec{u}}\approx \delta {\varvec{u}}^h = \sum _{I=1}^{n_\text {node}} \mathfrak {R}^{I}\delta {\varvec{u}}^{I},\\&d\approx d^h = \sum _{I=1}^{n_\text {node}} \mathfrak {R}^{I} d^{I} ,\quad \delta d \approx \delta d^h = \sum _{I=1}^{n_\text {node}} \mathfrak {R}^{I}\delta d^{I}, \end{aligned} \end{aligned}$$
(30)

where \(n_\text {node}\) is the number of control points in an element, and \({\varvec{u}}^{I}\) and \(d^{I}\) are the quantities at control points. Within a representative time interval \([t_{n}, \, t_{n+1}]\), the element residual vectors at the current time step \(t_{n+1}\) corresponding to the weak forms in Eqs. (27) and (28) are discretized as, respectively,

$$\begin{aligned} \begin{aligned} {\mathcal {R}}^I_{\varphi _i} = -\int _{{\mathcal {B}}_t} \dfrac{1}{J}\left( {\tau ^h}_{ij}\dfrac{\partial \mathfrak {R}^{I}}{\partial x_j}\right) \textsf {dv} \end{aligned} \end{aligned}$$
(31)
$$\begin{aligned} \begin{aligned} {\mathcal {R}}^I_{d}&=- \int _{{\mathcal {B}}_t}\dfrac{1}{J} \left\{ \dfrac{\partial g\left( d^h\right) }{\partial d}{\mathcal {H}}^{\textrm{e}}_{n+1}\mathfrak {R}^I \right. \\&\left. \quad +\dfrac{{H^*_{n+1}}}{l_\textrm{f}}d^h\mathfrak {R}^I+{{H^*_{n+1}}}{l_\textrm{f}}\dfrac{\partial d^h}{\partial x_a}F_{ak}\dfrac{\partial \mathfrak {R}^I}{\partial x_b}F_{bk} \right\} \textsf {dv}. \end{aligned} \end{aligned}$$
(32)

Throughout this paper, the body and traction forces are neglected and have been eliminated in the above-discretized equations. Also, the history variable has been introduced as

$$\begin{aligned} \begin{aligned} {\mathcal {H}}^{\textrm{e}}_{n+1}:= {\left\{ \begin{array}{ll} \Psi ^{\textrm{e}+}_{0,\,n+1}&{}\quad \text {if}\quad \Psi ^{\textrm{e}+}_{0,\,n+1}>{\mathcal {H}}^{\textrm{e}}_n\\ {\mathcal {H}}^{\textrm{e}}_n &{}\quad \text {otherwise} \end{array}\right. } , \end{aligned} \end{aligned}$$
(33)

which was originally proposed by Miehe et al. (2010). Thanks to this variable, the irreversibility of damage evolution is guaranteed.

In this study, the staggered algorithm (Miehe et al. 2010; Ambati et al. 2015a) is adopted to implicitly solve the coupled system of nonlinear algebraic equations. That is, the residual vectors for the mechanical field and damage field are solved alternately until both of the equilibrium states are satisfied at each loading step with reference to the following potential convergence criterion (convergence of a staggered iterative process):

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {Go to next loading step} &{}\quad \text {if}\; \log _{10}{\mathcal {R}}^{st}_{k+1} \le \text {Tolerance}\\ \text {One more cycle}&{}\quad \text {if}\;\log _{10}{\mathcal {R}}^{st}_{k+1} > \text {Tolerance} \end{array}\right. }. \end{aligned}$$
(34)

Here, \({\mathcal {R}}^{st}_{k+1}\) is the error in \({k+1}\) th staggered iteration, which is calculated as

$$\begin{aligned} {\mathcal {R}}^{st}_{k+1}=\text {min}\left[ \left| \dfrac{\Pi _{k+1}-\Pi _k}{\Pi _{k+1}}\right| , \, \left| \Pi _{k+1}-\Pi _k\right| \right] . \end{aligned}$$
(35)

If the error becomes smaller than Tolerance, we proceed to the next loading step. Otherwise, a new staggered iteration step is restarted. Within each staggered iteration step, the Newton-Raphson iteration is carried out to make each of the residuals in Eqs. (31) and (32) becomes small enough. In the following numerical simulations, a value of \(-4\) is used. For a detailed explanation of the staggered algorithm, refer to Ambati et al. (2015a).

By differentiating the residual force vectors in Eqs. (31) and (32) with respect to the principal variables, \({\varvec{\varphi }}\) and d, we obtain the corresponding linearized equations. Then, the tangent matrices are given as

$$\begin{aligned} \begin{aligned}&{\mathcal {K}}^{IJ}_{\varphi _i \varphi _j} =\int _{{\mathcal {B}}_t}\left( \dfrac{\partial \mathfrak {R}^I}{\partial x_k}{{\mathbb {C}}^h}_{ikjl}\dfrac{\partial \mathfrak {R}^J}{\partial x_l} \right) \textsf {dv}\\ \quad \text {with}\quad&{{\mathbb {C}}^h}_{ikjl}=\dfrac{1}{J}\left( \dfrac{\partial {\tau ^h}_{ik}}{\partial F_{ja}}F_{la}-{\tau ^h}_{il}\delta _{jk}\right) \end{aligned} \end{aligned}$$
(36)
$$\begin{aligned} \begin{aligned} {\mathcal {K}}^{IJ}_{dd}&= \int _{{\mathcal {B}}_t} \dfrac{1}{J}\left\{ \dfrac{\partial ^2 g\left( d^h\right) }{\partial d^2}{\mathcal {H}}^{\textrm{e}}_{n+1}\mathfrak {R}^I\mathfrak {R}^J +\dfrac{{H^*_{n+1}}}{l_\textrm{f}}\mathfrak {R}^I \mathfrak {R}^J \right. \\&\left. \quad + {H^*_{n+1}} l_\textrm{f}\dfrac{\partial \mathfrak {R}^I}{\partial x_a}F_{ak}\dfrac{\partial \mathfrak {R}^J}{\partial x_b}F_{bk} \right\} \textsf {dv}. \end{aligned} \end{aligned}$$
(37)

Note that the coupling terms between Eqs. (31) and (32) are unnecessary because of the staggered algorithm adopted in this study.

Remark 6

An assumption for \({H^*_{n+1}}\). Yin and Kaliske (2020) assumed \(\partial _{\alpha _{n+1}} {G^*_{\textrm{c},n+1}}\approx \partial _{\alpha _{n+1}} {G^*_{\textrm{c},n}}=0\) by noting that the degrading tendency of the fracture toughness has a “special non-linearity”. In the numerical implementation, we accept this assumption and let \({H^*_{n+1}}={H^*_{n}}\). Note that a similar assumption seems to be used in Dittmann et al. (2018) without mention.

Table 1 Fixed material parameters for Study 1
Full size table
Table 2 Five combination patterns of material parameters for Study 1
Full size table

4 Parameter studies: basic performance

Parameter studies are carried out to confirm the basic performance of the proposed model. In order to reduce the computational cost, the convergence calculation in the staggered iterative process is conducted when \(d_{\text {max}}>0.2\).

4.1 Study 1: Tensile failure of a square element

This parameter study is devoted to the verification of the ability of the proposed coupled plasticity-damage model in comparison with a decoupled plasticity-damage setup. We consider a two-dimensional square element having a side length of \(h_\textrm{e}=1\ \textrm{mm}\) subjected to the uni-directional loading to realize uniform deformation. The isotropic linear hardening law \(r^\textrm{p}\left( \alpha \right) =y_0+h\alpha \) is adopted for simplicity. The material parameters for the employed elastoplastic model are listed in Table 1, and the crack length scale parameter is fixed at \(l_\textrm{f}=2.0\ \textrm{mm}\) for all the cases. To highlight the feature of the proposed model, five cases with different parameters are considered as listed in Table 2; that is, no damage calculation (no damage), constant damage hardening modulus (\(H=\text {const.}\)), and three types of damage hardening modulus degraded by accumulated plastic strain, negative hydrostatic pressure and both of these (denoted by 1A, 1B and 1C), respectively. Note that the second case, \(H=\text {const.}\), is the decoupled plasticity-damage setup.

Fig. 2
figure 2

Load–displacement curves for Study 1

Full size image
Fig. 3
figure 3

Geometry and boundary conditions for Study 2

Full size image

The load–displacement curves obtained for all the cases are shown in Fig. 2. Here, after some manipulations on Eqs. (20) and (33) under the assumption of uniform deformation, the damage variable d yields

$$\begin{aligned} d=\dfrac{2{\mathcal {H}}^{\textrm{e}}}{H^*/l_\textrm{f}+2{\mathcal {H}}^{\textrm{e}}}. \end{aligned}$$
(38)

As can be seen, the maximum elastic strain energy \({\mathcal {H}}^{\textrm{e}}\) is dominant in determining damage evolution when the damage hardening modulus is constant. That means that, in plastic deformation, the rate of increase in elastic strain energy becomes relatively small compared to purely elastic deformation. Therefore, when the damage hardening modulus is constant, no significant reduction in material stiffness is expected in a plastic state when employing the decoupled plasticity-damage setup. Such a tendency can be confirmed from the black (no damage) and red dotted (\(H=\text {const.}\)) lines in Fig. 2.

On the other hand, the remaining three dotted lines in Fig. 2 show the results for the cases with three degradation types of the damage hardening modulus; that is, those degraded by accumulated plastic strain (1A: blue dotted line), negative hydrostatic pressure (1B: magenta dotted line), and both of them (1C: green dotted line), respectively. In each of these curves, a decrease in load can be observed after the material experiences a certain amount of deformation. It is obvious that the difference among these results has been brought by the different combinations of the material parameters, \(\beta _{\textrm{G}1}\) & \(\beta _{\textrm{G}2}\) in Eq. (23), as well as the threshold values, \(\tau _{\textrm{p},\textrm{cr}}\) & \(\alpha _{\textrm{cr}}\).

It seems reasonable to conclude from the discussions above that the proposed model can realize damage evolutions depending on plastic deformation or volume expansion.

4.2 Study 2: Mixed-mode failure for an asymmetrically notched specimen

The target of the second parameter study is a tensile test for a two-dimensional asymmetrically notched specimen illustrated in Fig. 3. Here, the same geometrical setup has also been studied by Ambati et al. (2015b) and others, in which cracks initiate from both notches and propagate toward the center of the specimen to form a single crack path in most cases. The main concern here is the difference in fracture modes depending on parameter values.

Table 3 Fixed material parameters for Study 2
Full size table
Table 4 Seven combination patterns of material parameters for Study 2
Full size table
Fig. 4
figure 4

Load–displacement curves for Study 2

Full size image

Fixed material parameters are listed in Table 3. In this particular example problem, the Voce hardening function \(r^\textrm{p}\left( \alpha \right) =y_0+h\alpha +\left( y_\infty -y_0\right) \exp \left( -\beta _\text {y}\alpha \right) \) is used for the hardening behavior of plastic deformation. We consider seven cases with different combinations of the material parameters for degrading the damage hardening modulus as listed in Table 4; i.e., damage hardening modulus degraded by accumulated plastic strain (2A1, 2A2), negative hydrostatic pressure (2B1, 2B2), and both accumulated plastic strain and negative hydrostatic pressure (2C1, 2C2, 2C3), respectively. Also, the crack length scale parameter is fixed at \(l_\textrm{f}=1.5\ \textrm{mm}\), and the element size in the potentially damaged region between two notches is set at \(h_\textrm{e}\approx 0.2\ \textrm{mm}\) for all the cases.

Fig. 5
figure 5

Detailed evolution of damage variable d, accumulated plastic strain \(\alpha \), damage hardening modulus \(H^*\) for Study 2: Cases 2A1 and 2A2 (\(H^*\) degraded by \(\alpha \))

Full size image
Fig. 6
figure 6

Detailed evolution of damage variable d, accumulated plastic strain \(\alpha \), damage hardening modulus \(H^*\) for Study 2: Cases 2B1 and 2B2 (\(H^*\) degraded by \(\tau _\textrm{p}\))

Full size image
Fig. 7
figure 7

Detailed evolution of damage variable d, accumulated plastic strain \(\alpha \), damage hardening modulus \(H^*\) for Study 2: Cases 2C1, 2C2 and 2C3 (\(H^*\) degraded by \(\alpha \) & \(\tau _\textrm{p}\))

Full size image

The simulated load–displacement curves are shown in Fig. 4. Also, Figs. 5, 6, and 7 show the distributions of the damage variable d, accumulated plastic strain \(\alpha \) and damage hardening modulus \(H^*\), respectively. First, let us examine the results of Cases 2A1 and 2A2, for which the damage hardening modulus is assumed to be degraded only by the accumulated plastic strain. As can be seen from Fig. 4a, the solid black line (2A1) reaches a peak around a forced displacement of \(u\approx 1.5\ \textrm{mm}\) and then exhibits a gradual decrease before a rapid drop around \(u\approx 2.0\ \textrm{mm}\). While a similar tendency is seen for Case 2A2, the degradation of the damage hardening modulus is delayed due to the threshold value \(\alpha _\textrm{cr}\) larger than that of Case 2A1. It is also found from Fig. 5 that, as the damage hardening modulus is degraded by the accumulation of plastic deformation, two single cracks subsequently initiate near the center between the notches, where the damage hardening modulus is severely degraded. It should be noted that the crack paths generated in each case are linearly inclined and directed to each other to form a single path. This kind of crack propagation was also obtained in the previous studies (Ambati et al. 2015b; Miehe et al. 2015; Dittmann et al. 2018; Yin and Kaliske 2020). Thus, the performance of the proposed model is similar to the existing models considering plasticity-induced damage evolution.

Next, we focus on the results of Cases 2B1 and 2B2, which assume the damage hardening modulus depends on the negative hydrostatic pressure only. The load–displacement curves are indicated by the blue and magenta dotted lines in Fig. 4a. As can be seen, rapid drops are exhibited once declines are confirmed. Also, the horizontal crack growths that are evident in corresponding distributions of the damage variable and the damage hardening modulus, as shown in Fig. 6, reflect the effect of negative hydrostatic pressure. Despite the horizontal cracks, the distribution of the accumulated plastic strain exhibits shear bands and is independent of the crack paths. The behavior looks like a brittle-like fracture caused by volume expansion, even though relatively large plastic deformation occurs. This suggests that the combination of negative hydrostatic pressure with accumulated plastic strain in the proposed model makes it possible to control the transition between brittle-like and ductile fractures.

To confirm the performance mentioned above, the results with Cases 2C1–2C3 are studied. In these cases, parameters \(\beta _{\textrm{G}1}\), \(\tau _{\textrm{p},\textrm{cr}}\) and \(\alpha _{\textrm{cr}}\) are fixed whereas \(\beta _{\textrm{G}2}\) is set in the descending order corresponding to \(\text {2C1}>\text {2C2}>\text {2C3}\); see Table 4. With this parameter setting, the effect of plastic deformation on the degradation of the damage hardening modulus is expected to be weaker, meaning the breaking elongations would be in the order corresponding to \(\text {2C1}<\text {2C2}<\text {2C3}\). As expected, the tendency in the load–displacement curves shown in Fig. 4b indicates that the specimen can sustain a larger elongation as \(\beta _{\textrm{G}2}\) becomes smaller. Also, the crack growth behavior in Fig. 7 becomes closer to that of Fig. 6 rather than Fig. 5 as \(\beta _{\textrm{G}2}\) becomes smaller. More specifically, in the case of a smaller \(\beta _{\textrm{G}2}\), the crack paths tend to evolve in the horizontal direction or, equivalently, in the direction of maximum principal stress at the onset but eventually transition to an inclined crack along the shear band formed by plastic deformation. This demonstrates that the proposed model is capable of controlling brittle-like and ductile crack growths.

In summary, both results in the parameter studies lead us to conclude that the proposed model is expected to demonstrate the crack propagation behavior reflecting the effects of both shear deformation (plastic deformation) and volume expansion (negative hydrostatic pressure).

Fig. 8
figure 8

Experimental setup for single notched specimen (Omiya et al. 2022)

Full size image

5 Numerical simulations of tensile failure of notched specimens

This section is devoted to demonstrating the ability of the proposed model to predict the breaking elongation, the transitional behavior from unstable to stable crack propagations, the load–displacement curves, and the crack initiation positions for single notched specimens subjected to tensile loading. The numerical results are compared with the experimental ones obtained by the corresponding tensile tests (Omiya et al. 2022) we have conducted for the purpose of verification.

5.1 Experimental setup and classification of crack growth behavior

A specimen is made of advanced high strength steel sheet (AHSS sheet) “JSC1180” or “JSC980”. Here, the number after “JSC” refers to its tensile strength in MPa units. The appearance of the experimental setup is shown in Fig. 8a, in which the specimen is fixed to the tension testing machine (MTS-810) by two jigs. Photos are taken by a high-speed camera (NAC MEMRECAM AC-1) and a CCD camera (Ximea MQ042MG-CM), focusing on the region where the crack initiates and propagates. As illustrated in Fig. 8b, two specimens with different notch geometries (\(\text {R}=5.0\ \textrm{mm}\) and \(\text {R}=0.5\ \textrm{mm}\)) are used, and the dark-gray region outside the parallel portion is sandwiched by two plate-like jigs. During experiments, a rate of forced displacement of \(1/6\ \textrm{mm}/\text {s}\) is applied to the entire surface of the topside jigs, while the downside jigs are immovably fixed; hereafter, this forced displacement is called “stroke displacement” and is denoted by \(u_\text {s}\). On the other hand, the relative displacement between the two points shown in Fig. 8b, which is measured by the CCD camera, is called “gauge displacement” and denoted by \(u_\text {g}\).

In general, crack propagation behavior can be classified into two states: “stable” and “unstable” (Anderson 2017). These can be used to classify the observed crack growth behavior in the experiments described above. When the crack growth does not continue without any external energy supply, it is called “stable crack propagation”, in which the crack resistance increases with crack propagation (R-curve). Since the speed of stable crack growth is relatively slow, the kinetic energy component may be insignificant. On the other hand, when the crack grows without any external energy supply, it is called “unstable crack propagation”. The material acquires kinetic energy from the inertia of the material surrounding the rapidly separating crack walls (Lawn 1993). In such dynamic cases, the static equilibrium conditions of Griffith and Irwin-Orowan no longer apply. Subsequent theoretical works done by Mott (1948), Yoffe (1951), and Broberg (1960) extended Griffith’s concept by adding the kinetic energy term in the expression of the total energy balance and exploring the terminal velocity in linear elastodynamics. Also, see Freund (1990).

From the above-described perspective, the crack propagation speed is a possible indicator for the purpose of classification. In our measurement, the shutter speed of the CCD camera is set at five fps, and one point for a load–displacement curve is plotted in every frame. In the following discussions, whether a crack growth is stable or unstable will be determined by the clearance between two adjacent points in the load–displacement curve, which corresponds to 0.2 s. That is, if the clearance is sufficiently large, so that curve plotted by points looks discontinuous, then the crack growth is regarded as an “unstable” state. Otherwise, it represents a “stable” crack propagation.

5.2 Experimental result

First, we summarize the experimental results for JSC1180. Fig. 9 shows the load–displacement curves and snapshots of crack growths for the specimens with notch radii of \(\text {R}=5.0\ \textrm{mm}\) and \(\text {R}=0.5\ \textrm{mm}\), respectively. Here, the black and gray plots in Fig. 9a and b indicate the gauge and stroke displacements, respectively. As can be seen from these figures, a characteristic response is observed for each of the specimens. Specifically, the load suddenly drops after the peak. During this decrease in load, the gauge displacement increases significantly from \(u_\text {g}\approx 0.37\ \textrm{mm}\) to \(u_\text {g}\approx 1.31\ \textrm{mm}\) for the specimen with \(\text {R}=5.0\ \textrm{mm}\) and \(u_\text {g}\approx 0.24\ \textrm{mm}\) to \(u_\text {g}\approx 1.05\ \textrm{mm}\) for the specimen with \(\text {R}=0.5\ \textrm{mm}\), while the stroke displacements \(u_\text {s}\) hardly increase. These tendencies result from the crack initiation and subsequent rapid growth, as can be recognized from Fig. 9c and d. Thus, the crack propagation can be categorized as an unstable crack growth. To be specific, within the time interval (about 0.2 s) starting from (C) to (D) for \(\text {R}=5.0\ \textrm{mm}\) specimen and (I) to (J) for \(\text {R}=0.5\ \textrm{mm}\) specimen, the crack initiates near the notch, propagates horizontally to the right and stops at about 3/4 of the width of specimen.

Fig. 9
figure 9

Experimental results for JSC1180 (Omiya et al. 2022)

Full size image

After the first unstable crack growth, a relatively stable crack growth is observed until each of the two specimens is finally broken. That is, the load versus stroke and gauge displacements shows almost the same tendency right after the peak load. During the stable crack growth, the load attains “the second peak” for both cases. This is surely due to the rotation of jigs since it allows the specimen to bend along with the crack growth. In fact, Fig. 9c and d show that the specimen is moving horizontally to the left; see the transitions from (C) to (D) and (I) to (J). As the bending mode reduces the effect of tensile loading around the right portion, it is considered that an increase in tensile load is required for subsequent crack propagation.

Fig. 10
figure 10

Experimental results for JSC980 (Omiya et al. 2022)

Full size image
Fig. 11
figure 11

Various crack initiation positions depending on different tensile strength and notch geometry (Omiya et al. 2022)

Full size image
Fig. 12
figure 12

Numerical setups for single notched specimens

Full size image

Next, let us describe the experimental results for JSC980. As for the case with JSC1180, Fig. 10 shows the load–displacement curves and snapshots of crack growths for the specimens with two different notch radii. It should be noted here that, unlike JSC1180, JSC980 shows different tendencies depending on the notch radius. That is, for the larger notch radius (\(\text {R}=5.0\ \textrm{mm}\)), unstable crack growth is confirmed like the results for JSC1180, while the \(\text {R}=0.5\ \textrm{mm}\) specimen reveals a stable crack propagation throughout the experiment. Specifically, as can be seen from Fig. 10a and b, a rapid drop in the load is observed for \(\text {R}=5.0\ \textrm{mm}\) but not for \(\text {R}=0.5\ \textrm{mm}\). These tendencies are also evident in the photos in Fig. 10c and d. To be more specific, in the case of \(\text {R}=5.0\ \textrm{mm}\), the crack initiates and propagates horizontally to the right until it extends to about 1/3 of the width of the specimen within the 0.2 s; see the transition from (O) to (P). On the other hand, from (U) to (X), such a rapid crack growth does not appear, and only a gradual crack propagation is observed. It can be inferred from these results that the notch radius is also an influential factor in the crack growth behavior as well as the tensile strength.

Additionally, the crack initiation positions for the four test cases should be noted. The photographs in Fig. 11 show the enlarged regions near the notches right after crack initiation. Here, we have added the results of two JSC590 specimens with the same set of notch radii, both of which were confirmed to exhibit stable crack growths. As can be seen from these photos, the position of crack initiation varies depending on both the tensile strength and notch radius. To be specific, in the case of the specimens with a larger notch radius, the crack initiates inside the specimen, and a higher tensile strength tends to be associated with the crack initiation occurring at a position away from the tip of the notch. This difference in crack initiation position is probably due to the difference in the relative magnitude of the failure resistances against shear deformation and volume expansion. Detailed discussions will be held later, along with numerical investigations. Meanwhile, the crack initiation position in the specimen with a notch radius of \(\text {R}=0.5\ \textrm{mm}\) hardly can be identified from the photos in Fig. 11 and therefore would be suitable targets for prediction by the proposed model.

Table 5 Material parameters for single notched specimens
Full size table

5.3 Exemplification

To exemplify the performance of the proposed model, we first identify the material parameters in the employed elastoplastic constitutive law. For that purpose, tensile tests were conducted on an I-shaped flat specimen made of JSC1180 and JSC980 using the same testing machine. Fig. 12a shows the experimentally obtained relationships between the true stress and equivalent plastic strain (drawn with black and gray markers) that have been converted from the relationships between the load and gauge displacement. By conducting calibration, we determined the material parameters as provided in Table 5 and obtained the fitted curves (the red and blue solid lines) in the same figure. Here, the Swift hardening function \(r^\textrm{p}\left( \alpha \right) =y_a\left( \alpha _b+\alpha \right) ^{\beta _c}\) is adopted for the hardening behavior of plastic deformation.

Table 6 Material parameters for damage hardening modulus
Full size table

As can be seen from Figs. 9 or 10, the stroke displacement is much larger than the gauge displacement, which indicates the stiffness of the testing machine is evidently reflected. It should also be noted that the bending of specimens is accompanied by the rotation of jigs. Thus, both the stiffness and rotational effects should be taken into account in our numerical simulations so that both the load versus the stroke and gauge displacements individually coincide with experimental results using the same set of material parameters. Otherwise, the relationship between the load and time would become unrealistic because the tensile loading (forced displacement) is in accord with time advance. However, modeling the actual jigs and other parts of the testing machine is not only unnecessarily cumbersome but also computationally expensive. Thus, to accommodate those effects, a “pseudo-arm” is attached to each of the ends of the numerical model of the specimen as shown in Fig. 12b along with the boundary conditions. This pseudo-arm is assumed to be a purely elastic material, and Young’s modulus and Poisson’s ratio are arbitrarily set at 210 GPa and 0.3. Then, its geometry is determined by trial and error so that the numerical results can reasonably be consistent with the experimental ones provided in Figs. 9a and b and 10a and b for all four cases. The fitted curves are shown in Fig. 12c for the purpose of comparison with the experimentally obtained curves. Note here that no damage computations have been conducted in this calibration process.

Next, the material parameters in the damage hardening modulus are determined so that the simulated load versus the stroke and gauge displacements matches as closely as possible to those of Figs. 9a and b and 10a and b. Here, the crack length scale parameter is fixed at \(l_\textrm{f}=0.6\ \textrm{mm}\), so that the element size in the potentially damaged region is set to be \(h_\textrm{e}\approx 0.25\sim 0.30\ \textrm{mm}\). A trial-and-error procedure is again carried out to finally determine the parameters provided in Table 6.

The numerical results for JSC1180 shown in Fig. 13 indicate that the simulated failure responses conform to the experimental ones. As can be seen from Fig. 13a for the case of \(\text {R}=5.0\ \textrm{mm}\), the load exhibits a sudden drop from its peak to about \(15\ \text {kN}\). During this decrease in load, the gauge displacement significantly increases from \(u_\text {g}\approx 0.47\) to \(u_\text {g}\approx 1.48\ \textrm{mm}\), whereas only a small increase in the stroke displacement \(u_\text {s}\) is obtained. Also, it can be seen from (B)–(D) in Fig. 13c that the crack rapidly grows right after the initiation. After this unstable crack growth, the fracture behavior becomes stable, and the crack grows with tensile loading, as indicated from (D)–(F) in this figure. By using the same set of material parameters, almost the same tendency of the fracture behavior can be simulated for the case of \(\text {R}=0.5\ \textrm{mm}\) as can be seen from Fig. 13d. Specifically, within the time interval (about 0.27 s) starting from (H) to (J), the crack initiates near the notch, propagates horizontally to the right, and stops when it reaches about 3/4 of the width of the specimen. After this point, the crack grows with tensile loading; see (J)–(L).

Meanwhile, Fig. 14 shows the simulation results for JSC980, which are also in close agreement with the experimental results. For the case of \(\text {R}=5.0\ \textrm{mm}\), unstable crack growth is again confirmed to be consistent with the experimental results. To be specific, the load significantly decreases from the peak to about \(30\ \text {kN}\), and the crack initiates near the edge of the notch and propagates to about 1/3 of the width of the specimen; see (N)–(O) in Fig. 14c. After this period of unstable crack growth, the stable crack growth is simulated until the specimen finally breaks. In contrast, the result for the case of \(\text {R}=0.5\ \textrm{mm}\) indicates stable crack growth throughout the numerical simulation. It is confirmed from Fig. 14d that the crack inconsiderably propagates after its initiation; see (T) and (U) in particular. This is probably due to the fact that the specimen with \(\text {R}=0.5\ \textrm{mm}\) attains less negative hydrostatic pressure (volume expansion) and exhibits more ductility than that of \(\text {R}=5.0\ \textrm{mm}\).

Fig. 13
figure 13

Numerical results for JSC1180

Full size image
Fig. 14
figure 14

Numerical results for JSC980

Full size image
Fig. 15
figure 15

Various crack initiation positions (left: before crack initiation, right: after crack initiation) depending on the degradation of damage hardening modulus for \(\text {R}=5.0\ \textrm{mm}\)

Full size image
Fig. 16
figure 16

Various crack initiation positions (left: before crack initiation, right: after crack initiation) depending on the degradation of damage hardening modulus for \(\text {R}=0.5\ \textrm{mm}\)

Full size image

In the above discussion, we have demonstrated that the proposed model successfully reproduces the failure behaviors of AHSS sheets. In what follows, its prediction ability for a crack initiation position is examined. As mentioned in relation to Fig. 11, the crack initiates inside the specimen but not on the notch surface in the case of \(\text {R}=5.0\ \textrm{mm}\). This is probably due to the effect of negative hydrostatic pressure (volume expansion) developed away from the notch surface, although the position of the maximum negative hydrostatic pressure and its magnitude seems to depend on the tensile strength as well as the notch size. Figure 15a shows the enlarged views around the obtained crack initiation position for the JSC1180 specimen using the damage hardening modulus degraded only by the accumulated plastic strain, which is conceptionally equivalent to the results of previous studies (Dittmann et al. 2018; Yin and Kaliske 2020). Note that the damage evolves in the order from the left view to the right view. As can be seen, the crack initiates from the edge of the notch, which is thought to have experienced the most significant plastic deformation. Additionally, Fig. 15b shows the corresponding results with the damage hardening modulus degraded only by the negative hydrostatic pressure. Since the damage contribution of plastic deformation is neglected in this case, the crack initiates at a position further away from the notch surface than the actual crack in the experiments. In this way, neither result is realistic nor consistent with the experimental results.

On the other hand, Fig. 15c and d show enlarged images of the vicinity of the crack initiation position for the specimen with a \(\text {R}=5.0\ \textrm{mm}\) notch taken from the numerical results, which correspond to the simulated fractures shown in Figs. 13c and 14c, respectively. In the cases of JSC1180 and JSC980, crack initiation occurred at almost the same position as those of the experiments. It is thus concluded that to accurately predict crack initiation, at least the damage contribution from both plastic deformation (shear dominant deformation) and negative hydrostatic pressure (volume expansion dominant deformation) should be properly taken into consideration. It should also be noted that since several previous models for ductile fracture (Ambati et al. 2015b; Miehe et al. 2015; Dittmann et al. 2018; Yin and Kaliske 2020) focus only on the plastic deformation-induced damage evolution, it might not be possible to represent this kind of characteristic feature of crack initiation.

Additionally, Fig. 16 shows the enlarged views around the crack initiation positions for the specimen with \(\text {R}=0.5\ \textrm{mm}\), which correspond to the simulated fracture behaviors shown in Figs. 13d and 14d. Again, for each figure, the damage evolves in the order from the left view to the right view. As can be seen from these results, the crack initiates slightly inside the specimen for each of the cases. It should be remembered that we could not identify the crack initiation position from the experiments because the phenomenon occurred within a very short period of time, and the notch radius is small. Given that the crack initiation positions are well reproduced for JSC1180/980 with \(\text {R}=5.0\ \textrm{mm}\), those obtained here can be presumed to be correct.

Here, let us summarize our experimental and numerical simulation results. In our experiments, the transitions from unstable to stable crack propagations are observed for AHSS sheets JSC1180/980. Also, we could observe crack initiation positions for JSC1180/980 with \(\text {R}=5.0\ \textrm{mm}\) but not for JSC1180/980 with \(\text {R}=0.5\ \textrm{mm}\). Meanwhile, in numerical simulations, we successfully simulated the failure tendency for JSC1180/980 with \(\text {R}=5.0\ \textrm{mm}\) after conducting calibration. Also, we simulated crack initiations from almost the same positions as in the experiments for them. Then, by conducting numerical simulations for JSC1180/980 with \(\text {R}=0.5\ \textrm{mm}\) using the same set of parameters, we found that the crack propagations, as well as the load–displacement curves, agreed with the experimental results. Therefore, we concluded that the simulated crack initiation positions for JSC1180/980 with \(\text {R}=0.5\ \textrm{mm}\) are also correct, even though they were not confirmed in our experiments.

5.4 Supplementary remarks

Thanks to the degradation of the damage hardening modulus by plastic deformation and volume expansion, the proposed model can reproduce or predict the crack propagation tendency as explored above, which is unable to be accomplished by previous studies that only consider plasticity-induced damage. In particular, the proposed model can be useful to simulate fracture behavior in metallic materials such as AHSS that exhibit volume expansion-induced fracture.

One area for improvement of the proposed model is the rational manner of determining the parameters for the degradation of the damage hardening modulus. Although the only way to determine them is calibration, it is common to most continuum damage models. With regard to this point, the proposed model cannot be a “predictive” one. Nevertheless, as investigated in this section, numerical simulations for the smaller notch radius \(\text {R}=0.5\ \textrm{mm}\) provided reasonable crack propagation tendencies, including crack initiation positions, once the parameters for the larger notch radius \(\text {R}=5.0\ \textrm{mm}\) have been determined. In this context, the proposed model is considered to be predictive, and we can argue the uniqueness of our study.

6 Conclusion

This study has presented a gradient damage model for ductile fracture, in which the damage hardening modulus is degraded by the accumulation of plastic deformation and the volume expansion caused by negative hydrostatic pressure based on phenomenological justification.

The governing equations are derived from energy minimization principles and discretized within the IGA framework. Three representative numerical examples are presented to demonstrate the ability and performance of the proposed model. From the numerical simulations in the first two parameter studies, in addition to providing the same ability as the existing models for ductile fracture, the proposed model has shown the ability to control crack propagation paths by changing the two degrading effects of the damage hardening modulus. Enjoying this feature, the last example successfully reproduced the fracture behavior of AHSS sheets observed in the actual experiments. For specimens with two different tensile strengths and notch radii, the proposed model realized the transition from/to unstable to/from stable crack growths.

Nevertheless, the degradation of the damage hardening modulus is still short of physical implication, and other factors, such as the Lode angle begs consideration. Also, a more quantitative estimate of experimental data is needed to understand better the failure mechanisms in AHSS sheets and other elastoplastic materials. These issues will be discussed in future work.