Skip to main content

Advertisement

SpringerLink
Log in

How to apply the dependence structure analysis to extreme temperature and precipitation for disaster risk assessment

  • Original Paper
  • Published:
Theoretical and Applied Climatology Aims and scope Submit manuscript

Abstract

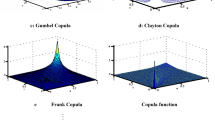
IPCC reports that a changing climate can affect the frequency and the intensity of extreme events. However, the extremes appear in the tail of the probability distribution. In order to know the relationship between extreme events in the tail of temperature and precipitation, an important but previously unobserved dependence structure is analyzed in this paper. Here, we examine the dependence structure by building a bivariate joint of Gumbel copula model for temperature and precipitation using monthly average temperature (T) and monthly precipitation (P) data from Beijing station in China covering a period of 1951–2015 and find the dependence structure can be divided into two sections, they are the middle part and the upper tail. We show that T and P have a strong positive correlation in the high tail section (T > 25.85 °C and P > 171.1 mm) (=0.66, p < 0.01) while they do not demonstrate the same relation in the other section, which suggests that the identification of a strong influence of T on extreme P needs help from the dependence structure analysis. We also find that in the high tail section, every 1 °C increase in T is associated with 73.45 mm increase in P. Our results suggested that extreme precipitation fluctuations by changes in temperature will allow the data dependence structure to be included in extreme affect for the disaster risk assessment under future climate change scenarios. Copula bivariate jointed probability distribution is useful to the dependence structure analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Abdi A, Hassanzadeh Y, Talatahari S, Fakheri-Fard A, Mirabbas R (2016) Parameter estimation of copula functions using an optimization-based method. Theor Appl Climatol 1–12

  • Allan RP, Soden BJ (2008) Atmospheric warming and the amplification of precipitation extremes. Science 321:1481–1484

    Article  Google Scholar 

  • Caesar J, Lowe JA (2012) Comparing the impacts of mitigation versus non-intervention scenarios on future temperature and precipitation extremes in the HadGEM2 climate model. J Geophys res. doi:10.1029/2012JD017762

  • De Luca G, Zuccolotto P (2015) Dynamic tail dependence clustering of financial time series. Stat Pap. doi:10.1007/s00362-015-0718-7

  • Feng J, Ning L, Zhang Z, Chen X (2017) The dual effect of vegetation green-up date and strong wind on the return period of spring dust storms. Sci Total Environ. doi:10.1016/j.scitotenv.2017.02.028

  • Fu YY, Yang XQ, Shen W (2013) The interdecadal variations and the correlation analysis of temperature and precipitation during winter in Jiangsu province. J Meteorol Sci 33(2):178–183 (in Chinese)

    Google Scholar 

  • Garcia-Aristizabal A, Bucchignani E, Palazzi E, D’Onofrio D, Gasparini P, Marzocchi W (2015) Analysis of non-stationary climate-related extreme events considering climate change scenarios: an application for multi-hazard assessment in the Dar es Salaam region, Tanzania. Nat Hazards 75(1):289–320

    Article  Google Scholar 

  • Huang S, Zang W, Xu M, Li X, Xie X, Li Z, Zhu J (2015) Study on runoff simulation of the upstream of Minjiang River under future climate change scenarios. Nat Hazards 75(2):139–154

    Article  Google Scholar 

  • IPCC (2013) Climate change 2013: the physical science basis. In: contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge

    Google Scholar 

  • Iyengar S (1998) Multivariate models and dependence concepts. Technometrics 40(4):353–353

    Article  Google Scholar 

  • Johns TC, Royer JF, Höschel I et al (2011) Climate change under aggressive mitigation: the ENSEMBLES multi-model experiment. Clim Dyn 37(9–10):1975–2003

    Article  Google Scholar 

  • Lengnick L (2015) The vulnerability of the US food system to climate change. J Environ Stud Sci 5(3):348–361

    Article  Google Scholar 

  • Li N, Liu X, Xie W, Wu J, Zhang P (2013) The return period analysis of natural disasters with statistical modeling of bivariate joint probability distribution. Risk Anal 33(1):134–145

    Article  Google Scholar 

  • Li Y, Gu W, Cui W, Chang Z, Xu Y (2015) Exploration of copula function use in crop meteorological drought risk analysis: a case study of winter wheat in Beijing, China. Nat Hazards 77(2):1289–1303

    Article  Google Scholar 

  • Liu ZY, Fan GZ, Lim KG (2009) Extreme events and the copula pricing of commercial mortgage-backed securities. J Real Estate Financ Econ 38(3):327–349

    Article  Google Scholar 

  • Maeda EE, Utsumi N, Oki T (2012) Decreasing precipitation extremes at higher temperatures in tropical regions. Nat Hazards 64(1):935–941

    Article  Google Scholar 

  • O’Gorman PA, Allan RP, Byrne MP, Previdi M (2012) Energetic constraints on precipitation under climate change. Theatr Surv 33(3–4):585–608

    Google Scholar 

  • Rana A, Moradkhani H, Qin Y (2016) Understanding the joint behavior of temperature and precipitation for climate change impact studies. Theor Appl Climatol 1–19

  • Romero YL, Bessembinder J, Van de Giesen NC, Van de Ven FH (2011) A relation between extreme daily precipitation and extreme short term precipitation. Clim Chang 106(3):393–405

    Article  Google Scholar 

  • Salazar Y, Ng WL (2015) Nonparametric estimation of general multivariate tail dependence and applications to financial time series. Stat Methods Appl 24(1):121–158

    Article  Google Scholar 

  • Serinaldi F (2008) Analysis of inter-gauge dependence by Kendall’s τK, upper tail dependence coefficient, and 2-copulas with application to rainfall fields. Stoch Environ Res Risk A 22(6):671–688

    Article  Google Scholar 

  • Sun W, Rachev S, Fabozzi FJ, Kalev PS (2009) A new approach to modeling co-movement of international equity markets: evidence of unconditional copula-based simulation of tail dependence. Empir Econ 36(1):201–229

    Article  Google Scholar 

  • Tao S, Dong S, Wang N, Soares CG (2013) Estimating storm surge intensity with Poisson bivariate maximum entropy distributions based on copulas. Nat Hazards 68(2):791–807

    Article  Google Scholar 

  • Tian Q, Yang S (2016) Regional climatic response to global warming: trends in temperature and precipitation in the Yellow, Yangtze and Pearl river basins since the 1950s. Quatern Int. doi:10.1016/j.quaint.2016.02.066

  • Zhang D, Yan D, Lu F, Wang Y, Feng J (2015) Copula-based risk assessment of drought in Yunnan province, China. Nat Hazards 75(3):2199–2220

    Article  Google Scholar 

  • Zhang L (2005) Multivariate hydrological frequency analysis and risk mapping. Dissertation, Beijing Normal University.

  • Zheng ZF, Zhang XL (2007) Extreme synoptic events in Beijing and their relation with regional climate change. J Nat Dis 16(3):55–59 (in Chinese)

    Google Scholar 

Download references

Acknowledgements

This work was supported by National Key Research and Development Program–Global Change and Mitigation Project: Global change risk of population and economic system: mechanism and assessment (2016YFA0602403); The Fundamental Research Funds for the Central Universities (310421101).

Author information

Authors and Affiliations

  1. State Key Laboratory of Earth Surface Processes and Resource Ecology, Faculty of Geographical Science, Beijing Normal University, Beijing, 100875, China

    Jieling Feng, Ning Li, Zhengtao Zhang & Xi Chen

  2. Key Laboratory of Environmental Change and Natural Disaster, MOE, Faculty of Geographical Science, Beijing Normal University, Beijing, 100875, China

    Jieling Feng, Ning Li, Zhengtao Zhang & Xi Chen

  3. Academy of Disaster Reduction and Emergency Management, Ministry of Civil Affairs & Ministry of Education, Faculty of Geographical Science, Beijing Normal University, Beijing, 100875, China

    Ning Li

Authors
  1. Jieling Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ning Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhengtao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xi Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ning Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Feng, J., Li, N., Zhang, Z. et al. How to apply the dependence structure analysis to extreme temperature and precipitation for disaster risk assessment. Theor Appl Climatol 133, 297–305 (2018). https://doi.org/10.1007/s00704-017-2187-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00704-017-2187-5

Search

Navigation