1 Introduction

Xinjiang is one of the western provinces in China located to the north of the Tibetan Plateau (Fig. 1). It is mostly covered with desert and grassland. In Xinjiang, the average rainfall among meteorological stations is about 163.5 mm year−1. The climate there is arid and semi-arid. Lives generally depend on the 16 rivers originating from mountain precipitation and glacier melting (Sorg et al. 2012; Immerzeel et al. 2013). Most of the rivers originate from the Tian Shan Mountains (43°N) and Kunlun Mountains (36°N; Fig. 1). Summer rainfall (about 42 % of annual total; Fig. 2a) is an important water source for those rivers. Recently, studies found that there is a significant relationship between the rainfall in central Asia and the sea surface temperature over the Indian Ocean (IOSST, e.g., Pourasghar et al. 2012; Ummenhofer et al. 2013). However, these studies mainly focus on southwestern central Asia (e.g., Iran). Thus, it is interesting to know whether the IOSST affects the summer rainfall over Xinjiang.

Fig. 1
figure 1

Location of Xinjiang, which is in the northwest of China, to the north of the Tibetan Plateau, and with the center of about 84°E/40°N in longitude/latitude. The border of Xinjiang encloses the 83 meteorological stations that are marked by black dots. The red line encloses the model domain used in the numerical experiments, and shading area with a color bar shows the height of the orography used in the model (in meters). The red-shaded area is the key region used in the sensitivity experiments. Kunlun Mountains is at the south border of Xinjiang and at the north border of the Tibetan Plateau; Tian Shan Mountains lies in the middle of Xinjiang. The Taklamakan Desert is between Kunlun Mountains and Tian Shan Mountains

Full size image
Fig. 2
figure 2

a Seasonal variation of the monthly rainfall (y-axis is in mm day−1) among 83 meteorological stations in Xinjiang during 1961–2007. b Spatial distribution of the rainfall (in mm day−1) in Xinjiang during June–August

Full size image

It is found that the IOSST plays an important role in the variation of the global climate (e.g., Ashok et al. 2003; Hu et al. 2003). Because the absolute value of the sea surface temperature (SST) is high over the Indian Ocean, even a small change in the IOSST can produce significant impacts on global climate (Palmer and Mansfield 1984; Murtugudde and Busalacchi 1999). For example, Graham et al. (2011) found that slight warming of the tropical Indian Ocean can induce a broad range of the medieval climate changes. The IOSST affects the winter rainfall in Australia (Ashok et al. 2003). The Indian summer rainfall is significantly impacted by the IOSST in the previous spring and winter (e.g., Li et al. 2001; Terray et al. 2003). The African rainfall is also influenced by the IOSST (e.g., Fontaine and Janicot 1996; Reason 2001). In central Asia, the rainfall is influenced by the IOSST (Mariotti 2007) and potentially affected by the East Asia summer monsoon and the subtropical high over the western North Pacific. Besides the above-mentioned factors, the large-scale circulation associated with the El Niño Southern Oscillation (ENSO) also impacts the rainfall in central Asia (Mariotti 2007). Moreover, many studies pointed out that the IOSST significantly correlates with the ENSO (e.g., Murtugudde and Busalacchi 1999; Xie and Annamalai 2002). Therefore, the IOSST and the annual rainfall in central Asia may be both covariant with the ENSO, but studies indicated that some components of the IOSST variation are independent from the ENSO (e.g., Saji et al. 1999). Overall, a question is raised: does the IOSST independently influence the summer rainfall over Xinjiang, and if it does, how?

In summer, the westerly jet stream at 200 hPa is located to the north of the Tibetan Plateau across Xinjiang. The precipitation in Xinjiang is dynamically induced by the eastward-moving synoptic disturbances along the jet stream (Barlow et al. 2005; Schiemann et al. 2008, 2009). In addition to the disturbances, another essential condition for the precipitation in Xinjiang is water vapor transport (Yatagai and Yasunari 1998; Sato et al. 2007). Yatagai and Yasunari (1998) found that the moisture from the Arabian Sea and the Bay of Bengal passed over the Tibetan Plateau accounts for nearly 10 % of the total moisture flux over southern Xinjiang; the rest of the flux is from the large lakes over western Siberia and East Asia. Bothe et al. (2012) found that the water vapor from the Indian Ocean is notable for the precipitation in Xinjiang. Moreover, previous studies suggested that the IOSST can alter the circulation over central Asia (e.g., Pourasghar et al. 2012; Ummenhofer et al. 2013), which may change the water transport and rainfall over Xinjiang.

So, in the present study, we analyzed observations and the results from a regional climate model to understand the relationship between the IOSST and Xinjiang summer rainfall. The structure of this paper is as follows. Section 2 describes the data and the analysis of the observations. In Section 3, the model experiments and results are presented. Section 4 provides summary and discussions.

2 Data and observations

2.1 Data

Station precipitation, global SST, and atmospheric data used in this study are described as follows. The daily precipitation of 83 stations (Fig. 1) in Xinjiang during 1961–2007 is supplied by the China Meteorology Administration. The precipitation is interpolated to a 0.5° × 0.5° grid using the Cressman (1959) objective analysis. The SST data during 1960–2007 is the monthly 2° × 2° resolution extended reconstructed SST (Reynolds et al. 2002) of the US National Oceanic and Atmospheric Administration (NOAA). The atmospheric data during 1961–2007 is the 6-hourly 2.5° × 2.5° resolution reanalysis (Kalnay et al. 1996) of the US National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR). The atmospheric data contains surface air pressure, air temperature, geopotential height, relative humidity, and horizontal wind. Except for the surface air pressure, the remaining data are on 17 pressure levels. The ENSO index is defined as the anomalies of the NOAA SST in the Niño 3.4 region (120°W–170°W/5°S–5°N, Trenberth 1997). The ENSO indices among December to March during 1961–2007 are used, and it is worth noting that the Decembers are of 1960–2006.

3 Observed Xinjiang rainfall and its relationship with the IOSST

Now we have a look at Xinjiang rainfall properties and its relationship with the IOSST. Figure 2 shows the seasonal variation and summer spatial distribution of the Xinjiang rainfall. It is found that the rainfall has a clear seasonal variation (Fig. 2a). The rainfall increases from March, reaching the maximum value in July. After July, it decreases, reaching the minimum value in January. In summer (June–August), the rainfall accounts for about 42 % of the annual total (Fig. 2a). The rainfall mainly occurs in the Tian Shan Mountains (43°N), and the maximum value is about 2.5 mm day−1 (Fig. 2b). To the south of the Tian Shan Mountains, the rainfall is very small in the Taklamakan Desert with a value of less than 0.5 mm day−1. To the north of the Tian Shan Mountains, the rainfall is about 1.0 mm day−1. It is noted that in the Taklamakan Desert and Kunlun Mountains, there is no station due to severe living condition. The stations are mainly around the desert and at the foot of the mountains (Fig. 1).

Figure 3a shows the annual variation of the Xinjiang rainfall in summer and the IOSST in March. The increasing trends of the two time series are both removed. The time series of the rainfall is the average among the 83 stations in summer. The IOSST is the average of the SST in the key region in March (Fig. 1). The two time series are well correlated with each other, and the correlation coefficient is about 0.49. The key region in the area of 50–95°E/20°S–20°N is the region with significant correlations between the Xinjiang summer rainfall and the SST over Indian Ocean. Figure 3b presents the correlation coefficients between the time series of the rainfall and the SST at each grid point in the Indian Ocean in March. The correlation between the SST and the rainfall is significant around the equator, in the middle and west of the tropical Indian Ocean, with the maximum value of about 0.55 to the northeast of Madagascar (Fig. 3b). In Fig. 3c, we also calculate the correlation coefficients between the time series of the IOSST in the key region in March and the grid rainfall in Xinjiang in summer. The correlation coefficients are generally positive over entire Xinjiang, and significant around the Tian Shan Mountains. The maximum correlation coefficient is about 0.50 in the west of the Tian Shan Mountains.

Fig. 3
figure 3

a Time series of the Xinjiang rainfall in summer (red) and the IOSST in March (blue) during 1961–2007. The rainfall is averaged among 83 stations in Xinjiang in summer, and the IOSST is averaged in the key region in the Indian Ocean in March. The key region is the red-shaded area shown in Fig. 1. Both time series are normalized by subtracting their mean and then dividing by their standard deviations for comparison. Thus, the two time series shown in a are dimensionless quantities. b Correlation coefficients between the time series of Xinjiang rainfall in summer (red line in a) and the SST at each grid point in the Indian Ocean in March during 1961–2007. The correlation in shading area is significant at 5 % level by the Student’s t test. c Correlation coefficients between the time series of the IOSST in March (blue line in a) and the rainfall at each grid point in Xinjiang in summer, during 1961–2007. The shaded area is significant at 5 % level by the Student’s t test. It is noted that the trends of the IOSST and the rainfall in the three panels are all removed

Full size image

Besides the IOSST in March, we have also examined the correlation between the summer rainfall in Xinjiang and the IOSST in the leading months (November to May), as well as the simultaneous correlation. It is found that the correlations between the rainfall and SST in the Indian Ocean in the other months are smaller than those in March (figures not shown).

The correlation coefficients between the IOSST in March and ENSO indices in December to March are about 0.68, 0.66, 0.62, and 0.56 (Table 1), and the relationship is significant and persistent from December to March. The correlations between the rainfall and the ENSO indices in December to March are about 0.22, 0.23, 0.25, and 0.32, respectively, and it is only significant in March (Table 1). We also checked the correlations between the rainfall and the ENSO indices from April to August, and it is only significant in April (0.36). The time series of the Xinjiang rainfall in summer and the IOSST in the key region in March are significantly correlated at the 5 % significant level (0.49; Table 1). Furthermore, the partial correlation between the rainfall and the IOSST in March controlling for the ENSO indices in December to March is about 0.48, 0.47, 0.44, and 0.40, which are all significant (Table 1). The partial correlations between the Xinjiang summer rainfall and the ENSO indices in December to March controlling for the March IOSST are not significant at all (Table 1). This indicates that the relationship between the IOSST in March and the Xinjiang rainfall in summer is independent from the ENSO. Moreover, the March IOSST being independent from the ENSO can explain about 16 % of the variance of the Xinjiang summer rainfall. Therefore, it is interesting to know how the March IOSST in the key region affects the summer rainfall in Xinjiang. It is worth noting that the trends in all the time series are removed. We also consider the influence of the autocorrelation on the degrees of freedom on the Student’s t test. We found that the number of degrees of freedom (47–2) is not influenced by the autocorrelation.

Table 1 Correlation and partial correlation coefficients between a pair of variables among Xinjiang rainfall in summer, the IOSST in March, and ENSO index among December–March (Niño 3.4), during 1961–2007 (the ENSO index in December is during 1960–2006). The partial correlation (in the brackets) is calculated between the two corresponding variables, controlling for the variable in the brackets in the first column
Full size table

4 Model experiments and results

4.1 Model experiments

In order to understand the mechanism behind the relationship between the summer rainfall in Xinjiang and the March IOSST, we conducted three sets of numerical sensitivity experiments using a regional climate model. Each set of the numerical experiments contains 15 simulations in which each simulation is integrated from March 1 to August 31 for each year between 1991 and 2005. One set of the numerical experiments is a control run, denoted by CON. The CON uses the monthly climatology of the SST during 1961–2007 that only includes the seasonal variation. The climatology of the SST is derived from the NOAA SST. The other two sets are the sensitivity experiments with added positive and negative anomalies to the climatological SST at the grids in the key region in March (red-shaded area in Fig. 1). The two experiments are denoted by POS and NEG, respectively. In Table 1, it is found that the influence of the IOSST on Xinjiang rainfall is not very strong, about 16–25 % of the variance of the rainfall can be explained by the IOSST. Therefore, we added double-positive (negative) standard deviations of the IOSST at each grid point in the key region in March as the anomalies of the IOSST in the POS (NEG). The only difference between the CON and POS (NEG) is the SST in the key region in March. The anomaly is only added in March in either POS or NEG. All the three experiments are driven by the same atmospheric condition during 1991–2005, which is the NCEP reanalysis.

The regional climate model used in the present study is RegCM4.3 (Giorgi and Anyah 2012, http://gforge.ictp.it). The model domain is ranging from the tropical Indian Ocean to the north of central Asia (Fig. 1). The model is configured with the rotated Mercator projection, and the horizontal resolution is 60 × 60 km at 18 sigma levels. The time-dependent lateral boundary scheme (Perkey and Kreitzberg 1976), the cumulus convection scheme of Grell et al. (1994), the planetary boundary layer scheme of Holtslag et al. (1990), and the biosphere-atmosphere transfer scheme (Dickinson et al. 1993) are used in the model. The model output is saved at daily intervals and interpolated to 11 pressure levels for analysis.

Using this experiment design, we can explore the impacts of the anomaly of the IOSST in the key region in March on the Xinjiang summer rainfall. We analyze the mean of the 15 simulations in each set to minimize the influence of the initial and lateral boundary conditions. Because the Xinjiang rainfall influenced by the IOSST is small, the differences between the POS and NEG are analyzed in the following subsection.

4.2 Model results

The mean of the summer rainfall in Xinjiang in the CON is shown in Fig. 4. Comparing to Fig. 2b, we find that the modeled rainfall has a similar pattern as that of the observed rainfall. The maximum rainfall mainly occurs around the Tian Shan Mountains (43°N, Fig. 4). However, there are differences between the modeled and observed rainfall. The rainfall is larger in the middle of the Tian Shan Mountains in the model than the observations. The rainfall to the north, in the east, and at the south foot of the Tian Shan Mountains is smaller in the model (Fig. 4). Around the south border of Xinjiang, the model generates a precipitation greater than 0.5 mm day−1 in the Kunlun Mountains, but in the observations, there is no rainfall. One possible reason is because of the lack of a meteorological station. Overall, the CON can reasonably reproduce the spatial pattern of the summer rainfall pattern in Xinjiang.

Fig. 4
figure 4

Average of the modeled rainfall (in mm day−1) in Xinjiang in summer during 1991–2005 in the CON

Full size image

In order to check the influence of the anomalous March IOSST on the summer rainfall in Xinjiang, the difference of the mean rainfall between the POS and NEG is shown in Fig. 5. It is found that to the east of 80°E, the rainfall is stronger in the POS than that in the NEG, with the maximum difference of about 0.3 mm day−1. Along the Tian Shan Mountains except for the middle of the mountains, the rainfall anomaly is positive (red contours in Fig. 5). This agrees with the positive correlation in Fig. 3c, but the significant differences (red shading in Fig. 5) are not in the center of the correlation. Furthermore, the significant positive differences of the rainfall are also located in a part of the Kunlun Mountains (36°N). To the west of 80°E, the rainfall is weaker in the POS (blue contours in Fig. 5), with the minimum difference of about −0.2 mm day−1. The negative differences are significant over western Xinjiang and a small part around the southeast border of Xinjiang (blue shading in Fig. 5). It is noted that the correlation between the IOSST and the rainfall is not significant over the area of the decreased rainfall in western Xinjiang (Fig. 3c). Because the significant areas over the Tian Shan and Kunlun Mountains are small, a field-significant test is conducted for the rainfall anomalies over the area of 74–98°E/35–50°N according to Wilks (2006). At each grid point, the p value of the local null hypothesis, that the rainfall difference is equal to zero, is calculated. It is found that the local p value of one grid point (990 in total) at the Kunlun Mountains is no greater than the global p value at the level of 0.1 (p FDR in the Eq. 7 in Wilks 2006). Thus, the field significance is declared for the rainfall differences. Generally, the model results are consistent with the correlation in observations. This indicates that the positive (negative) anomaly of the IOSST in March can cause the increase (decrease) of the rainfall in Xinjiang, especially around the Tian Shan Mountains and Kunlun Mountains. Moreover, it is interesting that the significant increases in the modeled rainfall are mainly in the Tian Shan Mountains and the Kunlun Mountains, which are the sources of the 16 rivers running across Xinjiang.

Fig. 5
figure 5

Differences of the mean rainfall (in mm day−1) between the POS and NEG during 1991–2005. The color bar is for both contour and shading. The shaded area shows the differences significant at 10 % level by the Student’s t test

Full size image

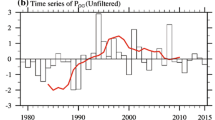
The variations of the June–August rainfall differences between the same years in POS and NEG during 1991–2005 are shown in Fig. 6 to check the robustness of the rainfall differences in Fig. 5. The rainfall is averaged in the area including part of the Tian Shan and Kunlun Mountains, where the rainfall differences between POS and NEG are generally positive and significant (80–90°E/35–44°N, within the green dash lines in Fig. 5). The 15 rainfall differences are plotted in bar chart, in which positive (negative) differences are in red (blue) bars. The differences are negative in 5 years but positive in the remaining 10 years. Moreover, the average of the rainfall differences is positive and significant at the 10 % level. Therefore, the positive change of the rainfall in the numerical experiments is robust.

Fig. 6
figure 6

June–August rainfall difference in each year of 1991–2005 between POS and NEG. The rainfall differences (y-axis is in mm day−1) are averaged over 80–90°E/35–44°N, which is the area within green dash lines shown in Fig. 5

Full size image

The difference of the average of the water vapor mixing ratio (also known as specific humidity) from surface pressure to 300 hPa in summer during 1991–2005 between the POS and NEG is shown in Fig. 7a. It is found that a positive anomalous center of moisture is located over the western Tibetan Plateau. Moisture is increased over southern and eastern Xinjiang. The positive anomaly is significant over some part of the Kunlun and Tian Shan Mountains, which is consistent with the increase of the rainfall. Similar to Fig. 5, a field-significant test is also conducted for the moisture anomalies over the area of 70–98°E/30–50°N according to Wilks (2006). It is found that the local p values of two grid points (1,754 in total) at the Tibetan Plateau are no greater than the global p value at the level of 0.1. Thus, the field significance is declared for moisture differences. Moisture decreases over the Persian Gulf, Iran, central India, the Bay of Bengal, and northern and western Xinjiang (Fig. 7a). Significantly negative anomalies are mainly located in central India and to the north of Xinjiang. It is found that the decrease of the moisture in western Xinjiang is corresponding to the decrease of the rainfall there (Fig. 7a). Figure 7b is the latitude–height plot of the specific humidity and the meridional circulation between 77 and 90°E. South wind blows over the Tibetan Plateau (Fig. 7b), and the air moisture increases over the Tibetan Plateau and southern Xinjiang. It is also found that the moisture decreases to the south of the Tibetan Plateau and to the north of the Tian Shan Mountains.

Fig. 7
figure 7

a Differences of the mean of water vapor mixing ratio (in 10−2 g kg−1) between the POS and NEG during 1991–2005. The water vapor mixing ratio is averaged from surface pressure to 300 hPa. The color bar is for both contour and shading. The shaded area is significant at 10 % level by the Student’s t test. b Latitude–height plot of the differences of the mean of water vapor mixing ratio (in 10−2 g kg−1) and the meridional circulation between the POS and NEG, and the differences are between 77 and 90°E. The shading area in gray is the average height of the topography between 77 and 90°E. The vertical wind speed is in −50 Pa s−1

Full size image

The changes of the air moisture are associated with the moisture flux. Figure 8a presents the anomalous moisture flux computed according to Trenberth (1991). The vector of the moisture flux is \( \mathbf{Q}=\frac{1}{g}{\displaystyle {\int}_{ps}^{300\mathrm{hPa}}q\mathbf{V} dp} \), where q is the specific humidity, V is the vector of horizontal wind, g is the gravity acceleration, and ps is the surface pressure. The moisture is transported from the Persian Gulf, the coast of Iran, and Pakistan to the south of the Tibetan Plateau, and then passes over the plateau to Xinjiang (Fig. 8a). Thus, the moisture over the Tibetan Plateau and southern Xinjiang increases. Meanwhile, the moisture over central India (about 15°N) is transported from land to the Arabian Sea. To the north of the Tian Shan Mountains, moisture is transported from northern Xinjiang to the Lake Balkhash, which decreases the local moisture. The moisture flux in Fig. 8a agrees with the moisture changes in Fig. 7a, b. Figure 8b shows the anomaly of the geopotential height and horizontal wind at 500 hPa, which is related to the anomalous moisture flux. It is found that a negative anomaly of geopotential height accompanying a cyclonic wind is located to the southwest of Xinjiang. Westerly wind is prevailing over the Persian Gulf and Iran, southwesterly wind over the Tibetan Plateau, and easterly wind over northern Xinjiang. Over the Arabian Sea, there is an anticyclonic circulation with easterly wind over central India and the Arabian Sea. Overall, the increase of the moisture over Xinjiang in summer is caused by the anomalous circulation over central Asia. This anomalous circulation transports the moisture from the Persian Gulf and the coast of Iran, passing over Pakistan and the Tibetan Plateau to Xinjiang.

Fig. 8
figure 8

a Differences of the moisture flux from surface to 300 hPa (in kg m s−1) between the POS and NEG (see text for details). b Differences of the geopotential height and horizontal wind at 500 hPa between the POS and NEG

Full size image

According to the experimental design, the anomalous circulation over central Asia in summer is induced by the anomalous IOSST in March. Figure 9 shows the time-latitude plot of the differences of the geopotential height at 500 hPa along 70°E during 1991–2005 between the POS and NEG. An 11-day running average is used to remove the synoptic scale disturbances. In March, due to the anomalous SST, a negative anomaly is formed over the equator. To the north of this anomaly, a positive anomaly is formed. During April to May, the negative anomaly breaks into two branches. One moves northwards in April, and the other stays over the ocean. During April to middle June, the negative anomaly over the ocean (around the equator) weakens. In early June, this negative anomaly propagates north again, with a speed of about 2–3 m s−1, and then stays around 35°N during summer, which is corresponding to the anomaly in Fig. 8b. After middle June, over the Indian Ocean, the negative anomaly induced by the anomalous IOSST becomes positive.

Fig. 9
figure 9

Time-latitude plot of the difference of the geopotential height at 500 hPa along 70°E between the POS and NEG. An 11-day running average is applied to the data

Full size image

So, to summarize, in March, the anomalous warm IOSST induces a negative anomalous geopotential height, which maintains over the ocean till June. The anomalous geopotential height then propagates north to central Asia. Moreover, the anomalous geopotential height stays over central Asia during the whole summer and influences the water transport.

5 Summary and discussions

In this study, we analyze the relationship between the summer rainfall in Xinjiang and the IOSST in March. In the observations, it is found that in Xinjiang most of the rainfall occurs in the Tian Shan Mountains. The rainfall and IOSST significantly correlate with each other, even in the partial correlation controlling for the ENSO indices among December to March. This indicates that the correlation between the IOSST and rainfall is independent from the ENSO. The IOSST being independent from the ENSO can explain about 16 % of the variance of the Xinjiang summer rainfall.

In addition to the observations, the model results are analyzed. It is found that the RegCM4.3 can reasonably represent the spatial pattern of the summer rainfall in Xinjiang, though there are some deviations. Those deviations probably are associated with the complicated topography over this region. One reason for the deviations over Kunlun Mountains is the lacking of meteorological station. The difference of the modeled rainfall between the POS and NEG is generally positive over Xinjiang and significant over some part of the Tian Shan Mountains and Kunlun Mountains. Those two mountains are the sources of the 16 rivers running across Xinjiang. Therefore, the IOSST significantly affects the water resource over Xinjiang. It is noted that because the Xinjiang summer rainfall influenced by the IOSST is small, in order to obtain a relative strong signal in the model, a rather strong forcing anomaly in the IOSST is used in the numerical sensitivity experiments.

The anomalous circulation and moisture transport over central Asia links the summer rainfall in Xinjiang and the March IOSST. When the IOSST is anomalously warm in March, a negative geopotential height at 500 hPa is excited. This anomalous height maintains over the Indian Ocean till June. It then propagates north to central Asia with a speed of about 2–3 m s−1, which is close to the propagating speeds of the Madden-Julian Oscillation (about 4–5 m s−1, Madden and Julian 1994; Zhang 2005). The negative geopotential height stays over central Asia and causes the anomalous moisture transport. The moisture is transported from the Persian Gulf and the coast of Iran, passing over Pakistan and the Tibetan Plateau to Xinjiang. The increase in the moisture in Xinjiang induces the significant increase in the rainfall over the Tian Shan and Kunlun Mountains. Overall, when the anomalous IOSST in March is positive (negative), there is an increase (a decrease) in summer rainfall in Xinjiang.

Besides the water vapor transport, the jet stream also plays an important role on the summer rainfall over Xinjiang. However, the model results show that the influence of the IOSST on the jet stream is very small. The difference of the zonal wind at 200 hPa between the POS and NEG is in the order of 0.5 m s−1 (figure not shown), which only accounts for 1–2 % of the wind speed of the jet stream (taken as 30–40 m s−1). Therefore, the influence of the IOSST on the locations and strength of the jet stream can be ignored in this study. In terms of the relationship between the IOSST and the Xinjiang rainfall, the water transport from the Indian Ocean is more important.

It is noted that the center of the rainfall differences between POS and NEG differ from the correlation center in the observations. Moreover, negative differences are found in the simulations while the correlation between the IOSST and Xinjiang summer rainfall is positive in the observations. These differences are probably caused by two reasons. First, the lasting of the IOSST anomaly is not considered in the simulations, and this probably decays the influence of the March IOSST anomaly on Xinjiang rainfall. The lasting of the IOSST anomaly may cause stronger moisture transport to the north of Tian Shan than that in the present study, and then produce more precipitation over this area, because the “memory” of the atmosphere is shorter than the ocean. Thus, a coupled regional atmosphere–ocean climate model may do a better job to reveal the relationship between the IOSST and Xinjiang summer rainfall. Second, the use of the regional model ignores the influence of the IOSST on the other parts of the world. The changes in the other parts of the world can, in turn, affect the summer rainfall in Xinjiang. For example, Saeed et al. (2011a, b) found a covariation between the summer rainfall over South Asia and East Asia, and the change of the heat over South Asia can influence the rainfall downstream over East Asia. In the present study, East Asia is not included by the model domain. Thus, the influence of the IOSST on East Asia and the in-turn influence from East Asia on the Xinjiang rainfall are not considered. Nevertheless, the present study shows that the IOSST significantly influences the air moisture and precipitation over Xinjiang.