1 Introduction

The presence of underground cavities as a result of past mining operations of soft rocks, used as building material, induces over time high risk conditions for overlying urbanised areas and infrastructures. In the Apulia region (south-eastern Italy), the extraction of soft and very soft carbonate rocks, as Pliocene or Pleistocene age calcarenites, was often carried out through the opening of underground quarries at variable depths, typically located at the boundaries of urban areas, which were abandoned later on, once the production phase stopped (Parise 2012, 2015). With time, the risk of sinkhole development affecting the built-up areas increased along with the urban expansion (Lollino et al. 2013). So that the assessment of stability of such underground caves nowadays represents a serious challenge for land and urban planning purposes (Parise and Gunn 2007). Several studies concerning the risk associated to man-made underground caves have been proposed in the literature, as those regarding the calcarenite caves in Southern Italy (Delle Rose et al. 2004; Parise 2010, 2015; Parise and Lollino 2011; Lollino et al. 2013; Fazio et al. 2017), the bell-shaped caverns in Israel (Hatzor et al. 2002), the metal mining caves in Canada (Bétournay 2009), the siltstone Longyou caverns in China (Li et al. 2009), an abandoned limestone mine in Korea (Sunwoo et al. 2010), and the limestone mines in the Netherlands and Belgium (Bekendam 1998), to mention a few. These failures are frequently associated to the occurrence of environmental weathering processes involving the soft porous rock in the long term, i.e. many years/decades after the end of the excavation, leading to the degradation of the mechanical properties of the rock surrounding the cave (Auvray et al. 2004; Castellanza and Nova 2004; Grgic et al. 2006; Andriani and Walsh 2007; Ciantia and Hueckel 2013; Ciantia et al. 2015a, b). Recently, numerical modelling has provided a powerful tool to explore the stress–strain state within the rock mass around the cave and investigate the corresponding displacement field induced by changes of loading or boundary conditions (Ferrero et al. 2010; Parise and Lollino 2011; Wang et al. 2011; Fazio et al. 2017; Castellanza et al. 2018; Ciantia et al. 2018).

Concerning the Apulia region, seismic actions might also represent a possible triggering factor for cave instabilities and sinkholes. As a matter of fact, in the cavities of the region, it is quite frequent to observe the presence of cracks and local block detachments from the roof, lateral walls as well as inner pillars. This can be the result of either environmental-induced weathering processes, i.e. related to humidity or infiltrating water, or seismic waves. The role of environmental factors on the triggering of cave instability processes has been widely investigated from the authors in previous scientific works, as Parise and Lollino (2011), Fazio et al. (2017), Castellanza et al. (2018), Perrotti et al. (2018), to mention a few. Seismic hazard in the Apulia region has been studied by INGV (Gruppo di Lavoro 2004), which point out that the largest earthquake motions recorded in the region are generated from the seismic faults mainly located along the Italian Apennines, the Gargano promontory as well as the Croatian coast (Del Gaudio et al. 2007). These earthquakes are capable of producing, in the central and northern areas of Apulia, peak ground accelerations, with a probability of 90% of not exceedance within 50 years, generally estimated in the range between 0.129 g and 0.231 g, with an average value equal to 0.177 g. Lower ground accelerations are instead estimated for the south-eastern areas of the region. The largest earthquake magnitudes felt in the last centuries throughout the study region have been estimated between 5 and 6.7 (Del Gaudio et al. 2007).

The role of dynamic stresses on the stability of man-made underground caves within soft rocks has been frequently underestimated or, at least, assessed only according to qualitative approaches (Sharma and Judd 1991). Several studies have focused on the effects of different seismic motion characteristics on the behavior of underground voids and tunnels as well as on the modification of the seismic motion at the ground surface as a consequence of the presence of the cavities. Lee and Karl (1992) and Smerzini et al. (2009) have shown that underground cavities generally produce, at the ground surface, attenuation of the rock displacements generated by a dynamic motion, if compared with green-field conditions, this being a function of the cave depth (Sanò 2011). Landolfi et al. (2011) have also stated that, in the zone of the cavity roof, interference processes between the incident and refracted wave motions reduce the amplification factors with respect to the green-field case. Also, attenuation is seen to depend on the cave size and the wave length, as well as on the cave depth and the cave shape. However, Conte and Dente (1993) have also stated that some wave amplification can be possible just above the cavity if the wave motion direction is not properly vertical. Genis and Gercek (2003) have first explored, by means of numerical approaches, the effects of dynamic stresses on the failure conditions of underground cavities. They have demonstrated the role of dynamic waves in the enlargement of the yield zone around the cave with respect to the static condition. They also investigated the influence of the wave direction, which is not seen to be really affecting, instead than the peak acceleration, which highly affects the yield zone size. Genis and Aydan (2007) have studied from a numerical point of view the effects of dynamic motion on a large underground opening and have highlighted the influence of the size of the yield zone on wave motion amplitude, frequency and direction. They also detect a threshold peak acceleration value capable of triggering yield zone enlargement with respect to the static case. Concerning an abandoned room and pillar underground lignite mine, based on visco-elastic one-dimensional analysis, the same authors clearly remark the increase of displacement values at the underground cave depth. Moreover, the results show that, at low acceleration peak values, tensile failure point generates along the cave roof, whereas shear failures also develop in the pillars when larger acceleration values are accounted for (Genis and Aydan 2008). The effects of the interaction between adjacent cavities have been also investigated by several authors, as Gercek (2005), Conte and Dente (1993) and Landolfi (2013). The studies have highlighted that the presence of cavities at short distances induces larger risk conditions under dynamic conditions. Finally, a recent study (Fabozzi et al. 2021) has proposed a method for assessing the stability of shallow cavities by calculating the safety factor as the ratio between the ultimate resistance moment and the loading moment at the most critical vertical section of the roof beam.

The purpose of this paper is to investigate the effects of earthquake motions, which are consistent with the regional seismicity recorded in the study region, on the stability of man-made underground cavities in calcarenite soft rocks. In particular, ideal geometries, representative of typical underground caves of the Apulia region, are accounted for. The effects of dynamic stresses are explored through the analysis of the evolution of the stress and strain field within the rock mass surrounding the cave, as well as the variation of safety conditions with respect to the failure occurrence. Both the case of a single cavity and that including two adjacent cavities are taken into account, the latter representing a condition more prone to instability.

Therefore, a schematic outline of the regional geology and a summary of the geotechnical properties of soft calcarenite rocks outcropping in large areas of the region are initially presented. Later on, the assumptions used in dynamic finite element analyses of ideal case studies represented by a single cavity and twin adjacent cavities are proposed, followed by a discussion of the numerical results in terms of variation of the yield zones, strain fields as well as variation of the stability conditions.

2 Geological Context and Geotechnical Characterization of the Rock Materials

The underground cavities examined in the present study have been excavated within deposits of soft calcarenites, which largely outcrop throughout the Apulia region (Fig. 1). These rocks can be classified as soft to very soft rocks according to their uniaxial compression strength (ISRM 1979; Dobereiner and De Freitas 1986). Generally, the calcarenite units outcropping within the Apulia region can be grouped into three main classes:

  • Upper Miocene calcarenites.

  • Upper Pliocene–Lower Pleistocene calcarenites.

  • Middle–Upper Pleistocene calcarenites (also named as Gravina calcarenites; Andriani and Walsh 2010).

Fig. 1
figure 1

Geological map showing only soft rock/hard soil units cropping out in the Apulia region and underground cavities detected in the same areas (Lepore et al. 2014)

Full size image

Since most of the Apulian underground caves located in the central area of the Apulia region have been excavated within the Gravina calcarenite, the mechanical properties of this rock unit are here discussed. The Gravina calcarenites are characterized by low and variable values of the uniaxial compressive strength, σc, under dry conditions, ranging between 1 and 9 MPa (Coviello et al. 2005; Andriani and Walsh 2010; Ciantia et al. 2015a, b). The degree of saturation significantly affects the rock strength, so that under full saturation conditions (Sr = 100%), the uniaxial compressive strength decreases to the range 0.3–6 MPa, in some cases even lower than 50% of the corresponding dry material strength (Andriani and Walsh 2010; Ciantia et al. 2015a, b). The tension strength, σt, measured using indirect tension tests, generally ranges between 0.2 and 2.0 MPa (Coviello et al. 2005; Andriani and Walsh 2010; Ciantia et al. 2015a, b). Therefore, the ratio between uniaxial compressive and tension strength is approximately equal to \(3 \div 12\). The aforementioned values need to be considered as approximate, because the petrographical and structural features affect the mechanical response of the rock masses, which are characterized by a high degree of heterogeneity among different study sites. Furthermore, the weathering processes related to both chemical-physical agents and drying-wetting cycles induce mechanical degradation, so that the rock strength values tend to decrease, accordingly.Previous works, such as Andriani and Walsh (2010) or Andriani et al. (2019), have observed a relationship between uniaxial strength and porosity of rock calcarenites, with UCS decrease with increasing porosity. In general, calcarenite porosity ranges between 26 and 55%. In particular, when porosity is lower than 40%, UCS value is measured to be in the range 2–6 MPa, whereas when porosity is larger than 40% UCS reduces down to a range between 0.2 and 4 MPa. A similar trend of reduction with increasing porosity is supposed to be valid for tensile strength. Also, Ciantia et al. (2015a, b) have shown that larger UCS loss upon wetting processes occurs for calcarenites with higher porosity.

Considering a range of the cavity depth between 2 and 20 m, from the linearization of the Hoek–Brown failure criterion, that can be derived from the aforementioned parameter values (assuming intact rock conditions and mi = 4), representative values of the Mohr–Coulomb strength parameters can be obtained for the calcarenite under study. In particular, rock cohesion, c′, can be assumed to range between 100 and 200 kPa, according to the different degrees of rock cementation. While a friction angle in the range ϕ′ = 30°\(\div\)35° and a dilation angle equal to ψ′ = 0° can be also considered as representative values of the material. Based on uniaxial compression test results, Young’s modulus is observed to range between 100 and 300 MPa at large strains. While, for very small and small strain levels, values larger than 1000 MPa have been indirectly determined from typical values of shear wave velocity observed in calcarenite deposits by means of down-hole tests (Gallipoli and Lupo 2012). A Poisson ratio equal to ν = 0.3 can be also adopted for this material.

3 2D Finite-Element Modelling

The aim of the numerical simulations hereafter described was to assess the influence of dynamic motions on the stress–strain field of soft rock masses around man-made underground cavities, as well as to investigate the possible evolution of the cave towards instability. All the simulations were carried out with a two-dimensional finite element approach using PLAXIS 2D (Brinkgreve et al. 2020). The use of 2D simulations is justified by the frequent existence in situ of plane-strain conditions, with simplified geometric and loading conditions (horizontal ground surface overlying homogeneous half-space in any direction; presence of regular geometry cavities with size in the 3rd direction, i.e. normal to the domain plane, that is frequently larger than those in the transverse plane). Moreover, 2D analyses are believed to be more conservative since disregarding the third component is in favor of stability. In detail, three calculation phases were defined:

  • An initial phase for the geostatic stress field initialization by assigning a coefficient of earth pressure at rest, K0. Therefore, the vertical stresses generated are in equilibrium with the self-weight of the soil, while the horizontal stresses were calculated using the specified value of K0.

  • A static phase simulates the excavation process by deactivating all clusters within the boundary of the cavity. A single-step excavation was imposed since it should be considered as a conservative hypothesis for cave stability.

  • A dynamic phase with the application of a time history of accelerations at the base of the model.

In addition, the stability of different cavity geometries was evaluated (by varying the ratio between cavity width and roof thickness) through a procedure described in detail in Sect. 3.1. In particular, factor of safety values, respectively, related to shear and tension failure mechanisms (i.e. FoSshear, FoStension), were calculated with respect to vertical slices of the problem domain. This allows to investigate the variation between the static and the dynamic phase, taking into account also the variation of the maximum peak ground acceleration, PGA.

Different boundary conditions were applied in the stages, as follows:

  • Static phase: the vertical model boundaries were horizontally fixed (ux = 0) and left free in the y-direction; the bottom boundary was fixed in both horizontal and vertical directions (ux = uy = 0); the ground surface was kept free in all directions.

  • Dynamic phase: free-field boundary conditions were used for the lateral boundaries of the model. These boundaries are widely recognized to reduce the reflection of the incident waves on the vertical boundary itself. The free-field conditions generate equivalent normal and shear forces applied to the main domain and consist of two dashpots, in the normal and shear directions, applied to each node of the boundary. The base of the geometrical scheme was assumed as a compliant base to model the propagation of the incident waves into the subsoil reducing the reflection to a minimum value. These conditions consist of viscous boundaries, which absorb downward waves, and line prescribed displacements in the x-direction at the base of the model, which allows to internally transform the prescribed displacement history into a dynamic history input (Brinkgreve et al. 2020).

15-node triangular elements, with a fourth-order interpolation for displacements and twelve stress points, have been used to generate the discretization mesh. The maximum size of the elements of the mesh was set to respect the relationship of Kuhlemeyer and Lysmer (1973):

$$h_{\max } = \frac{{V_{s} }}{{\begin{array}{*{20}c} {\left( {8 \div 10} \right)f_{\max } } \\ \end{array} }}$$
(1)

where \({V}_{s}\) is the shear wave velocity in the soil (i.e. for the calcarenite \({V}_{s}\) was set equal to 900 m/s) and \({f}_{\mathrm{max}}\) is the maximum frequency of the input signals. A low-pass filter with a cut-off frequency of 10 Hz was applied to all signals, thus \({h}_{\mathrm{max}}\) was fixed in the range 9\(\div\)11.25 m.

An implicit integration scheme, for which the solution of the differential equations in each calculation step depends on the value of its derivative in the next step, as implemented according to Newmark (1959) in the finite element code PLAXIS 2D. The displacement and the velocity at the point time t + Δt depends on the coefficients \({\alpha }_{N}\) and \({\beta }_{N}\), which control the accuracy of the numerical time integration. To obtain a stable solution, the coefficients must respect the modified Newmark condition proposed by Hilber et al. (1977):

$$\alpha_{N} = \frac{{\left( {1 + \gamma } \right)^{2} }}{4};\;\beta_{N} = \frac{1}{2} + \gamma$$
(2)

where γ represents a numerical dissipation parameter, which varies between 0 and 1/3. When γ = 0 the coefficients \({\alpha }_{N}\) and \({\beta }_{N}\) coincide with those of the original Newmark method, whereas if γ > 0 a numerical source of damping is introduced into the model. In this study, no numerical damping is considered, since a dissipation related to the soil damping has been assigned (i.e. Rayleigh formulation described below). In particular, when γ = 0, the coefficients are \({\alpha }_{N}\)= 0.25 and \({\beta }_{N}\)= 0.5, which lead to an unconditionally stable scheme (Visone et al. 2009).

To obtain reliable numerical results, the maximum time step should be set according to the following equation:

$$\Delta {t}_{\mathrm{max}}=\frac{{l}_{\mathrm{min}}}{{V}_{S}}$$
(3)

where \({l}_{\mathrm{min}}\) is the minimum distance between the pairs of vertices of the triangular mesh element (Brinkgreve et al. 2020). Accordingly, the dynamic analyses were performed adopting a time step equal to that of all the input signals (i.e. 0.01 s), thus fulfilling the aforementioned constraint.

To develop a preliminary study of the dynamic stability of underground artificial cavities existing in the study region, a simple constitutive model was chosen, i.e. the elastic-perfectly plastic model with the Mohr–Coulomb failure criterion. The required parameters are listed in Table 1. In detail, a non-associated flow rule (Ψ = 0°) was chosen as a conservative hypothesis (Vermeer and De Borst 1984) and a tension cut-off value was established.

Table 1 Parameters of Mohr–Coulomb constitutive model for calarenite
Full size table

To simulate the effects of dynamic damping, a viscous term proportional to the deformation rate was taken into account in the equation of motion. In PLAXIS 2D, this viscous damping is modeled according to the well-known Rayleigh formulation, for which the damping matrix is defined by the following equation:

$$\left[C\right]={\alpha }_{R}\left[M\right]+{\beta }_{R}\left[K\right]$$
(4)

The damping matrix [C] is a linear combination of the mass and the stiffness matrix, [M] and [K] respectively, with frequency-dependent coefficients \({\alpha }_{R}\) and \({\beta }_{R}\). In particular, these coefficients have been calculated using the following relationship (Chopra 1995; Clough and Penzien 1995):

$$\left\{ {\begin{array}{*{20}c} {\alpha_{R} } \\ {\beta_{R} } \\ \end{array} } \right\} = \frac{2D}{{\omega_{m} + \omega_{n} }}\left\{ {\begin{array}{*{20}c} {\omega_{m} \omega_{n} } \\ 1 \\ \end{array} } \right\}$$
(5)

where D is the damping associated to the two angular frequencies, \({\omega }_{m}\) and \({\omega }_{n}\), which are related to the target frequency interval, \(\left[ {f_{m} - f_{n} } \right]\). Several procedures exist in the literature to calibrate the aforementioned interval (Park and Hashash 2004; Amorosi et al. 2010; Tsai et al. 2014). In the analysis, here presented, a small damping rate was adopted, according to the procedure proposed by Park and Hashash (2004). In particular, the first target frequency \({f}_{m}\) has been set equal to the first natural frequency \({f}_{1}\) of the soil deposit, while the second one has been assigned equal to the closest odd integer larger than the ratio \({f}_{p}/{f}_{1}\), where \({f}_{p}\) is the predominant frequency of the dynamic input. In detail, the damping of calcarenite was assumed constant and equal to 0.5%, as typically chosen for soft rocks in the literature (Baranello et al. 2003; Fierro et al. 2020).

In accordance with the size of the numerical schemes here described (i.e. 60 m and 100 m) and the dominant frequency of all input signals (i.e. 3 Hz), the interval of target frequencies and the corresponding values of the Rayleigh coefficients used are reported in Table 2.

Table 2 Rayleigh calibration for material viscous damping
Full size table

A simple and easily controllable wave motion, the Ricker wavelet, was chosen as a seismic input according to literature studies (Smerzini et al. 2009; Landolfi 2013). This signal is defined in terms of acceleration through the following relationship:

$$a\left( t \right) = \left[ {1 - 2\pi^{2} f_{p} t^{2} } \right] \cdot {\text{e}}^{{ - \pi^{2} f_{p}^{2} t^{2} }}$$
(6)

where \({f}_{p}\) is the dominant frequency of the input signal and \(t\) is equal to (\(t-{t}_{p})\), with \({t}_{p}\) being the time when the wave reaches the maximum frequency.

Specifically, the dynamic inputs used, based on the Ricker wavelet, have the following features:

  • Single Ricker wavelet: wave following Eq. 6 with a single peak scaled to 0.2 g (PGA typically observed in recorded seismic events in the Apulian region) in Fig. 2a.

  • 4 times Ricker wavelet: dynamic input obtained from four times repetition of the single wavelet Ricker, with peak scaled to 0.2 g and 0.3 g, respectively, in Fig. 2b, c.

Fig. 2
figure 2

Dynamic input: a Single Ricker Wavelet − PGA = 0.2 g; b 4 times Ricker Wavelet − PGA = 0.2 g; c 4 times Ricker Wavelet − PGA = 0.3 g; d Real accelerogram − PGA = 0.22 g. From the left to right: accelerograms and Fourier spectra

Full size image

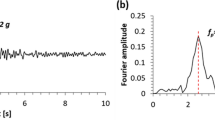
Moreover, the effects generated on the underground cavity systems by a dynamic input represented by a real accelerogram, which is comparable in terms of energy level with the above-mentioned signals, were also evaluated. The accelerogram is characterized by a dominant frequency of 2.9 Hz and has been filtered at 10 Hz, as well as scaled at 0.22 g (Fig. 2d).

3.1 Dynamic Stability of a Single Cavity

Two-dimensional finite element analyses were performed, first, on ideal schemes of single rectangular cavities to assess the influence of prescribed dynamic wave motions on the stability of the cavities.

All the numerical domains used for the analyses have a width of 100 m and a height of 60 m, thus sufficiently large to reduce any boundary effects with respect to the cavity area. To validate the choice of the model geometry, the corresponding boundary conditions and the adopted viscous formulation, the results of a 2D elasto-plastic model without cavity were compared with those obtained from a 1D analysis performed with the equivalent linear EERA software (Bardet et al. 2000). In particular, both the two analyses have highlighted the same response in terms of accelerogram at the ground surface, as shown in Fig. 3.

Fig. 3
figure 3

Comparison in terms of ground surface accelerogram between 2D elasto-plastic analysis without cavity (PLAXIS 2D) and 1D equivalent linear analysis (EERA)

Full size image

Figure 4a shows the general geometry of the problem and the discretization mesh used, which always respects the propagation condition of the highest frequencies of the signal, expressed by Eq. 1. To reach a higher calculation accuracy in the area around the cavity, where higher strain gradients are expected, a finer mesh was fixed with an average element size of about 1 m, as shown in Fig. 4b. Thus, a coefficient of 0.2 has been set in the area around the cavity, compared to the value 1 for more distant areas. The coarseness coefficient gives an indication of the triangular element size of a finer mesh with respect to the target element size.

Fig. 4
figure 4

a Numerical scheme and mesh adopted for the two-dimensional analyses with a single cavity (Htot = total height; Ltot = total width); b zoom on the refined mesh around the cavity (L = cavity width; h = cavity heigh; t = roof thickness)

Full size image

The parametric study here presented may be divided into two parts: in the first part, the effects of the cavity geometrical features on the stress–strain state of the rock mass under dynamic loading were investigated; in the second one, the effect of the assumed input wave was studied.

In particular, parametric analyses were carried out by varying separately the cavity width, L, the cavity height, h, and the thickness of the cave roof, t. In particular, values of the cavity width, respectively, equal to 5, 9, 15, and 21 m, cavity height equal to 3, 5, and 7 m, as well as roof thickness equal to 2, 5, 8, and 20 m, were assumed, following the typical values observed for the Apulian underground cavities (Perrotti et al. 2018).

The parametric analysis performed with respect to the cavity width, L, (keeping constant h = 5 m and t = 5 m) shows that no significant variation in the stability conditions emerges between the static phase and the dynamic one, for cavities with a width smaller than or equal to 9 m. This is illustrated in Fig. 5a in terms of plastic failure points and deviatoric strains. When L reaches 15 m (Fig. 5b), in the dynamic phase a slight increase of shear failure points, especially in the upper corner areas, where deviatoric strains are generated, is observed, although being limited. For L = 21 m (Fig. 5c), several plastic points are generated already in the static phase, but then increase when the dynamic input is applied at the base of the model. In this case, passing from the static phase to the dynamic one, the maximum deviatoric strains, in the roof of the cavity, increase by 0.3%.

Fig. 5
figure 5

Effect of the variation of cavity width, “L”: cavity dimensions a L = 9 m, h = 5 m, t = 5 m: b L = 15 m, h = 5 m, t = 5 m; c L = 21 m, h = 5 m, t = 5 m. Dynamic input: single Ricker wavelet with PGA = 0.2 g

Full size image

The variation in cavity height h (keeping constant L = 15 m and t = 5 m) has no significant influence on the numerical results obtained. As shown in Fig. 6, there are only very small increments of shear failure points and deviatoric strains passing from the static to the dynamic stage, which, however, do not vary with the increment of h.

Fig. 6
figure 6

Effect of the variation of cavity height, “h”: cavity dimensions a L = 15 m, h = 3 m, t = 5 m: b L = 15 m, h = 5 m, t = 5 m; c L = 15 m, h = 7 m, t = 5 m. Dynamic input: single Ricker wavelet with PGA = 0.2 g

Full size image

Conversely, the variation of the overburden thickness t (keeping constant L = 15 m and h = 5 m) has a more significant influence on the dynamic response of the cavity (Fig. 7). Although the deformations in the dynamic phase tend to decrease in magnitude by increasing the roof thickness, the differences between the maximum dynamic deviatoric strains and the static ones, as well as those between the shear failure points of the two stages, tend to increase. In particular, the deviatoric strains are seen to increase, from the static to the dynamic stage, from 0.01% for t = 2 m to 0.042% for t = 20 m. It should also be noted that as long as the L/t ratio, i.e. between cavity width and roof thickness, is higher than unit, the failure points are confined exclusively to the roof of the cavity. Whereas, if the ratio decreases (for example, see L/t = 0.75 in Fig. 7c), plastic points develop first along the vertical walls of the cavity and later on, in the dynamic phase, generate clear shear bands that propagate both upwards and downwards.

Fig. 7
figure 7

Effect of the variation of roof thickness, “t”: cavity dimensions a L = 15 m, h = 5 m, t = 2 m: b L = 15 m, h = 5 m, t = 8 m; c L = 15 m, h = 5 m, t = 20 m. Dynamic input: single Ricker wavelet with PGA = 0.2 g

Full size image

The single Ricker wavelet with PGA equal to 0.2 g is the dynamic input to which the results presented above refer. However, the influence of the input dynamic signal at the base of the model was also assessed. The different wave motions presented in Fig. 2 were applied and the results obtained for two case studies, respectively, with L/t < 1 and L/t > 1, are presented in Fig. 8, in terms of shear plastic points and deviatoric strains. It is straightforward pointing out that the results depend on the intensity of the dynamic input, which is a function of the maximum acceleration and energy content. In detail, the Ricker wavelet repeated 4 times slightly increases the instability of the cavity since the order of magnitude of the cumulated strains is increased, if compared with the single wavelet case previously presented. If the Ricker wavelet is scaled to a maximum acceleration of 0.3 g, a clear increase of the failure points and the range of deviatoric strains is obtained compared with the cases already analyzed. Lastly, the real accelerogram characterized by PGA = 0.22 g provides an intermediate response between the cases of Ricker wavelet repeated 4 times with peaks, respectively, at 0.2 g and 0.3 g.

Fig. 8
figure 8

Most relevant numerical results of the parametric analysis with varying the dynamic input, in terms of plastic failure point a L/t = 4.2; b L/t = 0.75 and deviatoric strains c L/t = 4.2; d L/t = 0.75 (note: L = cavity width, t = roof thickness)

Full size image

To assess from a quantitative point of view the stability of a single cavity under a dynamic input, both a shear and a tension Factor of Safety (FoSshear, FoStension) were calculated. In particular, the Factors of Safety were calculated by dividing the domain around the cavity into vertical slices, defined as clusters of the FEM domain. As noted in Fig. 9, the whole domain around the cavity was divided into two macrozones: the first concerns the roof area, the second concerns the areas adjacent to the vertical walls of the cavity. For the roof area, 10 vertical slices were considered above the whole cavity width, whereas 8 additional slices were considered for the outer lateral areas, for a total of 18 bands in the roof area (numbered from 1 to 18); for the area of vertical walls, 4 slices were defined for each side, for a total of 8 bands (numbered from 19 to 26). Values of the Factor of Safety within each slice were calculated, respectively, at the end of the static phase and the end of the dynamic one, varying the PGA (PGA = 0.2 g to PGA = 0.3 g) and considering as dynamic input the single Ricker wavelet.

Fig. 9
figure 9

Subdivision of the roof area and the vertical wall area into strips for the Factor of Safety (FoS) calculation

Full size image

From an analytical point of view, the FoSshear associated with each slice is calculated by means of the following formula:

$$Fo{S}_{\mathrm{shear}}=\frac{\sum_{e=1}^{n}{\tau }_{{\mathrm{max}}_{e}}{A}_{e}}{\sum_{e=1}^{n}{\tau }_{{\mathrm{mob}}_{e}}{A}_{e}}$$
(7)

where \({\tau }_{{\mathrm{max}}_{e}}\) is the maximum value of the shear strength obtained when the Mohr’s circle is expanded to touch the Mohr–Coulomb shear failure envelope, while keeping fixed the center of Mohr’s circle. It refers to the minimum value recorded by one of the 12 stress points i belonging to the triangular element e within each slice, according to Eq. 8. \({\tau }_{{\mathrm{mob}}_{e}}\) represents the maximum value of shear stress (i.e. the radius of the current Mohr stress circle) and refers to the maximum value recorded by one of the 12 stress points i belonging to the triangular element e in the slice, according to Eq. 9. \({A}_{e}\) is the area of the generic triangular element e belonging to the slice, for which the value of \({\tau }_{{\mathrm{max}}_{e}}\) and \({\tau }_{{\mathrm{mob}}_{e}}\) has been calculated. In detail, for each stress point i belonging to the element e in the slices:

$${\tau }_{{\mathrm{max}}_{e}}=\mathrm{min}\left({\tau }_{{\mathrm{max}}_{i}}\right)$$
(8)
$${\tau }_{{\mathrm{mob}}_{e}}=\mathrm{max}({\tau }_{{\mathrm{mob}}_{i}} )$$
(9)

Equation 10 is instead used to calculate the FoStension:

$${\mathrm{FoS}}_{\mathrm{tension}}=\frac{{\sigma }_{t}As}{\sum_{e=1}^{n}{\sigma }_{{3}_{e}}{A}_{e}}$$
(10)

where \({\sigma }_{t}\) is the tensile strength of the calcarenite and As is the slice area for which the FoStension is calculated. \({\sigma }_{{3}_{e}}\) is the largest tension principal stress recorded by one of the 12 stress points i belonging to the triangular element e in the slice, following Eq. 11. To assume conservative conditions, for compressive states (\({\sigma }_{{3}_{i}}\)< 0 kPa), a very low value of \({\sigma }_{{3}_{e}}\) was assumed, that is equal to 0.1 kPa. In detail, for each stress point i belonging to the element e in the slice:

$${\sigma }_{{3}_{e}}=\mathrm{max}\left({\sigma }_{{3}_{i}}\right)$$
(11)
$$\mathrm{if} {\sigma }_{{3}_{i}}<0 \mathrm{kPa};\; {\sigma }_{{3}_{i}}=0.1 \mathrm{kPa}$$
(12)

For the case study of a single cavity, three different geometric conditions were considered by varying the thickness of the roof, t, while keeping constant the cavity width, L = 21 m, to have the following ratios: L/t = 4; L/t = 1.25; L/t = 0.8. Figure 10 shows the numerical results obtained in terms of FoSshear for each slice in the roof area (slice numbers 1–18 in Fig. 9). The results have been calculated at both the end of the static phase and the end of the dynamic phase, as a function of the distance from the central axis of the cavity. A single Ricker wavelet is assumed as a dynamic input and PGA, respectively, equal to 0.2 g and 0.3 g are accounted for. In general, i.e. both under static and dynamic conditions, when the cavity deepens, i.e. L/t ratio decreases, the numerical results show a significant decrease in FoSshear in the lateral areas, outside the cavity width. Whereas, in the central part of the roof, immediately above the cavity opening, FoSshear increases. In particular, two different shear instabilities can be distinguished as a function of the ratio L/t. For shallow cavities, the area immediately above the cavity opening exhibits FoSshear rather low, while, outside the cavity width, FoSshear suddenly increases. With the deepening of the cavity, i.e. with the decrease of L/t, the central area of the cavity width becomes more stable in shear, while the outer parts exhibit a decrease in FoSshear.

Fig. 10
figure 10

Shear Factor of Safety (FoSshear) in the roof area as a function of the distance from the central cavity axis (Δx), for different values of the ratio L/t (PGA = 0.2 g and 0.3 g; Dynamic input: single Ricker wavelet)

Full size image

Moreover, when the ratio L/t decreases, the stability of the cavity seems to be more affected by the dynamic motion. In particular, FoSshear under dynamic conditions decreases with respect to the static phase, increasingly with the increase in PGA. Such a decrease becomes more important as the L/t ratio decreases and mainly affects the central area of the roof.

Figure 11 shows the results of FoSshear for each slice in the areas outside the lateral walls (slice numbers 19 to 26 in Fig. 9). As the L/t ratio decreases, a general progressive reduction in shear stability is observed, along with a larger shear instability in the dynamic phases than the static one.

Fig. 11
figure 11

Shear Factor of Safety (FoSshear) in the cavity vertical walls area as a function of the distance from the central cavity axis (Δx), for different values of the ratio L/t (PGA = 0.2 g and 0.3 g. Dynamic input: single Ricker wavelet)

Full size image

Figure 12 shows the variation of FoStension in the roof area for the three geometric ratios L/t considered. As the L/t ratio decreases, an increase in the tensile Factor of Safety, under both static and dynamic conditions, both in the roof area external to the cavity width and in the central roof area is observed, as well as a stronger effect in terms of a reduction of the cavity stability due to the dynamic input is recognized.

Fig. 12
figure 12

Tension Factor of Safety (FoStension), in the roof area, as a function of the distance from the central cavity axis (Δx), for different values of the ratio L/t (PGA = 0.2 g and 0.3 g. Dynamic input: single Ricker wavelet)

Full size image

As a matter of fact, two different tensile behaviours depending on the ratio L/t can be distinguished. For large values of L/t (i.e. L/t = 4), FoStension in the area immediately above the cavity width is rather low while in the lateral areas, external to the opening of the cavity, it grows. For lower L/t values (i.e. L/t = 0.8), the area immediately above the cavity opening has the central part with an increase of tension stability, while FoStension decreases in the area above the vertical walls, and after it again grows to very high values in the external roof areas (outside the cavity width). This indicates that a compressive stress state predominantly occurs in these areas.

Considering the dynamic effects on the cavity stability against tensile failure mechanisms, a remarkable effect of the dynamic input is observed when the ratio L/t decreases. In particular, when compared with the static phase, FoStension after the dynamic phase decreases with the increase of PGA. Such a decrease becomes important as the ratio L/t decreases and affects the overall roof area above the cavity opening.

3.2 Dynamic Stability of Two Adjacent Cavities

In the study area, situations characterized by adjacent cavities divided by walls or pillars, which represent weak elements for the general stability of the rock system, frequently occur (Fiore et al. 2018). For this reason, further 2D analyses were conducted on adjacent parallel cavities separated by a septum of different thicknesses. The objective is to investigate the interaction between the two cavities under dynamic actions and its influence on the general stability of the cave system. In detail, the ideal geometric scheme is formed by two parallel cavities, characterized by the same L/t ratio and separated by a septum of thickness “i”, which varies between 0.2L and 2L. Two different configurations, i.e. shallow cavities (L/t = 4) and deep cavities (L/t = 0.75), have been accounted for. The dynamic input is represented by a Ricker wavelet repeated 4 times with PGA = 0.2 g and 0.3 g. Figure 13a shows the geometry of the domain and the discretization mesh used, which is significantly finer in the area close to the cavities (Fig. 13b) and respects the propagation condition of the highest frequencies of the signal, expressed by Eq. 1.

Fig. 13
figure 13

a Numerical scheme and mesh adopted for the 2D analyses with two adjacent cavities (Htot = total height; Ltot = total width); b zoom on the refined mesh around the sistem of cavities (L = cavity width; h = cavity heigh; t = roof thickness; i = septum width)

Full size image

The numerical results (expressed in terms of shear failure points Fig. 14 and deviatoric stains Fig. 15) obtained for the case of twin shallow cavities (L/t = 4) indicate that there is no interaction between cavities until the septum thickness is larger than i = L. When i = 0.5L, a slight effect of the interaction between the two cavities starts to occur only in the dynamic phase, with an incipit of a shear band clearly identified at the bottom of the septum.

Fig. 14
figure 14

Numerical results in terms of failure shear points of the parametric analyses with variable septum width (L/t = 4; Dynamic input: 4 times Ricker wavelet with PGA = 0.2 g): left side: static phase; right side: dynamic phase

Full size image
Fig. 15
figure 15

Numerical results in terms of deviatoric strains of the parametric analyses with variable septum width (L/t = 4; Dynamic input: 4 times Ricker wavelet with PGA = 0.2 g): left side: static phase; right side: dynamic phase

Full size image

When i = 0.25L, a clear shear band is observed within the septum during the dynamic stage, which instead is not seen in the static phase. The septum collapses in the dynamic phase for a septum thickness value equal to i = 0.2L.

For a system of deep cavities (L/t = 0.75; Figs. 16, 17), no interaction between the cavities, neither in the static or the dynamic stage, is observed for septum thickness larger than 2L. However, for i = 1.5L, the progressive development of shear zones within the septum is calculated in the dynamic phase. Finally, for i = L, the septum shows shear collapse under dynamic conditions. Therefore, the comparison between the analyses performed with different cave depths highlights that, for deep twin cavities, dynamic effects start to occur with larger septum thicknesses than for shallow twin cavities. This should reflect the decay of FoSshear in the areas outside the walls, which has been observed for deep single cavities under dynamic conditions (Fig. 11).

Fig. 16
figure 16

Numerical results in terms of failure shear points of the parametric analyses with variable septum width (L/t = 0.75; Dynamic input: 4 times Ricker wavelet with PGA = 0.2 g): left side: static phase; right side: dynamic phase

Full size image
Fig. 17
figure 17

Numerical results in terms of deviatoric strains of the parametric analyses with variable septum width (L/t = 0.75; Dynamic input: 4 times Ricker wavelet with PGA = 0.2 g): left side: static phase; right side: dynamic phase

Full size image

Furthermore, for the same geometrical conditions, the effect of the variation of the input PGA has been explored by comparing a 4-times Ricker wavelet with PGA = 0.3 g with that considering a PGA of 0.2 g. Figure 18 shows that, for PGA = 0.3 g, the effect of the interaction between the twin cavities starts earlier than with the lower PGA. In detail, for a shallow cavity system, the interaction occurs for i = 0.5L, while for a deeper cavity system, it takes place even for i = 2L.

Fig. 18
figure 18

Shear failure points and deviatoric strains obtaind for a dynamic input represented by a 4 times Ricker wavelet with PGA = 0.3 g

Full size image

As for the case of single cavity, the factor of safety under shear conditions within the septum, at the end of the static phase and at the end of the dynamic phase (with PGA = 0.2 g and 0.3 g), was also assessed. In particular, FoSshear was calculated by dividing the thickness of the septum into vertical slices and using the analytical equations proposed in Sect. 3.1. Each septum was divided into five slices. The main results are shown in Fig. 19 for the shallow (L/t = 4) and deep (L/t = 0.8) cave system. The figure refers to values of the septum thickness, i, which produce an interaction between cavities mainly in the dynamic phase.

Fig. 19
figure 19

a Shear Factor of Safety (FoSshear) in the cavity septum area as a function of the distance from the central septum axis (Δx), for variable ratios L/t, calculated at the end of the static stage and at the end of the dynamic stages; b shear failure points at the end of the dynamic stage for L/t = 4 (left side) and L/t = 0.8 (right side)

Full size image

In the case of shallow cavities (L/t = 4), a decrease in the safety factor is clearly observed from the static to the dynamic stage, with both PGA = 0.2 g and PGA = 0.3 g, which is more enhanced with larger values of PGA. Shear plastic points tend to propagate from the corners of the cavities to the central part of the septum, thus giving rise to inclined shear bands that cross the whole septum. For deeper cavities (L/t = 0.8), wedge failures tend to appear along the vertical walls of the cavities, which propagate even in the central part of the septum, for PGA = 0.3 g.

4 Discussion

A numerical investigation of the dynamic behaviour of man-made underground caves in soft carbonate rocks specifically aimed at assessing the issues related to cave stability, a research topic that has been so far only marginally investigated in the literature, has been proposed in the present work. The study here presented derives from the need to advance the knowledge regarding the stability under seismic actions of a large number of cavities that are widespread throughout the Apulia region (south-eastern Italy). Both the seismic behaviour of single ideal caves and that of twin adjacent caves, divided by a septum, have been analyzed. To investigate the evolution of the stress–strain state of the cavity under dynamic loading and the corresponding equilibrium conditions, a parametric analysis was carried out. The parametric analysis was performed by varying both the geometrical features of the ideal cavity, in accordance with the typical values observed for the Apulian underground cavities system, and the seismic input characteristics. In fact, different dynamic signal inputs have been considered, as a simple and easily controllable signal, the Ricker wavelet, or a real accelerogram. To this purpose, a numerical procedure to calculate the factor of safety against either shear failure or tensile failure mechanisms of underground caves (i.e. FoSshear and FoStension) based on the partition of the rock mass area around the cave into vertical slices, has been proposed. The value of the factor of safety is then calculated, for each slice, as the ratio between the available shear and tensile strength and the corresponding mobilized strength throughout the different mesh elements.

In the study presented, an elastic-perfectly plastic Mohr–Coulomb model, integrated by viscous damping according to the frequency-dependent Rayleigh formulation, has been adopted. The choice was dictated by the lack of experimental data in the literature for a thorough mechanical dynamic characterization of the rock materials considered in the study. At the same time, an elastic-perfectly plastic model is supposed to be capable of catching the ultimate state behaviour of a rock mass under relatively strong earthquake motions, as those assumed in this work. However, the authors are aware that care should be given, when using such constitutive model in dynamic calculations, to the choice of the stiffness value aimed at correctly predicting wave velocities in the rock mass. Thus, the model overestimates the stiffness value, by simulating rock materials with a constant value of the shear modulus G until failure is reached, as well as adopts a stress-independent Young’s modulus. Moreover, additional damping must be included to account for dissipation in the elastic behaviour and during wave propagation to simulate the hysteretic energy dissipation in soil. To this purpose, in the analyses here presented, a Rayleigh damping formulation has been used, thus ensuring damping only over a limited frequency range. The limitations above described may be overcome using advanced constitutive models which simulate the non-linear behavior of soil from small strain levels.

The numerical results, obtained for the single cavity, indicate that dynamic loadings, with characteristics comparable with those considered in this study, produce an appreciable increment of shear failure points and deviatoric strains only in the case of wide cavities. Also, the overburden thickness has a significant influence on the dynamic response of the cavities. When the roof thickness increases, the difference between the static and the dynamic behaviour of the rock mass around the cave increases as a function of the dynamic input energy level. This is probably related to the combined effect between the increased shear stability of the roof for deeper cavities and the longer travel time of the shear wave within the thicker roof. This produces modifications of the seismic motion in the area around the cave, as already shown in the literature. No significant influence is instead observed, between static and dynamic phases, varying the cavity height. This seems to confirm previous results observed in the literature, where the cavity height is identified as the least influencing geometric component for the cavity stability under static conditions, regardless of the vertical position of the cavity itself.

For shallow cavities, a general tendency to failure mechanisms affecting the cave roof is observed, starting from the upper corners, under static as well as dynamic conditions. In this case, the increase in shear stress as a consequence of the dynamic loading mainly affects the upper corners of the cavity. For deep cavities, plastic points develop first along the vertical walls under static conditions, while later on, under dynamic conditions, shear bands propagating both upwards and downwards tend to generate. Based on previous numerical analyses carried out on the static behaviour of similar underground caves (see Parise and Lollino 2011; Perrotti et al. 2018; to mention a few), the generation of plastic points around the cavity, and specifically along the vertical walls, rather than at the top, should be the effect of high shear stresses induced by the cave excavation process, which represents the initial stress state before the application of the dynamic loading.

Concerning the effect of the dynamic input characteristics, a wavelet repeated signal increases the amount of deviatoric strains and shear failure points if compared with a single wavelet signal. This is a direct consequence of the increased energy content applied. Moreover, larger input accelerations induce more significant increments of deviatoric strains and shear failure points.

In terms of factors of safety with respect to shear failure mechanisms, under static conditions, when the cavity deepens, the numerical results show a significant decrease in FoSshear in the lateral areas, outside the cavity width, and an increase in the central part of the roof, immediately above the cavity opening. However, under dynamic conditions, when the ratio L/t decreases, FoSshear decreases with respect to the static phase, increasingly with the increase in PGA and more critically in the central area of the roof. As explained above, this is presumably a consequence of the different wave amplification effects with the cavity depth related to the different stability in the roof central part. Regarding the cavity stability against tensile failure mechanisms, a stronger reduction of the factor of safety under dynamic conditions is again observed in the roof area when the ratio L/t decreases, which is more significant with the increase of PGA.

For twin shallow cavities, some interaction between the two cavities starts to occur in the dynamic phase when the interaxis is about equal to the cavity width. The interaction increases significantly for lower values of the interaxis, with the development of a shear band and, later on, the general collapse of the septum. For twin deep cavities, no interaction between the cavities is observed under dynamic loading for septum thickness larger than 2L, while already for i = L, a septum shear collapse occurs. In general, it should be pointed out that, for deeper cavities, the effects of cave interaction are already evident for wider septa, if compared with the case of shallow cavities. This is valid both in the static phase and, in a more marked way, in the dynamic phase. Obviously, this is a consequence of the redistribution of the stress state following the cavity excavation process, which for deeper cavities favor the concentration of shear stresses along the cavity vertical wall. Thus, two adjacent deep cavities are more prone to instability as the thickness of the septum decreases, if compared with two superficial cavities, and such an effect is accentuated in the dynamic phase. Stronger effects on the cavity stability have been observed for larger peak ground accelerations, as expected. The failure mechanisms typically observed are represented by shear plastic points that tend to propagate from the corners of the cavities to the central part of the septum, thus giving rise to inclined shear bands that cross the whole septum.

5 Conclusions

The research presented has provided several insights into the dynamic behaviour of underground cavities within soft rock masses, highlighting the difference between the responses of deep and shallow cavities. The study has also proposed a methodology to calculate the factor of safety with respect to the occurrence of a general failure of underground cavities under dynamic conditions, which can be applied to similar case studies. The results show a significant influence of the dynamic signal on the stability of single cavities or cavity systems, which should not be neglected, as well as of the cave geometry.

However, future developments of this research could be represented by the adoption of advanced constitutive models that are capable of accounting more accurately for the non-linear dynamic response of the rock material examined.

A more comprehensive investigation of the response of underground cavities under a large set of real accelerometer input data is also recognized to be important to explore the cavity behaviour under seismic wave motion, to be developed in future scientific works. Moreover, the variation of the shape of the cavity, thus assuming more complex and realistic geometries, as for example with an arch-shaped or trapezoidal roof, could be also studied in terms of stability under dynamic stresses. From this point of view, applications of the methodology proposed to well-defined case studies can provide a way to validate the methodology itself.