Abstract
The behavior of deep tunnel is usually time dependent due to the sequential construction process as well as the rheological characteristic of the rock mass. Moreover, the uncertainty of different parameters such as the viscoelastic properties can play an essential role on the stability of tunnel and its supports. The reliability analysis based on the probabilistic approach, which has been largely applied in the last 2 decades to treat this kind of problems, presents an efficient tool but its application is usually limited in case of time-independent behavior of tunnel supported by a single liner. This study aims at assessment of time-dependent reliability of deep circular tunnel counting for rheological characteristic of rock mass and sequential construction of liners. Since the reliability analysis, using direct Monte Carlo Simulation and a FEM software could be very time-consuming, we establish firstly a closed form solution for the response of a deep tunnel excavated in the viscoelastic Burger rock accounting for the sequential installation of two liners. The validation of this analytical solution is performed by comparing the results of this solution with some previous existing analytical solutions as well as with numerical results obtained from the finite element simulation in some case studies. Once validated, this analytical solution is used as a fast tool for the time-dependent reliability analysis by direct Monte Carlo Simulation. The influence of different parameters on the probability of failure of a double liners tunnel in respect with its life service, by taking into account of the sequential construction, was discussed in the last part of the paper.















Similar content being viewed by others
Abbreviations
- \( R_{\text{ini}} \) :
-
Initial radius of the tunnel
- \( R_{\text{fin}} \) :
-
Final radius of the tunnel
- R(t):
-
Time-dependent radius during the excavation of the tunnel
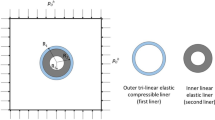
- \( R_{1} \) :
-
Exterior radius of the first liner
- \( R_{2} \)(\( R_{3} \)):
-
Interior radius of the first (second) liner
- \( l_{1} \) (\( l_{2} \)):
-
Thickness of the first (second) liner
- t :
-
Time
- \( s \) :
-
Variable in the Laplace transform
- \( r,\theta ,z \) :
-
Cylindrical coordinates
- \( t_{0} \) :
-
End time of the excavation of the tunnel
- \( t_{1} \) (\( t_{2} \)):
-
Installation time of the first (second) liner
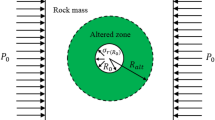
- \( p_{0}^{h} \) :
-
Hydrostatic far field stress
- \( p_{0} (t) \) :
-
Fictitious internal pressure applied on the tunnel’s perimeter
- \( \chi (t) \) :
-
Dimensionless parameter to account for the effect of the tunnel face advancement
- \( m_{1} \),\( m_{2} \) :
-
Parameters characterizing the curve of tunnel face advancement
- \( v_{\text{l}} \) :
-
Longitudinal excavation rate of tunnel
- \( v_{\text{r}} \) :
-
Radial excavation rate of tunnel
- \( p_{1} (t) \) :
-
Supported pressure at the outer face of the first liner
- \( p_{11} (t) \) :
-
Supported pressure at the outer face of the first liner due to the presence of the first liner and before the installation of the second liner (\( t_{1} \le t < t_{2} \))
- \( p_{12} (t) \) :
-
Supported pressure at the outer face of the first liner due the presence of the second liner (\( t \ge t_{2} \))
- \( p_{2} (t) \) :
-
Supported pressure at the outer face of the second liner
- \( p_{22} (t) \) :
-
Supported pressure at the outer face of the second liner after its installation (\( t \ge t_{2} \))
- \( G_{\text{M}} (G_{\text{K}} ) \) :
-
Shear elastic modulus of the Maxwell (Kelvin) element in the Burger model
- \( \eta_{\text{M}} (\eta_{\text{K}} ) \) :
-
Viscosity coefficient of the dashpot of the Maxwell (Kelvin) element in the Burger model
- \( G(t) \) :
-
Shear relaxation modulus
- \( G(s) \) :
-
Laplace transform of the shear relaxation modulus
- \( \delta (t) \) :
-
Delta function
- \( \sigma_{ij} (\varepsilon_{ij} ) \) :
-
Stress (strain) tensors
- \( s_{ij} (e_{ij} ) \) :
-
Deviatoric tensor of stress (strain)
- \( \sigma_{\text{r}} (\sigma_{\theta } ) \) :
-
Radial (hoop) stress in the rock mass
- \( \sigma_{\text{rL1}} (\sigma_{{\theta {\text{L}}1}} ) \) :
-
Radial (hoop) stress in the first liner
- \( \sigma_{\text{rL2}} (\sigma_{{\theta {\text{L}}2}} ) \) :
-
Radial (hoop) stress in the second liner
- \( u_{\text{r}} \) :
-
Radial displacement in the rock mass
- \( u_{\text{r1}} \) :
-
Radial displacement in the rock mass at the excavation stage (\( t < t_{0} \))
- \( u_{\text{r2}} \) :
-
Radial displacement in the rock mass after the excavation stage and before the installation of the first liner (\( t_{0} \le t < t_{1} \))
- \( u_{\text{r3}} \) :
-
Radial displacement in the rock mass after the installation of the first liner and before the installation of the second liner (\( t_{1} \le t < t_{2} \))
- \( u_{{{\text{r}}4}} \) :
-
Radial displacement in the rock mass after the installation of the second liner (\( t \ge t_{2} \))
- D1(t), D2(t), D3(t), D4(t):
-
Time-dependent coefficients
- G1(t), G2(t), G3(t), G4(t):
-
Time-dependent coefficients
- \( u_{\text{rL1}} (u_{\text{rL2}} ) \) :
-
Radial displacement in the first (second) liner
- \( u_{\text{max} } \) :
-
Allowable convergence of tunnel
- \( E_{\text{L1}} ,\nu_{\text{L1}} (E_{\text{L2}} ,\nu_{\text{L2}} ) \) :
-
Young’s modulus and Poisson ratio of the first (second) liner
- \( G_{\text{L1}} ,K_{\text{L1}} (G_{\text{L2}} ,K_{\text{L2}} ) \) :
-
Shear and bulk moduli of the first (second) liner
- K s :
-
Support stiffness
- \( {\mathbf{X}} = [G_{\text{M}} ,\eta_{\text{M}} ,G_{\text{K}} ,\eta_{\text{K}} ] \) :
-
Random variable vector of four parameters of the Burger rock in the reliability analysis
- \( G({\mathbf{X}},t) \) :
-
Time-dependent performance function
- \( G_{\text{Tunnel}} ({\mathbf{X}},t) \) :
-
Performance function defines the limit convergence on the tunnel boundary
- \( G_{{{\text{L}}1}} ({\mathbf{X}},t) \) :
-
Performance function defines the limit stress state in the first liner
- \( G_{{{\text{L}}2}} ({\mathbf{X}},t) \) :
-
Performance function defines the limit stress state in the second liner
- \( P_{\text{f}} (t) \) :
-
Time-dependent probability of failure
- \( q_{\text{L1}} (\varvec{X},t) = \left| {\sigma_{{\theta {\text{L1}}}} (\varvec{X},t) - \sigma_{\text{rL1}} (\varvec{X},t)} \right| \) :
-
Equivalent stress in the first liner
- \( q_{{{\text{L}}2}} (\varvec{X},t) = \left| {\sigma_{{\theta {\text{L2}}}} (\varvec{X},t) - \sigma_{\text{rL1}} (\varvec{X},t)} \right| \) :
-
Equivalent stress in the second liner
- \( \sigma_{\text{cL1}} (\sigma_{\text{cL2}} ) \) :
-
Allowable stresses of the first (second) liner
- \( N_{\text{total}} \) :
-
Total number of samples in the Monte Carlo Simulation
- \( f_{1}^{B} (f_{2}^{B} ) \) :
-
Free term of the integral equation
- \( E{}_{1},E{}_{2},\lambda_{1} ,\lambda_{2} \) :
-
Constant coefficients of the integral equation
- \( D_{a} \) :
-
Discriminant of the characteristic equation of the integral equation
- \( \mu_{1} ,\mu_{2} \) :
-
Two real roots of the characteristic equation of the integral equation
References
Arnau O, Molins C, Blom CB, Walraven JC (2012) Longitudinal time-dependent response of segmental tunnel linings. Tunn Under Space Tech 28:98–108
Au SK, Beck JL (2001) Estimation of small failure probabilities in high dimensions by subset simulation. Probab Eng Mech 16:263–277
Au SK, Ching J, Beck JL (2007) Application of subset simulation methods to reliability benchmark problems. Struct Saf 29:183–193
Barla G, Debernardi D, Sterpi D (2012) Time-dependent modeling of tunnels in squeezing conditions. Int Jour Geomech 12:697–710
Booth AJ, Marshall AM, Stace R (2016) Probabilistic analysis of a coal mine roadway including correlation control between model input parameters. Comput Geotech 74:151–162
Bui TA, Wong H, Deleruyelle F, Dufour N, Leo C, Sun DA (2014) Analytical modeling of a deep tunnel inside a poro-viscoplastic rock mass accounting for different stages of its life cycle. Comput Geotech 58:88–100
Code_Aster. www.code-aster.org
Fahimifar A, Tehrani FM, Hedayat A, Vakilzadeh A (2010) Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field. Tunn Under Space Tech 25:297–304
Fritz P (1984) An analytical solution for axisymmetric tunnel problems in elasto-viscoplastic media. Int Jour Num Anal Meth Geomech 8:325–342
Gasc-Barbier M, Chanchole S, Bérest P (2004) Creep behavior of Bure clayed rock. App Clay Sci 26:449–458
Hasofer AM, Lind NC (1974) Exact and invariant second-moment code format. J Eng Mech Div 100:111–121
Jaeger JC, Cook NGW, Zimmerman W (2007) Fundamentals of rock mechanics, 4th edn. Blackwell Publishing, USA
Jiang SH, Li DQ, Zhang LM, Zhou CB (2014) Time-dependent system reliability of anchored rock slopes considering rock bolt corrosion effect. Eng Geol 175:1–8
Laso E, Sagrario Gómez Lera M, Alarcón E (1995) A level II reliability approach to tunnel support design. Appl Math Model 19:371–382
Li HZ, Low BK (2010) Reliability analysis of circular tunnel under hydrostatic stress field. Comput Geotech 37:50–58
Low BK (2014) FORM, SORM and spatial modeling in geotechnical engineering. Struct Saf 49:56–64
Lü Q, Low BK (2011) Probabilistic analysis of underground rock excavations using response surface method and SORM. Comput Geotech 38:1008–1021
Lü Q, Chan CL, Low BK (2011) System assessment for a rock tunnel with multiple failure modes. Rock Mech Rock Eng 46:821–833
Mason DP, Abelman H (2009) Support provided to rock excavations by a system of two liners. Int J Rock Mech Min Sci 46:1197–1205
Miura K, Yagi H, Shiroma H, Takekuni K (2003) Study on design and construction method for the New Tomei-Meishin expressway tunnels. Tunn Under Space Tech 18:271–281
Mollon G, Dias D, Soubra AH (2009) Probabilistic analysis of circular tunnels in homogeneous soil using response surface methodology. J Geotech Geoenviron Eng 135:1314–1325
Nomikos P, Rahmannejad R, Sofianos A (2011) Supported axisymmetric tunnels within linear viscoelastic Burgers rocks. Rock Mech Rock Eng 44:553–564
Pan YW, Dong JJ (1991) Time-dependent tunnel convergence—II. Advance rate and tunnel-support interaction. Int J Rock Mech Min Sci Geomech 28:477–488
Polyanin AD, Manzhirov AV (2008) Handbook of integral equations, 2nd edn. Chapman & Hall/CRC, USA, p 147
Sakurai S (1978) Approximate time-dependent analysis of tunnel support structure considering progress of tunnel face. Int J Num Anal Meth Geomech 2:159–175
Sharifzadeh M, Daraei R, Broojerdi MS (2012) Design of sequential excavation tunneling in weak rocks through findings obtained from displacements based back analysis. Tunn Under Space Tech 28:10–17
Sharifzadeh M, Tarifard A, Ali Moridi M (2013) Time-dependent behavior of tunnel in weak rock mass based on displacement back analysis method. Tunn Under Space Tech 38:348–356
Song F, Wang HN, Jiang MJ (2018) Analytical solutions for lined circular tunnels in viscoelastic rock considering various interface conditions. Appl Math Model 55:109–130
Sulem J, Panet M, Guenot A (1987) An analytical solution for time-dependent displacement in a circular tunnel. Int J Rock Mech Min Sci Geomech 24:155–164
Tran-Manh H, Sulem J, Subrin D, Bilaux D (2015) Anisotropic time-dependent modeling of tunnel excavation in squeezing ground. Rock Mech Rock Eng 48:2301–2317
Vu TM, Sulem J, Subrin D, Monin N (2013) Semi-analytical solution for stresses and displacement in a tunnel excavated in transversely isotropic formation with non-linear behavior. Rock Mech Rock Eng 46:213–229
Wang Z, Wang P (2012) A nested extreme response surface approach for time-dependent reliability-based design optimization. J Mech Des 134:121007-1
Wang HN, Li Y, Ni Q, Utili S, Jiang MJ, Liu F (2013) Analytical solutions for the construction of the deeply buried circular tunnel with two liners in rheological rock. Rock Mech Rock Eng 46:1481–1498
Wang HN, Utili S, Jang MJ (2014) An analytical approach for the sequential excavation of axisymmetric lined tunnels in viscoelastic rock. Int J Rock Mech Min Sci 68:85–106
Zhang CL, Czaikowski O, Rothfuchs T (2010) Thermo-hydro-mechanical behavior of the Collovo-Oxfordian clay rocks. GRS-226. ISBN 978-3-939355-42-7
Zhang L, Liu Y, Yang Q (2016) Study on time-dependent behavior and stability assessment of deep-buried tunnels based on internal state variable theory. Tunn Under Space Tech 51:164–174
Zhang D, Han X, Jiang C, Liu J, Li Q (2017) Time-dependent reliability analysis through response surface method. J Mech Des 139:041404-1
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors of the present paper confirm that we have no conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Determination of the supporting pressures of two liners
Appendix 1: Determination of the supporting pressures of two liners
In this appendix, we detail the process to determine the supporting pressures of two liners by using the compatibility conditions of displacement at the interface between the rock mass and the first liner (Eq. 16) and at the interface of two liners (Eq. 17).
1.1 1.1. Determination of Supporting Pressures after the Installation of the First Liner
By substituting the Eq. (11) and Eq. (14a) in Eq. (16), the radial incremental displacement of rock from time t1 to the generic time t > t1 can be written in the integral form:
with:
Regarding with the conditions expressed in Eq. (4), the Eq. (46) written for the instant \( t \) with \( t_{1} \le t < t_{2} \) is:
This Eq. (48) results the second type Volterra equation (Polyanin and Manzhirov 2008) for \( p_{11} (t) \):
Substituting Eq. (13) into Eq. (49) yields this following equation:
which can be expanded in the form:
Supposing now \( \varphi_{1}^{B} (t) = p_{11} \left( t \right)\exp \left( {\frac{{G_{\text{K}} }}{{\eta_{\text{K}} }}t} \right) \), the following integral equation can be obtained:
Then by defining \( e_{1} = (R_{1} G_{H} )/(2G_{H} a_{00} - R_{1} ) \), we can rewrite Eq. (52) in form:
By defining:
with \( \lambda_{1}^{B} = e_{1} /\eta_{\text{K}} \) and posing:
the Eq. (54) can be rewritten as:
Thus, the function \( \varphi_{1}^{B} (t) \) in Eq. (53) can be simplified as:
This last equation presents in effect the standard integral equation as shown in (Eq. 18) with the free term \( f_{1}^{B} (t) \) and the Kernel \( \left( {\frac{{e_{1} }}{{\eta_{\text{K}} }} + \frac{{e_{1} }}{{\eta_{H} }}\exp \left( {\frac{{G_{\text{K}} }}{{\eta_{\text{K}} }}(t - \tau )} \right)} \right) \) whereas the corresponding parameters \( E{}_{1},E{}_{2},\lambda_{1} ,\lambda_{2} \) are respectively equal to \( E_{1} = - \frac{{e_{1} }}{{\eta_{\text{K}} }},\;E_{2} = - \frac{{e_{1} }}{{\eta_{H} }},\;\lambda_{1} = 0,\;\lambda_{2} = \frac{{G_{\text{K}} }}{{\eta_{\text{K}} }} \).
Due to the fact that \( \eta_{K} > 0,\,\,\eta_{H} \, > 0 \), the discriminant of the quadratic equation (Eq. 19) is positive (\( D_{a} > 0 \)), thus the solution \( \varphi_{1}^{B} (t) \) takes the same form of Eq. (21) which means that:
Correspondingly, the solution of \( p_{11} \left( t \right) \) can be calculated:
1.2 1.2. Determination of Supporting Pressure after the Installation of the Second Liner
The determination of the supporting pressure in the liners after the second installation stage consists of calculating the pressures \( p_{12} (t) \) and \( p_{22} (t) \) with \( t \ge t_{2} \).
Using the radial displacement in each liner expressed in Eqs. (14a) and (15a), the compatibility condition of the displacement at the interface of two liners (see Eq. 17) can be rewritten in the form:
with:
The Eq. (46) written for the instant \( t \) (with \( t \ge t_{2} \)) has the following form:
Using the relationship between \( p_{22} (t) \) and \( p_{12} (t) \) as shown in Eq. (60), one can deduce the following integral equation for \( p_{12} (t) \):
Substituting \( H(t) \) from Eq. (13) into Eq. (63), we have:
Defining \( \varphi_{2}^{B} (t) = p_{12} \left( t \right)\exp \left( {\frac{{G_{\text{K}} }}{{\eta_{\text{K}} }}t} \right) \), after some developments, the simplified form of the integral equation \( \varphi_{2}^{B} (t) \) can be obtained:
where
Defining \( e_{2} = \frac{{a_{11} G_{H} R_{1} }}{{2G_{H} \left( {a_{00} a_{11} - a_{01} a_{10} } \right) - R_{1} a_{11} }} \) and \( \lambda_{2}^{B} = e_{2} /\eta_{K} \), Eq. (65) can be rewritten in a more compact form:
where:
Defining \( A_{3} = \int_{{t_{1} }}^{{t_{2} }} {\chi (\tau )R^{2} (\tau )\exp \left( {\frac{{G_{\text{K}} }}{{\eta_{\text{K}} }}\tau } \right){\text{d}}\tau } \) with \( R(t) = R_{fin} \,\,\,{\text{if}}\,\,\,\,t_{1} \le t \) and:
Therefore, \( f_{2}^{B} (t) \) can be expressed in form:
We obtain also the following standard integral equation:
which has the Kernel \( \left( {\frac{{e_{2} }}{{\eta_{K} }} + \frac{{e_{2} }}{{\eta_{H} }}\exp \left( {\frac{{G_{K} }}{{\eta_{K} }}(t - \tau )} \right)} \right) \) and the free term \( f_{2}^{B} (t) \).
This integral equation with the corresponding parameters \( E_{1} = - \frac{{e_{2} }}{{\eta_{\text{K}} }},\quad E_{2} = - \frac{{e_{2} }}{{\eta_{H} }},\quad \lambda_{1} = 0,\quad \lambda_{2} = \frac{{G_{\text{K}} }}{{\eta_{\text{K}} }} \) results a positive discriminant (\( D_{a} > 0 \)) of the characteristic equation (Eq. 19). Thus, the solution of Eq. (71) has the same form as one presented in Eq. (22) meaning that:
From this last solution of \( \varphi_{2}^{B} \left( t \right) \), one can deduce the solution of \( p_{12} \left( t \right) \):
Through which the solution of \( p_{22} \left( t \right) \) can be determined using the Eq. (60) as shown in Eq. (25).
To simplify the presentation, the expressions of the supporting pressures as well as the displacements in the rock mass are written in the integral form but it is worth to note that their explicitly analytical expressions can be found without difficulty. The numerical integration is only needed for the functions containing the term \( \chi (t) \) determined in the range \( t < t_{0} \)(i.e. during the excavation stage) such as ones expressed in Eqs. (28 and 29) due to the present of time in both the numerator and denominator of the exponential function (see also Eq. 55a).
Rights and permissions
About this article
Cite this article
Do, DP., Tran, NT., Mai, VT. et al. Time-Dependent Reliability Analysis of Deep Tunnel in the Viscoelastic Burger Rock with Sequential Installation of Liners. Rock Mech Rock Eng 53, 1259–1285 (2020). https://doi.org/10.1007/s00603-019-01975-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-019-01975-6