Analytical and Numerical Simulations to Predict the Long-Term Behavior of Lined Tunnels Considering Excavation-Induced Damaged Zone

Abstract

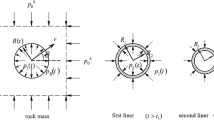
Tunnels embedded in soft rock masses experience time-dependent behaviour, and designing an appropriate supporting system is a challenging task. This condition can be more problematic when a damaged zone is also developed (due to poor quality blasting). In this paper, a theoretical solution is presented to predict long-term tunnel convergence and long-term induced lining pressure, considering the existence of an altered zone due to excavation. The rheological behaviour of rock mass and the altered zone is simulated by viscoelastic behaviour obeying the Burgers model. It is also assumed that a continuous lining, i.e., a shotcrete layer, is placed (with elastic behaviour) to confine the convergence. A comprehensive parametric study is performed by the presented solution to evaluate the effects of various parameters on the induced lining pressures and the tunnel convergence. Then, to have more practical conditions, the elastic–viscoplastic rheological model (known as CVISC) is assigned to the rock mass to consider its failure. The problem is further studied by only numerical approach using FDM. The results show that the support installation time and the radius of the altered zone have remarkable effects on the output results.

Highlights

• A new analytical method is proposed to obtain the tunnel displacement over time.

• The interaction of the tunnel and rheological rock mass is taken into account.

• The Burgers rheological model is assigned to altered and unaltered zones.

Appendices

Appendices

Appendix A: Detailed Solution of an Unsupported Tunnel Surrounded by the Altered Zone

In the initial rock mass, the radial displacement at radius ${R}_{\mathrm{alt}}$ can be calculated according to Eq. 5 as follows:

$${u}_{r}\left({R}_{\mathrm{alt}},t\right)=\frac{{R}_{\mathrm{alt}}}{2}\underset{0}{\overset{t}{\int }}\left({P}_{0}-{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right)\right){H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)d\tau .$$

(A1)

Note that ${\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}$ is the radial stress at radius ${R}_{\mathrm{alt}}$ before installation of the lining layer.

On the other hand, in the case of the altered zone, the above displacement is equal to

$${u}_{r}\left({R}_{\mathrm{alt}},t\right)=\frac{{R}_{0}^{2}}{2{R}_{\mathrm{alt}}\left(1-{c}_{v\left(\mathrm{alt}\right)}\right)}\underset{0}{\overset{t}{\int }}\left({\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right)-{\sigma }_{r\left({R}_{0}\right)}\left(\tau \right)\right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau .$$

(A2)

For the reason of continuity, these displacements must be equal. Thus:

$$\underset{0}{\overset{t}{\int }}\left({\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right)\left[\frac{{c}_{v\left(\mathrm{alt}\right)}}{1-{c}_{v\left(\mathrm{alt}\right)}}{H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)+{H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)\right]\right)d\tau $$

$$=\underset{0}{\overset{t}{\int }}{P}_{0}{H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)d\tau +\frac{{c}_{v\left(\mathrm{alt}\right)}}{1-{c}_{v\left(\mathrm{alt}\right)}}\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{0}\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau .$$

(A3)

Incorporating Eq. 6, the values of $\underset{0}{\overset{t}{\int }}{P}_{0}{H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)d\tau$ and $\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{0}\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau$ can be calculated as follows:

$$\underset{0}{\overset{t}{\int }}{P}_{0}{H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)d\tau ={P}_{0}\left[\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{t}{{\eta }_{M\left(\mathrm{ini}\right)}}+\frac{1}{{G}_{K\left(\mathrm{ini}\right)}}\left(1-{e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}\right)\right],$$

(A4)

$$\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{0}\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau =\alpha {P}_{0}\left[\frac{{e}^{-mt}}{{G}_{M\left(\mathrm{alt}\right)}}+\frac{1-{e}^{-mt}}{m{\eta }_{M\left(\mathrm{alt}\right)}}+\frac{{e}^{-mt}-{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}}{{G}_{K\left(\mathrm{alt}\right)}-m{\eta }_{K\left(\mathrm{alt}\right)}}\right].$$

(A5)

In these conditions, Eq. A3 can be written as follows:

$${\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(t\right)+\underset{0}{\overset{t}{\int }}\left(\left[\frac{{G}_{M\left(E\right)}}{{\eta }_{M\left(E\right)}}+\frac{{G}_{M\left(E\right)}{c}_{v\left(\mathrm{alt}\right)}}{{\eta }_{K\left(\mathrm{alt}\right)}\left(1-{c}_{v\left(\mathrm{alt}\right)}\right)}{e}^{-\frac{\left(t-\tau \right)}{{T}_{K\left(\mathrm{alt}\right)}}}+\frac{{G}_{M\left(E\right)}}{{\eta }_{K\left(\mathrm{ini}\right)}}{e}^{-\frac{\left(t-\tau \right)}{{T}_{K\left(\mathrm{ini}\right)}}}\right]\right){\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right)d\tau ={P}_{0}{G}_{M\left(E\right)}\left(\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{t}{{\eta }_{M\left(\mathrm{ini}\right)}}+\frac{1-{e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}}{{G}_{K\left(\mathrm{ini}\right)}}+\frac{\alpha {c}_{v\left(\mathrm{alt}\right)}}{1-{c}_{v\left(\mathrm{alt}\right)}}\left[{e}^{-mt}{P}_{1}+\frac{1}{m{\eta }_{M\left(\mathrm{alt}\right)}}-\frac{{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}}{{G}_{K\left(\mathrm{alt}\right)}-m{\eta }_{K\left(\mathrm{alt}\right)}}\right]\right),$$

(A6)

where

$${\eta }_{M\left(E\right)}=1/(\frac{1}{{\eta }_{M\left(\mathrm{ini}\right)}}+\frac{{c}_{v\left(\mathrm{alt}\right)}}{{\eta }_{M\left(\mathrm{alt}\right)}\left(1-{c}_{v\left(\mathrm{alt}\right)}\right)}), $$

(A7a)

$${G}_{M\left(E\right)}=1/\left(\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{{c}_{v\left(\mathrm{alt}\right)}}{{G}_{M\left(\mathrm{alt}\right)}\left(1-{c}_{v\left(\mathrm{alt}\right)}\right)}\right),$$

(A7b)

$${P}_{1}=\frac{1}{{G}_{M\left(\mathrm{alt}\right)}}-\frac{1}{m{\eta }_{M\left(\mathrm{alt}\right)}}+\frac{1}{{G}_{K\left(\mathrm{alt}\right)}-m{\eta }_{K\left(\mathrm{alt}\right)}},$$

(A7c)

$${T}_{K\left(\mathrm{alt}\right)}=\frac{{\eta }_{K\left(\mathrm{alt}\right)}}{{G}_{K\left(\mathrm{alt}\right)}},$$

(A7d)

$${T}_{K\left(\mathrm{ini}\right)}=\frac{{\eta }_{K\left(\mathrm{ini}\right)}}{{G}_{K\left(\mathrm{ini}\right)}}.$$

(A7e)

Equation A6 is similar to Eq. A8:

$$y\left(t\right)+\underset{0}{\overset{t}{\int }}\left(A{e}^{B\left(t-\tau \right)}+C{e}^{D\left(t-\tau \right)}+E{e}^{F\left(t-\tau \right)}\right)y\left(\tau \right)d\tau =f\left(t\right),$$

(A8)

in which

$$\begin{aligned}A&=\frac{{G}_{M\left(E\right)}}{{\eta }_{M\left(E\right)}},\\B&=0,\\C&=\frac{{G}_{M\left(E\right)}{c}_{v\left(\mathrm{alt}\right)}}{{\eta }_{K\left(\mathrm{alt}\right)}\left(1-{c}_{v\left(\mathrm{alt}\right)}\right)},\\D&=-\frac{1}{{T}_{K\left(\mathrm{alt}\right)}},\\ E&=\frac{{G}_{M\left(E\right)}}{{\eta }_{K\left(\mathrm{ini}\right)}},\\ F&=-\frac{1}{{T}_{K\left(\mathrm{ini}\right)}}.\end{aligned}$$

(A9)

Also, the right hand side of Eq. A6 is equal to $f\left(t\right)$, and $y={\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}$.

The solution of Eq. A8 is (Polyanin and Manzhirov 2008):

$$y\left(t\right)=f\left(t\right)+\underset{0}{\overset{t}{\int }}\left({B}_{1}{e}^{{z}_{1}\left(t-\tau \right)}+{B}_{2}{e}^{{z}_{2}\left(t-\tau \right)}+{B}_{3}{e}^{{z}_{3}\left(t-\tau \right)}\right)f\left(\tau \right)d\tau .$$

(A10)

The values of ${z}_{1}$, ${z}_{2}$, and ${z}_{3}$ are the roots of Eq. A11. It should be noted that Eq. A10 is valid only when these roots are real numbers and different.

$${z}^{3}+{z}^{2}\left(A+C-D+E-F\right)+z\left(FD-AF-AD-CF-ED\right)+ADF=0.$$

(A11)

The values of ${B}_{1}$, ${B}_{2}$, and ${B}_{3}$ are obtained by solving the system of Eq. A12:

$$\left\{\begin{array}{c}\frac{{B}_{1}}{-{z}_{1}}+\frac{{B}_{2}}{-{z}_{2}}+\frac{{B}_{3}}{-{z}_{3}}+1=0\\ \frac{{B}_{1}}{D-{z}_{1}}+\frac{{B}_{2}}{D-{z}_{2}}+\frac{{B}_{3}}{D-{z}_{3}}+1=0\\ \frac{{B}_{1}}{F-{z}_{1}}+\frac{{B}_{2}}{F-{z}_{2}}+\frac{{B}_{3}}{F-{z}_{3}}+1=0\end{array}\right..$$

(A12)

The value of radial stress in the boundary of the altered and initial rock masses is

$${\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}={P}_{0}{G}_{M\left(E\right)}\left[\sum_{i=1}^{3}{B}_{i}\left(\frac{{P}_{2\left(i\right)}}{{z}_{i}}\left({e}^{{z}_{i}t}-1\right)+\frac{t}{{\eta }_{M\left(\mathrm{ini}\right)}}\left(\frac{1}{3{B}_{i}}-\frac{1}{{z}_{i}}\right)+\frac{{e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}-{e}^{{z}_{i}t}}{{G}_{K\left(\mathrm{ini}\right)}\left({z}_{i}+\frac{1}{{T}_{K\left(\mathrm{ini}\right)}}\right)}+\frac{1}{3{B}_{i}}\left(\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{1}{{G}_{K\left(\mathrm{ini}\right)}}\left(1-{e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}\right)\right)+\frac{\alpha {c}_{v\left(\mathrm{alt}\right)}}{1-{c}_{v\left(\mathrm{alt}\right)}}\left({P}_{1}\left(\frac{{e}^{{z}_{i}t}-{e}^{-mt}}{m+{z}_{i}}+\frac{{e}^{-mt}}{3{B}_{i}}\right)+\frac{{e}^{{z}_{i}t}-1}{{z}_{i}m{\eta }_{M\left(\mathrm{alt}\right)}}+{P}_{3\left(i\right)}\left({e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}-{e}^{{z}_{i}t}\right)+\frac{1}{3{B}_{i}}\left(\frac{1}{m{\eta }_{M\left(\mathrm{alt}\right)}}-{P}_{3\left(i\right)}{P}_{4\left(i\right)}{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}\right)\right)\right)\right],$$

(A13)

where

$${P}_{2\left(i\right)}=\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{1}{{z}_{i}{\eta }_{M\left(\mathrm{ini}\right)}}+\frac{1}{{G}_{K\left(\mathrm{ini}\right)}},$$

(A14a)

$${P}_{3\left(i\right)}=\frac{1}{\left({G}_{K\left(\mathrm{alt}\right)}-m{\eta }_{K\left(\mathrm{alt}\right)}\right)\left({z}_{i}+\frac{1}{{T}_{K\left(\mathrm{alt}\right)}}\right)},$$

(A14b)

$${P}_{4\left(i\right)}={z}_{i}+\frac{1}{{T}_{K\left(\mathrm{alt}\right)}}.$$

(A14c)

It should be noted that ${P}_{2\left(i\right)}$, ${P}_{3\left(i\right)}$, and ${P}_{4\left(i\right)}$ depend on the value of ${z}_{i}$ ($i=1, \mathrm{2,3}$).

According to Eq. 5, the radial displacement at the tunnel boundary (${u}_{r}\left({R}_{0},t\right)$) is:

$${u}_{r}\left({R}_{0},t\right)=\frac{{R}_{0}}{2\left(1-{c}_{v\left(\mathrm{alt}\right)}\right)}\left[\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau -\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{0}\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau \right].$$

(A15)

The solution of the first term of Eq. A15 is

$$\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau =\frac{{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(t\right)}{{G}_{M\left(\mathrm{alt}\right)}}+\frac{{X}_{1}\left(t\right)}{{\eta }_{M\left(\mathrm{alt}\right)}}+\frac{{X}_{2}\left(t\right)}{{\eta }_{K\left(\mathrm{alt}\right)}},$$

(A16)

where

$${X}_{1}\left(t\right)={P}_{0}{G}_{M\left(E\right)}\left[\sum_{i=1}^{3}{B}_{i}\left(\frac{{P}_{2\left(i\right)}}{{z}_{i}}\left(\frac{{e}^{{z}_{i}t}-1}{{z}_{i}}-t\right)+\frac{{t}^{2}}{2{\eta }_{M\left(\mathrm{ini}\right)}}\left(\frac{1}{3{B}_{i}}-\frac{1}{{z}_{i}}\right)+\frac{\frac{1-{e}^{{z}_{i}t}}{{z}_{i}}+{T}_{K\left(\mathrm{ini}\right)}\left(1-{e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}\right)}{{G}_{K\left(\mathrm{ini}\right)}\left({z}_{i}+\frac{1}{{T}_{K\left(\mathrm{ini}\right)}}\right)}+\frac{1}{3{B}_{i}}\left(t\left(\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{1}{{G}_{K\left(\mathrm{ini}\right)}}\right)+\frac{{T}_{K\left(\mathrm{ini}\right)}\left({e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}-1\right)}{{G}_{K\left(\mathrm{ini}\right)}}\right)+\frac{\alpha {c}_{v\left(\mathrm{alt}\right)}}{1-{c}_{v\left(\mathrm{alt}\right)}}\left({P}_{1}\left(\frac{{e}^{{z}_{i}t}-1}{{z}_{i}\left(m+{z}_{i}\right)}+\left(\frac{1-{e}^{-mt}}{m}\right)\left(\frac{1}{3{B}_{i}}-\frac{1}{m+{z}_{i}}\right)\right)+\frac{\frac{{e}^{{z}_{i}t}-1}{{z}_{i}}-t}{{z}_{i}m{\eta }_{M\left(\mathrm{alt}\right)}}+{P}_{3\left(i\right)}\left({P}_{6}+\frac{1-{e}^{{z}_{i}t}}{{z}_{i}}\right)+\frac{1}{3{B}_{i}}\left(\frac{t}{m{\eta }_{M\left(\mathrm{alt}\right)}}-{P}_{3\left(i\right)}{P}_{4\left(i\right)}{P}_{6}\right)\right)\right)\right],$$

(A17a)

$${X}_{2}\left(t\right)={P}_{0}{G}_{M\left(E\right)}\left[\sum_{i=1}^{3}{B}_{i}\left(\frac{{P}_{2\left(i\right)}}{{z}_{i}}\left(\frac{{P}_{5}}{{P}_{4\left(i\right)}}-{P}_{6}\right)+\frac{{T}_{K\left(\mathrm{alt}\right)}\left(t-{P}_{6}\right)}{{\eta }_{M\left(\mathrm{ini}\right)}}\left(\frac{1}{3{B}_{i}}-\frac{1}{{z}_{i}}\right)+\frac{-\frac{{P}_{5}}{{P}_{4\left(i\right)}}+{P}_{7}}{{G}_{K\left(\mathrm{ini}\right)}\left({z}_{i}+\frac{1}{{T}_{K\left(\mathrm{ini}\right)}}\right)}+\frac{1}{3{B}_{i}}\left({P}_{6}\left(\frac{1}{{G}_{M\left(\mathrm{ini}\right)}}+\frac{1}{{G}_{K\left(\mathrm{ini}\right)}}\right)-\frac{{P}_{7}}{{G}_{K\left(\mathrm{ini}\right)}}\right)+\frac{\alpha {c}_{v\left(\mathrm{alt}\right)}}{1-{c}_{v\left(\mathrm{alt}\right)}}\left({P}_{1}\left(\frac{{P}_{5}}{{P}_{4\left(i\right)}\left(m+{z}_{i}\right)}+{P}_{8}\left(\frac{1}{3{B}_{i}}-\frac{1}{m+{z}_{i}}\right)\right)+\frac{1}{{z}_{i}m{\eta }_{M\left(\mathrm{alt}\right)}}\left(\frac{{P}_{5}}{{P}_{4\left(i\right)}}-{P}_{6}\right)+{P}_{3\left(i\right)}\left(t{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}-\frac{{P}_{5}}{{P}_{4\left(i\right)}}\right) +\frac{1}{3{B}_{i}}\left(\frac{{P}_{6}}{m{\eta }_{M\left(\mathrm{alt}\right)}}-t{P}_{3\left(i\right)}{P}_{4\left(i\right)}{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}\right)\right)\right)\right],$$

(A17b)

$${P}_{5}={e}^{{z}_{i}t}-{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}},$$

(A17c)

$${P}_{6}={T}_{K\left(\mathrm{alt}\right)}\left(1-{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}\right),$$

(A17d)

$${P}_{7}=\frac{{e}^{-\frac{t}{{T}_{K\left(\mathrm{ini}\right)}}}-{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}}{\frac{1}{{T}_{K\left(\mathrm{alt}\right)}}-\frac{1}{{T}_{K\left(\mathrm{ini}\right)}}},$$

(A17e)

$${P}_{8}=\frac{{e}^{-mt}-{e}^{-\frac{t}{{T}_{K\left(\mathrm{alt}\right)}}}}{\frac{1}{{T}_{K\left(\mathrm{alt}\right)}}-m}.$$

(A17f)

Also, the value of $\underset{0}{\overset{t}{\int }}{\sigma }_{r\left({R}_{0}\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau$ was calculated in Eq. A5.

Appendix B: Solving the Integral Equations Using Numerical Method

Finding a closed-form solution for a system of integral equations may be too difficult. Instead, it is possible to replace integrals by finite sums, and then approximate the solution.

Equation 20 can be written as Eq. B1 which is the linear Volterra integral equation of the second kind (Polyanin and Manzhirov 2008).

$$y\left(t\right)=f\left(t\right)+\underset{{t}_{0}}{\overset{t}{\int }}{K}^{\left(1\right)}\left(t,\tau \right)y\left(\tau \right)d\tau .$$

(B1)

If ${t}_{i}$ ($i=1,\dots ,n$) are the abscissas of the points of the integration interval $[{t}_{0},{t}^{*}]$, and ${A}_{ii}$ ($i=1,\dots ,n$) are numerical coefficient, for the trapezoidal rule, it can be written:

$${A}_{i1}={A}_{ii}=\frac{\Delta t}{2}, {A}_{i2}=\dots ={A}_{i,i-1}=\Delta t, i=2,\dots ,n,$$

(B2a)

$${t}_{i}={t}_{0}+\left(i-1\right)\Delta t, \Delta t=\frac{{t}^{*}-{t}_{0}}{n-1}, i=1,\dots ,n.$$

(B2b)

For $t={t}_{i}$, Eq. B1 can be written as:

$$y\left({t}_{i}\right)=f\left({t}_{i}\right)+\sum_{j=1}^{i}{A}_{ij}{K}^{\left(1\right)}\left({t}_{i},{t}_{j}\right)y\left({t}_{j}\right),$$

(B3)

or

$${y}_{1}={f}_{1}, {y}_{i}={f}_{i}+\sum_{j=1}^{i}{A}_{ij}{K}_{ ij}^{\left(1\right)}{y}_{j}, i=2,\dots ,n.$$

(B4)

In which $y\left({t}_{i}\right)={y}_{i}$, ${K}^{\left(1\right)}\left({t}_{i},{t}_{j}\right)={K}_{ ij}^{\left(1\right)}$, and $f\left({t}_{i}\right)={f}_{i}$.

Equation B4 can be simplified to

$${y}_{1}={f}_{1}, {y}_{i}=\frac{{f}_{i}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(1\right)}{y}_{j}}{1-{A}_{ii}{K}_{ii}^{\left(1\right)}}, i=2,\dots ,n.$$

(B5)

However, as two unknown parameters exist in Eq. 20 (${\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(2\right)}\left(t\right)$ and ${q}_{1}\left(t\right)$), Eq. B5 can be modified slightly according to the above procedure. Thus, it can be written:

$${y}_{1}={f}_{1}, {y}_{i}=\frac{{u}_{i}{a}^{\left(1\right)}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(2\right)}{u}_{j}+{Q}_{i}^{\left(1\right)}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(1\right)}{y}_{j}}{1-{A}_{ii}{K}_{ii}^{\left(1\right)}}, i=2,\dots ,n,$$

(B6)

in which

$${y}_{i}={\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(2\right)}\left(t\right),$$

(B7a)

$${u}_{i}={q}_{1}\left(t\right),$$

(B7b)

$${K}_{ij}^{\left(1\right)}=-\left(\frac{1}{{T}_{M\left(\mathrm{alt}\right)}}+\frac{{G}_{M\left(\mathrm{alt}\right)}}{{\eta }_{K\left(\mathrm{alt}\right)}}{e}^{-\frac{t-\tau }{{T}_{K\left(\mathrm{alt}\right)}}}\right),$$

(B7c)

$${K}_{ij}^{\left(2\right)}=-{K}_{ij}^{\left(1\right)},$$

(B7d)

$${Q}_{i}^{\left(1\right)}={W}_{1}{u}_{r}\left({R}_{0},{t}_{0}\right)+{G}_{M\left(\mathrm{alt}\right)}\left[\underset{0}{\overset{t}{\int }}\alpha {P}_{0}{e}^{-m\tau }{H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau -\underset{0}{\overset{{t}_{0}}{\int }}{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau \right],$$

(B7e)

$${a}^{\left(1\right)}=1+\frac{{W}_{1}{R}_{0}}{{k}_{s}}+{A}_{ii}\left(\frac{1}{{T}_{M\left(\mathrm{alt}\right)}}+\frac{{G}_{M\left(\mathrm{alt}\right)}}{{\eta }_{K\left(\mathrm{alt}\right)}}\right),$$

(B7f)

$${T}_{M\left(\mathrm{alt}\right)}=\frac{{\eta }_{M\left(\mathrm{alt}\right)}}{{G}_{M\left(\mathrm{alt}\right)}}.$$

(B7g)

Similarly, Eq. 25 can be written as

$${y}_{1}={f}_{1}, {y}_{i}=\frac{{u}_{i}{a}^{\left(2\right)}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(4\right)}{u}_{j}+{Q}_{i}^{\left(2\right)}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(3\right)}{y}_{j}}{1-{A}_{ii}{K}_{ii}^{\left(3\right)}}, i=2,\dots ,n,$$

(B8)

where

$${K}_{ij}^{\left(3\right)}=-\frac{1}{{W}_{2}}\left(\frac{1}{{\eta }_{M\left(\mathrm{alt}\right)}}+\frac{{e}^{-\frac{t-\tau }{{T}_{K\left(\mathrm{alt}\right)}}}}{{\eta }_{K\left(\mathrm{alt}\right)}}+\frac{1-{c}_{v\left(\mathrm{alt}\right)}}{{c}_{v\left(\mathrm{alt}\right)}}\left(\frac{1}{{\eta }_{M\left(\mathrm{ini}\right)}}+\frac{{e}^{-\frac{t-\tau }{{T}_{K\left(\mathrm{ini}\right)}}}}{{\eta }_{K\left(\mathrm{ini}\right)}}\right)\right),$$

(B9a)

$${K}_{ij}^{\left(4\right)}=-\frac{{K}_{ij}^{\left(1\right)}}{{G}_{M\left(\mathrm{alt}\right)}{W}_{2}},$$

(B9b)

$${Q}_{i}^{\left(2\right)}=\frac{1}{{W}_{2}}\left(\frac{1-{c}_{v\left(\mathrm{alt}\right)}}{{c}_{v\left(\mathrm{alt}\right)}}\left[\underset{0}{\overset{t}{\int }}{P}_{0}{H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)d\tau -\underset{0}{\overset{{t}_{0}}{\int }}{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right){H}_{\left(\mathrm{ini}\right)}\left(t-\tau \right)d\tau \right]+\underset{0}{\overset{t}{\int }}\alpha {P}_{0}{e}^{-m\tau }{H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau -\underset{0}{\overset{{t}_{0}}{\int }}{\sigma }_{r\left({R}_{\mathrm{alt}}\right)}^{\left(1\right)}\left(\tau \right){H}_{\left(\mathrm{alt}\right)}\left(t-\tau \right)d\tau \right),$$

(B9c)

$${a}^{\left(2\right)}=\frac{1}{{W}_{2}}\left(\frac{1}{{G}_{M\left(\mathrm{alt}\right)}}+{A}_{ii}\left(\frac{1}{{\eta }_{M\left(\mathrm{alt}\right)}}+\frac{1}{{\eta }_{K\left(\mathrm{alt}\right)}}\right)\right),$$

(B9d)

For $i=2,\dots ,n$, combining Eqs. B6 and B8 lead:

$${u}_{i}=\left(\frac{\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(4\right)}{u}_{j}+{Q}_{i}^{\left(2\right)}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(3\right)}{y}_{j}}{1-{A}_{ii}{K}_{ii}^{\left(3\right)}}-\frac{\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(2\right)}{u}_{j}+{Q}_{i}^{\left(1\right)}+\sum_{j=1}^{i-1}{A}_{ij}{K}_{ij}^{\left(1\right)}{y}_{j}}{1-{A}_{ii}{K}_{ii}^{\left(1\right)}}\right)\left(\frac{1}{\frac{{a}^{\left(1\right)}}{1-{A}_{ii}{K}_{ii}^{\left(1\right)}}-\frac{{a}^{\left(2\right)}}{1-{A}_{ii}{K}_{ii}^{\left(3\right)}}}\right).$$

(B10)