Skip to main content
SpringerLink
Log in

AC magnetohydrodynamic slip flow in microchannel with sinusoidal roughness

  • Technical Paper
  • Published:
Microsystem Technologies Aims and scope Submit manuscript

Abstract

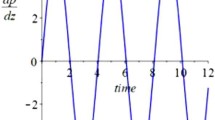
Perturbation solutions for the velocity and electric potential of a time periodic magnetohydrodynamic slip flow in a microchannel with sinusoidal wall corrugations are obtained using perturbation method. The effects of wall corrugations, slip length, Hartmann number and the frequency of the electric potential on the flow are analyzed theoretically and graphically. The results show that velocity and electric potential are significantly disturbed by wall roughness and that there exists a phase lag between the velocity and the electric potential. The velocity profile is characterized by the ratio of momentum diffusion time scale to the period of the applied electric field. The phase lag increases with frequency, slip length and decreases with Hartmann number, the wavenumber and phase difference of the wall corrugations. However, for a sufficiently small frequency, the phase lag is almost nonexistent. The effect of the phase difference of the wall corrugations on the phase lag becomes unimportant when the wavenumber is larger than 2. The velocity amplitude increases with slip length and decreases with frequency, wavenumber and phase difference. However, the phase difference becomes unimportant for sufficiently large wavenumber. When the frequency is large enough, the velocity amplitude is not influenced by slip length.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Abdullah M, Duwairi HM (2008) Thermal and flow analysis of two-dimensional fully developed flow in an AC magneto-hydrodynamic micropump. Microsyst Technol 14(8):1117–1123

    Article  Google Scholar 

  • Akyildiz FT, Siginer DA (2011) Fully developed laminar slip and no-slip flow in rough microtubes. Z Angew Math Phys (ZAMP) 62(4):741–748

    Article  MathSciNet  MATH  Google Scholar 

  • Andrade JS, Henriquea EAA, Almeidaa MP, Costa MHAS (2004) Heat transport through rough channels. Phys A 339:296–310

    Article  Google Scholar 

  • Buren M, Jian Y (2015) Electromagnetohydrodynamic (EMHD) flow between two transversely wavy microparallel plates. Electrophoresis 36(14):1539–1548

    Article  Google Scholar 

  • Buren M, Jian Y, Chang L (2014) Electromagnetohydrodynamic flow through a microparallel channel with corrugated walls. J Phys D Appl Phys 47(42):425501

    Article  Google Scholar 

  • Chen CK, Cho CC (2007) Electrokinetically-driven flow mixing in microchannels with wavy surface. J Colloid Interf Sci 312(2):470–480

    Article  Google Scholar 

  • Chu WKH (1996) Stokes slip flow between corrugated walls. Z Angew Math Phys (ZAMP) 47(4):591–599

    Article  MATH  Google Scholar 

  • Chun MS, Lee S (2005) Flow imaging of dilute colloidal suspension in PDMS-based microfluidic chip using fluorescence microscopy. Colloids Surfaces A Physicochem Eng Aspects 267(1):86–94

    Article  Google Scholar 

  • Davidson PA (2001) An introduction to magnetohydrodynamics. Cambridge University Press, Cambridge, UK

    Book  MATH  Google Scholar 

  • Duwairi H, Abdullah M (2007) Thermal and flow analysis of a magneto-hydrodynamic micropump. Microsyst Technol 13(1):33–39

    Article  Google Scholar 

  • Eijkel JCT, Dalton C, Hayden CJ, Burt JPH, Manz A (2003) A circular ac magnetohydrodynamic micropump for chromatographic applications. Sensor Actuat B: Chem 92(1):215–221

    Article  Google Scholar 

  • Erickson D, Li D (2003) Analysis of alternating current electroosmotic flows in a rectangular microchannel. Langmuir 19(13):5421–5430

    Article  Google Scholar 

  • Ibáñez G, Cuevas S, de Haro ML (2002) Optimization analysis of an alternate magnetohydrodynamic generator. Energ Convers Manage 43(14):1757–1771

    Article  Google Scholar 

  • Jang J, Lee SS (2000) Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sensor Actuat A Phys 80(1):84–89

    Article  Google Scholar 

  • Kiyasatfar M, Pourmahmoud N (2016) Laminar MHD flow and heat transfer of power-law fluids in square microchannels. Int J Therm Sci 99:26–35

    Article  Google Scholar 

  • Laser DJ, Santiago JG (2004) A review of micropumps. J Micromech Microeng 14(6):R35–R64

    Article  Google Scholar 

  • Leal LG (2007) Advanced transport phenomena: fluid mechanics and convective transport processes. Cambridge University Press, UK

    Book  MATH  Google Scholar 

  • Lemoff AV, Lee AP (2000) An AC magnetohydrodynamic micropump. Sensor Actuat B: Chem. 63(3):178–185

    Article  Google Scholar 

  • Lemoff AV, Lee AP (2003) An AC magnetohydrodynamic microfluidic switch for micro total analysis systems. Biomed Microdevices 5(1):55–60

    Article  Google Scholar 

  • Li L, Mo J, Li Z (2014) Flow and slip transition in nanochannels. Phys Rev E 90(3):033003

    Article  Google Scholar 

  • Moghaddam S (2012) Analytical solution of MHD micropump with circular channel. Int J Appl Electrom Mech 40(4):309–322

    MathSciNet  Google Scholar 

  • Müller U, Bühler L (2001) Magnetofluiddynamics in channels and containers. Springer-Verlag Berlin Heidelberg, New York

    Book  Google Scholar 

  • Ngoma GD, Erchiqui F (2007) Heat flux and slip effects on liquid flow in a microchannel. Int J Therm Sci 46(11):1076–1083

    Article  Google Scholar 

  • Nishimura T, Matsune S (1996) Mass transfer enhancement in a sinusoidal wavy channel for pulsatile flow. Heat Mass Transfer 32(1–2):65–72

    Article  Google Scholar 

  • Pamme N (2006) Magnetism and microfluidics. Lab Chip 6(1):24–38

    Article  Google Scholar 

  • Parsa MK, Hormozi F (2014) Experimental and CFD modeling of fluid mixing in sinusoidal microchannels with different phase shift between side walls. J Micromech Microeng 24(6):065018

    Article  Google Scholar 

  • Qian S, Bau HH (2009) Magneto-hydrodynamics based microfluidics. Mech Res Commun 36(1):10–21

    Article  MATH  Google Scholar 

  • Qin M, Bau HH (2011) When MHD-based microfluidics is equivalent to pressure-driven flow. Microfluids Nanofluids 10(2):287–300

    Article  Google Scholar 

  • Reddy PDS, Bandyopadhyay D, Joo SW, Sharma A, Qian S (2011) Parametric study on instabilities in a two-layer electromagnetohydrodynamic channel flow confined between two parallel electrodes. Phys Rev E 83(3):036313

    Article  Google Scholar 

  • Ritchie W (1832) Experimental researches in voltaic electricity and electro-magnetism. Phil Trans R Soc Lond 122:279–298

    Article  Google Scholar 

  • Rivero M, Cuevas S (2012) Analysis of the slip condition in magnetohydrodynamic (MHD) micropumps. Sensor Actuat B: Chem 166–167:884–892

    Article  Google Scholar 

  • Sahore V, Fritsch I (2015) Microfluidic rotational flow generated by redox-magnetohydrodynamics (MHD) under laminar conditions using concentric disk and ring microelectrodes. Microfluid Nanofluid 18(2):159–166

    Article  Google Scholar 

  • Sarkar S, Ganguly S (2015) Fully developed thermal transport in combined pressure and electroosmotically driven flow of nanofluid in a microchannel under the effect of a magnetic field. Microfluid Nanofluid 18(4):623–636

    Article  Google Scholar 

  • Sheikholeslami M, Gorji-Bandpy M, Vajravelu K (2015) Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3-water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder. Int J Heat Mass Transfer 80:16–25

    Article  Google Scholar 

  • Shit GC, Mondal A, Sinha A, Kundu PK (2016) Electro-osmotically driven MHD flow and heat transfer in microchannel. Phys A 449:437–454

    Article  MathSciNet  Google Scholar 

  • Shojaeian M, Shojaee SMN (2013) Viscous dissipation effect on heat transfer characteristics of mixed electromagnetic/pressure driven liquid flows inside micropumps. Korean J Chem Eng 30(4):823–830

    Article  Google Scholar 

  • Shojaeian M, Shojaeian M (2012) Analytical solution of mixed electromagnetic/pressure driven gaseous flows in microchannels. Microfluid Nanofluid 12(1–4):553–564

    Article  Google Scholar 

  • Si D, Jian Y (2015) Electromagnetohydrodynamic (EMHD) micropump of Jeffrey fluids through two parallel microchannels with corrugated walls. J Phys D Appl Phys 48(8):085501

    Article  Google Scholar 

  • Tretheway DC, Meinhart CD (2002) Apparent fluid slip at hydrophobic microchannel walls. Phys Fluids 14(3):L9–L12

    Article  Google Scholar 

  • Wang CY (1979) On Stokes flow between corrugated plates. J Appl Mech 46(2):462–464

    Article  MATH  Google Scholar 

  • Wang PJ, Chang CY, Chang ML (2004) Simulation of two-dimensional fully developed laminar flow for a magneto-hydrodynamic (MHD) pump. Biosens Bioelectron 20(1):115–121

    Article  MathSciNet  Google Scholar 

  • Wen CY, Yeh CP, Tsai CH, Fu LM (2009) Rapid magnetic microfluidic mixer utilizing AC electromagnetic field. Electrophoresis 30(24):4179–4186

    Article  Google Scholar 

  • Xia Z, Mei R, Sheplak M, Fan ZH (2009) Electroosmotically driven creeping flows in a wavy microchannel. Microfluids Nanofluids 6(1):37–52

    Article  Google Scholar 

  • Yang J, Kwok DY (2003) Microfluid flow in circular microchannel with electrokinetic effect and Navier’s slip condition. Langmuir 19(4):1047–1053

    Article  Google Scholar 

  • Zhao G, Jian Y, Chang L, Buren M (2015) Magnetohydrodynamic flow of generalized Maxwell fluids in a rectangular micropump under an AC electric field. J Magn Magn Mater 387:111–117

    Article  Google Scholar 

  • Zhong J, Yi M, Bau HH (2002) Magneto hydrodynamic (MHD) pump fabricated with ceramic tapes. Sensor Actuat A Phys 96(1):59–66

    Article  Google Scholar 

Download references

Acknowledgments

The work was supported by the National Natural Science Foundation of China (Grant Nos. 11472140, 11562014), the Inner Mongolia Grassland Talent (Grant No. 12000- 12102013) and the Natural Science Foundation of Inner Mongolia Autonomous Region of china (Grant Nos. 2016MS0106, 2015MS0110, 2015MS0113).

Author information

Authors and Affiliations

  1. School of Mathematical Science, Inner Mongolia University, Hohhot, China

    Mandula Buren, Yongjun Jian, Long Chang, Quansheng Liu & Guangpu Zhao

  2. School of Mathematics and Statistics, Chifeng University, Chifeng, China

    Mandula Buren

  3. School of Mathematics and Statistics, Inner Mongolia University of Finance and Economics, Hohhot, China

    Long Chang

Authors
  1. Mandula Buren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongjun Jian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Long Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Quansheng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guangpu Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yongjun Jian.

Appendices

Appendix A: Coefficients of the O(ε) problem

$$\begin{aligned} A_{11} & = \frac{{[1 - \cos (\theta )]\frac{{{\text{d}}\psi_{0} }}{{{\text{d}}y}}}}{2\sinh (k)},\;B_{11} = \frac{{[1 + \cos (\theta )]\frac{{{\text{d}}\psi_{0} }}{{{\text{d}}y}}}}{2\cosh (k)},\;\\ &A_{12} = \frac{{\sin (\theta )\frac{{{\text{d}}\psi_{0} }}{{{\text{d}}y}}}}{2\sinh (k)},\;B_{12} = \frac{{ - \sin (\theta )\frac{{{\text{d}}\psi_{0} }}{{{\text{d}}y}}}}{2\cosh (k)}, \\ C_{11} & = \frac{{f_{1u} + f_{1l} }}{{2[\cosh (\alpha_{1} ) + \alpha_{1} \beta \sinh (\alpha_{1} )]}},\;D_{11} = \frac{{f_{1u} - f_{1l} }}{{2[\sinh (\alpha_{1} ) + \alpha_{1} \beta \cosh (\alpha_{1} )]}}, \\ C_{12} & = \frac{{g_{1u} + g_{1l} }}{{2[\cosh (\alpha_{1} ) + \alpha_{1} \beta \sinh (\alpha_{1} )]}},\;D_{12} = \frac{{g_{1u} - g_{1l} }}{{2[\sinh (\alpha_{1} ) + \alpha_{1} \beta \cosh (\alpha_{1} )]}}, \\ \end{aligned}$$
$$\begin{aligned} f_{1u} & = \frac{HaSk}{{Ha^{2} + i\varOmega }}\left[ {\psi_{12} |_{z = 1} + \left. {\beta \frac{{{\text{d}}\psi_{12} }}{{{\text{d}}z}}} \right|_{z = 1} } \right], \\ f_{1l} & = \frac{HaSk}{{Ha^{2} + i\varOmega }}\left( {\psi_{12} |_{z = - 1} - \beta \frac{{{\text{d}}\psi_{12} }}{{{\text{d}}z}}|_{z = - 1} } \right) \\ & \quad + \sin (\theta )\left( {\left. {\beta \frac{{{\text{d}}^{2} U_{0} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}U_{0} }}{{{\text{d}}z}}} \right|_{z = - 1} } \right), \\ \end{aligned}$$
$$g_{1u} = - \frac{HaSk}{{Ha^{2} + i\varOmega }}\left( {\psi_{11} |_{z = 1} + \left. {\beta \frac{{{\text{d}}\psi_{11} }}{{{\text{d}}z}}} \right|_{z = 1} } \right)\, - \left( {\left. {\beta \frac{{{\text{d}}^{2} U_{0} }}{{{\text{d}}z^{2} }}} \right|_{z = 1} + \left. {\frac{{{\text{d}}U_{0} }}{{{\text{d}}z}}} \right|_{z = 1} } \right),$$
$$g_{1l} = - \frac{HaSk}{{Ha^{2} + i\varOmega }}\left( {\psi_{11} |_{z = - 1} - \left. {\beta \frac{{{\text{d}}\psi_{11} }}{{{\text{d}}z}}} \right|_{z = - 1} } \right) + \cos (\theta )\left( {\left. {\beta \frac{{{\text{d}}^{2} U_{0} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}U_{0} }}{{{\text{d}}z}}} \right|_{z = - 1} } \right).$$

Appendix B: Coefficients of the O(ε 2) problem

$$\begin{aligned} A_{21} = \frac{{\left. {\frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = 1} - \left. {\frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = - 1} }}{4k\sinh (2k)},\;B_{21} = \frac{{\left. {\frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = 1} + \left. {\frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = - 1} }}{4k\cosh (2k)}, \hfill \\ A_{22} = \frac{{\left. {\frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = 1} - \left. {\frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = - 1} }}{4k\sinh (2k)},\;B_{22} = \frac{{\left. {\frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = 1} + \left. {\frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = - 1} }}{4k\cosh (2k)}, \hfill \\ \end{aligned}$$

where

$$\left. {\frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = 1} = k^{2} \psi_{12} |_{z = 1} ,\;\left. {\frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = - 1} = k^{2} \cos (\theta )\psi_{12} |_{z = - 1} - k^{2} \sin (\theta )\psi_{11} |_{z = - 1},$$
$$\left. {\frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = 1} = - k^{2} \psi_{11} |_{z = 1} ,\;\left. {\frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = - 1} = - k^{2} \cos (\theta )\psi_{11} |_{z = - 1} - k^{2} \sin (\theta )\psi_{12} |_{z = - 1} .$$
$$C_{21} = \frac{{f_{2u} + f_{2l} }}{{2[\cosh (\alpha_{2} ) + \alpha_{2} \beta \sinh (\alpha_{2} )]}},\;D_{21} = \frac{{f_{2u} - f_{2l} }}{{2[\sinh (\alpha_{2} ) + \alpha_{2} \beta \cosh (\alpha_{2} )]}},$$
$$\begin{aligned} f_{2u} & = \frac{1}{2}\left[ {\left. {\beta \frac{{{\text{d}}^{2} U_{12} }}{{{\text{d}}z^{2} }}} \right|_{z = 1} + \left. {\frac{{{\text{d}}U_{12} }}{{{\text{d}}z}}} \right|_{z = 1} + \beta k^{2} U_{12} |_{z = 1} + \frac{1}{2}\left( {\left. {\beta \frac{{{\text{d}}^{ 3} U_{0} }}{{{\text{d}}z^{3} }}} \right|_{z = 1} + \left. {\frac{{{\text{d}}^{ 2} U_{0} }}{{{\text{d}}z^{2} }}} \right|_{z = 1}} \right.} \right. \\ & \quad \left.+\left.\left.\beta k^2\frac{\text{d}U_0}{\text{d}z}\right|_{z=1}\right)\right]+ \frac{2kHaS}{{Ha^{2} + i\varOmega }}\left( {\psi_{22} |_{z = 1} + \left. {\beta \frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}} \right|_{z = 1} } \right), \\ \end{aligned}$$
$$\begin{aligned} f_{2l} & = \frac{1}{2}\left[\sin (\theta )\left(\beta \left.\frac{{{\text{d}}^{ 2} U_{11} }}{{{\text{d}}z^{2} }}\right|_{z = - 1} \left.- \frac{{{\text{d}}U_{11} }}{{{\text{d}}z}}\right|_{z = - 1} + \left.\beta k^{2} U_{11} \right|_{z = - 1} \right) - \cos (\theta )\left(\left.\beta \frac{{{\text{d}}^{ 2} U_{12} }}{{{\text{d}}z^{2} }}\right|_{z = - 1} \right.\right.\\ & \quad\left.\left.\left.- \frac{{{\text{d}}U_{12} }}{{{\text{d}}z}}\right|_{z = - 1} + \left.\beta k^{2} U_{12} \right|_{z = - 1}\right)\right]+ \frac{2kHaS}{{Ha^{2} + i\varOmega }}\left(\left.\psi_{22} \right|_{z = - 1} -\left. \beta \frac{{{\text{d}}\psi_{22} }}{{{\text{d}}z}}\right|_{z = - 1} \right), \\ \end{aligned}$$
$$C_{22} = \frac{{g_{2u} + g_{2l} }}{{2[\cosh (\alpha_{2} ) + \alpha_{2} \beta \sinh (\alpha_{2} )]}},\;D_{22} = \frac{{g_{2u} - g_{2l} }}{{2[\sinh (\alpha_{2} ) + \alpha_{2} \beta \cosh (\alpha_{2} )]}},$$
$$\begin{aligned} g_{2u} & = - \frac{1}{2}\left( {\left. {\beta \frac{{{\text{d}}^{ 2} U_{11} }}{{{\text{d}}z^{2} }}} \right|_{z = 1} + \left. {\frac{{{\text{d}}U_{11} }}{{{\text{d}}z}}} \right|_{z = 1} + \beta k^{2} U_{11} |_{z = 1} } \right) \\ & \quad - \frac{2kHaS}{{Ha^{2} + i\varOmega }}\left( {\psi_{21} |_{z = 1} + \left. \beta \frac{\text{d}\psi_{21}}{\text{dz}} \right|_{z = 1} } \right), \\ \end{aligned}$$
$$\begin{aligned} g_{2l} & = \frac{1}{2}\left[ {\cos (\theta )\left( {\left. {\beta \frac{{{\text{d}}^{ 2} U_{11} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}U_{11} }}{{{\text{d}}z}}} \right|_{z = - 1} + \beta k^{2} U_{11} |_{z = - 1} } \right)} \right. \\ & \quad + \sin (\theta )\left( {\left. {\beta \frac{{{\text{d}}^{ 2} U_{12} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}U_{12} }}{{{\text{d}}z}}} \right|_{z = - 1} + \beta k^{ 2} U_{ 1 2} |_{z = - 1} } \right) \\ & \quad \left. { - \frac{1}{2}\sin (2\theta )\left( {\left. { - \beta \frac{{{\text{d}}^{ 3} U_{0} }}{{{\text{d}}z^{3} }}} \right|_{z = - 1} + \left. {\frac{{{\text{d}}^{ 2} U_{0} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\beta k^{2} \frac{{{\text{d}}U_{0} }}{{{\text{d}}z}}} \right|_{z = - 1} } \right)} \right] \\ & \quad - \frac{2kHaS}{{Ha^{2} + i\varOmega }}\left( {\psi_{21} |_{z = - 1} - \left. {\beta \frac{{{\text{d}}\psi_{21} }}{{{\text{d}}z}}} \right|_{z = - 1} } \right), \\ \end{aligned}$$
$$C_{23} = \frac{{h_{2u} + h_{2l} }}{{2[\cosh (\alpha_{0} ) + \alpha_{0} \beta \sinh (\alpha_{0} )]}},\;D_{23} = \frac{{h_{2u} - h_{2l} }}{{2[\sinh (\alpha_{0} ) + \alpha_{0} \beta \cosh (\alpha_{0} )]}},$$
$$\begin{aligned} h_{2u} & = \frac{1}{2}\left[ {\frac{1}{2}\left( { - \beta \frac{{{\text{d}}^{ 3} U_{0} }}{{{\text{d}}z^{3} }}|_{z = 1} - \frac{{{\text{d}}^{ 2} U_{0} }}{{{\text{d}}z^{2} }}|_{z = 1} + \beta k^{2} \frac{{{\text{d}}U_{0} }}{{{\text{d}}z}}|_{z = 1} } \right)} \right. \\ & \quad {\left. { - \left. {\beta \frac{{{\text{d}}^{ 2} U_{12} }}{{{\text{d}}z^{2} }}} \right|_{z = 1} - \left. {\frac{{{\text{d}}U_{12} }}{{{\text{d}}z}}} \right|_{z = 1} + \beta k^{2} U_{12} |_{z = 1} } \right]}, \\ \end{aligned}$$
$$\begin{aligned} h_{2l} & = \frac{1}{2}\left[ {\sin (\theta )\left( {\left. {\beta \frac{{{\text{d}}^{ 2} U_{11} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}U_{11} }}{{{\text{d}}z}}} \right|_{z = - 1} - \beta k^{2} U_{11} |_{z = - 1} } \right)} \right. \\ & \quad + \cos (\theta )\left( {\left. {\beta \frac{{{\text{d}}^{2} U_{12} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}U_{12} }}{{{\text{d}}z}}} \right|_{z = - 1} - \beta k^{2} U_{12} |_{z = - 1} } \right) \\ & \quad + \frac{1}{2}\left.\left( {\left. {\beta \frac{{{\text{d}}^{ 3} U_{0} }}{{{\text{d}}z^{3} }}} \right|_{z = - 1} - \left. {\frac{{{\text{d}}^{ 2} U_{0} }}{{{\text{d}}z^{2} }}} \right|_{z = - 1} - \left. {\beta k^{2} \frac{{{\text{d}}U_{0} }}{{{\text{d}}z}}} \right|_{z = - 1} } \right)\right]. \\ \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buren, M., Jian, Y., Chang, L. et al. AC magnetohydrodynamic slip flow in microchannel with sinusoidal roughness. Microsyst Technol 23, 3347–3359 (2017). https://doi.org/10.1007/s00542-016-3125-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00542-016-3125-7

Keywords

Search

Navigation