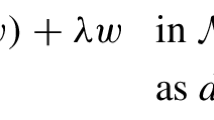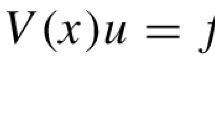Abstract
Let \({(\mathcal{M}, \tilde{g})}\) be an N-dimensional smooth compact Riemannian manifold. We consider the problem \({\varepsilon^2 \triangle_{\tilde{g}} \tilde{u} + V(\tilde{z})\tilde{u}(1-\tilde{u}^2)=0\; {\rm in}\; \mathcal{M}}\), where \({\varepsilon > 0}\) is a small parameter and V is a positive, smooth function in \({\mathcal{M}}\). Let \({\kappa \subset \mathcal{M}}\) be an (N − 1)-dimensional smooth submanifold that divides \({\mathcal{M}}\) into two disjoint components \({\mathcal{M}_{\pm}}\). We assume κ is stationary and non-degenerate relative to the weighted area functional \({\int_{\kappa}V^{\frac{1}{2}}}\). For each integer m ≥ 2, we prove the existence of a sequence \({\varepsilon = \varepsilon_\ell \rightarrow 0}\), and two opposite directional solutions with m-transition layers near κ, whose mutual distance is \({{\rm O}(\varepsilon | \log \varepsilon | )}\). Moreover, the interaction between neighboring layers is governed by a type of Jacobi–Toda system.
Similar content being viewed by others
References
Alikakos N., Chen X., Fusco G.: Motion of a droplet by surface tension along the boundary. Calc. Var. PDE 11, 233–306 (2000)
Allen S., Cahn J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta. Metall. 27, 1084–1095 (1979)
Bronsard L., Stoth B.: On the existence of high multiplicity interfaces. Math. Res. Lett. 3, 117–131 (1996)
Dancer E.N., Yan S.: multi-layer solutions for an elliptic problem. J. Differ. Equ. 194, 382–405 (2003)
del Pino M., Kowalczyk M., Wei J.: Concentration on curves for nonlinear Schrödinger equations. Commun. Pure Appl. Math. 70, 113–146 (2007)
del Pino M., Kowalczyk M., Wei J.: The Toda system and clustering interface in the Allen–Cahn equation. Arch. Ration. Mech. Anal. 190(1), 141–187 (2008)
del Pino M., Kowalczyk M., Pacard F., Wei J.: Multiple-end solutions to the Allen–Cahn equation in R 2. J. Funct. Anal. 258(2), 458–503 (2010)
del Pino M., Kowalczyk M., Wei J.: The Jacobi–Toda system and foliated interfaces. Discret. Contin. Dyn. Syst. A 28(3), 975–1006 (2010)
del Pino M., Kowalczyk M., Wei J., Yang J.: Interface foliation near minimal submanifolds in Riemannian manifolds with positive Ricci curvature. Geom. Funct. Anal. 20(4), 918–957 (2010)
Du Z., Gui C.: Interior layers for an inhomogeneous Allen–Cahn equation. J. Differ. Equ. 249, 215–239 (2010)
Du, Z., Lai, B.: Transition layers for an inhomogeneous Allen–Cahn equation in Riemannian manifolds, submitted
Du Y., Nakashima K.: Morse index of layered solutions to the heterogeneous Allen–Cahn equation. J. Differ. Equ. 238(1), 87–117 (2007)
Flores G., Padilla P.: Higher energy solutions in the theory of phase transitions: a variational approach. J. Differ. Equ. 169, 190–207 (2001)
Kohn R.V., Sternberg P.: Local minimizers and singular perturbations. Proc. R. Soc. Edinb. 11, 69–84 (1989)
Kowalczyk M.: On the existence and Morse index of solutions to the Allen–Cahn equation in two dimensions. Annali di Matematica Pura et Aplicata (4) 184(1), 17–52 (2005)
Mahmoudi F., Mazzeo R., Pacard F.: Constant mean curvature hypersurfaces condensing on a submanifold. Geom. Funct. Anal. 16(4), 924–958 (2006)
Malchiodi A., Montenegro M.: Multidimensional boundary layers for a singularly perturbed Neumann problem. Duke Math. J. 124(1), 105–143 (2004)
Malchiodi A., Wei J.: Boundary interface for the Allen–Cahn equation. J. Fixed Point Theory Appl. 1(2), 305–336 (2007)
Malchiodi A., Ni W.-M., Wei J.: Boundary clustered interfaces for the Allen–Cahn equation. Pac. J. Math. 229(2), 447–468 (2007)
Modica L.: The gradient theory of phase transitions and the minimal interface criterion. Arch. Ration. Mech. Anal. 98, 357–383 (1987)
Nakashima K.: Multi-layered stationary solutions for a spatially inhomogeneous Allen–Cahn equation. J. Differ. Equ. 191, 234–276 (2003)
Nakashima K., Tanaka K.: Clustering layers and boundary layers in spatially inhomogenerous phase transition problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 20(1), 107–143 (2003)
Pacard F., Ritoré M.: From constant mean curvature hypersurfaces to the gradient theory of phase transitions. J. Differ. Geom. 64, 359–423 (2003)
Padilla P., Tonegawa Y.: On the convergence of stable phase transitions. Commun. Pure Appl. Math. 51, 551–579 (1998)
Rabinowitz P.H., Stredulinsky E.: Mixed states for an Allen–Cahn type equation, I. Commun. Pure Appl. Math. 56, 1078–1134 (2003)
Rabinowitz P.H., Stredulinsky E.: Mixed states for an Allen–Cahn type equation, II. Calc. Var. Partial Differ. Equ. 21, 157–207 (2004)
Sternberg P., Zumbrun K.: Connectivity of phase boundaries in strictly convex domains. Arch. Ration. Mech. Anal. 141(4), 375–400 (1998)
Wei J., Yang J.: Toda system and cluster phase transition layers in an inhomogeneous phase transition model. Asymptot. Anal. 69(3–4), 175–218 (2010)
Yang, J., Yang, X.: Clustered interior phase transition layers for an inhomogeneous Allen–Cahn equation on higher dimensional domain, to appear
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Rights and permissions
About this article
Cite this article
Du, Z., Wang, L. Interface foliation for an inhomogeneous Allen–Cahn equation in Riemannian manifolds. Calc. Var. 47, 343–381 (2013). https://doi.org/10.1007/s00526-012-0521-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-012-0521-4