Skip to main content
SpringerLink
Log in

Extended isogeometric analysis of multi-material and multi-physics problems using hierarchical B-splines

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

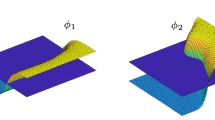
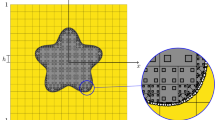
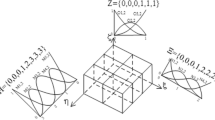
Abstract

This paper presents an immersed, isogeometric finite element framework to predict the response of multi-material, multi-physics problems with complex geometries using locally refined discretizations. To circumvent the need to generate conformal meshes, this work uses an extended finite element method (XFEM) to discretize the governing equations on non-conforming, embedding meshes. A flexible approach to create truncated hierarchical B-splines discretizations is presented. This approach enables the refinement of each state variable field individually to meet field-specific accuracy requirements. To obtain an immersed geometry representation that is consistent across all hierarchically refined B-spline discretizations, the geometry is immersed into a single mesh, the XFEM background mesh, which is constructed from the union of all hierarchical B-spline meshes. An extraction operator is introduced to represent the truncated hierarchical B-spline bases in terms of Lagrange shape functions on the XFEM background mesh without loss of accuracy. The truncated hierarchical B-spline bases are enriched using a generalized Heaviside enrichment strategy to accommodate small geometric features and multi-material problems. The governing equations are augmented by a formulation of the face-oriented ghost stabilization enhanced for locally refined B-spline bases. We present examples for two- and three-dimensional linear elastic and thermo-elastic problems. The numerical results validate the accuracy of our framework. The results also demonstrate the applicability of the proposed framework to large, geometrically complex problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27

Similar content being viewed by others

Notes

  1. Note that the union background mesh is not attained via a set union of the separate hierarchically refined meshes. Instead, elements in this set union that fully contain smaller elements in the set union do not belong to the union background mesh.

References

  1. Annavarapu C, Hautefeuille M, Dolbow JE (2012) A robust Nitsche’s formulation for interface problems. Comput Methods Appl Mech Eng 225–228:44–54. https://doi.org/10.1016/j.cma.2012.03.008

    Article  MathSciNet  MATH  Google Scholar 

  2. Babuška I, Melenk JM (1997) The partition of unity method. Int J Numer Methods Eng 40:727–758. https://doi.org/10.1002/(SICI)1097-0207(19970228)40:4<727::AID-NME86>3.0.CO;2-N

  3. Bazilevs Y, Calo VM, Cottrell JA, Evans JA, Hughes TJ, Lipton S, Scott MA, Sederberg TW (2010) Isogeometric analysis using t-splines. Comput Methods Appl Mech Eng 199:229–263. https://doi.org/10.1016/j.cma.2009.02.036

    Article  MathSciNet  MATH  Google Scholar 

  4. Belytschko T, Black T (1999) Elastic crack growth in finite elements with minimal remashing. Int J Numer Methods Eng 45:601–620

    Article  MATH  Google Scholar 

  5. Belytschko T, Gracie R, Ventura G (2009) A review of extended/generalized finite element methods for material modeling. Model Simul Materials Sci Eng 17:66. https://doi.org/10.1088/0965-0393/17/4/043001

    Article  Google Scholar 

  6. Bracco C, Buffa A, Giannelli C, Vázquez R (2019) Adaptive isogeometric methods with hierarchical splines: an overview. Discrete Continu Dyn Syst Ser A 39:241–262. https://doi.org/10.3934/dcds.2019010

    Article  MathSciNet  MATH  Google Scholar 

  7. Buffa A, Giannelli C (2017) Adaptive isogeometric methods with hierarchical splines: optimality and convergence rates. Math Models Methods Appl Sci 27:2781–2802. https://doi.org/10.1142/S0218202517500580

    Article  MathSciNet  MATH  Google Scholar 

  8. Burman E (2010) La pénalisation fantôme. Comptes Rendus Mathematique 348:1217–1220. https://doi.org/10.1016/j.crma.2010.10.006

    Article  Google Scholar 

  9. Burman E (2012) A penalty-free nonsymmetric Nitsche-type method for the weak imposition of boundary conditions. SIAM J Numer Anal 50:1959–1981. https://doi.org/10.1137/10081784X

    Article  MathSciNet  MATH  Google Scholar 

  10. Burman E, Hansbo P (2014) Fictitious domain methods using cut elements: III. A stabilized Nitsche method for stokes’ problem. ESAIM Math Model Numer Anal 48:859–874. https://doi.org/10.1051/m2an/2013123

    Article  MathSciNet  MATH  Google Scholar 

  11. D’Angella D, Kollmannsberger S, Rank E, Reali A (2018) Multi-level bézier extraction for hierarchical local refinement of isogeometric analysis. Comput Methods Appl Mech Eng 328:147–174. https://doi.org/10.1016/j.cma.2017.08.017

    Article  MATH  Google Scholar 

  12. de Boor C (1972) On calculating with B-splines. J Approx Theory 6:50–62

    Article  MathSciNet  MATH  Google Scholar 

  13. de Prenter F, Verhoosel CV, van Zwieten GJ, van Brummelen EH (2017) Condition number analysis and preconditioning of the finite cell method. Comput Methods Appl Mecha Eng 316:297–327. https://doi.org/10.1016/j.cma.2016.07.006

    Article  MathSciNet  MATH  Google Scholar 

  14. Divi SC, Verhoosel CV, Auricchio F, Reali A, van Brummelen EH (2020) Error-estimate-based adaptive integration for immersed isogeometric analysis. Comput Math Appl 80:2481–2516. https://doi.org/10.1016/j.camwa.2020.03.026

    Article  MathSciNet  MATH  Google Scholar 

  15. Duarte CA, Babusï I, Oden JT (2000) Generalized finite element methods for three-dimensional structural mechanics problems. Comput Struct 77:215–232

    Article  MathSciNet  Google Scholar 

  16. Düster A, Parvizian J, Yang Z, Rank E (2008) The finite cell method for three-dimensional problems of solid mechanics. Comput Methods Appl Mech Eng 197:3768–3782. https://doi.org/10.1016/j.cma.2008.02.036

    Article  MathSciNet  MATH  Google Scholar 

  17. D’Angella D, Zander N, Kollmannsberger S, Frischmann F, Rank E, Schröder A, Reali A (2016) Multi-level hp-adaptivity and explicit error estimation. Adv Model Simul Eng Sci. https://doi.org/10.1186/s40323-016-0085-5

    Article  Google Scholar 

  18. Elfverson D, Larson MG, Larsson K (2018) Cutiga with basis function removal. Adv Model Simul Eng Sci 5:1–19. https://doi.org/10.1186/s40323-018-0099-2

    Article  Google Scholar 

  19. Embar A, Dolbow J, Harari I (2010) Imposing Dirichlet boundary conditions with Nitsche’s method and spline-based finite elements. Int J Numer Methods Eng 83:877–898. https://doi.org/10.1002/nme.2863

    Article  MathSciNet  MATH  Google Scholar 

  20. Evans JA, Bazilevs Y, Babuška I, Hughes TJ (2009) n-widths, sup-infs, and optimality ratios for the k-version of the isogeometric finite element method. Comput Methods Appl Mech Eng 198:1726–1741. https://doi.org/10.1016/j.cma.2009.01.021

    Article  MathSciNet  MATH  Google Scholar 

  21. Garau EM, Vázquez R (2018) Algorithms for the implementation of adaptive isogeometric methods using hierarchical B-splines. Appl Numer Math 123:58–87. https://doi.org/10.1016/j.apnum.2017.08.006

    Article  MathSciNet  MATH  Google Scholar 

  22. Gerstenberger A, Wall WA (2008) An extended finite element method/Lagrange multiplier based approach for fluid–structure interaction. Comput Methods Appl Mech Eng 197:1699–1714. https://doi.org/10.1016/j.cma.2007.07.002

    Article  MathSciNet  MATH  Google Scholar 

  23. Giannelli C, Jüttler B, Speleers H (2012) THB-splines: the truncated basis for hierarchical splines. Comput Aided Geom Des 29:485–498. https://doi.org/10.1016/j.cagd.2012.03.025

    Article  MathSciNet  MATH  Google Scholar 

  24. Giannelli C, Bert J, Speleers H (2014) Strongly stable bases for adaptively refined multilevel spline spaces. Adv Comput Math 40:459–490. https://doi.org/10.1007/s10444-013-9315-2

    Article  MathSciNet  MATH  Google Scholar 

  25. Gunderman D, Weiss K, Evans JA (2021) Spectral mesh-free quadrature for planar regions bounded by rational parametric curves. Comput Aided Des 130:102944. https://doi.org/10.1016/j.cad.2020.102944

    Article  MathSciNet  Google Scholar 

  26. Hughes TJ, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195. https://doi.org/10.1016/j.cma.2004.10.008

    Article  MathSciNet  MATH  Google Scholar 

  27. Höllig K, Reif U, Wipper J (2001) Weighted extended b-spline approximation of Dirichlet problems. SIAM J Numer Anal 39:442–462. https://doi.org/10.1137/s0036142900373208

    Article  MathSciNet  MATH  Google Scholar 

  28. Kourounis D, Fuchs A, Schenk O (2018) Toward the next generation of multiperiod optimal power flow solvers. IEEE Trans Power Syst 33:4005–4014. https://doi.org/10.1109/TPWRS.2017.2789187

    Article  Google Scholar 

  29. Lang C, Makhija D, Doostan A, Maute K (2014) A simple and efficient preconditioning scheme for heaviside enriched XFEM. Comput Mech 54(5):1357–1374. https://doi.org/10.1007/s00466-014-1063-8

    Article  MathSciNet  MATH  Google Scholar 

  30. Makhija D, Maute K (2014) Numerical instabilities in level set topology optimization with the extended finite element method. Struct Multidisc Optim 49:185–197. https://doi.org/10.1007/s00158-013-0982-x

    Article  MathSciNet  Google Scholar 

  31. Marussig B, Hughes TJ (2018) A review of trimming in isogeometric analysis: challenges, data exchange and simulation aspects, vol 25. Springer, Netherlands, p 1183101792209. https://doi.org/10.1007/s11831-017-9220-9

    Book  Google Scholar 

  32. Mittal R, Iaccarino G (2005) Immersed boundary methods. Annu Rev Fluid Mech 37:239–261. https://doi.org/10.1146/annurev.fluid.37.061903.175743

    Article  MathSciNet  MATH  Google Scholar 

  33. Nguyen VP (2012) An introduction to standard and enriched isogeometric analysis through a simple Matlab code isogeometric analysis: a review and computer implementation aspects. Math Comput Simul 117:89–116. https://doi.org/10.1016/j.matcom.2015.05.008

    Article  Google Scholar 

  34. Nitsche J (1971) Über ein variationsprinzip zur lösung von dirichlet-problemen bei verwendung von teilräumen, die keinen randbedingungen unterworfen sind. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 36:9–15. https://doi.org/10.1007/BF02995904

    Article  MathSciNet  MATH  Google Scholar 

  35. Noël L, Schmidt M, Messe C, Evans JA, Maute K (2020) Adaptive level set topology optimization using hierarchical B-splines. Struct Multidiscip Optim 62:1669–1699. https://doi.org/10.1007/s00158-020-02584-6

    Article  MathSciNet  Google Scholar 

  36. Noël L, Schmidt M, Doble K, Evans JA, Maute K (2022) XIGA: an extended isogeometric analysis approach for multi-material problems. Comput Mech. https://doi.org/10.1007/s00466-022-02200-y

    Article  MathSciNet  MATH  Google Scholar 

  37. Parvizian J, Düster A, Rank E (2007) Finite cell method : h- and p-extension for embedded domain problems in solid mechanics. Comput Mech 41:121–133. https://doi.org/10.1007/s00466-007-0173-y

    Article  MathSciNet  MATH  Google Scholar 

  38. Peskin CS (2002) The immersed boundary method. Acta Numer 11:479–517. https://doi.org/10.1017/S0962492902000077

    Article  MathSciNet  MATH  Google Scholar 

  39. Remacle J, Lambrechts J, Seny B (2012) Blossom-quad: a non-uniform quadrilateral mesh generator using a minimum-cost perfect-matching algorithm. International 104:1102–1119. https://doi.org/10.1002/nme

    Article  MathSciNet  MATH  Google Scholar 

  40. Rodgers T (2015) Exploration of process-structure linkages in simulated additive manufacturing microstructures. Harv Dataverse. https://doi.org/10.7910/DVN/KJMK9Z

    Article  Google Scholar 

  41. Saad Y (2003) Iterative methods for sparse linear systems. Soc Ind Appl Math. https://doi.org/10.1137/1.9780898718003

    Article  MATH  Google Scholar 

  42. Schillinger D, Rank E (2011) An unfitted hp-adaptive finite element method based on hierarchical b-splines for interface problems of complex geometry. Comput Methods Appl Mech Eng 200:3358–3380. https://doi.org/10.1016/j.cma.2011.08.002

    Article  MathSciNet  MATH  Google Scholar 

  43. Schillinger D, Ruess M (2015) The finite cell method: a review in the context of higher-order structural analysis of cad and image-based geometric models. Arch Comput Methods Eng 22:391–455. https://doi.org/10.1007/s11831-014-9115-y

    Article  MathSciNet  MATH  Google Scholar 

  44. Schillinger D, Dedè L, Scott MA, Evans JA, Borden MJ, Rank E, Hughes TJR (2012) An isogeometric design-through-analysis methodology based on adaptive hierarchical refinement of NURBS, immersed boundary methods, and T-spline CAD surfaces. Comput Methods Appl Mech Eng 249–252:116–150. https://doi.org/10.1016/j.cma.2012.03.017

    Article  MathSciNet  MATH  Google Scholar 

  45. Schillinger D, Ruthala PK, Nguyen A (2016) Lagrange extraction and projection for nurbs basis functions: a direct link between isogeometric and standard nodal finite element formulations. Int J Numer Methods Eng 66:1102–1119. https://doi.org/10.1002/nme.3279/full

    Article  MathSciNet  Google Scholar 

  46. Shemon ER, Attaway CW (2014) User manual for exodus ii mesh converter. www.anl.gov

  47. Strouboulis T, Copps K, Babuska I (2000) The generalized finite element method: an example of its implementation and illustration of its performance. Int J Numer Methods Eng 47:1401–1417. https://doi.org/10.1002/(SICI)1097-0207

  48. Terada K, Asai M, Yamagishi M (2003) Finite cover method for linear and non-linear analyses of heterogeneous solids. Int J Numer Methods Eng 58:1321–1346. https://doi.org/10.1002/nme.820

    Article  MATH  Google Scholar 

  49. Thiagarajan V, Shapiro V (2016) Adaptively weighted numerical integration in the finite cell method. Comput Methods Appl Mech Eng 311:250–279

    Article  MathSciNet  MATH  Google Scholar 

  50. Verhoosel CV, van Zwieten GJ, van Rietbergen B, de Borst R (2015) Image-based goal-oriented adaptive isogeometric analysis with application to the micro-mechanical modeling of trabecular bone. Comput Methods Appl Mech Eng 284:138–164. https://doi.org/10.1016/j.cma.2014.07.009

    Article  MathSciNet  MATH  Google Scholar 

  51. Villanueva CH, Maute K (2014) Density and level set-XFEM schemes for topology optimization of 3-D structures. Comput Mech 54:133–150. https://doi.org/10.1007/s00466-014-1027-z

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first, second, fourth, and fifth authors acknowledge the support for this work from the Defense Advanced Research Projects Agency (DARPA) under the TRADES program (Agreement HR0011-17-2-0022). The first author acknowledges partial auspice of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 (LLNL-JRNL-842737). The third and fifth authors acknowledge the support of Sandia National Laboratories under PO 2120843. The fourth and fifth authors acknowledge the support of the National Science foundation under Grant 2104106. The opinions and conclusions presented in this paper are those of the authors and do not necessarily reflect the views of the sponsoring organization.

Author information

Authors and Affiliations

  1. Computational Engineering Division, Lawrence Livermore National Laboratory, 7000 East Ave, Livermore, CA, 94550, USA

    Mathias Schmidt

  2. Department of Precision and Microsystems Engineering, Faculty of Mechanical, Maritime and Materials Engineering, Delft University of Technology, Mekelweg 2, 2628 CD, Delft, The Netherlands

    Lise Noël

  3. Department of Aerospace Engineering Sciences, Aerospace Mechanics Research Center, University of Colorado Boulder, 3775 Discovery Dr, Boulder, CO, 80309-0429, USA

    Keenan Doble, John A. Evans & Kurt Maute

Authors
  1. Mathias Schmidt
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lise Noël
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Keenan Doble
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. John A. Evans
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Kurt Maute
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mathias Schmidt.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schmidt, M., Noël, L., Doble, K. et al. Extended isogeometric analysis of multi-material and multi-physics problems using hierarchical B-splines. Comput Mech 71, 1179–1203 (2023). https://doi.org/10.1007/s00466-023-02306-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-023-02306-x

Keywords

Search

Navigation