A generalised multi-scale Peridynamics–DEM framework and its application to rigid–soft particle mixtures

Abstract

The discrete element method (DEM) is the most dominant method for the numerical prediction of dynamic behaviour at grain or particle scale. Nevertheless, due to its discontinuous nature, the DEM is inherently unable to describe microscopic features of individual bodies which can be considered as continuous bodies. To incorporate microscopic features, efficient numerical coupling of the DEM with a continuous method is generally necessary. Thus, a generalised multi-scale PD–DEM framework is developed in this work. In the developed framework, meshfree discretised Peridynamics (PD) is used to describe intra-particle forces within bodies to capture microscopic features. The inter-particle forces of rigid bodies are defined by the DEM whereas a hybrid approach is applied at the PD–DEM interface. In addition, a staggered multi-scale time integration scheme is formulated to allow for an efficient numerical treatment of both methods. Validation examples are presented and the applicability of the developed framework to capture the characteristics mixtures with rigid and deformable bodies is shown.

1 Introduction

In the last decades, the computational mechanics community has gradually grown and various numerical methods have been developed. Thanks to the significant increase in computational resources and efficiency it is now possible to tackle highly complex problems. This involves the coupling of different numerical methods to overcome the drawbacks of individual methods, allowing to capture more complex phenomena. In this work a three-dimensional framework for the efficient numerical treatment of coupled continuous and discontinuous material behaviour is developed. The motivation behind this is the ability to describe the discontinuous dynamics of a particle system, whilst capturing the microscopic features of individual particles by a continuous description. A possible application is the simulation of grain collisions, in which microscopic phenomena of individual grains such as deformability or fragmentation are considered. Real-life examples include the compaction of powders [1], the compaction of powder mixtures [2], the identification of fracture origins in ceramics [3] and the characterisation of particle mixtures with hard and soft grains [4].

In the following, suitable numerical methods have to be picked to develop the desired coupling framework. The most widespread and well-established method applied in computational mechanics is the Finite Element Method (FEM) (e.g. [5,6,7]), which is based on the consideration of continuous media. Within the method, the media is discretised by finite elements and associated nodal points. The degrees of freedom, e.g. displacements or temperature, are only defined and solved for these discrete points within the continua. Up to now, the FEM is the method of choice for most standard solid mechanics applications. However, there are various problems for which the FEM is not applicable. One crucial shortcoming of the classical FEM is its inability to capture fracture and crack propagation. To consider this phenomenon the so-called eXtended Finite Element Method (XFEM) (cf. [8, 9]), can be applied. It is based on the enrichment of ansatzfunctions with discontinuous functions within the FEM. Besides the additional numerical cost, the main disadvantage is that discontinuities are not naturally considered within the method. To overcome this problem Peridynamics (PD) was introduced as an alternative total Lagrangian formulation to classical continuum mechanics [10]. In contrast to classical methods, the underlying equations are integro-differential equations without spatial derivatives. Consequently, discontinuities in space are naturally considered within the non-local framework, even though the underlying integral equations describe continuous media. Moreover, the integro-differential equations allow for a direct meshfree discretisation using nodal integration. Up to now, a major shortcoming in PD is the treatment of contact. Initially, short-range force were applied to account for the contact between peridynamic bodies [11]. In [12] an overview of various possibilities to tread contact within PD is given. Additionally, a complex peridynamic specific contact model is introduced, conserving angular momentum during collision.

When it comes to the description of the dynamics of soil and granular materials the Discrete Element Method (DEM), introduced in [13], is commonly applied. Within the DEM, the underlying dynamics are captured on grain level on the basis of contact forces, formulated with respect to micro-mechanical parameters. Generally, the solid or granular material is represented by rigid particles with an associated particle size distribution. It is also possible to capture microscopic effects on grain level using the DEM. Examples are the modelling of progressive failure in fractured rock masses [14], the approximation of grain deformations under the consideration of compressible effects using the implicitly formulated deformable DEM [15] and the bonded sphere approach in which the microscopic behaviour of a rubber grain is described by a deformable agglomerate of rigid particles being able to move relative to each other [4]. Note that to describe the microscopic behaviour, these approaches are still based on discontinuous approaches relying on micro-mechanical parameters. Generally, it is numerically advantageous to describe grains as continua to capture their microscopic behaviour. The reason behind this is that the associated material models of continuum methods are formulated with respect to measurable material parameters, having a real physical meaning. In contrast to macroscopic material parameters, the micro-mechanical parameters represent fitting parameters which are not size independent and can depend on particle size distribution and particle shapes. Consequently, a problem-dependent complex numerical calibration on the basis of experimental measurements, e.g. triaxial compression tests, is always necessary (see e.g. [16]). In contrast, classical macroscopic material parameters, e.g. elastic, viscous and plastic properties, can be directly determined by standard experimental tests without the necessity of complex calibrations.

The most promising combination to capture the discontinuous dynamics of grains, whilst taking into account microscopic effects on the grain level, is the combination of DEM and PD. Firstly, the DEM is perfectly capable to capture the dynamics on the grain level and various contact models have been developed in the last decades. Secondly, PD allows to describe individual grains as continua and to capture their microscopic behaviour by applying peridynamic material models. Besides elasticity models, this includes fracture models as shown in [17,18,19], amongst others. An application of peridynamic fracture models for grain crushing is further considered in [20, 21]. Thus, a PD–DEM coupling framework is superior to FEM–DEM coupling frameworks (see e.g. [22, 23]) and to the ‘meshfree numerical tool’ developed for the simulation of mixtures of hard and soft grains (see e.g. [24, 25]). The reason behind is that fracture is naturally included in the PD formulation and has been intensively studied (see e.g. [18, 26]). Consequently, the discontinuous–continuous approach is applicable for a wider range of applications. A different continuum approach is presented in [27], considering flexible DEM particles of arbitrary polyhedral shapes on the basis of the Virtual Element Method.

Recently a PD–DEM framework for the prediction of fracture of colliding grains in two-dimensional space has been implemented [28]. In the framework, the intra-particle forces within the arbitrarily shaped grains are computed on the basis of a peridynamic formulation. The inter-particle interactions, i.e. the forces between two grains coming into contact, are computed by DEM-like contact laws between particles of distinct discretised bodies. Moreover, in [29] the coupling of PD and DEM is considered from a computational point of view with respect to the software library ParticLS, in which meshfree methods and the DEM are considered. A shortcoming of the existing framework in [28], which is tackled in this work, is that all grains are treated as peridynamic bodies. However, it is not necessary to consider all grains on the microscopic scale for various applications. An example are deformable–rigid mixtures of soft and hard grains, where all rigid grains can be treated as DEM grains, i.e. as a single discrete particle. Incorporating rigid DEM grains as well as microscopic phenomena in PD grains within the same framework constitutes a multi-scale approach. Consequently, it is desirable to have the possibility of a multi-scale time integration scheme. In the following, the term grain is replaced by body to allow the description of arbitrary objects in a generalised framework. Moreover, in discretised form bodies consists of particles.

This contribution targets an efficient numerical coupling of discontinuous and continuous material behaviour by developing a generalised multi-scale PD–DEM coupling framework. The fundamentals of the PD–DEM framework, i.e. conservation principles, PD and DEM, are recapitulated in Sect. 2. The proposed generalised multi-scale PD–DEM coupling framework is then introduced in Sect. 3. It is focused on the generalised force coupling as well as on the staggered solution scheme for the multi-scale time integration. In Sect. 4.1, the PD–DEM coupling is verified using a 3D Hertzian contact problem and the multi-scale time integration is verified in Sect. 4.2. Furthermore, numerical examples of coupled discontinuous–continuous material behaviour are presented in Sect. 5 in terms of simultaneous consideration of deformable and rigid bodies. Finally, the main findings are summarised and possible extensions of the current work are discussed in Sect. 6.

2 Fundamentals of methodology

2.1 Conservation principles in mechanics

In numerical frameworks, it is crucial to obey fundamental laws of physics with respect to associated physical values to allow reliable predictions. In the case of dynamic systems, the fundamental laws are the conservation of linear and angular momentum.

To conserve linear momentum it is necessary to fulfil Newton’s second law

$$\begin{aligned} \mathbf {f} = \frac{\,\text {d}\mathbf {p}}{\,\text {d}t} = \frac{m\,\text {d}\mathbf {v}}{\,\text {d}t}= m {\ddot{\mathbf{u}}}= m \mathbf {a} \end{aligned}$$

(1)

as well as Newton’s third law $\mathbf {f}_A = - \mathbf {f}_B$. Newton’s second law states that the resulting force $\mathbf {f}$ is directly proportional to the change of linear momentum $\mathbf {p}$, i.e for a system with constant mass m, proportional to the change of velocity $\mathbf {v}$ and thus proportional to the second time derivative of the positional vector $\mathbf {u}$ which is the acceleration $\mathbf {a}$. Newton’s third law states that the force between two points A and B in contact is equal in magnitude with opposed direction. When fulfilling Newton’s third law, the accumulated point-wise intra-particle forces within a generalised body $\mathcal {B}$ with volume v and boundary $\partial \mathcal {B}$ with area a vanish. Consequently, only traction forces $\mathbf {t}$ with associated normal direction $\mathbf {n}$ on $\partial \mathcal {B}$ have to be considered for the fulfillment of Eq. (1). Thus, including body forces $m_i \mathbf {b}_i$, where $\mathbf {b}$ is the specific body force, it yields

$$\begin{aligned} \sum \mathbf {f} = \sum m \mathbf {a} =\sum _{i \in \partial \mathcal {B}} \mathbf {t}_i {a}_i + \sum _{i \in \mathcal {B}} m_i \mathbf {b} \end{aligned}$$

(2)

for a discontinuous particle system. For continuous bodies with infinitesimal particle volumes it yields

$$\begin{aligned} \int _{\mathcal {B}} \rho \mathbf {a} \,\text {d}v = \int _{\partial \mathcal {B}} \mathbf {t} \,\text {d}a + \int _{\mathcal {B}} \rho \mathbf {b} \,\text {d}v = \int _{\mathcal {B}} \,\text {div}\varvec{\sigma } + \rho \mathbf {b} \,\text {d}v \end{aligned}$$

(3)

and locally

$$\begin{aligned} \rho \mathbf {a} = \,\text {div}\varvec{\sigma } + \rho \mathbf {b}, \end{aligned}$$

(4)

where $\rho$ is the density in the current configuration and $\,\text {div}\varvec{\sigma }$ the divergence of the Cauchy stress tensor.

To conserve angular momentum L, it is necessary to fulfil

$$\begin{aligned} \dot{\mathbf {L}} = I \dot{\varvec{\omega }} = \mathbf {M}^{act}, \end{aligned}$$

(5)

where I is the moment of inertia and $\dot{\varvec{\omega }}$ the rate of angular velocity. Moreover, $\mathbf {M}^{act}$ is the sum of acting moments, either directly applied as external moments or generated by interaction forces (e.g. contact forces or rolling resistance). Thus, Eq. (5) states that acting moments lead to a change of angular momentum.

In the case of the classical continuum description (Eq. 4), angular momentum is automatically conserved when the stress tensor is symmetric, i.e. $\varvec{\sigma } = \varvec{\sigma }^T$. In contrast, for discontinuous particle systems it is required to consider the angular velocities in the degrees of freedom and to solve Eq. (5) with respect to the acting moments.

2.2 Peridynamics

In the theory of Peridynamics (PD), firstly introduced in [10], non-local particle interactions over a specific radius within the family $\mathcal {H}$ are considered. Considering a master particle I, its family represents the domain of influence and contains all neighbouring particles J whose distances are less equal than the horizon size $\delta$, as depicted in Fig. 1.

Fig. 1

Family $\mathcal {H}$ of particle I with interacting neighbouring particles J

In contrast to the updated Lagrangian type smoothed-particle hydrodynamics (SPH) method (cf. [30]), the original framework of PD is of total Lagrangian type. As a consequence, the neighbourhoods of particles do not change during the computation. Thus, scalars corresponding to material properties in the governing equations are defined with respect to the reference configuration and vectorial quantities are defined with respect to initial positions $\mathbf {X}$ and time t.

Compared to classical continuum mechanics, the resulting equations in PD are integro-differential equations without spatial derivatives. In the context of the preservation of linear momentum, this leads to the replacement of the classical divergence of the stress tensor ${\text {div} \varvec{\sigma }}$, cf. Eq. (4), by its peridynamic counterpart $\mathcal {L}$. Thus, the operator $\mathcal {L}$ represents the resulting force density from a peridynamic material model and the associated equation of motion is defined by

$$\begin{aligned} \rho \mathbf {a}(\mathbf {X},t) = \mathcal {L} + \rho \mathbf {b}(\mathbf {X},t). \end{aligned}$$

(6)

Consequently, the peridynamic force is defined with respect to the volume V of the initial configuration by

$$\begin{aligned} \mathbf {f}^{\text {PD}} = \mathcal {L} V. \end{aligned}$$

(7)

Similar to classical continuum mechanics, the conservation of angular momentum is directly handled via the material model. Thus, a fundamental requirement for peridynamic material models is that no angular momentum is generated due to deformation. To define peridynamic material models, the deformations of bonds $\varvec{\xi } = \mathbf {X}'- \mathbf {X}$, defined as the vectors between the initial position of master particle $\mathbf {X}$ and all initial positions $\mathbf {X'}$ of particles within its family $\mathcal {H}_{\mathbf {X}}$, are considered. Generally, it is distinguished between bond-based and state-based PD, whereby the difference lays in the bond-force computation, cf. [31]. In bond-based models, the bond-force between two particles depends on the deformation of the associated bond only, whereas the bond-force between two particles depends on the collective deformation of bonds within the family for state-based peridynamic models.

In the following, the force density computation for bond-based as well as state-based models is explained and specific elastic material models are introduced. Bond-based models are derived from a central potential and the force densities are computed with respect to a pairwise force function $\mathbf {t}$, which generally depends on the relative displacement (displacement field ${\mathbf {w}}$) and the bond vector itself. Thus, it yields

$$\begin{aligned} \mathcal {L} = \int _{\mathcal {H}_{\mathbf {X}}} \mathbf {t}\big ({\mathbf {w}}(\mathbf {X}',t) - {\mathbf {w}}(\mathbf {X},t),\mathbf {X}'- \mathbf {X} \big ) \mathrm {d} V_{\mathbf {X'}}. \end{aligned}$$

(8)

Note, that bond-based models are automatically restricted to a Poisson’s ratio of 0.25 within three-dimensional approaches due to the derivation from a central potential. Thus, there are generally not applicable for the modelling of nearly incompressible materials like rubber. The force vector between two particles is always parallel to its deformed bond vector $\varvec{\eta }$, i.e. the bond force densities are represented by

$$\begin{aligned}&\mathbf {t} = \frac{ \varvec{\xi }+ \varvec{\eta }}{\Vert \varvec{\xi }+ \varvec{\eta }\Vert } t, \end{aligned}$$

(9)

where t is the scalar bond-force. Consequently, angular momentum is automatically preserved. In the further course, the micro-elastic brittle material model is utilised and the scalar bond-force is defined by

$$\begin{aligned} t = \phi c s. \end{aligned}$$

(10)

Within Eq. (10) $s = \frac{\Vert \varvec{\xi }+ \varvec{\eta }\Vert -\Vert \varvec{\xi }\Vert }{\Vert \varvec{\xi }\Vert }$ is the bond stretch, $c = \frac{18 K}{\pi \delta ^4}$ a spring constant and $\phi$ a damage function. The spring constant can be defined with respect to the classical compression modulus K and is obtained by postulating the same stress power for the linear elastic continuum mechanical material model and the presented peridynamic model. Note that the correspondence between micro and macro material parameters is formulated with the assumption of compact support. Thus, the assumption is violated for particles whose initial distances to the surface are smaller than $\delta$. In the scope of this work, no surface correction is applied. However, a study about different surface correction procedures is conducted in [32]. Moreover, in this work bond breakage is not considered and $\phi =1$ is used.

Similar to [33, 34], Eq. (6) is discretised in a meshfree fashion. Neglecting the body force term, it yields on particle level

$$\begin{aligned} \rho _{I} \mathbf {a}_I= \sum _{J \in \mathcal {H}_{\mathbf {X}_I}} \mathbf {t}_{IJ} V_J . \end{aligned}$$

(11)

Thus, the peridynamic forces exerted on particle I due to its interactions within its family are defined by

$$\begin{aligned} \mathbf {f}^{\text {PD}}_I = \mathcal {L}_I V_I = \sum _{J \in \mathcal {H}_{\mathbf {X}_I}} \mathbf {t}_{IJ} V_J V_I. \end{aligned}$$

(12)

Note that the result of the meshfree discretised PD is a particle system. However, the system is describing a continuum body in a non-local manner.

As the name indicates, state-based PD are formulated with respect to states. From a mathematical point of view, states are generalised second-order tensors representing the mapping of bond vectors $\varvec{\xi } \in \mathcal {H}_{\mathbf {X}}$ to either a scalar or a vector. In the following, states are indicated by an underscore. The equation of motion in state-based PD is formulated with respect to force state densities ${{\underline{\varvec{T}}}}$. This leads to the general state-based expression of

$$\begin{aligned} \mathcal {L} = \int _{\mathcal {H}_{\mathbf {X}}} {{\underline{\varvec{T}}}}[\mathbf {X},t] \langle \mathbf {X'}- \mathbf {X} \rangle - {{\underline{\varvec{T}}}}[\mathbf {X'},t] \langle \mathbf {X}- \mathbf {X'} \rangle \mathrm {d} V_{\mathbf {X'}} \end{aligned}$$

(13)

for the non-local operator $\mathcal {L}$. Applying nodal integration and multiplying by volume leads to the force definition on particle level

$$\begin{aligned} \mathbf {f}^{\text {PD}}_I = \mathcal {L}_I V_I = \sum _{J \in \mathcal {H}_{\mathbf {X}_I}} ({{\underline{\varvec{T}}}}_I \langle \varvec{\xi }_{IJ}\rangle - {{\underline{\varvec{T}}}}_J \langle \varvec{\xi }_{JI}\rangle ) V_J V_I. \end{aligned}$$

(14)

Within the discretised version the force state density ${{\underline{\varvec{T}}}}_I$ contains the collective information about forces exerted on/from particle I within its family. Consequently, ${{\underline{\varvec{T}}}}_I \langle \varvec{\xi }_{IJ}\rangle$ maps the bond vector $\varvec{\xi }_{IJ}$ into a force vector per unit volume square. In the formulation of associated material laws the deformation state, which maps the bond vector into the deformed bond vector, is defined by ${{\underline{\varvec{Y}}}}[\mathbf {X},t] \langle \mathbf {X'}- \mathbf {X} \rangle = \varvec{\eta }$.

In the following, Linear Peridynamic Solid (LPS) [31] will be used. In order to define the force state density, the scalar reference state

$$\begin{aligned} \Vert {\underline{X}} \Vert = \Vert \varvec{\xi }\Vert , \end{aligned}$$

(15)

the scalar deformation state

$$\begin{aligned} \Vert {\underline{Y}} \Vert = \Vert {{\underline{\varvec{Y}}}}\Vert \end{aligned}$$

(16)

as well as the deformed direction state

$$\begin{aligned} {{\underline{\varvec{M}}}}({{\underline{\varvec{Y}}}}) = \frac{{{\underline{\varvec{Y}}}}}{\Vert {\underline{Y}} \Vert } \end{aligned}$$

(17)

are introduced. In this way, the bond extensions are defined with respect to the scalar extension state by

$$\begin{aligned} {\underline{e}} = \Vert {\underline{Y}}\Vert - \Vert {\underline{X}}\Vert . \end{aligned}$$

(18)

Moreover, the extension state is split into an isotropic $\underline{e}^i$ and a deviatoric part ${\underline{e}}^d$. For their definitions it is necessary to define the scalar weighted volume

$$\begin{aligned} m = ({\underline{w}} \Vert {\underline{X}} \Vert ) \bullet \Vert {\underline{X}} \Vert \end{aligned}$$

(19)

and the peridynamic dilatation

$$\begin{aligned} \theta = \frac{3}{m}({\underline{w}} \Vert {\underline{X}} \Vert ) \bullet {\underline{e}} \end{aligned}$$

(20)

with respect to the the weighting influence function ${\underline{w}}$, which is further assumed to be 1. Note that the peridynamic dot product between two states is a scalar and is defined by

$$\begin{aligned} {{\underline{\varvec{A}}}} \bullet {{\underline{\varvec{B}}}} = \int _{\mathcal {H}_{\mathbf {X}}} {{\underline{\varvec{A}}}}\langle \mathbf {X'} - \mathbf {X} \rangle \cdot {{\underline{\varvec{B}}}}\langle \mathbf {X'}- \mathbf {X} \rangle \mathrm {d} V_{\mathbf {X'}}. \end{aligned}$$

(21)

Using Eqs. (18) and (20), the deviatoric scalar extension state is defined by

$$\begin{aligned} {\underline{e}}^d ={\underline{e}} - {\underline{e}}^i= {\underline{e}} - \frac{\theta \Vert {\underline{X}} \Vert }{3}= \Vert {\underline{Y}}\Vert - \Vert {\underline{X}}\Vert - \frac{\theta \Vert {\underline{X}} \Vert }{3}. \end{aligned}$$

(22)

Finally, the force state densities are defined with respect to the deformed direction state (Eq. 17) and the scalar force state ${\underline{t}}({{\underline{\varvec{Y}}}})$ by

$$\begin{aligned} {{\underline{\varvec{T}}}}({{\underline{\varvec{Y}}}}) = {\underline{t}}({{\underline{\varvec{Y}}}}) {{\underline{\varvec{M}}}}({{\underline{\varvec{Y}}}}). \end{aligned}$$

(23)

Note that angular momentum is automatically conserved using the LPS formulation. The scalar force state in Eq. (23) consists of a co-isotropic and co-deviatoric part, i.e. $\underline{t}= {\underline{t}}^i+{\underline{t}}^d$, whereby the parts are defined with respect to the peridynamic free energy function

$$\begin{aligned} \Psi ({\underline{e}}^i(\theta ), {\underline{e}}^d) = \frac{K}{2} \theta ^2 + \frac{\alpha }{2} ({\underline{w}} \ {\underline{e}}^d) \bullet {\underline{e}}^d \end{aligned}$$

(24)

by

$$\begin{aligned} \begin{aligned}&{\underline{t}}^i = \frac{\partial \Psi }{\partial {\underline{e}}^i} = \frac{\partial \Psi }{\partial \theta }\frac{\partial \theta }{\partial {\underline{e}}^i}= \frac{3}{m}{\underline{w}} \Vert {\underline{X}} \Vert \frac{\partial \Psi }{\partial \theta } = \frac{3 K \theta }{m} {\underline{w}} \Vert {\underline{X}} \Vert \\&{\underline{t}}^d = \frac{\partial \Psi }{\partial {\underline{e}}^i}= \alpha {\underline{w}} {\underline{e}}^d. \end{aligned} \end{aligned}$$

(25)

The material parameter $\alpha$ is the micro shear modulus which can be related to the macroscopic shear modulus G by $\alpha = \frac{15 G}{m}$. Note that similar to the bond-based approach, the missing compact support leads to inaccurate $\alpha$’s near the surface. An extension of the described model to elasto-plasticity with von Mises plasticity is shown in [35].

In this work, fractions of the so-called PD correspondence formulation, which is based on a non-local stress tensor, is used. Based on the discretised shape tensor

$$\begin{aligned} \mathbf {K}_I = \sum _{J \in \mathcal {H}_{\mathbf {X}_I}} \underline{w} \langle \varvec{\xi }_{IJ}\rangle \varvec{\xi }_{IJ} \otimes \varvec{\xi }_{IJ} \end{aligned}$$

(26)

the non-local deformation gradient is defined by

$$\begin{aligned} \mathcal {F}_I = \left( \sum _{J \in \mathcal {H}_{\mathbf {X}_I}} {\underline{w}}\langle \varvec{\xi }_{IJ}\rangle \mathbf {u}_{IJ} \otimes \varvec{\xi }_{IJ} V_J \right) \mathbf {K}_I^{-1}. \end{aligned}$$

(27)

Based on this non-local deformation gradient, a classical material model can be utilised for the stress computation. The only requirement is the application of the same macro-mechanical material parameters. Thus, the material parameters of the bond-based as well as state-based elastic model needs to be transformed into the Lame constants $\lambda$ and G. Applying the compressible Neo-Hookean free energy function with the compressible part of Ciarlet [36]

$$\begin{aligned} W(I_C,J)= & {} \frac{1}{2} G \left( I_C-3 \right) + \frac{\lambda }{4}(J^2-1) \nonumber \\&- \lambda \frac{\ln J}{2} - G \ln J , \end{aligned}$$

(28)

the second Piola-Kirchhoff stress tensor is computed by [37]

$$\begin{aligned} \mathbf {S} = G(\text {1}- \mathbf {C}^{-1}) + \frac{\lambda }{2}(J^2-1) \mathbf {C}^{-1} \end{aligned}$$

(29)

where $\mathbf {C}=\mathcal {F}^T\mathcal {F}$ is the right Cauchy-Green tensor, $I_C$ its first invariant and $J= \det \mathcal {F}$ the Jacobean. As a result, the mechanically more meaningful non-local Cauchy-stresses are obtained by

$$\begin{aligned} \varvec{\sigma } = \frac{1}{J} \mathcal {F} \mathbf {S} \mathcal {F}^T. \end{aligned}$$

(30)

Moreover, in engineering practise the Green-Lagrange strain tensor $\mathbf {E}=\frac{1}{2}\left( \mathbf {C} - \mathbf {1}\right)$ is commonly used for the evaluation of finite strains.

2.3 Discrete element method

The second method considered within the developed coupling scheme is the Discrete Element Method (DEM). In contrast to the continuum based PD, in the DEM discrete bodies are considered and thus, no discretisation is necessary.

In the following, spherical bodies are considered, whilst generally arbitrary shaped discrete elements can be used. Their equation of motion is defined with respect to Eq. (1) by

$$\begin{aligned} m \mathbf {a} = \mathbf {f}^{\text {DEM}} + m \mathbf {b}, \end{aligned}$$

(31)

where $m \mathbf {b}$ are body forces and $\mathbf {f}^{\text {DEM}}$ inter-particle DEM forces. The DEM forces are classically composed of normal and shear forces of adjacent discrete elements being in contact via

$$\begin{aligned} \mathbf {f}^{\text {DEM}} = \mathbf {f}_n^{\text {DEM}} + \mathbf {f}_s^{\text {DEM}}, \end{aligned}$$

(32)

whilst the direct neighbours of bodies are progressively updated.

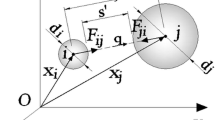
The used rheological model for the DEM-force computation between two spherical bodies is depicted in Fig. 3. It consists of a divider, a spring in normal direction with normal stiffness $k_n$, a spring in tangential direction with shear stiffness $k_s$ and a slider. In contrast to other numerical methods, the interpenetration of bodies is not prohibited within the DEM and the resulting overlap represents the basis for the force computation. The resulting forces of two overlapping spherical bodies A and B is visualised in Fig. 2. The normal forces

$$\begin{aligned} \mathbf {f}_n^{\text {DEM}} = k_n \mathbf {d}_n \end{aligned}$$

(33)

are defined with respect to the overlap in normal direction $\mathbf {d}_n$ and normal stiffness $k_n$. The incremental shear forces between two colliding bodies A and B are defined by

$$\begin{aligned} \Delta \mathbf {f}_s^{\text {DEM}} = k_s \dot{\mathbf {d}}_s \Delta t, \end{aligned}$$

(34)

where $\dot{\mathbf {u}}_s$ is the relative shear velocity and $k_s$ the shear stiffness. Note that the normal and shear stiffness can both be a function of the overlap in normal direction $\mathbf {d}_n$. The total shear force is limited by a Coulomb-like slip model, i.e.

$$\begin{aligned} \mathbf {f}_s^{DEM} \le \mu \mathbf {f}_n^{DEM} \end{aligned}$$

(35)

where $\mu$ is the friction coefficient. The divider in Fig. 3 indicates the absence of forces when two adjunct particles do not overlap.

The no slip non-linear Hertz-Mindlin (HM) contact model, cf. [38], is used in this work where contact stiffnesses are defined as:

$$\begin{aligned} \begin{aligned} k_n&= \frac{4}{3} {\bar{E}}_c \sqrt{{\bar{R}} \mathbf {d}_n}\\ k_s&= 8 {\bar{G}}_c \sqrt{{\bar{R}} \mathbf {d}_n} , \end{aligned} \end{aligned}$$

(36)

with respect to the equivalent sphere radius $\bar{R}=(1/R_A+1/R_B)^{-1}$, the equivalent Young’s modulus ${\bar{E}}_c= \left[ \left( 1- \nu _c^{A^2}\right) /E_c^A + \left( 1- \nu _c^{B^2} \right) E_c^B \right] ^{-1}$ and the equivalent shear modulus $\bar{G}_c= \left[ \left( 2- \nu _c^{A}\right) /G_c^A + \left( 1- \nu _c^{B} \right) /G_c^B \right] ^{-1}$. The associated shear moduli $G_c^A$ and $G_c^B$ are computed by $G_c^{*} = E_c^{*} / \left[ 2\left( 1+ \nu _c^{*}\right) \right]$ with $* = A, B$.

Besides contacts between two spherical bodies, contacts between spheres and kinematically constraint rigid walls are considered. The associated contact forces are defined analogously to the sphere–sphere interaction. Since walls do not possess a radius, their radii are assumed to be equivalent to the radii of their spherical contacts for the computation of the equivalent sphere radius ${\bar{R}}$.

As mentioned in Sect. 2.1, the conservation of angular momentum is not automatically fulfilled in the DEM and it is required to consider the angular velocities as degrees of freedom. In this work no external moments are considered and thus, the acting moments $\mathbf {M}^{act}$ result solely from interaction forces, cf. Fig. 2. As a result, it yields with respect to Eq. (5)

$$\begin{aligned} \dot{\mathbf {L}} = I \dot{\varvec{\omega }} = \mathbf {M}^{act} = \underbrace{\mathbf {R}_c\times \mathbf {f}_n^{\text {DEM}}}_{= 0} + \mathbf {R}_c \times \mathbf {f}_s^{\text {DEM}}, \end{aligned}$$

(37)

where $\mathbf {R}_c$ represents the radial vector from spheres origin to the contact point. Consequently, besides the equation of motion, the first-order differential equation

$$\begin{aligned} I \dot{\varvec{\omega }} = \mathbf {R}_c\times \mathbf {f}_s^{\text {DEM}} \end{aligned}$$

(38)

has to be solved for all DEM bodies as well.

3 Generalised multi-scale PD–DEM formulation

3.1 Generalised force coupling

A generalised PD–DEM force coupling scheme is introduced based on the framework discussed in Sect. 2. All possible contact variations on the basis of three PD and three DEM bodies are depicted in Fig. 4. The associated bodies are colour-coded in green (DEM) and grey (PD), whilst the centers of discrete elements are depicted by squares and the discretised peridynamic particles by crosses. Moreover, hybrid particles acting as peridynamic particle as well as DEM body are highlighted in red. In the following, DEM bodies are also denoted by discrete particles.

Fig. 2

Resulting forces and moments from two spherical bodies A and B in contact

Fig. 3

Rheological model of two overlapping spherical bodies within the DEM

Fig. 4

Illustration of generalised contact treatment between PD and DEM bodies. DEM bodies are colour coded in green and PD bodies in grey. Hybrid particles acting as peridynamic particle as well as DEM body are highlighted in red. (Color figure online)

The inter-particle forces between two discrete elements (DEM–DEM) are obtained by the DEM (Eq. 32). The macroscopic intra-particle forces within a peridynamic body $\mathbf {f}^{\text {PD}}$ are defined by Eqs. (12) and (14) for a bond-based and state-based peridynamic model, respectively.

The key of the developed formulation is the introduction of hybrid particles at the interface of PD and DEM. Indeed, all surface particles of the peridynamic bodies are also treated as discrete elements. This allows the computation of inter-particle forces between discrete elements and the surface of peridynamic bodies (PD–DEM), inter-particle forces between two peridynamic bodies (PD–PD), as well as self-contact of peridynamic bodies by DEM contact forces. An example where self-contact of a peridynamic body can take place is the compression of a highly deformable hollow sphere under compression when the top and bottom boundary of the hollow sphere come into contact. The resulting forces are further denoted by $\mathbf {f}^{\text {Coupling}}$ and are computed by Eq. (32). A problem in the definition of hybrid particles is that the underlying peridynamic particles do not inherently have a radius. They represent integration points with associated volumes as integration weights accounting for the fraction of continuous volume they are representing. Therefore, the quasi radii R of the hybrid particles required for contact detection and force computation are defined on the basis of the associated volumes V of the integration points via

$$\begin{aligned} R = \left( \frac{3 V}{4 \pi }\right) ^{\frac{1}{3}}. \end{aligned}$$

(39)

Hence, the required DEM part of hybrid particles (i.e. contact forces) can be calculated. Note that the DEM contact model for $\mathbf {f}^{\text {DEM}}$ and $\mathbf {f}^{\text {Coupling}}$ can be different.

Since hybrid particles only represent integration points with their volume as weighting within the peridynamic framework, they do not possess the rotational degree of freedom of DEM bodies. Thus, the quasi radii R of hybrid particles are only used for contact detection and contact force computation, whereby the resulting contact forces are applied on the associated peridynamic integration points. Moreover, self-contact in peridynamic bodies is not considered for particles within the same family. In the proposed formulation the drawback of the lacking kronecker-delta property resulting from the meshfree peridynamic discretisation diminished. Due to the hybrid approach at the surface of peridynamic bodies, boundaries are indirectly applied by the resulting coupling forces.

Summarising, the forces of the particle system are defined as the superposition of intra-particle peridynamic, inter-particle DEM, inter-particle coupling and body forces by

$$\begin{aligned} \mathbf {f} = \underbrace{\mathbf {f}^{\text {PD}}}_{\text {Intra-particle}} +\underbrace{\mathbf {f}^{\text {DEM}}}_{\text {Inter-particle}} + \underbrace{\mathbf {f}^{\text {Coupling}}}_{\text {Inter-particle}} +\underbrace{m \mathbf {b}}_{\text {body forces}}. \end{aligned}$$

(40)

3.2 Multi-scale time integration

The state-of-the-art for PD as well as DEM is to perform an inherently conditionally stable explicit time integration for the equation of motion. A detailed investigation of different stability criteria for classical peridynamic models is done in [39]. In this work, the CFL-criterion (cf. [40])

$$\begin{aligned} \Delta t_{\text {crit}}^{\text {PD}} = \frac{h}{c}, \end{aligned}$$

(41)

where h is the characteristic length and c the wave speed, defined by

$$\begin{aligned} c = \sqrt{\frac{K}{\rho }}, \end{aligned}$$

(42)

is applied. As discussed in [41], it is not obvious what the characteristic length within the peridynamic framework is. However, it is said that the time step estimation by the CFL-criterion is conservative when the particle spacing is assumed to be the characteristic length.

The critical time step $\Delta t_{\text {crit}}^{\text {DEM}}$ of the DEM is defined on the basis of the equivalent per-particle stiffness ${\bar{k}}$ which is composed of the associated stiffnesses of all contacts (see e.g. [42]). Thus, each particle has an individual critical time step and the global critical time step is generally defined as the minimum of local critical time steps, i.e.

$$\begin{aligned} \Delta t_{\text {crit}}^{\text {DEM}} = \min _i \sqrt{\frac{m_i}{{\bar{k}}_i}}. \end{aligned}$$

(43)

The reader is referred to [42] for the computation of the equivalent per-particle stiffness ${\bar{k}}$. An extension to include rotational degrees of freedom is presented in [43].

The leapfrog time integration algorithm is applied to discretise the equation of motion, Eq. (1) or with generalised forces Eq. (40), in time. Thus, the velocities and positions are updated as follows

$$\begin{aligned} \begin{aligned} \mathbf {v}_{n+\frac{1}{2}}&= \mathbf {v}_{n-\frac{1}{2}} + \mathbf {a}_n \Delta t\\ \mathbf {u}_{n+1}&= \mathbf {u}_{n} + \mathbf {v}_{n+\frac{1}{2}} \Delta t + \mathbf {a}_n \Delta t^2. \end{aligned} \end{aligned}$$

(44)

Moreover, the rotational accelerations of pure DEM bodies, cf. Eq. (38), have to be integrated to fulfil the conservation of angular momentum. Thus, the same time integration as for the translational kinematics, cf. Eq. (44), is applied and it yields

$$\begin{aligned} \varvec{\omega }_{n+\frac{1}{2}}^{DEM} = \varvec{\omega }_{n-\frac{1}{2}}^{DEM} + \frac{\mathbf {R}_{c_{n+\frac{1}{2}}}\times \mathbf {f}_{s_{n+\frac{1}{2}}}^{\text {DEM}}}{I} \Delta t. \end{aligned}$$

(45)

Based on the simultaneous use of PD and DEM with associated critical time steps defined in Eq. (41) and Eq. (43), two distinct critical time steps have to be considered within simulations. The straightforward approach is to define the critical time step as the minimum of both, i.e. $\Delta t_{\text {crit}} = \min (\Delta t_{\text {crit}}^{\text {PD}}, \Delta t_{\text {crit}}^{\text {DEM}})$, compute all forces and update the kinematics monolithically using Eq. (44). However, the use of a single time step is computationally highly inefficient. The main issue is that the length scales of PD and DEM may vary in magnitudes due to the targeted multi-scale approach. This may result in a significantly smaller critical time step $\Delta t_{\text {crit}}^{\text {PD}}$. This is why a staggered integration scheme is developed. Based on Eqs. (41) and (43), the maximal integral multiple m between $\Delta t_{\text {crit}}^{\text {PD}}$ and $\Delta t_{\text {crit}}^{\text {DEM}}$ or vise versa is determined. Even though $\Delta t_{\text {crit}}^{\text {PD}} < \Delta t_{\text {crit}}^{\text {DEM}}$ is expected, both possibilities are considered to formulate the generalised multi-scale time integration scheme.

The key idea of the implemented staggered solution scheme is the successive update of kinematics resulting from peridynamic and DEM forces with respect to their associated critical time steps. The simplified update scheme for equivalent critical time steps is illustrated in Eq. (46):

$$\begin{aligned} \mathbf {u}_{n} \xrightarrow {\mathbf {f}^{\text {DEM}}_{n+1}, \mathbf {f}^{\text {Coupling}}_{n+1}} \mathbf {u}_{n+1}^{\text {DEM},\text {Coupling}} \xrightarrow {\mathbf {f}^{\text {PD}}_{n+1}} \mathbf {u}_{n+1} \,. \end{aligned}$$

(46)

Based on the updated kinematics of the last time step $\mathbf {u}_{n}$, the inter-particle forces $\mathbf {f}^{\text {DEM}}_{n+1}$ and $\mathbf {f}^{\text {Coupling}}_{n+1}$ are computed. The kinematics of the associated particles are then updated, leading to new positions $\mathbf {u}_{n+1}^{\text {DEM},\text {Coupling}}$ for discrete and hybrid particles. Afterwards, the peridynamic forces $\mathbf {f}^{\text {PD}}_{n+1}$ are computed and the associated kinematics are updated. Thus, the hybrid particles are updated a second time, but now with respect to the intra-particle forces. Note, that it is essential to consider body forces of hybrid particles only once during the staggered time integration. Thus, they are always taken into account at the same time as the coupling forces. Consequently, body forces of peridynamic surface particles being in contact, i.e. they are hybrid particles, are always considered during the DEM time integration step. In order to simplify the treatment of body forces within the staggered time integration, the body forces of peridynamic particles are also considered in the first step.

For the staggered time integration of hybrid particles and $\Delta t^{\text {DEM}}=\Delta t^{\text {PD}}$ this yields to

$$\begin{aligned} \begin{aligned} \mathbf {v}_{n+\frac{1}{2}}^{\text {Coupling}}&= \underbrace{\mathbf {v}_{n-\frac{1}{2}}}_{\mathbf {{\bar{v}}}} + \mathbf {a}_n^{\text {Coupling}} \Delta t^{\text {DEM}}\\ \mathbf {x}_{n+1}^{\text {Coupling}}&= \mathbf {x}_{n} + \Delta t^{\text {DEM}}\mathbf {v}_{n+\frac{1}{2}}^{\text {Coupling}} \\ \mathbf {v}_{n+\frac{1}{2}}&= \underbrace{\mathbf {v}_{n+\frac{1}{2}}^{\text {Coupling}}}_{\mathbf {{\bar{v}}}} + \mathbf {a}_n^{\text {PD}} \Delta t^{\text {PD}}\\ \mathbf {x}_{n+1}&= \mathbf {x}_{n+1}^{\text {Coupling}}+\Delta t^{\text {PD}}\mathbf {v}_{n+\frac{1}{2}}. \end{aligned} \end{aligned}$$

(47)

Note that the mean velocities $\varvec{{\bar{V}}}$ in the velocity updates are always defined with respect to their values of the last incremental update. Thus, for varying peridynamic and DEM time step sizes the symplecticity of the leapfrog integration is violated for the kinematic update of hybrid particles. The implementation of the generalised multi-scale time integration algorithm is explained in detail in Sect. 3.3.

3.3 Implementation

The open-source DEM framework Yade [44] is chosen as a basis for the implementation. This comes with a high variety of already implemented DEM models to choose from for DEM and hybrid force computation. In this paper, only the simple model introduced in Sect. 2.3 will be applied. An additional advantage of using Yade is that an optimised collider for contact detection as well as time integration schemes are already available. Model generation including definitions of DEM and peridynamic bodies with related discretisation are further handled via the available Python interface.

The peridynamic framework and the peridynamic material models described in Sect. 2.2 are implemented based on the pre-existing software architecture. Moreover, a coupling engine is implemented to account for the PD–DEM coupling formulation and the applied staggered time integration scheme outlined in Sect. 3.2. In the following, the extended simulation loop within Yade, cf. Algorithm 1, is explained first before focusing on the implementation of the multi-scale time integration. Yade is run via a Python-interface and its classical simulation loop consists of the resetting of forces and the action of fundamental DEM engines. Note, that the fundamental DEM engines have to be defined in a specific order: approximate collision detection, exact collision detection with overlap computation, definition of physical properties of new interactions, DEM force computation via constitutive laws and time integration. The highlighted step Coupling Engine is the required extension for the generalised multi-scale PD–DEM coupling time integration.

Since Yade is a DEM based framework, the global time step is set to $\Delta t_{\text {crit}}^{\text {DEM}}$ and the iteration number n is incremented with respect to this time step. As described in Sect. 3.2, the maximum integral multiple m between both critical time steps is computed in the beginning and is further used in the simulation. Before the coupling engine is called, the classical DEM steps of neighbouring search and DEM force computation are performed. The kinematics of the associated particles are then updated, leading to new positions $\mathbf {u}_{n+1}^{\text {DEM},\text {Coupling}}$ for discrete and hybrid particles.

The pseudo code of the coupling engine is shown in Algorithm 2. It is distinguished between the two possible cases $\Delta t_{\text {crit}}^{\text {PD}} >= \Delta t_{\text {crit}}^{\text {DEM}}$ and $\Delta t_{\text {crit}}^{\text {PD}} < \Delta t_{\text {crit}}^{\text {DEM}}$. In case of $\Delta t_{\text {crit}}^{\text {PD}} >= \Delta t_{\text {crit}}^{\text {DEM}}$ it is checked if the current time $t_n$ is a m-mulitple of $\Delta t_{\text {crit}}^{\text {PD}}$. If this is the case, the peridynamic forces $\mathbf {f}^{\text {PD}}_{n+1}$ are computed and the kinematics of corresponding particles are updated. The associated time integration is performed with respect to $\Delta t_{\text {crit}}^{\text {PD}} = m \Delta t_{\text {crit}}^{\text {DEM}}$. Otherwise, no time integration of peridynamic particles is performed.

The second and most probable case is $\Delta t_{\text {crit}}^{\text {PD}} < \Delta t_{\text {crit}}^{\text {DEM}}$. Similar to the first case, the time integration of peridynamic particles takes place in the coupling engine. However, an incremental time integration with $\Delta t_{\text {inc}}=\Delta t_{\text {crit}}^{\text {PD}} = \frac{\Delta t^{\text {DEM}}}{m}$ is necessary to account for the smaller peridynamic time step. Thus, the peridynamic forces and corresponding kinematic quantities are m times updated incrementally. After the last incremental update, $t_{n+1}$ is reached.

4 Verification of implementations

4.1 PD–DEM coupling

In order to verify the implemented PD–DEM coupling scheme, the solution for the contact of a rigid sphere with an elastic half space obtained by Hertzian contact theory (cf. [45]) is considered. Dependent on the penetration depth d, the corresponding analytical normal force is defined by

$$\begin{aligned} F_n = \frac{4}{3} {\bar{E}} R^{1/2}d^{3/2}, \end{aligned}$$

(48)

where ${\bar{E}}$ is the effective Young’s modulus and R the radius of the sphere.

Fig. 5

Visualisation of 3D Hertzian contact problem with a solid sphere on an elastic half-space

Table 1 DEM and PD material parameters for the computation of Hertzian contact

Within the numerical PD–DEM approach, the rigid sphere is represented by a discrete DEM particle of radius $R^{\text {DEM}}={5}\,\hbox {cm}$ while the elastic half-space is approximated by a peridynamic body of dimensions ${45}\,\hbox {cm} \times {45}\,\hbox {cm} \times {22.5}\,\hbox {cm}$, as illustrated in Fig. 5. The peridynamic body is discretised by $30 \times 30 \times 15 = 13500$ particles based on a regular particle spacing of $\Delta _x={1.5}\,\hbox {cm}$. Using Eq. (39), the representative radius of the hybrid particles is $R^{\text {PD}}={0.93}\,\hbox {cm}$. The kinematics of surface/hybrid particles are constrained in associated normal directions whilst all internal peridynamic particles are unconstrained for the purpose of representing the elastic half space. An exception are the hybrid particles in the plane of the initial contact surface which are unconstrained as well.

To obtain the numerical force response, the described Hertz-Mindlin contact model with normal force definition in Eq. (33) is used for the DEM-like coupling forces between two bodies. Both the bond-based (Eq. 12) and state-based (Eq. 14) peridynamic models are used. The applied material parameters are listed in Table 1, whilst friction is not considered in this example, i.e. $\mu =0$. In contrast to the analytical approach, the resulting coupling forces are DEM-like forces which generally depend on the micro-mechanical contact parameters between DEM bodies. When applying the Hertz-Mindlin contact model, the microscopic DEM parameters are represented by their macroscopic counterpart and the analytical Hertzian contact force is obtained for the contact of two single DEM bodies with associated radii $R^{\text {DEM}}_A$ and $R^{\text {DEM}}_B$. Thus, the numerical contact forces are computed locally between spherical particles, whereas the analytical solution describes the global behaviour between a rigid sphere and an elastic half space. For this reason, a perfect match between predicted and analytical results is not expected. Nevertheless, the overall trend of the analytical result should be captured. It should be mentioned that a perfect match can be obtained by calibration, e.g. [16, 46], however, this is not the aim of the current study.

In the simulations a prescribed velocity of $v_z=-{1}\,\small {\frac{\mathrm {cm}}{{\mathrm {s}}}}$ is applied for the discrete particle in the z-direction using a fixed time step of $\Delta t = 10^{-4}\,\hbox {s}$ . Thus, the penetration depth is indirectly used as control parameter and the acting normal forces are measured. The measurement is done incrementally by setting the velocity to zero at certain times, iterating until quasi-static conditions are reached and measuring the resulting normal force. This procedure is performed with an incremental penetration depth of $\Delta d={0.05}\,\hbox {cm}$ until $d={1}\,\hbox {cm}$ is reached.

The comparison of analytical (green), PD bond-based (blue) and PD state-based (orange) normal force response with respect to the penetration depth is depicted in Fig. 6. Overall, the trend of the analytical Hertzian solution is captured well by the PD–DEM coupling framework applying the bond-based as well as state-based material model. In comparison to the analytical solution, the numerical contact force is underestimated for both the bond-based and the state-based PD material model. Moreover, the state-based solution is approaching the analytical solution with increasing penetration depth. Based on the fact that no calibration is performed for the micro-mechanical contact parameters, Hertzian contact is properly represented within the developed framework. Since the focus and goal of this contribution is the efficient numerical coupling of discontinuous and continuous material behaviour using the example of grain mixtures, it is relinquished to perform a calibration for the micro-mechanical contact parameters. Thus, a successful verification of the PD–DEM coupling framework has been performed and it is meaningful to use the framework for more complex applications.

4.2 Multi-scale time integration

In a next step the verification of the multi-scale time integration is performed. The verification example consists of a peridynamic body of dimensions ${40}\,\hbox {cm} \times {40}\,\hbox {cm} \times {10}\,\hbox {cm}$ sitting on a static wall below. The peridynamic body is discretised by 2000 particles. On top of the peridynamic body are $9\times 9=81$ discrete DEM particles with $R^{\text {DEM}}={2}\,\hbox {cm}$ (Fig. 7). A velocity of $v_z={-1}\,\frac{{\mathrm {cm}}}{{\mathrm {s}}}$ is continuously applied to all discrete particles until a compression of ${0.2}\,\hbox {cm}$ is reached. Moreover, the displacements in the x–y plane are constraint for all peridynamic particles at the bottom. The material parameters listed in Table 1 are applied and the state-based PD formulation is used. Measured are the resulting normal forces on the wall with respect to the norm of applied displacements, u, of discrete particles in the z-direction. The normal forces are measurements under fully dynamic conditions (no damping) in order to investigate possible differences between monolithic and staggered time integration for the developed coupling approach.

Fig. 6

Comparison of analytic (green), PD bond-based (blue) and PD state-based (orange) normal force response with respect to the penetration depth of a solid sphere on an elastic half-space. (Color figure online)

Fig. 7

Dimensions for multi-scale time integration example consisting of 81 discrete particles, a peridynamic body and a wall

In the following, all three different possibilities arising from the developed and implemented multi-scale time integration (Sects. 3.2 and 3.3) are considered. The first one is the classical monolithic solution of DEM and PD. The second possibility is the application of the staggered integration scheme using the same time step for both methods. The last one is the staggered solution with different time steps. For the sake of comparability, a time step of $\Delta t = 10^{-4}\,\hbox {s}$ is used in the first two options whereas $\Delta t^{\text {DEM}} = 10^{-4}\,\hbox {s}$ and $\Delta t^{\text {PD}} = 2 \times 10^{-5}\,\hbox {s}$ are used for the multi-scale time integration.

Fig. 8

Comparison of resulting normal forces using monolithic, staggered and staggered multi-scale (MS) time integration

The resulting normal forces are plotted against the norm of enforced displacement of discrete particles in the z-direction in Fig. 8. Overall, the normal forces are oscillating due to the fully dynamic approach, whilst the peak values increase with respect to increasing displacements. On the one hand, there are no differences in normal forces between the staggered scheme with identical time steps compared to the staggered multi-scale scheme. Thus, even though the symplecticity of the integrator is violated, no negative effects are observable in the multi-scale time integration. On the other hand, there are differences between the results for the monolithic and the staggered scheme. The period length of the oscillations is slightly smaller for the staggered scheme and the magnitudes in normal forces are also lower. These effects result solely from the postulated successive integration of motion for hybrid particles and are expected. By applying the DEM like coupling forces on hybrid particles and updating their kinematics before the peridynamic forces are computed, a higher ’constraint’ is applied on the peridynamic body. The reason behind is that the updated positions of hybrid particles are used to compute the peridynamic forces. Thus, the peridynamic force response is slightly higher than for the monolithic integration, leading to a reduced wave speed as well as to a reduced accumulated force within a total time step. In other words, the dynamic impact of discrete particles upon peridynamic bodies is slightly reduced in the staggered time integration scheme.

Finally, the computational efficiency of the implemented multi-scale time integration is evaluated. Therefore, normalised computation times obtained on a single Intel Core i7-7560U (2.40 GHz) processor are compared. As a reference solution the monolithic approach with $\Delta t = 10^{-4}\,\hbox {s}$ is considered. The normalised computation times for the multi-scale simulations with $\Delta t^{\text {PD}} = 10^{-4}\,\hbox {s}$ and $\Delta t^{\text {DEM}} = m \Delta t^{\text {PD}}$ with $m= 1,2,4,6$ are evaluated and listed in Table 2. Overall, the normalised computation time decreases with increasing m. In case of equal time steps the staggered computation time is ${27}\,\%$ higher than the monolithic computation time. Equal normalised computation times are obtained for $m=2$. A reduction of ${16}\,\%$ and ${21}\,\%$ is observed for the staggered multi-scale integration for $m=4$ and $m=6$, respectively. This proofs the computational advantage of the multi-scale time integration over the monolithic one. In the considered example the number of discrete particles is with 81 significantly smaller than the number of peridynamic particles (2000). On the one hand, it is obvious that the computational advantage increases with an increasing number of discrete DEM particles. On the other hand, when only a few DEM discrete particles are used and the applicable factor m between critical DEM and PD time step is not sufficiently high, the computational overhead might be higher than the gain obtained by the multi-scale integration.

Table 2 Normalised computation times ${\bar{t}}_{CPU}$ with respect to monolithic solution time for various time step factors m

5 Numerical examples

5.1 General set-up

In the following, the potential of the developed multi-scale PD–DEM coupling formulation is presented on the basis of deformable–rigid mixture applications. A real-life example for this are rubber–sand mixtures. The rigid bodies are assumed to be perfect spheres and are represented by single discrete particles. In contrast, the deformable bodies are assumed to be of arbitrary shape. In the following, the simulations are performed on the cm scale and not on the length scale of real grain mixtures to save computational costs. This is sufficient for the present approach since it is the goal to reveal the potential of the multi-scale coupling framework and not to reproduce experimental based observations.

For all numerical examples the inherent body forces including gravity are neglected and loads are induced by kinematic boundary conditions. Moreover, the state-based PD formulation (Eq. 14) is applied to account for incompressible behaviour of deformable bodies which cannot be covered by the bond-based approach with fixed Poisson’s ratio of $\nu =0.25$. In the following, the deformable bodies are modelled as weakly compressible with $\nu =0.48$ to avoid additional kinematic constraints in the material model. The DEM and PD parameters used for the numerical examples are listed in Table 3.

Table 3 DEM and PD material parameters in the numerical examples

5.2 Compression of deformable cube via generalised force coupling

In the first example, a three body interaction bounded by two walls, as depicted in Fig. 9, is considered. The centre body is a cubic rubber body of length 30 cm, discretised by 8000 peridynamic particles of volumes 3.375 $\hbox {cm}^3$. The other two bodies are rigid and represented by discrete particles of radii $R^{\text {DEM}}= {15}\,\hbox {cm}$. In this example friction is not considered, i.e. $\mu =0$. Both walls have a prescribed velocity of $v_{wall}= {\pm 1}\small {\frac{\mathrm {cm}}{{{\mathrm {s}}}}}$ in the z-direction to induce an indirect compression of the peridynamic cube. With a fixed time step of $\Delta t = 10^{-4}\,{\hbox {s}}$ the simulation is run for $t={12}\,{\mathrm{s}}$.

In this approach all forces of the developed generalised force coupling scheme, cf. Eq. (40), are coexisting. Inter-particle DEM forces are acting between the walls and the adjacent discrete particles whereas intra-particle forces are acting between the peridynamic particles of the cube. Finally, PD–DEM coupling forces exist between the discrete particles and the surface of the cube (i.e. hybrid particles).

Fig. 9

Problem definition and dimensions for the compression of a deformable cube via PD–DEM coupling forces

Fig. 10

Resulting strains a $E_{zz}$, b $E_{xx}$ as well as c, d von Mises stresses at $t={12}\,{\mathrm{s}}$ for the peridynamic cube

Fig. 11

Dimensions for numerical example to investigate the capability of the developed framework to capture morphology changes in deformable–rigid mixtures

The final results at $t={12}\,{\mathrm{s}}$ are depicted in Fig. 10. Note that particles on the edges are not visualised due to their missing compact support, cf. Sect. 2.2. As shown in all subfigures, the elastic peridynamic cube is deformed due to the indirectly induced penetration of discrete particles. The associated strains in loading direction $E_{zz}$ are depicted in Fig. 10a. The extrema $E_{zz}= 0.134$ are located in the centres of the free surfaces in the x–y plane, thus, at the centres of contact between the discrete particles and the peridynamic cube. In consequence of its penetration from top and bottom together with a nearly incompressible material, the elastic cube is squeezed perpendicular to the applied loading direction. This is reflected by the resulting strains $E_{xx}$ (Fig. 10b). Based on the introduced non-local deformation gradient in Eq. (27) and the associated Cauchy stresses Eq. (30), the von Mises stresses are computed and plotted in Fig. 10c and Fig. 10d. As expected, the highest von Mises stresses of $\sigma _{VM}={1.292}\,{\hbox {N}}\,/{\mathrm{cm}}^2$ are obtained at the centre of the contact between the discrete particles and the peridynamic cube since it is the point of highest deformation. The capability of the developed framework to overcome the shortcoming of purely DEM based frameworks to predict stresses in soft particles is proven.

Overall, the induced deformations of the peridynamic cube are well captured using the developed generalised force coupling scheme. Meaningful elastic deformations and stresses of the considered deformable block, related to its weakly compressible material, are observed based on the penetration. Thus, an application to real life problems where the penetration of rubber objects by solid objects plays the superordinate role, is feasible.

5.3 Morphology changes in deformable–rigid mixtures

In the second example, the capability of the developed framework to account for major morphology changes in deformable–rigid mixtures is investigated on the basis of a simplified problem. Considered is a rectangular deformable body of dimensions $60 \times 15 \times 7.5\, \hbox {cm}^3$ sitting on two static discrete particles of radius $R^{\text {DEM}}= {5}\,\hbox {cm}$ and subjected to a induced loading by a discrete particle with same radius on top with a prescribed velocity of $v={1}\frac{\mathrm {cm}}{\mathrm {s}}$ in the z-direction, as depicted in Fig. 11. The deformable body is equidistantly discretised by 2000 peridynamic particles with corresponding volumes of $V^{\text {PD}}= {3.375}\,\hbox {cm}^3$. In contrast to the previous example, friction is considered with a contact friction coefficient of $\mu =0.546$.

The aim of this example is to investigate if it is possible to capture the squeezing of a lengthy deformable body through a network of rigid bodies thanks to their deformability induced via the elastic PD formulation. Performed is a completely dynamic simulation using $\Delta t = {10^{-4}} \,{\hbox {s}}$ for $t = {22.15}\,{\hbox {s}}$. The resulting displacements in the x and z-direction of the deformable block are shown at three different time instances in Fig. 12. Over time, i.e. from $t = {7.5}\,{\hbox {s}}$ (Fig. 12a and Fig. 12b), $t = {17.5}\,{\hbox {s}}$ (Fig. 12c and Fig. 12d) to $t = {22.15}\,{\hbox {s}}$ (Fig. 12e and Fig. 12f) the initially straight block is gradually bend until it slips between the two static rigid discrete particles. Consequently, the block is compressed in the x-direction over time with maximum absolute values of ${4.6}\,{\hbox {cm}}$, ${17.6}\,{\hbox {cm}}$ and ${24.6}\,{\hbox {cm}}$ for the associated displacements. In contrast, the ends of the block are deflected in the z-direction, taking the maximum value of ${7.6}\,{\hbox {cm}}$ at $t = {17.5}\,{\hbox {s}}$ (Fig. 12d) before the bend block slips through the static kinematic boundary particles and the displacements in the z-direction continuously decrease.

Based on the captured dynamics, the capability of the developed coupling framework to account for major morphology changes in deformable–rigid mixtures is shown.

Fig. 12

Displacements of lengthy deformable body induced by kinematic constraints of discrete particles at $t = {7.5}\,{\hbox {s}}$ in a x-direction, b z-direction, at $t = {17.5}\,{\hbox {s}}$ in c x-direction, d z-direction as well as at $t = {22.15}\,{\hbox {s}}$ in e x-direction and f z-direction

5.4 Compression of sphere pack

The last and most complex example is the constraint compression of a sphere pack consisting of a mix of 8 deformable and 8 rigid bodies, as illustrated in Fig. 13. All bodies have a radius of $R= {15}\,{\hbox {cm}}$, whereby each deformable body is uniformly discretised by 4166 peridynamic particles with $V^{\text {PD}}={3.375}\,{\hbox {cm}^3}$. Note that by applying the uniform discretisation, the bodies of volume $V= {14137}\,{\hbox {cm}^3}$ are each represented by an accumulated PD volume of $V^{\text {dis}}=4166 \cdot {3.375}\,{\hbox {cm}^3}= {14060}\,{\hbox {cm}^3}$. Consequently, a volumetric discretisation error of ${0.55}\,\%$ is induced.

In total, the problem consists of 8 discrete particles, 33328 peridynamic particles and 6 walls surrounding the deformable–rigid mixture. Similar to the compression of a single cube in Sect. 5.2, the loading is induced by the application of kinematic boundaries in terms of $v_{wall}=\pm {10}\small {\frac{\mathrm {cm}}{{{\mathrm {s}}}}}$ for the walls in the x-z plane. The surrounding walls are modelled as static to induce constraints perpendicular to the compression direction. Similar to the previous example in Sect. 5.3, friction is considered with a contact friction coefficient of $\mu =0.546$. A simulation time of $t= {3}\,{\hbox {s}}$ with $\Delta t = {10^{-4 }}\,{\hbox {s}}$ is considered.

Fig. 13

Problem definition and dimensions for the uniaxial compression of a deformable–rigid sphere pack consisting of 8 discrete elements and 8 deformable PD bodies

For the evaluation, the displacements of peridynamic particles in the z-direction as well as their norm of displacements in the x–y plane are considered at different times. The results at $t=1$, $t=2$ and $t = {3}\,{\hbox {s}}$ are illustrated in Fig. 14. At the beginning, at $t = {1}\,{\hbox {s}}$ (Fig. 14a, b) the peridynamic particles start to be compressed and a slight misalignment in the x–y plane is observable. However, the spherical bodies are still stacked on top of each other and the maximum norm of displacement in the x–y plane is ${6.07}\,{\hbox {cm}}$. After $t = {2}\,{\hbox {s}}$ (Fig. 14c, d), a morphology change is observable and the bodies are not aligned on top of each other any more. On the one hand, PD bodies are compressed further and start clinging to the discrete element at the bottom. On the other hand, a discrete element is now located in the centre of the compressed packing. The morphology change is reflected in a significant increase in the maximum norm of displacement in the x–y plane with ${34.26}\,{\hbox {cm}}$. Due to the further compression, at the final time $t = {3}\,{\hbox {s}}$ the change in morphology continues and the porosity decreases further. As depicted in Fig. 14c, d, the sphere pack appears to be a single clump of material, whereby the maximum norm of displacement in the x–y plane has slightly decreased to ${33.79}\,{\hbox {cm}}$. The reason for the slightly decreased maximum norm of displacement is the ongoing morphology change of individual bodies in the packing, i.e. peridynamic bodies are not only further compressed over time, but are still moving. This can lead to increasing or decreasing norms of displacement in the x–y plane of the associated peridynamic particles.

In order to quantify the results further, the mean of the norm of displacements in the x–y plane from all peridynamic particles are computed. The value gradually increases from 2.35 at $t=1$ and 8.32 at $t=2$ to ${11.21}\,{\hbox {cm}}$ at $t = {3}\,{\hbox {s}}$. This increase of values reflects the continuous squeezing of deformable peridynamic bodies in the x–y plane. The final result of a more or less single clump of material where the deformable bodies cling to the discrete rigid particles is exactly as expected for deformable–rigid mixtures.

The results obtained for the sphere pack mixture at $t = {3}\,{\hbox {s}}$ are now compared against sphere packs where all considered bodies are either rigid (DEM) or deformable (PD). The associated particle configurations including displacements in z-direction and the norm of displacements in the x–y plane are depicted in Fig. 15. In the compression of purely DEM bodies, none of the spheres is deflected in the x–y plane as shown in Fig. 15a, b. In contrast, the behaviour with PD bodies only, cf. Fig. 15c, d, is similar to the behaviour of the mixture (Fig. 14). Overall, morphology changes in the sphere pack are observable and the bodies start to form a single clump of material. The maximum norm of displacements in the x–y plane is with ${32.21}\,{\hbox {cm}}$ slightly smaller than the one for the mixture (${33.79}\,{\hbox {cm}}$). Similar, the mean of the norm of displacements in the x–y plane is with ${8.64}\,{\hbox {cm}}$ smaller in comparison to ${11.21}\,{\hbox {cm}}$. The reason why the mean deformations in the x–y plane for the purely deformable sphere pack are inferior to the mean deformations for the sphere mixture is related to the impact of the discrete particles in the mixture. Since the DEM bodies are rigid the entire deformation in the sphere pack mixture is carried by the deformable PD bodies and thus, by a total of eight bodies. In contrast, in the purely deformable sphere pack the deformation is distributed over all 16 bodies. Thus, the average deformation in a single deformable bodies is smaller.

Fig. 14

Positions of discrete and peridynamic particles including displacements of peridynamic particles at $t = {1}\,{\hbox {s}}$ in a z-direction, b the x–y plane, at $t = {2}\,{\hbox {s}}$ in c z-direction, d the x–y plane as well as at $t = {3}\,{\hbox {s}}$ in e z-direction, f the x–y plane

Fig. 15

Final particle configurations at $t = {3}\,{\hbox {s}}$ including displacements in z-direction and norm of displacements in the x–y plane for a, b DEM bodies and c, d PD bodies

6 Conclusion

In this contribution an efficient numerical coupling of discontinuous and continuous material behaviour based on an interface contact scheme is developed. In a first step, a generalised force coupling scheme is introduced, consisting of the superposition of inter-particle DEM, intra-particle peridynamic and inter-particle coupling forces. The key part in the formulation are surface particles of peridynamic bodies acting as hybrid particles. Based on the formulation, a multi-scale time integration scheme is proposed leading to the generalised multi-scale PD–DEM coupling framework.

It is shown that the trend of the analytical 3D Hertzian contact theory is captured reasonably well within the developed PD–DEM coupling framework, without calibrating the micro-mechanical DEM contact parameters. Thus, a proper force coupling of the discontinuous–continuous numerical approach is verified. The multi-scale time integration is verified on the basis of a fully dynamic example. It is shown that the staggered integration leads to a slightly smaller dynamic impact than the monolithic scheme due to subsequent kinematic updates of hybrid particles within a global time step. However, the general behaviour is similar. Comparing the computational efficiency it is possible to reduce the computation time up to 21 % when using the staggered scheme for the simple example considered. It is expected that the computational efficiency significantly increases for more complex simulations with higher number of peridynamic particles. The reason behind is the general non-linear scaling of the computation time with respect to the number of particles considered. Most of the computation time is spend for collision detection, which is considerably decreased when applying the multi-scale time integration in case of $\Delta t^{\text {DEM}} < \Delta t^{\text {PD}}$.

The coupling framework is then applied to the simulation of systems with deformable and rigid bodies. Firstly, the successful simulation of the penetration of rigid discrete elements into an elastic body is shown. Secondly, the ability of the framework to represent the major morphology change of squeezing a lengthy deformable body through rigid spheres is presented. Since it is essential to capture this phenomena in the simulation of deformable–rigid grain mixtures under compressible loads, it verifies the applicability of the developed framework for this kind of problems. In the last numerical example the actual compression of a deformable–rigid sphere mixture is considered. Using this example, the capability of the framework to capture the effect of deformable bodies being squeezed and clinging to rigid bodies is proven. As a consequence, a successful application of the developed numerical continuous–discontinuous coupling framework for the simulation of grain mixtures is presented.

In future it is desirable to apply the approach for real-life grain mixtures, e.g. for rubber–sand mixtures. In order to predict their dynamic behaviour appropriately, only two steps are necessary. Firstly, it is required the calibrate the macroscopic material parameters of the rubber by laboratory experiments. In a subsequent step a classical calibration of required DEM contact parameters is necessary, whilst already applying the rubber parameters. Besides specific grain mixtures, the framework could also be applied to capture the penetration of tires by stones on gravel road with stones being possibly trapped in grooves of the tire thread.

Overall, there are numerous possibilities to use the developed approach or to make it applicable to other problems with simple extensions or changes. One of these approaches is the simulation of grain crushing of specific stones in sand grain mixtures. Whilst the sand can still be modelled by DEM bodies it would only be necessary to model the crushable stones by PD bodies and to apply a material law including fracture.

The implementation of the coupling scheme into Yade offers new extensive additional possibilities. Generally, DEM bodies do not have to be spherical particles and more complex DEM shapes can be applied within the framework. Moreover, the applications are not limited to the presented Hertz-Mindlin contact model since various contact models have already been implemented. Generally, it is also possible to apply different contact models within a mixture.

Further, the PD–DEM force coupling scheme is implemented in a generalised object-orientated manner with respect to the applied multi-scale time integration scheme. Thus, the performed contact coupling in Yade is not limited to PD–DEM couplings and can be straight forward extended to other DEM coupling schemes.