A new homogenization scheme for beam and plate structures without a priori requirements on boundary conditions

Abstract

This contribution picks up on a novel approach for a first order homogenization procedure based on the Irving-Kirkwood theory and provides a finite element implementation as well as applications to beam and plate structures. It does not have the fundamental problems of dependency from representative volume element (RVE) size in determining the shear and torsional stiffness for beams and plates, that is present in classic Hill-Mandel methods. Due to the possibility of using minimal boundary conditions whilst simultaneously reusing existing homogenization algorithms, creation of models and numerical implementation are much more straight forward. The presented theory and FE formulation are limited to materially and geometrically linear problems. The approach to determining shear stiffness is based on the assumption of a quadratic shear stress distribution over the height (and width in case of the beam), which causes warping of the cross-section under transverse shear loading. Results for the homogenization scheme are shown for various beam and plate configurations and compared to values from well known analytical solutions or computed full scale models.

1 Introduction

When modeling large structures, there are two main concepts to reduce model complexity and with it computational costs. One is the use of beam, plate and shell elements, if the geometric prerequisites are met by the structure of interest. The other is a multiscale approach, that uses two layers of models - a macro level with a coarse mesh, in which the structure is assumed to be at least partwise homogeneous and a micro/meso level that accounts for inhomogeneities. The micro/meso scale serves the purpose of generating a material law for every point of the macro scale by arguments of separation of scales and homogenization. We use the term micro/meso scale as for beams and plates the lengths of inhomogeneties can be of the same order of magnitude as the lengths of the cross-sections. Therefore, the cross-section is modeled in full length in the micro/meso scale which makes it more of a meso than a micro scale for beams and plates. For more details, see Sect. 4.2.2.

For a maximum reduction of computational costs, it is desirable to use both techniques at the same time. Using the well established Hill-Mandel FE2 methods, see e.g. [1, 2], for multiscale modeling in combination with structural elements such as beams, plates and shells, leads to significant challenges, see e.g. [3,4,5,6,7]. Solutions for these difficulties have only recently been introduced for shells in [8, 9] and for beams in [7]. In [8] a higher order homogenization scheme was introduced for shells with shear soft kinematics and successfully tested on complex structures. However, the authors did not provide any benchmark results for well known properties of homogeneous structures. In [9] a classic Hill-Mandel FE2 approach was considered for shells, but lead to transverse shear stiffness parameters, that were dependent on the size of the RVE, as was shown in [10]. In [7] the classic Hill-Mandel FE2 approach was applied to shear soft beams and additional inner constraints were introduced via interface elements on the micro/meso level. This method leads to well established cross-sectional values for linear elastic benchmark tests and shows results in accordance with full scale models for complex structures with nonlinear geometry and materials. However, the method relies on interface elements for additional constraints and periodic boundary conditions on the micro/meso scale. Both are not easy to use in a practical sense as they have special requirements regarding meshing of the structure. They need to be taken into consideration by the user and are not easy to meet, depending on the nature of the modeled structure.

The aim of this contribution is to show a homogenization scheme for shear soft structures such as beams and plates, that is not based on the Hill-Mandel condition. Instead, it uses the more recently developed homogenization scheme based on the Irving-Kirkwood theory, that was presented in [11, 12]. This approach does not need any interface elements when applied to shear soft beams or plates and has no a-priori requirements concerning boundary conditions, as the micro/meso scale is no longer loaded via boundary conditions but rather via an additional, global constraint that links strains between macro and micro/meso scale.

Main properties of the presented multiscale approach for beams and plates are:

• The macro structure is modeled with a shear soft kinematic as Timoshenko beam and Reissner-Mindlin plate. Therefore, basic elements with six degrees of freedom for spatial beams and five degrees of freedom for plates, including membrane deformation, are used.

• On macro and micro/meso level all strains are assumed to be small. A linear geometry and linear elastic materials are considered.

• RVEs on the micro/meso scale are modeled in three dimensions and allow the modeling of arbitrary inhomogenieties.

• Results for homogenized properties are independent of the RVE’s length without any further adjustments.

• Benchmark tests show perfect accordance with well-known values, except for shear correction factors in more complex geometry. The latter still show good estimates and reasons for their deviation are identified and discussed.

• Inhomogenieties in beam axis direction and reference surface directions are considered and reactions of the macro structure show good accordance with full scale reference solutions.

2 Beam and plate theory

We limit the theory to small strains and thus linear geometry. Furthermore, we make the following assumptions and simplifications for beams and plates:

beams:

• prismatic with straight, untwisted reference axis,

• reference axis through centroids of cross-sections,

• cross-sections are doubly symmetric,

• no warping of cross-sections,

• stresses $S_{xx}, S_{xy}, S_{xz}$ are small and can be neglected.

plates:

• reference surface is plane and the mid surface,

• inextensibility in thickness direction

• no warping of cross-sections,

• in-plane strains of reference surface are included,

• thickness normal stresses $S_{zz}$ are small and can be neglected.

We denote the linear strain tensor by $\hat{{\varvec{\varepsilon }}}$. To avoid confusion with beam and plate strains, denoted by ${\varvec{\varepsilon }}_\text {B}$ and ${\varvec{\varepsilon }}_\text {P}$, we rename its Voigt’s notation with respect to a cartesian base system $\{{\varvec{e}}_x, {\varvec{e}}_y, {\varvec{e}}_z\}$ to ${\varvec{E}}_\text {V}={\varvec{\varepsilon }}_\text {V}=[E_{xx},E_{yy},E_{zz},2E_{xy},2E_{xz},2E_{yz}]^\text {T} =[{\hat{\varepsilon }}_{xx},{\hat{\varepsilon }}_{yy},{\hat{\varepsilon }}_{zz}, 2{\hat{\varepsilon }}_{xy},2{\hat{\varepsilon }}_{xz}, 2{\hat{\varepsilon }}_{yz}]^\text {T}$.

For a beam, the relevant parts are denoted by ${\varvec{E}}_\text {B}=[E_{xx},2E_{xz},2E_{yz}]^\text {T}$ and for a plate by ${\varvec{E}}_\text {P}=[E_{xx},E_{yy},2E_{xy},2E_{xz},2E_{yz}]^\text {T}$.

Analogous to the strains, the stress tensor is denoted by $\hat{{\varvec{\sigma }}}$ and its Voigt’s notation renamed to ${\varvec{S}}_\text {V}={\varvec{\sigma }}_\text {V}=[S_{xx},S_{yy},S_{zz},S_{xy},S_{xz},S_{yz}]^\text {T} =[{\hat{\sigma }}_{xx},{\hat{\sigma }}_{yy},{\hat{\sigma }}_{zz},{\hat{\sigma }}_{xy}, {\hat{\sigma }}_{xz},{\hat{\sigma }}_{yz}]^\text {T}$ to avoid confusion with beam and plate stress resultants, denoted by ${\varvec{\sigma }}_\text {B}$ and ${\varvec{\sigma }}_\text {P}$. Relevant parts of the stresses for beams are denoted by ${\varvec{S}}_\text {B}=[S_{xx},S_{xy},S_{xz}]^\text {T}$ and for plates by ${\varvec{S}}_\text {P}=[S_{xx},S_{yy},S_{xy},S_{xz},S_{yz}]^\text {T}$.

2.1 Kinematics

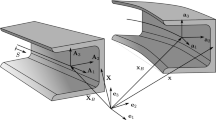
Let ${\mathcal {B}}_0$ be the body of interest (beam or plate) and $\{{\varvec{e}}_x,{\varvec{e}}_y, {\varvec{e}}_z\}$ an orthonormal base system. For a beam, the base system is chosen in a way that ${\varvec{e}}_x$ aligns with the undeformed beam axis. For a plate, ${\varvec{e}}_x$ and ${\varvec{e}}_y$ span the plane of the undeformed reference surface.

Fig. 1

Kinematics of a spatial beam

Fig. 2

Kinematics and stress resultants of a plate

In accordance with the Timoshenko beam theory, displacements $\bar{{\varvec{u}}}=[{\bar{u}}_x,{\bar{u}}_y,{\bar{u}}_z]^\text {T}$ of any point in the beam with coordinates ${\varvec{x}} =[x,y,z]^\text {T}$ are given with respect to the displacements and rotations ${\varvec{u}}_\text {B}^{} =[u_x, u_y, u_z, \beta _x, \beta _y, \beta _z]^\text {T}$ of the reference axis as

$$\begin{aligned} {\bar{u}}_x(x,y,z)&= u_x(x) + z\,\beta _y(x) - y\,\beta _z(x) \, \nonumber \\ {\bar{u}}_y(x,y,z)&= u_y(x) - z\,\beta _x(x) \,\nonumber \\ {\bar{u}}_z(x,y,z)&= u_z(x) + y\,\beta _x(x). \end{aligned}$$

(1)

Then the relevant strains are given with $(\cdot )'=\frac{\text {d} (\cdot )}{\text {d} x}$ as

$$\begin{aligned} E_{xx}&= {\bar{u}}_{x,x} = u'_{x} + z\,\beta '_y -y\, \beta '_z \, \nonumber \\ 2 E_{xy}&= {\bar{u}}_{x,y} + {\bar{u}}_{y,x} = -\beta _z + u'_y - z\,\beta '_x \, \nonumber \\ 2 E_{xz}&= {\bar{u}}_{x,z} + {\bar{u}}_{z,x} = \beta _y + u'_z + y\,\beta '_x \, . \end{aligned}$$

(2)

The six independent beam strains ${\varvec{\varepsilon }}_\text {B} = [ \varepsilon _{x}, \gamma _{xy}, \gamma _{xz}, \kappa _{x}, \kappa _{y}, \kappa _{z}]_\text {B}^\text {T}$ are defined and connected to the relevant strains:

$$\begin{aligned} {\varvec{E}}_\text {B}&= \begin{bmatrix} E_{xx} \\ 2E_{xy} \\ 2E_{xz} \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 &{}0 &{} 0&{} 0&{} z &{} -y \\ 0 &{}1 &{} 0&{} -z&{} 0 &{} 0 \\ 0 &{}0 &{} 1&{} y&{} 0 &{} 0 \\ \end{bmatrix}}_{\displaystyle {{\varvec{A}}_\text {B}}} \begin{bmatrix} \varepsilon _{x} \\ \gamma _{xy} \\ \gamma _{xz} \\ \kappa _{x} \\ \kappa _{y} \\ \kappa _{z} \end{bmatrix}_\text {B} \nonumber \\ {\varvec{E}}_\text {B}&= {\varvec{A}}_\text {B}^{} \, {\varvec{\varepsilon }}_\text {B}^{} \,, \end{aligned}$$

(3)

$$\begin{aligned} {\varvec{\varepsilon }}_\text {B}^{}&= \begin{bmatrix} \varepsilon _{x} \\ \gamma _{xy} \\ \gamma _{xz} \\ \kappa _{x} \\ \kappa _{y} \\ \kappa _{z} \end{bmatrix}_\text {B} = \begin{bmatrix} u'_x\\ u'_y-\beta _z\\ u'_z+\beta _y\\ \beta '_x\\ \beta '_y\\ \beta '_z \end{bmatrix}. \end{aligned}$$

(4)

For plates, a Reissner-Mindlin kinematic is used. The displacements and rotations of the reference surface are given by ${\varvec{u}}_\text {P}^{} = [u_x,u_y,u_z,\beta _x,\beta _y]^\text {T}$. The displacements $\bar{{\varvec{u}}}=[{\bar{u}}_x,{\bar{u}}_y,{\bar{u}}_z]^\text {T}$ of any point within the plate with coordinates ${\varvec{x}}=[x,y,z]^\text {T}$ are then given by

$$\begin{aligned} {\bar{u}}_x&= u_x(x,y) + z\,\beta _x(x,y)\,\nonumber \\ {\bar{u}}_y&= u_y(x,y) + z\,\beta _y(x,y)\,\nonumber \\ {\bar{u}}_z&= u_z(x,y)\,. \end{aligned}$$

(5)

The relevant strains are

$$\begin{aligned} E_{xx}&= {\bar{u}}_{x,x}=u_{x,x}+z\, \beta _{x,x}\, \nonumber \\ E_{yy}&= {\bar{u}}_{y,y}=u_{y,y}+z\, \beta _{y,y}\, \nonumber \\ 2 E_{xy}&= {\bar{u}}_{x,y} + {\bar{u}}_{y,x} = u_{x,y} + z\,\beta _{x,y} + u_{y,x} + z\,\beta _{y,x}\, \nonumber \\ 2 E_{xz}&= {\bar{u}}_{x,z} + {\bar{u}}_{z,x} = \beta _{x}+u_{z,x}\, \nonumber \\ 2 E_{yz}&= {\bar{u}}_{y,z} + {\bar{u}}_{z,y} = \beta _y + u_{z,y}\, . \end{aligned}$$

(6)

The eight plate strains ${\varvec{\varepsilon }}_\text {P}^{} =[\varepsilon _x, \varepsilon _y,\gamma _{xy},\kappa _x, \kappa _y,\kappa _{xy},\gamma _{xz},\gamma _{yz}]_\text {P}^\text {T}$ are defined and connected to the relevant strains:

$$\begin{aligned} {\varvec{E}}_\text {P}^{}&= \begin{bmatrix} E_{xx}\\ E_{yy} \\ 2 E_{xy}\\ 2 E_{xz}\\ 2 E_{yz} \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 &{} 0 &{} 0 &{} z &{} 0 &{}0 &{}0&{}0\\ 0 &{} 1 &{} 0 &{} 0 &{} z &{}0 &{}0&{}0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{}z &{}0&{}0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 &{}1&{}0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 &{}0&{}1 \end{bmatrix}}_{\displaystyle {{\varvec{A}}_\text {P}}} \begin{bmatrix} \varepsilon _x\\ \varepsilon _y\\ \gamma _{xy}\\ \kappa _x\\ \kappa _y\\ \kappa _{xy}\\ \gamma _{xz}\\ \gamma _{yz} \end{bmatrix}_\text {P} \end{aligned}$$

(7)

$$\begin{aligned} {\varvec{\varepsilon }}_\text {P}^{}&= \begin{bmatrix} \varepsilon _x\\ \varepsilon _y\\ \gamma _{xy}\\ \kappa _x\\ \kappa _y\\ \kappa _{xy}\\ \gamma _{xz}\\ \gamma _{yz} \end{bmatrix}_\text {P} = \begin{bmatrix} u_{x,x}\\ u_{y,y}\\ u_{x,y}+u_{y,x}\\ \beta _{x,x}\\ \beta _{y,y}\\ \beta _{x,y}+\beta _{y,x}\\ \beta _x + u_{z,x}\\ \beta _y + u_{z,y}\\ \end{bmatrix}. \end{aligned}$$

(8)

We solely include the in-plane strains of the plate to showcase the potential of the presented theory for extension to shell structures. The in-plane parts are not an area of focus in this contribution, but it can be shown that the corresponding entries in the homogenized stiffness matrix are computed as the analytical values for a homogeneous material [13].

2.2 Constitutive equations for the stress resultants

The beam stress resultants are normal and transverse forces as well as torsional and bending moments, which are arranged in a vector

$$\begin{aligned} {\varvec{\sigma }}_\text {B}^{} (x)&= \begin{bmatrix} N \\ Q_y\\ Q_z \\ M_x\\ M_y\\ M_z \end{bmatrix} = \int \limits _{A} \begin{bmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\\ 0 &{} -z&{} y\\ z &{} 0 &{} 0\\ -y&{} 0 &{} 0 \end{bmatrix} \begin{bmatrix} S_{xx} \\ S_{xy} \\ S_{xz} \end{bmatrix} \text { d}A \nonumber \\ {\varvec{\sigma }}_\text {B}^{} (x)&= \int \limits _{A} {\varvec{A}}_\text {B}^\text {T} \, {\varvec{S}}_\text {B}^{} \text { d}A \, . \end{aligned}$$

(9)

Here, A denotes the area of the beam cross-section.

A linear elastic isotropic material model is used to compute the stresses

$$\begin{aligned} {\varvec{S}}_\text {B}= \begin{bmatrix} S_{xx} \\ S_{xy} \\ S_{xz} \end{bmatrix}= \underbrace{ \begin{bmatrix} E &{}0 &{}0 \\ 0&{} G &{}0 \\ 0&{} 0 &{}G \end{bmatrix}}_{\displaystyle {{\varvec{C}}_\text {B}}} \begin{bmatrix} E_{xx} \\ 2E_{xy} \\ 2E_{xz} \end{bmatrix} = {\varvec{C}}_\text {B} \, {\varvec{E}}_\text {B}\,. \end{aligned}$$

(10)

Where E and $G=E/[2(1+\nu )]$ denote Young’s and shear modulus, respectively, and $\nu$ the Poisson’s ratio.

Introducing (10) into (9) yields

$$\begin{aligned} {\varvec{\sigma }}_\text {B}^{} = \int \limits _{A} {\varvec{A}}_\text {B}^\text {T} {\varvec{C}}_\text {B}^{} {\varvec{A}}_\text {B}^{} \text { d}A \, \,{\varvec{\varepsilon }}_\text {B}^{} = {\varvec{D}}_\text {B}^{} \,{\varvec{\varepsilon }}_\text {B}^{} \, . \end{aligned}$$

(11)

The material matrix ${\varvec{D}}_\text {B}$ for the beam is modified to

$$\begin{aligned} {\varvec{D}}_\text {B} = \begin{bmatrix} EA &{} 0 &{} 0&{} 0 &{} 0 &{} 0\\ 0 &{} \varkappa _y GA &{} 0&{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \varkappa _z GA&{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0&{} GI_T &{} 0 &{} 0\\ 0 &{} 0 &{} 0&{} 0 &{} EI_y &{} 0\\ 0 &{} 0 &{} 0&{} 0 &{} 0 &{} EI_z\\ \end{bmatrix} \end{aligned}$$

(12)

with shear correction factors $\varkappa _y$ and $\varkappa _z$. They are introduced to correct the overly stiff response to transverse shear loading. The area moments of inertia are denoted by $I_y$ and $I_z$ while $I_T$ denotes the torsional moment of inertia.

In an analogous way, stress resultants for a plate with thickness h are defined as

$$\begin{aligned} {\varvec{\sigma }}_\text {P}^{}&= \begin{bmatrix} n_x\\ n_y\\ n_{xy}\\ m_x\\ m_y\\ m_{xy}\\ q_x\\ q_y \end{bmatrix} = \int \limits _{-h/2}^{h/2} \begin{bmatrix} 1&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0\\ z&{}0&{}0&{}0&{}0\\ 0&{}z&{}0&{}0&{}0\\ 0&{}0&{}z&{}0&{}0\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{bmatrix} \begin{bmatrix} S_{xx}\\ S_{yy}\\ S_{xy}\\ S_{xz}\\ S_{yz} \end{bmatrix} \text { d}z \nonumber \\ {\varvec{\sigma }}_\text {P}^{}&= \int \limits _{-h/2}^{h/2} {\varvec{A}}_\text {P}^\text {T}\, {\varvec{S}}_\text {P}^{} \text { d}z \, . \end{aligned}$$

(13)

Again, a linear elastic isotropic material model is used to connect stresses and strains and then introduced into (13):

$$\begin{aligned} {\varvec{S}}_\text {P}&= \begin{bmatrix} S_{xx}\\ S_{yy}\\ S_{xy}\\ S_{xz}\\ S_{yz} \end{bmatrix} = \dfrac{E}{1-\nu ^2} \begin{bmatrix} 1&{}\nu &{}0&{}0&{}0\\ \nu &{}1&{}0&{}0&{}0\\ 0&{}0&{}\frac{1-\nu }{2}&{}0&{}0\\ 0&{}0&{}0&{}\frac{1-\nu }{2}&{}0\\ 0&{}0&{}0&{}0&{}\frac{1-\nu }{2} \end{bmatrix} \begin{bmatrix} E_{xx}\\ E_{yy} \\ 2 E_{xy}\\ 2 E_{xz}\\ 2 E_{yz} \end{bmatrix}\nonumber \\ {\varvec{S}}_\text {P}&= {\varvec{C}}_\text {P} {\varvec{E}}_\text {P} \, . \end{aligned}$$

(14)

$$\begin{aligned} {\varvec{\sigma }}_\text {P}^{}&= \int \limits _{-h/2}^{h/2} {\varvec{A}}_\text {P}^\text {T} {\varvec{C}}_\text {P}^{} {\varvec{A}}_\text {P}^{} \text { d}z \, {\varvec{\varepsilon }}_\text {P}^{}={\varvec{D}}_\text {P}^{}\, {\varvec{\varepsilon }}_\text {P}^{}\, . \end{aligned}$$

(15)

The material matrix ${\varvec{D}}_\text {P}$ contains the entries

$$\begin{aligned} {\varvec{D}}_\text {P} = \begin{bmatrix} {\varvec{D}}_\text {m} &{} {\varvec{0}} &{}{\varvec{0}} \\ {\varvec{0}} &{} {\varvec{D}}_\text {b} &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{0}} &{}{\varvec{D}}_\text {s} \end{bmatrix} \end{aligned}$$

(16)

where

$$\begin{aligned} {\varvec{D}}_\text {m}&= \dfrac{Eh}{1-\nu ^2} \begin{bmatrix} 1&{}\nu &{}0\\ \nu &{}1&{}0\\ 0&{}0&{}\frac{1-\nu }{2} \end{bmatrix},\nonumber \\ {\varvec{D}}_\text {b}&= \dfrac{Eh^3}{12(1-\nu ^2)} \begin{bmatrix} 1&{}\nu &{}0\\ \nu &{}1&{}0\\ 0&{}0&{}\frac{1-\nu }{2} \end{bmatrix},\nonumber \\ {\varvec{D}}_\text {s}&= \varkappa \dfrac{Eh}{(1-\nu ^2)} \begin{bmatrix} \frac{1-\nu }{2}&{}0\\ 0&{}\frac{1-\nu }{2} \end{bmatrix}. \end{aligned}$$

(17)

Analogous to the beam, the shear part ${\varvec{D}}_\text {s}$ is modified to incorporate a shear correction factor $\varkappa$ to correct the overly stiff response to transverse shear loading.

3 Multiscale framework

3.1 Basics

This section briefly describes the relevant parts of the findings presented in [12]. There, a homogenization framework for solid bodies was presented, that is based on the Irving-Kirkwood theory (see [14]). It does not depend on any a priori assumptions on boundary conditions or loading conditions of the micro/meso scale, but only assumes volumetric averaging between micro/meso and macro scale solely for basic extensive mechanical quantities mass, linear momentum and energy.

A body ${\mathcal {B}}$ is described in two scales. On a first, macro scale it is assumed to be homogeneous. On a second, micro/meso scale, a lot more details are incorporated, including inhomogeneities or a micro/meso structure with characteristic lengths, that are small compared to those of the macro structure of the body. For details regarding size requirements between macro and micro/meso scale and inhomogenizations, see for example [15,16,17].

The body ${\mathcal {B}}$ takes up the region $\Omega$ with boundary $\partial \Omega$. Its macro scale representation is described in an ortho-normal base system $\{{\varvec{e}}_{y_1},{\varvec{e}}_{y_2},{\varvec{e}}_{y_3}\}$, its micro/meso scale representation accordingly in $\{{\varvec{e}}_{x_1},{\varvec{e}}_{x_2},{\varvec{e}}_{x_3}\}$. A point within the body can then be identified with its coordinates ${\varvec{y}}$ and ${\varvec{x}}$ in macro and micro/meso scale, respectively.

With $\rho$ the mass density, ${\varvec{v}}$ the velocity of a material point, ${\varvec{t}}$ the boundary force vector on $\partial \Omega$ and ${\varvec{b}}$ the body force vector, the continuity equation for mass and the balance of linear momentum can be formulated independently from each other for the whole body in the macro scale and for a small subsection ${\mathcal {P}}$ with boundary $\partial {\mathcal {P}}$ of the micro/meso scale. Entities of the macro scale are denoted by superscript $(\cdot )^\text {M}$, those of the micro/meso scale with $(\cdot )^\text {m}$.

The continuity of mass then reads as

$$\begin{aligned} \dfrac{\text {d}}{\text {d}t}\int \limits _{\Omega }\rho ^\text {M} \text { d}v^\text {M}&=0 \, , \end{aligned}$$

(18)

$$\begin{aligned} \dfrac{\text {d}}{\text {d}t}\int \limits _{{\mathcal {P}}}\rho ^\text {m} \text { d}v^\text {m}&=0 \, \end{aligned}$$

(19)

and the balance of linear momentum as

$$\begin{aligned} \dfrac{\text {d}}{\text {d}t}\int \limits _{\Omega }\rho ^\text {M}\,{\varvec{v}}^\text {M} \text { d}v^\text {M}&= \int \limits _{\partial \Omega } {\varvec{t}}^\text {M} \text { d}a^\text {M} + \int \limits _{\Omega } {\varvec{b}}^\text {M} \text { d}v^\text {M} \, , \end{aligned}$$

(20)

$$\begin{aligned} \dfrac{\text {d}}{\text {d}t}\int \limits _{{\mathcal {P}}}\rho ^\text {m}\,{\varvec{v}}^\text {m} \text { d}v^\text {m}&= \int \limits _{\partial {\mathcal {P}}} {\varvec{t}}^\text {m} \text { d}a^\text {m} + \int \limits _{{\mathcal {P}}} {\varvec{b}}^\text {m} \text { d}v^\text {m} \, . \end{aligned}$$

(21)

To connect the entities of both scales, an averaging theorem for mass density and linear momentum is introduced

$$\begin{aligned} \rho ^\text {M}({\varvec{y}})&= \dfrac{1}{v^\text {m}}\int \limits _{{\mathcal {P}}} \rho ^\text {m}({\varvec{x}}) \text { d}v^\text {m} \, , \end{aligned}$$

(22)

$$\begin{aligned} \rho ^\text {M}({\varvec{y}}){\varvec{v}}^\text {M}({\varvec{y}})&= \dfrac{1}{v^\text {m}}\int \limits _{{\mathcal {P}}}\rho ^\text {m}({\varvec{x}})\,{\varvec{v}}^\text {m}({\varvec{x}}) \text { d}v^\text {m} \, . \end{aligned}$$

(23)

For this averaging theorem, it is essential, that the subsection ${\mathcal {P}}$ is a small surrounding area of the point ${\varvec{y}}$. It is in fact the RVE corresponding to ${\varvec{y}}$.

The authors in [11] and [12] showed that this theorem connects both scales in a consistent manner and that they bring about averaging equations for the body force vector and stress tensor, that can be described for the quasi-static case as

$$\begin{aligned} {\varvec{b}}^\text {M}&=\dfrac{1}{v^\text {m}}\int \limits _{{\mathcal {P}}}{\varvec{b}}^\text {m} \text { d}v^\text {m} \, , \end{aligned}$$

(24)

$$\begin{aligned} \hat{{\varvec{\sigma }}}^\text {M}&=\dfrac{1}{v^\text {m}}\int \limits _{{\mathcal {P}}}\hat{{\varvec{\sigma }}}^\text {m}\text { d}v^\text {m} \, . \end{aligned}$$

(25)

For entities of the reference configuration, analogous homogenization equations can be derived.

3.2 Macro to micro/meso transition

On macro level, the strong form of the boundary value problem is described by

$$\begin{aligned} \text {Div}\left( \hat{{\varvec{\sigma }}}^\text {M}\right) + {\varvec{b}}^\text {M}&=0 \qquad&\text {in } \Omega \end{aligned}$$

(26)

$$\begin{aligned} {\varvec{u}}^\text {M}&= \bar{{\varvec{u}}} \qquad&\text {on } \partial \Omega ^{{\varvec{u}}} \end{aligned}$$

(27)

$$\begin{aligned} {\varvec{t}}^\text {M}&= \bar{{\varvec{t}}} \qquad&\text {on } \partial \Omega ^{{\varvec{t}}} \, . \end{aligned}$$

(28)

Where $\Omega$ with boundary $\partial \Omega$ is the region occupied by the body. ${\varvec{\sigma }}^\text {M}$ is the stress tensor, ${\varvec{b}}^\text {M}$ denotes the body force vector. The boundary $\partial \Omega$ is divided into a part $\partial \Omega ^{{\varvec{u}}}$ with given boundary displacements $\bar{{\varvec{u}}}$ and a part $\partial \Omega ^{{\varvec{t}}}$ with given boundary forces $\bar{{\varvec{t}}}$. The union of both parts makes up the full boundary: $\partial \Omega = \partial \Omega ^{{\varvec{u}}} \cup \partial \Omega ^{{\varvec{t}}}$.

On micro/meso level, the equilibrium equation for stresses and body forces holds, but as mentioned before, there are no a priori boundary conditions so far (apart from restraining rigid body motions):

$$\begin{aligned} \text {Div}\left( \hat{{\varvec{\sigma }}}^\text {m}\right) + {\varvec{b}}^\text {m}=0 \qquad \text {in } {\mathcal {P}}. \end{aligned}$$

(29)

In order to define a load on the micro/meso level consistent with the macro level, a homogenization of the strain tensor analogous to the homogenization Eqs. (22)-(25) is assumed [12]:

$$\begin{aligned} \hat{{\varvec{\varepsilon }}}^{M}=\dfrac{1}{V^\text {m}}\int \limits _{{\mathcal {P}}}\hat{{\varvec{\varepsilon }}}^{\text {m}}\text { d}V^\text {m}. \end{aligned}$$

(30)

Since the micro/meso region ${\mathcal {P}}$ corresponds to a single point in the macro scale, the macro strains $\hat{{\varvec{\varepsilon }}}^{M}$ are constant throughout ${\mathcal {P}}$. Therefore,

$$\begin{aligned} \int \limits _{{\mathcal {P}}}\left( \hat{{\varvec{\varepsilon }}}^{M}-\hat{{\varvec{\varepsilon }}}^{\text {m}}\right) \text { d}V^\text {m}=0 \end{aligned}$$

(31)

holds. This is essentially an additional constraint for the micro/meso scale boundary value problem, that can be introduced into the weak form of (29) in Voigt’s notation via Lagrange parameters:

$$\begin{aligned}&{\bar{g}}({\varvec{u}}, \delta {\varvec{u}}, {\varvec{\lambda }}_\text {V},\delta {\varvec{\lambda }}_\text {V})\nonumber \\&\quad = \,g({\varvec{u}}, \delta {\varvec{u}}) + \int \limits _{{\mathcal {P}}}\delta {\varvec{\lambda }}_\text {V}^\text {T}\left( {\varvec{E}}_\text {V}^\text {M}-{\varvec{E}}_\text {V}^\text {m}\right) \text { d}V \nonumber \\&\qquad + \int \limits _{{\mathcal {P}}}{\varvec{\lambda }}_\text {V}^\text {T}\left( \delta {\varvec{E}}_\text {V}^\text {M}-\delta {\varvec{E}}_\text {V}^\text {m}\right) \text { d}V =\,0 \,. \end{aligned}$$

(32)

Here, $g({\varvec{u}}, \delta {\varvec{u}})$ denotes the weak form of (29) and $\delta (\cdot )$ denotes the variation of the quantity $(\cdot )$. A vector of Lagrange parameters ${\varvec{\lambda }}_\text {V} \in {\mathbb {R}}^6$ is used to enforce (31). They clearly show to be stresses.

We assume ${\varvec{E}}_\text {V}^\text {M}$, ${\varvec{E}}_\text {V}^\mathrm{m}$ and ${\varvec{\lambda }}_\text {V}$ as unknown. Assuming ${\varvec{E}}_\text {V}^\mathrm{M}$ as an unknown quantity leads to a symmetric system matrix in the finite element formulation and also makes it possible to use already existing algorithms to generate the homogenized entities later on. The given values of ${\varvec{E}}_\text {V}^\mathrm{M}$ will then be provided by means of boundary conditions.

Equation (32) shows the need for appropriate ansatz functions for ${\varvec{\lambda }}_\text {V}$ in order to fulfill the side conditions in a weighted average instead of a point wise manner. A point wise fulfillment of the side condition would mean a uniform strain across all of ${\mathcal {P}}$ and simply lead to Voigt’s bound for homogenized entitites, which does not account for the internal structure and material distribution within ${\mathcal {P}}$. In essence, the micro/meso scale needs to allow for more complex deformation than the macro scale to make the concept of homogenization worthwhile.

The complete weak form for the micro/meso scale without boundary and body forces then reads

$$\begin{aligned}&{\bar{g}}({\varvec{u}}, \delta {\varvec{u}}, {\varvec{\lambda }}_\text {V},\delta {\varvec{\lambda }}_\text {V})\nonumber \\&\quad = \int \limits _{{\mathcal {P}}}\delta {{{\varvec{E}}}_\text {V}^\text {m}}^\text {T}\left( {\varvec{S}}_\text {V}^{} -{\varvec{\lambda }}_\text {V}\right) \text { d}V + \int \limits _{{\mathcal {P}}}\delta {\varvec{\lambda }}_\text {V}^\text {T}\left( {\varvec{E}}_\text {V}^\text {M}-{\varvec{E}}_\text {V}^\text {m}\right) \text { d}V\nonumber \\&\qquad +\int \limits _{{\mathcal {P}}}\delta {{{\varvec{E}}}_\text {V}^\text {M}}^\text {T}\,{\varvec{\lambda }}_\text {V}^{} \text { d}V \; . \end{aligned}$$

(33)

4 Finite element formulation and application to beams and plates

4.1 Required element formulations

A standard isoparametric, displacement-based finite element formulation is invoked. We use the same basic scheme for brick, plate and beam elements. The region $\Omega$, that is occupied by the body of interest ${\mathcal {B}}$, is approximated with a finite number of elements $\Omega ^e$: $\Omega \approx \Omega ^\text {h}=\bigcup \limits _{e=1}^{numel}\Omega ^e$. The superscript h refers to the finite element approximation and numel is the total number of elements.

Geometry, displacements and rotations, as well as virtual quantities are interpolated with functions $N_K$. We use linear and quadratic functions $N_K(\xi )$ for beam elements, bilinear/biquadratic $N_K(\xi ,\eta )$ for plates and trilinear/triquadratic $N_K(\xi ,\eta ,\zeta )$ for brick elements, where $\xi$, $\eta$, $\zeta$ are the coordinates in parameter space with $\xi , \eta , \zeta \in [-1,1]$. The interpolations then are

$$\begin{aligned} {\varvec{X}}^\text {h}&= \sum \limits _{K=1}^{nel}N_K {\varvec{X}}_K \,, \quad {\varvec{x}}^\text {h} = \sum \limits _{K=1}^{nel}N_K {\varvec{x}}_K \,, \end{aligned}$$

(34)

$$\begin{aligned} {\varvec{u}}^\text {h}&= \sum \limits _{K=1}^{nel} N_K {\varvec{v}}_K \,, \quad \delta {\varvec{u}}^\text {h} = \sum \limits _{I=1}^{nel} N_I \delta {\varvec{v}}_I\, , \end{aligned}$$

(35)

$$\begin{aligned} {\varvec{\varepsilon }}^\text {h}&= {\varvec{L}} {\varvec{u}}^\text {h} = \sum \limits _{K=1}^{nel}{\varvec{L}} N_K {\varvec{v}}_K = \sum \limits _{K=1}^{nel} {\varvec{B}}_K^{} {\varvec{v}}_K \,,\end{aligned}$$

(36)

$$\begin{aligned} \delta {\varvec{\varepsilon }}^\text {h}&= \sum \limits _{I=1}^{nel} {\varvec{B}}_I \delta {\varvec{v}}_I. \end{aligned}$$

(37)

Here, nel denotes the number of nodes per element and ${\varvec{L}}$ describes a differential operator that connects the displacement vector to the strain vector. It is different for each application (3D body/ plate/ beam). For a 3D body (brick element) a displacement vector ${\varvec{u}}_\text {V}=[u_x,u_y,u_z]^\text {T}$ with three translational degrees of freedom is used. The strains are ${\varvec{\varepsilon }}_\text {V}={\varvec{E}}_\text {V}$ and the corresponding differential operator ${\varvec{L}}_\text {V}$ reads

$$\begin{aligned} {\varvec{\varepsilon }}_\text {V}^{}= \begin{bmatrix} E_{xx}\\ E_{yy}\\ E_{zz}\\ 2E_{xy}\\ 2E_{xz}\\ 2E_{yz} \end{bmatrix} = \begin{bmatrix} \partial _x &{}0&{}0\\ 0&{}\partial _y&{}0\\ 0&{}0&{}\partial _z\\ \partial _y&{}\partial _x&{}0\\ \partial _z&{}0&{}\partial _x\\ 0&{}\partial _z&{}\partial _y\\ \end{bmatrix} \begin{bmatrix} u_x\\ u_y\\ u_z \end{bmatrix} = {\varvec{L}}_\text {V}^{} {\varvec{u}}_\text {V}^{} \, . \end{aligned}$$

(38)

For a beam, a displacement vector ${\varvec{u}}_\text {B} = [u_x,u_y,u_z,\beta _x,\beta _y,\beta _z]^\text {T}$ with three displacements and three rotations of the reference axis is used. The corresponding differential operator reads

$$\begin{aligned} {\varvec{\varepsilon }}_\text {B}^{}&= \begin{bmatrix} \varepsilon _{x} \\ \gamma _{xy} \\ \gamma _{xz} \\ \kappa _{x} \\ \kappa _{y} \\ \kappa _{z} \end{bmatrix} = \begin{bmatrix} u'_x\\ u'_y-\beta _z\\ u'_z+\beta _y\\ \beta '_x\\ \beta '_y\\ \beta '_z \end{bmatrix} \nonumber \\ {\varvec{\varepsilon }}_\text {B}^{}&= \begin{bmatrix} \partial _x &{}0 &{}0 &{}0 &{}0 &{}0\\ 0&{}\partial _x&{}0 &{}0&{}0&{}-1\\ 0&{}0&{}\partial _x&{}0&{}1&{}0\\ 0&{}0&{}0&{}\partial _x&{}0&{}0\\ 0&{}0&{}0&{}0&{}\partial _x&{}0\\ 0&{}0&{}0&{}0&{}0&{}\partial _x\\ \end{bmatrix} \begin{bmatrix} u_x\\ u_y\\ u_z\\ \beta _x\\ \beta _y \\ \beta _z \end{bmatrix}= {\varvec{L}}_\text {B}^{}\, {\varvec{u}}_\text {B}^{} \,. \end{aligned}$$

(39)

For a plate, a displacement vector ${\varvec{u}}_\text {P}^{} = {[}u_x,u_y,u_z, \varphi _x, \varphi _y]^\text {T}$ with three translations and two rotations of the reference surface is used. The two rotations $\varphi _x=-\beta _y$ and $\varphi _y=\beta _x$ are used for easier application of boundary conditions and readability of results. The corresponding differential operator ${\varvec{L}}_\text {P}$ reads

$$\begin{aligned} {\varvec{\varepsilon }}_\text {P}^{}&= \begin{bmatrix} \varepsilon _x\\ \varepsilon _y\\ \gamma _{xy}\\ \kappa _x\\ \kappa _y\\ \kappa _{xy}\\ \gamma _{xz}\\ \gamma _{yz} \end{bmatrix} = \begin{bmatrix} u_{x,x}\\ u_{y,y}\\ u_{x,y}+u_{y,x}\\ \beta _{x,x}\\ \beta _{y,y}\\ \beta _{x,y}+\beta _{y,x}\\ \beta _x + u_{z,x}\\ \beta _y + u_{z,y}\\ \end{bmatrix}\nonumber \\ {\varvec{\varepsilon }}_\text {P}^{}&= \begin{bmatrix} \partial _x &{}0&{}0&{}0&{}0\\ 0&{}\partial _y&{}0&{}0&{}0\\ \partial _y&{}\partial _x&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}\partial _x\\ 0&{}0&{}0&{}-\partial _y&{}0\\ 0&{}0&{}0&{}-\partial _x&{}\partial _y\\ 0&{}0&{}\partial _x&{}0&{}1\\ 0&{}0&{}\partial _y&{}-1&{}0 \end{bmatrix} \begin{bmatrix} u_x\\ u_y\\ u_z\\ \varphi _x\\ \varphi _y \end{bmatrix} ={\varvec{L}}_\text {P}^{}\,{\varvec{u}}_\text {P}^{} \, . \end{aligned}$$

(40)

The approximations (34)-(37) are inserted into the weak form in vector notation on the macro scale. Omitting the subscripts $(\cdot )_\text {V}$, $(\cdot )_\text {P}$ and $(\cdot )_\text {B}$ for a general representation, standard procedure leads to

$$\begin{aligned} g({\varvec{u}}^\text {h}, \delta {\varvec{u}}^\text {h})&= \sum \limits _{e=1}^{numel}\delta {\varvec{v}}^{e\text {T}}\left( {\varvec{k}}^{e} {\varvec{v}}^{e} +{\varvec{f}}^{e}\right) \nonumber \\ g({\varvec{u}}^\text {h}, \delta {\varvec{u}}^\text {h})&=\delta {\varvec{v}}^\text {T}\left( {\varvec{K}} {\varvec{v}} +{\varvec{F}}\right) =0 \,. \end{aligned}$$

(41)

The quantities ${\varvec{K}}$, ${\varvec{v}}$ and ${\varvec{F}}$ are generated by assembling all element quantities ${\varvec{k}}^e$, ${\varvec{v}}^e$, ${\varvec{f}}^e$ into one corresponding system quantity each.

For beam and plate elements, a selectively reduced integration scheme is used to mitigate the effects of transverse shear locking. One fewer Gauss point is used per element dimension to integrate the shear parts of the element stiffness matrix ${\varvec{k}}^e$ than is used for the other parts.

4.2 Elements on micro/meso level

On micro/meso scale, 3D brick elements are used. For approximation of displacement quantities and micro/meso strains in the weak form (33), we use the method described in Sect. 4.1. The approximation of Lagrange parameters is dependent on the type of elements used on macro level as they need to account for the relations between beam or plate on macro level and 3D body on micro/meso level. We first develop an implementation for use with 3D bodies on macro level to show differences between the approaches presented here and in [12]. We do not showcase any numerical examples for 3D bodies as this was already done there.

4.2.1 3D bodies

When brick elements are used on macro level to describe a three dimensional body, macro and micro/meso scale both use the same strains within their respective elements. Therefore, the macro strain vector ${\varvec{\varepsilon }}_\text {V}^\text {M} = {\varvec{E}}_\text {V}^\text {M}$ is directly available for use in the weak form on micro/meso level (33) and none of its entries are zero by definition. This means, an approximation for ${\varvec{E}}_\text {V}^\text {M}$ and ${\varvec{\lambda }}_\text {V}$ with constant functions as in

$$\begin{aligned} {{\varvec{E}}_\text {V}^\text {M}}^\text {h}&= {\varvec{A}}_\text {V}^{}\,{\varvec{\varepsilon }}_\text {V}^\text {M} \, , \qquad \delta {{\varvec{E}}_\text {V}^\text {M}}^\text {h} = {\varvec{A}}_\text {V}^{} \,\delta {\varvec{\varepsilon }}_\text {V}^\text {M} \, ,\nonumber \\ {\varvec{\lambda }}_\text {V}^\text {h}&= \bar{{\varvec{A}}}_\text {V}^{}\,{\varvec{\lambda }}_\text {V} \, , \qquad \delta {\varvec{\lambda }}_\text {V}^\text {h} = \bar{{\varvec{A}}}_\text {V}^{}\,\delta {\varvec{\lambda }}_\text {V} \end{aligned}$$

(42)

with

$$\begin{aligned} {\varvec{A}}_\text {V} = \bar{{\varvec{A}}}_\text {V} = \text {diag}\{1,1,1,1,1,1 \} \end{aligned}$$

(43)

is feasible. The assumption of constant Lagrange parameters for the whole micro/meso model leads to a fulfillment of the side condition (31) only in an averaged manner as desired (see Sect. 3.2). Inserting those approximations together with (34)-(37) into (33) leads to

$$\begin{aligned} {\bar{g}}^\text {h}=&\sum \limits _{e=1}^{numel}\left[ \delta {{\varvec{v}}^{e}}^\text {T}\left( {{\varvec{f}}_v^e} + {\varvec{k}}^{e} {\varvec{v}}^{e} - {{\varvec{M}}_\text {V}^e}\,{\varvec{\lambda }}_\text {V}^{}\right) \right. \\&+\delta {\varvec{\lambda }}_\text {V}^\text {T} \left( {{\varvec{f}}_\lambda ^e} +{{\varvec{T}}_\text {V}^e}\,{\varvec{\varepsilon }}_\text {V}^\text {M} - {{\varvec{M}}_\text {V}^e}^\text {T}\, {\varvec{v}}^{e}\right) \\&\left. + \, \delta {\varvec{\varepsilon }}_\text {V}^\text {M} \left( {{\varvec{f}}_{\varepsilon }^e} + {{\varvec{T}}_\text {V}^e}\,{\varvec{\lambda }}_\text {V}^{}\right) \right] \end{aligned}$$

where

$$\begin{aligned} {\varvec{M}}_\text {V}^e&= \begin{bmatrix} {{\varvec{M}}_\text {V}^e}_1\\ \vdots \\ {{\varvec{M}}_\text {V}^e}_I\\ \vdots \\ {{\varvec{M}}_\text {V}^e}_{nel} \end{bmatrix}, \quad {{\varvec{f}}^e_v} = \begin{bmatrix} {{\varvec{f}}^e_v}_1\\ \vdots \\ {{\varvec{f}}^e_v}_I\\ \vdots \\ {{\varvec{f}}^e_v}_{nel} \end{bmatrix},\\ {{\varvec{T}}_\text {V}^e}&= \int \limits _{{\mathcal {P}}^e}\bar{{\varvec{A}}}_\text {V}^\text {T}{{\varvec{A}}}_\text {V}^{} \text { d}V^e \,, \\ {{\varvec{f}}^e_\lambda }&= \int \limits _{{\mathcal {P}}^e}\bar{{\varvec{A}}}_\text {V}^\text {T} \left( {\varvec{E}}_\text {V}^\text {M} -{\varvec{E}}_\text {V}^\text {m}\right) \text { d}V^e \,, \nonumber \\ {{\varvec{f}}^e_\varepsilon }&= \int \limits _{{\mathcal {P}}^e}{\varvec{A}}_\text {V}^\text {T}{\varvec{\lambda }}_\text {V}^{} \text { d}V^e \end{aligned}$$

with

$$\begin{aligned} {{\varvec{M}}_\text {V}^e}_I&= \int \limits _{{\mathcal {P}}^e}{\varvec{B}}_I^\text {T}\bar{{\varvec{A}}}_\text {V}^{} \text { d}V^e \end{aligned}$$

(44)

and

$$\begin{aligned} {{\varvec{f}}^e_v}_I = \int \limits _{{\mathcal {P}}^e}{\varvec{B}}_I^\text {T} \left( {\varvec{S}}_\text {V}^{} -{\varvec{\lambda }}_\text {V}^{}\right) \text { d}V^e \, . \end{aligned}$$

Assembly of element quantities into system quantities leads to

$$\begin{aligned} {\bar{g}}^\text {h}=&\, \delta {\varvec{v}}^\text {T}\left( {\varvec{F}}_v^{}+ {\varvec{K}} {\varvec{v}} - {\varvec{M}}_\text {V}^{}\,{\varvec{\lambda }}_\text {V}^{}\right) \nonumber \\&+\delta {\varvec{\lambda }}_\text {V}^\text {T} \left( {\varvec{F}}_\lambda ^{} + {\varvec{T}}_\text {V}^{}\,{\varvec{\varepsilon }}_\text {V}^\text {M} - {{\varvec{M}}_\text {V}^\text {T}}\, {\varvec{v}}\right) \nonumber \\&+\delta {\varvec{\varepsilon }}_\text {V}^\text {M} \left( {{\varvec{F}}_{\varepsilon }^{}} + {{\varvec{T}}_\text {V}^{}}\,{\varvec{\lambda }}_\text {V}^{}\right) =0 \end{aligned}$$

(45)

or

$$\begin{aligned} {\bar{g}}^\text {h}= \begin{bmatrix} \delta {\varvec{v}} \\ \delta {\varvec{\lambda }}_\text {V}\\ \delta {\varvec{\varepsilon }}_\text {V}^\text {M} \end{bmatrix}^\text {T}&\left( \begin{bmatrix} {\varvec{K}} &{} -{{\varvec{M}}_\text {V}} &{} {\varvec{0}}\\ -{\varvec{M}}_\text {V}^\text {T} &{} {\varvec{0}}&{}{\varvec{T}}_\text {V}\\ {\varvec{0}} &{} {\varvec{T}}_\text {V}^\text {T} &{} {\varvec{0}} \end{bmatrix} \begin{bmatrix} {\varvec{v}}\\ {\varvec{\lambda }}_\text {V}\\ {\varvec{\varepsilon }}_\text {V}^\text {M} \end{bmatrix}\right. \nonumber \\&\left. \; + \begin{bmatrix} {\varvec{F}}_v\\ {\varvec{F}}_\lambda \\ {\varvec{F}}_\varepsilon \end{bmatrix} \right) =0. \end{aligned}$$

(46)

As mentioned before, the system matrix shows to be symmetric.

The additional degrees of freedom for ${\varvec{\varepsilon }}_\text {V}^\text {M}$ and ${\varvec{\lambda }}_\text {V}^{}$ are associated with additional global nodes, that are shared by all elements on micro/meso level, see Fig. 3. Degrees of freedom, that are used for storage of ${\varepsilon _\text {V}^\text {M}}_{i}$, are fixed at their respective values.

Fig. 3

Some elements within an RVE with black element nodes (displacement dof) and blue global nodes shared by all elements (${\varepsilon _\text {V}^\text {M}}_{i}$ and ${\lambda _\text {V}}_{i}$ dofs). (Color figure online)

Fig. 4

RVE for a beam: on top the reference axis with assigned cross-section, below a corresponding RVE

4.2.2 Beams

When using beam elements on macro level, the macro strains ${\varvec{E}}_\text {V}^\text {M}$ needed for the weak form on micro/meso level are not directly accessible as those elements internally use the beam strains ${\varvec{\varepsilon }}_\text {B}$. However, they can easily be converted by using Eq. (4): ${\varvec{E}}_\text {B}^\text {M} = {\varvec{A}}_\text {B}^{} \, {\varvec{\varepsilon }}_\text {B}^\text {M}$. As there are only three strains in ${\varvec{E}}_\text {V}^\text {M}$, that are non-zero, a meaningful side condition can only be invoked for those three. The following is introduced for a consistent notation:

$$\begin{aligned} {\varvec{\lambda }}_\text {V}&= \begin{bmatrix} \lambda _{xx}\\ 0\\ 0\\ \lambda _{xy}\\ \lambda _{xz}\\ 0 \end{bmatrix} = \underbrace{ \begin{bmatrix} 1&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1\\ 0&{}0&{}0 \end{bmatrix}}_{\displaystyle {{\varvec{\Lambda }}_\text {B}}} \underbrace{ \begin{bmatrix} \lambda _{xx}\\ \lambda _{xy}\\ \lambda _{xz}\\ \end{bmatrix}}_{\displaystyle {\bar{{\varvec{\lambda }}}_\text {B}}} ={\varvec{\Lambda }}_\text {B}\,\bar{{\varvec{\lambda }}}_\text {B} \,, \nonumber \\ {\varvec{E}}_\text {B}^\text {m}&= {\varvec{\Lambda }}_\text {B}^\text {T}\, {\varvec{E}}_\text {V}^\text {m} \,. \end{aligned}$$

(47)

This leads to an expression of the weak form in the micro/meso scale as

$$\begin{aligned} {\bar{g}}({\varvec{u}}, \delta {\varvec{u}}, {\varvec{\lambda }}_\text {V},\delta {\varvec{\lambda }}_\text {V})&= \int \limits _{{\mathcal {P}}}\delta {{\varvec{E}}_\text {V}^\text {m}}^\text {T} \left( {\varvec{S}}_\text {V} - {\varvec{\Lambda }}_\text {B}\bar{{\varvec{\lambda }}}_\text {B}\right) \, \text {d}V \nonumber \\&\quad + \int \limits _{{\mathcal {P}}}\delta \bar{{\varvec{\lambda }}}_\text {B}^\text {T}\left( {\varvec{A}}_\text {B}^{}\, {\varvec{\varepsilon }}_\text {B}^\text {M}-{\varvec{\Lambda }}_\text {B}^\text {T}\,{\varvec{E}}_\text {V}^\text {m}\right) \, \text {d}V\nonumber \\&\quad +\int \limits _{{\mathcal {P}}}\delta {{\varvec{\varepsilon }}_\text {B}^\text {M}}^\text {T}{\varvec{A}}_\text {B}^\text {T}\,\bar{{\varvec{\lambda }}}_\text {B}^{} \text { d}V\,. \end{aligned}$$

(48)

In this representation, the Lagrange parameters are stresses. This leads to some problems, that need to be addressed.

When using a 3D body on macro scale, the micro/meso scale is viewed as a point of the continuum and a very small surrounding with negligible lengths in all three dimensions compared to the characteristic lengths of the macro scale. This makes it possible to assume constant Lagrange parameters (see Sect. 4.2.1), that represent an averaged stress quantity. They describe the averaged reaction of the 3D body to the imposed macro strains at that macro point with sufficient information.

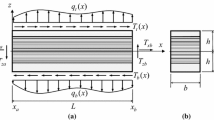
When using a beam on macro level, the argument of separation of scales only holds true for one dimension - the direction of the beam axis. The cross-section of the beam needs to be represented in full within the micro/meso scale because there is no separation of length scales for the remaining two dimensions (see Figure 4). This also means, that there cannot be constant Lagrange parameters $\lambda _{ij}$ associated with averaged stress entities, that accurately describe the beam’s reactions to the imposed macro strains without major information loss. For example, a beam experiencing bending would react with a linear normal stress $S_{xx}$ across its width or height. An over the cross-section averaged normal stress, and subsequently the corresponding Lagrange parameter, would be zero and all information on the beam’s reaction would be lost. Therefore, the Lagrange parameters cannot be assumed constant, but need appropriate global ansatz functions with associated parameters to accurately describe the beam’s reactions. The ansatz functions need to be global in order to fulfill the side condition (31) only in an averaged manner.

In the stress resultants, there is a quantity that is constant for each cross-section and can easily be connected to the stresses. Therefore, they are used as new parameters and ansatz functions are built around them. Thus the vector ${\varvec{\lambda }}_\text {B}=[\lambda _N, \lambda _{Q_y}, \lambda _{Q_z},\lambda _{M_x},\lambda _{M_y},\lambda _{M_z}]^\text {T}$ is introduced and connected to the Lagrange parameters by

$$\begin{aligned} \bar{{\varvec{\lambda }}}_\text {B} = \bar{{\varvec{A}}}_\text {B}\, {\varvec{\lambda }}_\text {B} \end{aligned}$$

(49)

where

$$\begin{aligned} \bar{{\varvec{A}}}_\text {B} = \begin{bmatrix} 1&{}0&{}0&{}0&{}z&{}-y\\ 0&{}1-\left( \frac{y}{y_\text {max}}\right) ^2&{}0&{}-z&{}0&{}0\\ 0&{}0&{}1-\left( \frac{z}{z_\text {max}}\right) ^2&{}y&{}0&{}0 \end{bmatrix}\,. \end{aligned}$$

(50)

This leads to constant normal stresses for a normal force and linear normal stresses for bending moments. A torsional moment leads to shear stresses, that are proportional to the distance from the beam axis. Torsional warping is not accounted for. This limits the applicability of the proposed theory to either warp-free cross-sections or problems, where torsion is negligible.

Shear stresses caused by transverse forces are assumed to be quadratic in an attempt to account for shear warping without giving up the Timoshenko theory on the macro level. They are assumed quadratic as this is the easiest enhancement from constant shear stresses and fulfills the stress boundary condition for free boundaries. The effects of this assumption are studied in Sect. 5.

The presented approximations are now introduced into the weak form and analogous equations and quantities to Sect. 4.2.1 are derived:

$$\begin{aligned} {\bar{g}}({\varvec{u}}, \delta {\varvec{u}}, {\varvec{\lambda }},\delta {\varvec{\lambda }})&= \int \limits _{{\mathcal {P}}}\delta {{\varvec{E}}_\text {V}^\text {m}}^\text {T} \left( {\varvec{S}}_\text {V}^{} -{\varvec{\Lambda }}_\text {B}^{}\,\bar{{\varvec{A}}}_\text {B}^{}\,{\varvec{\lambda }}_\text {B}^{}\right) \text { d}V \nonumber \\&\quad + \int \limits _{{\mathcal {P}}}\delta {\varvec{\lambda }}_\text {B}^\text {T}\,\bar{{\varvec{A}}}_\text {B}^\text {T}\left( {\varvec{A}}_\text {B}^{}\, {\varvec{\varepsilon }}_\text {B}^\text {M}-{\varvec{\Lambda }}_\text {B}^\text {T}\,{\varvec{E}}_\text {V}^\text {m}\right) \text { d}V\nonumber \\&\quad +\int \limits _{{\mathcal {P}}}\delta {{{\varvec{\varepsilon }}}_\text {B}^\text {M}}^\text {T}{\varvec{A}}_\text {B}^\text {T}\,\bar{{\varvec{A}}}_\text {B}^{}\,{\varvec{\lambda }}_\text {B}^{} \text { d}V \, , \end{aligned}$$

(51)

$$\begin{aligned} {\bar{g}}^\text {h}&= \sum \limits _{e=1}^{numel}\left[ \delta {{\varvec{v}}^{e}}^\text {T}\big ( {{\varvec{f}}_v^e} + {\varvec{k}}^{e} {\varvec{v}}^{e} - {{\varvec{M}}_\text {B}^e}\,{\varvec{\lambda }}_\text {B}^{}\big ) \right. \nonumber \\&\quad +\delta {\varvec{\lambda }}_\text {B}^\text {T} \left( {{\varvec{f}}_\lambda ^e} +{{\varvec{T}}_\text {B}^e}\,{\varvec{\varepsilon }}_\text {B}^\text {M} - {{\varvec{M}}_\text {B}^e}^\text {T} {\varvec{v}}^{e}\right) \nonumber \\&\quad \left. +\delta {\varvec{\varepsilon }}_\text {B}^\text {M} \left( {{\varvec{f}}_{\varepsilon }^e} + {{\varvec{T}}_\text {B}^e}^\text {T}\,{\varvec{\lambda }}_\text {B}^{}\right) \right] \end{aligned}$$

(52)

where

$$\begin{aligned} {\varvec{M}}_\text {B}^e&= \begin{bmatrix} {{\varvec{M}}_\text {B}^e}_1\\ \vdots \\ {{\varvec{M}}_\text {B}^e}_I\\ \vdots \\ {{\varvec{M}}_\text {B}^e}_{nel} \end{bmatrix}, \quad {{\varvec{f}}^e_v} = \begin{bmatrix} {{\varvec{f}}^e_v}_1\\ \vdots \\ {{\varvec{f}}^e_v}_I\\ \vdots \\ {{\varvec{f}}^e_v}_{nel} \end{bmatrix}, \\ {{\varvec{T}}_\text {B}^e}&= \int \limits _{{\mathcal {P}}^e}\bar{{\varvec{A}}}_\text {B}^\text {T} \,{{\varvec{A}}}_\text {B}^{} \text { d}V^e \,, \\ {{\varvec{f}}^e_\lambda }&= \int \limits _{{\mathcal {P}}^e}\bar{{\varvec{A}}}_\text {B}^\text {T} \left( {\varvec{A}}_\text {B}^{}{\varvec{\varepsilon }}_\text {B}^\text {M} -{\varvec{\Lambda }}_\text {B}^\text {T}\,{\varvec{E}}_\text {V}^\text {m}\right) \text { d}V^e \,, \\ {{\varvec{f}}^e_\varepsilon }&= \int \limits _{{\mathcal {P}}^e}{\varvec{A}}_\text {B}^\text {T}\,\bar{{\varvec{\lambda }}}_\text {B}^{} \text { d}V^e \end{aligned}$$

with

$$\begin{aligned}{{\varvec{M}}_\text {B}^e}_I&= \int \limits _{{\mathcal {P}}^e}{\varvec{B}}_I^\text {T}{\varvec{\Lambda }}_\text {B}^{}\bar{{\varvec{A}}}_\text {B}^{} \text { d}V^e \end{aligned}$$

and

$$\begin{aligned} {{\varvec{f}}^e_v}_I = \int \limits _{{\mathcal {P}}^e}{\varvec{B}}_I^\text {T} \left( {\varvec{S}}_\text {V}^{} -{\varvec{\lambda }}_\text {V}^{}\right) \text { d}V^e \, . \end{aligned}$$

Assembly of element quantities into system matrices leads to the expression

$$\begin{aligned} {\bar{g}}^\text {h}&= \begin{bmatrix} \delta {\varvec{v}} \\ \delta {\varvec{\lambda }}_\text {B}\\ \delta {\varvec{\varepsilon }}_\text {B}^\text {M} \end{bmatrix}^\text {T} \left( \begin{bmatrix} {\varvec{K}} &{} -{{\varvec{M}}_\text {B}} &{} {\varvec{0}}\\ -{\varvec{M}}_\text {B}^\text {T} &{} {\varvec{0}}&{}{\varvec{T}}_\text {B}\\ {\varvec{0}} &{} {\varvec{T}}_\text {B}^\text {T} &{} {\varvec{0}} \end{bmatrix} \begin{bmatrix} {\varvec{v}}\\ {\varvec{\lambda }}_\text {B}\\ {\varvec{\varepsilon }}_\text {B}^\text {M} \end{bmatrix}+ \begin{bmatrix} {\varvec{F}}_v\\ {\varvec{F}}_\lambda \\ {\varvec{F}}_\varepsilon \end{bmatrix} \right) \nonumber \\ {}&=0 \, . \end{aligned}$$

(53)

4.2.3 Plates

Using plate elements on macro level leads to very similar problems as using beam elements. Subsequently, analogous strategies can be applied.

First, the plate strains are converted: ${\varvec{E}}_\text {P}^\text {M} = {\varvec{A}}_\text {P}^{} \, {\varvec{\varepsilon }}_\text {P}^\text {M}$. Second, the number of Lagrange parameters is set according to the number of non-zero strains and an analogous notation is invoked:

$$\begin{aligned} {\varvec{\lambda }}_\text {V}&= \begin{bmatrix} \lambda _{xx}\\ \lambda _{yy}\\ 0\\ \lambda _{xy}\\ \lambda _{xz}\\ \lambda _{yz}\\ \end{bmatrix} = \underbrace{ \begin{bmatrix} 1&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{bmatrix}}_{\displaystyle {{\varvec{\Lambda }}_\text {P}}} \underbrace{ \begin{bmatrix} \lambda _{xx}\\ \lambda _{yy}\\ \lambda _{xy}\\ \lambda _{xz}\\ \lambda _{yz}\\ \end{bmatrix}}_{\displaystyle {\bar{{\varvec{\lambda }}}_\text {P}}} ={\varvec{\Lambda }}_\text {P}\bar{{\varvec{\lambda }}}_\text {P} \,, \nonumber \\ {\varvec{E}}_\text {P}^\text {m}&= {\varvec{\Lambda }}_\text {P}^\text {T}\, {\varvec{E}}_\text {V}^\text {m} \,. \end{aligned}$$

(54)

In a third step, an ansatz for the Lagrange parameters is chosen, that is based on the stress resultants and quadratic shear stresses, such that ${\varvec{\lambda }}_\text {P} \in {\mathbb {R}}^8$ with

$$\begin{aligned} \bar{{\varvec{\lambda }}}_\text {P}= \bar{{\varvec{A}}}_\text {P} {\varvec{\lambda }}_\text {P} \end{aligned}$$

(55)

where

$$\begin{aligned} \bar{{\varvec{A}}}_\text {P} = \begin{bmatrix} 1&{}0&{}0&{}z&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}z&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}z&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1-\left( \frac{z}{z_\text {max}}\right) ^2&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1-\left( \frac{z}{z_\text {max}}\right) ^2 \end{bmatrix}. \end{aligned}$$

(56)

Finally, the micro/meso problem can be described with same equations as the beam by substituting quantities with subscript $(\cdot )_\text {B}$ with respective quantities with subscript $(\cdot )_\text {P}$, see Eqs. (51) - (53).

4.3 Consistent boundary deformations

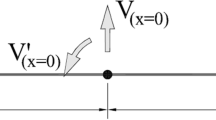
Using the described theory and approximations and FE interpolations without any boundary conditions other than to restrict rigid body motions may lead to inconsistent boundary displacements. This is due to the fact, that the additional constraints and therefore the kinematic relations between macro and micro/meso scale are only fulfilled in an averaged manner, when implementing the Lagrange parameters as described. As this average fulfillment includes the boundary of the micro/meso scale, boundary displacements are not subjected to any hard, point wise requirements, so they deform as if they are free boundaries. But the micro/meso model is essentially a subsection of the whole body and therefore its boundaries are not free. They are interfaces to the remainder of the body’s continuum, except for the outer boundaries of the cross-section for the beam and the top and bottom surfaces for the plate, which are real outer boundaries and therefore free in their deformation.

These interfaces to the body’s continuum cannot undergo arbitrary deformations if basic physics are to be respected. Especially they cannot deform in a way, that would lead to holes or interpenetration within the whole continuum. Rather, they need to be periodic. Boundary deformations of opposing boundaries (if they are continuum interfaces) need to fit together without any holes or interpenetration.

4.3.1 Displacement boundary conditions

The most obvious way to make opposing boundaries deform periodically is to apply periodic or linear displacement boundary conditions. The former are rather complicated to implement and need special consideration when discretizing the micro/meso problem, which contradicts the aim of an easy to use, one for all homogenization scheme. This leads to the consideration of linear displacement boundary conditions (DBC). They are easily implemented and impose no requirements on the used discretization.

Fig. 5

Effect of scaled Lagrange parameters; top: no scaling, bottom: with scaling according to local stiffness

For 3D bodies, DBC are applied onto the continuum interface boundaries of the micro/meso scale using the following expressions for the boundary displacements ${\varvec{u}}^\text {R}$

$$\begin{aligned} {\varvec{u}}^\text {R}&= \begin{bmatrix} E_{xx} &{} E_{xy} &{} E_{xz} \\ E_{xy} &{} E_{yy} &{} E_{yz} \\ E_{xz} &{} E_{yz} &{} E_{zz} \\ \end{bmatrix}^\text {M} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \nonumber \\ {\varvec{u}}^\text {R}&= \underbrace{\begin{bmatrix} x&{}0&{}0&{}\frac{1}{2}y&{}\frac{1}{2}z&{}0\\ 0&{}y&{}0&{}\frac{1}{2}x&{}0&{}\frac{1}{2}z\\ 0&{}0&{}z&{}0&{}\frac{1}{2}x&{}\frac{1}{2}y\\ \end{bmatrix}}_{\displaystyle {{\varvec{R}}_\text {V}^{}}} \begin{bmatrix} E_{xx} \\ E_{yy} \\ E_{zz} \\ 2E_{xy} \\ 2E_{xz}\\ 2E_{yz} \end{bmatrix}^\text {M} \nonumber \\ {\varvec{u}}^\text {R}&={\varvec{R}}_\text {V}^{}\, {\varvec{E}}_\text {V}^\text {M} \; . \end{aligned}$$

(57)

For beams, shear deformations are applied to $u_x^\text {R}$ only and the expression

$$\begin{aligned} {\varvec{u}}^\text {R}&= \begin{bmatrix} \varepsilon _{x}+z\kappa _y-y\kappa _z &{} \gamma _{xy} &{} \gamma _{xz} \\ -z\kappa _x &{} 0 &{} 0 \\ y\kappa _x &{} 0 &{} 0 \\ \end{bmatrix}^\text {M} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \nonumber \\ {\varvec{u}}^\text {R}&= {\begin{bmatrix} x&{}y&{}z&{}0&{}xz&{}-xy\\ 0&{}0&{}0&{}-xz&{}0&{}0\\ 0&{}0&{}0&{}xy&{}0&{}0\\ \end{bmatrix}} \begin{bmatrix} \varepsilon _{x} \\ \gamma _{xy} \\ \gamma _{xz} \\ \kappa _{x} \\ \kappa _{y}\\ \kappa _{z} \end{bmatrix}^\text {M}\, \end{aligned}$$

(58)

arises. However, if DBC are applied like this to $u_y^\text {R}$ and $u_z^\text {R}$, they lead to wrong results for the bending and extensional stiffness, similar to the findings in [9]. As those boundary conditions only apply torsional deformations and there are no incompatible boundary deformations caused by torsional loads because torsional warping is neglected, they can be omitted. Accordingly, DBC are only applied to $u_x^\text {R}$:

$$\begin{aligned} u_x^\text {R}&= \underbrace{\begin{bmatrix} x&y&z&0&xz&-xy \end{bmatrix}}_{\displaystyle {{\varvec{R}}_\text {B}}} \begin{bmatrix} \varepsilon _{x} \\ \gamma _{xy} \\ \gamma _{xz} \\ \kappa _{x} \\ \kappa _{y}\\ \kappa _{z} \end{bmatrix}^\text {M} ={\varvec{R}}_\text {B}^{} \, {\varvec{\varepsilon }}_\text {B}^\text {M} \;. \end{aligned}$$

(59)

For plates, analogous arguments hold for applying DBC and therefore only $u_x^\text {R}$ and $u_y^\text {R}$ are subject to prescribed boundary displacements using

$$\begin{aligned} \begin{bmatrix} u_x \\ u_y \end{bmatrix}^\text {R}&= \underbrace{\begin{bmatrix} x&{}0&{}\frac{1}{2}y&{}xz&{}0&{}\frac{1}{2}yz&{}z&{}0\\ 0&{}y&{}\frac{1}{2}x&{}0&{}yz&{}\frac{1}{2}xz&{}0&{}z \end{bmatrix}}_{\displaystyle {{\varvec{R}}_\text {P}}} \begin{bmatrix} \varepsilon _{x}\\ \varepsilon _{y} \\ \gamma _{xy} \\ \kappa _{x} \\ \kappa _{y} \\ \kappa _{xy} \\ \gamma _{xz} \\ \gamma _{yz} \end{bmatrix}^\text {M} \nonumber \\ \begin{bmatrix} u_x \\ u_y \end{bmatrix}^\text {R}&={\varvec{R}}_\text {P}^{}\, {\varvec{\varepsilon }}_\text {P}^\text {M} \; . \end{aligned}$$

(60)

4.3.2 Scaling of Lagrange parameters

A less obvious way to achieve consistent boundary deformations, but one without the need for boundary conditions, is a slight modification of the ansatz for the Lagrange parameters. However, it can only be applied if beam or plate elements are used on the macro scale and special requirements for the internal structure of the material are met.

If the body consists of a layered structure with each consisting of a homogeneous material, the previously proposed ansatz of overall constant $\lambda _{xx}$ for a given $\varepsilon _x^\text {M}$ leads to non-uniform strains across the layers, but constant normal stress $S_{xx}$ in accordance with constant $\lambda _{xx}$ (see top row of Figure 5). If the ansatz is modified in a way, that the Lagrange parameter is not overall constant, but only constant within each layer and the value dependent on the stiffness of the layer, the strains would become uniform across all layers and thus consistent boundary deformations would be achieved (see bottom row of Figure 5).

This method can obviously only be applied if there is no change of material along the direction of the beam axis or within the directions of the reference surface of the plate. Would there be such an inhomogeneity, there would then be a jump in the normal stresses at the material interface, that would violate the equilibrium conditions. For the same reason it cannot be applied to 3D bodies.

In detail, the necessary modifications to the Lagrange parameters affect only the ones related to stresses in beam axis direction and the directions of the reference surface of the plate. Those Lagrange parameters will be multiplied with the associated entries of the material matrix ${\varvec{C}} \in {\mathbb {R}}^{6\times 6}$ in Voigt notation for a 3D continuum:

$$\begin{aligned} \bar{{\varvec{A}}}_\text {B}&= \begin{bmatrix} C_{11}&{}0&{}0&{}0&{}C_{11}z&{}-C_{11}y\\ 0&{}1-\left( \frac{y}{y_\text {max}}\right) ^2&{}0&{}-z&{}0&{}0\\ 0&{}0&{}1-\left( \frac{z}{z_\text {max}}\right) ^2&{}y&{}0&{}0 \end{bmatrix}\,, \end{aligned}$$

(61)

$$\begin{aligned} \bar{{\varvec{A}}}_\text {P}&= \begin{bmatrix} C_{11}&{}0&{}0&{}C_{11}z&{}0&{}0&{}0&{}0\\ 0&{}C_{22}&{}0&{}0&{}C_{22}z&{}0&{}0&{}0\\ 0&{}0&{}C_{44}&{}0&{}0&{}C_{44}z&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1-\left( \frac{z}{z_\text {max}}\right) ^2&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1-\left( \frac{z}{z_\text {max}}\right) ^2 \end{bmatrix}. \end{aligned}$$

(62)

4.4 Micro/meso to macro transition

In order to generate the homogenized quantities from the solution of the micro/meso problem, we adapt the algorithm presented in [9].

The overall discretized, coupled problem is described by its weak form as in

$$\begin{aligned}&g^\text {h}({\varvec{u}}^\text {M},\delta {\varvec{u}}^\text {M},{\varvec{u}}^\text {m},\delta {\varvec{u}}^\text {m},{\varvec{\lambda }},\delta {\varvec{\lambda }}) \nonumber \\&\quad =\sum \limits _{e=1}^{numel}\Bigg (\delta {{{\varvec{v}}^e}^\text {M}}^\text {T} {{\varvec{k}}^e}^\text {M} {{\varvec{v}}^e}^\text {M} + {{\varvec{f}}^e}^\text {M} \nonumber \\&\qquad + \sum \limits _{i=1}^{NGP} \dfrac{1}{\Gamma _i}\,{\bar{g}}_i({\varvec{u}}_i^\text {m},\delta {\varvec{u}}_i^\text {m},{\varvec{\lambda }}_i,\delta {\varvec{\lambda }}_i)\Bigg ). \end{aligned}$$

(63)

Here, $\Gamma _i$ denotes the averaging quantity dependent on the macro problem (RVE volume for 3D body, RVE mid surface area for plate, RVE length for beam) and NGP denotes the number of Gauss points per macro element. For every macro Gauss point, there is one micro/meso problem described by its weak form ${\bar{g}}_i$.

Using the FE discretization described previously and combining all degrees of freedom, system matrices and load vectors of each micro/meso problem together with $\Gamma _i$ into new generalized entities $\hat{{\varvec{v}}}^\text {m}$, $\hat{{\varvec{K}}}^\text {m}$ and $\hat{{\varvec{F}}}^\text {m}$, the coupled problem is represented by

$$\begin{aligned} g^\text {h}&=\sum \limits _{e=1}^{numel} { \begin{bmatrix} {\delta {\varvec{v}}^\text {M}}\\ {\delta \hat{{\varvec{v}}}_1^\text {m}}\\ \vdots \\ {\delta \hat{{\varvec{v}}}_{NGP}^\text {m}} \end{bmatrix}^e}^\text {T} \left\{ \begin{bmatrix} {\varvec{k}}^\text {M} &{} {\varvec{0}} &{} \cdots &{} {\varvec{0}}\\ {\varvec{0}} &{} \hat{{\varvec{K}}}_1^\text {m} &{}\cdots &{}{\varvec{0}}\\ \vdots &{} \vdots &{}\ddots &{}\vdots \\ {\varvec{0}} &{} {\varvec{0}} &{}\cdots &{}\hat{{\varvec{K}}}_{NGP}^\text {m} \end{bmatrix}^e \right. \nonumber \\&\quad \left. \times \begin{bmatrix} {\varvec{v}}^\text {M}\\ \hat{{\varvec{v}}}_1^\text {m}\\ \vdots \\ \hat{{\varvec{v}}}_{NGP}^\text {m}\\ \end{bmatrix}^e + \begin{bmatrix} {\varvec{f}}^\text {M}\\ \hat{{\varvec{F}}}_1^\text {m}\\ \vdots \\ \hat{{\varvec{F}}}_{NGP}^\text {m}\\ \end{bmatrix}^e \right\} . \end{aligned}$$

(64)

The element stiffness matrix ${{\varvec{k}}^e}^\text {M}$ and element load vector ${{\varvec{f}}^e}^\text {M}$ of the macro system are dependent on the solution of the micro/meso problems. But the entities describing the micro/meso problem are independent from each other, so they can be solved independently in parallel computations.

The overall structure of the equation describing the micro/meso problem is the same for 3D bodies, plates and beams

$$\begin{aligned} \dfrac{1}{\Gamma _i}{\bar{g}}_i&= \dfrac{1}{\Gamma _i} \begin{bmatrix} \delta {\varvec{v}} \\ \delta {\varvec{\lambda }}\\ \delta {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i^\text {T}\nonumber \\&\quad \times \left( \begin{bmatrix} {\varvec{K}} &{} -{{\varvec{M}}} &{} {\varvec{0}}\\ -{{\varvec{M}}}^\text {T} &{} {\varvec{0}} &{}{\varvec{T}}\\ {\varvec{0}} &{} {\varvec{T}}^\text {T} &{}{\varvec{0}} \end{bmatrix}_i \begin{bmatrix} {\varvec{v}}\\ {\varvec{\lambda }}\\ {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i + \begin{bmatrix} {\varvec{F}}_v\\ {\varvec{F}}_\lambda \\ {\varvec{F}}_\varepsilon \end{bmatrix}_i \right) \end{aligned}$$

(65)

or with element representation:

$$\begin{aligned} \dfrac{1}{\Gamma _i}{\bar{g}}_i&= \dfrac{1}{\Gamma _i} \sum \limits _{e=1}^{numel} \begin{bmatrix} \delta {\varvec{v}}^e \\ \delta {\varvec{\lambda }}\\ \delta {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i^\text {T} \nonumber \\&\quad \times \left( \begin{bmatrix} {\varvec{k}}^e &{} -{{\varvec{M}}^e} &{} {\varvec{0}}\\ -{{\varvec{M}}^e}^\text {T} &{} {\varvec{0}} &{}{\varvec{T}}^e\\ {\varvec{0}} &{} {{\varvec{T}}^e}^\text {T} &{}{\varvec{0}} \end{bmatrix}_i \begin{bmatrix} {\varvec{v}}^e\\ {\varvec{\lambda }}\\ {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i + \begin{bmatrix} {\varvec{f}}_v^e\\ {\varvec{f}}_\lambda ^e \\ {\varvec{f}}_\varepsilon ^e \end{bmatrix}_i \right) . \end{aligned}$$

(66)

For this representation, it is assumed, that all rigid body motions are already restrained by boundary conditions and all corresponding degrees of freedom are accounted for by static condensation. This leads to ${\varvec{K}}$ being regular.

In cases, where there are any additional displacement boundary conditions, displacements ${\varvec{v}}^e$ can be split into a part ${\varvec{v}}_\text {R}^e$ subjected to boundary conditions and a free part ${\varvec{v}}_\text {F}^e$. The latter can be connected to the overall displacement vector ${\varvec{v}}$ using the assembly matrix ${\varvec{a}}^e$ while ${\varvec{v}}_\text {R}^e$ can be connected to the macro strains using the matrix ${\varvec{R}}_I$ according to Sect. 4.3:

$$\begin{aligned} {\varvec{v}}^e = \begin{bmatrix} {\varvec{v}}_\text {F}^{} \\ {\varvec{v}}_\text {R}^{} \end{bmatrix}^e = \begin{bmatrix} {\varvec{a}}^e \,{\varvec{v}} \\ {\varvec{R}}^e {\,} {\varvec{\varepsilon }}^\text {M} \end{bmatrix} \end{aligned}$$

(67)

and

$$\begin{aligned} \delta {\varvec{v}}^e = \begin{bmatrix} \delta {\varvec{v}}_\text {F}^{} \\ \delta {\varvec{v}}_\text {R}^{} \end{bmatrix}^e = \begin{bmatrix} {\varvec{a}}^e \,\delta {\varvec{v}} \\ {\varvec{R}}^e {\,} \delta {\varvec{\varepsilon }}^\text {M} \end{bmatrix} \, , \end{aligned}$$

(68)

where

$$\begin{aligned} {\varvec{R}}^e = \begin{bmatrix} \delta _1 {\varvec{R}}_1 \\ \vdots \\ \delta _I^{} {\varvec{R}}_I^{} \\ \vdots \\ \delta _{nel} {\varvec{R}}_{nel} \end{bmatrix} \end{aligned}$$

(69)

with

$$\begin{aligned} \delta _I^{} ={\left\{ \begin{array}{ll} 1 &{} \text {for boundary condition present on node } I,\\ 0 &{} \text { else.} \end{array}\right. } \end{aligned}$$

Inserting (68) into (66) and introducing corresponding splits for ${\varvec{k}}^e$, ${\varvec{M}}^e$ and ${\varvec{f}}_v^e$ into

$$\begin{aligned} {\varvec{k}}^e&= \begin{bmatrix} {\varvec{k}}_\text {FF}^e &{} {\varvec{k}}_\text {FR}^e \\ {\varvec{k}}_\text {RF}^e &{} {\varvec{k}}_\text {RR}^e \end{bmatrix} \,, \qquad {\varvec{M}}^e = \begin{bmatrix} {\varvec{M}}_\text {F}^e\\ {\varvec{M}}_\text {R}^e \end{bmatrix} \,, \nonumber \\ {\varvec{f}}_v^e&= \begin{bmatrix} {{\varvec{f}}_v^e}_\text {F}\\ {{\varvec{f}}_v^e}_\text {R} \end{bmatrix} \end{aligned}$$

(70)

leads to

$$\begin{aligned} \dfrac{1}{\Gamma _i}{\bar{g}}_i&= \dfrac{1}{\Gamma _i} \sum \limits _{e=1}^{numel} \begin{bmatrix} \delta {\varvec{v}} \\ \delta {\varvec{\varepsilon }}^\text {M}\\ \delta {\varvec{\lambda }}\\ \delta {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i^\text {T}\nonumber \\&\quad \times \left( \begin{bmatrix} {{\varvec{a}}^e}^\text {T} {\varvec{k}}_\text {FF}^e \, {\varvec{a}}^e &{} {{\varvec{a}}^e}^\text {T} {\varvec{k}}_\text {FR}^e {\varvec{R}}^e &{} -{{\varvec{a}}^e}^\text {T} {{\varvec{M}}}_\text {F}^e &{} {\varvec{0}}\\ {{\varvec{R}}^e}^\text {T} {\varvec{k}}_\text {RF}^e \, {\varvec{a}}^e &{} {{\varvec{R}}^e}^\text {T} {\varvec{k}}_\text {RR}^e {\varvec{R}}^e &{} -{{\varvec{R}}^e}^\text {T}{{\varvec{M}}}_\text {R}^e &{} {\varvec{0}}\\ -{{{\varvec{M}}}_\text {F}^e}^\text {T} {\varvec{a}}^e &{} -{{{\varvec{M}}}_\text {R}^e}^\text {T} {\varvec{R}}^e&{} {\varvec{0}} &{}{\varvec{T}}\\ {\varvec{0}} &{} {\varvec{0}} &{}{\varvec{T}}^\text {T} &{}{\varvec{0}} \end{bmatrix}_i\right. \nonumber \\&\left. \quad \times \begin{bmatrix} {\varvec{v}}\\ {\varvec{\varepsilon }}^\text {M}\\ {\varvec{\lambda }}\\ {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i +\begin{bmatrix} {{\varvec{a}}^e}^\text {T}{{\varvec{f}}}_\text {F}^e\\ {{\varvec{R}}^e}^\text {T}{{\varvec{f}}}_\text {R}^e\\ {\varvec{f}}_\lambda ^e \\ {\varvec{f}}_\varepsilon ^e \end{bmatrix}_i \right) . \end{aligned}$$

(71)

Combining the two ${\varvec{\varepsilon }}^\text {M}$ and $\delta {\varvec{\varepsilon }}^\text {M}$ rows and columns and introducing

$$\begin{aligned} {\varvec{K}}_\text {FF}&= \sum \limits _{e=1}^{numel} {{\varvec{a}}^e}^\text {T} \, {\varvec{k}}_\text {FF}^e \, {\varvec{a}}^e \,, \\ {{\varvec{K}}_\text {RR}}&= \sum \limits _{e=1}^{numel} {{\varvec{R}}^e}^\text {T} {\varvec{k}}_\text {RR}^e {\varvec{R}}^e \,, \\ {\varvec{K}}_\text {RF}&= {\varvec{K}}_\text {FR}^\text {T} = \sum \limits _{e=1}^{numel} {{\varvec{R}}^e}^\text {T} {\varvec{k}}_\text {RF}^e \, {\varvec{a}}^e \,, \\ {{\varvec{M}}}_\text {F}&= \sum \limits _{e=1}^{numel} {{\varvec{a}}^e}^\text {T}{{\varvec{M}}}_\text {F}^e \,, \\ {{\varvec{M}}}_\text {R}&= \sum \limits _{e=1}^{numel} {{\varvec{R}}^e}^\text {T}{{\varvec{M}}}_\text {R}^e \,, \\ {{\varvec{F}}}_\text {F}&= \sum \limits _{e=1}^{numel} {{\varvec{a}}^e}^\text {T}{{\varvec{f}}}_\text {F}^e\,, \\ {{\varvec{F}}}_\text {R}&= \sum \limits _{e=1}^{numel} {{\varvec{R}}^e}^\text {T}{{\varvec{f}}}_\text {R}^e \,, \\ {{\varvec{F}}}_\lambda&= \sum \limits _{e=1}^{numel} {{\varvec{f}}}_\lambda ^e \, , \\ {{\varvec{F}}}_\varepsilon&= \sum \limits _{e=1}^{numel} {\varvec{f}}_\varepsilon ^e \end{aligned}$$

leads to

$$\begin{aligned} \dfrac{1}{\Gamma _i}&{\bar{g}}_i = \dfrac{1}{\Gamma _i} \begin{bmatrix} \delta {\varvec{v}} \\ \delta {\varvec{\lambda }}\\ \delta {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i^\text {T} \nonumber \\&\quad \times \left( \begin{bmatrix} {\varvec{K}}_\text {FF} &{} -{{\varvec{M}}}_\text {F} &{} {\varvec{K}}_\text {FR}\\ -{{\varvec{M}}}_\text {F}^\text {T} &{} {\varvec{0}} &{}{\varvec{T}}-{{\varvec{M}}}_\text {R}^\text {T}\\ {\varvec{K}}_\text {FR}^\text {T} &{} {\varvec{T}}^\text {T}-{{\varvec{M}}}_\text {R}&{} {\varvec{K}}_\text {RR} \\ \end{bmatrix}_i \begin{bmatrix} {\varvec{v}}\\ {\varvec{\lambda }}\\ {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i \right. \nonumber \\&\quad + \left. \begin{bmatrix} {{\varvec{F}}}_\text {F}\\ {\varvec{F}}_\lambda \\ {\varvec{F}}_\varepsilon + {{\varvec{F}}}_\text {R}\\ \end{bmatrix}_i \right) \,. \end{aligned}$$

(72)

Lastly, unknown degrees of freedom for displacements and Lagrange parameters are combined

$$\begin{aligned}&\bar{{\varvec{v}}} = \begin{bmatrix} {\varvec{v}}\\ {\varvec{\lambda }}\end{bmatrix} \, , \quad \delta \bar{{\varvec{v}}} = \begin{bmatrix} \delta {\varvec{v}}\\ \delta {\varvec{\lambda }}\end{bmatrix} \end{aligned}$$

(73)

and correspondingly

$$\begin{aligned} \bar{{\varvec{K}}}_\text {FF}^{}&= \begin{bmatrix} {\varvec{K}}_\text {FF}^{} &{} -{{\varvec{M}}}_\text {F}^{}\\ -{{\varvec{M}}}_\text {F}^\text {T} &{} {\varvec{0}} \end{bmatrix} \, , \nonumber \\ \bar{{\varvec{K}}}_\text {FR}^{}&= \begin{bmatrix} {\varvec{K}}_\text {FR} \\ {\varvec{T}} -{{\varvec{M}}}_\text {R}^\text {T} \end{bmatrix}\, , \nonumber \\ \bar{{\varvec{F}}}_\text {F}^{}&= \begin{bmatrix} {\varvec{F}}_\text {F}^{}\\ {\varvec{F}}_\lambda ^{} \end{bmatrix} \quad \text { and } \quad \bar{{\varvec{F}}}_\varepsilon ^{} = {\varvec{F}}_\varepsilon ^{} + {{\varvec{F}}}_\text {R}^{} \end{aligned}$$

(74)

are introduced, which then leads to

$$\begin{aligned} \dfrac{1}{\Gamma _i}{\bar{g}}_i&= \dfrac{1}{\Gamma _i} \begin{bmatrix} \delta \bar{{\varvec{v}}} \\ \delta {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i^\text {T}&\left( \begin{bmatrix} \bar{{\varvec{K}}}_\text {FF}^{} &{} \bar{{\varvec{K}}}_\text {FR}^{}\\ \bar{{\varvec{K}}}_\text {FR}^\text {T} &{} {\varvec{K}}_\text {RR}^{} \end{bmatrix}_i \begin{bmatrix} \bar{{\varvec{v}}}\\ {\varvec{\varepsilon }}^\text {M} \end{bmatrix}_i + \begin{bmatrix} {\bar{{\varvec{F}}}_F^{}}\\ \bar{{\varvec{F}}}_\varepsilon ^{} \end{bmatrix}_i \right) \nonumber \\&=0\,. \end{aligned}$$

(75)

Using $[\delta \bar{{\varvec{v}}}^\text {T}, \delta {{\varvec{\varepsilon }}^\text {M}}^\text {T}]_i \not = {\varvec{0}}$, static condensation is possible. The unknown displacements and Lagrange parameters can be obtained from the first row with

$$\begin{aligned}&\bar{{\varvec{K}}}_\text {FF}^{} \, \bar{{\varvec{v}}} +\bar{{\varvec{K}}}_\text {FR}^{} \, {\varvec{\varepsilon }}^\text {M} +{\bar{{\varvec{F}}}_F^{}} =0 \nonumber \\&\Rightarrow \bar{{\varvec{v}}} = -\bar{{\varvec{K}}}_\text {FF}^{-1} \left( \bar{{\varvec{K}}}_\text {FR}^{}\, {\varvec{\varepsilon }}^\text {M} +{\bar{{\varvec{F}}}_F^{}}\right) \, . \end{aligned}$$

(76)

This can be inserted into the second row of (75) and the homogenized entities can be obtained by comparing coefficients

$$\begin{aligned}&\delta {{\varvec{\varepsilon }}_i^\text {M}}^\text {T}\left[ {{\varvec{D}}}^\text {M}{\varvec{\varepsilon }}^\text {M} + {\varvec{\sigma }}^\text {M}\right] _i \nonumber \\&\quad =\dfrac{1}{\Gamma _i}\delta {{\varvec{\varepsilon }}_i^\text {M}}^\text {T} \left[ \left( {\varvec{K}}_\text {RR}^{} -\bar{{\varvec{K}}}_\text {FR}^\text {T}\, \bar{{\varvec{K}}}_\text {FF}^{-1}\,\bar{{\varvec{K}}}_\text {FR}^{}\right) {\varvec{\varepsilon }}^\text {M} \right. \nonumber \\&\qquad \left. + \bar{{\varvec{F}}_\varepsilon ^{}}-\bar{{\varvec{K}}}_\text {FR}^\text {T}\,\bar{{\varvec{K}}}_\text {FF}^{-1}\,\bar{{\varvec{F}}}_F^{}\right] _i . \end{aligned}$$

(77)

The homogenized material matrix ${\varvec{D}}_i^\text {M}$ and the vector of homogenized stresses or stress resultants ${\varvec{\sigma }}_i^\text {M}$ at Gauss point i in element e of the macro problem are given by

$$\begin{aligned} {\varvec{D}}_i^\text {M}&= \dfrac{1}{\Gamma _i}\left( {\varvec{K}}_\text {RR}^{} -\bar{{\varvec{K}}}_\text {FR}^\text {T}\,\bar{{\varvec{K}}}_\text {FF}^{-1}\,\bar{{\varvec{K}}}_\text {FR}^{}\right) _i \,, \end{aligned}$$

(78)

$$\begin{aligned} {\varvec{\sigma }}_i^\text {M}&= \dfrac{1}{\Gamma _i}\left( \bar{{\varvec{F}}_\varepsilon ^{}}-\bar{{\varvec{K}}}_\text {FR}^\text {T}\,\bar{{\varvec{K}}}_\text {FF}^{-1}\,\bar{{\varvec{F}}}_F^{}\right) _i \,. \end{aligned}$$

(79)

5 Examples

The developed models are programmed in FEAP [18]. All computations are done with FEAP, if not explicitly stated otherwise.

In this section, we use abbreviations according to Table 1.

Table 1 Used abbreviations in numerical examples

Normalized values $W_\text {norm}$ and relative errors / relative deviations $\Delta W_{\text {rel}}$ are computed by

$$\begin{aligned} W_\text {norm}=\dfrac{W_\text {hom}}{W_\text {ref}}\, , \qquad \Delta W_{\text {rel}} = W_\text {norm} - 1 \,. \end{aligned}$$

(80)

Here $W_\text {hom}$ denotes a value received from the presented homogenization scheme and $W_\text {ref}$ a reference value obtained from literature results or a full scale model.

For beams, only plane macro problems are investigated as torsional warping is neglected and all other deformations can be linear superposed for the different directions, due to the linear elastic material and linear geometry.

5.1 Influence of RVE length, boundary conditions and order of ansatz functions

In contrast to classic Hill-Mandel homogenization scheme, where torsional and shear stiffness of beams (and plates) are dependent on boundary conditions and RVE length, if no further adjustments are made (see [7, 10]), the homogenization scheme presented here does not show any such effects.

Solely the use of linear displacement boundary conditions leads to expected boundary effects, because they stand in opposition to the assumption of quadratic shear stresses by using a quadratic ansatz funktion for the corresponding Lagrange parameters. The influence of those boundary effects decreases with increasing RVE length (see the following examples in this section).

In Sect. 5.2, results show that elements with quadratic ansatz functions have much better convergence rates over linear elements (see Fig. 6 and 7 ). Therefore, only quadratic elements are used in all following examples.

Fig. 6

Convergence of homogenized bending stiffness for beam RVE with length identical to height $L_\text {RVE}=h$ and homogeneous square cross-section

Fig. 7

Convergence of homogenized shear stiffness for beam RVE with length identical to height $L_\text {RVE}=h$ and homogeneous square cross-section

5.2 Homogeneous, isotropic beam with square cross-section

A homogeneous isotropic beam with a square cross-section is used as a benchmark to demonstrate basic functionality of the proposed homogenization method.

We consider a square cross-section with a width of $b=h=1\,\hbox {cm}$ and a linear elastic, isotropic material with $E=21\, 000\,\hbox {kN/cm}^{2}$ and $\nu = 0.3$. This leads to a reference material matrix ${\varvec{D}}_\text {B}=\text {diag}\{D_{11},D_{22},D_{33},D_{44},D_{55},D_{66}\}$, where

$$\begin{aligned} D_{11}&= EA = \, 21\,000\,\hbox {kN} \,, \nonumber \\ D_{22}&=D_{33}= \varkappa GA = \, \varkappa \cdot 8\,077\,\hbox {kN} \,, \\ D_{44}&= GI_P=G(I_y+I_z) =\, 1\,346 \, \hbox {kN cm}^{2}\,, \\ D_{55}&= D_{66} = EI =\, 1\,750\,\hbox {kN cm}^{2}\,. \end{aligned}$$

For the shear correction factor $\varkappa$, a lot of literature can be found, e.g. [19,20,21,22,23,24], in which some depend on the value of $\nu$, but their deviation from $\nu =0$ is minimal for a square cross-section and $\nu =0.3$. Therefore, we use the universal $\varkappa =5/6$ as reference value. The proposed beam kinematics do not account for torsional warping, which is why $I_P=I_y+I_z$ is used for reference instead of $I_T$.

Table 2 summarizes results obtained with the newly proposed homogenization scheme.

The correct diagonal structure for ${\varvec{D}}_B$ is obtained. There are no erroneous coupling terms. Extensional and torsional stiffness are always exact. Bending stiffness is always exact for quadratic elements and converges correctly with increasing discretization if linear elements are used (Fig. 6). The shear stiffness converges with increasing discretization against the correct value (Fig. 7). Although there is a boundary effect caused by application of DBC, its influence decreases with increasing RVE length (Fig. 8). This is due to the DBC hindering shear warping displacements near the boundary. With larger RVE lengths this effect becomes negligible.

Comparison with results from our previously proposed homogenization scheme [7], which is based on a classical Hill-Mandel approach, shows, that only the torsional stiffness differs. The previous approach yielded the Saint-Venant torsional stiffness $GI_T=1\,130\,\hbox {kN cm}^{2}$ instead of $GI_P=1\,346\, \hbox {kN cm}^{2}$.

Table 2 Results for beam RVE with homogeneous square cross-section

Fig. 8

Relative error in homogenized shear stiffness for beam RVE with homogeneous square cross-section and configuration DBC with varied RVE length $L_\text {RVE}$; element edge length of $l_e=0.25\,H_\text {RVE}$

5.3 Beam with layered cross-section

As a more complex example, a layered cross-section with geometry according to Fig. 9 is studied. The fraction $\rho _C=h_C/h$ describes the ratio of core height $h_C$ to total height $h=h_C+2h_L$ and is varied as well as the stiffness ratio $\alpha =E_C/E_L$ of Young’s modulus $E_C$ of the core and Young’s modulus $E_L$ of the face layers. The Young’s modulus of the face layers is fixed at $E_L=1\,000\, \hbox {kN/cm}^{2}$ and Poisson’s ratio for face layers and core is chosen as $\nu =0.3$.

5.3.1 Homogenized material matrix

Considering a typical use of such structures, focus lies in studying results for extensional stiffness $D_{11}={\overline{EA}}$, bending stiffness $D_{55}={\overline{EI}}_y$ and shear stiffness $D_{33}=\varkappa _z {\overline{GA}}$.

Analytical values for the considered stiffness parameters $D_{ii}$ are given by

$$\begin{aligned} D_{11}&={\overline{EA}} =E_Lb\left( \alpha h_C+2h_L\right) \nonumber \\ D_{55}&={\overline{EI}}_y=E_Lb\left( \alpha \dfrac{h_C^3}{12} +2\left[ \dfrac{h_L^3}{12}+s_L^2h_L\right] \right) \nonumber \\ D_{33}&={\overline{GA}}_{S_z}=\varkappa _z G_Lb\left( \alpha h_C+2h_L\right) \,. \end{aligned}$$

(81)

Here, $s_L=(h_C+h_L)/2$ and $\varkappa _z$ can be computed according to [25] with

$$\begin{aligned} \varkappa _z=\dfrac{4}{9}\dfrac{T_1^2}{T_2T_4} \end{aligned}$$

(82)

and

$$\begin{aligned} {\tilde{A}}&=\dfrac{(1-\rho _C)^3}{15}\left( 3\rho _C^2+9\rho _C+8\right) \,,\nonumber \\ T_1&=\left( 1-\rho _C^3\right) +\rho _C^3\,\alpha \,,\nonumber \\ T_2&=\dfrac{1-\rho _C}{\alpha }+\rho _C \,,\nonumber \\ T_3&=\left( 1-\rho _C^2\right) ^2+\dfrac{8}{15}\alpha ^2\rho _C^4 +\dfrac{4}{3}\alpha \,\rho _C^2\left( 1-\rho _C^2\right) \,,\nonumber \\ T_4&={\tilde{A}}\,\alpha + \rho _CT_3 \, . \end{aligned}$$

(83)

Fig. 9

Geometry of the layered beam cross-section with overall lengths $b=h=h_C+2h_L=1\,\hbox {cm}$

Table 3 Results for a beam with layered cross-section

These analytical values are also achieved with our previous approach based on classical Hill-Mandel homogenization presented in [7] and henceforth referred to as reference values. Table 3 summarizes results of the computations. Again, ${\varvec{D}}_B$ is computed correctly as diagonal matrix and the values for ${\overline{EA}}$ and ${\overline{EI}}_y$ are exactly the reference values (Fig. 10 and 11 ). The boundary effect of the DBC configuration is stronger than for the homogeneous cross-section and much higher RVE length and discretization are needed for the deviation in $\varkappa _z$ between DBC and Scal configuration to become negligible (Fig. 13). The DBC configuration is therefore deemed to be not feasible for this example and all further investigations are made within the Scal configuration.

The computed shear correction factor $\varkappa _z$ shows to be near the reference values for all considered combinations of $\rho _C$ and $\alpha$ but does not meet it exactly (Fig. 12). The relative deviation between computed and reference value increases with increasing core height and increasing stiffness ratio to up to $16.6\,{\%}$. For a detailed study into the reason for this deviation, see Sect. 5.3.2.

Fig. 10

Comparison of numerical and analytical extensional stiffness EA for beam with layered cross-section

Fig. 11

Comparison of numerical and analytical bending stiffness $EI_y$ for beam with layered cross-section

Fig. 12

Comparison of numerical and analytical shear correction factor $\varkappa _z$ for beam with layered cross-section

Fig. 13

Relative deviation for shear correction factor $\varkappa _z$ between configurations Scal and DBC for $\alpha =0.1$, $\rho _C=0.6$ for varying RVE length; discretization with constant element length over all computations

5.3.2 Multiscale model

In order to better understand the influence of the error in shear stiffness, a macro problem of a clamped beam is considered (see Fig. 14). It is loaded with a concentrated load in its center. We study the maximum displacement w and the stresses $S_{xx}$ and $S_{xz}$ for two exemplary configurations with $\alpha =0.5, \rho _C=0.5$ (I) and $\alpha =0.01, \rho _C=0.8$ (II).

Fig. 14

Clamped beam with concentrated load $F_z$ and vertical displacement w

Table 4 Comparison of the maximum displacement w of the beam axis between full scale reference model and FE2 model for the layered beam

Considering symmetry of the system, only half of the beam is simulated. The macro problem is discretized with 20 linear Timoshenko beam elements according to Sect. 4.1. For the micro/meso problem 24 quadratic brick elements are used per direction with eight elements over the height for each layer. For reference, we use a full scale model with quadratic brick elements and same discretization density as for the micro/meso problem ($15\,360$ brick elements overall).

Table 4 shows results for the displacement w of both models. The error in the displacement is slightly lower than, but clearly increasing with, the error in shear stiffness.

Taking a look at stress distributions $S_{xx}(z)$ and $S_{xz}(z)$ at $x=7.75\,\hbox {cm}$ in Fig. 15 and 16 , the normal stresses show perfect accordance with the full scale model. The shear stresses however show a significant deviation. While the RVE can only show a quadratic shear stress distribution due to the ansatz in Eqs. (50) and (61), the full scale model shows a more complex distribution. For configuration (I), deviation from a quadratic parabola is small, but for configuration (II) it is much more significant and hence the error in shear stiffness is much larger.

Fig. 15

Comparison of $S_{xx}(z)$ at $x=7.75\,\hbox {cm}$ between full scale / reference model and FE2 model for the layered beam

Fig. 16

Comparison of $S_{xz}(z)$ at $x=7.75\,\hbox {cm}$ between full scale / reference model and FE2 model for the layered beam

5.4 Beam with soft inclusions

Figure 18 shows the geometry of a beam with soft inclusions, that shall be studied in this section. Main material and inclusions are again linear elastic, isotropic with Young’s modulus $E_1=21\,000\,\hbox {kN/cm}^{2}$ and Poisson’s ratio $\nu _1=0.3$ for the main material and $E_2=10\hbox {kN/cm}^{2}$, $\nu _2=0$ for the inclusions.

As the beam is inhomogeneous in direction of the beam axis, the RVE can only be modeled by means of the DBC configuration instead of the Scal configuration. Considering results from previous examples, a convergence study is conducted considering RVE length and RVE discretization. This shows a RVE consisting of three inclusions ($L_\text {RVE}=60\,\hbox {mm}$) discretized with quadratic brick elements with edge length $l_e\approx 0.9\,\hbox {mm}$ is sufficient. One inclusion is then discretized with eight elements per direction and the main material accordingly. The used RVE can be seen in Fig. 19.

As macro problem, a clamped beam is chosen (see Fig. 17). The midpoint of the beam is displaced by $w=18\,\hbox {mm}$ and reaction forces are studied. For reference, a full scale model with 27-node quadratic brick elements is used. The full scale model is discretized with the same density as the RVE ($41\,472$ elements overall). The macro model of the FE2 study is discretized with 16 linear beam elements according to Sect. 4.1.

Fig. 17

Clamped beam with prescribed displacement w

Fig. 18

Geometry of beam with soft inclusions; width in y-direction: $8\,\hbox {mm}$

Fig. 19

RVE for the beam with soft inclusions

Table 5 shows results for reaction force and reaction moment. Both quantities show good accordance between full scale and FE2 model with only 1.10 - $1.85\,{\%}$ lower quantities in the FE2 model. As the inclusions lower reactions by $7.5\,{\%}$ ($F_z$) and $6.6\,{\%}$ ($M_y$) in comparison to a beam consisting only of the main material, the FE2 model only slightly overestimates the weakening effect caused by the inclusions.

Table 5 Comparison of reaction force $F_z$ and reaction moment $M_y$ between full scale / reference model and FE2 model for the beam with soft inclusions

5.5 Plate with inclusions

As examples for a homogeneous and a layered plate lead to very similar results as the homogeneous and layered beam, they are not discussed in detail. Instead, a more complex example of a plate with periodically distributed cube shaped inclusions is considered. The geometry of one such inclusion and its surroundings are displayed in Fig. 20.

Fig. 20

Geometry of an inclusion within the plate

The matrix material of the plate is chosen as $E_1=21\,000\, \hbox {kN/cm}^{2}$ and $\nu _1=0.3$. The inclusion material is chosen as $E_2=100\,\hbox {kN/cm}^{2}$ and $\nu _2=0.45$. The plate has a thickness of $h=50\,\hbox {cm}$, the distance between two inclusions is $30\,\hbox {cm}$ for both x- and y-direction.

Again, convergence studies considering RVE length and discretization are carried out. They show a RVE length of $100\,\hbox {cm}$ in both directions and an element edge length of $l_e\approx 5.6\,\hbox {cm}$ to be sufficient when using quadratic elements. This means, one inclusion is discretized with three quadratic elements per direction. The discretized RVE is displayed in Fig. 22.

Fig. 21

Clamped plate under constant loading

Fig. 22

RVE for plate with cube shaped inclusions

For the macro problem, a clamped plate under constant loading is studied (Fig. 21). Using symmetry arguments, only a quarter of the plate is simulated. For reference, a full scale model with quadratic brick elements is used, where the load is applied on the upper surface of the plate. It is computed in ABAQUS CAE 6.14 [26] with elements of type 3D20 (20-node brick element with quadratic ansatz functions), because of memory issues in FEAP due to the size of the model. Convergence studies lead to a discretization of the full scale model with 5.19 million degrees of freedom. The macro model of the FE2 model is discretized with 50 linear elements per direction (elements according to Sect. 4.1).

Results in Table 6 show good accordance between FE2 and full scale model and only minimal deviation of $0.27\,{\%}$ in the vertical displacement at the midpoint of the plate. Comparison with a homogeneous plate shows that the inclusions cause a $1.0\,{\%}$ increase of the vertical displacement in the reference models. The weakening effect is not as strong as for the beam with inclusions, but still measurable and the FE2 model is able to display this effect in good accordance with the reference model.

Table 6 Comparison of vertical displacement of the midpoint of the plate with cube shaped inclusions for full scale reference model and FE2 model

6 Conclusions

A first order homogenization scheme based on the Irving-Kirkwood theory is presented and applied to shear soft beam and plate structures. The micro/meso scale is loaded via a side condition, that enforces the macro scale strains to be the volumetric average of the micro/meso scale strains. No boundary conditions are needed to enforce the macro deformations on the micro/meso scale. Nontheless, minimal boundary conditions must be applied to prevent rigid body motions and additional ones can be applied for other purposes if necessary, e.g. to incorporate boundary conditions in an RVE located at the support of the macro structure.

The side condition and 3D modeling of the RVE allow for broader capabilities than just simple cross-sectional modeling within the Timoshenko or Reissner kinematic of the macro scale. A simple extension to quadratic shear stresses over the cross-section within the RVE leads to decent results for shear correction factors, even for non-homogeneous cross-sections. Macro quantities like reaction forces, reaction moments, in-plane stresses and displacements show good accordance between the proposed multiscale modeling and full scale models.