Mixed strain/stress gradient loadings for FFT-based computational homogenization methods

Abstract

In this article, the Lippmann–Schwinger equation for nonlinear elasticity at small-strains is extended by mixed strain/stress gradient loadings. Such problems occur frequently, for instance when validating computational results with three-point bending tests, where the strain in the bending direction varies linearly over the thickness of the sample. To control all components of the effective strain/stress gradient the periodic boundary conditions are combined with constraints that enforce the periodically deformed boundary to approximate the kinematically fully prescribed boundary in an average sense. The resulting fixed point and Fletcher–Reeves algorithms preserve the positive characteristics of existing FFT-algorithms, like low memory consumption and extraordinary computational speed. The accuracy and power of the proposed methods is demonstrated with a series of numerical examples, including continuous fiber reinforced laminate materials.

1 Introduction

The digital design of thin walled lightweight components made of carbon-fiber-reinforced plastics (CFRP) needs accurately calibrated material models on so-called coupon tests [2]. Due to the high in-plane stiffness of the CFRP, tensile measurements turn out to be very difficult, especially the clamping method plays a fundamental role [28]. Therefore, the effective mechanical material parameters are typically measured by three-point or four-point bending tests [3, 4, 38]. The same holds true for materials like concrete, which have a low tensile strength [1, 24].

The measured plate bending stiffness can be predicted for laminate structures made of unidirectional fiber-reinforced laminas, see Fig. 1, very well by using the classical laminate theory [26] in a two-step approach.

• 1. Calculate the effective lamina stiffness based on the elastic parameters of the fibers and matrix material and the volume fraction and orientation of the fibers (see [26, Section 2.2.2]). This leads to the homogenized laminate structure shown in Fig. 2.

• 2. Based on the stacking of the homogenized laminas, the effective plate bending stiffness is obtained by using the plane stress assumption (see [26, Section 3.3.5]).

Fig. 1

Upper half of the laminate which will be used in Sect. 5.5

Fig. 2

Upper half of the homogenized laminate, see Fig. 1

If the lamina exhibits a more complex geometry, e.g., due to fiber waviness, the first step can be replaced by numerical approaches. Especially, the FFT-based homogenization method of Moulinec–Suquet [20, 21] has proven to be a powerful tool for the computation of effective mechanical properties of micro-heterogeneous materials. An overview of the improvements of this method is given in [31].

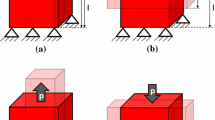
When nonlinear effects enter the stage, a direct simulation of the bending is unavoidable. In the early contribution of Nguyen et al. [22], the authors obtained the force and moment resultants for plates by adding a linear function (with zero mean value) to the ansatz of the strain field and derived a Green’s operator for mixed periodic and stress-free boundary conditions. Recently, Gélébart [7] extended the first idea to torsional loadings of beams and applied stress-free boundary conditions by symmetrically extending the plate resp. beam by pore space instead of using the special Green’s operator. In spite of the significant progress accomplished in his contribution, the loading direction still has to be grid-aligned. For practical applications, however, it is often useful to apply a bending in an arbitrary direction without using defective geometrical operations, i.e., rotation of the original unit cell and cutting out a smaller unit cell for computations. From a computational perspective, the extension by pore space typically decreases the convergence speed and enforces the usage of finite element [16, 34, 42] or finite difference discretizations [33]. Even more severe is the limitation that only the 9 components of the strain gradient which control bending and torsion (see Fig. 3) can be prescribed, and thus direct integration of stress gradient loadings is impossible.

Following Kouznetsova et al.[15] we combine the periodic boundary condition for the displacement fluctuations with kinematic constraints to resolve this issue (see Sect. 2). These constraints enforce the periodically deformed boundary to approximate the kinematically fully prescribed boundary in an average sense and can be automatically fulfilled if the unit cell has certain symmetries with respect to the applied strain gradient loading. E.g., for pure bending loadings it would be sufficient to use PMUBC boundary conditions [10] to obtain zero entries for the 9 additional components of the strain gradient. In the absence of such symmetries, the additional constraints can even strongly influence the solution of pure tensile tests, as we will show with an analytical solution for a two-phase laminate.

Inspired by the higher order homogenization [37, 43,44,45] and multiscale second-order computational homogenization [6, 15, 40] the kinematic constraints are formulated in terms of strain gradient measures. By transferring the previously developed framework for arbitrary mixed strain/stress boundary conditions [12] to mixed strain/stress gradients in Sect. 3, we derive a Lippmann–Schwinger equation for small strain elasticity with mixed first order boundary conditions.

The algorithms for solving the corresponding fixed point iteration are discussed in Sect. 4. In Sect. 5 we first validate our method with the analytical solution derived in Sect. 2, and then compare it for linear elastic material behavior with the classical laminate theory and numerical results of Nguyen et al. [22] and Gélébart [7] for grid-aligned bending. Afterwards, we extend this comparison to arbitrary loading directions. Finally, we investigate the linear and nonlinear behavior of the 2 mm thick $(-\,45^\circ /0^\circ /+\,45^\circ /0^\circ )_{\text {s}}$¹ laminate shown in Fig. 1.

2 FFT-based homogenization with strain gradient boundary conditions

Before introducing first order boundary conditions, we will shortly repeat the definition of zero order boundary conditions for FFT-based homogenization [20, 21]. For prescribed macroscopic symmetric strain $E\in {\text {Sym}}_3$ and given stress/strain relation $\sigma (\varepsilon )$, where we suppress the x-dependence for notational clarity, we seek a periodic displacement fluctuation $u:Y\rightarrow \mathbb {R}^3$ on the unit cell $Y = [-L_1/2,L_1/2] \times [-L_2/2,L_2/2] \times [-L_3/2,L_3/2]$ satisfying the equilibrium equation

$$\begin{aligned} \text {div}\sigma (\varepsilon )=0, \quad \varepsilon =E + \nabla ^su, \end{aligned}$$

(1)

where $\nabla ^su = \frac{1}{2}(\nabla u + \nabla u^T )$ denotes the strain due to the displacement fluctuation.

The volumetric components of the macroscopic strain E can be used to apply tensile loads, while the diagonal components allow shear loads to be imposed. For linear elastic material behavior, these load cases are used to compute the effective linear elastic stiffness of the material.

2.1 Strain gradient boundary conditions

A naive extension of the equilibrium equation (1) with first order boundary conditions may be obtained by modifying the corresponding optimization problem

$$\begin{aligned} \langle w(E + \nabla ^s u) \rangle _Y \rightarrow \min _{u \in H^1_{\#}(Y)^3} \end{aligned}$$

(2)

for the stress potential w, where the subscript $\#$ denotes function spaces with vanishing mean value [11].

By adding a linear function $E^\nabla \cdot x$ to the argument of the stress potential resp. the definition of $\varepsilon$, the bending response of the material can be computed by solving

$$\begin{aligned} \langle w(E + E^\nabla \cdot x + \nabla ^s u) \rangle _Y \rightarrow \min _{u \in H^1_{\#}(Y)^3} \end{aligned}$$

(3)

Its solution satisfies the equilibrium equation

$$\begin{aligned} \text {div}\sigma (\varepsilon )=0, \quad \varepsilon =E+E^\nabla \cdot x + \nabla ^su. \end{aligned}$$

(4)

With $E^\nabla \in {\text {Sym}}_3^{3}$ we want to prescribes the macroscopic gradient of $\varepsilon$. The relevant components of $E^\nabla$ for bending loadings are

$$\begin{aligned} E^\nabla _{112},E^\nabla _{113},E^\nabla _{221},E^\nabla _{223},E^\nabla _{331},E^\nabla _{332} \end{aligned}$$

(5)

and for torsional loadings

$$\begin{aligned} E^\nabla _{231},E^\nabla _{132},E^\nabla _{123}. \end{aligned}$$

(6)

These loadings are visualized in Fig. 3.

Fig. 3

Bending and torsional loadings

Similar to zero order boundary conditions, where the macroscopic strain E is determined by volume averaging of $\varepsilon$, we want an easy to compute measure for the macroscopic strain gradient $E^\nabla$. Inspired by the work of Kouznetsova et al.[15, equation (A4)] we define the effective bending resp. torsion of the unit cell Y as

$$\begin{aligned} \langle \varepsilon \otimes x \rangle _Y^\nabla = \frac{\int _Y \varepsilon \otimes x\, dx}{\int _Y (\mathbb {1}^\nabla \cdot x) \otimes x\, dx} \end{aligned}$$

(7)

with component wise division and $\mathbb {1}^\nabla \in {\text {Sym}}_3^3$ denoting the constant strain gradient tensor with only ones, i.e., $\mathbb {1}^\nabla _{ijk} = 1$ for $i,j,k=1,2,3$.

By using integration by parts we can show that the following relation holds

$$\begin{aligned} \begin{aligned} \langle \varepsilon _{ij} \otimes&x_k \rangle _Y^\nabla \\&=\frac{\int _{Y} \left[ E_{ij}+E^\nabla _{ijl} x_l + \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i} \right) \right] x_k \, dx}{\int _{Y} (x_1+x_2+x_3)x_k \, dx} \\&= E^\nabla _{ijk} + \frac{\frac{1}{2}\int _{Y}\left( \frac{\partial u_i}{\partial x_j}x_k +\frac{\partial u_j}{\partial x_i} x_k\right) \, dx}{\int _{Y} x_k^2 \, dx} \\&= E^\nabla _{ijk} + \frac{6}{L_k^2}\langle u_i \delta _{jk}+u_j \delta _{ik}\rangle _{Y_k^+}, \end{aligned} \end{aligned}$$

(8)

where $\langle \cdot \rangle _{Y_k^+}$ denotes the average value over $Y_k^+ = x\in Y: x_k = L_k/2$. Consequently, only the components of the macroscopic strain gradient for bending (5) and for torsion (6) directly coincide with the definition (7) for periodic displacement fields u.

2.2 Lippmann–Schwinger reformulation for strain gradient boundary conditions

Defining $\tilde{\varepsilon } = E + \nabla ^s u$ as well as $\tilde{\sigma } = \sigma (\tilde{\varepsilon } + E^\nabla \cdot x)$ allows us to interpret the problem (3) as zeroth-order homogenization with a fancy stress operator. The corresponding Lippmann–Schwinger equation reads

$$\begin{aligned} \tilde{\varepsilon } = E - \varGamma ^0:(\tilde{\sigma }(\tilde{\varepsilon }) - \mathbb {C}^0:\tilde{\varepsilon }), \end{aligned}$$

(9)

where $\varGamma ^0=\nabla ^s G^0 \text {div}: [L^2(Y)]^{3\times 3} \rightarrow [L^2(Y)]^{3\times 3}$ denotes the Lippmann–Schwinger operator and $G^0: [H_{\#}^{-1}(Y)]^{3} \rightarrow [H_{\#}^{1}(Y)]^{3}$ the solution operator of the linear reference problem, which associates to a right-hand side f the solution of the variational equation

$$\begin{aligned} \int _{Y} \nabla ^sv : \mathbb {C}^0 : \nabla ^su \,dx = -\int _{Y} f \cdot v \,dx, \end{aligned}$$

(10)

for all $v \in [H^1_{\#}(Y)]^3$. Using the definitions for $\tilde{\varepsilon }$ and $\tilde{\sigma }$ we obtain

$$\begin{aligned} \begin{aligned} \varepsilon&= E + E^\nabla \cdot x - \varGamma ^0:\left( \sigma (\varepsilon )-\mathbb {C}^0:\varepsilon \right) \\&\quad -\,\varGamma ^0:\mathbb {C}^0:E^\nabla \cdot x. \end{aligned} \end{aligned}$$

(11)

If $\mathbb {C}^0$ is isotropic, i.e., $\mathbb {C}^0_{ijkl} = \mu _0 (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}) + \lambda _0\delta _{ik}\delta _{jl}$ with Lamé’s moduli $\lambda _0$ and $\mu _0$, this equation can be simplified. Let $u^0_{E^\nabla } \in H^1_\#(Y)^3$ be the periodic displacement fluctuation defined by

$$\begin{aligned} u^0_{E^\nabla }(x) = \frac{1}{2}\left( \begin{array}{c} E^\nabla _{\perp ^0 111}x_1^2 + E^\nabla _{122}x_2^2 + E^\nabla _{133}x_3^2 \\ E^\nabla _{211}x_1^2 + E^\nabla _{\perp ^0 222}x_2^2 + E^\nabla _{233}x_3^2 \\ E^\nabla _{311}x_1^2 + E^\nabla _{322}x_2^2 + E^\nabla _{\perp ^0 333}x_3^2 \end{array}\right) \end{aligned}$$

(12)

with

$$\begin{aligned} E^\nabla _{\perp ^0 111}&= E^\nabla _{111} + \frac{\lambda _0}{2\mu _0 + \lambda _0} (E^\nabla _{221} + E^\nabla _{331}), \end{aligned}$$

(13)

$$\begin{aligned} E^\nabla _{\perp ^0 222}&= E^\nabla _{222} + \frac{\lambda _0}{2\mu _0 + \lambda _0} (E^\nabla _{112} + E^\nabla _{332}), \end{aligned}$$

(14)

$$\begin{aligned} E^\nabla _{\perp ^0 333}&= E^\nabla _{333} + \frac{\lambda _0}{2\mu _0 + \lambda _0} (E^\nabla _{113} + E^\nabla _{223}) \end{aligned}$$

(15)

and let $f^0_{E^\nabla } = \text {div}(\mathbb {C}^0:E^\nabla \cdot x) \in H_{\#}^{-1}(Y)^{3}$ be the constant function with components $f_i(x) \equiv \mathbb {C}^0_{ijkl} E^\nabla _{klj}$, $i=1,2,3$. Using the definition of $\mathbb {C}^0$ we obtain

$$\begin{aligned} \begin{aligned} f^0_{E^\nabla }&= 2\mu _0 \left( \begin{array}{c} E^\nabla _{111} + E^\nabla _{122} + E^\nabla _{133} \\[2pt] E^\nabla _{211} + E^\nabla _{222} + E^\nabla _{233} \\[2pt] E^\nabla _{311} + E^\nabla _{322} + E^\nabla _{333} \end{array}\right) \\&\quad +\,\lambda _0 \left( \begin{array}{c} E^\nabla _{111} + E^\nabla _{221} + E^\nabla _{331} \\[2pt] E^\nabla _{112} + E^\nabla _{222} + E^\nabla _{332} \\[2pt] E^\nabla _{113} + E^\nabla _{223} + E^\nabla _{333} \end{array}\right) \end{aligned} \end{aligned}$$

(16)

By simple calculus we can show for all interior points of Y

$$\begin{aligned} \text {div}\left( \mathbb {C}^0:\nabla ^s u^0_{E^\nabla }\right) = f^0_{E^\nabla }. \end{aligned}$$

(17)

In other words, $u^0_{E^\nabla }$ is the solution of the reference problem (10) for $f^0_{E^\nabla }$, i.e. $u^0_{E^\nabla } = G^0f^0_{E^\nabla } = G^0\text {div}(\mathbb {C}^0:E^\nabla \cdot x)$. For the symmetric strain we obtain using Voigt notation

$$\begin{aligned} \varGamma ^0:\mathbb {C}^0:E^\nabla \cdot x=\underbrace{\left( \begin{array}{ccc} E^\nabla _{\perp ^0 111} &{} 0 &{} 0 \\ 0 &{} E^\nabla _{\perp ^0 222} &{} 0 \\ 0 &{} 0 &{} E^\nabla _{\perp ^0 333} \\ 0 &{} E^\nabla _{232} &{} E^\nabla _{233} \\ E^\nabla _{131} &{} 0 &{} E^\nabla _{133} \\ E^\nabla _{121} &{} E^\nabla _{122} &{} 0 \end{array}\right) }_{=:E^\nabla _{\perp ^0}} \cdot x \end{aligned}$$

(18)

Consequently, the extended Lippmann–Schwinger equation (11) can be written as

$$\begin{aligned} \varepsilon = E + E^\nabla _{\parallel ^0} \cdot x - \varGamma ^0:\left( \sigma (\varepsilon )-\mathbb {C}^0:\varepsilon \right) , \end{aligned}$$

(19)

with

$$\begin{aligned} E^\nabla _{\parallel ^0} = E^\nabla - E^\nabla _{\perp ^0} = \left( \begin{array}{ccc} E^\nabla _{\parallel ^0 111} &{} E^\nabla _{112} &{} E^\nabla _{113} \\[2pt] E^\nabla _{221} &{} E^\nabla _{\parallel ^0 222} &{} E^\nabla _{223} \\[2pt] E^\nabla _{331} &{} E^\nabla _{332} &{} E^\nabla _{\parallel ^0 333} \\[2pt] E^\nabla _{231} &{} 0 &{} 0 \\ 0 &{} E^\nabla _{132} &{} 0 \\ 0 &{} 0 &{} E^\nabla _{123} \end{array}\right) \end{aligned}$$

(20)

and

$$\begin{aligned} E^\nabla _{\parallel ^0 111}&= - \frac{\lambda _0}{2\mu _0 + \lambda _0} (E^\nabla _{221} + E^\nabla _{331}), \end{aligned}$$

(21)

$$\begin{aligned} E^\nabla _{\parallel ^0 222}&= - \frac{\lambda _0}{2\mu _0 + \lambda _0} (E^\nabla _{112} + E^\nabla _{332}), \end{aligned}$$

(22)

$$\begin{aligned} E^\nabla _{\parallel ^0 333}&= - \frac{\lambda _0}{2\mu _0 + \lambda _0} (E^\nabla _{113} + E^\nabla _{223}). \end{aligned}$$

(23)

Therefore, a fixed-point iteration based on this extended Lippmann–Schwinger equation (19) allows to prescribe only the components of $E^\nabla _{\parallel ^0}$ visualized in Fig. 3. This confirms the observation of Gélébart [7], that “...due to the use of periodic boundary conditions, among the 18 strain gradient components, only 9 can be really prescribed.”. The remaining 9 components are an outcome of the equilibrium equation (4).

In the following Sect. 2.3 we will heavily rely on Eq. (8) to incorporate additional constraints into our extended Lippmann–Schwinger equation (19) that will enforce the equality of $\langle \varepsilon \otimes x \rangle _Y^\nabla$ and $E^\nabla$ for all components.

2.3 Kinematically constrained extended Lippmann–Schwinger equation

Without being able to to subject the unit cell to the full gradient $E^\nabla$, it is impossible to incorporate stress gradient loadings into the extended Lippmann–Schwinger equation (19). In other words, more restrictive boundary conditions are needed for mixed strain/stress gradient loadings. Kouznetsova et al. introduced the concept of “generalized” periodicity, which adds the missing 9 constraints [15, equation (25)]

$$\begin{aligned} \langle u_i\rangle _{Y_k^+} = 0, \quad i,k = 1,2,3. \end{aligned}$$

(24)

Then the deformed boundary approximates the kinematically fully prescribed boundary in an average sense. Therefore, in the following we call the generalized periodic boundary conditions of Kouznetsova et al. more expressively kinematically constrained periodic. According to (8) the kinematic constraints (24) are equivalent to

$$\begin{aligned} \langle \nabla ^s u \otimes x \rangle _Y^\nabla = 0 \end{aligned}$$

(25)

and therefore all components of the macroscopic strain gradient can be obtained by volume averaging of the local strain field

$$\begin{aligned} \langle \varepsilon \otimes x \rangle _Y^\nabla = E^\nabla . \end{aligned}$$

(26)

The (linear) constrained optimization problem for the bending response under kinematically constrained periodicity condition reads

$$\begin{aligned} \langle w(E + E^\nabla \cdot x + \nabla ^s u) \rangle _Y \rightarrow \min _{u \in H^1_{\#}(Y)^3, \langle \nabla ^s u \otimes x \rangle _Y^\nabla = 0} \end{aligned}$$

(27)

and has the Lagrangian saddle-point formulation

(28)

(29)

By endowing the space $H^1_{\#}(Y)^3$ with the Korn-type inner product

$$\begin{aligned} \langle u,v\rangle _{H^1_{\#}} = \langle \nabla ^s u : \mathbb {C}^0 : \nabla ^s v \rangle _Y \end{aligned}$$

(30)

we can compute the KKT condition as

$$\begin{aligned} 0&= G^0\text {div}\left[ \sigma (E + E^\nabla \cdot x + \nabla ^s u) + \varLambda ^\nabla \cdot x\right] , \end{aligned}$$

(31)

$$\begin{aligned} 0&= \langle \nabla ^s u \otimes x \rangle _Y. \end{aligned}$$

(32)

Therefore, the alternating gradient descent ascent method (Alt-GDA) [47] for the primal-dual pair $(u,\varLambda ^\nabla )$ reads

$$\begin{aligned} u^{n+1}&= u^n -s^n G^0\text {div}\left[ \sigma (E + E^\nabla \cdot x + \nabla ^s u^n) \right. \nonumber \\&\left. \quad +\, \varLambda ^{\nabla ,n} \cdot x \right] , \end{aligned}$$

(33)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \varLambda ^{\nabla ,n} + t^n \langle \nabla ^s u^{n+1} \otimes x \rangle _Y, \end{aligned}$$

(34)

for a sequence of positive step-sizes $s^n$ and $t^n$. To turn $\varLambda ^\nabla$ into a stress gradient we endow additionally ${\text {Sym}}_3^3$ with the inner product

(35)

where $\mathbb {Y}^\nabla$ is the six-order tensor that scales every entry of a third order tensor with the corresponding entry of $\langle (\mathbb {1}^\nabla \cdot x) \otimes x\rangle _Y$. Then the gradient of $L(u,\varLambda ^\nabla )$ with respect to $\varLambda ^\nabla$ is changed to $\mathbb {C}^0:\langle \nabla ^s u \otimes x \rangle _Y^\nabla$ and the Alt-GDA algorithm reads

$$\begin{aligned} u^{n+1}&= u^n -s^n G^0\text {div}\left( \sigma (E + E^\nabla \cdot x + \nabla ^s u^n) \right. \nonumber \\&\left. \quad +\, \varLambda ^{\nabla ,n} \cdot x \right) , \end{aligned}$$

(36)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \varLambda ^{\nabla ,n} + t^n \mathbb {C}^0:\langle \nabla ^s u^{n+1} \otimes x \rangle _Y^\nabla , \end{aligned}$$

(37)

For $t^n=1$ and $s^n=1$ we obtain using $\nabla ^s u^{n} = \varGamma ^0 : \mathbb {C}^0: \nabla ^s u^{n}$ for the strain fields the following GDA algorithm

$$\begin{aligned} \varepsilon ^{n+1}&= E+E^\nabla \cdot x - \varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right. \nonumber \\&\left. \quad +\,\left[ \varLambda ^{\nabla ,n}+\mathbb {C}^0:E^\nabla \right] \cdot x \right) , \end{aligned}$$

(38)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \varLambda ^{\nabla ,n} + \mathbb {C}^0:\langle \nabla ^s u^{n+1} \otimes x \rangle _Y^\nabla . \end{aligned}$$

(39)

This can be further simplified to

$$\begin{aligned} \varepsilon ^{n+1}&= E+\left[ E^\nabla _{\parallel ^0}-\varLambda ^{\nabla ,n}_{\perp ^0}\right] \cdot x \nonumber \\&\quad -\,\varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right) , \end{aligned}$$

(40)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \varLambda ^{\nabla ,n} + \langle \varepsilon ^{n+1} \otimes x \rangle _Y^\nabla -E^\nabla . \end{aligned}$$

(41)

or equivalently

$$\begin{aligned} \varepsilon ^{n+\frac{1}{2}}&= E+E^\nabla _{\parallel ^0} \cdot x - \varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right) , \end{aligned}$$

(42)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \langle \varepsilon ^{n+\frac{1}{2}} \otimes x \rangle _{Y}^\nabla - E^\nabla , \end{aligned}$$

(43)

$$\begin{aligned} \varepsilon ^{n+1}&= \varepsilon ^{n+\frac{1}{2}} - \varLambda ^{\nabla ,n}_{\perp ^0} \cdot x. \end{aligned}$$

(44)

This can be transformed into

$$\begin{aligned} \varepsilon ^{n+\frac{1}{2}}&= E - \varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right) , \end{aligned}$$

(45)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= E^\nabla - \langle \varepsilon ^{n+\frac{1}{2}} \otimes x \rangle _{Y}^\nabla , \end{aligned}$$

(46)

$$\begin{aligned} \varepsilon ^{n+1}&= \varepsilon ^{n+\frac{1}{2}} + \left[ E^\nabla _{\parallel ^0} + \varLambda ^{\nabla ,n}_{\perp ^0}\right] \cdot x. \end{aligned}$$

(47)

Therefore, the limit strain field $\varepsilon$ satisfies the kinematically constrained extended Lippmann–Schwinger equation

$$\begin{aligned}&\varepsilon + \varGamma ^0 : \left( \sigma (\varepsilon )-\mathbb {C}^0:\varepsilon \right) \nonumber \\&\quad =E\! + \!\left[ E^\nabla \!+\! \langle \varGamma ^0 \!: \left( \sigma (\varepsilon )-\mathbb {C}^0:\varepsilon \right) \otimes x \rangle _{Y,\perp ^0}^\nabla \right] \cdot x. \end{aligned}$$

(48)

and its corresponding Lagrange parameters can be computed by

$$\begin{aligned} \varLambda ^{\nabla } = E^\nabla + \langle \varGamma ^0 : \left( \sigma (\varepsilon )-\mathbb {C}^0:\varepsilon \right) \otimes x \rangle _{Y}^\nabla . \end{aligned}$$

(49)

2.4 Kinematically constrained periodic boundary conditions

To better understand the effect of the kinematic constraints let us consider the two-phase laminate with thickness $h=L_3$ shown in Fig. 4 under pure tensile loading in $x_1$-direction, i.e.

$$\begin{aligned} E=\left( \begin{array}{cccccc} E_{11}&0&0&0&0&0 \end{array}\right) ^T, \quad E^\nabla = 0 \end{aligned}$$

(50)

Fig. 4

Two-phase laminate

The two phases of the laminate are isotropic linear elastic with with Lamé’s moduli $\lambda ^\pm$ and $\mu ^\pm$. According to Appendix A of [13] the solution of the unconstrained problem (2), i.e. for periodic boundary conditions, has the phase wise constant strain

$$\begin{aligned} \varepsilon ^{\pm }=\left( \begin{array}{cccccc} E_{11}&0&\pm \frac{a_3}{2}&0&0&0 \end{array}\right) ^T. \end{aligned}$$

(51)

with the rank-one jump given by

$$\begin{aligned} a_3 = 2E_{11}\frac{\lambda ^- - \lambda ^+}{\lambda ^- + \lambda ^+ + 2(\mu ^- + \mu ^+)}. \end{aligned}$$

(52)

This solution has the in general non vanishing effective strain gradient component

$$\begin{aligned} \langle \varepsilon _{33} \otimes x_3 \rangle _Y^\nabla =\frac{\int _{0}^{h/2}a_3x_3 dx_3}{\int _{-h/2}^{h/2}x_3^2 dx_3} = \frac{3a_3}{2h} \end{aligned}$$

(53)

To obtain the solution for kinematically constrained boundary conditions (27) we need to start with a phase wise affine liner ansatz

$$\begin{aligned} \varepsilon ^{\pm }=\left( \begin{array}{cccccc} E_{11}&0&a_3^\pm + b_3^\pm x_3&0&0&0 \end{array}\right) ^T \end{aligned}$$

(54)

for the strain of the solution. By enforcing the effective strain and strain gradient as well as the continuity of the normal stress at the interface, i.e.

$$\begin{aligned}&\langle \varepsilon _{33} \rangle _Y = \frac{\int _{0}^{h/2}\varepsilon ^+_{33} dx_3 + \int _{-h/2}^{0}\varepsilon ^-_{33} dx_3}{h} = 0, \end{aligned}$$

(55)

$$\begin{aligned}&\langle \varepsilon _{33} \otimes x_3 \rangle _Y^\nabla =\frac{\int _{-h/2}^{h/2}\varepsilon _{33} x_3 dx_3}{\int _{-h/2}^{h/2}x_3^2 dx_3} = 0, \end{aligned}$$

(56)

$$\begin{aligned}&\sigma ^+_{33}(x_1,x_2,0) - \sigma ^-_{33}(x_1,x_2,0) =0 \end{aligned}$$

(57)

three of the four parameters of the ansatz can be eliminated and we are left with an one dimensional minimization problem for the elastic energy. Simple calculus leads to the following solution

$$\begin{aligned} a_3^\pm&= \pm \gamma \left( \lambda ^\pm + 7\lambda ^\mp + 2(\mu ^\pm + 7\mu ^\mp )\right) E_{11}, \end{aligned}$$

(58)

$$\begin{aligned} b_3^\pm&= -24\gamma \left( \lambda ^\mp + 2\mu ^\mp \right) \frac{E_{11}}{h} \end{aligned}$$

(59)

where

$$\begin{aligned} \gamma = \frac{\lambda ^- - \lambda ^+}{\tilde{\lambda } + 4\lambda ^+(7\mu ^- + \mu ^+) + 4\lambda ^-(\mu ^- + 7\mu ^+) + \tilde{\mu }} \end{aligned}$$

(60)

with

$$\begin{aligned} \tilde{\lambda }&= (\lambda ^-)^2 + 14 \lambda ^-\lambda ^+ + (\lambda ^+)^2, \end{aligned}$$

(61)

$$\begin{aligned} \tilde{\mu }&= (\mu ^-)^2 + 14 \mu ^-\mu ^+ + (\mu ^+)^2. \end{aligned}$$

(62)

Due to

$$\begin{aligned} \text {div}\sigma ^{\pm }&=b_3^\pm \left( \begin{array}{c} \lambda ^\pm \\ \lambda ^\pm \\ (\lambda ^\pm +2\mu ^\pm ) \end{array}\right) \end{aligned}$$

(63)

$$\begin{aligned}&=-24\gamma \frac{E_{11}}{h}\left( \begin{array}{c} \lambda ^\pm \left( \lambda ^\mp + 2\mu ^\mp \right) \\ \lambda ^\pm \left( \lambda ^\mp + 2\mu ^\mp \right) \\ (\lambda ^\pm +2\mu ^\pm )\left( \lambda ^\mp + 2\mu ^\mp \right) \end{array}\right) \end{aligned}$$

(64)

the corresponding stress does not satisfy the equilibrium equation (1) for $\gamma \ne 0$, i.e. $\lambda ^- \ne \lambda ^+$.

In Figs. 5 and 6 the non vanishing components of the strain resp. stress fields are visualized for $E^+ =1$ GPa, $E^-=10$ GPa, $\nu ^\pm = 0.3$, $h=1$mm and $E_{11} = 10$%. Clearly, even at the chosen low phase contrast, the local stress and strain fields differ significantly due to the kinematic constraints. Also the average stresses change notably. Additionally, the solution for kinematically constrained periodic boundary conditions depends on the choice of the center point of the RVE. When choosing a point in the middle of one of the two layers as the center point, the symmetries of the RVE automatically enforce the kinematic constraints and both solutions - with and without kinematic constraints - would coincide.

Fig. 5

Local strain field of the two-phase laminate shown in Fig. 4 under pure tensile loading

Fig. 6

Local stress field of the two-phase laminate shown in Fig. 4 under pure tensile loading

Fig. 7

Local displacement field of the two-phase laminate shown in Fig. 4 under pure tensile loading

For the situation at hand, the displacements for kinematically constrained periodic boundary conditions also satisfy zero Dirichlet boundary conditions, compare Fig. 7. Nevertheless, the displacements are completely different inside the RVE, because the kinematically constrained solution does not fulfill the equilibrium equation (1). Put differently, in general it is impossible to satisfy the equilibrium equation (1), periodic boundary conditions and the kinematic constraints all at once. The solution for kinemtically constrained periodic boundary conditions is the energetic optimal deformation that satisfies the periodic boundary conditions and at the same time the kinematic boundary conditions in an average sense.

In Sect. 5 we will use this solution to validate our numerical algorithms and to investigate the local solution quality for different discretizations. Since from an engineering point of view non-symmetric plates that lead to effective bending under tensile loading are not desirable, all other considered examples are symmetric with respect to the center plane. Consequently, the additional constraints would have no effect on the results of (in-plane) tensile simulations and we can use the standard FFT-based algorithms for computing the tensile stiffness then.

Before proceeding with mixed first order boundary conditions, some remarks are in order.

• 1. Due to the identity

  

  (65)

  the constraints (25) are equivalent to

  $$\begin{aligned} \langle E^\nabla \cdot x : \nabla ^s u \rangle _Y^\nabla = 0 \quad \forall E^\nabla \in {\text {Sym}}_3^3 \end{aligned}$$

  (66)

  which makes the decomposition

  $$\begin{aligned} \varepsilon = E + E^\nabla \cdot x + \nabla ^s u \end{aligned}$$

  (67)

  unique.

• 2. The solution of the kinematically constrained extended Lippmann–Schwinger equation (48) will in general no longer satisfy the equilibrium equation (4).

• 3. The additional constraints (24) makes it possible to use periodic boundary conditions for the micro scale of a gradient-enhanced FE$^2$ scheme. Kouznetsova et al. [15] implemented these constraints for the displacements.

• 4. For displacement based FFT-based schemes [16, 18] the constraints can be enforced by using the surface integrals (24) and a kinematically constrained extended Lippmann–Schwinger equation for the displacements similar to (48) can be derived.

• 5. When the Nyquist frequencies are set to zero [41], the relation (18) is only approximately correct but the resulting linear difference is removed due to the additional constraints (25).

• 6. The above formulas for $E^\nabla _{\parallel ^0}$ and $E^\nabla _{\perp ^0}$ simplify when the reference material is chosen as a scalar multiple of the identity [11, Section 3.1]. Nevertheless, the derivation continues to hold for general isotropic $\mathbb {C}^0$.

3 FFT-based homogenization with mixed first order boundary conditions

Thanks to the developments of the previous section, i.e. the kinematically constrained extended Lippmann–Schwinger equation (48), the full gradient $E^\nabla$ can be prescribed. We now have the tools in hand to integrate stress gradient boundary conditions, which we will present below, and thus derive a kinematically constrained extended Lippmann–Schwinger equation for mixed first-order boundary conditions.

3.1 Stress gradient boundary conditions

Similar to the strain gradient boundary conditions, we must first introduce a measure of the effective stress gradient that is easy to compute.

Using the following extension of the Hill–Mandel energy condition

(68)

Kouznetsova et al.[15, equation (38)] and Schmidt et al. [29] introduced the effective higher-order stress measure

$$\begin{aligned} \langle \sigma \otimes x \rangle _Y = \frac{1}{|Y|}\int _{Y} \sigma \otimes x \, dx. \end{aligned}$$

(69)

Therefore, we can introduce as an alternative higher order boundary condition the effective stress gradient $S^\nabla \in {\text {Sym}}_3^{3}$ defined by

$$\begin{aligned} S^\nabla = \langle \sigma \otimes x \rangle _Y^\nabla = \frac{\int _Y \sigma \otimes x\, dx}{\int _Y (\mathbb {1}^\nabla \cdot x) \otimes x\, dx}. \end{aligned}$$

(70)

In contrast to the effective strain gradient studied so far, all components of the effective stress gradient can be computed from the local stress field $\sigma$ for any periodic displacement field u.

Before extending the Lippmann–Schwinger equation to mixed first order boundary conditions in the next section, we note that the same extension (68) of the Hill–Mandel lemma is used for higher order homogenization of first strain gradient theories. The macroscopic energy density for elastic material behavior is of the form [37]

$$\begin{aligned} \begin{aligned} \left<\sigma : \varepsilon \right>_Y&= E:\mathbb {C}^{0,0}:E + 2L E:\mathbb {C}^{0,1}:E^\nabla \\&\quad +\,L^2 E^\nabla :\mathbb {C}^{1,1}:E^\nabla , \end{aligned} \end{aligned}$$

(71)

with $L=L_1=L_2=L_3$. Consequently, by solving (27) for a suitable sequence of loads $E, E^\nabla$, one can obtain the effective stiffness matrices $\mathbb {C}^{0,0},\mathbb {C}^{1,1}$ and $\mathbb {C}^{0,1}$. Keep in mind, that e.g. for the two-phase laminate shown in Fig. 4, the effective stiffness matrix $\mathbb {C}^{0,0}$ in general does not coincide with the effective stiffness obtained by standard homogenization methods.

3.2 Mixed boundary conditions and projectors

To conveniently describe mixed zero order boundary conditions Kabel et al. [12] made use of projectors, i.e., 4-tensors $\mathbb {P}$ with minor symmetries which are idempotent

$$\begin{aligned} \mathbb {P}:\mathbb {P}:T=\mathbb {P}:T \quad \text {for all} \quad T\in {\text {Sym}}_3 \end{aligned}$$

(72)

and have major symmetry

$$\begin{aligned} \langle \mathbb {P}:S,T\rangle = \langle S,\mathbb {P}:T\rangle \quad \text {for all} \quad S, T\in {\text {Sym}}_3. \end{aligned}$$

(73)

The first property (72) has the important consequence that every $T\in {\text {Sym}}_3$ can be (uniquely) decomposed in the form

$$\begin{aligned} T=T_1 + T_2 \quad \text {with} \quad \mathbb {P}:T_1=T_1 \quad \text {and} \quad \mathbb {P}:T_2=0. \end{aligned}$$

(74)

Furthermore, $T_1$ and $T_2$ can be computed via

$$\begin{aligned} T_1 = \mathbb {P}: T \quad \text {and} \quad T_2 = T-T_1 = \mathbb {Q}:T \end{aligned}$$

(75)

with the complementary projector $\mathbb {Q}=\mathbb {I}-\mathbb {P}$, where $\mathbb {I}$ is the identity $4-$tensor, i.e., $\mathbb {I}:T=T$ for all $T\in \mathbb {R}^{3\times 3}$. Furthermore, the operators $\mathbb {P}$ and $\mathbb {Q}$ annihilate each other, i.e.,

$$\begin{aligned} \mathbb {P}:\mathbb {Q}=0 \quad \text {and} \quad \mathbb {Q}:\mathbb {P}=0. \end{aligned}$$

(76)

For higher order mixed boundary conditions we additionally need projectors for 3-tensors. For the applications we have in mind it is sufficient to consider only 6-tensors $\mathbb {P}^\nabla$ that can be represented by three projectors $\mathbb {P}^1,\mathbb {P}^2$ and $\mathbb {P}^3$ for 2-tensors in the following way

$$\begin{aligned} \mathbb {P}^\nabla _{ijklmn} = \delta _{kn}\mathbb {P}^k_{ijlm}. \end{aligned}$$

(77)

Using the identity $6-$tensor $\mathbb {I}^\nabla$, i.e., for all $T^\nabla \in \mathbb {R}^{3\times 3 \times 3}$, we obtain the complementary projector $\mathbb {Q}^\nabla = \mathbb {I}^\nabla - \mathbb {P}^\nabla$.

With these preparations in hand, we can neatly formulate mixed boundary conditions for the kinematically constrained extended Lippmann–Schwinger equation (48). Given projectors $\mathbb {P},\mathbb {P}^\nabla$ and some $E,S\in {\text {Sym}}_3$ as well as $E^\nabla ,S^\nabla \in {\text {Sym}}_3^3$ we seek periodic $u:Y\rightarrow \mathbb {R}^3$ satisfying the optimization problem (27) and the boundary conditions

(78)

(79)

where $\langle \varepsilon \rangle _Y$ and $\langle \sigma (\varepsilon )\rangle _Y$ are denoting the average of the strain resp. stress field over Y. Similarly $\langle \varepsilon \otimes x \rangle _{Y}^\nabla$ is the effective bending resp. torsion and $\langle \sigma (\varepsilon ) \otimes x \rangle _Y^\nabla$ is the effective stress gradient defined in Eq. (7) resp. (70).

Dimension counting shows that (78) and (79) are overdetermined if E and S or $E^\nabla$ and $S^\nabla$ are unconstrained. Due to the mutual annihilation property (76), a necessary condition for (78) and (79) to be reasonable are the four constraints

(80)

(81)

rendering the optimization problem (27) with boundary conditions (78) and (79) sensible. To illustrate the concept, we give some examples for the choice of the projectors.

• 1. If $\mathbb {P}=\mathbb {I}$ and $\mathbb {P}^{\nabla }=\mathbb {I}^{\nabla }$, the boundary conditions are equivalent to the constraints $\langle \varepsilon \rangle _Y=E$ and $\langle \varepsilon \otimes x \rangle _{Y}^\nabla =E^\nabla$. Using for example the loading (in Voigt notation)

  $$\begin{aligned} E=\left( \begin{array}{cccccc} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right) , \quad E^\nabla =\left( \begin{array}{ccc} 0 &{} 0 &{} E^\nabla _{113} \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right) \end{aligned}$$

  (82)

  allows to prescribe the bending visualized in the top left of Fig. 3.

• 2. By rotating these loadings E and $E^\nabla$ by $45^\circ$ in the $x_1$-$x_2$ plane, the bending shown in Fig. 8 can be applied.

• 3. For the projectors $\mathbb {P}=0$ and $\mathbb {P}^{\nabla }=0$ the stresses $\langle \sigma (\varepsilon ) \rangle _Y = S$ and $\langle \sigma (\varepsilon ) \otimes x \rangle _Y^\nabla =S^\nabla$ are prescribed. By multiplying the stress gradient with the half of the thickness of a plate resp. the length of a bar, one can easily estimate the maximal occurring tensile stress in the outer layers of a bended plate resp. the maximal shear stress at the end of a twisted bar.

• 4. Bending of a plate in the $x_1$-$x_2$ plane under plane stress conditions can be performed for $\mathbb {P}=\mathbb {I}- e_3\otimes e_3\otimes e_3\otimes e_3$ and $\mathbb {P}^i=\mathbb {I}- e_i\otimes e_i\otimes e_i\otimes e_i$, $i=1,2,3$, with the loading

  $$\begin{aligned} E=\left( \begin{array}{cccccc} 0&0&*&0&0&0 \end{array}\right) ^T, \quad S = \left( \begin{array}{cccccc} *&*&0&*&*&* \end{array}\right) ^T \end{aligned}$$

  (83)

  and

  $$\begin{aligned} E^\nabla =\left( \begin{array}{ccc} * &{} 0 &{} E^\nabla _{113} \\ 0 &{} * &{} 0 \\ 0 &{} 0 &{} * \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right) , \quad S^\nabla =\left( \begin{array}{ccc} 0 &{} * &{} * \\ * &{} 0 &{} * \\ * &{} * &{} 0 \\ * &{} * &{} * \\ * &{} * &{} * \\ * &{} * &{} * \\ \end{array}\right) . \end{aligned}$$

  (84)

  In contrast to example 1, the plate can become thinner with this type of boundary conditions due to the Poisson effect.

• 5. By also rotating the projectors by $45^\circ$ in addition to the loads in example 2, the bending shown in Fig. 8 can also be performed under plane stress conditions. A detailed comparison of the results of this simulation setup with laminate theory is presented in Sect. 5.

Fig. 8

Rotated bending loading

Similar to the work at hand, Schneider [32] extended the usage of projectors. In his work, he uses projectors to apply mixed zero order boundary conditions in polarization methods.

3.3 The kinmatically constrained Lippmann–Schwinger equation for mixed boundary conditions

Given projectors $\mathbb {P},\mathbb {P}^{\nabla }$ and prescribed loads $E,S\in {\text {Sym}}_3$ as well as $E^\nabla ,S^\nabla \in {\text {Sym}}_3^{3}$ satisfying the constraints (80) and (81) the mixed boundary conditions (78) and (79) are incorporated into the optimization problem (27)

(85)

Following the ideas of Sect. 2.3 we use this constrained optimization problem to derive an extended Lippmann–Schwinger equation that generalizes (48) by mixed boundary conditions.

The constrained optimization problem (85) has the Lagrangian saddle-point formulation

(86)

with

(87)

By endowing the affine linear subspaces $\mathbb {P}: \bar{\varepsilon } = E$ of ${\text {Sym}}_3$ and of ${\text {Sym}}_3^3$ with the inner products

(88)

(89)

and keeping the inner product for the space ${\text {Sym}}_3^3$ of Lagrange parameters

(90)

Using the Moore–Penrose pseudoinverse [19, 25] $\mathbb {M}=\left( \mathbb {Q}:\mathbb {C}^0:\mathbb {Q}\right) ^\dagger$ as well as whose components are given by

$$\begin{aligned} \mathbb {M}^{\nabla }_{ijklmn} = \delta _{kn}\left( \mathbb {Q}^k:\mathbb {C}^0:\mathbb {Q}^k\right) ^\dagger _{ijlm}, \end{aligned}$$

(91)

we can compute the KKT condition as

(92)

(93)

(94)

(95)

Therefore, the alternating gradient descent ascent (Alt-GDA) [47] reads

(96)

(97)

(98)

(99)

for a sequence of positive step-sizes $s^n$ and $t^n$. For $t^n=1$ and $s^n=1$ we obtain using $\nabla ^s u^{n} = \varGamma ^0 : \mathbb {C}^0: \nabla ^s u^{n}$ for the strain fields the following GDA algorithm

(100)

(101)

(102)

(103)

Due to

(104)

(105)

the update of the average strain and its gradient can be written as

(106)

(107)

The two other equations can be simplified to

$$\begin{aligned} \varepsilon ^{n+1}&= \bar{\varepsilon }^{n+1}+\left[ \bar{\varepsilon }^{\nabla ,n+1}_{\parallel ^0}-\varLambda ^{\nabla ,n}_{\perp ^0}\right] \cdot x \nonumber \\&\quad -\, \varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right) , \end{aligned}$$

(108)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \varLambda ^{\nabla ,n} + \langle \varepsilon ^{n+1} \otimes x \rangle _Y^\nabla -\bar{\varepsilon }^{\nabla ,n+1}. \end{aligned}$$

(109)

or equivalently

$$\begin{aligned} \varepsilon ^{n+\frac{1}{2}}&= \bar{\varepsilon }^{n+1}+\bar{\varepsilon }^{\nabla ,n+1}_{\parallel ^0} \cdot x \nonumber \\&\quad -\,\varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right) , \end{aligned}$$

(110)

$$\begin{aligned} \varLambda ^{\nabla ,n+1}&= \langle \varepsilon ^{n+\frac{1}{2}} \otimes x \rangle _{Y}^\nabla - \bar{\varepsilon }^{\nabla ,n+1}, \end{aligned}$$

(111)

$$\begin{aligned} \varepsilon ^{n+1}&= \varepsilon ^{n+\frac{1}{2}} - \varLambda ^{\nabla ,n}_{\perp ^0} \cdot x. \end{aligned}$$

(112)

This can be transformed into

$$\begin{aligned} \varepsilon ^{n+\frac{1}{2}} =&\bar{\varepsilon }^{n+1} - \varGamma ^0 : \left( \sigma (\varepsilon ^n)-\mathbb {C}^0:\varepsilon ^n \right) , \end{aligned}$$

(113)

$$\begin{aligned} \varLambda ^{\nabla ,n+1} =&\bar{\varepsilon }^{\nabla ,n+1} - \langle \varepsilon ^{n+\frac{1}{2}} \otimes x \rangle _{Y}^\nabla , \end{aligned}$$

(114)

$$\begin{aligned} \varepsilon ^{n+1} =&\varepsilon ^{n+\frac{1}{2}} + \left[ \bar{\varepsilon }^{\nabla ,n+1}_{\parallel ^0} + \varLambda ^{\nabla ,n}_{\perp ^0}\right] \cdot x. \end{aligned}$$

(115)

so that the complete algorithm using the variable $\tau$ for the polarization reads

(116)

(117)

(118)

(119)

(120)

(121)

Therefore, the limit strain field $\varepsilon$ satisfies the kinematicall constrained extended Lippmann–Schwinger equation with mixed first order boundary conditions

(122)

where $\langle \varGamma ^0 : \cdot \otimes x \rangle _{Y,\perp ^0}^\nabla$ and are shorthand notations for the operators

$$\begin{aligned} T\mapsto \langle \varGamma ^0 : T \otimes x \rangle _{Y,\perp ^0}^\nabla , \quad T:Y\rightarrow {\text {Sym}}_3 \end{aligned}$$

(123)

and

(124)

The corresponding Lagrange parameters of the strain field $\varepsilon$ can be computed by

(125)

(126)

The equation (122) can be simplified if the projectors $\mathbb {P},\mathbb {P}^{\nabla }$ and the reference tensor $\mathbb {C}^0$ commute, i.e.,

(127)

holds for all $T\in \mathbb {R}^{3\times 3}$ and $T^\nabla \in \mathbb {R}^{3\times 3 \times 3}$. This is automatically satisfied if $\mathbb {C}^0$ is chosen as a multiple of the identity tensor $\mathbb {I}$. Conversely, (127) holds for all projectors $\mathbb {P},\mathbb {P}^{\nabla }$ if and only if $\mathbb {C}^0$ is a multiple of the identity. Then, equation (122) simplifies to

(128)

where $\mathbb {D}^0$ denotes the inverse of $\mathbb {C}^0$.

An alternative derivation more in the line of [12] can be found in the Appendix 1

4 FFT-based algorithms

In this section we will derive FFT-based algorithms to solve the extended Lippmann–Schwinger equation (122). The projected gradient descent method [23, 27] will use $\varLambda ^{\nabla ,n+1}_{\perp ^0}$ instead of the last iterate $\varLambda ^{\nabla ,n}_{\perp ^0}$ for the update of $\varepsilon ^n$ in equation (121) and can therefore be seamlessly integrated into existing (nonlinear) conjugate gradient (CG) methods [30, 46].

4.1 Projected gradient descent

After the derivations of Sect. 3.3 it seems natural to use the gradient descent ascent method [47] for the solution of the extended Lippmann–Schwinger (122). It is known, however, that even the convergence speed of gradient descent methods is limited [11] and that one should use (nonlinear) CG methods whenever possible [30].

Since it seems to be difficult to integrate the gradient descent ascent algorithm (116)–(121) into a CG method, we decided to use the projected gradient descent (PGD) method [23, 27]. This method projects the iterates of the standard gradient descent method for the unconstrained problem onto the (affine linear) subspace of admissible functions satisfying the constraints. From an algorithmic point of view this can be achieved by only changing the update of the strain field in the gradient descent ascent algorithm. More precisely, using $\varLambda ^{\nabla ,n+1}_{\perp ^0}$ instead of the last iterate $\varLambda ^{\nabla ,n}_{\perp ^0}$ for the update of $\varepsilon ^n$ allows to eliminate the Lagrange parameters

(129)

(130)

(131)

(132)

(133)

While the first part (129)–(132) performs the classical basic scheme of Moulinec–Suquet on the unconstrained extended Lippmann–Schwinger equation, the last step (133) projects the next iterate on an admissible state.

Unfortunately, as the visualization in Fig. 9 shows, the projection is in general not orthogonal to the subspace of admissible solutions.

Fig. 9

Projected gradient descent method

The projection can only be interpreted as ascent step in orthogonal direction to the (affine linear) subspace of admissible solutions.

Using the equivalent steps

$$\begin{aligned} \varepsilon ^{n+\frac{1}{2}} =\,&\bar{\varepsilon }^{n+1} - \varGamma ^0 : \tau ^n, \end{aligned}$$

(134)

$$\begin{aligned} \varepsilon ^{n+1} =\,&\varepsilon ^{n+\frac{1}{2}} + \left[ \bar{\varepsilon }^{\nabla ,n+1} - \langle \varepsilon ^{n+\frac{1}{2}} \otimes x \rangle _{Y,\perp ^0}^\nabla \right] \cdot x. \end{aligned}$$

(135)

instead of (132) and (133) this method can be implemented as shown in Algorithm 1.

Notice that the operators $\mathbb {M}=\left( \mathbb {Q}:\mathbb {C}^0:\mathbb {Q}\right) ^\dagger$ and have to be computed only once in preprocessing of each loading step, when $\mathbb {C}^0$ is adapted by setting it to the average of the maximal and minimal (positive) eigenvalue of the tangential stiffness $d\sigma /d\varepsilon$ [11].

Similar as described by Kabel et al. [12] for unidirectional tensile tests, the following affine linear extrapolation improves the convergence speed for strain gradient simulations without superimposed stretch

$$\begin{aligned} \varepsilon _k = \varepsilon _{k-2} + \frac{\left\| E^\nabla _{k} - E^\nabla _{k-2}\right\| }{\left\| E^\nabla _{k-1} - E^\nabla _{k-2}\right\| } (\varepsilon _{k-1} - \varepsilon _{k-2}). \end{aligned}$$

(136)

4.2 Conjugate gradient methods

In the case of linear material behavior, i.e. $\sigma (\varepsilon ) = \mathbb {C}: \varepsilon$, the extended Lippmann–Schwinger equation with mixed first order boundary conditions (122) is a linear relation and therefore the conjugate gradient (CG) method can be used. This method was first applied by Zeman et al. [46] for FFT-based homogenization. It needs four instead of one solution vector but can be expected to have a significantly improved convergence behavior, see the detailed comparison of Schneider [30] for standard boundary conditions.

The implementation shown in Algorithm 2 is based on the Moulinec–Suquet iterate for computing the matrix vector product on the left hand side of (122), which was previously used as core function of the PGD implementation shown in Algorithm 1.

In the case of nonlinear material behavior we suggest using the Fletcher–Reeves (FR) nonlinear CG [30] for solving (122), see Algorithm 3. The implementation proposed by Schneider [30] can be stabilized by limiting the factor $\frac{\gamma }{\gamma _{\text {old}}}$, compare line 10 of Algorithm 3. It needs one solution vector less but typically also converges slower than the standard CG method in the linear elastic case. To reduce memory requirements, both the CG and FR methods could also be implemented by using additional displacement vectors instead of additional strain vectors [9, 11].

In Sect. 5.4 we will compare the convergence speed of all three methods.

5 Examples

In the following we will discuss multiple examples of laminate structures. At first, we will use in Sect. 5.1 our analytical solution for the two-phase laminate shown in Fig. 4 under pure tension with the additional constraints to study the influence of the discretization on the local solution quality. After discussing the relation of the force and moment resultant with the effective stress and stress gradient in Sect. 5.2 we will then investigate in Sect. 5.3 the examples of Nguyen et al. [22] and Gélébart [7] for which only grid-aligned loadings are applied. Afterward, we will modify one of their examples and validate our extended Lippmann–Schwinger equation in the linear elastic regime by comparison with the classical laminate theory [26] in Sect. 5.4. Finally, in Sect. 5.5 we will study the effective linear and nonlinear behavior of a multilayer laminate subjected to tensile and bending loadings. All simulations results were obtained with FeelMath [5] which is distributed as part of GeoDict².

Fig. 10

Local numerical solution fields of the two-phase laminate under pure tensile loading and their corresponding error for the Hex8R discretization of Willot [42] and the staggered grid discretization [34] at different resolutions. Left column: Displacement. Middle column: Strain. Right column: Stress

5.1 Strain gradient boundary conditions

In this section, the analytical solution shown in Figs. 5, 6 and 7 for a two-phase laminate under tensile loading and with suppressed strain gradient is used to validate our method and to investigate the local solution quality.

In the middle column of Fig. 10 we compare the local strain fields for three different resolution and two discretizations. Obviously, the staggered grid discretization [34] exhibits a significantly higher local accuracy than the Hex8R discretization [42]. This is at least partly related to the fact, mentioned earlier, that for the Hex8R discretization the Nyquist frequencies are set to zero [41]. Somewhat surprisingly, the Hex8R discretization does not show comparable solution quality even at doubled resolution. Only the (phase-wise) averages are of similar accuracy, compare Table 1.

Table 1 Phase-wise averages of the local strain and global average of the stress field shown in Fig. 10

Since the displacement field is obtained by integrating the strain field according to the formulas derived in [10], we make the same observation for the local displacement field shown in the left column of Fig. 10.

The non-trivial stress components $\sigma _{11}$ and $\sigma _{22}$ are not shown because their errors are only a constant rescaling of the error for $\sigma _{33}$ that is visualized in the right column of Fig. 10. This is due to the fact that the numerical error for $\varepsilon _{11}$ is equal zero. Therefore, the phase-wise scaling factor of the error coincides with $\lambda ^\pm /(\lambda ^\pm +2\mu ^\pm )$, which for both phases is equal to 3/7.

Despite these observations, we will only use the Hex8R discretization in the following. Otherwise, our results would not be comparable to the benchmark results of Gélébart [7] in Sect. 5.3 and the subsequent extension to arbitrary loading directions.

5.2 Force and moment resultant

To be able to compare our simulation results for a plate $Y = [-L_1/2,L_1/2] \times [-L_2/2,L_2/2] \times [-h/2,h/2]$ with thickness h in the x-y-plane with the benchmark results of Nguyen et al. [22] and Gélébart [7] in Sect. 5.3 as well as classical results of the laminate theory [26] in Sects. 5.4 and 5.5 we first discuss the relation between the force resultant N and the moment resultant M with the effective stress $\langle \sigma \rangle _Y$ and the effective stress gradient $\langle \sigma \otimes x \rangle _Y^\nabla$ of the plate.

Since the components of the force and moment resultants are defined by

$$\begin{aligned} N_{ij}&= \frac{1}{L_1 L_2} \int _{Y}\sigma _{ij} dx \end{aligned}$$

(137)

$$\begin{aligned} M_{ij}&= \frac{1}{L_1 L_2} \int _{Y}x_3\sigma _{ij} dx \end{aligned}$$

(138)

for $i,j \in \{1,2\}$ we obtain

$$\begin{aligned} N_{ij}&= h \langle \sigma _{ij} \rangle _Y \end{aligned}$$

(139)

$$\begin{aligned} M_{ij}&= h \langle x_3 \sigma _{ij} \rangle _Y^\nabla \nonumber \\&= \langle \sigma _{ij} \otimes x_3 \rangle _{Y}^\nabla \frac{h}{|Y|}\int _Y (\mathbb {1}^\nabla x)_{ij} \otimes x_3\, dx \nonumber \\&= \langle \sigma _{ij} \otimes x_3 \rangle _{Y}^\nabla \int _{-h/2}^{h/2} x_3^2\, dx_3 \nonumber \\&= \frac{h^3}{12} \langle \sigma _{ij} \otimes x_3 \rangle _{Y}^\nabla , \end{aligned}$$

(140)

where $\langle \sigma _{ij} \otimes x_k \rangle _{Y}^\nabla$ denotes the ijk component of $\langle \sigma \otimes x \rangle _{Y}^\nabla$. These tensors are set into relation with the prescribed average in-plane strain components $E_{11},E_{22},E_{12}$ and their average gradient in thickness direction $E^\nabla _{113},E^\nabla _{223},E^\nabla _{123}$

(141)

To simulate plates with plane stress assumption and to directly obtain coefficients of the extensional stiffness matrix A and bending stiffness matrix B we apply the following loadings in Voigt notation

• 1. Tension: $\mathbb {P}=e_1\otimes e_1\otimes e_1\otimes e_1 + e_2\otimes e_2\otimes e_2\otimes e_2 + e_1\otimes e_2\otimes e_1\otimes e_2$ and $\mathbb {P}^{\nabla }_1=\mathbb {P}^{\nabla }_2=\mathbb {P}^{\nabla }_3=\mathbb {I}$ with

  $$\begin{aligned} E=\left( \begin{array}{cccccc} E_{11}&0&*&*&*&0 \end{array}\right) ^T, \quad S = \left( \begin{array}{cccccc} *&*&0&0&0&* \end{array}\right) ^T \end{aligned}$$

  (142)

  and

  $$\begin{aligned} E^\nabla =\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right) , \quad S^\nabla =\left( \begin{array}{ccc} * &{} * &{} * \\ * &{} * &{} * \\ * &{} * &{} * \\ * &{} * &{} * \\ * &{} * &{} * \\ * &{} * &{} * \\ \end{array}\right) . \end{aligned}$$

  (143)

• 2. Bending: Using $\mathbb {P}^{\nabla }_i = \mathbb {I}- e_i\otimes e_i\otimes e_i\otimes e_i$ and $\mathbb {P}= \mathbb {P}^{\nabla }_3$ with

  $$\begin{aligned} E=\left( \begin{array}{cccccc} 0&0&*&0&0&0 \end{array}\right) ^T, \quad S = \left( \begin{array}{cccccc} *&*&0&*&*&* \end{array}\right) ^T \end{aligned}$$

  (144)

  and

  $$\begin{aligned} E^\nabla =\left( \begin{array}{ccc} * &{} 0 &{} E^\nabla _{113} \\ 0 &{} * &{} 0 \\ 0 &{} 0 &{} * \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right) ,\quad S^\nabla =\left( \begin{array}{ccc} 0 &{} * &{} * \\ * &{} 0 &{} * \\ * &{} * &{} 0 \\ * &{} * &{} * \\ * &{} * &{} * \\ * &{} * &{} * \\ \end{array}\right) . \end{aligned}$$

  (145)

Then — depending on the applied loading $E_{11}$ resp. $E^\nabla _{113}$ — it is possible to directly compute entries of the extensional resp. bending stiffness matrix from the local stress field

• 1. Tension:

  $$\begin{aligned} A_{11} = \frac{N_{11}}{E_{11}} = h \frac{\langle \sigma _{11} \rangle _Y}{E_{11}} \end{aligned}$$

  (146)

• 2. Bending:

  $$\begin{aligned} D_{11} = \frac{M_{11}}{E^\nabla _{113}} = \frac{h^3}{12} \frac{\langle \sigma _{11} \otimes x_3 \rangle _{Y}^\nabla }{E^\nabla _{113}} \end{aligned}$$

  (147)

If Y is symmetrically extended by pore space in thickness direction, as proposed by Gélébart [7], the same formulas apply when h is replaced by the thickness of the extended plate.

The closed-form solution for the effective stiffnesses of the Kirchhoff plate with n layers are given by the following relations [26]

$$\begin{aligned} A&= \sum _{k=1}^{n} (h_k - h_{k-1}) \mathbb {C}_k \end{aligned}$$

(148)

$$\begin{aligned} B&= \frac{1}{2} \sum _{k=1}^{n} (h_k^2 - h_{k-1}^2) \mathbb {C}_k \end{aligned}$$

(149)

$$\begin{aligned} D&= \frac{1}{3} \sum _{k=1}^{n} (h_k^3 - h_{k-1}^3) \mathbb {C}_k \end{aligned}$$

(150)

where $\mathbb {C}_k$ denotes the two-dimensional stiffness matrix under plane stress assumption for the kth layer of the plate located between the points $x_3=h_{k-1}$ and $x_3=h_k$ in thickness direction. Under the assumption of isotropic material behavior described by Young’s modulus E and Poison’s ratio $\nu$ the stiffness matrix is given by

$$\begin{aligned} \mathbb {C}_k = \frac{E}{1-\nu ^2}\begin{pmatrix} 1 &{} \nu &{} 0 \\ \nu &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1-\nu }{2} &{} \end{pmatrix}, \end{aligned}$$

(151)

and, more generally, for transversely isotropic material behavior with Young’s moduli $E_1$, $E_2$, in-plane shear modulus $G_{12}$ and in-plane Poisson’s ratio $\nu _{12}$ ($\nu _{21}= \nu _{12} E_2/E_1$)

$$\begin{aligned} \begin{aligned} \mathbb {C}_k&= \begin{pmatrix} \frac{1}{E_1} &{} -\frac{\nu _{21}}{E_2} &{} 0 \\ -\frac{\nu _{12}}{E_1} &{} \frac{1}{E_2} &{} 0 \\ 0 &{} 0 &{} \frac{1}{G_{12}} &{} \end{pmatrix}^{-1} \\&= \begin{pmatrix} \frac{E_1}{1-\nu _{12}\nu _{21}} &{} \frac{\nu _{12}E_2}{1-\nu _{12}\nu _{21}} &{} 0 \\ \frac{\nu _{12}E_2}{1-\nu _{12}\nu _{21}} &{} \frac{E_2}{1-\nu _{12}\nu _{21}} &{} 0 \\ 0 &{} 0 &{} G_{12} &{} \end{pmatrix}. \end{aligned} \end{aligned}$$

(152)

The four independent parameters are related to the five independent parameters of a transversely isotropic material in the following way

$$\begin{aligned} E_1&= E_\parallel \end{aligned}$$

(153)

$$\begin{aligned} E_2 = E_3&= E_{\perp ^0} \end{aligned}$$

(154)

$$\begin{aligned} G_{12} = G_{13}&= G_\parallel \end{aligned}$$

(155)

$$\begin{aligned} \nu _{12} = \nu _{13}&= \nu \end{aligned}$$

(156)

$$\begin{aligned} G_{23}&= G_{\perp ^0} \end{aligned}$$

(157)

$$\begin{aligned} \nu _{21} = \nu _{31}&= \frac{E_{\perp ^0}}{E_\parallel } \nu \end{aligned}$$

(158)

$$\begin{aligned} \nu _{23} = \nu _{32}&= \frac{E_{\perp ^0}}{2 G_{\perp ^0}} - 1 \end{aligned}$$

(159)

The plate stiffness matrices A, B and D of a rotated plate can be obtained by rotating the stiffness matrices $\mathbb {C}_k$ for each layer [8].

Fig. 11

Microstructures used by Nguyen et al. [22] and Gélébart [7]. Top: Laminate plate. Bottom: Plate with periodic inclusion. Middle: Central part of the plate with periodic inclusions which is first homogenized in the two-step homogenization approach in Sect. 5.4

Table 2 Material parameters for the laminate plate and the parameter sets for the plate with periodic inclusions

5.3 Grid-aligned loading directions

In the following we compare the results of our approach for grid-aligned loading directions with the benchmark results of Nguyen et al. [22] and Gélébart [7]. The first benchmark example is a laminate plate with moderate phase contrast, see Fig. 11 and Table 2. In this case, the results with and without extension by pore space coincide if the correct thickness is used for the formulas (146) and (147). Therefore, in Tables 3 and 4 we only show the values without extension. Since we do not increase the phase contrast by an extension, our approach converges for the conjugate gradient method shown in Algorithm 2 with fewer iterations and also gives more precise results at the same time.

Table 3 Extensional stiffness obtained for the laminate case (without extension by pore space)

Table 4 Bending stiffness obtained for the laminate case (without extension by pore space)

Fig. 12

Local stress in the plate with periodic inclusion under tensile loading for $E_{\text {inclusion}}=10$ GPa and $E_{\text {matrix}}=1$ GPa. Top: Without extension by pore space. Bottom: With extension by pore space. The wireframe indicates the discretization and deformed position of the inclusion

Fig. 13

Local stress in the plate with periodic inclusion under bending loading for $E_{\text {inclusion}}=10$ GPa and $E_{\text {matrix}}=1$ GPa. Top: Without extension by pore space. Bottom: With extension by pore space. The wireframe indicates the discretization and deformed position of the inclusion

For the second benchmark example of a plate with periodic inclusions and three different sets of material parameters, see Fig. 11 and Table 2, it is not possible to reproduce the FEM reference solution of Nguyen et al. [22] without using an extension by pore space. Mixed boundary conditions [12] only allow to prescribe zero average stress but not zero surface stress as prescribed in Nguyen et al. [22]. The resulting stress fields for the third parameter set are visualized in Fig. 12 for tensile and in Fig. 13 for bending loadings. Consequently, we show in Tables 5, 6, 7, 8, 9 and 10 the results of our approach for the microstrucuture with pore space extension to obtain comparable results under tensile loadings. Following the observation of Gélébart, we used mixed boundary conditions, i.e., $\mathbb {P}=e_1\otimes e_1\otimes e_1\otimes e_1 + e_2\otimes e_2\otimes e_2\otimes e_2 + e_1\otimes e_2\otimes e_1\otimes e_2$, on the extended geometry to reduce the number of iterations. Nevertheless, for this infinite contrast problem only the conjugate gradient method 2 and the Fletcher–Reeves algorithm 3 converge at a moderate number of iterations.

For these results, we did not use the energy based convergence criterion proposed by Nguyen et al. [22] because it leads to inaccurate solutions when combined to our approach. With our strain based convergence criterion[11]

$$\begin{aligned} \frac{\left| \left\Vert \varepsilon ^{\mathrm {new}}\right\Vert ^2 - \left\Vert \varepsilon ^{\mathrm {old}}\right\Vert ^2 \right| }{\left\Vert \varepsilon ^ {\mathrm {initial}}\right\Vert ^2} < \mathrm {tolerance}, \end{aligned}$$

(160)

we obtain in general more accurate solutions than Nguyen et al. [22] and Gélébart [7] especially for the coarsest resolution. On the other hand, we also need significantly more iterations for convergence. Without the extension by pore space, this would not be the case. We will study the convergence behavior and the influence of the extension on the convergence speed in detail for arbitrary loading directions in the next section.

Table 5 Extensional stiffness obtained for the inclusion case (with extension by pore space) for $E_{\text {inclusion}}=0$ GPa and $E_{\text {matrix}}=10$ GPa

Table 6 Bending stiffness obtained for the inclusion case (with extension by pore space) for $E_{\text {inclusion}}=0$ GPa and $E_{\text {matrix}}=10$ GPa

Table 7 Extensional stiffness obtained for the inclusion case (with extension by pore space) for $E_{\text {inclusion}}=1$ GPa and $E_{\text {matrix}}=1000$ GPa

Table 8 Bending stiffness obtained for the inclusion case (with extension by pore space) for $E_{\text {inclusion}}=1$ GPa and $E_{\text {matrix}}=1000$ GPa

Table 9 Extensional stiffness obtained for the inclusion case (with extension by pore space) for $E_{\text {inclusion}}=10$ GPa and $E_{\text {matrix}}=1$ GPa

Table 10 Bending stiffness obtained for the inclusion case (with extension by pore space) for $E_{\text {inclusion}}=10$ GPa and $E_{\text {matrix}}=1$ GPa

Fig. 14

Comparison of the laminate theory with the two-step homogenization approach and the direct simulation results on the resolved geometry of the plate with inclusion shown in Fig. 11. Left: Extensional/Bending stiffness. Right: Corresponding number of iterations needed for convergence

Fig. 15

Relative difference for the numerically calculated stiffness to the laminate theory for homogenized layers. Left: Two-step homogenization. Right: Simulation on the resolved geometry of the plate with inclusion shown in Fig. 11

5.4 Arbitrary loading direction

To validate the derived Lippmann–Schwinger equation for mixed boundary conditions, we compare in the following the results of our approach with the 2-step homogenization approach described in the introduction of this paper. Contrary to the previous section, we now use mixed (strain/stress) boundary conditions only on the geometries without extension.

As test geometry we use the plate with inclusion from the previous section with the third parameter set, i.e., $E_{\text {inclusion}}=10$ GPa and $E_{\text {matrix}}=1$ GPa. Numerically homogenizing the central part of the plate with inclusion shown in the middle of Fig. 11 we obtain the anisotropic stiffness parameters shown in Table 11. In Fig. 14 we compare five different results.

• 1. The results of the laminate theory using the parameters of Table 11.

• 2. Numerical results for the laminate structure without extension by pore space.

• 3. Numerical results for the laminate structure with extension by pore space.

• 4. Direct numerical results on the plate with inclusion without extension by pore space.

• 5. Direct numerical results on the plate with inclusion with extension by pore space.

The left part of Fig. 15 shows that the first three results coincide independently of the loading direction. The last two results on the resolved geometry with and without extension coincide only for the bending stiffness but not for the extensional stiffness due to the boundary effects discussed in the previous section. Then the plane strain and zero surface stress boundary conditions lead to a softer response.

The relative difference of the results on the resolved geometry and the two-step approach is below $4\%$ for the extensional and below $8\%$ for the bending stiffness, see right part of Fig. 15. For tensile and bending loadings in fiber direction (y-direction) the five results are even in perfect agreement.

The number of iterations necessary for convergence, shown on the right side of Fig. 14 is robust with respect to the loading direction and the resolution of the geometry, but extending the geometry by pore space significantly decreases the convergence speed.

5.5 Multilayer laminate

For representative volume elements the boundary effects, enforcing us to use an extension by pore space in Sect. 5.3, are by definition negligible. Therefore, for our representative microstructure of a multilayer laminate, see Fig. 1, we will only discuss the results obtained without extension. The (-45$^\circ$/0$^\circ$/+45$^\circ$/0$^\circ$)$_{\text {s}}$ laminate has a total thickness of 2mm. Each unidirectional layer has a carbon fiber volume content of 40%. The transversely isotropic elastic material parameters of the carbon fibers are shown in Table 12. Since for bending always a combination of tensile and compressive loading occurs, the tension-compression asymmetry of epoxy has to be taken into account by the material model. Therefore, we model the epoxy matrix material by an elasto-plastic material model of Stier et al. [36] that incorporates different yield strengths in tension and compression. The material parameters of Table 13 were calibrated by Ullah et al. [39] according to the measurements of Stier et al. [36] on pure epoxy samples, see Fig. 16.

At first we compare — similar to the previous section — in the first row of Fig. 17 the extensional and bending stiffness predicted by the following three methods.

• 1. Laminate theory for the numerically homogenized unidirectional layers, see Fig. 2.

• 2. Two-step numerical homogenization.

• 3. Direct numerical homogenization on the resolved geometry.

The iteration numbers shown in the second row of Fig. 17 reveal that also for this complicated geometry, the convergence speed is not influenced by the loading direction. As to be expected for the homogenized unidirectional layers the FFT-based homogenization methods needs fewer iterations.

Table 11 Anisotropic stiffness of the central part of the plate with inclusions shown in the middle of Fig. 11 for the third parameter set of Table 2

Table 12 Material parameters for carbon fibers [36]

Table 13 Material parameters for epoxy [39]

The last row of Fig. 17 shows the difference between the predictions of the three approaches. The two-step numerical homogenization approach is closer to the laminate theory, because it uses the same intermediate results. For any loading direction, the relative difference of the extensional and bending stiffness is below 0.15% resp. 0.5%.

Fig. 16

Calibrated material model for epoxy [39]

Fig. 17

Comparison of the laminate theory with the two-step homogenization approach and the direct simulation results on the resolved geometry of the ($-\,45^\circ /0^\circ /+\,45^\circ /0^\circ )_{\text {s}}$ laminate shown in Fig. 1. Left: Tensile loadings. Right: Bending Loadings

Fig. 18

Loading direction dependent force/moment resultant curves and number of iterations for convergence. Top row: Tensile loading. Bottom row: Bending

Fig. 19

Local solution fields in the upper half of the $(-\,45^\circ /0^\circ /+\,45^\circ /0^\circ )_{\text {s}}$ laminate microstructure at the end of the bending simulation in $0^\circ$ direction. Left: Strain component $\varepsilon _{11}$ in the epoxy phase. Middle: Stress component $\sigma _{11}$ in the carbon fibers. Right: Equivalent plastic strain in the epoxy phase

Fig. 20

Orientation dependent Rp02 value of the force resultant [MPa m] (left) and moment resultant [kN] (right)

At this point one could argue, that deriving an extended Lippmann–Schwinger equation is not really helpful, because it only reproduces the results of classical laminate theory and the original version of the Lippmann–Schwinger equation [20, 21] would be sufficient to derive the stiffness of the unidirectional layers. When nonlinear effects enter the stage, this is no longer true. Only the direct simulation approach can be applied to physically nonlinear material behavior without any changes. On the left of Fig. 18 the force and moment resultant under increasing tensile resp. bending loadings for different loading directions are shown. For tensile loadings the stacking order of the unidirectional layer does not influence the force resultant. Therefore, the force resultant for $\alpha ^\circ$ and $180^\circ -\alpha ^\circ$ coincide. For the moment resultant under bending loadings this is not true because the outer layers of the (-45$^\circ$/0$^\circ$/+45$^\circ$/0$^\circ$)$_{\text {s}}$ laminate, e.g., the $-45^\circ$ layers, are submitted to higher loadings.

By post-processing of these force and moment resultants and the corresponding evolution of the average plastification, the yield surfaces under tensile and bending loadings shown in Fig. 20 were derived. For tensile loadings the yield stress is the highest in the main fiber direction of $0^\circ$. Under bending loadings the yield surface is reoriented into the direction of the outermost fiber orientation.

The computational effort for tensile and bending simulations could be kept limited thanks to the application of the Fletcher–Reeves algorithm 3. The iteration numbers for convergence of each loading step on the right of Fig. 18 were obtained with affine linear extrapolation (136) between the loading steps. Only for the first iterate, these numbers are independent of the loading direction. Then the plastic evolution changes the convergence behavior significantly. Since bending loadings lead to higher local plastifications than comparable tensile loadings, the iteration numbers are approximately 50% higher for this type of loading.

6 Conclusion

In this work, we first extended the Lippmann–Schwinger equation to strain gradient boundary conditions. To be able to prescribe the full strain gradient of the solution, it was necessary to introduce additional kinematic constraints. This allowed us to also integrate stress gradient boundary conditions and to enforce mixed first order boundary conditions with respect to an arbitrary coordinate system. Thanks to the use of a projected gradient descent method, the kinematic constraints can be easily implemented in existing FFT-based algorithms. This extension makes it possible, for example, to simulate plate bending. In contrast to the simulation of tensile experiments, a volume element can only be representative for bending simulations if it contains the entire thickness of the plate.

When applied to the test cases with grid-aligned loadings of Nguyen et al. [22], our method gave more accurate predictions at coarse resolutions. By extending the example to anisotropic material behavior, we could validate our approach for arbitrary loading directions with the classical laminate theory. It turned out that the approach of Gélébart [7] to extend the domain by pore space significantly decreases the convergence speed. The difference in the boundary conditions due to the pore space extension, e.g., zero surface stress instead of periodic stress, did not influence the predicted effective response.

Regarding the multilayer laminate example, in the linear elastic regime the predictions of our approach coincide with the classical laminate theory, if the boundary conditions are set properly. By applying the Fletcher–Reeves method [30] we were able to predict the force and moment resultant under arbitrary loading directions at moderate computational effort. Thereby, we could also determine the yield surface of the laminate under tensile and bending loadings.

It should be remarked, that our derivation directly carries over to problems of finite strains. Therefore, our FFT-based solver for the kinematically constrained extended Lippmann–Schwinger equation could replace—similar to previously developed FE-FFT methods [14, 35]—the micro-scale solver in higher order FE$^2$ methods [15, 29, 40] at small and finite strains.

Appendix

1.1 Alternative derivation of the extension to mixed strain/stress gradient boundary conditions

Given projectors $\mathbb {P},\mathbb {P}^{\nabla }$ and prescribed loads $E,S\in {\text {Sym}}_3$ as well as $E^\nabla ,S^\nabla \in {\text {Sym}}_3^{3}$ satisfying the constraints (80) and (81) we want to incorporate the boundary condition (79) into the Lippmann–Schwinger equation (48)

Adding a zero the boundary condition (79) for the stress gradient is equivalent to

(161)

Invoking the splitting

(162)

the last equation can be rewritten as

(163)

As $\mathbb {C}^0$ is positive definite, the last equation can be solved for . More precisely, using the Moore–Penrose pseudoinverse [19, 25] $\mathbb {M}^{\nabla }$ whose components are given by

$$\begin{aligned} \mathbb {M}^{\nabla }_{ijklmn} = \delta _{kn}\left( \mathbb {Q}^k:\mathbb {C}^0:\mathbb {Q}^k\right) ^\dagger _{ijlm}, \end{aligned}$$

(164)

we arrive at the equation

(165)

By using again the splitting (162) we obtain

(166)

Inserting the last identity (166) into the extended Lippmann–Schwinger equation (48) yields

(167)

or expressed more compactly

(168)

where $\langle \varGamma ^0 : \cdot \otimes x \rangle _{Y,\perp ^0}^\nabla$ and are shorthand notations for the operators

$$\begin{aligned} T\mapsto \langle \varGamma ^0 : T \otimes x \rangle _{Y,\perp ^0}^\nabla , \quad T:Y\rightarrow {\text {Sym}}_3 \end{aligned}$$

(169)

and

(170)

This extended Lippmann–Schwinger equation with mixed first order boundary conditions can be combined with zero order mixed boundary conditions [12, 17, 32]

(171)

where $\mathbb {M}=\left( \mathbb {Q}:\mathbb {C}^0:\mathbb {Q}\right) ^\dagger$.