A computational phase transformation model for selective laser melting processes

Abstract

Selective laser melting (SLM) has gained large interest due to advanced manufacturing possibilities. However, the growing potential also necessitates reliable predictions of structures in particular regarding their long-term behaviour. The constitutive and structural response is thereby challenging to reproduce, due to the complex material behaviour. This motivates the aims of this contribution: To establish a material model that accounts for the behaviour of the different phases occurring during SLM but that still allows the use of (basic) process simulations. In particular, the present modelling framework explicitly takes into account the mass fractions of the different phases, their mass densities, and specific inelastic strain contributions. The thermomechanically fully coupled framework is implemented into the software Abaqus. The numerical examples emphasise the capabilities of the framework to predict, e.g., the residual stresses occurring in the final part. Furthermore, a postprocessing of averaged inelastic strains is presented yielding a micromechanics-based motivation for inherent strains.

1 Introduction

Additive manufacturing (AM) refers to processes where a part is fabricated by sequential addition of material rather than by subtractive manufacturing or moulding. Thus, the final part has little geometrical and material restrictions. Customised parts can be produced within a reasonably low cost range and comparative short amount of time. AM is often called a near-net-shaping technique, as the part is directly built based on a computer aided design (CAD) model. The CAD model is then converted into a standard triangulation language (STL) format which is widely used for all AM machines. It represents the geometry of the CAD model by a simple mesh. This file is digitally sliced into thin cross-sectional layers and can then be constructed by the chosen AM process. The layering is carried out through deposition and bonding of these layers. Thus, no tools are required to initiate the AM process (except for necessary post-processing). Nowadays, there are various technologies, differing in the used material (mostly powder or wire), in the heat source and in the procedure in general.

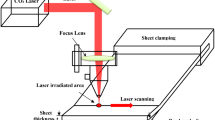
In this contribution, the focus lies on the selective laser melting (SLM) process, also referred to as laser powder-bed fusion as summarised in, e.g. [14], where a work piece is manufactured in a—in this case—metal powder bed. The process uses a laser beam as the heat source to selectively melt the metallic powder particles of the layer according to the CAD model. The material then re-solidifies after a cooling period. Afterwards, the building platform is lowered and a new layer of powder is applied. This process is repeated until the final geometry of the work piece is achieved. A detailed view of the three specific material states—powder, melting pool, and re-solidified material—is shown in Fig. 1 for the SLM process. Hence, it is possible to manufacture parts by melting metallic powder in a layer-upon-layer technique. It also improves lightweight construction due to the possibility of arbitrarily shaped parts. Especially the aerospace and automotive sector, as well as the biomedical sector investigate the SLM process.

Fig. 1

Detailed view of the SLM process, referring to the three different material states, namely powder, molten pool and re-solidified material. (Color figure online)

So far, the prediction of the influence of the additive manufacturing process on the properties of the final workpiece is still challenging. The temperature gradients and cooling rates present will vary significantly depending on the position of the laser beam and the considered particle. In addition, the three different states of the material exhibit significantly different mass densities so that the phase changes evoke relevant process-induced eigenstrains. Furthermore, inhomogeneously distributed thermal strains are present. Overall, these inelastic strains cause eigenstresses which may have a major impact on the properties of the final workpiece, in particular with respect to the long-term behaviour and its lifetime. In addition, these eigenstresses of the part are directly affected by the various process parameters. So far, experiments have mostly been used to identify the optimal parameter configuration on a purely empirical level. Therefore, simulations with physically well-motivated models are necessary in order to gain a deeper understanding of the relation between process parameters and the quality of the SLM part.

Over the last twenty years, starting with [44], different approaches for simulations using the Finite Element (FE) method have been available in literature regarding the modelling of the SLM process on a small scale: purely thermal models, see for example [12, 15, 26, 29, 30, 38, 42, 45] and more sophisticated thermomechanical small strain models, i.e. [11, 16, 22, 36, 37, 43, 49, 51]. Thermomechanical models enable the prediction of residual stresses and the geometry, as well as the influence on scanning strategies. Within these contributions, there are different approaches to model the phase changes, i.e. [22] enhances the Stefan-Neumann equation and [26] uses a mathematical phase change function calibrated by experiments. In [39], a purely thermal model is used which explicitly incorporates two state variables for both the phase and the porosity. This enables the capturing of the consolidation of the material. However, most researchers use the melting point temperature to indicate the phase changes, so that these are purely temperature driven.

The effect of volume shrinkage of the powder bed due to porosity has been investigated in [12] by using a purely thermal model. In [16, 37] a thermomechanical model is used, where a pseudo-thermal expansion is implemented to take into account not only the thermal expansion of the material, but also the shrinkage of the powder bed. The advantage of a thermomechanical model and the difference in the temperature evolution is also stated in [16]. In [48], a thermomechanical finite deformation framework is developed to predict the melting and solidification process on the powder scale.

For industrial usage, the influence of process parameters, product quality and the prediction of deformation and residual stresses still remains challenging for a physically real component. Researchers are presently focusing on advanced models for the numerical investigation of rather large parts in contrary to a single-line melt tracks. On the one hand, high performing FE-algorithms are developed to speed up computation time, for example in [27, 33, 34]. On the other hand, the models are simplified at the macro scale: Multiscale approaches where the micro, meso, and macro scale are taken into account, as for example described in [9, 24, 28]. In particular, simulating each layer at the same time is used to speed up the process, see for example [17]. A similar approach is the inherent strain method which was first introduced for metal welding applications in [21, 50]. This method is now applied to additive manufacturing processes, see for instance [24, 31, 40, 41]. The challenge in using this method lies in the determination of the inherent strains, either through simulation or experiments. Altogether, there are different formulations available for the simulation of the micro and macro scale with help of the FE method. However, from our point of view, no frameworks exist which take into account the mechanical material model and phase change in a physically well-motivated approach.

Based on the framework for solid-solid phase transformations in shape memory alloys, see e.g. [3], this contribution focuses on the advancement of the model presented in [2]. The model is based on the explicit consideration of phase energy densities, where each state of the material—powder, molten and re-solidified—is a single phase (see Fig. 1). During the transformation process, the material first melts and then solidifies. These phase energy densities are combined by using a specific homogenisation assumption which yields the averaged energy density—and with this the constitutive model—for the possible phase mixture. Several inelastic strain contributions are taken into account within the material models of the single phases. More precisely speaking, viscous strains and transformation strains are considered in the molten phase as well as thermal strains, plastic strains, and transformation strains in the solid phase. The transformation strains are introduced as material constants and capture the significant change of the mass densities during the phase changes. The internal state variables including the mass fractions of the different phases are calculated by using thermomechanically consistent evolution equations solved at the material point level. The formulation of the material model as well as the FE model consider full thermomechanical coupling. The present investigations aim at the accurate prediction of essential process-induced quantities such as eigenstresses. Furthermore, the present modelling framework could be used to calculate effective inherent strains which could then be used in simpler yet faster process simulations.

This article is set up as follows: A brief summary of the thermomechanical field equations is given Sect. 2, where a focus is set on the thermomechanical coupling and mechanical dissipation contributions. In Sect. 3, the phase energy densities and the irreversible strains are specified to introduce the constitutive material model which is based on mass fractions. We provide deeper insight into the local algorithm and Abaqus implementation of the framework at hand in Sect. 4. Calculations at the material point level designed to yield a proof of concept as well as representative three-dimensional boundary value problems are studied in Sect. 5, before we finally conclude our findings in Sect. 6.

2 Thermomechanical framework

This section provides general information on the kinematics and the thermodynamically fully coupled balance equations. At this stage, the small strain theory is considered to be appropriate. Thus, the linearised strain measure

$$\begin{aligned} \varvec{\varepsilon }:= \frac{1}{2}\,\left[ \nabla {\varvec{u}} + [\nabla {\varvec{u}}]^{\mathrm {t}} \right] \end{aligned}$$

(1)

with the displacement field denoted as ${\varvec{u}}$ is applied. In general, the total strains can be decomposed additively as follows

$$\begin{aligned} \varvec{\varepsilon }=\varvec{\varepsilon }^{\mathrm {el}}+\varvec{\varepsilon }^{\mathrm {irr}} \end{aligned}$$

(2)

into an elastic part $\varvec{\varepsilon }^{\mathrm {el}}$ and an irreversible part $\varvec{\varepsilon }^{\mathrm {irr}}$. The irreversible strains describe inelastic effects e.g. viscous, thermal or plastic strains and the combination thereof, and transformation strains, i.e. eigenstrains, capturing the phase transformation of the material, as explained in subsequent sections.

To simulate the underlying SLM-process, a fully coupled thermomechanical model is proposed. The problem at hand is based on the balance of linear momentum and on the energy equation which follows from the first law of thermodynamics, i.e.

$$\begin{aligned} {\varvec{0}}&= \nabla \cdot \varvec{\sigma } + {\varvec{b}}, \end{aligned}$$

(3)

$$\begin{aligned} 0&= - \nabla \cdot {\varvec{q}} + r^\mathrm {ext} + \varvec{\sigma } : \dot{\varvec{\varepsilon }} - \rho \, {\dot{e}} , \end{aligned}$$

(4)

respectively. In these equations, $\varvec{\sigma }$ denotes the stress tensor, ${\varvec{b}}$ describes the body forces, ${\varvec{q}}$ represents the heat flux vector, $r^\mathrm {ext}$ denotes the external heat supply, $\rho$ is the mass density and e symbolises the specific internal energy. The absolute temperature is denoted by $\theta$. In general, notation ${\dot{\bullet }}$ is used to describe the time derivative of the respective quantity $\bullet$. As this work proceeds, all body forces shall be neglected, i.e. ${\varvec{b}} \equiv {\varvec{0}}$.

In the following, the second law of thermodynamics, respectively the entropy inequality, is used to introduce the internal dissipation. As proposed by [10], the specific Helmholtz free energy $\varPsi$ shall be used for a thermodynamic consistent derivation. In order to reformulate the problem depending on the temperature $\theta$ as state variable rather than the entropy s, the specific Helmholtz free energy $\varPsi$ is obtained via the Legendre transformation

$$\begin{aligned} e&=\, \varPsi + s \, \theta , \end{aligned}$$

(5)

$$\begin{aligned} \Rightarrow {\dot{e}}&=\, {\dot{\varPsi }} + s\,{\dot{\theta }} + {\dot{s}}\, \theta . \end{aligned}$$

(6)

In general, the Helmholtz free energy $\varPsi (\varvec{\varepsilon }, \theta , {\mathcal {V}})$ depends on the total strains $\varvec{\varepsilon }$, the temperature $\theta$ and—at this point not further specified—on internal variables ${\mathcal {V}}$. With this at hand, the time derivative of the Helmholtz free energy results in

$$\begin{aligned} {\dot{\varPsi }} = \frac{\partial \varPsi }{\partial {\varvec{\varepsilon }} } :\dot{{\varvec{\varepsilon }}}+ \frac{\partial \varPsi }{\partial \theta }\, {{\dot{\theta }}} + \frac{\partial \varPsi }{\partial {\mathcal {V}} } \bullet \dot{{\mathcal {V}}} . \end{aligned}$$

(7)

Following the Colemann-Noll procedure, cf. [10], the entropy inequality

$$\begin{aligned} s \ge 0 \end{aligned}$$

(8)

is used and, combining (8) with the energy equation (4), the second law of thermodynamics reads

$$\begin{aligned} \rho \,\theta \,{\dot{s}} - r^\mathrm {ext} + \nabla \cdot {\varvec{q}} - \frac{1}{\theta } \,{\varvec{q}} \cdot \nabla \theta \ge 0 . \end{aligned}$$

(9)

This can be reformulated in terms of the dissipation symbolised with ${\mathcal {D}}$ and split into a mechanical and thermal part, i.e.

$$\begin{aligned} {\mathcal {D}}&= {\mathcal {D}}_\mathrm {mech} + {\mathcal {D}}_\mathrm {therm} \ge 0. \end{aligned}$$

(10)

Moreover, each contribution is assumed to be non negative. This results in the Fourier inequality for the thermal contribution on the one hand,

$$\begin{aligned} {\mathcal {D}}_\mathrm {therm}&= - \frac{1}{\theta } \,{\varvec{q}} \cdot \nabla \theta \ge 0 , \end{aligned}$$

(11)

and in the Clausius-Planck inequality on the other,

$$\begin{aligned} {\mathcal {D}}_\mathrm {mech}&=\theta \, \rho \,{\dot{s}} - r^\mathrm {ext} + \nabla \cdot {\varvec{q}} \ge 0 . \end{aligned}$$

(12)

By recalling (4) and using (6), it is possible to reformulate (12) such that

$$\begin{aligned} {\mathcal {D}}_\mathrm {mech} = \varvec{\sigma }:\dot{\varvec{\varepsilon }} - \rho \, s\,{\dot{\theta }} -\rho \,{\dot{\varPsi }} . \end{aligned}$$

(13)

Inserting (7) into (13) and rearranging terms for the purpose of simplification results in

$$\begin{aligned} \left[ \varvec{\sigma }- \rho \,\frac{\partial \varPsi }{\partial \varvec{\varepsilon }} \right] :\dot{\varvec{\varepsilon }} - \rho \left[ s + \frac{\partial \varPsi }{\partial \theta } \right] {\dot{\theta }} - \rho \, \frac{\partial \varPsi }{\partial {\mathcal {V}}} \bullet \dot{{\mathcal {V}}} \ge 0 , \end{aligned}$$

(14)

where $\bullet$ represents a generalised scalar product. Following the lines of the Coleman-Noll procedure, the constitutive equations based on the Helmholtz free energy density can be directly extracted, i.e.

$$\begin{aligned} \varvec{\sigma }&= \rho \, \frac{\partial \varPsi }{\partial {\varvec{\varepsilon }}} , \end{aligned}$$

(15)

$$\begin{aligned} s&= - \frac{\partial \varPsi }{\partial \theta } \, . \end{aligned}$$

(16)

From this, the definition of entropy and stresses can be determined in a straightforward manner. As a further abbreviation, the driving forces

$$\begin{aligned} {\mathcal {F}} = - \rho \,\frac{\partial \varPsi }{\partial {\mathcal {V}}} \end{aligned}$$

(17)

of the internal variables are introduced. Substituting these results into (14) finally leads to the reduced form of the mechanical dissipation as

$$\begin{aligned} {\mathcal {D}}_\mathrm {mech} = {\mathcal {F}} \bullet \dot{{\mathcal {V}}} \ge 0 . \end{aligned}$$

(18)

With these derivations at hand, (4) can be rewritten in the more convenient form

$$\begin{aligned} 0&= -\,\nabla \cdot {\varvec{q}} + r^\mathrm {ext} - \rho \,{c}\,{\dot{\theta }} \nonumber \\&\quad + {\mathcal {D}}_\mathrm {mech} + \theta \,\partial _\theta \left[ \,\varvec{\sigma } : \dot{\varvec{\varepsilon }} - {\mathcal {D}}_\mathrm {mech} \,\right] , \end{aligned}$$

(19)

where the specific heat capacity is defined by

$$\begin{aligned} c = - \theta \,\frac{\partial ^2 \varPsi }{\partial \theta \, \partial \theta }. \end{aligned}$$

(20)

In the following sections, it is assumed that the (unspecific) Helmholtz free energy density is defined as $\psi = \rho \, \varPsi$.

3 Constitutive framework

The thermomechanical material model based on phase energy densities is introduced in this section. The overall material behaviour is determined according to a phase transformation model. Furthermore, the specifications of the thermal problem are introduced. Altogether, both models are thermomechanically fully coupled.

3.1 Phase energy densities

As already indicated in Sect. 1, each state of the material is represented by an energy density. Altogether, the material response of the complete model is determined with the help of a homogenisation approach, rather than by relying on solely temperature-dependent material parameters. At this point, three distinct phases representing the different states of the material, namely powder, molten, and re-solidified, are explicitly taken into account. All of these phases are modelled as a solid continuum, which may be arguable in particular for the molten phase with respect to the (viscous) solid approach and for the powder phase regarding the continuum ansatz. Motivations for these simplifications are, however, provided in the subsequent sections.

The material model is based on the averaged Helmholtz free energy density ${\overline{\psi }}$, where additively decomposed energy densities $\psi _i$ each of which consists of two parts, are chosen for each phase denoted by the index i. The first part describes the mechanical energy density $\psi _i^\mathrm {mech}$, while the second part $\psi _i^\mathrm {cal}$ is a purely caloric contribution due to the temperature dependence of the material model. This results in an energy density

$$\begin{aligned} \psi _i := \psi ^\mathrm {mech}_i + \psi ^\mathrm {cal}_i , \end{aligned}$$

(21)

where the index i refers to all possible phases. The mechanical part of the energy density is defined as

$$\begin{aligned} \psi ^\mathrm {mech}_i := \dfrac{1}{2}\,\left[ \varvec{\varepsilon }_i - \varvec{\varepsilon }_i^\mathrm {irr}\right] :{{{\mathbf {\mathsf{{E}}}}}}_i\, :\left[ \varvec{\varepsilon }_i - \varvec{\varepsilon }_i^\mathrm {irr}\right] , \end{aligned}$$

(22)

whereas the caloric part is a function of temperature and specific material parameters and which is to be defined later. While $\varvec{\varepsilon }_i$ denote the total strains of each phase, $\varvec{\varepsilon }_i^\mathrm {irr}$ describe the irreversible strains and ${{{\mathbf {\mathsf{{E}}}}}}_i$ represents an fourth-order elasticity tensor of the respective phase. The influence of the caloric part and the irreversible strains are visualised in Fig. 2. Each energy density represents a potential well which is shifted due to $\psi _i^\mathrm {cal}$ and $\varvec{\varepsilon }^\mathrm {irr}_i$. In the following paragraphs, the corresponding phase energy densities $\psi _i$ will be discussed in detail.

Fig. 2

Influence of the different contributions on the phase energy densities

3.1.1 Powder phase

Powder particles are assumed to move freely due to the high degree of porosity between the powder grains. Therefore, the material behaves solely elastic. It has to be kept in mind that only compression strains are admissible within the powder particles. In the framework at hand, the powder is modelled as a continuum with a significantly higher compliance than the solid material. Overall, the powder shall not undergo states of high stress or strain level. In the initial state, only the powder phase is present. In addition, due to the high porosity of the powder phase, any thermal strains are neglected for this state of the material. Thus, the powder is considered as the parent phase so that no irreversible strains are incorporated for this phase, i.e. $\varvec{\varepsilon }_\mathrm {pow}^\mathrm {irr} = {\varvec{0}}$. The energy density of the powder is approximated by

$$\begin{aligned} \psi _\mathrm {pow}&:= \frac{1}{2}\,\varvec{\varepsilon }_\mathrm {pow}: {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {pow} : \varvec{\varepsilon }_\mathrm {pow} \nonumber \\&\quad -c_\mathrm {pow} \,\theta \ln (\theta ) + L_\mathrm {pow}\, \frac{\theta -\theta ^\mathrm {ref}_\mathrm {pow}}{\theta ^\mathrm {ref}_\mathrm {pow}}, \end{aligned}$$

(23)

where ${c_\mathrm {pow}= \rho _\mathrm {pow}\,c}$ is the weighted heat capacity of the powder, and where ${L_\mathrm {pow}=\rho _\mathrm {pow}\, L}$ describes the weighted latent heat of the powder at a constant reference temperature $\theta _\mathrm {pow}^\mathrm {ref}$. The weighted values are calculated by the mass density of the powder $\rho _\mathrm {pow}$ and the specific value of the heat capacity c and latent heat L, respectively.

3.1.2 Molten phase

The molten phase shall also be approximated as a solid type phase. This behaviour is assumed to be appropriate, as the molten pool is only present for a brief time span. Fluid effects like the Marangoni flow are therefore neglected. However, to include a fluid-like behaviour of the molten pool in the material model, a viscous strain contribution $\varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}$ is included, which shall be used to enable full stress relaxation within the molten phase. Furthermore, the mass density of the three phases varies considerably. To take into account the shrinkage from the powder material to the molten phase, a transformation strain $\varvec{\varepsilon }^\mathrm {trans}_\mathrm {mel}$ is incorporated. Both irreversible strains will be further defined in what follows. Overall, an additive split of the irreversible strains is used for the molten phase, i.e.

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {irr}_\mathrm {mel} = \varvec{\varepsilon }^\mathrm {trans}_\mathrm {mel} + \varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}. \end{aligned}$$

(24)

As the molten phase is the high temperature phase, the influence of the latent heat is only integrated into the powder and re-solidified phase. With this at hand, the specific energy density of the molten phase is defined as

$$\begin{aligned} \psi _\mathrm {mel}&:= \frac{1}{2}\,\left[ \varvec{\varepsilon }_\mathrm {mel}- \varvec{\varepsilon }^\mathrm {irr}_\mathrm {mel}\right] : {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {mel} : \left[ \varvec{\varepsilon }_\mathrm {mel}- \varvec{\varepsilon }^\mathrm {irr}_\mathrm {mel}\right] \nonumber \\&\quad -c_\mathrm {mel}\, \theta \ln (\theta ) , \end{aligned}$$

(25)

with the heat capacity defined as ${c_\mathrm {mel} =\rho _\mathrm {mel} \, c}$ and the mass density of the molten phase denoted as $\rho _\mathrm {mel}$.

3.1.3 Re-solidified phase

An additive decomposition of the irreversible strains into three parts is chosen according to

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {irr}_\mathrm {sol}= \varvec{\varepsilon }^\mathrm {th}_\mathrm {sol} +\varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol} +\varvec{\varepsilon }^\mathrm {trans}_\mathrm {sol}\, \end{aligned}$$

(26)

for the re-solidified phase. The transformation strains $\varvec{\varepsilon }^\mathrm {trans}_\mathrm {sol}$ take into account the volume changes of the material during the phase transition from the molten phase to the re-solidified phase due to the changing mass densities. In contrast to the previously introduced phases, two further inelastic strain contributions are considered. Plastic deformation can arise due to high eigenstrains after the phase transformation and due to high temperature gradients present. A plastic strain tensor $\varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol}$ is used to capture this behaviour whose evolution will be further defined in Sect. 3.4. Furthermore, thermal strains $\varvec{\varepsilon }^\mathrm {th}_\mathrm {sol}$ are considered in the re-solidified phase to take into account inelastic strains stemming from the high temperature changes during the process. These strains will be further defined in Sect. 3.5. Finally, the energy density of the re-solidified phase is defined by analogy with the previously introduced energies as

$$\begin{aligned} \psi _\mathrm {sol}&:= \dfrac{1}{2}\left[ \varvec{\varepsilon }_\mathrm {sol}-\varvec{\varepsilon }_{\mathrm {sol}}^\mathrm {irr}\right] : {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol} : \left[ \varvec{\varepsilon }_\mathrm {sol}-\varvec{\varepsilon }_\mathrm {sol}^\mathrm {irr}\right] + \dfrac{H_\mathrm {sol}}{2}\,[k^\mathrm {hard}_\mathrm {sol}]^2 \nonumber \\&\quad -c_\mathrm {sol} \,\theta \ln (\theta ) + L_\mathrm {sol}\, \dfrac{\theta -\theta ^\mathrm {ref}_\mathrm {sol}}{\theta ^\mathrm {ref}_\mathrm {sol}} . \end{aligned}$$

(27)

The heat capacity and the latent heat are defined in an analogous manner as ${c_\mathrm {sol}=\rho _\mathrm {sol} \,c}$ and ${L_\mathrm {sol}=\rho _\mathrm {sol}\, L}$. The mass density of the solid phase is denoted by $\rho _\mathrm {sol}$. In addition, $H_\mathrm {sol}$ defines the hardening modulus of the solid phase, whereas $k^\mathrm {hard}_\mathrm {sol}$ indicates the accumulated equivalent plastic strain related to isotropic hardening.

3.2 Specification of transformation strains

The transformation strains $\varvec{\varepsilon }^\mathrm {trans}_i$ of the molten and re-solidified phases shall be introduced next, as they are solely dependent on the transformation process and on material parameters previously introduced. These strains shall capture the volume changes of the material during phase transitions due to the different mass densities. In fact, the validity of the small strain theory needs to be carefully scrutinised in view of physically plausible transformation strains. Initially, the material solely consists of powder with the mass contribution $\mathrm {d}m_0$, thus

$$\begin{aligned} \mathrm {d}V_0 = \frac{\mathrm {d}m_0}{\rho _\mathrm {pow}}\, , \end{aligned}$$

(28)

Hypothetically assuming that this infinitesimal volume element of the parent powder phase fully transforms into one of the other phases, i.e. molten and re-solidified material, the volume of the new phase is given by

$$\begin{aligned} \mathrm {d}V_\bullet = \frac{\mathrm {d}m_0}{\rho _{\bullet }} = [1 + \mathrm {tr}(\varvec{\varepsilon }^\mathrm {trans}_\bullet )]\,\mathrm {d}V_0. \end{aligned}$$

(29)

Here it is assumed that the mass contribution $\mathrm {d}m_0$ is constant (conservation of mass). Using (28) and (29) together with the physically sound assumption of $\varvec{\varepsilon }^\mathrm {trans}_\bullet$ being purely volumetric, these transformation strains are specifically given by

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {trans}_\bullet&= \frac{1}{3}\left[ \frac{\rho _\mathrm {pow}}{\rho _\bullet } - 1\right] {\varvec{I}}, \end{aligned}$$

(30)

where ${\varvec{I}}$ corresponds to the second order identity tensor. This results in the transformation strains

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {trans}_\mathrm {mel}&= \frac{1}{3}\left[ \frac{\rho _\mathrm {pow}}{\rho _\mathrm {mel}} - 1\right] {\varvec{I}} \end{aligned}$$

(31)

for the molten phase and

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {trans}_\mathrm {sol}&= \frac{1}{3}\left[ \frac{\rho _\mathrm {pow}}{\rho _\mathrm {sol}} - 1\right] {\varvec{I}} \end{aligned}$$

(32)

for the re-solidified phase.

3.3 Homogenisation via convexification

In the context of additive manufacturing and the related phase changes of the underlying material, the mass densities of the powder, molten phase and re-solidified material differ significantly. Thus, conservation of mass does not coincide with conservation of volume. The volume consequently cannot be used as a conserved quantity and the homogenisation algorithm needs to be reformulated accordingly.

Material models for solid-solid phase transformation, see, e.g. [3, 4, 23, 25], mainly use the respective volume fractions as state variables and as conserved quantity. This is motivated by the fact that the mass densities of, e.g., austenite and martensite can be considered identical. Therefore, the algorithm has in general been introduced with respect to volume fractions

$$\begin{aligned} \xi _i = \frac{\mathrm {d}V_i}{\mathrm {d}V_0} , \end{aligned}$$

(33)

where $\mathrm {d}V_0$ denotes the (infinitesimal) initial volume and where $\mathrm {d}V_i$ is the corresponding volume of the respective phase.

First of all, the averaged energy density ${\overline{\psi }}$ is introduced via a volume averaging as

$$\begin{aligned} {{\overline{\psi }}} = \sum _{i=1}^{n_\mathrm {ph}}\xi _i \,{{\psi }_i} \end{aligned}$$

(34)

subject to $0 \le \xi _i \le 1$ and $\sum _i \xi _i = 1$ as constraints for the volume fraction. The number of phases is given by $n_\mathrm {ph}$. The volume—also the mass for equal mass densities—is hereby used as conserved quantity. Furthermore, an additional constraint in terms of the compatibility condition

$$\begin{aligned} {\varvec{r}}^{\varvec{\varepsilon }} = \varvec{\varepsilon } - \sum _{i=0}^{n_\mathrm {ph}} \xi _i \, {\varvec{\varepsilon }}_i = {\varvec{0}} \, \end{aligned}$$

(35)

has to be considered.

For the application at hand, the algorithm needs to be enhanced and re-formulated with respect to the mass fractions

$$\begin{aligned} \zeta _i = \dfrac{\mathrm {d} m_i}{\mathrm {d}m_0}. \end{aligned}$$

(36)

These mass fractions can be related to the volume fractions via

$$\begin{aligned} \zeta _i = \dfrac{\rho _i \,\mathrm {d} V_i}{\mathrm {d}m_0} = \dfrac{\rho _i \, \xi _i \, \mathrm {d} V_0}{\mathrm {d} m_0} \quad \Leftrightarrow \quad \xi _i = \dfrac{\zeta _i \, \mathrm {d}m_0}{\rho _i \,\mathrm {d} V_0} . \end{aligned}$$

(37)

For the sake of consistency, the algorithm shall now be developed based on mass fractions and on the averaged mass specific energy ${{\overline{\varPsi }}}$. While working with mass fractions $\zeta _i$, some adaptions to the aforementioned approach have to be made. The overall energy ${{\overline{\varPsi }}}$ is analogously calculated via a linear mixture rule of the mass specific phases $\varPsi$, thus

$$\begin{aligned} {{\overline{\varPsi }}} = \sum _{i=1}^{n_\mathrm {ph}} \zeta _i\,\varPsi _i = \frac{\mathrm {d}V_0}{\mathrm {d}m_0}\, \sum _{i=1}^{n_\mathrm {ph}} \xi _i\,{\psi }_i , \end{aligned}$$

(38)

where the relation between the volume and mass specific energy density ${\psi _i = \rho _i \, \varPsi _i}$ still holds. The use of mass fractions in particular affects the compatibility condition

$$\begin{aligned} {\varvec{r}}^{\varvec{\varepsilon }} = \varvec{\varepsilon } - \sum _{i=1}^{n_\mathrm {ph}}\zeta _i\, {\varvec{\varepsilon }}_i= {\varvec{0}}, \end{aligned}$$

(39)

as well as

$$\begin{aligned} 0 \le \zeta _i \le 1 \quad \text {and} \quad \sum _{i=1}^{n_\mathrm {ph}} \zeta _i = 1 \end{aligned}$$

(40)

as constraints for the mass fractions. One can see the similarities between (38) and (34). This is advantageous for the implementation, as will be explained in Sect. 4.2.

For the specific material model at hand, three phases are present so that $n_\mathrm {ph} = 3$, namely powder, molten pool and solid. The averaged or, in other words, effective energy density explicitly used in the present modelling framework is given by

$$\begin{aligned} {{\overline{\varPsi }}} = \frac{\mathrm {d}V_0}{\mathrm {d}m_0}&\left[ \,\xi _\mathrm {pow}\,{\psi }_{\mathrm {pow}}\left( {\varvec{\varepsilon }}_{\mathrm {pow}},\ldots \right) + \xi _{\mathrm {mel}}\,{\psi }_{\mathrm {mel}}\left( {\varvec{\varepsilon }}_{\mathrm {mel}},\ldots \right) \right. \nonumber \\&\, \left. + \, \xi _{\mathrm {sol}}\,{\psi }_{\mathrm {sol}}\left( {\varvec{\varepsilon }}_{\mathrm {sol}},\ldots \right) \right] . \end{aligned}$$

(41)

This averaged energy density has to be minimised subject to the constraints regarding the domain of feasible mass fractions $\zeta _\bullet \in {\mathcal {A}}$ with

$$\begin{aligned} {{\mathcal {A}} = \left\{ 0\le \zeta _\bullet \le 1 ,\quad \zeta _\mathrm {pow} + \zeta _{\mathrm {mel}} + \zeta _{\mathrm {sol}} = 1 \right\} } \end{aligned}$$

(42)

and the domain of the admissible strain distributions $\varvec{\varepsilon }_\bullet \in {\mathcal {E}}$ with

$$\begin{aligned} {\mathcal {E}} = \left\{ \zeta _\mathrm {pow}\, {\varvec{\varepsilon }}_{\mathrm {pow}} + \zeta _\mathrm {mel}\,{\varvec{\varepsilon }}_{\mathrm {mel}} + \zeta _\mathrm {sol} \, {\varvec{\varepsilon }}_{\mathrm {sol}} = \varvec{\varepsilon } \right\} . \end{aligned}$$

(43)

This constrained minimisation problem results in the so called convexification of ${{\overline{\varPsi }}}$, i.e.

$$\begin{aligned} \mathrm {C}{{\overline{\varPsi }}} = \inf _{\zeta _\bullet \in {\mathcal {A}}} \, \inf _{\varvec{\varepsilon }_\bullet \in {\mathcal {E}}} \, {\overline{\varPsi }}, \end{aligned}$$

(44)

Thus, $\mathrm {C}{{\overline{\varPsi }}}$ is also known as the convex hull, which is qualitatively visualised in Fig. 3.

Fig. 3

Qualitative illustration of the convex hull $C{\overline{\varPsi }}$ of two energy potential wells $\varPsi _1$ and $\varPsi _2$

In contrast to standard solid-solid phase transformation, an additional constraint is necessary regarding the evolution of the powder phase. Due to the physical behaviour of powder particles, the melting of powder is not reversible. Thus,

$$\begin{aligned} {\dot{\zeta }}_\mathrm {pow} \le 0 \end{aligned}$$

(45)

has to be fulfilled in addition to (42).

At this point, only the determination of the optimal strains shall be discussed. The evolution equations of the mass fractions will be considered in detail in Sect. 3.4. The strain states in each phase shall minimise the averaged specific energy density while considering (43). The aforementioned minimisation problem subject to the respective equality constraint can be solved with help of a Lagrangian

$$\begin{aligned} {\mathcal {L}} = {\overline{\varPsi }} + \varvec{\lambda } :{\varvec{r}}^{\varvec{\varepsilon }} \, \end{aligned}$$

(46)

with the Lagrange multipliers contained in $\varvec{\lambda }$. Accordingly, the necessary conditions for the minimisation are determined as

$$\begin{aligned} \partial _{\varvec{\varepsilon }_\mathrm {pow}} {\mathcal {L}} = {\varvec{0}}, \quad \partial _{\varvec{\varepsilon }_\mathrm {mel}} {\mathcal {L}} = {\varvec{0}}, \quad \partial _{\varvec{\varepsilon }_\mathrm {sol}} {\mathcal {L}} = {\varvec{0}}. \end{aligned}$$

(47)

It is possible to derive an explicit expression for the optimal strain distributions by using (47) and by solving these equations with respect to the Lagrange multipliers

$$\begin{aligned} \varvec{\lambda } = \frac{1}{\rho _\bullet } \,\frac{\partial \psi _\bullet }{\partial {\varvec{\varepsilon }}_\bullet }. \end{aligned}$$

(48)

After taking into account (43) and (48), the following analytical results are obtained for the respective optimal strains of each phase

$$\begin{aligned} \varvec{\varepsilon }_\mathrm {pow}^\star&=\widetilde{{{{\mathbf {\mathsf{{E}}}}}}}\, ^{-1} : \left[ \rho _\mathrm {pow}\, {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol}: {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {mel}: \varvec{\varepsilon }^\mathrm {el} \right] , \end{aligned}$$

(49)

$$\begin{aligned} \varvec{\varepsilon }_\mathrm {mel}^\star&= \widetilde{{{{\mathbf {\mathsf{{E}}}}}}}\, ^{-1} : \left[ \rho _\mathrm {mel}\, {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol}: {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {pow}: \varvec{\varepsilon }^\mathrm {el} \right] + \varvec{\varepsilon }_\mathrm {mel}^\mathrm {irr} , \end{aligned}$$

(50)

$$\begin{aligned} \varvec{\varepsilon }_\mathrm {sol}^\star&= \widetilde{{{{\mathbf {\mathsf{{E}}}}}}} \,^{-1} : \left[ \rho _\mathrm {sol}\, {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {mel}: {{{\mathbf {\mathsf{{E}}}}}}_\mathrm {pow}: \varvec{\varepsilon }^\mathrm {el} \right] + \varvec{\varepsilon }_\mathrm {sol}^\mathrm {irr} , \end{aligned}$$

(51)

with the abbreviation

$$\begin{aligned} \widetilde{{{{\mathbf {\mathsf{{E}}}}}}}&= \zeta _\mathrm {pow} \,\rho _\mathrm {pow}\,{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol} :{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {mel} + \zeta _\mathrm {mel} \,\rho _\mathrm {mel}\,{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol} :{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {pow}\nonumber \\&\quad + \zeta _\mathrm {sol} \,\rho _\mathrm {sol}\,{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {pow} :{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {mel},\end{aligned}$$

(52)

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {el}&= \varvec{\varepsilon } - \zeta _\mathrm {mel} \, \varvec{\varepsilon }_\mathrm {mel}^\mathrm {irr}- \zeta _\mathrm {sol} \, \varvec{\varepsilon }^\mathrm {irr}_\mathrm {sol}. \end{aligned}$$

(53)

Finally, the overall stress

$$\begin{aligned} \varvec{\sigma } = \frac{\partial {\overline{\psi }}}{\partial \varvec{\varepsilon }} = \frac{\mathrm {d}m_0}{\mathrm {d}V_0}\, \widetilde{{{{\mathbf {\mathsf{{E}}}}}}}\,^{-1} : {{{\mathbf {\mathsf{{E}}}}}}^\star : \varvec{\varepsilon }^\mathrm {el} \end{aligned}$$

(54)

can be determined in a compact form by using the abbreviation ${ {{{\mathbf {\mathsf{{E}}}}}}^\star ~=~{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol}:{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {mel}:{{{\mathbf {\mathsf{{E}}}}}}_\mathrm {sol}}$. The consolidated notation for (49)-(51) and (54) can only be derived in case ${{{\mathbf {\mathsf{{E}}}}}}_\bullet$ is an isotropic tensor. This assumption seems to be appropriate for the material at hand, as defined in Sect. 5.

3.4 Evolution equations

In line with, e.g., [7], it is possible to derive evolution equations for state variables ${\mathcal {V}}$ from a dissipation function ${\mathcal {C}}$, i.e.

$$\begin{aligned} \partial _{{\mathcal {V}}} \,{\overline{\psi }} + \partial _{\dot{{\mathcal {V}}}} \,{\mathcal {C}} = - \varGamma \, \partial _{{\mathcal {V}}} \,r, \end{aligned}$$

(55)

with the consistency parameter $\varGamma$ and the generalised inequality constraint ${r\le 0}$. For specific cases, it may be more convenient to use the dual dissipation function ${\mathcal {C}}^\star$ instead. This quantity depends on the driving force

$$\begin{aligned} {\mathcal {F}} = -\frac{\partial {\overline{\psi }}}{\partial {\mathcal {V}} }\, \end{aligned}$$

(56)

and can be computed by applying the Legendre-Fenchel transformation

$$\begin{aligned} {\mathcal {C}}^\star = \max _{\dot{{\mathcal {V}}}} \left\{ {\mathcal {F}} \,\dot{{\mathcal {V}}} - {\mathcal {C}} \right\} . \end{aligned}$$

(57)

As an alternative to (55), the evolution equation is then given by

$$\begin{aligned} \dot{{\mathcal {V}}} - \partial _{{\mathcal {F}}} \, {\mathcal {C}}^\star = - \varGamma \, \partial _{{\mathcal {V}}}\, r . \end{aligned}$$

(58)

This concept is now applied in order to derive the evolution equations for the model-specific independent internal state variables

$$\begin{aligned} {\mathcal {V}} = \lbrace \xi _\mathrm {mel},\varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}, \xi _\mathrm {sol} , \varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol}, k^\mathrm {hard}_\mathrm {sol} \rbrace . \end{aligned}$$

(59)

The mass fraction of the powder is substituted by

$$\begin{aligned} {\zeta _\mathrm {pow} = 1 - \zeta _{\mathrm {mel}} - \zeta _{\mathrm {sol}}} \end{aligned}$$

(60)

according to conservation of mass. As the volume and mass fractions can be converted into one another, compare (37), the following framework is derived based on volume fractions $\xi _\bullet$. This enables the enforcement of the minimisation based on the Helmholtz free energy ${\overline{\psi }}$ without weighting the equation itself with the respective mass density $\rho _\bullet$. The stresses can then be calculated in a straightforward manner via (54).

3.4.1 Volume fractions

In view of establishing evolution equations for the volume fractions $\xi _{\mathrm {mel}}$ and $\xi _{\mathrm {sol}}$, the dissipation function

$$\begin{aligned} {\mathcal {C}}^{\xi } = \frac{\eta ^\xi }{2}\, \left[ {\dot{\xi }}_\mathrm {mel}^2 + {\dot{\xi }}_\mathrm {sol}^2 + {\dot{\xi }}_\mathrm {pow}^2\right] , \end{aligned}$$

(61)

is introduced together with the inequality constraints

$$\begin{aligned} r_\mathrm {mel}&= - \xi _\mathrm {mel} \le 0, \end{aligned}$$

(62)

$$\begin{aligned} r_\mathrm {sol}&= - \xi _\mathrm {sol} \le 0, \end{aligned}$$

(63)

$$\begin{aligned} r_\mathrm {pow}&= - 1 + \zeta _\mathrm {mel} + \zeta _{\mathrm {sol}} \le 0 , \end{aligned}$$

(64)

$$\begin{aligned} r_{\Delta }&= {\dot{\zeta }}_{\mathrm {pow}} \le 0, \end{aligned}$$

(65)

derived from (42). The evolution of phase fractions is supposed to occur over a finite temperature range rather than jumping from zero to one at a specific temperature. Therefore, this development is considered dissipative. Altogether, two Biot-equations

$$\begin{aligned} -{\mathcal {F}}_{\xi _\mathrm {mel}}' + \partial _{{\dot{\xi }}_\mathrm {mel}} {\mathcal {C}}^\xi&= - \varGamma _\mathrm {mel}\, \partial _{\xi _\mathrm {mel}}\, r_\mathrm {mel} - \varGamma _\mathrm {pow} \, \partial _{\xi _\mathrm {mel}}\, r_\mathrm {pow} \nonumber \\&\quad - \varGamma _{\varDelta }\, \partial _{\xi _\mathrm {mel}}\, r_{\Delta } \end{aligned}$$

(66)

$$\begin{aligned} -{\mathcal {F}}_{\xi _\mathrm {sol}}' + \partial _{{\dot{\xi }}_\mathrm {sol}} {\mathcal {C}}^\xi&= - \varGamma _\mathrm {sol}\, \partial _{\xi _\mathrm {sol}}\, r_\mathrm {sol} - \varGamma _\mathrm {pow} \, \partial _{\xi _\mathrm {sol}}\, r_\mathrm {pow} \nonumber \\&\quad - \varGamma _{\varDelta }\, \partial _{\xi _\mathrm {sol}}\, r_{\Delta } \end{aligned}$$

(67)

are carried out which govern the evolution of the independent volume fractions. In this case,

$$\begin{aligned} {\mathcal {F}}'_\bullet = -\frac{\partial {\overline{\varPsi }}}{\partial {\mathcal {V}}_\bullet } \end{aligned}$$

(68)

refers to the driving force based on the free energy density ${\overline{\varPsi }}$.

3.4.2 Viscous strains

The evolution of viscous strains $\varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}$ within the molten pool is determined via a visco-elastic and thus rate dependent primal dissipation function

$$\begin{aligned} {\mathcal {C}}^\mathrm {vis} = \frac{\eta _\mathrm {mel}^\mathrm {vis}}{2} \, \Vert \dot{\varvec{\varepsilon }}^\mathrm {vis}_\mathrm {mel}\Vert ^2. \end{aligned}$$

(69)

Therein, $\eta _\mathrm {mel}^\mathrm {vis}$ denotes a viscosity related material constant. For this evolution equation, no inequality constraints have to be taken into account, therefore the right hand side in (55) equals zero when applied to the evolution of viscous strain contributions. In general, the driving force is calculated via (56), such that the standard driving force for the viscous strains is defined as

$$\begin{aligned} {\mathcal {F}}^\mathrm {vis} := - \frac{\partial {\overline{\psi }}}{\partial \varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}} = \zeta _{\mathrm {mel}} \, \varvec{\sigma }. \end{aligned}$$

(70)

Here, the driving force ${\mathcal {F}}^\mathrm {vis}$ equals the stress tensor weighted with $\zeta _{\mathrm {mel}}$. However, this driving force is a quantity averaged over a domain due to the homogenisation framework applied, whereas the domain can contain multiple phases and changing mass fractions, as visualised in Fig. 4. This domain corresponds to an infinitesimal surrounding of a material point. As a consequence, a local driving force

$$\begin{aligned} {\mathcal {F}}^\mathrm {vis}_\mathrm {loc} := - \frac{1}{\zeta _{\mathrm {mel}}}\, \frac{\partial {\overline{\psi }}}{\partial \varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}} = \varvec{\sigma } \end{aligned}$$

(71)

has to be defined that affects only the molten phase within the domain considered, see Fig. 4 and also Remark 1. This driving force is incorporated into the evolution equation, such that

$$\begin{aligned} \dot{\varvec{\varepsilon }}^\mathrm {vis}_\mathrm {mel} = \frac{1}{\eta _\mathrm {mel}^\mathrm {vis}} \, \varvec{\sigma }. \end{aligned}$$

(72)

The viscous strains incorporate a fluid-like response, as a complete relaxation of the stresses is enabled.

Fig. 4

Explanation of the standard driving force ${\mathcal {F}}^\mathrm {vis}$ taking into account the whole domain, in contrast to the local driving force ${\mathcal {F}}_\mathrm {loc}^\mathrm {vis}$ being effective in the molten phase $p_2$ (grey), whereas $p_1$ (white) corresponds to all other possible phases present, also including $p_2$

3.4.3 Plastic strains

For the rate-independent evolution of the plastic strains $\varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol}$ as well as of the variable $k^\mathrm {hard}_\mathrm {sol}$ related to the isotropic hardening, the following dual dissipation function

$$\begin{aligned} {\mathcal {C}}^{\star \mathrm {pl}} = \lambda \, \varPhi = 0 \end{aligned}$$

(73)

is used. In the aforementioned equation, $\lambda$ denotes the Lagrange multiplier and $\varPhi$ refers to the yield function. Following the same argumentation as in the previous section, the yield function

$$\begin{aligned} \varPhi = {\widehat{\varPhi }}({\mathcal {F}}^\mathrm {pl}_\mathrm {loc},\,\kappa _\mathrm {loc}) \end{aligned}$$

(74)

depends on the local driving forces

$$\begin{aligned} {\mathcal {F}}^\mathrm {pl}_\mathrm {loc}&:= - \frac{1}{\zeta _\mathrm {sol}}\, \frac{\partial {\overline{\psi }}}{\partial \varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol}} \,\, = \varvec{\sigma }, \end{aligned}$$

(75)

$$\begin{aligned} \kappa _\mathrm {loc}&:= - \frac{1}{\zeta _\mathrm {sol}}\, \frac{\partial {\overline{\psi }}}{\partial k^\mathrm {hard}_\mathrm {sol}} = - \frac{\xi _{\mathrm {sol}}}{\zeta _{\mathrm {sol}}}\, H_\mathrm {sol}\, k_\mathrm {sol}^\mathrm {hard}, \end{aligned}$$

(76)

which yields the associated evolution equation for the plastic strains

$$\begin{aligned} \dot{\varvec{\varepsilon }}^\mathrm {pl}_\mathrm {sol}&= \lambda \, \dfrac{\partial \varPhi }{\partial {\mathcal {F}}^\mathrm {pl}_\mathrm {loc}} , \end{aligned}$$

(77)

and for the hardening variable

$$\begin{aligned} {\dot{k}}^\mathrm {hard}_\mathrm {sol}&= \lambda \, \dfrac{\partial \varPhi }{\partial \kappa _\mathrm {loc}}. \end{aligned}$$

(78)

The yield function is specifically chosen as

$$\begin{aligned} \varPhi&:= \left\| {\mathcal {F}}^\mathrm {pl}_\mathrm {loc,dev} \right\| - \sqrt{\frac{2}{3}} \, \left[ \sigma _\mathrm {sol}^\mathrm {y} - \kappa _\mathrm {loc} \right] \end{aligned}$$

(79)

$$\begin{aligned}&= \left\| \varvec{\sigma }^\mathrm {dev}\right\| - \sqrt{\frac{2}{3}} \, \left[ \sigma _\mathrm {sol}^\mathrm {y} + \frac{\xi _{\mathrm {sol}}}{\zeta _{\mathrm {sol}}}\, H_\mathrm {sol}\, k_\mathrm {sol}^\mathrm {hard} \right] , \end{aligned}$$

(80)

where $\sigma _\mathrm {sol}^\mathrm {y}$ refers to the yield stress of the solid phase and where ${\bullet ^\mathrm {dev} := \bullet - \frac{1}{3}\,\mathrm {tr}(\bullet )}\,{\varvec{I}}$ denotes the deviator of the quantity $\bullet$. With this, the flow direction can then be specified as

$$\begin{aligned} \varvec{\nu }&:= \frac{\partial \varPhi }{\partial {\mathcal {F}}^\mathrm {pl}_\mathrm {loc}} = \frac{\varvec{\sigma }_\mathrm {dev}}{\Vert \varvec{\sigma }_\mathrm {dev}\Vert }, \end{aligned}$$

(81)

together with $\partial \Phi / \partial \kappa _\mathrm {loc} = \sqrt{2/3}$.

Remark 1

In general, a driving force ${\mathcal {F}} = - \partial _{{\mathcal {V}}}\,{\overline{\psi }}$ is calculated for all internal variables ${\mathcal {V}}$. However, the evolution of the internal state variables $\dot{{\mathcal {V}}}$ of the corresponding material only depends on the local driving force ${\mathcal {F}}_{\mathrm {loc}}$, as discussed before. In contrast, the mechanical dissipation entry ${\mathcal {D}}_\mathrm {mech} = {\mathcal {F}}\,\dot{{\mathcal {V}}}$ regards the complete driving force, as the thermodynamic consistent driving force ${\mathcal {F}}$ is already weighted within ${\mathcal {D}}_\mathrm {mech}$ due to the homogenisation approach applied for ${\overline{\varPsi }}$.

3.5 Heat effects

All standard heat transfer mechanisms, particularly heat expansion, conduction, radiation and convection, are considered within the model formulation and shall be briefly discussed in what follows. With respect to the heat expansion model and related thermal strains $\varvec{\varepsilon }_{\mathrm {sol}}^\mathrm {th}$, a standard linear relation

$$\begin{aligned} {\varvec{\varepsilon }}_{\mathrm {sol}}^{\mathrm {th}} := \alpha _{\mathrm {sol}}\,\left[ \theta -\theta _{\mathrm {ref}}\right] \,{\varvec{I}}\, , \end{aligned}$$

(82)

is used, where $\alpha _{\mathrm {sol}}$ represents the (isotropic) heat expansion coefficient of the solid phase and where $\theta _{\mathrm {ref}}$ denotes the reference temperature. The heat expansion of the powder and molten phase is negligible compared to the expansion of the solid phase.

In addition, a standard isotropic Fourier-type form is used for the heat conduction model, viz.

$$\begin{aligned} {\varvec{q}}_\mathrm {cond} = -\,{\widetilde{k}}\,\nabla \theta \,{\varvec{I}} . \end{aligned}$$

(83)

In this relation,

$$\begin{aligned} {\widetilde{k}} := \left[ \frac{\zeta _\mathrm {pow}}{k_{\mathrm {pow}}} + \frac{\zeta _{\mathrm {mel}}}{k_{\mathrm {mel}}} + \frac{\zeta _{\mathrm {sol}}}{k_{\mathrm {sol}}}\right] ^{-1}, \end{aligned}$$

(84)

represents the averaged heat conduction coefficient of the phase mixture according to a Reuss-type homogenisation with $k_\bullet$ as the respective heat conductivity of each phase.

Moreover, heat convection and radiation are regarded on the outer boundaries. In a standard manner, heat convection is considered by

$$\begin{aligned} q_\mathrm {conv} = - h\,[\theta _\mathrm {surf} - \theta _\mathrm {amb}], \end{aligned}$$

(85)

where h refers to the convective heat transfer coefficient, i.e. the reference film coefficient. Furthermore, $\theta _\mathrm {sur}$ and $\theta _\mathrm {sink}$ denote the surface and ambient (sink) temperature, respectively. In addition, radiation heat flow can be given by

$$\begin{aligned} q_\mathrm {rad} = -\sigma _\mathrm {boltz}\, \epsilon _\mathrm {emiss}\,\left[ [\theta - \theta ^\mathrm {Z}]^4 - [\theta _\mathrm {amb} - \theta ^\mathrm {Z}]^4\right] , \end{aligned}$$

(86)

with $\sigma _\mathrm {boltz} = 1.38064852\times 10^{-23}$ $\hbox {m}^2$kg $\hbox {s}^{-2}\hbox {K}^{-1}$ corresponding to the Stefan-Boltzmann constant, $\epsilon _\mathrm {emiss}$ being the emissivity coefficient, $\theta ^\mathrm {Z}$ defining the value of absolute zero on the specific temperature scale used and with $\theta ^\mathrm {amb}$ referring to the ambient temperature of the surrounding media. For further insight into the heat transfer mechanism the interested reader is referred to, e.g., [6].

As introduced in (19) and (20), the balance equations depend on the effective specific heat capacity which is here given by

$$\begin{aligned} {\widetilde{c}}&:= -\, \theta \,\partial ^2_{\theta \theta }{{\overline{\varPsi }}} \nonumber \\&=\frac{\mathrm {d}V_0}{\mathrm {d}m_0}\,[\xi _\mathrm {pow}\,c_{\mathrm {pow}} + \xi _{\mathrm {mel}}\,c_{\mathrm {mel}} + \xi _{\mathrm {sol}}\,c_{\mathrm {sol}}] - \chi . \end{aligned}$$

(87)

It is worth noting that the specific heat capacity is dependent on the volume fraction $\xi _\bullet$ rather than on the mass fraction $\zeta _\bullet$. This is due to the direct dependence of the effective specific heat capacity with the averaged specific energy ${{\overline{\psi }}}$. Besides, quantity $\chi$ stems from the thermoelastic coupling via the thermal strains in the solid phase and is defined as

$$\begin{aligned} \chi = \frac{\mathrm {d}m_0}{\mathrm {d}V_0}\,\alpha _{\mathrm {sol}}^2\, \zeta _{\mathrm {sol}}^2 \, [\widetilde{{{{\mathbf {\mathsf{{E}}}}}}}\,^{-1} : {\varvec{I}}] : [ {\varvec{I}} : {{{\mathbf {\mathsf{{E}}}}}}^\star ] \, . \end{aligned}$$

(88)

However, in the present framework, this contribution turns out to be negligible due to the dependence on the square of the heat expansion coefficient.

4 Implementation and algorithmic treatment

The framework at hand has been realised with help of the commercial FE-based software Abaqus. For the FE implementation, not only the time discretisation and the evolution of the volume fractions are necessary, but various user subroutines also need to be specified to implement the present modelling framework. For example, the constitutive model defined in Sect. 3 has to be incorporated into Abaqus via the subroutine UMAT, whereas the thermal material model is adapted within UMATHT. In general, the strong form of the energy balance is defined as

$$\begin{aligned} \rho \, {\dot{e}}&=-\nabla \cdot {\varvec{q}} + r^* \end{aligned}$$

(89)

in Abaqus, see [13], where $r^*$ symbolises all effective heat sources. Following the derivations in Sect. 2, some differences are visible. Overall, the heat sources in a thermomechanical problem can be additively decomposed into the sum of external heat supply $r_\mathrm {ext}$ and the volumetric heat generation caused by mechanical working of the material

$$\begin{aligned} r_\mathrm {mech}&= {\mathcal {D}}_\mathrm {mech} + \theta \,\partial _\theta \left[ \,\varvec{\sigma } : \dot{\varvec{\varepsilon }} - {\mathcal {D}}_\mathrm {mech} \,\right] . \end{aligned}$$

(90)

This results in

$$\begin{aligned} r^*&=r_\mathrm {ext}+r_\mathrm {mech} . \end{aligned}$$

(91)

All terms contributing to $r_\mathrm {mech}$ are calculated within the user subroutine UMAT as contributions to the variable RPL as defined in [13]. In a thermomechanical analysis, this contribution—if specified—is automatically added to the external heat sources. In doing so, it is possible to directly include the influence of mechanical working and dissipation in Abaqus. To complete the model, the moving heat flux representing the laser beam is added in the user subroutine DFLUX. In addition, an internal strategy of Abaqus (*Model Change) is used to model the layer construction during the SLM process. For further information, see [2] and the references cited therein.

4.1 Global finite-element-based algorithm

In this section, the discretised weak forms of (3) and (19) as introduced in Sect. 2 are defined, where the contributions from both mechanical equilibrium in the absence of mechanical body forces and heat equation for a thermomechanically fully coupled system are considered. The completely discretised weak form can be given by

$$\begin{aligned}&\mathop {{{{\mathbf {\mathsf{{A}}}}}}}\limits _{\begin{array}{c} A=1 \\ e=1 \end{array}}^{\begin{array}{c} n_{\mathrm {el}} \\ n_{\mathrm {en}}^u \end{array}} \left[ \,\int _{\partial {\mathcal {B}}^e} \varvec{t} \, N_A^u \, \mathrm {d}S_0 - \int _{{\mathcal {B}}^e} \varvec{\sigma }\cdot \nabla _{\varvec{x}} \, N_A^u\, \mathrm {d} V_0 \right] = \varvec{0} , \end{aligned}$$

(92)

$$\begin{aligned}&\mathop {{{{\mathbf {\mathsf{{A}}}}}}}\limits _{\begin{array}{c} C=1 \\ e=1 \end{array}}^{\begin{array}{c} n_{\mathrm {el}} \\ n_{\mathrm {en}}^\theta \end{array}} \left[ \,\int _{\partial {\mathcal {B}}^e} q_{{\varvec{n}}}\,N^\theta _C\,\mathrm dS_0 + \int _{{\mathcal {B}}^e} {\varvec{q}} \cdot \nabla N^\theta _C\,\mathrm d V_0 \right. \nonumber \\&\quad \left. \quad + \int _{{\mathcal {B}}^e} r^\mathrm {ext}\,N^\theta _C\,\mathrm d V_0 - \int _{{\mathcal {B}}^e} \rho \,{\widetilde{c}}\, {{\dot{\theta }}}\,N^\theta _C\,\mathrm d V_0 \right. \nonumber \\&\quad \left. \quad + \int _{{\mathcal {B}}^e} {\mathcal {D}}_\mathrm {mech}\,N^\theta _C\,\mathrm d V_0 \right. \nonumber \\&\quad \left. \quad + \, \theta \int _{{\mathcal {B}}^e} \partial _\theta [\varvec{\sigma }:\dot{\varvec{\varepsilon }} - {\mathcal {D}}_\mathrm {mech}] \,N^\theta _C\,\mathrm d V_0 \right] = {\varvec{0}} , \end{aligned}$$

(93)

where ${{{\mathbf {\mathsf{{A}}}}}}$ denotes the assembly operator, $N_A^u,$ and $N^\theta _C$ symbolise the corresponding set of shape functions, $\rho$ refers to the current density, see also Remark 2, surface tractions per unit area are represented by ${{\varvec{t}} = \varvec{\sigma }\cdot {\varvec{n}}}$ and the heat flux vector is given by ${q_{{\varvec{n}}} = - {\varvec{q}}\cdot {\varvec{n}}}$, with ${\varvec{n}}$ describing the outward normal unit vector. The derivation of the discretised weak form is given in the Appendix A.

Remark 2

In analogy to (41), the current density is defined as $\rho = \zeta _\mathrm {pow}\,\rho _\mathrm {pow} + \zeta _{\mathrm {mel}} \,\rho _\mathrm {mel} + \zeta _{\mathrm {sol}}\, \rho _\mathrm {sol}$. At the beginning of the simulation, the material completely consists of powder material, thus $\rho := \rho _\mathrm {pow}$. The effective density obviously changes during the process due to the evolution of the mass fractions. This can be implemented within the user subroutine UMATHT, where the density is artificially adapted, cf. the explanations in [2].

4.2 Local algorithm

In general, all time derivatives ${\dot{\bullet }}$ are approximated by a forward difference quotient

$$\begin{aligned} {\dot{\bullet }} \approx \left[ {^{n+1}\bullet } -\,^{n}\bullet \right] / {\varDelta t}, \end{aligned}$$

(94)

wherein $^n\bullet$ refers to the previous and $^{n+1}\bullet$ to the current time step of the quantity $\bullet$. The time increment is defined as $\varDelta t = \,^{n+1}t - \,^n t$. This time discretisation is applied not only for the temperature and strain field rate, ${\dot{\theta }}$ and $\dot{\varvec{\varepsilon }}$, respectively, but also for all rates of internal variables $\dot{{\mathcal {V}}}$. The solution of the time-discretised versions of the evolution equations given by (66), (67), (72) and (78) with respect to ${}^{n+1}{\mathcal {V}}$ is discussed in the following. Evolution equation (72) can be explicitly solved for $\varvec{\varepsilon }_\mathrm {mel}^\mathrm {vis}$ by using the backward Euler scheme, such that

$$\begin{aligned} ^{n+1} \varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel} = \frac{\varDelta t \, \varvec{\sigma }( ^{n+1}\xi _\mathrm {mel}, {}^{n+1}\xi _\mathrm {sol} , {}^{n+1}\varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol})}{\eta _\mathrm {mel}^\mathrm {vis}} + {} ^n \varvec{\varepsilon }^\mathrm {vis}_\mathrm {mel}. \end{aligned}$$

(95)

Consecutively, the viscous strains are replaced with this analytical expression throughout the algorithm. The constraint (45) can be further reformulated by inserting relation (60) and by applying the forward difference quotient so that

$$\begin{aligned} {\dot{\zeta }}_\mathrm {pow} = -\frac{\,^{n+1}\zeta _{\mathrm {mel}} -\,^n\zeta _{\mathrm {mel}}}{\varDelta t} - \frac{\,^{n+1}\zeta _{\mathrm {sol}} -\,^n\zeta _{\mathrm {sol}}}{\varDelta t} . \end{aligned}$$

(96)

With these conversion at hand, the distinct set of inequality constraints introduced in (62)-(65) is now defined by

$$\begin{aligned} r_\mathrm {mel}&= - \,^{n+1}\xi _\mathrm {mel} \le 0, \end{aligned}$$

(97)

$$\begin{aligned} r_\mathrm {sol}&= - \,^{n+1}\xi _\mathrm {sol} \le 0, \end{aligned}$$

(98)

$$\begin{aligned} r_\mathrm {pow}&= - 1 + {}^{n+1}\zeta _\mathrm {mel} + {}^{n+1}\zeta _{\mathrm {sol}} \le 0 , \end{aligned}$$

(99)

$$\begin{aligned} r_{\Delta }&= -\,^{n+1}\zeta _{\mathrm {mel}} + {}^n\zeta _{\mathrm {mel}} - {}^{n+1}\zeta _{\mathrm {sol}} + {}^n\zeta _{\mathrm {sol}} \le 0, \end{aligned}$$

(100)

which has to be fulfilled by the algorithm. The first two residuals emanating from the evolution equations with respect to the volume fractions of the molten and solid phase are specifically given by

$$\begin{aligned} r_1 =&\, \frac{\mathrm {d}V_0}{\mathrm {d}m_0}\,\frac{\partial {\overline{\psi }}}{\partial \xi _{\mathrm {mel}}} - \varGamma _\mathrm {mel} + \frac{\rho _\mathrm {mel}\,\mathrm {d}V_0}{\mathrm {d}m_0}\, \varGamma _\mathrm {pow} \nonumber \\&- \frac{\rho _\mathrm {mel}\,\mathrm {d}V_0}{\mathrm {d}m_0} \, \varGamma _{\varDelta } + \frac{\eta ^\xi }{\varDelta t}\left[ ^{n+1}\xi _{\mathrm {mel}} - {}^{n}\xi _{\mathrm {mel}}\right] \nonumber \\&- \frac{\eta ^\xi }{\varDelta t}\,\frac{\rho _\mathrm {mel}}{\rho _\mathrm {pow}} \left[ ^{n+1}\xi _{\mathrm {pow}} - {}^{n}\xi _{\mathrm {pow}} \right] , \end{aligned}$$

(101)

$$\begin{aligned} r_2 =&\, \frac{\mathrm {d}V_0}{\mathrm {d}m_0}\,\frac{\partial {\overline{\psi }}}{\partial \xi _{\mathrm {sol}}} - \varGamma _\mathrm {sol} + \frac{\rho _\mathrm {sol}\,\mathrm {d}V_0}{\mathrm {d}m_0} \, \varGamma _\mathrm {pow} \nonumber \\&- \frac{\rho _\mathrm {sol}\,\mathrm {d}V_0}{\mathrm {d}m_0} \,\varGamma _{\varDelta } + \frac{\eta ^\xi }{\varDelta t} \left[ \,^{n+1}\xi _{\mathrm {sol}} - \,^{n}\xi _{\mathrm {sol}}\right] \nonumber \\&-\frac{\eta ^\xi }{\varDelta t} \, \frac{\rho _\mathrm {sol}}{\rho _\mathrm {pow}} \left[ \,^{n+1}\xi _{\mathrm {pow}} - \,^{n}\xi _{\mathrm {pow}} \right] , \end{aligned}$$

(102)

where the dissipation function specified in (61) is analogously discretised by using (94), and where the explicit definition for $\xi _{\mathrm {pow}}$ is not inserted because the terms are already rather lengthy. The compatibility conditions belonging to the constraints (97)–(100) shall be transformed into equality constraints by using the regularised Fischer–Burmeister nonlinear complementarity function, as applied in [2] and explained in the references cited therein. For a more general overview and further insight, cf. [5]. Thus, the residual entries

$$\begin{aligned} r_3&= \sqrt{\varGamma _\mathrm {mel}^2 + r_\mathrm {mel}^2 + 2\,\delta ^2} + r_\mathrm {mel} - \varGamma _\mathrm {mel} \end{aligned}$$

(103)

$$\begin{aligned} r_4&= \sqrt{\varGamma _\mathrm {sol}^2 + r_\mathrm {sol}^2 + 2\,\delta ^2} + r_\mathrm {sol} - \varGamma _\mathrm {sol} \end{aligned}$$

(104)

$$\begin{aligned} r_5&= \sqrt{\varGamma _\mathrm {pow}^2 + r_\mathrm {pow}^2 + 2\,\delta ^2} + r_\mathrm {pow} - \varGamma _\mathrm {pow} \end{aligned}$$

(105)

$$\begin{aligned} r_6&= \sqrt{\varGamma _\varDelta ^2 + r_\varDelta ^2 + 2\,\delta ^2} + r_\varDelta - \varGamma _\varDelta \end{aligned}$$

(106)

can be implemented into the framework, where the perturbation parameter $\delta = 10^{-10}$ is used. With this parameter, a continuously differentiable function exists.

Furthermore, (77) and (78) are discretised in time by using a backward Euler scheme, resulting in

$$\begin{aligned} {\varvec{r}}_7&= \, ^n\varvec{\varepsilon }_\mathrm {sol}^\mathrm {pl} - \, ^{n+1}\varvec{\varepsilon }_\mathrm {sol}^\mathrm {pl} \nonumber \\&\quad \, +\varDelta t \,\lambda \, \varvec{\nu }( ^{n+1}\xi _\mathrm {mel}, {}^{n+1}\xi _\mathrm {sol} , {}^{n+1}\varvec{\varepsilon }^\mathrm {pl}_\mathrm {sol}), \end{aligned}$$

(107)

$$\begin{aligned} r_8&= \, ^n k_\mathrm {sol}^\mathrm {hard} - \,^{n+1}k_\mathrm {sol}^\mathrm {hard} + \varDelta t \, \lambda \, \sqrt{2/3} . \end{aligned}$$

(108)

To calculate the consistency parameter $\lambda$ in (107) and (108), the complementarity conditions related to the evolution of plastic strains are incorporated via

$$\begin{aligned} r_9 = \sqrt{\lambda ^2 + \varPhi ^2 + 2\,\delta ^2} + \varPhi - \lambda . \end{aligned}$$

(109)

The final residual

$$\begin{aligned} {\underline{r}}&= [ \,r_1 ,\, r_2 ,\, r_3 , \,r_4 ,\, r_5 ,\, r_6 ,\,{\underline{r}}_7 ,\, r_8,\, r_9\,]^{\mathrm{{t}}} = {\underline{0}} , \end{aligned}$$

(110)

has to be solved with respect to

$$\begin{aligned} {\underline{f}}&= [ \xi _{\mathrm {mel}}, \,\xi _{\mathrm {sol}}, \,\varGamma _\mathrm {mel},\,\varGamma _\mathrm {sol},\,\varGamma _\mathrm {pow}, \,\varGamma _{\Delta } , \,{\underline{\varepsilon }}_{\mathrm {sol}}^\mathrm {pl},\, k_\mathrm {sol}^\mathrm {hard} , \, \lambda \,]^{\mathrm{{t}}} \, , \end{aligned}$$

(111)

where the tensorial quantities ${\varvec{r}}_7$ and $\varvec{\varepsilon }_{\mathrm {sol}}^\mathrm {pl}$ are rewritten as vectors with the help of the Kelvin notation, resulting in vectorial entries ${\underline{r}}_7$ and ${\underline{\varepsilon }}_{\mathrm {sol}}^\mathrm {pl}$.

Using the Fischer-Burmeister nonlinear complementarity function has the advantage that a standard solver, such as the Newton-Raphson scheme, is applicable even though inequality conditions have to be fulfilled. This method is then used to solve (110) for (111), where the norm of the residuum is checked in every iteration with a tolerance $\epsilon = 10^{-8}$.

5 Numerical examples

In this section, different numerical examples are discussed. The material model is adapted to a $\hbox {Ti}_6\hbox {Al}_4\hbox {V}$ titanium aluminium alloy with material parameters according to Table 1. The transformation strains are directly defined via the mass densities. The parameter $\eta ^\xi$ incorporated in the dissipation potential ${\mathcal {D}}^\xi$ is set to $\eta ^\xi = 0.005$ for the examples at hand. This parameter can be used to adjust the temperature range, in which the phase changes occur in comparison to experimental findings. Moreover, it can be used to potentially stabilise the global FE scheme in terms of numerical robustness. In addition, the viscous strain parameter is chosen as $\eta _\mathrm {mel}^\mathrm {vis} = 70$, so that a high relaxation within the molten (fluid) phase is feasible. The mechanical parameters, i.e. Poisson’s ratio $\nu$, Young’s modulus E and yield limit $\sigma ^\mathrm {y}$, are taken from the literature, see [32, 36, 46]. The hardening modulus $H_\mathrm {sol}$ is, at this stage, chosen without particular literature reference. The thermal material parameters, i.e. the expansion coefficient $\alpha$, the specific heat capacity c, the conductivity k and the latent heat L, as well as the initial temperature $\theta ^\mathrm {ini}$ and the reference temperature $\theta ^\mathrm {ref}$ are parameters based on [32, 36]. The respective effective counterparts which are used to calculate the material response follow from the homogenisation approach introduced in the previous chapters in contrast to material models which directly incorporate temperature-dependent averaged material properties. Furthermore, it shall be remarked that the difference in the mass densities of the material’s phases is rather large and, in consequence, the volume changes captured by the transformation strains. Therefore, one could argue that the used small strain approach may not be appropriate. However, we consider the small strain formulation acceptable, as little rotations are present (see Remark 3) and the rather large transformation strains are completely volumetric.

Table 1 Overview of the used material parameters of $\hbox {Ti}_6\hbox {Al}_4\hbox {V}$ adopted from [32, 36, 46]

Remark 3

The deformation gradient ${\varvec{F}}$ can be multiplicatively split into a rotation tensor ${\varvec{R}}$ and a stretch tensor ${\varvec{U}}$, so that ${\varvec{F}} = {\varvec{R}}\cdot {\varvec{U}}$. The general definition of the small strain tensor has been introduced in (1). In general, the strain measure is introduced via the deformation gradient, so that, e.g., $\varvec{\varepsilon }:= \frac{1}{2}\, [{\varvec{F}} + {\varvec{F}}^\mathrm {T}] - {\varvec{I}}$. For negligible rotation ${\varvec{R}}\approx {\varvec{I}}$, it follows that $\varvec{\varepsilon } \approx {\varvec{U}} - {\varvec{I}}$. For the model at hand, $\varvec{\varepsilon } = \frac{1}{2}\left[ \nabla {\varvec{u}} + [\nabla {\varvec{u}}]^{\mathrm {t}} \right] \approx {\varvec{U}} - {\varvec{I}}$ is valid.

5.1 Proof of concept

In order to investigate the pure material response of the proposed framework, a temperature cycle is prescribed at material point level with zero Neumann boundary conditions as a proof of concept. At the beginning, the temperature is linearly increased in a time interval ${\varDelta t = 1\,}$ms from ${\theta = 873}\,$K to ${\theta = 2873}\,$K, then decreased back to $\theta = 873\,$K in the same time span, see Fig. 5a. The resulting strain evolution is shown in Fig. 5b, while Fig. 6 illustrates the corresponding evolution of mass and volume fractions. The significant changes in the strains occur simultaneously to the evolution of phase fractions. For constant phase fractions, the strains are therefore also constant, except for the re-solidified phase where the strains decrease while the material cools down due to heat expansion. Due to the zero Neumann boundary conditions, no stresses arise, so that no viscous or plastic strains are present in this conceptual proof.

Fig. 5

Proof of concept via thermal cycle at material point level: a prescribed temperature evolution and b resulting strain evolution. The significant drops in the strain evolution occur during the transitions between powder, molten, and re-solidified material

Fig. 6

Evolution of the respective mass and volume fractions over time and temperature for the three phases: a powder phase, b molten phase and c re-solidified material, with prescribed temperature evolution according to Fig. 5a

In Fig. 6, particularly the difference in the evolution of the mass and volume fractions for the three phases can be examined. The material initially purely consists of powder, thus ${\xi _{\mathrm {pow}}= \zeta _\mathrm {pow}=1}$. With increasing temperature, the first phase change towards the molten phase starts at approximately ${\theta \approx 1880}\,$K and finishes at ${\theta \approx 2330}\,$K. The solidification process begins at ${\theta \approx 1870}\,$K and ends at ${\theta \approx 1520}\,$K. As already indicated above, the parameter $\eta ^\xi$ governs the time span in which the phase transition occurs and thereby significantly affects the temperature interval as well. In other words, it is possible to affect the mushy region between the solidus and liquidus temperature with this parameter, as it controls the rate dependent behaviour of the evolution equation (61). From this numerical example, it can be concluded that a volume change of approximately $36\, \%$ occurs during the process.

5.2 Simulation of basic SLM processes

In the following, the modelling and simulation of basic SLM processes are presented. The main geometrical model with all boundary conditions on $\partial {\mathcal {B}}$ is conceptually illustrated in Fig. 7 for the representative building chamber. For the example at hand, homogeneous Dirichlet boundary conditions are prescribed for the displacement, so that

$$\begin{aligned}&\partial {\mathcal {B}}_2: \quad u_3 = 0 \quad \forall \quad x_3= d, \end{aligned}$$

(112)

$$\begin{aligned}&\partial {\mathcal {B}}_3: \quad u_2 = 0 \quad \forall \quad x_2= w ,\end{aligned}$$

(113)

$$\begin{aligned}&\partial {\mathcal {B}}_4: \quad u_2 = 0 \quad \forall \quad x_2= 0, \end{aligned}$$

(114)

$$\begin{aligned}&\partial {\mathcal {B}}_5: \quad u_1 = 0 \quad \forall \quad x_1= l, \end{aligned}$$

(115)

$$\begin{aligned}&\partial {\mathcal {B}}_6: \quad u_1 = 0 \quad \forall \quad x_1= 0. \end{aligned}$$

(116)

The temperature at the bottom surface is prescribed based on

$$\begin{aligned} \partial {\mathcal {B}}_2: \quad&\theta = 373.15\,\mathrm {K} \quad \forall \quad x_3= d. \end{aligned}$$

(117)

Additional heat flux terms due to convection $q_\mathrm {conv}$ and radiation $q_\mathrm {rad}$ are present at the top surface, i.e.

$$\begin{aligned}&\partial {\mathcal {B}}_1: \quad q_\mathrm {conv} \quad \forall \quad x_3= 0, \end{aligned}$$

(118)

$$\begin{aligned}&\partial {\mathcal {B}}_1: \quad q_\mathrm {rad} \quad \forall \quad x_3= 0. \end{aligned}$$

(119)

In addition, the laser beam heat input which is represented by the volume-distributed heat source $r_\mathrm {ext}$ exists along the respective scanning path.

Various models exist for the application of the heat flux $r_\mathrm {ext}$ generated by the laser beam as accurately as possible, see e.g. [20, 22, 26, 47]. For this model, a volumetric heat source as proposed in [19] for welding is adjusted for SLM, such that the external heat source is defined within the Abaqus subroutine DFLUX by

$$\begin{aligned} r_\mathrm {ext}(x_1^\prime ,x_2^\prime ,x_3^\prime )=\frac{4\,\sqrt{2}\,P}{r_{0}^3\,\pi \sqrt{\pi }}\,\exp \left( { -\frac{2\,({x^\prime _1}^2 + {x^\prime _2}^2 + {x^\prime _3}^2)}{r_{0}^2}} \right) , \end{aligned}$$

(120)

where P defines the laser power, $r_0$ is the characteristic (focus) radius of the laser beam and $x_i^\prime$ refers to the moving coordinate system whose origin lies in the centre of the laser beam at the top surface of the current powder layer, see Fig. 7. Coordinates $x_1^\prime$ and $x_2^\prime$ are needed to define the laser movement in dependence of the laser velocity ${\overline{v}}_\mathrm {lsr}$ within the $x_1$-$x_2$-plane. Coordinate $x_3^\prime$ depends on the height $h_\mathrm {lyr}$ of a single layer and on the current number of applied layers $n_\mathrm {lyr}$, so that ${x^\prime _3 = x_3 + n_\mathrm {lyr} \,h_\mathrm {lyr}\,}$.

For the following simulations, the laser power is set to $P=130\,\hbox {W}$ with velocity ${\overline{v}}_\mathrm {lsr}=1\,\hbox {m s}^{-1}$ and focus radius $r_{0}=150\,\mu \hbox {m}$. A convective heat transfer coefficient of air $h = 25\,\hbox {W}\,\hbox {K}^{-1}\, \hbox {m}^{-2}$ is used, whereas the emissivity of the titanium alloy is set to ${\epsilon _\mathrm {emiss} = 0.19}$, cf. [1]. A layer height ${h_{\mathrm {lyr}}=50}\,\upmu \hbox {m}$ is used, whereas the height of the base material is chosen to be larger ($150\,\upmu \hbox {m}$). Overall, a part made out of three layers ${n_\mathrm {lyr} = 3}$ will be simulated. To model the application of different layers, the element birth and death method implemented in Abaqus is used (*Model Change). More insight into the laser beam model and layer construction model can be found in [2]. Different models for the laser beam impact as well as models for the heat transfer mechanisms could be incorporated into the algorithm in a straight-forward manner.

Fig. 7

Definition of boundaries for basic process simulations. (Color figure online)

Fig. 8

Geometry of the straight laser path model in [mm] with a layer height of 0.05 mm and a height of the base material of 0.15 mm. In addition, the corresponding mesh is visualised. (Color figure online)

The initial part only consists of powder material where the first layer of material is already activated. At first, the building chamber is homogeneously pre-heated to ${{\overline{\theta }}=373}\,$K subject to the respective boundary conditions. Afterwards, the laser beam is applied along the predefined scanning path and a cooling time is given before the next layer of powder is activated. This procedure is repeated until all three layers have been activated and until the laser beam has been applied. Finally, the work piece cools down to the building chamber temperature ${{\overline{\theta }}}$. For the simulation, the element type C3D8HT is chosen. Due to high temperature gradients and laser velocity, a dense mesh is used close to the laser beam path. Within this region, a characteristic element length of $l_\mathrm {char} \approx 20\,\upmu$m is applied, as visualised for the straight laser path in Fig. 8. For the L-shaped laser path, a constant mesh of $l_\mathrm {char} \approx 20\,\upmu$m is used, as shown in Fig. 9. For both examples, three elements per layer are used in thickness direction. During the simulation, the automatic time incrementation included within Abaqus is used. The simulations are performed on the Linux HPC cluster (LiDO3) at TU Dortmund University, where one compute node using eight cores is taken for both simulations.

5.2.1 Straight laser path

For this example, the laser beam moves $1\,$mm along the $x_1$-direction. The geometry considered, respectively half of the geometry, is specified by $l=3.3\,$mm, $w = 1\,$mm and $d=0.3\,$mm for the boundary conditions introduced in (112)–(117). In Fig. 10, the temperature evolution $\theta ({\varvec{x}},t)$ and the evolution of the mass fraction of the molten phase $\zeta _{\mathrm {mel}}$ is illustrated. The deformed mesh (with scale factor one) is plotted for all consecutive figures. The depth of the molten pool increases as can be seen in Fig. 10b, c compared to Fig. 10a due to the higher conductivity of the already re-solidified layers. This allows the connection of newly added layers to previous ones so that there is one compound. The volume shrinkage of the material during the melting is indicated in Fig. 10. After the application of all three layers and the consecutive cooling, the final re-solidified part can be identified in terms of the volume fraction $\xi _\mathrm {sol}$, see Fig. 11a, b, where in the latter figure the solid part has been virtually extracted. These two Figures show the re-solidified material after applying the laser beam to three layers in contrast to Fig. 10c, where only the current state of the molten material during the third scanning is visualised. The maximum value of the volume fraction of the solid phase equals 0.633 (i.e. $\max \xi _{\mathrm{sol}} = \rho _{\mathrm{pow}}/\rho _{\mathrm{sol}} = 0.633$) in contrast to the related mass fraction ($\max \zeta _\mathrm {sol} =1$), compare Fig. 6c.

Fig. 9

Geometry of the L-shaped laser path model in [mm] with a layer height of 0.05 mm and a height of the base material of 0.15 mm. In addition, the corresponding mesh is visualised. (Color figure online)

Fig. 10

Distribution of temperature $\theta$ (NT11) in [K] on the left side and the respective mass fraction $\zeta _\mathrm {mel}$ of the molten phase on the right side for the same time step while scanning a layer 1, b layer 2 and c layer 3, where the laser beam has reached the end of each straight line. (Color figure online)

Fig. 11

Final distribution of a the re-solidified volume fraction $\xi _\mathrm {sol}$ and b the final virtually extracted part with re-solidified mass fraction $\zeta _\mathrm {sol}$ (cut at the red line displayed in (a) and rotated; red dot used for graphs in Fig. 13) after cooling down to the building chamber temperature. (Color figure online)

The incorporation of $r_\mathrm {mech}$ in the subroutine UMAT as defined in (91) is quite important. Without the coupling term RPL, the maximum temperature within the molten pool would be overestimated by approximate $200\,$K. Within $r_\mathrm {mech}$, not only the dissipative effects due to the internal state variables ${\mathcal {V}}$ are included, but also the latent heat effects are thermomechanically consistent incorporated into the framework. For example, the latent heat terms in $\psi _\mathrm {pow}$ and $\psi _{\mathrm {sol}}$ change the heat conduction and cooling speed. In the literature, mostly the apparent heat capacity method as introduced by [8] is used to capture the effects of the latent heat in an artificial increase of the heat capacity, e.g. [11, 15, 18, 42, 45, 48]. An in-depth study on different methods to include latent heat effects during phase changes can be found in [35]. In [42], the influence of the latent heat for the solely thermal problem has been specifically examined, where similar results were obtained compared to our studies. Overall, (91) mainly regulates the temperature evolution and thus the melt pool geometry rather than the absolute stress values. In general, the laser beam parameters influence the melt pool geometry which affects the hatching strategy and the layer height while simulating a complete part.

The residual stresses stemming from heat expansion and, more significantly, the volume changes due to the phase transitions, are illustrated in Fig. 12. These stresses are particularly significant within the re-solidified part, as the powder material exhibits a small Young’s modulus (Fig. 12d). In the contour plots, it is observable in Fig. 12a that particularly high tensile normal stresses are present in $x_1$-direction of the third layer, in other words along the direction of the moving heat source. In addition, high compressive normal stresses exist in $x_2$-direction which is perpendicular to the direction of the moving heat source, see Fig. 12b. Negligible stresses are present in $x_3$-direction as presented in Fig. 12c. Not pictured are the shear stresses, as these stresses are negligible (for the coordinate system considered) compared to the highlighted normal stress contributions.

Fig. 12

Distribution of normal stresses in [GPa] of the virtually extracted final re-solidified part in a $x_1$-direction (S, S11), b $x_2$-direction (S, S22) and c $x_3$-direction (S, S33). The von Mises equivalence stress $\sigma _\mathrm {v.M.}$ (S, Mises) for the overall part is shown in (d). (Color figure online)

To gain a better understanding of the stress evolution, a centred element in the first layer shall be considered in detail indicated by a red dot, see Fig. 11. In Fig. 13a, the related temperature and the molten mass fraction are illustrated. A steep temperature increase is found when the laser beam is applied. During the second scanning, the top material re-melts, whereas during the scanning of the third layer, the first layer does not completely re-melt again. When examining the stress evolution in Fig. 13c, the relaxation of the stress $\sigma _{11}$ is noticeable during the scanning of the second layer. In contrast, stress $\sigma _{22}$ increases, as the expansion and contraction of the material in $x_2$-direction is hindered.

The temporal evolution of various significant quantities is exemplarily presented for one element of the first layer in Fig. 13. The values of the nodes are averaged for the element. In Fig. 13c, the stress evolution is shown. High total strains are present for $\varepsilon _{22}$ and $\varepsilon _{33}$ in Fig. 13b. After cooling down for the third time, see Fig. 13a, a steady-state is reached for the strains and stresses, as visualised in Fig. 13b, c.

Fig. 13

Temporal evolution t in [ms] of representative quantities for the element as indicated in Fig. 11a: a averaged temperature evolution $\theta$ (TEMP_avg) in [K] and molten mass fraction $\zeta _\mathrm {mel}$ (zetamel_avg), b averaged total strains $\varepsilon _{ii}$ (Eii_avg), c averaged normal stress evolution $\sigma _{ii}$ (Sii_avg) in [GPa] and d accumulated irreversible strains $\varepsilon ^\mathrm {irr}_{ii}$ (INii_avg) in $x_1$-, $x_2$- and $x_3$-direction. (Color figure online)

As mentioned before, various models use a phenomenological approach to define a macroscopic inelastic strain contribution that accumulates all irreversible processes. This is often denoted as the inherent strain method, see e.g. [24, 31, 40, 41]. In a post processing step, the accumulated irreversible strains ${\varvec{\varepsilon }}^\mathrm {irr}$ can be evaluated with the introduced model. These are then defined as

$$\begin{aligned} \varvec{\varepsilon }^\mathrm {irr} = \zeta _{\mathrm {mel}} \, [{\varvec{\varepsilon }}_{\mathrm {mel}}^\mathrm {trans} +{\varvec{\varepsilon }}_{\mathrm {mel}}^\mathrm {vis} ] + \zeta _{\mathrm {sol}} \, [{\varvec{\varepsilon }}_{\mathrm {sol}}^\mathrm {trans} +{\varvec{\varepsilon }}_{\mathrm {sol}}^\mathrm {pl} + {\varvec{\varepsilon }}_{\mathrm {sol}}^\mathrm {th} ]. \end{aligned}$$

(121)

The evolution of this averaged inherent strain of one element is exemplarily plotted in Fig. 13d. Due to the volumetric transformation strains, the evolution of inherent strains is (quasi) volumetric for the particular boundary value problem considered until the part solidifies. Then the accumulated inelastic strain evolution differs: larger strains are only found in $x_2$- and $x_3$-direction, while these strains almost coincide again during the second re-melting. After cooling, almost no further changes occur. Only one small peak is visible when the third layer is applied and molten. This is in accordance with Fig. 13a, as the element does not completely remelt during the third cycle. In the final state, high irreversible strains for the $x_2$- and $x_3$-direction are present.

Fig. 14

Distribution of total strains ${\varepsilon }_{ij}$ (E, EIJ) of the virtually extracted final re-solidified part: a normal and b shear strains. (Color figure online)

Fig. 15

Distribution of normal stresses in [GPa] of the virtually extracted final re-solidified part in a $x_1$-direction (S, S11), b $x_2$-direction (S, S22) and c $x_3$-direction (S, S33). (Color figure online)

5.2.2 L-shaped laser path

In addition to the aforementioned case, a more complicated laser beam path is simulated. For this example, the laser beam moves $0.75\,$mm along the $x_1$-direction and $0.75\,$mm along the $x_2$-direction. Similar to the example before, three layers are consecutively added. The boundary conditions defined in (112)–(117) are referred to a geometry with $l=1.6\,$mm, $w = 1.6\,$mm and $d=0.3\,$mm, cf. Figs. 7 and 9. In theory, it is possible to model even more complex geometries. However, the computational time increases considerably with a larger number of elements and longer laser beam paths. When comparing both simulations, the straight laser path needs approximately 17 hours, where $27\,693$ elements are used. Overall, the model exhibits $151\,821$ degrees of freedom. The example of the L-shaped laser path, however, is applied using $108\,800$ elements and a total of $581\,192$ degrees of freedom. Altogether, the computational time increases to almost 8 days. The final results of the L-shaped path are presented in what follows, where the solid part has been virtually extracted for all illustrations.

First of all, the normal and shear strain distribution is pictured in Fig. 14, where the deformed mesh (with scale factor one) is presented. Here, a couple of effects are striking: the dependence of the strains and the laser path orientation is obvious, compare Fig. 14a for $\varepsilon _{11}$ and $\varepsilon _{22}$. While the beam moves along the $x_1$-direction, small tensile strains $\varepsilon _{11}$ are present. The values of the strains change as soon as the laser beam turns and moves along the $x_2$-direction. The strains $\varepsilon _{11}$ switch from tensile to compressive strains and small tensile strains $\varepsilon _{22}$ are present. In addition, especially high normal compressive strains $\varepsilon _{33}$ are found within the part, as it shrinks the most in depth. Due to the changing laser beam path, shear stresses are induced, as illustrated in Fig. 14b. Large negative shear strains $\varepsilon _{23}$ change to high positive shear strains $\varepsilon _{13}$ after the kink, as a symmetry is present with respect to a plane parallel to $-x_1 = x_2$. Altogether, the strains are rather constant along the width of the re-solidified part and within one direction of each layer. In contrast—with an increasing number of layers—the magnitude of the strains increases.

Although the laser beam path, respectively the objective geometry, is symmetric with respect to the underlying symmetry plane and although the distribution of the strains is almost symmetric as well, the distribution of the resulting solid part is not completely symmetric. The widths of the two sides differ slightly. This can be explained by the rather coarse discretisation. In addition, the depth of the simulated workpiece increases at the turning point of the laser beam and the part is notably wider at the kink. Due to the turning of the laser, the heat influence takes place over a longer time period compared to the positions further afield and the straight lines considered in Sect. 5.2.1. This effect has to be borne in mind when manufacturing more complex components.

Figure 15 shows the normal stresses which are significantly larger than the related shear stresses. In analogy to Fig. 14a, the stresses vary according to the laser beam movement. This becomes especially visible when comparing Fig. 15a, b. High tensile stresses $\sigma _{11}$ and $\sigma _{22}$, respectively, can be found along the movement of the laser beam. High compressive strains exist perpendicular to the laser movement, especially in the lower portion of each layer. In $x_3$-direction, less normal stresses $\sigma _{33}$ are computed.

Finally, the equivalent irreversible strain ${\overline{\varepsilon }}^\mathrm {irr}$ (in analogy to the equivalent von Mises stress) shall be analysed, as illustrated in Fig. 16. Overall, the results show a symmetric distribution of ${\overline{\varepsilon }}^\mathrm {irr}$ with respect to the loading path. This coincides with the inherent strain method, where the orientation of the laser beam path is of immense importance, cf. [24]. In summary, the values of strains and stresses themselves significantly change with respect to the loading path, but correlate to one another when taking into account the movement of the laser beam.

Fig. 16

Equivalent irreversible strain ${\overline{\varepsilon }}^\mathrm {irr}$ (analogous to von Mises stress) of the virtually extracted final re-solidified part. (Color figure online)

6 Conclusion

In this contribution we presented a three dimensional and thermomechanically consistent fully coupled framework for the simulations of Selective Laser Melting processes based on a phase transformation model. The different states of the material—powder, molten and re-solidified—are explicitly taken into account with the respective mass densities, where the mass fractions are determined via homogenisation and energy minimisation. The phase distribution is not coupled one-to-one to the temperature distribution, e.g. the melting point, but is a result of the calculated distribution of the mass fractions which is defined within the minimisation problem. Furthermore, we consider the volume change during the changes of the material state through physically sound motivated transformation strains. In addition, further inelastic strain contributions are considered, i.e. a viscous strain in the molten phase and a plastic strain in the re-solidified phase, which are derived via dissipation functionals. Moreover, a thermal strain is included in the re-solidified material. This constitutive model is then implemented into the commercial finite element program Abaqus to simulate the SLM process. To model the manufacturing process, further models are applied, e.g. for the laser beam heat source and the layer build-up. Due to the micromechanically properly motivated material model, it is possible to predict the process induced residual stresses and the temperature evolution in a reasonable manner. In a post-processing step, the accumulated inelastic strains present are calculated. This information can be incorporated in a phenomenological model by using an averaged inherent strain tensor.

In future work, the previously derived and computed irreversible strains shall be averaged to an inherent strain tensor and applied to more complex geometries. With the enhanced material model at hand, it is possible to establish an efficient simulation framework to predict residual stresses and the final geometry for larger process simulations. Thus, the idea of the inherent strain method, to model more complex geometries and laser beam paths, without the need for extremely time consuming simulations, can be applied based on the previously shown simulation results. In addition, a mesh optimisation and code optimisation could save further computational time. It shall be emphasised that the material model at hand can also be used for the simulation of other additive manufacturing processes based on metallic powder, for example laser cladding. Furthermore, the used phase transformation model allows the incorporation of multiple solid phases which could preferably form depending on the specific local cooling rate and stress state. In view of the titanium alloy considered here, the related $\alpha$- and $\beta$-phase could also be taken into account. This is supposed to have a significant effect on the residual stress prediction and may therefore improve the results. In addition, the material model can be further enhanced, for example the necessity of a temperature-dependent yield limit for the plastic strains or of temperature-dependent material parameters needs to be investigated. In the long term, due to the highly changing mass densities, it may be necessary to enhance the constitutive framework by using a large strain framework. In view of the model verification, some parameters still need to be identified which requires comparisons to available experimental data. In this way, the material and process parameters can be calibrated accordingly to further improve the simulation results.

Appendices

Appendices

Finite element framework

The discretised weak forms of (3) and (19) shall be derived in detail by considering the contributions from both mechanical equilibrium in the absence of mechanical body forces and heat equation for a thermomechanically fully coupled system as introduced in Sect. 2. The weak form is obtained by multiplying (3) and (19) by an admissible test function for the displacement and temperature field, $\delta {\varvec{u}}$ and $\delta \theta$, respectively. Subsequently, the resulting equations are integrated with respect to the volume of the body ${\mathcal {B}}$. Finally, integration by parts and the divergence theorem are applied. This yields

$$\begin{aligned}&\displaystyle \int _{\partial {\mathcal {B}}} [\varvec{\sigma }\cdot {\varvec{n}}]\cdot \delta {\varvec{u}}\,\mathrm d S_0 -\int _{{\mathcal {B}}} \varvec{\sigma }: \nabla \delta {\varvec{u}}\,\mathrm d V_0 = {0} , \end{aligned}$$

(122)

$$\begin{aligned}&-\displaystyle \int _{\partial {\mathcal {B}}}{\varvec{q}}\cdot {\varvec{n}}\,\delta \theta \,\mathrm dS_0 + \int _{{\mathcal {B}}} {\varvec{q}} \cdot \nabla \delta \theta \,\mathrm d V_0 + \int _{{\mathcal {B}}} \,r^\mathrm {ext}\,\delta \theta \,\mathrm d V_0 \nonumber \\&\quad - \int _{{\mathcal {B}}} \rho \, {{\widetilde{c}}}\, {{\dot{\theta }}}\,\delta \theta \,\mathrm d V_0 + \int _{{\mathcal {B}}} {\mathcal {D}}_\mathrm {mech}\,\delta \theta \,\mathrm d V_0 \nonumber \\&\quad \displaystyle + \int _{{\mathcal {B}}} \theta \, \partial _\theta [\varvec{\sigma }:\dot{\varvec{\varepsilon }} - {\mathcal {D}}_\mathrm {mech}] \,\delta \theta \,\mathrm d V_0 = 0, \end{aligned}$$

(123)

where $\rho$ denotes the current density, and where ${\varvec{n}}$ describes the outward normal unit vector. Using Cauchy’s theorem, surface tractions per unit area are represented by ${{\varvec{t}} = \varvec{\sigma }\cdot {\varvec{n}}}$ and the heat flux vector ${q_{{\varvec{n}}} = - {\varvec{q}}\cdot {\varvec{n}}}$ is analogously defined.

To discretise the problem in space, body ${\mathcal {B}}$ is decomposed into $n_\mathrm {el}$ finite elements, thus

$$\begin{aligned}&\sum _{e=1}^{n_\mathrm {el}} \left[ \, \int _{\partial {\mathcal {B}}^e} \varvec{t} \cdot \delta \varvec{u}^e \, \mathrm {d}S_0 - \int _{{\mathcal {B}}^e} \varvec{\sigma }:\nabla _{\varvec{x}} \, \delta \varvec{u}^e\, {\mathrm {d} V_0} \right] = {0} , \end{aligned}$$

(124)

$$\begin{aligned}&\sum _{e=1}^{n_\mathrm {el}} \left[ \int _{\partial {\mathcal {B}}^e} q_{{\varvec{n}}}\,\delta \theta ^e\,\mathrm dS_0 + \int _{{\mathcal {B}}^e} {\varvec{q}} \cdot \nabla \delta \theta ^e\,\mathrm d V_0 + \int _{{\mathcal {B}}^e} r^\mathrm {ext}\,\delta \theta ^e\,\mathrm d V_0\right. \nonumber \\&\quad \,\left. - \int _{{\mathcal {B}}^e} \rho \, {\widetilde{c}}\, {{\dot{\theta }}}\,\delta \theta ^e\,\mathrm d V_0 + \int _{{\mathcal {B}}^e} {\mathcal {D}}_\mathrm {mech}\,\delta \theta ^e\,\mathrm d V_0 \right. \nonumber \\&\quad \,\left. + \int _{{\mathcal {B}}^e} \theta \, \partial _\theta [\varvec{\sigma }:\dot{\varvec{\varepsilon }} - {\mathcal {D}}_\mathrm {mech}] \,\delta \theta ^e\,\mathrm d V_0 \right] = 0 . \end{aligned}$$

(125)

In addition, the test functions are analogously discretised element-wise

$$\begin{aligned} \delta \varvec{u}^e \approx \sum _{A=1}^{n_\mathrm {en}^u} N_A^u \,\delta \varvec{u}^{eA} , \quad \delta \theta ^e \approx \sum _{C=1}^{n_\mathrm {en}^\theta } N_C^\theta \, \delta \theta ^{eC}\, , \end{aligned}$$

(126)

for each element node ${n_\mathrm {en}}$, where $N_A^u,\, N^\theta _C$ denote the corresponding set of shape functions. For the problem at hand, the same type of shape functions are used for both fields. The contributions $\delta \varvec{u}^{eA}$ and $\delta \theta ^{eC}$ represent the respective values of the test function at the nodes. With these relations at hand, and by additionally defining the assembly operator ${{{\mathbf {\mathsf{{A}}}}}}$, the completely discretised weak form can finally be given, see (92) and (93).