Poroelastic model parameter identification using artificial neural networks: on the effects of heterogeneous porosity and solid matrix Poisson ratio

Abstract

Predictive analysis of poroelastic materials typically require expensive and time-consuming multiscale and multiphysics approaches, which demand either several simplifications or costly experimental tests for model parameter identification.This problem motivates us to develop a more efficient approach to address complex problems with an acceptable computational cost. In particular, we employ artificial neural network (ANN) for reliable and fast computation of poroelastic model parameters. Based on the strong-form governing equations for the poroelastic problem derived from asymptotic homogenisation, the weighted residuals formulation of the cell problem is obtained. Approximate solution of the resulting linear variational boundary value problem is achieved by means of the finite element method. The advantages and downsides of macroscale properties identification via asymptotic homogenisation and the application of ANN to overcome parameter characterisation challenges caused by the costly solution of cell problems are presented. Numerical examples, in this study, include spatially dependent porosity and solid matrix Poisson ratio for a generic model problem, application in tumour modelling, and utilisation in soil mechanics context which demonstrate the feasibility of the presented framework.

1 Introduction

A poroelastic medium consists of a solid porous material (solid matrix) interacting with fluid percolating its pores. Having a pore scale much smaller than the average size of the body, even in the most idealised cases, it is computationally expensive to work with a model including all geometrical details and solve the solid-fluid interaction problem via Direct Numerical Simulation (DNS). This issue imposes the need to reduce the complexity/order of the model, which can be carried out employing multiscale approaches. Phenomenological methods either consider only the macroscale behaviour (e.g. Biot’s theory of poroelasticity [1]) or include upscaling techniques such as volume averaging [2, 3]. They provide the same macroscale governing equations that include some characteristic parameters. However, direct relationships between macro- and microscale properties are not considered.

A detailed comparison between different upscaling approaches is provided in [4]. The average-field theory is based on volume average of microscale strains and stresses which results in the effective properties that characterise macroscale response of the medium. This approach can be extended to a nonlinear constitutive behaviour of the sub-phases, however, the coefficients are typically not entirely related to the underlying microstructure [5,6,7].

In contrast, asymptotic homogenisation [8,9,10], which results in the same macroscale equations as the mentioned phenomenological methods, provides analytical relationships between their coefficients and underlying microscale properties, allowing for much simpler material characterisation tests. The calculation of the mentioned mathematical relationships has recently been carried out for a wide range of microscale properties in three-dimensions via DNS in [5], which demonstrates the viability of this method in a wide range of applications. This framework is then extended in [10, 11] by solving the actual macroscale system of PDEs via Finite Element Method to visualise the role of Microscale Solid Matrix Compressibility (MSMC). However, it is difficult to apply the above-mentioned framework in the latter studies to more complex problems, e.g. spatially dependent properties, non-linear problems, considering growth and remodelling [9], etc. The reason is that the macroscale coefficients should be calculated several times (because the microscale properties can be varied at each coordinate and time increment), which is a time-consuming process. This motivates us to find an improved alternative to such upscaling techniques.

Data science, together with powerful modern computers, have provided us with the “fourth paradigm” of science, namely, data-driven modelling and computing that its integration into mechanics is becoming increasingly successful. There are several Machine Learning (ML) approaches that are applicable within the field of mechanics and can be found in several descriptive pieces of literature such as [12,13,14]. Here, we make use of the well-known method Artificial Neural Network (ANN) [15] as it is a powerful tool based on interpolation and optimisation techniques aiming at describing the input-output relationship of a provided dataset. This method is inspired by the architecture of the human brain and consists of input and output and some hidden layers of neurons between them. Each layer adopts an arbitrary number (to be determined by sensitivity analysis) of neurons that are connected to the ones in the adjacent layers via some weights (different from weighted residual method) and biases. An activation function is also applied to each neuron to control if a neuron should be active or not so that a highly accurate approximation of a complex non-linear relationship is possible using simple linear or non-linear piece-wise hierarchical interpolations.

In mechanics, Machine Learning (ML) approaches are exploited to replace either the whole or a part (e.g. constitutive equations) of DNS to make the analysis more efficient and accurate (or one of them) [16,17,18,19,20]. Recently, the capabilities of this paradigm were applied to the multiscale analysis of heterogeneous materials in 2D [21,22,23] and 3D [24] [25]. Nevertheless, in the field of poroelasticity, to the best of our knowledge, the potential of ML is not well exploited. This technique is used to estimate some of the poroelastic material parameters based on their response under certain loading conditions via ultrasound tomography such as [26]. In a recent study [27], a Convolutional Neural Network (CNN) is used to bypassing the numerical homogenisation procedure. However, due to the unbounded randomness of this method, and as CNN is based on interpolation, there is the risk of extrapolation. Moreover, Biot’s coefficient and modulus, which are essential properties of Biot’s theory of poroelasticity, and have shown to be highly dependent on porosity and MSMC [5], are assumed to be constant.

In contrast, in asymptotic homogenisation, the unit pressure and dynamic viscosity are non-dimensionalised. Thus, the inputs of the problem could be only porosity and Solid Matrix Poisson Ratio (SMPR) which are non-dimensional and bounded. Moreover, in this technique, the effective properties are determined by solving specified problems derived from a robust analytical upscaling process and are based on microscopic properties.

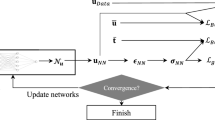
In this study, we aim at bypassing the process of macroscale properties identification derived from asymptotic homogenisation by providing an ANN that efficiently computes the coefficients of the macroscale system of PDEs without solving the cell problems. For this purpose, first, we need to create a sufficiently rich dataset mapping (microscale properties) as the input to the model coefficients at the macroscale (as the output data), which is constructed by solving a certain number of the cell problems derived from asymptotic homogenisation via DNS. This dataset should cover a wide range of Poisson ratios and porosities so that the machine-learnt model be applicable in a wide range of scenarios of interest thus reducing the risk of extrapolation. Next, we choose an appropriate ANN architecture, activation function, and learning rule from sensitivity analysis, considering that the feed-forward process must be fast enough to be called several times. However, as the training procedure itself is a one-time calculation and its efficiency here is not of great importance, we do not investigate more complex and advanced ML techniques such as Long short-term memory (LSTM) for exploding and vanishing gradient problems [28]. The trained network, here, is introduced as a further constitutive relationship to the macroscale system of PDEs and its Finite Element (FE) discretisation via the open-source FE package FEniCS [29] so that, the parameters required to characterise the macroscale behaviour are microscale properties such as porosity and MSMC instead of coefficients computed with a homogenisation technique.

The provided framework is a general one which can be employed in a wide range of applications from soil mechanics to the modelling of biological tissues by choosing appropriate characteristic properties specific to the scenario of interest. This paper focuses on the modelling of poroelastic bodies under different Boundary Conditions (BCs) with spatially dependant porosity and SMPR. We study three types of problems. One with heterogeneous porosity under mechanical pressure and other Neumann and Dirichlet BCs. A second problem class, with similar BCs but different geometry, includes an impermeable object inside a poroelastic one with spatially dependent pore fluid volume fraction. The third problem type with heterogeneous porosity, as well as SMPR, under no mechanical pressure but a constant cavity/pore pressure (resembling drug injection into a tumour mass) is subject to specific displacement and drainage BCs. The presented results demonstrate the feasibility of the ANN-supported framework for such complex problems. Furthermore, the importance of flexibly considering additional aspects in poroelastic problems is highlighted. In the present discussion an isotropic solid matrix and rotational invariance of the cell geometry with respect to permutation of the three orthogonal axes are assumed.

The remainder of the work is organised as follows. In the next section, we introduce the governing equations derived from asymptotic homogenisation together with the variational formulation of the cell problems. We discuss the advantages and downsides of the described upscaling process together with the application of ANN to bypass the process of solving the cell problems derived from homogenisation in Sect. 3. This is followed by providing a training dataset, mentioning the ANN features and architecture, and testing the trained network. In Sect. 4, we apply the latter into the macroscale system of PDEs as an additional relationship which is followed by solving poroelastic problems using the provided framework. The concluding remarks and future perspective are presented in Sect. 5.

2 Governing equations

In this section, for the reader’s convenience and understanding, the basic equations for poroelastic media derived from asymptotic homogenisation that are originally developed in [8] and revisited in [9, 10] are recalled. in addition to the mentioned equations, we exploit the cell problems derived from asymptotic homogenisation to provide a training dataset for ANN.

2.1 Multiscale technique

Let us assume that the poroelastic medium has the average pore size d much smaller than the medium size L (e.g. as shown in Fig. 1). Its solid matrix is linear elastic interacting with incompressible Newtonian fluid that percolates its pores with no-slip boundary condition on the solid-fluid interface.

At this stage, non-dimensionalisation with respect to appropriate characteristic quantities in terms of leng- th scales and velocity fields is carried out as in [8]. For example,

$$\begin{aligned} {\varvec{x}}=L{\varvec{x}}', \quad {\varvec{v}}=\frac{Cr^2}{\mu _c}{\varvec{v}}',\quad \mu =\mu _c \mu ', \quad {\mathbb {C}}=CL {\mathbb {C}}', \end{aligned}$$

(1)

where CL, r, and $\mu _c$ are characteristic pressure, pore radius, and fluid dynamic viscosity, respectively.

Fig. 1

A poroelastic medium on the right which is assumed to be constructed from periodic microscale cells such as the one on the left. The solid matrix is the black part and the fluid phase is the blue one. (Color figure online)

A very small length scale separation parameter $\epsilon =d/L \ll 1$ allows to make use of asymptotic homogenisation technique. We assume that ${\varvec{x}}$ and ${\varvec{y}}$ (${\varvec{y}}={\varvec{x}}/\epsilon$) indicate two formally independent macroscale and microscale spatial variables, respectively. Then, the differential operators transform into two independent ones for macroscale and microscale as

$$\begin{aligned} \nabla \rightarrow \nabla _{{\varvec{x}}}+\frac{1}{\epsilon } \nabla _{{\varvec{y}}} \end{aligned}$$

(2)

which separates the problem into two scales.

Equating the coefficients of $\epsilon ^0$ and $\epsilon ^1$, by replacing every field by its power of series representation, $\psi _{\epsilon }({\varvec{x}},{\varvec{y}})=\sum _{l=0}^{\infty }\psi ^{(l)}({\varvec{x}},{\varvec{y}})\epsilon ^ l$, yields zero-th and first order equations which are the principal ones of the upscaling process. The first result of these equations is that the leading order hydrostatic pressure $p^{(0)}$ and solid displacement ${\varvec{u}}^{(0)}$ are microscale independent (locally constant) and could be referred to as macroscale variables.

As the relative fluid velocity and the solutions of the cell problems (will be defined later) are not constant at the microscale, we apply the integral average

$$\begin{aligned} \left\langle \psi \right\rangle _k= \frac{1}{|\varOmega |}\int _{\varOmega _k}\psi ({\varvec{x}},{\varvec{y}})\,\text {d}{\varvec{y}} \quad k=f,s, \end{aligned}$$

(3)

to exploit the acquired equations in the homogenisation process and macroscale. Following complex mathematical machinery, assuming ${\varvec{y}}$-periodicity, and no-growth limit [9], the closed differential problem governing the macroscale is obtained as

$$\begin{aligned} \displaystyle \nabla _{{\varvec{x}}}\cdot {\mathsf {\varvec{\tau }}}_E&={\varvec{0}}, \end{aligned}$$

(4)

$$\begin{aligned} {\mathsf {\varvec{\tau }}}_E{:}&= {\tilde{\mathbb {C}}}\, {:}\, {\varvec{\varepsilon }}-\tilde{{\mathsf {{\varvec{\alpha }}}}}p^{(0)} \end{aligned}$$

(5)

$$\begin{aligned} {\dot{p}}^{(0)}&=-M[\,\tilde{{\mathsf {{\varvec{\alpha }}}}}\, {:}\, \dot{{\varvec{\varepsilon }}} + \nabla _{{\varvec{x}}}\cdot {\varvec{v}}_{rf}] \end{aligned}$$

(6)

$$\begin{aligned} {\varvec{v}}_{rf}&=-\varvec{{\mathsf {K}}} \nabla _{{\varvec{x}}}p^{(0)}. \end{aligned}$$

(7)

where ${\mathsf {\varvec{\tau }}}_E$ and ${\varvec{v}}_{rf}$ indicate effective stress and relative fluid velocity. ${\varvec{\varepsilon }}$ is the solid strain define usually as

$$\begin{aligned} {\varvec{\varepsilon }}= \frac{1}{2} \left[ \nabla _{{\varvec{x}}}{\varvec{u}}^{(0)} + [\nabla _{{\varvec{x}}}{\varvec{u}}^{(0)}]^t \right] \end{aligned}$$

(8)

This system of PDEs is characterised by some coefficients, namely, effective elasticity tensor, Biot coefficient and modulus, and hydraulic conductivity, that are defined, respectively, as

$$\begin{aligned} \tilde{{\mathbb {C}}}{:}&=\left\langle {\mathbb {C}}+{\mathbb {C}}{\mathbb {M}}\right\rangle _s, \quad \tilde{{\mathsf {{\varvec{\alpha }}}}}{:}=\phi \varvec{{\mathsf {I}}} - {{\,\mathrm{Tr}\,}}{\left\langle {\mathbb {M}}\right\rangle _s}, \\ M{:}&=-\frac{1}{\left\langle {{\,\mathrm{Tr}\,}}{\varvec{{\mathsf {Q}}} }\right\rangle _s}, \quad \quad \varvec{{\mathsf {K}}} {:}= \left\langle \varvec{{\mathsf {W}} } \right\rangle _f, \end{aligned}$$

where ${\mathbb {C}}$ and $\phi$ indicate the elasticity tensor of solid matrix and porosity (i.e. volume fraction of fluid phase), respectively.

From the asymptotic homogenisation technique developed in [8] and revisited in [9], the fourth rank tensor ${\mathbb {M}}$ and the second rank tensors $\varvec{{\mathsf {Q}}}$ and $\varvec{{\mathsf {W}}}$ are the solutions of the following systems of PDEs, respectively.

$$\begin{aligned} \nabla _{{\varvec{y}}} \cdot ({\mathbb {C}} \xi _{{\varvec{y}}} ({\mathcal {A}}))&={\varvec{0}} \quad \text {in}\,\,\ \varOmega _s \end{aligned}$$

(9)

$$\begin{aligned} ({\mathbb {C}} \xi _{{\varvec{y}}} ({\mathcal {A}})) {\varvec{n}} + {\mathbb {C}} {\varvec{n}}&={\varvec{0}} \quad \text {on}\,\,\, \varGamma \end{aligned}$$

(10)

$$\begin{aligned} \left\langle {\mathcal {A}}\right\rangle _s&={\varvec{0}}, \end{aligned}$$

(11)

$$\begin{aligned} \nabla _{{\varvec{y}}}\cdot \left( {\mathbb {C}}\xi _{{\varvec{y}}} ({\varvec{a}})\right)&={\varvec{0}}\quad \quad \text {in}\,\,\varOmega _s \end{aligned}$$

(12)

$$\begin{aligned} \quad ({\mathbb {C}}\xi _{{\varvec{y}}} ({\varvec{a}})){\varvec{n}}+{\varvec{n}}&={\varvec{0}}\quad \quad \text {on}\,\,\varGamma \end{aligned}$$

(13)

$$\begin{aligned} \left\langle {\varvec{a}} \right\rangle _s&={\varvec{0}} , \end{aligned}$$

(14)

$$\begin{aligned} \nabla ^2_{{\varvec{y}}}{\varvec{{\mathsf {W}}} }^{\mathsf {T}}-\nabla _{{\varvec{y}}}{\varvec{P}}+\varvec{{\mathsf {I}}}&={\varvec{0}}\quad \text {in}\,\,\varOmega _f\end{aligned}$$

(15)

$$\begin{aligned} \nabla _{{\varvec{y}}}\cdot {\varvec{{\mathsf {W}}} }^{\mathsf {T}}&={\varvec{0}}\quad \text {in}\,\,\varOmega _f\end{aligned}$$

(16)

$$\begin{aligned} \varvec{{\mathsf {W}}}&={\varvec{0}}\quad \text {on}\,\,\varGamma \end{aligned}$$

(17)

$$\begin{aligned} \left\langle {\varvec{P}} \right\rangle _f&={\varvec{0}} . \end{aligned}$$

(18)

Where $\varOmega _s$, $\varOmega _f$, $\varGamma$, ${\mathcal {A}}$, and ${\varvec{a}}$ represent the solid and fluid domains, their interface, a third rank tensor and a vector, respectively. ${\varvec{n}}$ is the inward unit vector normal to the solid-fluid interface $\varGamma$, and

$$\begin{aligned} {\mathbb {M}}{:}=\xi _{{\varvec{y}}} ({\mathcal {A}}), \quad \varvec{{\mathsf {Q}}} {:}=\xi _{{\varvec{y}}} ({\varvec{a}}), \end{aligned}$$

(19)

with

$$\begin{aligned} \xi _{{\varvec{y}}}(\bullet ) = \frac{1}{2}\left[ \nabla _{{\varvec{y}}}(\bullet )+[\nabla _{{\varvec{y}}}(\bullet )]^t\right] . \end{aligned}$$

(20)

${\varvec{P}}$ is an auxiliary vector that encodes microscale information by relating the first order hydrostatic pressure to $\nabla _{{\varvec{x}}} p^{(0)}$ ($p^{(1)}=-{\varvec{P}}\cdot \nabla _{{\varvec{x}}}p^{(0)}$), and $\varvec{{\mathsf {I}}}$ is the second rank identity tensor.

In the following, we take the approach that was developed in [5, 9] to solve the above-mentioned cell problems via the finite element method and determine the coefficients of the macroscale system PDEs.

2.2 Solid cell problems

The system of Eqs. (9)–(11) is rewritten component-wise as follows

$$\begin{aligned} \frac{\partial }{\partial y_{j}}\left( C_{ijkl} M_{lk\nu \gamma }\right) =0&\quad \text {in}\,\,\varOmega _s\end{aligned}$$

(21)

$$\begin{aligned} C_{ijkl}M_{lk\nu \gamma }n_{j}=-C_{ij\nu \gamma }n_{j}&\quad \text {on}\,\,\varGamma \end{aligned}$$

(22)

$$\begin{aligned} \left\langle A_{ijk}\right\rangle _s=0\,\,\,\, \forall \,\, i,j,k&=1\ldots 3. \end{aligned}$$

(23)

The solution of the problem ($M_{lk\nu \gamma }$) can be obtained, using Voigt notation by concatenating the average solution (strain components) of six linear elastic-type cell problems that are achieved by fixing the couple of indices $(\nu , \gamma )$.

Assuming that the elastic matrix is isotropic at the pore scale, we have the following Neumann boundary conditions on $\varGamma$ for each problem

$$\begin{aligned} \nu \gamma =11{:}\, \,&{\varvec{f}}=\lambda {\varvec{n}} + 2 \mu n_1{\varvec{e_1}} \end{aligned}$$

(24)

$$\begin{aligned} \nu \gamma =22{:}\, \,&{\varvec{f}}=\lambda {\varvec{n}} + 2 \mu n_2{\varvec{e_2}} \end{aligned}$$

(25)

$$\begin{aligned} \nu \gamma =33{:}\, \,&{\varvec{f}}=\lambda {\varvec{n}} + 2 \mu n_3{\varvec{e_3}} \end{aligned}$$

(26)

$$\begin{aligned} \nu \gamma =23{:}\, \,&{\varvec{f}}=\mu ( n_3{\varvec{e_2}}+n_2{\varvec{e_3}}) \end{aligned}$$

(27)

$$\begin{aligned} \nu \gamma =13{:}\, \,&{\varvec{f}}= \mu ( n_3{\varvec{e_1}}+n_1{\varvec{e_3}} ) \end{aligned}$$

(28)

$$\begin{aligned} \nu \gamma =12{:}\, \,&{\varvec{f}}=\mu ( n_2{\varvec{e_1}}+n_1{\varvec{e_2}}) \end{aligned}$$

(29)

Where $n_1$, $n_2$, $n_3$ are the components of the inward unit vector normal to the interface $\varGamma$, $\lambda$ and $\mu$ are the Lamé constants derived from ${\mathbb {C}}$, and ${\varvec{e_1}}$, ${\varvec{e_2}}$ and ${\varvec{e_3}}$ are the standard unit vectors in the Cartesian coordinate system. At this stage, we can describe the auxiliary problems presented in system of PDEs (9)–(11) which represent six linear elastic problems in the solid phase of the cell under the Neumann BCs in Eqs. (24)–(29) and periodic conditions on $\partial \varOmega _s \setminus \varGamma$.

The weak form of such an elastic problem reads

$$\begin{aligned} 0 =&\int _{\varOmega _s} {\mathsf {\varvec{\tau }}} {:} (\nabla _{{\varvec{y}}} \delta {\varvec{u}}) \;\mathrm{d}\varOmega - \int _{\varGamma } {\varvec{f}} \cdot \delta {\varvec{u}} \;\mathrm{d}\varGamma \qquad \forall \;\delta {\varvec{u}} \end{aligned}$$

(30)

where ${{\mathsf {\varvec{\tau }}}}$ is the Cauchy stress tensor and $\delta {\varvec{u}}$ is the virtual displacement.

Moreover, the cell problem (12)–(13) reads as a linear elastic problem equipped with inhomogeneous Neumann interface conditions on $\varGamma$ (a unit inner pressure) and periodic conditions on $\partial \varOmega _s \setminus \varGamma$.

In fact, by choosing a cubic cell with rotational invariance with respect to the three orthogonal axes and an isotropic solid matrix, the effective elasticity tensor with cubic symmetry is obtained. This allows to conduct the analysis of the elastic moduli in terms of the effective Young’s modulus, Poisson’s ratio and shear modulus $E_p$, $\nu _p$, and $\mu _p$, respectively, which are related to the independent components of $\tilde{{\mathbb {C}}}$, namely, ${\tilde{C}}_{11},{\tilde{C}}_{12}, {\tilde{C}}_{44}$ via the following relationships [5, 6, 30]

$$\begin{aligned} E_p&=\frac{{\tilde{C}}_{11}({\tilde{C}}_{11}+{\tilde{C}}_{12})-2{\tilde{C}}^2_{12}}{{\tilde{C}}_{11}+{\tilde{C}}_{12}} \end{aligned}$$

(31)

$$\begin{aligned} \nu _p&=\frac{{\tilde{C}}_{12}}{{\tilde{C}}_{11}+{\tilde{C}}_{12}} \end{aligned}$$

(32)

$$\begin{aligned} \mu _p&={\tilde{C}}_{44}. \end{aligned}$$

(33)

2.3 Fluid cell problems

The system of Eqs. (15)–(17) can be rewritten component-wise as follows

$$\begin{aligned}&\mu \frac{\partial W_{ji}}{\partial y_k \partial y_k} - \frac{\partial P_i}{\partial y_j} + \delta _{ij} =0 \quad \text {in}\,\,\varOmega _f \end{aligned}$$

(34)

$$\begin{aligned}&\frac{\partial W_{ji}}{\partial y_j} = 0 \quad \text {in}\,\,\varOmega _f \end{aligned}$$

(35)

$$\begin{aligned}&W_{ij}=0 \quad \text {on}\,\,\varGamma . \end{aligned}$$

(36)

This problem corresponds to three Stokes’ problems for $i=1, 2, 3$. However, since a geometry with rotational invariance with respect to the three orthogonal axes is chosen, the solution of this problem can be obtained by solving, for example, by $i=1$ only, i.e.

$$\begin{aligned}&\nabla ^2_{{\varvec{y}}}{\varvec{v}} - \nabla _{{\varvec{y}}} p + {\varvec{e_1}} = {\varvec{0}} \quad \text {in}\,\,\varOmega _f \end{aligned}$$

(37)

$$\begin{aligned}&\nabla _{{\varvec{y}}} \cdot {\varvec{v}} = 0 \quad \text {in}\,\,\varOmega _f \end{aligned}$$

(38)

$$\begin{aligned}&{\varvec{v}}= {\varvec{0}} \quad \text {on}\,\,\varGamma , \end{aligned}$$

(39)

where $p=P_1$. The above problem formally reads as a periodic Stokes’ problem for an incompressible fluid driven by a unit body force directed along ${\varvec{e_1}}$ and the solution ${\varvec{v}}$ is related to the components of the tensor $\varvec{{\mathsf {W}}}$ by the following convention

$$\begin{aligned} v_1=W_{11}=W_{22}=W_{33}. \end{aligned}$$

(40)

Note, that for this specific setting, the other components of $\varvec{{\mathsf {W}}}$ are very small and assumed to be zero.

Finally, in order to solve this problem approximately, the variational formulation of Eqs. (37) to (39) is written as

$$\begin{aligned} 0 =&\int _{\varOmega _f} \nabla _{{\varvec{y}}} {\varvec{v}} {:} \nabla _{{\varvec{y}}} \delta {\varvec{v}} \; \mathrm{d}\varOmega - \int _{\varOmega _f} \nabla _{{\varvec{y}}} \cdot \delta {\varvec{v}} \, p \; \mathrm{d}\varOmega \nonumber \\&+ \int _{\varOmega _f} {\varvec{e_1}} \cdot \delta {\varvec{v}} \; \mathrm{d}\varOmega + \int _{\varOmega _f} \nabla _{{\varvec{y}}} \cdot {\varvec{v}}\,\delta p \; \mathrm{d}\varOmega \qquad \forall \;\delta {\varvec{v}},\,\delta p, \end{aligned}$$

(41)

where $\delta {\varvec{v}}$ and $\delta p$ are test functions.

Having solved the cell problems and determined the coefficients of the macroscale system of PDEs, the macroscale problems can be tackled as is done in [10, 11]. However, it is crucial to know the advantages and limits of this framework and, more importantly, how to overcome the latter, which is the core and novelty of this study.

3 Application of ANN

In this section, we discuss the advantages and downsides of the described upscaling process and introduce the application of ANN to eliminate the limits imposed by the time-consuming process of macroscale properties identification.

The advantages of asymptotic homogenisation can be summarised as

• Existence of analytical relationships between microscale and macroscale properties opening the possibility to study the mutual effects of microscale properties and macroscale response during the analysis;

• Avoids unnecessary experimental tests to determine the macroscale properties;

• Solid matrix elasticity tensor and fluid dynamic viscosity are non-dimensionalised, and the most important inputs (porosity and MSMC) are bounded.

On the other hand, the approach suffers from the following limits

• In the case of heterogeneity of the underlying material properties, we need to determine the macroscale properties at each spatial coordinate which is neither practical not efficient;

• Restriction to linear cases which means that we are limited to small deformations;

• Although considerable effort has been made (e.g. in [9]) the effects of the macroscale response on the physical scale (and consequently microscale) mass, property, and shape change [31] (growth, remodelling and morphogenesis) are not fully considered in the upscaling process.

At this point, it seems that we need to find an alternative approach for determination of macroscale properties to overcome the mentioned limits and to determine the coefficients of macroscale system of PDEs in a fast and reliable way so that we can consider more details of a problem. ANNs are a promising tool for the purpose of determining the relationship between micro and macro scale properties.

In general, the identification of the coefficients of the macroscale system of equations can be summarised by indicating the inputs and outputs. The former consists of solid matrix Young modulus and Poisson ratio, porosity (representing the cell geometry shown in Fig. 1), and fluid dynamic viscosity. The outputs are effective Young modulus, Poisson ratio, and shear modulus as well as Biot modulus and coefficient, and hydraulic conductivity. This transfer can be written as

$$\begin{aligned} f(E, \nu , \phi , \mu )= (E_p, \nu _p, \mu _p, K_{11}, M, \alpha ) \end{aligned}$$

(42)

where due to invariant geometry with respect to permutation of the three orthogonal axes,

$$\begin{aligned}\varvec{{\mathsf {K}}} = \langle W_{11} \rangle _f \varvec{{\mathsf {I}}} = K_{11} \varvec{{\mathsf {I}}}\end{aligned}$$

and

$$\begin{aligned}\tilde{{\mathsf {{\varvec{\alpha }}}}} = \alpha {\mathsf {I}}.\end{aligned}$$

such a transfer can be constructed by means of ANN. Considering that the elasticity tensor and viscosity are non-dimensionalised before the upscaling process (as is shown in Sect. 2.1), one can reduce the above mapping to

$$\begin{aligned} {\bar{f}}(\nu , \phi )= (E'_p, \nu _p, \mu '_p, K'_{11}, M', \alpha ) , \end{aligned}$$

(43)

and enforce the effects of the characteristic values on the outputs of Eq. (43). This not only renders the ANN smaller and more efficient but also avoids extrapolation, which is crucial because ANN is based on interpolation.

An ANN, typically, consists of one input layer, one output layer, and some layers in between which act as an intermediate that determines the output from input data. Each layer has several processors called neurons. The value of each neuron is determined by adding a scalar called bias to the summation of all the neurons of the previous layer, where each one is multiplied by a coefficient called weight, and passing it to the activation function. The latter is a function that determines if a neuron should be active (has a value) or not (zero value) which, in turn, provides a somewhat piece-wise interpolation. In order to reach an accurate prediction of the output, we need to train the network using a dataset of the known values. The ANN training aims at achieving the best weights, and biases, which minimises a distance function called Cost function, of the ANN output and known values. Having a priori training procedure, this is called a supervised ANN.

3.1 Training dataset

In order to train an ANN, first, we need a training dataset which consists of a sufficient number of input sets and their respective output sets. In this study, we create the latter by performing a parametric study in which we change the porosity and solid matrix Poisson ratio. We choose 50 different porosities ranging from 0.082 to 0.783, that correspond to the pore radii of 0.1d and 0.4d (with the steps equal to 0.008), respectively. The same number of Poisson ratios are also chosen to consider the role of solid matrix compressibility spanning from 0.02 to 0.498. In this study, we vary neither solid matrix Young modulus nor fluid dynamic viscosity as the results are non-dimensionalised with respect to their characteristic values in the upscaling process according to Eq. (1). The Young modulus and viscosity are chosen to be the same as the ones in a previous study in the literature [5] ($E=13.5[-]$ and $\mu = 1[-]$) which are non-dimensionalised with arbitrary unit pressure and viscosity. Then, we can validate our training dataset by comparing it with published results. Figure 2 provides the reader with a quick comparison of the results with the ones in [5].

Fig. 2

The non-linear profile of Biot modulus and coefficient derived from microscale properties via asymptotic homogenisation, see [5]

3.2 ANN features and architecture

There are several methods for ANN architecture, features, optimisation, learning etc. in the literature (see, e.g. [32, 33]). The choice of the relevant elements and methods is application dependent. Here, we make use of Deep Neural Network (DNN) with $ReLU(x) = \max (0,x)$ as the activation function. The ANN training process starts from, in this case, a linear Feed Forward which can be expressed as

$$\begin{aligned} z^{(i)}_k&=w^{(i)}_{kj}a^{(i-1)}_j+b^{(i)}_k \end{aligned}$$

(44)

$$\begin{aligned} a^{(i)}_k&=ReLU(z^{(i)}_k) \end{aligned}$$

(45)

where $a^{(i)}_k$ is the value of the k -th neuron in the (i) -th layer, $(i)\quad i \in (0,1,..,L)$ is the number of hidden layers, k and j indicate the number of the neurons in the (i) -th and $(i-1)$ -th layers, respectively.

Having computed the output, we can now calculate the cost function. From a sensitivity analysis Itakura–Saito Distance (ISD) [34] is chosen as the Cost function which reads as

$$\begin{aligned} C&= \frac{1}{n} \sum _m^n \left( \frac{y_m}{a_m^{(L)}} - \log \frac{y_m}{a_m^{(L)}} -1 \right) \end{aligned}$$

(46)

$$\begin{aligned} \nabla _a C&= \frac{1}{n} \left( \frac{a_m^{(L)}- y_m}{(a_m^{(L)})^2} \right) , \end{aligned}$$

(47)

where C, n, $a_m^{(L)}$, $y_m$ are cost function, the number of training pieces of data, ANN output, and known value. $(a_m^{(L)})^2$ is an element-wise square.

Next, an optimisation algorithm to update the weig- hts and biases according to the cost function and complete training cycle is needed. We choose the Adam optimiser as it is based on adaptive estimates of lower-order (first and second) moments [35]. In this algorithm, the weights and biases are updated in each iteration via

$$\begin{aligned} w^{(i)}_{kj}&:=w^{(i)}_{kj}- n_w \frac{{\bar{m}}_w}{\sqrt{{\bar{v}}_w}+ {\bar{\epsilon }}} \end{aligned}$$

(48)

$$\begin{aligned} b^{(i)}_k&:=b^{(i)}_k- n_b \frac{{\bar{m}}_b}{\sqrt{{\bar{v}}_b}+ {\bar{\epsilon }}} \end{aligned}$$

(49)

where $n_w$ and $n_b$ are the learning rates or step size, ${\bar{\epsilon }}$ is a term to improve the numerical stability. ${\bar{m}}_w$, ${\bar{v}}_w$, ${\bar{m}}_b$, and ${\bar{v}}_b$ are defined and updated in each iteration as

$$\begin{aligned} {\bar{m}}_w&:= \frac{m_w}{1-\beta _1^t} \quad \quad \quad \quad {\bar{v}}_w := \frac{v_w}{1-\beta _2^t} \end{aligned}$$

(50)

$$\begin{aligned} {\bar{m}}_b&:= \frac{m_b}{1-\beta _1^t} \quad \quad \quad \quad {\bar{v}}_b := \frac{v_b}{1-\beta _2^t}, \end{aligned}$$

(51)

where t is the number of iteration and $\beta _1$ and $\beta _2$ are exponential decay rates for the moment estimates. Finally, the terms $m_w$, $v_w$, $m_b$, and $v_b$ are defined and updated in each iteration as

$$\begin{aligned} m_w&:=\beta _1 m_w +(1-\beta _1) \frac{\partial C}{\partial w^{(i)}_{kj}} \end{aligned}$$

(52)

$$\begin{aligned} v_w&:=\beta _2 v_w +(1-\beta _2) \left( \frac{\partial C}{\partial w^{(i)}_{kj}}\right) ^2 \end{aligned}$$

(53)

$$\begin{aligned} m_b&:=\beta _1 m_b +(1-\beta _1) \frac{\partial C}{\partial b^{(i)}_k} \end{aligned}$$

(54)

$$\begin{aligned} v_b&:=\beta _2 v_b +(1-\beta _2) \left( \frac{\partial C}{\partial b^{(i)}_k}\right) ^2. \end{aligned}$$

(55)

We choose the initial values of $m_w$, $v_w$, $m_b$, $v_b$, and t equal to zero. In each iteration, after computing the cost function, the parameters are updated from Eq. (55) to (48) until we reach the target accuracy. As $w^{(i)}_{kj}$ is not directly related to C we need to use the chain rule, for example, the following

$$\begin{aligned}&\frac{\partial C}{\partial w^{(i)}_{kj}}= \frac{\partial C}{\partial a^{(L)}_l} \frac{\partial a^{(L)}_l}{\partial a^{(i)}_k} \frac{\partial a^{(i)}_k}{\partial w^{(i)}_{kj}} \end{aligned}$$

(56)

$$\begin{aligned}&\frac{\partial C}{\partial b^{(i)}_k}=\frac{\partial C}{\partial a^{(L)}_l} \frac{\partial a^{(L)}_l}{\partial a^{(i)}_k} \frac{\partial a^{(i)}_k}{\partial b^{(i)}_k}. \end{aligned}$$

(57)

In this study, we use the “gradient” feature of the open-source framework PyTorch [36].

Fig. 3

ANN results showing a good agreement with known upscaling results

Fig. 4

A comparison between the known values out of the upscaling process and ANN results highlights its reliability

Having a comparative look at the outputs, which are the coefficients of macroscale system of PDEs, (see, for instance, Figs. 2, 3, 4, 5) we note that the values are of very different orders of magnitude. For example, the non-dimensional maximum Biot modulus is around 5220 while the one of hydraulic conductivity is 0.012, although they are both significant in material characterisation. Consequently, we normalise the values of all outputs by dividing them by their maximum values (which means they all could range between 0 and 1) and re-scale, after training the network.

Finally, choosing an appropriate ANN architecture is an essential factor that affects the efficiency and accuracy. Here, the architecture is identified by a sensitivity analysis. The training time is not a major concern, as it is a one-time effort, but the size of the network is important because it affects the output computation time. Consequently, we choose the smallest network architecture that provides us with the desired ISD ($1.0^{-6}$), which was three hidden layers with 200 neurons per layer.

3.3 ANN performance

After determining the ANN features and training it, we test the network with a test dataset. The latter is a dataset with values different from the ones in the training dataset to double-check our ANN. For this purpose, we solve the cell problems with the same framework as in Sect. 2.2, this time, for solid matrix Poisson ratios 0.136, 0.251, 0.366, 0.481 each one for pore radii from 0.12 to 0.40 with steps of 0.2 (15 different ones) which correspond to porosities from 0.116 to 0.783.

Moreover, to check the results of a different solid matrix Young modulus, we set $E = 1$ kPa. Thus, as our ANN is trained for the cases with $E' = 13.5$ kPa, which is assumed to be equal to the unit pressure, we need to multiply effective Young, shear, and Biot moduli of ANN output by $E/E'$ to reach the dimensional values. Figures 3, 4, 5 show that the provided ANN is reliable to be introduced to practical problems.

The dimensional value $K_{11}$ shown in Fig. 5b can be obtained by multiplying the dimensionless values by $\frac{d^2}{\mu }$. Consequently, the unit of time can be identified from the unit of fluid dynamic viscosity $\mu$.

Fig. 5

ANN results showing a good agreement with known values out of the upscaling process

4 Macroscale response

This study, so far, was intended to provide a basis for solving several complex problems such as macroscopic heterogeneity of microscale properties, growth, and remodelling of poroelastic media. Here, we focus on the first one and solve a simple problem to demonstrate the application of the provided framework. Heterogeneous porosity is known to affect the macroscale response of porous material [37,38,39], however, the full effects of it are not investigated yet.

4.1 Variational formulation

Table 1 The effective poroelastic properties derived from the underlying microstructural properties

Variational formulation of Eqs. (4) to (7) is necessary to obtain the weakly continuous form of them to visualise the macroscale response via FE method. The weak form is obtained by integrating mentioned equations with respect to the corresponding volume and multiplying them with arbitrary test functions. The latter, respectively, consists of the variation of the macroscale displacement vector field $\delta {\varvec{u}}^{(0)}$ and the variation of the macroscale pressure $\delta p^{(0)}$ applied to Eqs. (4) and (6), which then reads

$$\begin{aligned} {0} =&\int _{{\mathcal {B}}} \left[ \nabla _{{\varvec{x}}}\cdot \varvec{{\tau }}_E\right] \cdot \delta {\varvec{u}}^{(0)} \, \mathrm {d} V \nonumber \\&+ \int _{{\mathcal {B}}} \left[ {\dot{p}}^{(0)} + M\left[ \nabla _{{\varvec{x}}}\cdot {\varvec{v}}_{rf} + \tilde{\varvec{\alpha }}:\dot{{\varvec{\varepsilon }}} \right] \right] \delta p^{(0)} \, \mathrm {d}V \nonumber \\&\quad \forall \;\delta {\varvec{u}}^{(0)},\,\delta p^{(0)}. \end{aligned}$$

(58)

Then, to be able to prescribe or measure surface traction and relative fluid velocity (in the direction of the surface normal vector) we apply the divergence theorem which results in the following form

$$\begin{aligned} {0} =&\int _{\partial {\mathcal {B}}} {\varvec{t}} \cdot \delta {\varvec{u}}^{(0)} \, \mathrm {d}S - \int _{{\mathcal {B}}} \varvec{{\tau }}_E {:} \nabla _{{\varvec{x}}} \, \delta {\varvec{u}}^{(0)}\, \mathrm {d}V \nonumber \\&+ \int _{{\mathcal {B}}} \frac{1}{M} \,{\dot{p}}^{(0)} \, \delta p^{(0)} \, \mathrm {d} V + \int _{\partial {\mathcal {B}}} {\varvec{v}}_{rf} \cdot {\varvec{n}} \, \delta p^{(0)} \, \mathrm {d}S \nonumber \\&- \int _{{\mathcal {B}}} {\varvec{v}}_{rf} \cdot \nabla _{{\varvec{x}}} \, \delta p^{(0)} \, \mathrm {d} V + \int _{{\mathcal {B}}} \tilde{\varvec{\alpha }}:\dot{{\varvec{\varepsilon }}} \, \delta p^{(0)} \, \mathrm {d} V \nonumber \\&\quad \forall \;\delta {\varvec{u}}^{(0)},\,\delta p^{(0)}. \end{aligned}$$

(59)

Furthermore, free drainage can be introduced on a surface by enforcing

$$\begin{aligned} {\varvec{v}}_{rf} = \varvec{{\mathsf {K}}} \frac{p^{(0)}}{\varDelta x} \quad \quad \text {on}\quad \quad S_{fd} \end{aligned}$$

(60)

where $\varDelta x$ is the distance between the surface of free drainage ($S_{fd}$) and the environment which is practically zero but here is a very small number. This could be introduced as a part of the fourth term on the right hand side of Eq. (59). Noteworthy is that if we do not introduce the latter on a boundary surface, an impermeable boundary condition is imposed.

The weak formulation is the starting point for discretising and solving the macroscale problem using FEniCS, more detail regarding FE implementation of the macroscale problem can be found in [10].

Verification

The verification of the FE implementation in FEniCS is done by solving the same problem and acquisition of the same results as in the benchmark part of references [10, 11].

Fig. 6

The mesh setup of the model at macroscale. The elements have quadratic and linear interpolation functions for displacements and pore pressure, respectively

Fig. 7

A representative sketch of the model including the employed conventions such as degrees of freedom. Mechanical pressure and free drainage BC are applied on $\varGamma _{top}$. Displacements on $\varGamma _{sides}$ are free only in z direction while they are zero in all directions on $\varGamma _{bottom}$. The dimensions are $h=15$ m and $b=0.1$ m

4.2 Example: 1D problem with heterogeneous porosity

Let us assume a column of a poroelastic material with spatially dependent porosity (e.g. a column of consolidated soil under self-weight effects after a long time [39]). Note that, such properties could also vary with time, stress level, etc. due to macroscale response, growth, etc. [31] which are the subject of future research. Solid matrix Young modulus and Poisson ratio are assumed to be $E = 15\,$(MPa) and $\nu = 0.3$, respectively, and porosity is assumed $\phi = 0.03z + 0.25[-]$, where z is the axial coordinate varying from 0 at the bottom to 15 m at the top. Figure 6 shows the mesh and geometry setup of the model. The conventions that are used throughout this example such as sides, bottom, degrees of freedom etc. are shown in Fig. 7. For the sake of comparison, we solve similar problems with constant porosities $\phi = 0.7[-]$ (the upper bound), $\phi =0.25[-]$ (the lower bound) and $\phi = 0.475[-]$ (the average). Moreover, the fluid is assumed to be water with dynamic viscosity $\mu _f = 8.9\times 10^{-4}$ Pa.s and the average cell dimension to be $d = 10^{-4}$ m. Table 1 shows the effective poroelastic properties derived from the underlying microstructural properties of the mentioned cases.

The counterplot for the heterogeneous case shows a good agreement with the literature and also with Figs. 3, 4, 5. For example the definite minimum reported in [5] and Fig. 4b can be seen in the last row of Table 1. Moreover, in all the cases, drainage is allowed only from the top surface of the column where a constant mechanical pressure $P_m = 10^4$ Pa in the direction $-z$ is applied. Zero displacements boundary condition is imposed on the bottom surface. We only allow displacements in z (axial) direction of the column so that it resembles a 1D problem.

The load is applied instantly at the beginning of the problem, causing an overpressure which decreases at the top of the column with a high spatial gradient (due to the free drainage condition) as shown in Fig. 9a. The latter drives fluid to percolate through the pores towards the top surface (Fig. 10) resulting in a decrease in the maximum value of pore pressure and its gradient (see, for example, Fig. 9d after 1000 s).

Figures 8, 9, 10 show the solution of all the mentioned problems at different times along the axial direction. The general finding of this example is that introducing non-uniform porosity has considerable effects such as a non-linear settlement profile at $t=1000$ s shown in Fig. 8. This, as expected, does not follow the overall response of any of the cases with constant porosity which highlights the importance of such factors. Furthermore, the profile of settlement ($-u^{(0)}_z$) of the heterogeneous case is close to the one with $\phi =0.25[-]$ at the bottom tending to the one with the highest porosity as we move towards the top of the column which causes a higher polynomial degree of the characteristic relation.

The profile of pore pressure is one of the most important factors to be studied as it has considerable effects on the critical phenomena observed in several disciplines ranging from fracture net pressure [40] and fault reactivation [41] in soil and rock mechanics to abnormal therapeutic agents flow in tumour [42] and rearrangement of its properties [43]. Figure 9 shows the considerable difference that spatially dependent porosity distribution induces. Although similar maximum interstitial hydrostatic pressure of all the cases is shown in Fig. 9a this quantity, as is discussed later, reduces at higher rate in the heterogeneous case than the other ones as shown in Fig. 9d.

Figure 10 shows relative fluid velocity induced by the pore pressure gradient. A specific fluid flow profile can be the final goal of several applications such as controlled drug delivery in biology [44] which imposes the need of gaining a better understanding of the effects of different parameters. As shown in Fig. 10a, after a short time ($t = 1$ (s)), the heterogeneous case demonstrates similar profile to the case of constant high porosity ($\phi = 0.7[-]$) as the considerable pore pressure gradient is located near the top of the column where the porosity is high (see Fig. 9a). However, for longer simulation times, e.g. $t = 100$ s in Fig. 10c, when pore pressure propagates to the height of the model, the profile of relative fluid velocity diverges from the one of $\phi = 0.7[-]$.

Fig. 8

A comparison of the settlements of four cases, with constant and spatially dependent porosities, at four different times. The profile of the heterogeneous case (solid line) is non-linear even after a long time ($t = 1000 s$)

Fig. 9

The pore pressure profile of four cases, with constant and spatially dependent porosities. The heterogeneous case (solid line) shows higher polynomial degree of the characteristic relation. At quasi steady-state ($t=1000s$) the gradient of the pore pressure in the heterogeneous case is very small compared with the other cases as discussed in the Sect. 4.2

Fig. 10

The relative pore fluid velocity profile of the heterogeneous case shortly after the application of load ($t=1s$) is similar to the case with high porosity. However, time passing, it decreases at higher rates compared to other cases

The observed profile of relative fluid velocity and pore pressure motivates to monitor the volume change of fluid. This is possible by computing the volumetric integral of $\nabla \cdot {\varvec{v}}_{rf}$ which, using divergence theorem and for this case could be simplified as

$$\begin{aligned} \varDelta \epsilon _{vrf} = A_{fd} \, \varDelta t \, v_{rf}^d \end{aligned}$$

(61)

where $\varDelta \epsilon _{vrf}$ is the relative fluid volume change in the body of the model in one time increment, $A_{fd}$ is the area of the drainage surface, $v_{rf}^d = {\varvec{v}}_{rf} \cdot {\varvec{n}}$ indicates relative fluid velocity at the mentioned surface in its normal direction which is, in this case, the axial direction of the column (the only nonzero component) and $\varDelta t$ is the time increment. Figure 11a shows the fact that although the fluid volume change rate of heterogeneous case at early times is very high and near the case with $\phi = 0.7[-]$, after passing more or less 500 s it becomes much smaller than for other cases (the fluid volume change is almost constant). The latter, considering Eq. 6, implies that the problem is approaching the steady-state condition which means ${\dot{p}}^{(0)} \rightarrow 0$. Having no external fluid source together with a free drainage surface (which results in no excess pore pressure), the mentioned condition means that the excess pore pressure in the poroelastic body is approaching to zero which is shown in Fig. 12.

Fig. 11

The profile of maximum settlement, which represents the solid volume change, is similar to the one of relative fluid volume change. In the heterogeneous case, both of them become almost constant (indicating the steady-state condition) faster than other cases

Finally, it is important to note that although the stored volume of the fluid in both, heterogeneous case and the one with $\phi =0.475[-]$, are equal, this does not necessarily mean that the fluid volume change and other results should be equal. The reason is that the spatial profile of the coefficients that characterise the macroscale response change non-linearly at different porosities. For example, from Fig. 4b, one can see that not only the profile of Biot modulus is non-linear, but also it can have a definite minimum.

4.3 Example: 3D model of a rock within soil

Let us assume a unit cube of fully saturated soil, with similar material properties as the one in Sect. 4.2, inside which a crystalline spherical rock with radius $r=0.2$ m is located. We assume that the latter is impermeable (as its porosity is very low) and considerably stiff compared to the background soil, so that only rigid body movement is probable. Consequently, the rock is modelled with material properties $\alpha =0$, $K=0$, $M \rightarrow \infty$, $E_p= 60,000$ MPa, and $\nu _p= 0.25$ [45]). The soil has a heterogeneous porosity distribution $\phi =0.25z+0.25[-]$. We also model three more cases (for the sake of comparison) with homogeneous porosities $\phi =0.25[-]$, $\phi =0.375[-]$, and $\phi =0.5[-]$ which are the porosities of the bottom, middle, and the top of the heterogeneous model, respectively. The microscale solid matrix Young modulus and Poisson ratio are $E=15$  MPa and $\nu =0.3$ and the fluid dynamic viscosity and the average microscale cell size are $\mu _f=8.9 \times 10^{-4} \,Pa.s$ and $d=10^{-4}\,m$, respectively. We impose a constant mechanical pressure $P_m = 10$ kPa on the surface at the top of the model ($z=1$ m) in the direction $-z$ where the fluid drainage is free. The latter (drainage) is not allowed from the sides and the bottom of the model as in the 1D problem in Sect. 4.2. Figure 13 shows the geometry and the employed conventions in this example.

Early in the process, the applied load causes a high excess pore pressure in the body that decreases with a high gradient at the free drainage surface as shown in Fig. 14a. Note, that the latter is a Neumann BC which results in a pore pressure that is almost equal to the environment pressure (which is assumed zero) where it is applied. The maximum pore pressure decreases sharply over time in all models creating a profile as shown in Fig. 15. We also note that the heterogeneous case stands below other cases, thus leaving room for targeted optimisation.

Figure 14a shows that, almost instantly after the load application, the pore pressure increases from $z=0$ to $z=0.3$ which is due to the pore pressure concentration around the rock. This behaviour is not observed at later times, such as in Fig. 14b, which will be studied in detail. As time passes, the maximum gradient of the pore pressure decreases and its distribution in the depth of the model is more flat. The pore pressure in the homogeneous cases has inverse relationship with porosity (i.e. the higher the porosity the lower the pore pressure at a specific time after $t=1$). This is due to the direct relation of the porosity with hydraulic conductivity $(\mathrm{m^2/Pa.s)}$ which is one of the parameters controlling the reduction rate of the excess pore pressure. On the other hand, from Fig. 14d and Fig. 15, it is concluded that the heterogeneous porosity distribution imposes higher reduction rate of pore pressure (as in the 1D example) which is one of its essential effects.

In order to study the pore pressure concentration near the rock we provide Fig. 16 which shows the pore pressure along the circumference of the inclusion at the plane $x=0.5$ m. Figure 16a shows the instant pore pressure profile before considerable consolidation occurs, showing that this parameter decreases moving from $z=0.3$ m and 0.7 m to $z=0.5$ m (from the top and bottom towards the middle of the rock) and from $y=0.5$ m to $y = 0.7$ m and 0.3 m. This profile at $t=1$ s is affected by the drainage from the top of the cube creating a profile, as shown in Fig. 16b, that is the highest at the bottom (($\theta =1.5$ rad) and lowest at the top ($\theta =0.5$ rad) showing that, near the rock, fluid flows from the bottom to the sides and the top. The pore pressure concentration results in nominal stress alternation that can, in practical scenarios, induce seismic activities [46] as an example.

Fig. 12

The pore pressure in the body with spatially dependent porosity reduces at higher rates than in the cases with constant porosities

Fig. 13

A representative sketch of the geometry where $b=1$ m and $r=0.2$ m. Zero displacements on $\varGamma _{bottom}$ are imosed in all directions and on $\varGamma _{sides}$ are imposed in x and y directions. Mechanical pressure and free drainage are introduced on $\varGamma _{top}$

The profiles of the settlement (displacements in $-z$ direction in cartesian coordinate system) shown in Fig. 17 have considerable differences with the one in 1D example without inclusion (see Fig. 8). The instant settlement, which reflects the undrained elastic response of the medium, has direct relationship with the porosity which agrees the equation of the maximum instant settlement (of an isotropic and homogeneous 1D problem) $u_{0max} = LP_m/(2\mu _p+\lambda _p)$ where L is the depth of the model, $P_m$ is the mechanical pressure, and $\mu _p$ and $\lambda _p$ are the effective lame constants [11]. Note, that the latter have an inverse relationship with porosity in the cases in this section. At this stage the heterogeneous case remains near the case with $\phi =0.375[-]$. However, as a consequence of consolidation process, after 1 s the mentioned relationship becomes inverse such that the higher the porosity the smaller the settlement (see Fig. 17b). At later times, such as $t=10$ s in Fig. 17c, when the settlement profile is similar to its profile in the steady-state, the case with spatially dependent fluid volume ratio at $z=0$ m is similar to the case with low porosity and tends to the case of $\phi = 0.5[-]$ approaching to $z=1$ m. We again highlight that the fluid volume ratio of the mentioned case (heterogeneous) is equal to $\phi =0.25[-]$ at $z=0$ m and to $\phi =0.5[-]$ at $z=1$ m.

Fig. 14

Pore pressure profile in z direction of the model at $x=0.5$ and $y=0.5$. The black arrow in Fig. 14a shows the coordinates indicated on the horizontal axis in the model. Inside the rock there is no pore pressure, so that the lines, here, are only connected linearly from one side to the other side of the rock showing no physical information

Figure 18a shows that moving from $y=0.5$ m to $y=0.7$ m in the plane $x=0.5$ m the effects of the rock exists but to a smaller extent. It is shown in Fig. 18b that at the edge of the mentioned plane ($y=1$ m) this effect is not considerable and the profile is similar to a model without inclusion. This motivates us to study the displacements along the line with $(x,z)=(0.5,0.5)$ in y direction. Figure 19 shows that the displacement decreases monotonically from the circumference of the rock ($y=0.7$ m and $y=0.3$ m), with high gradient, to the edge of the plane ($y=1$ m and $y=0$ m), with small gradient, while it is constant inside the rock. It is noteworthy that the mentioned effect is more notable in the heterogeneous case.

Last but not least, as shown in Fig. 20, the maximum settlement of the model with spatially dependent porosity, initially follows the profile of the case with high porosity while approaching to the steady-state it stands close to the case with average porosity ($\phi =0.375[-]$).

4.4 Example: 2D model of a tumour tissue

In many studies in the literature, the effective properties of poroelastic tissues such as Poisson ratio (PR), Young modulus (YM), and permeability/hydraulic conductivity are either averaged (in macroscale) to be homogeneous and isotropic, or consist of some layers including different effective properties with sharp interfaces [47]. However, using poroelastography and atomic force microscopy methods together with powerful machine learning approaches it is seen that, for example, in tumours, these properties vary gradually from one point in the space to another [48, 49]. There are different and sometimes contradictory reports of the material properties of healthy and malignant tissues. For instance, in some studies, in which they make use of the nanomechanical indentation and topography tests via atomic force microscopy, it is concluded that at the tumour core, where there exist more cancer cells, the tissue shows softer behaviour than the outer part (see, for example, [49] and references therein). It is also reported that the cancer cells are more compressible than the normal ones [50, 51]. However, in several studies, the PR and YM of healthy tissues are considerably less than the cancerous ones [52,53,54]. We embrace the reports that the tissue at the core of a tumour mass have the properties of cancerous tissues while moving towards the outer boundaries its properties tend to the healthy ones [49, 55, 56].

Fig. 15

The maximum pore pressure profile in time

In this study, we make use of the values measured via poroelastography in [48], which provides some contour plots demonstrating non-uniform YM and PR of a tumour mass of a mouse animal. Based on the latter, we assume that PR ranges from 0.45 at the tumour core to 0.3 at the adjacent peripheral region and, for the sake of simplicity, solid matrix YM of 50 kPa is constant in the whole space and time domain. The reported values of the porosities of cancerous tissues are higher compared with the healthy tissues (see, for example, [58, 59] and the references therein). The porosity of the highly cancerous tumour core is assumed 50%, which decreases to 20% at the peripheral region. Having assumed the microscale properties at the inner and outer boundaries of the homogenised model, we choose a linear relationship (for the sake of simplicity) describing how these properties vary depending on the spatial location. The identified microscale properties at every specific coordinate are the inputs of our ANN. The outputs of the latter are the coefficients of the macroscale system of PDEs at the associated coordinate. Furthermore, the adjacent peripheral region of a tumour, where we impose zero displacement BC, is stiffened due to the collagen alignment [49].

Fig. 16

Pore pressure concentration around the inclusion at a plane with $x=0.5$ (m), in the cartesian system, and $r=0.2$ m along $\theta \, (rad)$ (azimuthal direction), in the cylindrical system. Note, that the point $(r,\theta )=(0.2,0)$ is located at $(x,y,z)=(0.5,0.7,0.5)$. The resultant instant fluid flow is from the top and bottom of the rock towards the middle of it ($z=0.5$ m) while after 1 s it is affected by the drainage and is from bottom to the top

Fig. 17

Settlement profile along the depth of the model at $(x,y)=(0.5,0.5)$ showing that it remains constant inside the rock as it is considerably stiffer than the soil. The zero displacements at the bottom of the model are due to the prescribed Boundary Conditions

Table 2 The microscopic properties of the considered models

Table 3 The effective poroelastic properties of the considered models

Fig. 18

Settlement profile at different distances from the centre of the inclusion

Fig. 19

Displacements in z direction along the line with $(x,z)=(0.5,0.5)$ versus the location in y direction showing that the inclusion has greater effects on the heterogeneous case

In order to minimise the effects of the geometry and focus on the material properties, we choose a spherical geometry for the tumour mass with the radius $R_t=1$ cm from which a qualitatively small cavity with the radius $R_c = 0.05 R_t$ is cored out. A continuous injection with a constant cavity pressure $P_c = 1$ kPa is applied on the inner boundary as in [11, 60]. Figure 21 shows the geometry and labelling used throughout this example. Having a cubic microscale cell with rotational invariance with respect to the three orthogonal axes and with an isotropic solid matrix material, as highlighted in [5], the obtained effective elasticity tensor has a cubic symmetry. Considering symmetric geometry and BCs, we reduce the 3D model to a 2D model assuming that the model response in the azimuthal direction represents the polar one. Zero displacements and the cavity pressure applied at $r = R_t$ and $r = R_c$ are the Dirichlet BCs and the free drainage condition at $r = R_t$ is the Neumann BC.

Fig. 20

Maximum settlement of heterogeneous case stays at values near to the case with average porosity when approaching to the steady-state while at short times such as $t<1$  (s) it is near the case with $\phi =0.5[-]$

Fig. 21

A representative sketch of the geometry where $R_c=0.05$ cm and $R_t=1\,$(cm). We impose zero displacements and free drainage on $\varGamma _{outer}$ and the cavity pressure $P_c=1$ kPa on $\varGamma _{cavity}$

We study six cases among which three cases, for the sake of comparison, have homogeneous material properties with the assumptions of tumour core, outer area and their average, respectively, while the fourth/fifth case has non-uniform porosity/Poisson ratio in the radial direction. The sixth case has both heterogeneous porosity and Poisson ratio in the radial direction. Table 2 shows the details of the chosen microscale properties of each model.

The resultant coefficients of macroscale system of PDEs are provided in Table 3 including colourmaps for the heterogeneous cases which agree with the results provided in [5].

Figure 22 shows the profile of pore pressure $p^{(0)}$ along the radius highlighting that at short times (e.g. 1 s) this pressure is distributed only very near to the cavity interface with high spatial gradient where the differences between the models are not considerable. However, when the fluid percolates inside the poroelastic domain, the pore pressure at larger distances from the cavity (e.g. $r = 0.2$ cm) and the effects of different material properties increase. For example, if we consider $p^{(0)}$ at $r = 0.2$ cm in Fig. 22a the differences between the models are not considerable, however, at longer times such as in Fig. 22b they are easily noticeable. The latter highlights that the spatial profile of pore pressure depends on the porosity of the medium such that the models with the heterogeneous porosity (Case4 and Case6) have the highest $p^{(0)}$ followed by Case1 with greatest, Case5 and Case3 with average, and Case2 with the lowest homogeneous porosity. Case4 and Case6 are the first models that reach the steady-state (as in the 1D example in the last section) which is again followed by the same order of homogeneous models. For example, by comparing Fig. 22c and d, one would notice that Case2 with the lowest porosity is the last model that (almost) reaches the steady-state. We do not observe considerable effects of the various solid matrix Poisson ratio, which agrees with Eq. (7). According to the latter hydraulic conductivity is the only parameter relating relative fluid velocity to spatial gradient of pore pressure. This parameter depends on porosity, geometry of the pore (e.g. straight or tortuous), characteristic cell dimension, dynamic fluid viscosity, etc. which, except porosity (the lower porosity, the smaller Hydraulic conductivity [5]), are all the same in our models. Note, that in the previous example, we did not have an external source of cavity pressure so, unlike this example, the final state of the problem was zero pore pressure and relative fluid velocity. The considerable pore pressure difference between the cases with homogeneous and heterogeneous porosity distribution, shown in Fig. 22d, highlight the importance of considering more realistic porosity distribution for real-world problems as this factor has a significant impact on tumour growth and drug delivery inside the tumour mass [42, 43, 57].

Figure 23 shows that the norm of maximum radial relative fluid velocity $v_{rf}^r$ decreases as time passes which agrees with the spatial gradient of the $p^{(0)}$. In other words, at the beginning of the problem, when the pore pressure decreases sharply along the radius, we observe high relative fluid velocity (which is also in agreement with Eq. (7)) and, as time passes and we have smoother pore pressure spatial distribution, the maximum $v_{rf}^r$ decreases and its minimum increases (smoother relative fluid velocity distribution). Moreover, at the beginning of the analyses, when we have $\nabla p^{(0)}$ only near the inner boundary, the profile of relative fluid velocity of Case6 and Case4 is similar to the Case1 which is the upper bound of porosity (as shown in Fig. 22a. This is due to the close values of Hydraulic conductivity of the mentioned cases in that region. However, close to the end of the process, such as in Fig. 22c and d the profile of Case6 and Case4 approach the profile of the average porosity (Case5 and Case3).

Fig. 22

Pore pressure along the radius showing a high spatial gradient near the inner boundary at $t=1$ s. The high difference between the cases with homogeneous porosity (Case1, Case2, Case3, and Case5) and heterogeneous one is an important parameter with special importance in the tumour growth and therapy [57]

Fig. 23

Radial relative fluid velocity (cm/s) along the radius. The maximum value is at the inner boundary where pore pressure spatial gradient is the highest

Fig. 24

Radial displacement distribution (cm) at $\theta = 0$ rad in the radial direction. The negative values at the inner boundary shows swelling of the model. The cases with higher porosity have greater maximum value of displacements

As solid matrix Poisson’s ratio does not affect the Hydraulic conductivity, we do not observe a considerable effect of this parameter on Figs. 22 and 23. This parameter, instead, has a considerable effect on Biot coefficient, Biot modulus, and effective Poisson ratio and small impact on effective Young and shear moduli (see, for example, Table 3) which, in turn, affect the displacement response of the media as shown in Fig. 24. This plot shows that the displacements at short times such as $t = 1$ s in Fig. 24a are considerably smaller than the ones at $t = 1000$ s in Fig. 24d. Moreover, from the radial displacement distribution of the problem at $\theta = 0$ rad (where $\theta$ is the azimuthal coordinate) along the radius at short times one can observe that the effect of heterogeneous solid matrix Poisson ratio is not considerable while at longer times it becomes considerable. In other words, the profiles of Case6 and Case4 (Case5 and Case3) are well separated in Fig. 24c and d.

One important point in Fig. 24 is that the radial displacement at the inner boundary has a negative value that, considering zero displacement BC on the outer boundary, is an indicator of the swelling of the model due to the injection of the fluid which is shown in Fig. 25. The higher pore pressures of Case4 and Case6 shown in Fig. 22 also agree with this observation as it is directly added to the volumetric part of the stress tensor in Eq. (5) (note that $\tilde{{\varvec{\alpha }}}$ is a diagonal second rank tensor). In the models with homogeneous porosity (Case1, Case2, Case3, and Case5) which have the similar pore pressure profiles after 1000 s, as shown in Fig. 22d, the final value of the model volume change directly obeys the Biot coefficient value as it is the pore pressure-displacement coupling term (i.e. the more the Biot coefficient, the more the change in the volume due to the fluid injection).

Another effect of a compressible solid matrix is more “deviation from isotropy” ($\mu _p/\mu _{iso}$) introduced in [11] (and in different notation in [6]) which is the ratio of the effective shear modulus derived from effective elasticity tensor (which is anisotropic with cubic symmetry) to an isotropic shear modulus calculated from effective Young modulus and Poisson ratio with isotropy assumption ($\mu _{iso} = E_p/2(1+\nu _p)$). It is shown in [11] that the more compressible the solid matrix the more the deviation from isotropy which results in a more deviation from homogeneous displacement distribution in azimuthal direction. Note, that the porosity can also affect this parameter. Figure 26 shows the difference between the radial displacements at $\theta = 45$ deg and $\theta = 0$ deg at the inner boundary ($r = 0.05$ cm) along the time. From this plot and the ones provided in Fig. 24 and by comparing, on the one hand, Case6 and Case4 and, on the other hand, Case5 and Case3, it could be concluded that the effect of spatially dependent solid matrix Poisson ratio is larger when we have heterogeneous porosity (i.e. the difference between Case6 and Case4 is more than the one of Case5 and Case3).

5 Concluding remarks and future work

In this study, we have presented a computational framework using Artificial Intelligence (AI) to identify the macroscale parameters of poroelastic media in an efficient approach. In particular, we have provided an ANN which gives the coefficients of the macroscale system of PDEs from microscale properties in almost real-time (0.003 s). We have trained the network by a dataset of known values which is acquired by solving numerous cell problems of asymptotic homogenisation in 3D. This technique uses the non-dimensional form of parameters such as solid Young modulus and fluid dynamic viscosity so that, one can include their effects directly on the outputs of ANN which reduces the inputs to SMPR and porosity for this specific case. As these properties are bounded, we avoid extrapolation, which is a major concern of using an interpolation-based technique such as ANN. Although here, we assume that the solid phase is isotropic, the cell geometry is invariant with respect to permutation of three orthogonal axes, the pores are straight, etc. this framework is readily applicable to more complex cases by providing an appropriate dataset. We introduce the trained ANN as an additional relationship, established at the beginning of the macro-scale simulation, which determines the effective properties of macroscale governing equations of the model at every spatial coordinate.

Fig. 25

Radial displacement at $\theta =0$ deg and $r=0.05$ cm representing the change in the volume of the model along time. Case6 and Case 4 have the most volume change as they have more pore pressure as shown in Fig. 22d

Fig. 26

The difference between the radial displacement at $\theta = 45$ deg and $\theta = 0$ deg and both at $r = 0.05$ cm is and indicator of heterogeneous displacement distribution along azimuthal direction. The maximum value is before reaching the steady-state while the most difference between the models with similar porosity distribution can be measured after reaching steady-state

Heterogeneous porosity is known to affect the macro-scale response of porous material [37,38,39]. However, the full effects of it were not investigated. Hence, we study the macroscale response of two distinct problems with this type of poroelastic material and one with spatially dependent porosity and SMPR. The presented numerical results highlight significant effects of modelling heterogeneous porosity that is not possible to be captured by choosing a constant one for the whole model. The contour plot of the coefficients of the macroscale system of equations show non-linear dependence of them on porosity distribution. We have also provided the profiles of displacements, pore pressure, and relative fluid velocity in space and time as they have significant effects on several phenomena in different disciplines from soil and rock to tumour mechanics [40,41,42,43,44]. In case of the first and second example a poroelastic material with and without inclusion, respectively, is modelled. In both cases, higher polynomial degree of the characteristic relation of the profile of displacements, pore pressure, and relative fluid velocity together with higher drainage temporal rates are the most important consequences of heterogeneous porosity among many others. Moreover, the role of fluid drainage, and consequently heterogeneous porosity, which alters the profile of pore pressure concentration around the spherical impermeable inclusion has been studied. Finally, we have modelled a spherical tumour mass with spatially dependent pore volume fraction and SMPR under constant cavity pressure. Our findings highlight that the value of pore pressure along the radius is significantly higher in the cases with non-uniform porosity (except the zones with prescribed conditions) which results in a greater volume change of the model. The heterogeneous SMPR affects the displacement profile, which is more notable when studying no-uniform radial displacement distribution along the azimuthal direction.

The present work provides a basis to develop a computational framework for multiscale appositional growth [9] and rearrangement of the microstructural features due to the macroscale mechanical and hydraulic response [10, 31]. Extension of the presented data-driven approach to multiscale problems in multi-physics contexts, in particular fluid-solid interaction [61, 62] and neural network supported rheological characterisation of interfaces [63], is the subject of ongoing research.