A hysteretic multiscale formulation for nonlinear dynamic analysis of composite materials

Abstract

A new multiscale finite element formulation is presented for nonlinear dynamic analysis of heterogeneous structures. The proposed multiscale approach utilizes the hysteretic finite element method to model the micro-structure. Using the proposed computational scheme, the micro-basis functions, that are used to map the micro-displacement components to the coarse mesh, are only evaluated once and remain constant throughout the analysis procedure. This is accomplished by treating inelasticity at the micro-elemental level through properly defined hysteretic evolution equations. Two types of imposed boundary conditions are considered for the derivation of the multiscale basis functions, namely the linear and periodic boundary conditions. The validity of the proposed formulation as well as its computational efficiency are verified through illustrative numerical experiments.

1 Introduction

Composite materials have long been utilized in construction and manufacturing in various forms. Nowadays, their scope of applicability spans a large area including, though not limited to the aerospace, automobile and sports industries [28]. Their appeal lies in the fact that composites exhibit some enhanced mechanical properties, such as high strength to weight ratio, high stiffness to weight ratio, high damping, negative Poisson’s ratio and high toughness. In the field of Civil Engineering, composite materials are used either in the form of fiber reinforcing or more recently as textile composites in various applications such as retrofitting and strengthening of damaged structures [11], or supporting cables for cable stayed bridges and high strength bridge decks [26] amongst many others. This vast and multidisciplinary implementation of composites results in the need for better understanding of their mechanical behaviour. Research efforts are oriented towards further improving the mechanical properties of composites while at the same time alleviating some of their disadvantages such as high production/ implementation costs and damage susceptibility [52].

Composites are mixtures of two or more mechanically separable solid materials. As such, they exhibit a heterogeneous micro-structure whose specific morphology affects the mechanical behaviour of the final product [34]. Within this framework, composites are intrinsically multiscale materials since the scale of the constituents is of lower order than the scale of the resulting material. Furthermore, the resulting structure, that is an assemblage of composites, can be of an even larger scale than the scale of the constituents (e.g. a textile strengthened masonry structure [24], a bio-sensor consisting of several nano-wires [44]). Thus, the required modelling approach has to account for such a level of detail that spreads through scales of significantly different magnitude. Throughout this paper, the term macroscopic (or coarse) scale corresponds to the structural level whereas the term microscopic (or fine) scale corresponds to the composite micro-structure properties such as the sizes, morphologies and distributions of heterogeneities that the material consists of.

The derivation of reliable numerical models for the simulation of mechanical processes occurring across multiple scales can aid both the design and/or optimization of new composite systems. Using appropriate modelling assumptions accounting for plasticity and damage [38], estimates on the damage susceptibility of composites can be readily derived and parametric models can be established where micro-material properties are identified based on experimentally measured quantities.

Modelling of structures that consist of composites could be accomplished using the standard finite element method [65]. However, a finite element model mesh accounting for each micro-structural heterogeneity would require significant computational resources (both in CPU power and storage memory). In general, the computational complexity of a finite-element solution procedure is of the order of $O\left( n_{z} ^{3/2} \right)$ where $n_{z}$ is the number of degrees of freedom of the underlying finite element mesh [37]. Therefore, the finite element scheme is usually restricted to small scale numerical experiments of a representative volume element (RVE) [1, 53].

To properly capture the micro-structural effects in the large scale more refined methods have been developed. Instead of implementing the standard finite element method, upscaled or multiscale methods have been proposed to account for such types of problems, therefore significantly reducing the required computational resources [36, 59, 67]. Upscaling techniques rely on the derivation of analytical forms to describe a coarser (i.e. large scale) model based on smaller scale properties [40]. Usually this is accomplished by analytically defining a homogenized constitutive law from the individual constitutive relations of the constituents. Thus, a continuous mathematical model that is problem dependent replaces the fine scale information. On the other hand, multiscale methods use the fine scale information to formulate a numerically equivalent problem that can be solved in a coarser scale, usually through the finite element method [2, 55]. An extensive review on the subject can be found in [33].

In general, multiscale methods can be separated in two groups, namely multiscale homogenization methods [45] and multiscale finite element methods (MsFEMs) [20]. Within the framework of the averaging theory for ordinary and partial differential equations, multiscale homogenization methods are based on the evaluation of an averaged strain and corresponding stress tensor over a predefined space domain (i.e. the RVE) [5]. Amongst the various homogenization methods proposed [25], the asymptotic homogenization method has been proven efficient in terms of accuracy and required computational cost [61].

However, these methods rely on two basic assumptions, namely the full separation of the individual scales and the local periodicity of the RVEs. In practice, the heterogeneities within a composite are not periodic as in the case of fiber-reinforced matrices . In order to adapt to general heterogeneous materials, the size of RVE must be sufficiently large to contain enough microscopic heterogeneous information [3, 54], thus increasing the corresponding computational cost. Furthermore, in an elasto-plastic problem, periodicity on the RVEs also dictates periodicity on the damage induced which could result in erroneous results.

The MsFEM is a computational approach that relies on the numerical evaluation of a set of micro-scale basis functions. These are used to map the micro-structure information onto the larger scale. These basis functions depend both on the micro-structural geometry and constituent material properties. Therefore, the heterogeneity can be accounted for through proper manipulation of the underlying finite element meshes defined at different scales. MsFEM was first introduced in [31] although a variant of the method was earlier introduced in [7] for one-dimensional problems and later for the multi-dimensional case [6]. Along the same lines, domain-decomposition [66] and sub-structuring [68] approaches have also been introduced for the solution of elastic micro-mechanical assemblies.

Although MsFEMs have been extensively used in linear and nonlinear flow simulation analysis [19, 27] the method has not been implemented in structural mechanics problems. This is attributed to the inherent inability of the method to treat the bulk expansion/ contraction phenomena (i.e. Poisson’s effect). To overcome this problem, the enhanced multiscale finite element method (EMsFEM) has been proposed for the analysis of heterogeneous structures [62]. EMsFEM introduces additional coupling terms into the fine-scale interpolation functions to consider the coupling effect among different directions in multi-dimensional vector problems. The method has been also extended to the nonlinear static analysis of heterogeneous structures [63]. Recently, the geometric multiscale finite element method was introduced [14] along with a novel approach for the numerical derivation of displacement based shape functions for the case of linear elastic problems.

However, a limiting factor in a nonlinear analysis procedure, is the fact that the numerical basis functions need to be evaluated at every incremental step due to the progressive failure of the constituents. In [63] the initial stiffness approach is implemented for the solution of the incremental governing equations, thus avoiding the re-evaluation of the basis functions. Nevertheless, this method is known to face serious convergence problems and usually requires a large number of iterations to achieve convergence [46]. The computational cost increases even further for the case of a nonlinear dynamic analysis, where a time integration scheme is also required on top of the iterative procedure [30].

In this work, a modified multiscale finite element analysis procedure is presented for the nonlinear static and dynamic analysis of heterogeneous structures. In this, the evaluation of the micro-scale basis functions is accomplished within the hysteretic finite element framework [56]. In the hysteretic finite element scheme, inelasticity is treated at the element level through properly defined evolution equations that control the evolution of the plastic part of the deformation component. Using the principle of virtual work, the tangent stiffness matrix of the element is replaced by an elastic and a hysteretic stiffness matrix both of which remain constant throughout the analysis.

Along these lines, a multi-axial smooth hysteretic model is implemented to control the evolution of the plastic strains that is derived on the basis of the Bouc–Wen model of hysteresis [10]. The smooth model used in this work accounts for any kind of yield criterion and hardening law within the framework of classical plasticity [38]. Smooth hysteretic modelling has proven very efficient with respect to classical incremental plasticity in computationally intense problems such as nonlinear structural identification [12, 35, 43], hybrid testing [13] and stochastic dynamics [58]. Furthermore, the proposed hysteretic scheme can be extended to account for cyclic damage induced phenomena such as stiffness degradation and strength deterioration [4, 22]. The thermodynamic admissibility of smooth hysteretic models with stiffness degradation has proven on the basis of an equivalence principle to the endochronic theory of plasticity [21]. However, such concepts are beyond the scope of this work.

The present paper is organized as follows. The smooth hysteretic model together with the hysteretic finite element scheme that form the basis of the proposed method are described in Sect. 2. In Sect. 3, the enhanced multiscale finite element method (EMsFEM) is briefly described. In Sect. 4, the proposed hysteretic multiscale finite element method is presented. The method used for the solution of the governing equations at the coarse mesh is described in Sect. 5. The latter is based on the simulation of the governing equations of motion in time using the Newmark direct-integration method [17]. In Sect. 6 a set of benchmark problems is presented to verify both the accuracy and the efficiency of the proposed multiscale formulation.

2 Hysteretic modelling

2.1 Multiaxial modelling of hysteresis

Classical associative plasticity is based on a set of four governing equations, namely the additive decomposition of strain rates, the flow rule, the hardening rule and the consistency condition [38, 49].

The additive decomposition of the total strain rate into reversible elastic and irreversible plastic components [41] is established as:

$$\begin{aligned} \left\{ \dot{\varepsilon }\right\} =\left\{ \dot{\varepsilon }^{{el} } \right\} +\left\{ \dot{\varepsilon }^{{pl} } \right\} \Rightarrow \left\{ \dot{\varepsilon }^{{el} } \right\} =\left\{ \dot{\varepsilon }\right\} -\left\{ \dot{\varepsilon }^{{pl} } \right\} \end{aligned}$$

(1)

where $\left\{ \dot{\varepsilon }\right\}$ is the rate of the total deformation tensor, $\left\{ \dot{\varepsilon }^{{el} } \right\}$ is the rate of the elastic part of the total deformation vector, $\left\{ \dot{\varepsilon }^{{pl} } \right\}$ is the rate of the plastic part of the total deformation vector while $\left( .\right)$ denotes differentiation with respect to time. Based on observations, the unloading stiffness of a plastified material is considered equal to the elastic and thus the following relation holds between the total stress tensor $\left\{ \sigma \right\}$ and the elastic part of the strain rate:

$$\begin{aligned} \left\{ \dot{\sigma }\right\} =\left[ D\right] \left\{ \dot{\varepsilon }^{{el} } \right\} \end{aligned}$$

(2)

where $\left[ D\right]$ is the elastic constitutive matrix.

The plastic deformation rate is determined through the flow rule using the following relation

$$\begin{aligned} \left\{ \dot{\varepsilon }^{pl} \right\} =\dot{\lambda }\frac{\partial \varPhi \left( \left\{ \sigma \right\} ,\left\{ \eta \right\} \right) }{\partial \left\{ \sigma \right\} } \end{aligned}$$

(3)

where $\dot{\lambda }$ the plastic multiplier, $\varPhi$ is the yield surface and $\left\{ \eta \right\}$ the back-stress tensor. The consistency condition or normality rule of associative plasticity [38] is defined as:

$$\begin{aligned} \dot{\lambda }\dot{\varPhi }=0 \end{aligned}$$

(4)

The evolution of the back-stress $\left\{ \eta \right\}$, determines the type of kinematic hardening introduced in the material model during subsequent cycles of loading and unloading and corresponds to the gradual shift of the yield surface in the stress-space. A commonly used type of hardening is the linear kinematic hardening assumption which dictates a constant plastic modulus during plastic loading such that:

$$\begin{aligned} \left\{ \dot{\eta }\right\} =C\left\{ \dot{\varepsilon }^{pl} \right\} \end{aligned}$$

(5)

where $C$ is defined as the hardening material constant. During a plastic process the current stress state, the plastic multiplier and consequently the vector of plastic deformations are readily evaluated through the solution of the nonlinear system of Eqs. (1)–(5) [49].

Substituting Eq. (3) into relation (1) and using relation (2) the following equation is derived:

$$\begin{aligned} \left\{ \dot{\sigma }\right\} =\left[ D\right] \left( \left\{ \dot{\varepsilon }\right\} -\dot{\lambda }\left\{ \alpha \right\} \right) \end{aligned}$$

(6)

where

$$\begin{aligned} \left\{ \alpha \right\} =\partial \varPhi / \partial \left\{ \sigma \right\} \end{aligned}$$

is a $6\times 1$ column vector. From the consistency condition defined in Eq. (4) the following relation is established:

$$\begin{aligned} \dot{\lambda }\dot{\varPhi }=0\Rightarrow \dot{\lambda }\left( \left\{ \alpha \right\} ^{T} \left\{ \dot{\sigma }\right\} +\left\{ b\right\} ^{T} \left\{ \dot{\eta }\right\} \right) =0 \end{aligned}$$

(7)

where

$$\begin{aligned} \left\{ b\right\} ={\partial \varPhi / \partial \left\{ \eta \right\} } \end{aligned}$$

where again $\left\{ b\right\}$ is a $6 \times 1$ column vector.

The plastic multiplier assumes a positive value when the material yields $\dot{\lambda } >$0 and thus relation (7) reduces to:

$$\begin{aligned} \left\{ \alpha \right\} ^{T} \left\{ \dot{\sigma }\right\} +\left\{ b\right\} ^{T} \left\{ \dot{\eta }\right\} =0\Rightarrow \left\{ \alpha \right\} ^{T} \left\{ \dot{\sigma }\right\} =-\left\{ b\right\} ^{T} \left\{ \dot{\eta }\right\} \end{aligned}$$

(8)

Pre-multiplying relation (6) with $\left\{ \alpha \right\} ^{T}$ the following equation is derived:

$$\begin{aligned} \left\{ \alpha \right\} ^{T} \left\{ \dot{\sigma }\right\} =\left\{ \alpha \right\} ^{T} \left[ D\right] \left( \left\{ \dot{\varepsilon }\right\} -\dot{\lambda }\left\{ \alpha \right\} ^{T} \right) \end{aligned}$$

(9)

Substituting Eq. (8) into Eq. (9) the following relation is established:

$$\begin{aligned} -\!\left\{ b\right\} ^{T} \left\{ \dot{\eta }\right\} =\left\{ \alpha \right\} ^{T} \left[ D\right] \left( \left\{ \dot{\varepsilon }\right\} -\dot{\lambda }\left\{ \alpha \right\} \right) \end{aligned}$$

(10)

In classical plasticity the hardening law is defined as a relation between the back-stress tensor and the plastic strain tensor. This relation can be either rate dependent or rate independent. In any case, the back-stress is finally derived as a function of the plastic multiplier $\dot{\lambda }$ and one can write:

$$\begin{aligned} \left\{ \dot{\eta }\right\} =\dot{\lambda }{\fancyscript{G}}\left( \left\{ \eta \right\} ,\varPhi \right) \end{aligned}$$

(11)

where ${\fancyscript{G}}$ is defined herein as the hardening function. Substituting relation (11) into Eq. (10) the following relation is derived:

$$\begin{aligned} -\!\left\{ b\right\} ^{T} \dot{\lambda }{\fancyscript{G}}\left( \left\{ \eta \right\} ,\varPhi \right) =\left\{ \alpha \right\} ^{T} \left[ D\right] \left( \left\{ \dot{\varepsilon }\right\} -\dot{\lambda }\left\{ \alpha \right\} \right) \end{aligned}$$

(12)

Rearranging and solving for the plastic multiplier the following expression is derived:

$$\begin{aligned} \dot{\lambda }=\kappa \left\{ \alpha \right\} ^{T} \left[ D\right] \left\{ \dot{\varepsilon }\right\} \end{aligned}$$

(13)

where $\kappa$ is a scalar that assumes the following form:

$$\begin{aligned} \kappa = {\left( { - \underbrace{{{\left\{ b \right\} }^T}}_{1{\times }6}\underbrace{{\fancyscript{G}}\left( {\left\{ \eta \right\} ,\varPhi } \right) }_{6{\times }1} + \underbrace{{{\left\{ \alpha \right\} }^T}}_{1{\times }6}\underbrace{\left[ D \right] }_{6{\times }6}\underbrace{\left\{ \alpha \right\} }_{6{\times }1}} \right) ^{ - 1}} \end{aligned}$$

(14)

In the case of the elastic perfectly plastic material ${\fancyscript{G}}=0$, and relation (13) coincides with the Karray–Bouc formulation described in [15]. Equations (8)–(13) hold when yielding has occurred, either in the positive or in the negative semi-plane and thus by introducing the following Heaviside functions:

$$\begin{aligned} H_{1} \left( \varPhi \right) = \left\{ \begin{array}{l} 1, \quad \varPhi =0 \\ 0,\quad \varPhi <0 \end{array}\right. ,\quad H_{2} \left( \dot{\varPhi }\right) = \left\{ \begin{array}{l} 1,\quad \dot{\varPhi }>0\\ 0,\quad \dot{\varPhi }<0 \end{array}\right. \end{aligned}$$

(15)

a single relation is established for the plastic multiplier, in the whole domain of the strain tensor:

$$\begin{aligned} \dot{\lambda }=H_{1} H_{2} \kappa \left\{ \alpha \right\} ^{T} \left[ D\right] \left\{ {\dot{\varepsilon }}\right\} \end{aligned}$$

(16)

Instead of describing the cyclic behavior of a material in a step-wise approach considering the domains of non-smooth Heaviside functions [Eq. (15)], Casciati [15], proposed the smoothening of the latter, introducing additional material parameters. According to this approach, the two Heaviside functions are approximated using the following expressions:

$$\begin{aligned} H_{1} =\left| \frac{\varPhi \left( \left\{ \sigma \right\} ,\left\{ \eta \right\} \right) }{\varPhi _{0} } \right| ^{N} ,\quad N\ge 2 \end{aligned}$$

(17)

and:

$$\begin{aligned} H_{2} =\beta +\gamma sgn\left( \dot{\varPhi }\right) \end{aligned}$$

(18)

where $N,\,\beta$ and $\gamma$ are model parameters and $\varPhi _{0}$ is the maximum value of the yield function or yield point. In the special case where $\beta =\gamma =0.5$, the unloading stiffness is equal to the elastic one. The total derivative $\dot{\varPhi }$ in Eq. (18) is derived from the following expression

$$\begin{aligned} \dot{\varPhi }=\frac{\partial {\varPhi }}{\partial \{\sigma \}}\dot{\{\sigma \}}+\frac{\partial {\varPhi }}{\partial \{\eta \}}\dot{\{\eta \}} \end{aligned}$$

(19)

Substituting the plastic multiplier from Eq. (16) into relation (6) and rearranging, the following expression is derived:

$$\begin{aligned} \left\{ \dot{\sigma }\right\} =\left[ D\right] \left( \left[ I\right] -H_{1} H_{2} \left[ R\right] \right) \left\{ \dot{\varepsilon }\right\} \end{aligned}$$

(20)

where $\left[ I\right]$ is the $6 \times 6$ identity matrix and $\left[ R\right]$ is evaluated as:

$$\begin{aligned} \underbrace{\left[ R \right] }_{6{\times }6} = \kappa \underbrace{\left\{ \alpha \right\} }_{6{\times }1}\underbrace{{{\left\{ \alpha \right\} }^T}}_{1{\times }6}\underbrace{\left[ D \right] }_{6{\times }6} \end{aligned}$$

(21)

Matrix $\left[ R\right]$ in equation determines the interaction relation between the components of the stress tensor at yield so that the consistency condition in relation (7) is satisfied.

The corresponding smooth back-stress evolution law can be derived accordingly by substituting Eq. (16) into Eq. (11):

$$\begin{aligned} \left\{ \dot{\eta }\right\} =H_{1} H_{2} {\fancyscript{G}}\left( \left\{ \eta \right\} ,\varPhi \right) \left[ \tilde{R}\right] \left\{ \dot{\varepsilon }\right\} \end{aligned}$$

(22)

where $\big [\tilde{R}\big ]$ is the corresponding hardening interaction matrix defined by the following relation

$$\begin{aligned} \left[ \tilde{R}\right] =\left( -\left\{ b\right\} ^{T} {\fancyscript{G}}\left( \left\{ \eta \right\} ,\varPhi \right) +\left\{ \alpha \right\} ^{T} \left[ D\right] \left\{ \alpha \right\} \right) ^{-1} \left\{ \alpha \right\} ^{T} \left[ D\right] \nonumber \\ \end{aligned}$$

(23)

Equations (20) and (22) define a smooth plasticity model, valid on the overall domain of the material cyclic response. In classical plasticity the transition from the elastic to the inelastic regime, and vice-versa, is controlled through the definition of the yield function and the accompanying hardening law (Fig. 1a). In this work, this transition is smoothed through the introduction of parameters $H_{1}$ and $H_{2}$ thus allowing for a more versatile approach on the hysteretic modelling of materials. In Fig. 1b, the corresponding evolution of the smooth Heaviside functions $H_{1}$ and $H_{2}$ is schematically presented over a full loading-unloading-reloading cycle. It is deduced from Eqs. (17), (18) and (20) that when either $H_{1}$ or $H_{2}$ is equal to zero, the material behaves elastically. The elastic material behaviour corresponds to either small values of the ratio $\varPhi / \varPhi _{0}$ or elastic unloading (in which case $\dot{\varPhi }<0$). On the other hand, when both $H_{1} =1$ and $H_{2} =1$ the material yields.

Fig. 1

a Classical plasticity hysteresis. b Smoothed plasticity hysteresis

Although rate forms are used herein for the sake of formalism, an incremental procedure is implemented for their solution, described in Sect. 5.3. The continuum tangent modulus of the model is readily derived from Eq. (20) as

$$\begin{aligned} \left[ D\right] _{T}=\left[ D\right] \left( \left[ I\right] -H_{1} H_{2} \left[ R\right] \right) \end{aligned}$$

(24)

In the case where a return-mapping scheme is implemented for the solution of Eqs. (20) and (22), a consistent, smooth, modulus can also be defined, following the procedure introduced in [50]. The implications of the selection of an appropriate material modulus in conjunction with the solution procedure implemented are also discussed in [56].

2.2 Test case

The behaviour of the smoothed Heaviside function is presented through an illustrative example. A von-Mises no hardening material is considered with the following material properties, namely $E=210$ GPa, $\sigma _{y} =235$ MPa, $N=2,\,\beta =0.1$ and $\gamma =0.9$. One cycle of imposed strain is applied and the corresponding time history is presented in Fig. 2a. The resulting stress–strain hysteresis loop is presented in Fig. 2b. Due to the small value of parameter $N$, the transition from the elastic to the inelastic regime of the response is smooth. Furthermore, the particular choice of parameters $\beta$ and $\gamma$ with $\beta <\gamma$ results in a bulge hysteresis loop, since the material stiffness at the beginning of unloading is slightly larger than the stiffness of elastic loading.

Fig. 2

a Imposed strain. b Stress–strain hysteresis loop. c Time history of smoothed Heaviside function $H_{1}$. d Evolution of $H_1$ (normalized by the sign of the stress component) with respect to the imposed strain. e Time-history of Heaviside function $H_{2}$, f evolution of $H_2$ with respect to the imposed strain

In Fig. 2c, the time history of the smoothed Heaviside function $H_{1}$ is presented. The graph displays subsequent regions of elastic loading, yielding and elastic unloading corresponding to the stress–strain hysteresis loop presented in Fig. 1b. In Fig. 2d $H_{1}$ is multiplied by the sign of the corresponding normal stress and plotted with respect to the strain. Small values of imposed strain correspond to small values of $H_{1}$ and the elastic response is retrieved in Fig. 2b. Finally, in Fig. 2e and f the evolution of function $H_{2}$ is presented with respect to time and strain respectively. As predicted by the model, in elastic loading it holds that $H_{1} =1$ in both directions of strain. However, during unloading the value of $H_{1}$ turns into $H_{1} =\beta -\gamma =-0.8$. As long as the value $H_{1}$ is not sufficiently small, the stiffness retrieved during unloading is different than that of the elastic loading.

The smooth hysteretic model implemented in this work is based on the Karray–Bouc model of hysteresis [16]. However, instead of relying on the assumptions of von-Mises yield and linear kinematic hardening, the constitutive formulation proposed herein accounts for any type of yield function and kinematic hardening, within the framework of classical rate-independent plasticity. The advantages of a Bouc–Wen type model accounting for deformation dependent hardening were recently highlighted in [47, 60] where the linear kinematic hardening coefficient of the Bouc–Wen model is substituted by a continuous function derived from calibration of experimental data.

2.3 The hysteretic finite element scheme

Substituting Eq. (1) into (2) the following relation is established

$$\begin{aligned} \left\{ \dot{\sigma }\right\} =\left[ D\right] \left\{ \dot{\varepsilon }^{el} \right\} =\left[ D\right] \left( \left\{ \dot{\varepsilon }\right\} -\left\{ \dot{\varepsilon }^{pl} \right\} \right) \end{aligned}$$

(25)

Comparing Eqs. (20) and (25) the following expression for the evolution of the plastic strain component is readily derived:

$$\begin{aligned} \left\{ \dot{\varepsilon }^{pl} \right\} =H_{1} H_{2} \left[ R\right] \left\{ \dot{\varepsilon }\right\} \end{aligned}$$

(26)

where the interaction matrix $\left[ R\right]$ is defined in Eq. (21). The discrete formulation is derived on the basis of the following rate form of the principle of virtual displacements [57]

$$\begin{aligned} \int \limits _{V_{e} }\left\{ \varepsilon \right\} ^{T} \left\{ \dot{\sigma }\right\} dV_{e} =\left\{ d\right\} ^{T} \left\{ \dot{f}\right\} \end{aligned}$$

(27)

where $\left\{ d\right\}$ is the vector of nodal displacements over the finite mesh, $\left\{ f\right\}$ is the corresponding vector of nodal forces and $V_{e}$ is the finite volume of a single element. Only nodal loads are considered herein for brevity however the evaluation of body loads and surface tractions can be treated accordingly. Substituting Eq. (25) into the variational principle (27) the following relation is derived:

$$\begin{aligned} \int \limits _{V_{e} }\left\{ \varepsilon \right\} ^{T} \left[ D\right] \left\{ \dot{\varepsilon }\right\} dV_{e} -\int \limits _{V_{e} }\left\{ \varepsilon \right\} ^{T} \left[ D\right] \left\{ \dot{\varepsilon }^{pl} \right\} dV_{e} =\left\{ d\right\} ^{T} \left\{ \dot{f}\right\} \nonumber \\ \end{aligned}$$

(28)

The following interpolation scheme is considered for the continuous displacement field $\left\{ u\right\}$

$$\begin{aligned} \left\{ u\right\} =\left[ N\right] \left\{ d\right\} \end{aligned}$$

(29)

with the accompanying strain-displacement compatibility relation:

$$\begin{aligned} \left\{ \varepsilon \right\} =\left[ B\right] \left\{ d\right\} \end{aligned}$$

(30)

where $\left\{ d\right\}$ is the vector of displacements at the finite element nodes, $\left[ N\right]$ is the matrix of shape functions, $\left\{ \varepsilon \right\}$ is the vector of strains evaluated at the nodes and $\left[ B\right] =\partial \left[ N\right]$ is the strain-displacement matrix [18]. Substituting Eq. (30) into Eq. (28) the following relation is derived:

$$\begin{aligned} \int \limits _{V_{e} }\left[ B\right] ^{T} \left[ D\right] \left[ B\right] dV_{e} \left\{ \dot{d}\right\} {-}\int \limits _{V_{e} }\left[ B\right] ^{T} \left[ D\right] \left\{ \dot{\varepsilon }^{pl} \right\} dV_{e} =\left\{ \dot{f}\right\} \nonumber \\ \end{aligned}$$

(31)

Next, a set of interpolation functions $\left[ N_{\sigma } \right]$ for the plastic part of the strain $\left\{ \varepsilon ^{pl} \right\}$ is introduced, namely:

$$\begin{aligned} \left\{ \dot{\varepsilon }^{pl} \right\} =\left[ N_{\sigma } \right] \left\{ \dot{\varepsilon }_{cq}^{pl} \right\} \end{aligned}$$

(32)

where $\left\{ \varepsilon _{cq}^{pl} \right\}$ is the vector of plastic strains measured at properly defined collocation points

$$\begin{aligned} \left\{ {\varepsilon _{cq}^{pl}} \right\} = {\left\{ {\begin{array}{*{20}{c}} {{{\left\{ {\varepsilon _{cq}^{pl}} \right\} }^1}}&{{{\left\{ {\varepsilon _{cq}^{pl}} \right\} }^2}}&\ldots&{{{\left\{ {\varepsilon _{cq}^{pl}} \right\} }^{{n_{cq}}}}} \end{array}} \right\} ^T} \end{aligned}$$

(33)

where $n_{cq}$ is the total number of collocation points within the element. Substituting Eq. (32) in relation (31) the following relation is finally derived:

$$\begin{aligned} \left[ k^{el} \right] \left\{ \dot{d}\right\} -\left[ k^{h} \right] \left\{ \dot{\varepsilon }_{cq}^{pl} \right\} =\left\{ \dot{f}\right\} \end{aligned}$$

(34)

where $\left[ k^{el} \right]$ is the elastic stiffness matrix of the element

$$\begin{aligned} \left[ k^{el} \right] =\int \limits _{V_{e} }\left[ B\right] ^{T} \left[ D\right] \left[ B\right] dV_{e} \end{aligned}$$

(35)

and $\left[ k^{h} \right]$ is the hysteretic matrix of the element.

$$\begin{aligned} \left[ k^{h} \right] =\int \limits _{V_{e} }\left[ B\right] ^{T} \left[ D\right] \left[ N_{\sigma } \right] dV_{e} \end{aligned}$$

(36)

Both $\left[ k^{el} \right]$ and $\left[ k^{h} \right]$ are constant and inelasticity is controlled at the collocation points through the accompanying plastic strain evolution equations defined in Eq. (26). The latter is based on the smooth plasticity model presented in Sect. 2.1. However, any type of plastic evolution law can be implemented.

The exact form of the interpolation matrix $\left[ N_{\sigma } \right]$ depends on the element formulation and is also relevant to the stress recovery procedure implemented within the finite element formulation [56]. In this work the collocation points are chosen to coincide with the Gauss quadrature points where stresses are evaluated in standard FEM [65]. Furthermore, smooth evolution equations of the form of relation (26) are implemented. The classical formulation of classical plasticity however can be also used by considering the flow rule defined in relation (3).

Equation (34) is the rate form of the equilibrium equation. Considering zero initial conditions for brevity, rates are dropped and the equilibrium equation of the hysteretic finite element scheme assumes the following form

$$\begin{aligned} \left[ {{k^{el}}} \right] \left\{ d \right\} - \left[ {{k^h}} \right] \left\{ {\varepsilon _{cq}^{pl}} \right\} = \left\{ f \right\} \end{aligned}$$

(37)

Equation (37) is supplemented by the set of nonlinear equations accounting for the evolution of the plastic part of the deformation components defined at the collocation points. These are the rates of the plastic strain vector defined in Eq. (33) and assume the following form at the component level

$$\begin{aligned} {\left\{ {\dot{\varepsilon }_{cq}^{pl}} \right\} ^{iq}} = H_1^{iq}H_2^{iq}{\left[ R \right] ^{iq}}{\left\{ {{\dot{\varepsilon }_{cq}}} \right\} ^{iq}}, \quad iq=1, \ldots , n_{cq} \end{aligned}$$

(38)

Equations (37) and (38) form the governing equations of the hysteretic finite element scheme. The latter is then used to describe the micro-scale nonlinear behaviour of the multiscale scheme introduced in this work.

3 The enhanced multiscale finite element method

3.1 Overview

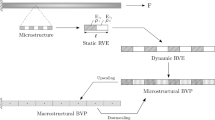
The EMsFEM is briefly presented in this section as a reference for subsequent derivations. In Fig. 3 the FEM computational model of a composite heterogeneous structure is presented. A 2D periodic structure, meshed with quadrilateral plane stress elements is considered for brevity. However, the numerical method presented in this work is also established for the case of 3D meshes. The corresponding applications are presented in Sect. 6. Since EMsFEM is a computational multiscale scheme, no requirements exist on the periodicity of the underlying mesh [39].

Fig. 3

Multiscale finite element procedure

In the MsFEM the structure consists of two layers, namely a fine-meshed layer up to the scale of the heterogeneities and a coarse mesh of the macro-scale where the solution of the discrete problem is performed. In Fig. 3, the fine element mesh consists of 54 quadrilateral micro-elements and 70 micro-nodes while the coarse mesh consists of 6 quadrilateral macro-elements and 12 macro-nodes. Furthermore, two displacement fields are established corresponding to each level of discretization.

Thus, in the fine mesh the displacement of a micro-material point $p$ is described by the micro-displacement vector field

$$\begin{aligned} \left\{ d_{m} \right\} =\left\{ \begin{array}{cc} {u_{m} \left( x,y\right) }&{v_{m} \left( x,y\right) } \end{array}\right\} ^{T} \end{aligned}$$

Accordingly, the macro-displacement field is described by the vector

$$\begin{aligned} \left\{ d_{M} \right\} =\left\{ \begin{array}{cc} {u_{M} \left( x,y\right) }&{v_{M} \left( x,y\right) } \end{array}\right\} ^{T} \end{aligned}$$

In general, the subscript $m$ is used throughout this work to denote a micro-measure while the capital $M$ is used to denote a macro-measure of the indexed quantity.

Instead of implementing a one-step approach, i.e. solving the fine meshed FEM model, a two-step solution procedure is performed. In the first step, a mapping is numerically evaluated that maps the fine mesh within each coarse-element to the corresponding macro-nodes. Next, the solution procedure is performed in the coarse mesh. Finally, the fine-mesh stress and strain history is retrieved by implementing the inverse micro-mapping procedure onto the results obtained on the coarse mesh.

3.2 Numerical evaluation of micro-scale basis functions

The numerical mapping is established by considering each type of coarse element and its corresponding fine mesh as a sub-structure. Considering groups of coarse-elements that bare the same geometrical and mechanical properties these coarse element types can be grouped into sets of representative volume elements (RVE). In this work the term RVE will be used to denote the coarse element together with its underlying fine mesh structure as in [62]. For each RVE a homogeneous equilibrium equation is established considering specific boundary conditions. The solution of this equilibrium problem forms a vector of basis functions that maps the displacement components of the fine mesh within the element to the macro-nodes of the RVE.

In Fig. 4, the RVE finite element mesh of the periodic composite structure (Fig. 3) is presented. This mesh is assigned a local nodal numbering since it is solved as an independent structure.

EMsFEM is based on the assumption that the discrete micro-displacements within the coarse element are interpolated at the macro-nodes using the following scheme:

$$\begin{aligned} u_{m} \left( x_{i} ,y_{i} \right)&= \sum \limits _{j=1}^{n_{Macro} }N_{ijxx} u_{M_{j} } + \sum \limits _{j=1}^{n_{Macro} }N_{ijxy} v_{M_{j} } \nonumber \\ v_{m} \left( x_{i} ,y_{i} \right)&= \sum \limits _{j=1}^{n_{Macro} }N_{ijxy} u_{M_{j} } + \sum \limits _{j=1}^{n_{Macro} }N_{ijyy} v_{M_{j}} \end{aligned}$$

(39)

$$\begin{aligned}&N_{ijxx}= N_{jxx} \left( x_{i}, y_{i} \right) ,\quad N_{ijyy} =N_{jyy} \left( x_{i} ,y_{i} \right) ,\\&N_{ijxy}= N_{jxy} \left( x_{i} ,y_{i} \right) , \quad i=1, \ldots ,n_{micro} \end{aligned}$$

where $u_{m} ,\,v_{m}$ are the horizontal and vertical components of the micro-nodes, $n_{micro}$ is the number of micro-nodes within the coarse element, $n_{Macro}$ is the number of macro-nodes of the coarse element, $\left( x_{i} ,y_{i} \right)$ are the local coordinates of the micro-nodes, $u_{M_{j} } ,\,v_{M_{j} }$ are the horizontal and vertical displacement components of the macro-nodes and $N_{jxx} ,\,N_{jxy} ,\,N_{jyy}$ are the micro-basis functions. In MsFEM as well as the interpolation techniques of the standard displacement based finite element procedure [8] the interpolated displacement fields are considered uncoupled. However in EMsFEM the coupling terms $N_{ijxy}$ are introduced that are more consistent with the observation that a unit displacement in the boundary of a deformable body may induce displacements in both directions within the body.

It can be demonstrated [20, 62] that a necessary and sufficient condition for relations (39) to hold is that the micro-basis functions adhere to the following property

$$\begin{aligned} \begin{array}{*{20}{c}} {\sum \limits _{i = 1}^{n_{Macro}} {{N_{ijxx}} = 1} }&{}{\sum \limits _{i = 1}^{n_{Macro}} {{N_{ijxy}} = 0} } \\ {\sum \limits _{i = 1}^{n_{Macro}} {{N_{ijyx}} = 0} }&{}{\sum \limits _{i = 1}^{n_{Macro}} {{N_{ijyy}} = 1} } \end{array},\quad j = 1, \ldots , n_{Macro}\nonumber \\ \end{aligned}$$

(40)

Further details on the numerical evaluation of the micro-basis functions are given in the Appendix section.

Fig. 4

Finite element mesh of an RVE

Considering the micro to macro-displacement mapping introduced in relation (39), the following equation can be established in the micro-elemental level

$$\begin{aligned} \left\{ d\right\} _{m(i)} =\left[ N\right] _{m(i)} \left\{ d\right\} _{M} \end{aligned}$$

(41)

where $\left\{ d\right\} _{m(i)}$ is the nodal displacement vector of the $i_{th}$ micro-element, $\left[ N\right] _{m(i)}$ contains the micro-basis shape functions evaluated at the nodes of the $i_{th}$ micro-element while $\left\{ d\right\} _{M}$ is the vector of nodal displacements of the corresponding macro-nodes. For the case of micro-element #6 of the coarse-element presented in Fig. 4, the corresponding micro and macro-displacement vectors assume the following form, namely

$$\begin{aligned} \left\{ d\right\} _{m\left( 6\right) } =\left\{ \begin{array}{cccccccc} {u_{m9} }&{v_{m9} }&{u_{m10} }&{v_{m10} }&{u_{m14} }&{v_{m14} }&{u_{m13} }&{v_{m13} } \end{array}\right\} ^{T}\nonumber \\ \end{aligned}$$

(42)

and

$$\begin{aligned} \left\{ d\right\} _{M} =\left\{ \begin{array}{cccccccc} {u_{M1} }&{v_{M1} }&{u_{M2} }&{v_{M2} }&{u_{M6} }&{v_{M6} }&{u_{M5} }&{v_{M5} } \end{array}\right\} ^{T} \end{aligned}$$

(43)

respectively. Variables $u_{mi}$ and $v_{mi}$ in Eq. (42) stand for the horizontal and vertical displacement component of micro-node $i$ while $u_{Mj}$ and $v_{Mj}$ in Eq. (43) are the corresponding macro-displacement components of coarse node $j$. The micro-basis shape function matrix is defined as:

$$\begin{aligned}&\!\!\!\! {\left[ N \right] _{m\left( 6 \right) }}\nonumber \\&= \left[ {\begin{array}{*{20}{c}} {{N_{9,1xx}}}&{}{{N_{9,1xy}}}&{}{{N_{10,1xx}}}&{}{{N_{10,1xy}}}&{}{{N_{14,1xx}}}&{}{{N_{14,1xy}}}&{}{{N_{13,1xx}}}&{}{{N_{13,1xy}}} \\ {{N_{9,1xy}}}&{}{{N_{9,1yy}}}&{}{{N_{10,1xy}}}&{}{{N_{10,1yy}}}&{}{{N_{14,1xy}}}&{}{{N_{14,1yy}}}&{}{{N_{13,1xy}}}&{}{{N_{13,1yy}}} \\ {{N_{9,2xx}}}&{}{{N_{9,2xy}}}&{}{{N_{10,2xx}}}&{}{{N_{10,2xy}}}&{}{{N_{14,2xx}}}&{}{{N_{14,2xy}}}&{}{{N_{13,2xx}}}&{}{{N_{13,2xy}}} \\ {{N_{9,2xy}}}&{}{{N_{9,2yy}}}&{}{{N_{10,2xy}}}&{}{{N_{10,2yy}}}&{}{{N_{14,2xy}}}&{}{{N_{14,2yy}}}&{}{{N_{13,2xy}}}&{}{{N_{13,2yy}}} \\ {{N_{9,3xx}}}&{}{{N_{9,3xy}}}&{}{{N_{10,3xx}}}&{}{{N_{10,3xy}}}&{}{{N_{14,3xx}}}&{}{{N_{14,3xy}}}&{}{{N_{13,3xx}}}&{}{{N_{13,3xy}}} \\ {{N_{9,3xy}}}&{}{{N_{9,3yy}}}&{}{{N_{10,3xy}}}&{}{{N_{10,3yy}}}&{}{{N_{14,3xy}}}&{}{{N_{14,3yy}}}&{}{{N_{13,3xy}}}&{}{{N_{13,3yy}}} \\ {{N_{9,4xx}}}&{}{{N_{9,4xy}}}&{}{{N_{10,4xx}}}&{}{{N_{10,4xy}}}&{}{{N_{14,4xx}}}&{}{{N_{14,4xy}}}&{}{{N_{13,4xx}}}&{}{{N_{13,4xy}}} \\ {{N_{9,4xy}}}&{}{{N_{9,4yy}}}&{}{{N_{10,4xy}}}&{}{{N_{10,4yy}}}&{}{{N_{14,4xy}}}&{}{{N_{14,4yy}}}&{}{{N_{13,4xy}}}&{}{{N_{13,4yy}}} \end{array}} \right] \nonumber \\ \end{aligned}$$

(44)

The $\left( 2n_{micro} \times 1\right)$ vector of nodal displacements of the micro-mesh $\left\{ d\right\} _{m}$ is evaluated as:

$$\begin{aligned} \left\{ d\right\} _{m} =\left[ N\right] _{m} \left\{ d\right\} _{M} \end{aligned}$$

(45)

where in this example

$$\begin{aligned} \left\{ d\right\} _{m} =\left\{ \begin{array}{ccccccccc} {u_{m1} }&{v_{m1} }&{u_{m2} }&{v_{m2} }&{u_{m3} }&{v_{m3} }&{\ldots }&{u_{m16} }&{v_{m16} } \end{array}\right\} ^{T}\nonumber \\ \end{aligned}$$

(46)

and $\left\{ d\right\} _{M}$ is defined in Eq. (43).

Matrix $\left[ N\right] _{m}$ in Eq. (45) is a $32\times 8$ matrix containing the components of the micro-basis shape functions evaluated at the nodal points $\left( x_{j} ,y_{j} \right) , j=1, \ldots , 16$ of the micro-mesh. According to the property introduced in Eq. (40), each column of $\left[ N\right] _{m}$ corresponds to a deformed configuration of the RVE where the corresponding macro-degree of freedom is equal to unity and all of the remaining macro-degrees of freedom are equal to zero.

Deriving micro-basis functions with these properties can be accomplished by considering the following boundary value problem

$$\begin{aligned}&\left[ K\right] _{RVE} \left\{ d\right\} _{m} =\left\{ \emptyset \right\} \nonumber \\&\left\{ d\right\} _{S} =\left\{ \bar{d}\right\} \end{aligned}$$

(47)

where $\left[ K\right] _{RVE}$ is the stiffness matrix of the RVE, $\left\{ d\right\} _{S}$ is a vector containing the nodal degrees of freedom defined at the boundary $S$ of the RVE and $\left\{ \bar{d}\right\}$ is a vector of prescribed displacements. The r.h.s vector in Eq. (47) stands for the zero vector.

The RVE stiffness matrix $\left[ K\right] _{RVE}$ is formulated using the standard finite element method [8]. Thus, $\left[ K\right] _{RVE}$ is assembled by evaluating the contribution of the individual stiffness of each micro-element in the stiffness of the RVE, the latter being considered as a stand-alone structure. In this work, the direct stiffness method [65] is implemented for that purpose. In the example case presented in Fig. 4, the RVE consists of $16$ nodes and $9$ quadrilateral plane stress elements. Therefore, the corresponding $\left[ K\right] _{RVE}$ is a $32 \times 32$ matrix.

Each column of the shape function matrix $\left[ N\right] _{m}$ in Eq. (45) corresponds to a displacement pattern derived from the solution of the linear system introduced in Eq. (47) for a specific set of boundary conditions. Thus, for the example case presented in Fig. 4, eight (8) different prescribed displacement vectors $\left\{ \bar{d}\right\}$ need to be defined and the corresponding solutions need to be performed. In this work, the solution of the boundary value problem established in Eq. (47) is performed using the Penalty method [9, 23].

The type of the boundary conditions implemented for the evaluation of the micro-basis shape functions significantly affects the accuracy of EMsFEM. Four different types of boundary conditions are established in the literature namely linear boundary conditions, periodic boundary conditions, oscillatory boundary conditions with oversampling and periodic boundary conditions with oversampling. In the first case, the displacements along the boundaries of the coarse element are considered to vary linearly. Periodic boundary conditions are established by considering that the displacement components of periodic nodes lying on the boundary of the coarse element differ by a fixed quantity that varies linearly along the boundary of the coarse element. The oscillatory boundary condition method with oversampling considers a super-element of the coarse element whose basis functions are evaluated using the linear boundary condition approach. Finally, the periodic boundary conditions with oversampling combine the oversampling technique with the periodic boundary condition method, thus allowing for the implementation of the latter in non-periodic RVE meshes [39, 63].

In this work, the cases of linear and periodic boundary conditions are considered. An example on the application of the periodic boundary conditions is described in the Appendix, however further details on the procedure implemented for the derivation of the micro-basis functions can be found in [20, 63].

3.3 Macro equivalent micro-nodal forces

The interpolation scheme introduced in Eq. (45) maps the macro-displacement vector to the micro-displacement components of the fine mesh. Through this approximation, the solution of the structural problem can be performed in the coarse mesh. Consequently, the external applied loads have to also be defined in the coarse mesh nodes. Therefore, a procedure is required that maps the external applied loads acting on the micro-mesh to equivalent loads acting on the coarse mesh nodes. By means of equivalence of the potential energy between the macro and the micro-scale [63], the following relation is derived for the equivalent macro-loads

$$\begin{aligned} \left\{ F\right\} _{M\left( i\right) } =\left[ N\right] _{m\left( i\right) }^{T} \left\{ F\right\} _{m\left( i\right) } \end{aligned}$$

(48)

where $\left\{ F\right\} _{M\left( i\right) }$ is the equivalent force vector of the micro-nodal forces $\left\{ F\right\} _{m\left( i\right) }$ of the $i_{th}$ micro-element. Since these equivalent forces are derived in terms of an energy equivalence principle, compatibility within the fine mesh needs to be enforced by calculating a set of “perturbed” micro-forces. The micro-forces, acting on the micro-nodes will result in the correct stress distribution within the fine mesh without altering the displacement assumption along the boundary of the coarse-element.

Therefore, an additive decomposition scheme is enforced where the effect of a micro-force nodal vector $\left\{ f\right\} _p$ acting on a micro-node $p$ is decomposed into the effect of the same force on the fine mesh but considering fixed boundaries and the effect of the macro-equivalent forces on the coarse element (Fig. 5).

Fig. 5

Micro to macro-force equivalence

The local effect of the “perturbed” micro-forces on the micro-mesh is numerically evaluated from the solution of the following equilibrium equation

$$\begin{aligned}&\left[ K\right] _{RVE} \left\{ \tilde{d}\right\} _{m} =\left\{ \tilde{F}\right\} _{m} \nonumber \\&\left\{ \tilde{d}\right\} _{S} =\left\{ \bar{d}\right\} \end{aligned}$$

(49)

where $\left\{ \tilde{F}\right\} _{m}$ is the vector of nodal “perturbed” micro-forces, $\left\{ \tilde{d}\right\} _{m}$ is the corresponding nodal displacement vector, while $\left\{ \tilde{d}\right\} _{S}$ is the vector of imposed boundary conditions $\left\{ \bar{d}\right\}$. The boundary conditions considered are similar to the boundary conditions implemented for the evaluation of the micro to macro mapping [Eq. (47)] [62, 63] .

The evaluation of the “perturbed” micro-displacement vector is crucial for the efficiency of the multiscale scheme and will be further treated in Sect. 5.2 where the numerical aspects of the proposed method are presented. Equivalently, the actual stress field within the micro-element needs to be evaluated taking into account the contribution of both the micro-forces evaluated from the micro to macro-mapping and the “perturbed” forces.

4 The hysteretic multiscale analysis scheme

4.1 Equilibrium in the fine scale

In this work the hysteretic finite element scheme defined by Eqs. (37) and (38) is used to formulate the governing equations of the micro-scale. Thus, at the micro-scale the following relations are defined

$$\begin{aligned} \left[ k^{el} \right] _{m\left( i\right) } \left\{ d\right\} _{m\left( i\right) } -\left[ k^{h} \right] _{m\left( i\right) } \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) } =\left\{ f\right\} _{m\left( i\right) } \end{aligned}$$

(50)

and

$$\begin{aligned} {\left\{ {\dot{\varepsilon }_{cq}^{pl}} \right\} ^{iq}_{m\left( i\right) }} = H_1^{iq}H_2^{iq}{\left[ R \right] ^{iq}}{\left\{ {{\dot{\varepsilon }_{cq}}} \right\} ^{iq}_{m\left( i\right) }},\quad iq=1, \ldots , n_{cq}\nonumber \\ \end{aligned}$$

(51)

where the index $m\left( i\right)$ denotes the corresponding measure of the $i_{th}$ micro-element. Substituting Eq. (41) into Eq. (50) and pre-multiplying with $\left[ N\right] _{m\left( i\right) }^{T}$ the following relation is derived:

$$\begin{aligned} \left[ k^{el} \right] _{m\left( i\right) }^{M} \left\{ d\right\} _{M} -\left[ k^{h} \right] _{m\left( i\right) }^{M} \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) } =\left\{ f\right\} _{m\left( i\right) }^{M} \end{aligned}$$

(52)

where

$$\begin{aligned} \left[ k^{el} \right] _{m\left( i\right) }^{M} =\left[ N\right] _{m\left( i\right) }^{T} \left[ k^{el} \right] _{m\left( i\right) } \left[ N\right] _{m\left( i\right) } \end{aligned}$$

(53)

is the elastic stiffness matrix of the $i_{th}$ micro-element mapped onto the macro-element degrees of freedom while $\left[ k^{h} \right] _{m\left( i\right) }^{M}$ is the corresponding hysteretic matrix of the $i_{th}$ micro-element, evaluated by the following relation:

$$\begin{aligned} \left[ k^{h} \right] _{m\left( i\right) }^{M} =\left[ N\right] _{m\left( i\right) }^{T} \left[ k^{h} \right] _{m\left( i\right) } \end{aligned}$$

(54)

Finally, $\left\{ f\right\} _{m\left( i\right) }^{M}$ in Eq. (52) is the equivalent nodal force vector of the micro-element mapped onto the macro-nodes of the coarse element and is evaluated from Eq. (55) below

$$\begin{aligned} \left\{ f\right\} _{m\left( i\right) }^{M} =\left[ N\right] _{m\left( i\right) }^{T} \left\{ f\right\} _{m\left( i\right) } \end{aligned}$$

(55)

Rearranging terms, Eq. (52) can be cast in the following form

$$\begin{aligned} \left[ k^{el} \right] _{m\left( i\right) }^{M} \left\{ d\right\} _{M}=\left\{ f\right\} _{m\left( i\right) }^{M}-\left\{ f_h\right\} _{m\left( i\right) }^{M} \end{aligned}$$

(56)

where

$$\begin{aligned} \left\{ f_h\right\} _{m\left( i\right) }^{M}=-\left[ k^{h} \right] _{m\left( i\right) }^{M} \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) } \end{aligned}$$

(57)

can be considered as a nonlinear correction to the externally applied load vector $\left\{ f\right\} _{m\left( i\right) }^{M}$.

Equation (52) is a multiscale equilibrium equation involving the displacement vector $\left\{ d\right\} _{M}$ that accounts for the nodal displacements of the coarse-element nodes and the plastic part of the strain tensor $\left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) }$ that is evaluated at collocation points within the micro-scale element mesh. Using the micro-displacement to macro-displacement interpolation relation [Eq. (41)] the micro-element state matrices, namely the elastic stiffness matrix and the hysteretic matrix, defined in Eqs. (35) and (36) respectively are mapped onto their multiscale counterparts $\left[ k^{el} \right] _{m\left( i\right) }^{M}$ and $\left[ k^{h} \right] _{m\left( i\right) }^{M}$.

The derived multiscale elastic stiffness and hysteretic matrices are constant and need only be evaluated once during the analysis procedure. Therefore, the corresponding micro-basis functions introduced in relation (47) are also evaluated once, thus significantly reducing the required computational cost.

4.2 Micro to macro scale transition

Having established the micro-element equilibrium in Eq. (52) in terms of macro-displacements using the micro-basis mapping introduced in Eq. (41), a procedure is required to also formulate the global structural equilibrium equations in terms of macro-quantities. Denoting with a subscript $M$ the corresponding macro-measures over the volume $V$ of the coarse element, the Principle of Virtual Work is established at the coarse scale as

$$\begin{aligned} \int \limits _{V_{M} }\left\{ \varepsilon \right\} _{M}^{T} \left\{ \sigma \right\} _{M} dV_{M} =\left\{ d\right\} _{M}^{T} \left\{ f\right\} _{M} \end{aligned}$$

(58)

where $\left\{ f\right\} _{M}$ is the vector of nodal loads imposed at the coarse element nodes. Equivalently to relation (34) the variational principle of equation (58) gives rise to the following equation:

$$\begin{aligned} \int \limits _{V_{M} }\left\{ \varepsilon \right\} _{M}^{T} \left\{ \sigma \right\} _{M} dV_{M}&= \left[ K^{el}\right] _{CR\left( j\right) }^{M} \left\{ d\right\} _{M}\nonumber \\&-\left[ K^{h} \right] _{CR\left( j\right) }^{M} \left\{ \varepsilon _{cq}^{pl} \right\} _{M} \end{aligned}$$

(59)

where $\left[ K^{el}\right] _{CR\left( j\right) }^{M},\,\left[ K^{h} \right] _{CR\left( j\right) }^{M}$ are the equivalent elastic stiffness and hysteretic matrix of the $j_{th}$ coarse element respectively while $\left\{ \varepsilon _{cq}^{pl} \right\} _{M}$ is the vector of plastic strains defined at the collocation points. Within the multiscale finite element framework, these quantities are not known a priori and need to be expressed in terms of micro-scale measures, thus accounting for the micro-scale effect upon the macro-scale mesh. This is accomplished by postulating that the strain energy of the coarse element is additively decomposed into the contributions of each micro-element within the coarse-element. Thus, the following relation is established:

$$\begin{aligned} \int \limits _{V}\left\{ \varepsilon \right\} _{M}^{T} \left\{ \sigma \right\} _{M} dV= \sum _{i=1}^{m_{el} }\int \limits _{V_{m\left( i\right) } }\left\{ \varepsilon \right\} _{m\left( i\right) }^{T} \left\{ \sigma \right\} _{m\left( i\right) } dV_{\left( i\right) } \end{aligned}$$

(60)

where $\left\{ \varepsilon \right\} _{m\left( i\right) } ,\,\left\{ \sigma \right\} _{m\left( i\right) }$ are the micro-strain and micro-stress field defined over the volume $V_{m\left( i\right) }$ of the $i_\mathrm{th}$ micro-element. Using relation (37), the following equation is established for the r.h.s of equation (60)

$$\begin{aligned}&\sum _{i=1}^{m_{el} }\int \limits _{V_{m\left( i\right) } }\left\{ \varepsilon \right\} _{m\left( i\right) }^{T} \left\{ \sigma \right\} _{m\left( i\right) } dV_{\left( i\right) }\nonumber \\&=\sum _{i=1}^{m_{el} }\left( \left\{ d\right\} _{m\left( i\right) }^{T} \left[ k^{el} \right] _{m\left( i\right) } \left\{ d\right\} _{m\left( i\right) } \right. \nonumber \\&\left. \quad -\left\{ d\right\} _{mi}^{T} \left[ k^{h} \right] _{m\left( i\right) } \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) } \right) \end{aligned}$$

(61)

Substituting relation (45) into relation (61) gives rise to the following expression

$$\begin{aligned}&\sum _{i=1}^{m_{el} }\int \limits _{V_{mi} }\left\{ \varepsilon \right\} _{m\left( i\right) }^{T} \left\{ \sigma \right\} _{m\left( i\right) } dV_{i} =\left\{ d\right\} _{M}^{T}\nonumber \\&\quad \cdot \sum _{i=1}^{m_{el} }\left( \left[ N\right] _{M\left( i\right) }^{T} \left[ k^{el} \right] _{m\left( i\right) } \left[ N\right] _{M\left( i\right) } \left\{ d\right\} _{M}\right. \nonumber \\&\quad \left. -\left[ N\right] _{M\left( i\right) }^{T} \left[ k^{h} \right] _{m\left( i\right) } \left\{ \varepsilon _{cq}^{pl} \right\} _{_{m\left( i\right) } } \right) \end{aligned}$$

(62)

Substituting Eqs. (59) and (62) into Eq. (60), the following expression is derived:

$$\begin{aligned}&\left[ K^{el}\right] _{CR\left( j\right) }^{M} \left\{ d\right\} _{M}-\left[ K^{h} \right] _{CR\left( j\right) } \left\{ \varepsilon ^{pl} \right\} _{cq} \nonumber \\&=\sum _{i=1}^{m_{el} }\left[ k^{el} \right] _{m\left( i\right) }^{M} \left\{ d\right\} _{M}-\sum _{i=1}^{m_{el} }\left[ k^{h} \right] _{m\left( i\right) }^{M} \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) } \end{aligned}$$

(63)

Relation (63) holds for every compatible vector of nodal displacements $\left\{ d\right\} _{M}$ as long as:

$$\begin{aligned} \left[ K^{el}\right] _{CR\left( j\right) }^{M} =\sum _{i=1}^{m_{el} }\left[ k^{el} \right] _{m\left( i\right) }^{M} \end{aligned}$$

(64)

and

$$\begin{aligned} \left[ K^{h} \right] _{CR\left( j\right) }^{M} \left\{ \varepsilon _{cq}^{pl} \right\} _{M}=\sum _{i=1}^{m_{el} }\left[ k^{h} \right] _{m\left( i\right) }^{M} \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) } \end{aligned}$$

(65)

thus, substituting in relation (59) the following multiscale equilibrium equation is derived for the coarse element:

$$\begin{aligned} \left[ K^{el}\right] _{CR\left( j\right) }^{M} \left\{ d\right\} _{M} =\left\{ f\right\} _{M} -\left\{ f_{h} \right\} _{M} \end{aligned}$$

(66)

Vector $\left\{ f_{h} \right\} _{M}$ in Eq. (66) is the nonlinear correction to the external force vector. This correction is evaluated by considering the micro to macro mapping arising from the evolution of the plastic strains within the micro-structure.

$$\begin{aligned} {\left\{ {{f_h}} \right\} _M} = - \sum \limits _{i = 1}^{{m_{el}}} {\left[ {{k^h}} \right] _{m\left( i \right) }^M} {\left\{ {\varepsilon _{cq}^{pl}} \right\} _{m\left( i \right) }} = \sum \limits _{i = 1}^{{m_{el}}} {\left\{ {{f_h}} \right\} _{m\left( i \right) }^M} \end{aligned}$$

(67)

where ${\left\{ {{f_h}} \right\} _{m\left( i \right) }^M}$ has been defined in Eq. (57) while the plastic strain vectors $\left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) }$ are considered to evolve according to relation (26).

Equations (66) and (67) are used to derive the equilibrium equation at the structural level as will be described in the next section. In analogy to the equilibrium equation of the micro-element (mapped onto the coarse element) defined in relation (56), the hysteretic force nodal load vector $\left\{ f_{h} \right\} _{M}$ is the nonlinear correction to the external force vector $\left\{ f\right\} _{M}$ at the coarse element level. However, the evolution of $\left\{ f_{h} \right\} _{M}$ is manifested through the evolution of the plastic deformations at the micro-level and is therefore the link between the inelastic processes occurring at the fine scale and the macroscopically observed nonlinear structural behaviour.

The coarse element stiffness matrices are evaluated considering only their individual micro-mesh properties. Thus, they are independent and their evaluation can be performed in parallel.

5 Solution procedure

5.1 Governing equations in the macro-scale

Considering the general case of a coarse mesh with $ndof_{M}$ free macro-degrees of freedom and using Eq. (66), the global equilibrium equations of the composite structure can be established in the coarse mesh. In the dynamic case the following equation is established:

$$\begin{aligned}&\left[ M\right] _{CR} \left\{ \ddot{U}\right\} _{M} +\left[ C\right] _{CR} \left\{ \dot{U}\right\} _{M}\nonumber \\&\quad +\left[ K^{el} \right] _{CR} \left\{ U\right\} _{M} =\left\{ F\right\} _{M} -\left\{ F_{h} \right\} _{M} \end{aligned}$$

(68)

where $\left[ M\right] _{CR} ,\,\left[ C\right] _{CR} ,\,\left[ K^{el} \right] _{CR}$ are the $\left( ndof_{M} \times ndof_{M} \right)$ macro-scale mass, viscous damping and stiffness matrix respectively, evaluated at the coarse mesh.

The formulation of the mass matrix, defined at the coarse mesh, is established on the grounds of the micro-basis shape functions presented in Sect. 3. This leads to a multi-scale consistent mass matrix formulation where the derived mass matrix is non-diagonal. Well-known mass diagonalization techniques can then be performed to derive an equivalent lumped mass matrix [18]. However, the implications of such approaches are beyond the scope of this work. Similarly, the viscous damping can be of either the classical or non-classical type [17].

The global stiffness matrix of the structure, defined at the coarse mesh, is formulated through the direct stiffness method from the contributions of the coarse elements equivalent stiffness matrices $\left[ K^{el}\right] _{CR\left( j\right) }^{M}$ [Eq. (64)]. Accordingly, the $\left( ndof_{M} \times 1\right)$ vector $\left\{ U\right\} _{M}$ consists of the nodal macro-displacements.

The external load vector $\left\{ F\right\} _{M}$ and the hysteretic load vector $\left\{ F_{h} \right\} _{M}$ are assembled considering the equilibrium of the corresponding elemental contributions $\left\{ f\right\} _{M}$ and $\left\{ f_{h} \right\} _{M}$, defined in Eqs. (58) and (67) respectively, at coarse nodal points.

Equation (68) is supplemented by the evolution equations of the micro-plastic strain components defined at the collocation points within the micro-elements. These equations can be established in the following form:

$$\begin{aligned} \left\{ \dot{E}_{cq}^{pl} \right\} _{m} =\left[ G\right] \left\{ \dot{E}_{cq} \right\} _{m} \end{aligned}$$

(69)

where the vector

$$\begin{aligned} \left\{ \dot{E}_{cq}^{pl} \right\} _{m} =\left\{ \begin{array}{llll} {\left\{ \dot{\varepsilon }_{cq}^{pl} \right\} _{m\left( 1\right) } }&{\left\{ \dot{\varepsilon }_{cq}^{pl} \right\} _{m\left( 2\right) } }&{\ldots }&{\left\{ \dot{\varepsilon }_{cq}^{pl} \right\} _{m\left( m_{el}\right) }} \end{array}\right\} ^{T} \end{aligned}$$

(70)

holds the plastic strain components evaluated at the collocation points of each micro-element and

$$\begin{aligned} \left\{ \dot{E}_{cq} \right\} _{m} =\left\{ \begin{array}{llll} {\left\{ \dot{\varepsilon }_{cq} \right\} _{m\left( 1\right) } }&{\left\{ \dot{\varepsilon }_{cq} \right\} _{m\left( 2\right) } }&{\ldots }&{\left\{ \dot{\varepsilon }_{cq}^{} \right\} _{m\left( m_{el} \right) } } \end{array}\right\} ^{T} \end{aligned}$$

(71)

are the corresponding total strain components. Index $m_{el}$ denotes the total number of micro-elements within each coarse element. Matrix $\left[ G\right]$ in relation (69) is a block diagonal matrix that assumes the following form

$$\begin{aligned} \left[ G \right] {=}\!\left[ \!\!{\begin{array}{*{20}{c}} {{{\left[ \!\!{\begin{array}{*{20}{c}} {\left[ {{g_1}} \right] }&{}{}&{}{} \\ {}&{} {\ddots } &{}{} \\ {}&{}{}&{}{\left[ {{g_{{n_{cq}}}}} \right] } \end{array}} \right] }_{\left( 1 \right) }}}&{}{}&{}{} \\ {}&{} {\ddots } &{}{} \\ {}&{}{}&{}{{{\left[ {\begin{array}{*{20}{c}} {\left[ {{g_1}} \right] }&{}{}&{}{} \\ {}&{} {\ddots } &{}{} \\ {}&{}{}&{}{\left[ {{g_{{n_{cq}}}}} \right] } \end{array}} \right] }_{\left( {{m_{el}}} \right) }}} \end{array}} \right] \nonumber \\ \end{aligned}$$

(72)

where $\left[ g_{iq}\right] , iq=1, \ldots , n_{cq}$ are $6\times 6$ sub-matrices defined as

$$\begin{aligned} {g_{iq\left( i \right) }} = H_{1m\left( i \right) }^{iq}H_{2m\left( i \right) }^{iq}\left[ R \right] _{m\left( i \right) }^{iq} \end{aligned}$$

and $n_{cq}$ is the total number of collocation points within each micro-element.

Equations (69) are independent and thus can be solved in the micro-element level resulting in an implicitly parallel scheme. Both relations (69) and (72) depend on the current micro-stress state within each micro-element and consequently on the micro-strain and micro-displacement distribution. Thus, a procedure needs to be established that downscales the macro-displacements $\left\{ U\right\} _{M}$ evaluated at the coarse mesh to the micro-displacements of the micro-nodes within the fine mesh.

5.2 Downscale computations

Considering that the value of the coarse mesh displacements $\left\{ U\right\} _{M}$ is known, the interpolation scheme introduced in relation (39) can be used to derive the micro-displacement components within each coarse element. Extracting the nodal macro-displacements $\left\{ d\right\} _{M}$ of a macro-element from $\left\{ U\right\} _{M}$ the corresponding micro-displacement vector of the $i_{th}$ micro-element $\left\{ d\right\} _{m\left( i\right) }$ is derived through relation (41) that is re-written here for brevity

$$\begin{aligned} \left\{ d\right\} _{m(i)} =\left[ N\right] _{m(i)} \left\{ d\right\} _{M} \end{aligned}$$

(73)

However, this micro-displacement vector only contains information derived from the macro to micro-displacement mapping and does not take into account the local effect of the micro-displacement on the neighbouring micro-nodes, as discussed in Sect. 3.3. Therefore, the actual displacement vector $\left\{ \bar{d}\right\} _{m(i)}$ that is compatible with the strain field within the micro-element is evaluated as

$$\begin{aligned} \left\{ \bar{d}\right\} _{m(i)} =\left\{ d\right\} _{m(i)} +\left\{ \tilde{d}\right\} _{m(i)} \end{aligned}$$

(74)

where $\left\{ \tilde{d}\right\} _{m(i)}$ is evaluated from relation (49). The total strain vector at the collocation points is then evaluated by using the strain-displacement relation defined in Eq. (30)

$$\begin{aligned} \left\{ \varepsilon _{cq} \right\} _{m\left( i\right) }^{iq} =\left[ B\right] _{m\left( i\right) }^{iq} \left\{ \bar{d}\right\} _{m(i)} ,\quad iq=1,\ldots ,n_{cq} \end{aligned}$$

(75)

where $n_{cq}$ is the number of collocation points within the element and $\left[ B\right] _{m\left( i\right) }^{iq}$ is the strain-displacement matrix evaluated at each collocation point $iq$. The rate of total strains is derived accordingly through

$$\begin{aligned} \left\{ \dot{\varepsilon }_{cq} \right\} _{m\left( i\right) }^{iq} =\left[ B\right] _{m\left( i\right) }^{iq} \left\{ \dot{\bar{d}}\right\} _{m(i)},\quad iq=1,\ldots ,n_{cq} \end{aligned}$$

(76)

The total stresses at the collocation points are evaluated by integrating Eqs. (25) and (22) defined at the micro-scale as

$$\begin{aligned} \left\{ \dot{\sigma }_{cq} \right\} _{m\left( i\right) }^{iq} =\left[ D\right] _{m\left( i\right) } \left( \left\{ \dot{\varepsilon }_{cq} \right\} _{m\left( i\right) }^{iq} -\left\{ \dot{\varepsilon }_{cq}^{pl} \right\} _{m\left( i\right) }^{iq} \right) \end{aligned}$$

(77)

and

$$\begin{aligned}&\!\!\! \left\{ {{{\dot{\eta }}_{cq}}} \right\} _{m\left( i \right) }^{iq}\nonumber \\&\quad = H_{1m\left( i \right) }^{iq}H_{2m\left( i \right) }^{iq}{\fancyscript{G}}\left( {\left\{ \eta \right\} _{m\left( i \right) }^{iq},\varPhi _{m\left( i \right) }^{iq}} \right) \left[ {\tilde{R}} \right] _{m\left( i \right) }^{iq}\left\{ {{{\dot{\varepsilon }}_{cq}}} \right\} _{m\left( i \right) }^{iq}\nonumber \\ \end{aligned}$$

(78)

respectively. Equations (77) and (78) are supplemented by the following set of evolution equations for the plastic strain

$$\begin{aligned} \left\{ \dot{\varepsilon }_{cq}^{pl} \right\} _{m\left( i\right) }^{iq} =H_{1m\left( i \right) }^{iq}H_{2m\left( i \right) }^{iq} \left[ R\right] _{m\left( i\right) }^{iq} \left\{ \dot{\varepsilon }_{cq} \right\} _{m\left( i\right) }^{iq} \end{aligned}$$

(79)

Since the current micro-stress state is required to evaluate the Heaviside functions $H_{1m\left( i\right) }^{iq} ,\,H_{2m\left( i\right) }^{iq}$ [Eqs. (17) and (18) respectively] and the interaction matrix $\left[ R\right] _{m\left( i\right) }$ [Eq. (21)] an iterative procedure is required at the micro-element level.

5.3 Newton iterative scheme

In this section, the nonlinear static analysis procedure implemented is presented for clarity, while the dynamic case is treated accordingly using the Newmark average acceleration method to integrate the equations of motion [17].

Dropping the inertia and viscous damping terms from Eq. (68) the following equation is derived:

$$\begin{aligned} \left[ K^{el} \right] _{CR} \left\{ d\right\} =\left\{ F\right\} _{M} -\left\{ F_{h} \right\} _{M} \end{aligned}$$

(80)

Considering an iterative Newton–Raphson incremental scheme the following equation is established

$$\begin{aligned} \left[ {{K^{el}}} \right] _{CR} {_i^j\left\{ {\Delta d} \right\} } = _i^j\left\{ {\Delta P} \right\} - {_i^j{\left\{ {\Delta {F_h}} \right\} _M}} \end{aligned}$$

(81)

where $j$ stands for the current iteration within the current loading step $i,\,{}_{i}^{j} \left\{ \Delta P\right\}$ is the current externally applied force increment that at the beginning of the load increment is evaluated as:

$$\begin{aligned} _{i}^{0} \left\{ \Delta P\right\} ={}_{i} \left\{ P^{ext} \right\} -{}_{i-1} \left\{ P^{ext} \right\} \end{aligned}$$

(82)

while ${_i^j{\left\{ {\Delta {F_h}} \right\} _M}}$ is the incremental nonlinear correction to the externally applied load vector assembled considering the individual contribution of each coarse element vector ${\left\{ {{f_h}} \right\} _M}$ defined in Eq. (67). Equation (81) is supplemented by $n_{el}\times n_{m_{el}} \times n_{cq}$ incremental equations of the plastic component of the strain tensors, defined at the fine-scale

$$\begin{aligned} _{i}^{j} \left\{ \Delta E_{cq}^{pl} \right\} _{m} ={_{i}^{j}\left[ G\right] } {_{i}^{j} \left\{ \Delta E_{cq} \right\} _{m}} \end{aligned}$$

(83)

where $n_{el}$ is the total number of coarse elements.

Thus, considering that convergence has been established at the $\left( i-1\right) _{th}$ incremental step, the following procedure is used to evaluate the structural response at the next incremental step, solving equation

$$\begin{aligned} \left[ K^{el} \right] {}_{i}^{1} \left\{ \Delta d\right\} ={_{i}^{1} \left\{ \Delta P\right\} }-{_i^1{\left\{ {\Delta {F_h}} \right\} _M}} \end{aligned}$$

(84)

where the incremental plastic deformation vector at the beginning the $i_{th}$ step has been evaluated at the end ($j_{th}$ iteration) of the previous step, thus:

$$\begin{aligned} {}_{i}^{0} \left\{ \Delta E_{cq}^{pl} \right\} _{m} ={}_{i-1}^{j} \left\{ \Delta E_{cq}^{pl} \right\} _{m} \end{aligned}$$

(85)

Solving Eqs. (84) and (85), the current increment of the displacement vector $_{i}^{1}\left\{ \Delta d\right\}$ is evaluated. Next, the corresponding incremental strains need to be evaluated at the collocation points of the fine-scale mesh taking into account both the macro-displacement contribution and the perturbed displacement contribution (Eq. (74)).

Therefore, for each coarse element the following procedure is established:

• 1. Solve Eq. (49) for the fine-scale residual forces evaluated at the beginning of the step and retrieve the perturbed displacement vector ${}_{i}^{1} \left\{ \Delta \tilde{d}\right\} _{m(i)}$

• 2. Evaluate the fine-scale incremental displacement components from Eq. (73)

  $$\begin{aligned} {}_{i}^{1} \left\{ \Delta d\right\} _{m(i)} =\left[ N\right] _{m(i)} {_{i}^{1} \left\{ d\right\} _{M}} \end{aligned}$$

  (86)

• 3. The total strains at the collocation points are then derived as

  $$\begin{aligned} {}_{i}^{1} \left\{ \varepsilon _{cq} \right\} _{m\left( i\right) }^{iq}&= \left[ B\left( \xi ,\eta \right) \right] \left( _{i-1} \left\{ d\right\} +_{i}^{1} \Delta \left\{ d\right\} _{m\left( i\right) }\right. \nonumber \\&\left. +{}_{i}^{1} \left\{ \Delta \tilde{d}\right\} _{m(i)} \right) \end{aligned}$$

  (87)

The total stresses are derived by integrating Eqs. (77)–(79). This is a system of first order nonlinear differential equations. In this work, an Euler scheme is implemented to retrieve the updated stress field at the Gauss points for brevity. However, more refined sub-stepping explicit [32, 51] or implicit methods [49] can be implemented for the solution of the incremental equations of plasticity.

Thus, at the end of the iterative procedure, both the current stress field and the interaction matrix $\left[ R\right]$ are evaluated. Therefore, the updated plastic strain vector is derived as:

$$\begin{aligned} {}_{i}^{1} \left\{ \varepsilon _{cq}^{pl} \right\} _{m\left( i\right) }^{iq} ={_{i}^{1}H_{1}^{iq}} {_{i}^{1}H_{2}^{iq}}{_{i}^{1}\left[ R\right] ^{iq}}{_{i}^{1} \left\{ \varepsilon _{cq} \right\} _{m\left( i\right) }^{iq}} \end{aligned}$$

(88)

Having evaluated the nodal displacement field and plastic strain field at the micro-element level the corresponding incremental micro-forces ${}_{i}^{1} \left\{ \Delta f\right\} _{m\left( i\right) }$ can be evaluated using relation (50). These are then used to derive the next increment of the perturbed micro-displacement vector ${}_{i}^{2} \left\{ \Delta \tilde{d}\right\} _{m(i)}$, using relation (49) as well as the increment of the macro equivalent nodal forces using relation (55). Assembling at the coarse element level the increment of the internal forces, defined at the coarse level is readily derived as:

$$\begin{aligned} \left\{ P^{int} \right\} _{i}^{1} =\left\{ P^{int} \right\} _{i}^{0} +\left[ K^{el} \right] _{i}^{1}\left\{ \Delta d\right\} -\left[ K^{pl} \right] _{i}^{1}\left\{ \Delta \varepsilon _{_{p}}^{pl}\right\} \nonumber \\ \end{aligned}$$

(89)

The current internal force vector is then compared to the external applied load vector through an appropriate convergence criterion and the iterative procedure continues until convergence. Any type of convergence criterion can be used; a work based criterion is implemented herein assuming the following form [23]:

$$\begin{aligned} W_{i}^{1} =\left\{ \Delta U_{i}^{1} \right\} \left( \left\{ P^{ext} \right\} _{i} -\left\{ P^{int} \right\} _{i}^{1} \right) \le \varepsilon \end{aligned}$$

(90)

where $\varepsilon$ is a user defined tolerance. Usually $\varepsilon$ is chosen such that $10^{-7} \le \varepsilon \le 10^{-4}$.

Relations (80)–(89) define an explicit Newton solution scheme, where the state matrices remain constant throughout the analysis procedure. The resulting iterative scheme relies on constant global matrices and does not require the re-evaluation and re-factorization of the global stiffness matrix. Inelasticity is introduced as an additional load vector that acts as a nonlinear correction to the externally applied load. This hysteretic load vector is evaluated by considering the evolution of the plastic strain at collocation points defined in the micro-scale.

Consequently, the re-evaluation of the micro to macro numerical mapping [relation (47)] is not required either. The numerical schema described herein can be extended for the case of nonlinear dynamic analysis by introducing a time-marching method on top of the iterative procedure. Both the static and dynamic analysis case has been treated and their corresponding results are discussed in the Sect. 6.

5.4 Comparison to the classical iterative solution procedure

The EMsFE method significantly reduces the size of the finite element mesh to be solved, since the solution procedure is applied in the coarse mesh. This is accomplished by the evaluation of a numerical mapping that interpolates the displacement components of the fine mesh onto the displacement components of the coarse mesh through relation (39).

The evaluation of this numerical mapping is performed through the procedure described in Sect. 3.2. This procedure involves the solution of an indeterminate structure and thus the derived micro-basis shape functions depend on the mechanical properties of the constituents of the micro-mesh. Thus, in a nonlinear analysis procedure where these mechanical properties depend on the value of the current displacement, the evaluation of the micro-basis function needs to be performed in every computational step. This leads into a significant increase on the computational cost of the proposed numerical scheme. A schema of the nonlinear analysis procedure of an EMsFEM is presented in Fig. 6.

Fig. 6

Schematic flow chart of the classical multiscale finite element scheme implementing a N–R iterative procedure

However, in the proposed computational scheme that is schematically presented in Fig. 7 the need for re-evaluation of the micro to macro displacement mapping is alleviated. This is accomplished by treating inelasticity at the local micro-level through the introduction of the additional hysteretic components [Eq. (32)]. These, account for the plastic part of the strain tensor, measured at specific collocation points. In this work, these points are so chosen to coincide with the Gauss quadrature points of the micro-elements. The proposed procedure expands the vector of unknown quantities and introduces an additional set of nonlinear equations that need to be solved [Eq. (69)]. However, the solution of these equations is performed at the local micro-level. Each set of equations is independent and can be solved in parallel, thus significantly enhancing the computational efficiency of the proposed scheme.

Since the proposed scheme is based on constant state matrices the corresponding rate of convergence is expected to be slower than the full Newton–Raphson method that guarantees quadratic convergence. Nevertheless, the significant reduction of the order of the computational model in conjunction with the implicit parallelicity of the proposed algorithm render the hysteretic scheme an efficient method for the solution of multiscale problems.

Fig. 7

Schematic flow chart of the proposed hysteretic multiscale finite element scheme

6 Examples

In this section examples are presented for the verification of the proposed methodology. All analyses were performed on an Intel Xeon PC fitted with 16 GB of RAM. The Abaqus commercial code [29] is used for the validation of the derived multiscale numerical scheme. The implementation of the latter has been performed using the FORTRAN 2003 programming language.

6.1 Compression experiment of a cubic specimen

In this example, a cubic specimen is examined (Fig. 8) as a benchmark problem to verify the accuracy and the efficiency of the proposed multiscale scheme under monotonic loading. Two cases are considered. In the first, the specimen is homogeneous while in the second, a band of heterogeneity is introduced within its volume. Results are derived with the proposed methodology and compared with solutions derived using the standard FEM methodology and Abaqus commercial code [29].

Fig. 8

Concrete cube under uniform compression and multiscale model (8 coarse elements—64 fine scale elements each)

The model is considered fixed at its base, while a uniform pressure is applied at its top edge. The elastic parameters considered are $E_{m} =10$ GPa and $\nu =0.2$ for the Young’s modulus and the Poisson’s ration respectively. An associative linear Drucker–Prager plasticity model is used to model the nonlinear behaviour of the matrix. The following values are considered for the friction angle and the Drucker–Prager cohesion namely $\phi =30^{\circ }$ and $d=2000$ kPa respectively.

To establish the FEM solution that will serve as a reference for further comparisons, three different discretization schemes are considered, namely a 16, 512 and 4096 hex element mesh. All analyses are performed using the displacement based 8-node hex element implementing the b-bar integration scheme [29]. A full Newton–Raphson procedure in 1000 incremental steps is used in Abaqus with the same ammount of steps being applied in the proposed formulation for comparison purposes. The specimen is loaded up to a vertical displacement equal to $2.0\times 10^{-6}\hbox { m}$ . In Fig. 9a, the derived pressure-displacement paths are shown for the three different discretization schemes.

Fig. 9

a FEA derived pressure-displacement path for different discretization schemes. b Comparison of the proposed hysteretic multiscale formulation and Abaqus 512 element mesh

The hysteretic multiscale finite element method is implemented considering 8 coarse elements. Each coarse element is meshed into 64 micro-elements so that the total number of fine elements remains equal to 512. The corresponding pressure-displacement path is presented in Fig. 9b. The obtained solution is compared to the derived solution from the standard FE analysis. The difference between the two formulations is less than 1.0 %. Furthermore, while the Abaqus analysis procedure concluded in 51 s, the multiscale analysis module concluded in 13 s resulting in a 70 % reduction of the computational time.

Next, a “heterogeneous” band is introduced within the volume of the specimen. The assumed pattern is presented in Fig. 10a. The band material is considered elastic with the following material properties, namely $E_{b} =0.1$ GPa and $v_{b} =0.3$ for the Young’s modulus and the Poisson’s ratio respectively.

Fig. 10

a Material pattern. b Deformed configuration (FEM model)

The derived pressure displacement path is presented in Fig. 11a, where the displacement is measured at node #6 (Fig. 10a). Although the multiscale solution with linear boundary conditions succeeds in capturing both the elastic stiffness of the body as well as the maximum attained pressure, the overall difference from the 512 finite element mesh solution is greater than 5 %. On the contrary, the multiscale solution obtained using the periodic boundary HMsFEM solution practically coincides with the FEM solution.

The linear boundary constraint imposed on the coarse element cannot compensate for the curvature variation along the edges of the solid as shown in Fig. 10b. Further increasing the number of coarse elements reduces the discrepancy at the cost of increasing the required computational time. In Fig. 17b, results obtained considering a multiscale model comprising of 64 coarse elements (each one including 8 fine-scale elements) are presented.

6.2 Cantilever with periodic micro-structure

In this example, a composite cantilever beam is examined. The beam (Fig. 12a) consists of a $30\times 6$ matrix of RVEs. The RVE presented in Fig. 12b comprises of a square matrix and a circular inclusion. Two test cases are examined, a homogeneous case where the matrix and the inclusion share the same material and a heterogeneous one.

Fig. 11

a 8 coarse elements. b 64 coarse elements

Fig. 12

a Cantilever composite beam ($30\times 6$ coarse element mesh). b RVE

Nodes in sector AB are considered fixed in both directions (Fig. 12a. A traction load $T$ is applied at the free end of the cantilever.

Using the Abaqus commercial code [29] a detailed FEM model is formulated, to serve as a reference model for the validation of the proposed methodology. The derived model consists of 76380 nodes and 75686 quadrilateral plane stress elements.

Due to the periodicity of the structure, a periodic finite element mesh is derived accordingly. Thus, using the multiscale finite element method, a single fine mesh component needs to be evaluated comprising of 353 nodes and 320 quadrilateral plane stress elements. The corresponding coarse-element structure (Fig. 12a) consists of 217 nodes and 180 elements. Therefore, using the proposed methodology, the computational complexity of the initial finite element problem reduced from a magnitude of $O\left( 76380^{2} \right)$ to that of $O\left( 353^{2} \right)$.

The micro-mesh considered for the RVE together with the material properties considered in the two test cases are presented in Fig. 13, where $E_{m} ,\,n_{m}$ and $E_{i} ,\,n_{i}$ are the elastic properties of the matrix and the inclusion respectively. Furthermore, $\sigma _{y}$ and $c_{}$ stand for the yield stress and the linear kinematic hardening constant. For both materials, the following smooth hysteretic model material parameters are used, namely $n=6,\,\beta =0.5$ and $\gamma =0.5$. A displacement control monotonic analysis is performed, with the maximum controlled displacement (centroidal node at the tip) set to $u_{c} =10$ cm.

Fig. 13

RVE micro-mesh

The derived load-displacement path for both the homogeneous and heterogeneous cases are presented in Fig. 14a and b respectively. In the first case, both the linear boundary condition (HMsFEM-L) and periodic boundary solution (HMsFEM-P) coincide with the exact FEM solution. Differences emerge in the heterogeneous case; however, the average error with respect to the exact (FEM) solution is less than 1.5 % in both cases.

Fig. 14

a Homogeneous structure. b Heterogeneous structure

These differences are observed during the inelastic regime of the cantilever response, with the HMsFEM-L solution being stiffer than the exact one and the HMsFEM-P solution being more flexible than the exact one. In this case, the error introduced by the linear boundary condition assumption are reduced, with respect to the case examined in Example 1. However in the case considered herein, the actual cantilever deformed configuration can be adequately reproduced with a piece-wise linear displacement distribution, provided that the number of coarse elements along the length of cantilever is sufficient enough.

Next, a dynamic analysis is performed considering a varying amplitude sinusoidal excitation of the following form

$$\begin{aligned} T\left( t\right) =\frac{260}{8} t\sin \left( 3{\pi /2} t\right) \end{aligned}$$

Only the heterogeneous case is examined in this loading scenario. To further examine the efficiency of the proposed scheme, the structure is driven well beyond its yield limit. Also, an average acceleration Newmark scheme is implemented in all cases with a constant time step $dt=0.0002$ s. The load is applied for a total duration of $T=10$ s, thus the total number of requested incremental steps is equal to $N_{steps}=50000$.

A lumped mass matrix approach is implemented considering the following densities, namely $\gamma _{m} =1\mathrm{{KN/ m^{3}} }$ and $\gamma _{i} =0.1\mathrm{{KN/m^{3}}}$ for the matrix and the inclusion respectively. The time history of the tip vertical displacement for the two formulations is presented in Fig. 15a where in the multiscale case both linear (HMsFEM-L) and periodic boundary (HMsFEM-P) conditions are considered. Similar to the monotonic case, the solution derived with linear boundary conditions is stiffer. This is evident during the last cycle of the cantilever response where severe inelastic deformations occur.

However in this case, the relative error between the linear boundary condition case (HMsFEM-L) and the FEM solution assumes the maximum value of 2.75 % while the corresponding error for the HMsFEM-P solution is less than 1.5 %. The evolution of the relative error for the three different models is presented in Fig. 16. The relative error assumes its maximum value at the time instant $t=8.20$ s where plastic deformation initiates and remains constant for the remaining of the analysis procedure. This error is attributed to the evaluation of the additional “perturbed” micro-displacements that are used to evaluate the total vector of micro-strains [Eqs. (73) and (74)]. As described in Sect. 3.3, the evaluation of the vector of “perturbed” micro-displacements $\left\{ \tilde{d}\right\} _{m(i)}$ depends on the RVE boundary condition assumption.

The corresponding load displacement paths for the multiscale and FEM solution are presented in Fig. 15b. As far as the analysis time is concerned while the standard finite element procedure concludes in 1756 min the proposed hysteretic multiscale scheme concludes in $432$ min. Although the time integration parameters implemented on this example are not necessary for the accurate evaluation of the structural response, they do yield a computationally intensive case, thus revealing the advantages of both the hysteretic scheme and the derived multiscale formulation.

Fig. 15

a Tip vertical displacement time-history. b Applied-traction—vertical displacement hysteretic loop

Fig. 16

Relative error time history

6.3 Masonry wall under earthquake excitation

In this example, the cantilever masonry wall presented in Fig. 17a is examined. The wall consists of layers of masonry and mortar, while a layer of composite reinforcement is considered at its exterior. An additional mass of 10 tn is considered at the top of the wall.

Fig. 17

a Cantilever masonry wall. b Finite element mesh

The elastic material properties considered for each of the constituents are presented in Table 1. Isotropic elastic constants are used for both stone and mortar [48]. Accordingly, a von-Mises plasticity model is considered for the stone layer while Mohr–Coulomb yield is used to model the nonlinear behaviour of mortar.

Table 1 Stone and mortar material properties

A homogenized orthotropic elastic material is used for the textile composite layer [24]. The corresponding properties are presented in Table 2.

Table 2 Textile composite material properties

A finite element model is constructed in Abaqus for verification, using 2204 8-node displacement based hex elements. To avoid numerical instabilities stemming from the implementation of the Mohr–Coulomb plasticity model, equivalent properties for the more robust Drucker–Prager model are acquired using the following relations [29]

$$\begin{aligned}&\begin{array}{cc} {\tan \beta =\frac{\sqrt{3} \sin \phi }{\sqrt{1+\frac{1}{3} \sin ^{2} \phi } } =32.17^{\circ } }&{d=\frac{\sqrt{3} \cos \phi }{\sqrt{1+\frac{1}{3} \sin ^{2} \phi } } } \end{array}\\&c=0.157\,\text {MPa} \end{aligned}$$

Since the exact representation of masonry behaviour is out of the scope of the present work, associative plasticity rules are considered for brevity.

Ten coarse elements are used in the proposed formulation. Two coarse element types are consequently defined for the implementation of the proposed multiscale scheme. The first one consists of stone, mortar and composite layers, while the second one consists of stone and composite layers only and accounts for the top coarse element of the wall (Fig. 18).

Fig. 18

Coarse element assignment

The wall is subjected to the Lefkada ground excitation record (Lefkada 2003) presented in Fig. 19. The peak ground acceleration of the record is approximately $\alpha _{\max } =0.33g$ at $t=6.8$ s and the sampling time is $dt_{acc}=0.01$ s. The average acceleration Newmark integration method is used in both cases, with a constant time step $dt=0.001$ s. The first 20 s of the ground motion record are considered in this example. The time-history of the relative horizontal displacement measured at the top of the masonry wall is presented in Fig. 20a. The two solution methods yield practically the same results. Differences are observed during the last 5 s of the response. These are attributed to the different plasticity formulations (and the accompanying integration algorithms) implemented in the two approaches that result in different values for the corresponding residual deformations. In Fig. 20b a stress–strain hysteretic loop is presented derived at micro-element ‘#’19 (Fig. 17b). The values presented are the average values of the corresponding components evaluated at the 8 Gauss quadrature points. The two solutions are in good agreement.

Fig. 19

Lefkada ground acceleration record (Lefkada 2003)

In Fig. 21, the time history of the relative error between the two solutions for the normal stress–strain hysteretic loops of Fig. 20b is presented. The relative error in this case is evaluated as:

$$\begin{aligned} Err=\sqrt{\frac{{{{\left( {{\sigma _{FEM}} - {\sigma _{HMsFEM}}} \right) }^2} + {{\left( {{\varepsilon _{FEM}} - {\varepsilon _{HMsFEM}}} \right) }^2}}}{{\sigma _{FEM}^2 + \varepsilon _{FEM}^2}}} \end{aligned}$$

The maximum error is $1.18\,\%$ and corresponds to the time increment where the maximum plastic deformations occur. The average error is $0.63\,\%$.

Fig. 20

a Tip horizontal displacement time-history (relative). b Normal stress–strain hysteretic loop—element ‘#’19

Fig. 21

Stress–strain hysteretic loop relative error

Finally, the proposed formulation concludes in approximately 49 min while the standard FEM procedure requires 195 min, thus leading to a 75 % reduction of the required computational time.

7 Conclusions

In this work, a novel multi-scale finite element method is presented for the nonlinear analysis of heterogeneous structures. The proposed method is derived within the framework of the enhanced multiscale finite element method. However, the necessary re-evaluation of the the micro to macro basis functions is avoided by implementing the hysteretic finite element formulation at the micro-level. Consequently, inelasticity is treated at the micro-level through the introduction of local inelastic quantities. These are assembled at the macro-level in the form of an additional load vector that acts as a nonlinear correction to the externally applied loads. As a result, the state matrices of the multiscale problem need only to be evaluated once at the beginning of the analysis procedure.

The evolution of the additional inelastic quantities, e.g. the plastic part of the strain tensor, are bound to evolve according to a generic smooth hysteretic law. The hysteretic model implemented is a generalized form of the Bouc–Wen model of hysteresis, allowing for a more versatile approach on material modelling. In the application section, examples are presented that verify the computational efficiency of the proposed formulation as well as its accuracy.

8 Appendix

In this section, the procedure for the evaluation of the micro-basis shape functions of the RVE presented in Fig. 4 is briefly presented. The RVE comprises 9 quadrilateral plane stress micro-elements with corresponding stiffness matrices $\left[ k^{el}\right] _{m\left( i\right) }$ where $i=1\dots 9$. By means of the direct stiffness method [65], the stiffness matrix of the RVE is evaluated as

$$\begin{aligned} \left[ K\right] _{RVE}=\mathop A\limits _{i = 1}^9 {\left[ {{k^{el}}} \right] _{m\left( i \right) }} \end{aligned}$$

where $\mathop A\limits _{i = 1}^9$ denotes the direct stiffness assemblage operator. The resulting size of $\left[ K\right] _{RVE}$ is $32\times 32$.

The stiffness matrix $\left[ K\right] _{RVE}$ is used to evaluate the micro-basis shape functions that are readily derived as solutions of the boundary value problem defined in relation (47). The boundary conditions imposed are evaluated in such a way that the fundamental property of the micro-basis functions defined in relation (40) holds. A set of values satisfying relations (40) can be retrieved by means of the following reasoning; For the first set of equations (40) to hold it suffices that a micro-basis function mapping the micro-displacement components along $x$ to a macro-displacement along the same direction $x$ of a coarse-node is equal to unity at that specific coarse-node and zero to every other coarse-node. Moreover, the second set of equations (40) is satisfied if and only if a micro-basis function mapping the micro-displacement component along $x$ to the macro-displacement component along the direction $y$ is equal to zero in every coarse-node.

Based on this rationale, the following procedure is utilized to evaluate the micro-basis functions defined in relation (39), namely:

The definition of vector $\left\{ \bar{d}\right\} ^{iM}_{jM}$ depends on the boundary condition assumption utilized. The implementation of the periodic boundary condition assumption is presented in this example for the evaluation of micro-basis function $N_{9,j}$ [e.g. the first column of matrix $\left[ N\right] _{m}$ in Eq. (45)]. The periodic boundary condition kinematic constraint is based on the assumption that the displacement components of opposite nodes of a periodic mesh on a pre-defined direction will defer by a small perturbation. The periodic boundary nodes are defined by the edge pairs $S_{12}-S_{34}$ and $S_{14}-S_{23}$. For the evaluation of $N_{9,j}$ the following relations are applied between the periodic nodes (Fig. 22):

$$\begin{aligned} {\left\{ u\right\} _{{S_{12}}}}&= {\left\{ u\right\} _{{S_{43}}}} + \Delta \left\{ u\right\} \\ {\left\{ v\right\} _{{S_{12}}}}&= {\left\{ v\right\} _{{S_{43}}}} \\ {\left\{ u\right\} _{{S_{14}}}}&= {\left\{ u\right\} _{{S_{23}}}} + \Delta \left\{ u\right\} \\ {\left\{ v\right\} _{{S_{14}}}}&= {\left\{ v\right\} _{{S_{23}}}} \end{aligned}$$

where $\Delta \left\{ u\right\}$ is the imposed perturbation. The latter, is not a periodic function of the RVE geometry but varies linearly from $\Delta u=1$ to $\Delta u=0$ along the corresponding boundary. Thus, the boundary conditions for the boundary pair $\left( S_{12}-S_{43}\right)$ are defined as

$$\begin{aligned} \left( {{S_{12}} - {S_{43}}} \right) \rightarrow \left\{ \begin{array}{lr} {{u_1} = {u_4} + 1}&{}{{v_1} = {v_4}}\\ {{u_5} = {u_{15}} + {2 /3}}&{}{{v_5} = {v_{15}}}\\ {{u_6} = {u_{16}} + {1 {/3}}}&{}{{v_6} = {v_{16}}}\\ {{u_2} = {u_3}}&{}{{v_2} = {v_3}} \end{array} \right. \end{aligned}$$

(91)

The deformation pattern introduced in relation (91) does not exclude rigid body motions. These are avoided by constraining also the displcement components at micro-node 3 (Fig. 4), thus setting

$$\begin{aligned} \begin{array}{{cc}} {{u_3} = 0} \\ {{v_3} = 0} \end{array} \end{aligned}$$

(92)

Equations (91) and (92) constitute a set of multi-freedom non-homogeneous constraints that are treated in this work using the Penalty method [9, 23]. For this purpose, Eqs. (91) are augmented to account for the whole RVE and the imposed boundary condition relation assumes the following form

$$\begin{aligned} \left[ A \right] \left\{ d\right\} _{m} = \left\{ c \right\} \end{aligned}$$

(93)

where $\left\{ d\right\} _{m}$ is the $18\times 1$ nodal displacement vector of the RVE defined in relation (46), $\left[ A \right]$ is the following $10\times 32$ constraint coefficient matrix

(94)

and $\left\{ c \right\}$ is a $32 \times 1$ column vector assuming the following form

$$\begin{aligned} \left\{ c \right\} = {\left\{ {\begin{array}{*{20}{c}} 1&0&{\frac{2}{3}}&0&{\frac{1}{3}}&0&0&0&0&0&0&0&0&0&0&0&0&0&0&0 \end{array}} \right\} ^T} \end{aligned}$$

(95)

Fig. 22

Periodic boundary conditions of the evalation of $N_{9,j}$

The periodic boundary conditions introduce a numerical perturbation on the displacement field of periodic boundary nodes. Thus, they can in principle be used in non-periodic media (i.e. RVEs with non-periodic material distribut0ions). However in this case the size of the RVE should be small enough for the considered perturbation to be valid, i.e. for the displacements of periodic boundary nodes to differ by a small variation of the displacement field. Furthermore, the applicability of the method is restricted on periodic micro-element meshes. To alleviate such problems, a procedure has been established for the generalization of the periodic boundary condition assumption allowing its application to non-structured, non-periodic meshes [42]. Also, refined boundary condition assumptions such as the oversampling technique [19] and the generalized periodic boundary condition method (combining periodic boundary conditions with oversampling) have been effectively used in [63] for non-periodic media. The effect of different boundary condition assumptions on the accuracy of the EMsFEM method is examined in [64].