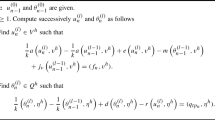Abstract
For the numerical analysis of dynamic contact problem where the contact constraint is imposed by a very stiff massless spring between the bodies, it is shown that a stabilized time integration solution can be obtained without spurious oscillations by imposing the velocity and acceleration constraints as well as the displacement constraint on the contact point. For the velocity and acceleration contact constraints which are crucial for the numerical stability, the time derivatives of the spring deformation are computed by using the Newmark time integration rule of structural dynamics. With the numerical experiments the necessity of the velocity and acceleration contact constraints and the necessity of unconditionally stable time integration rule for the very stiff spring are demonstrated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Shabana AA, Zaazaa KE, Escalona JL, Sany JR (2004) Development of elastic force model for wheel/rail contact problems. J Sound Vib 269: 295–325
Shabana AA, Zaazaa KE, Sugiyama H (2008) Railroad vehicle dynamics a computational approach. CRC Press, Boca Raton
Cardona A, Geradin M (1993) Kinematic and dynamic analysis of mechanism with cams. Comput Methods Appl Mech Eng 103: 115–134
Potra FA, Anitescu M, Gavrea B, Trinkle J (2006) A linearly implicit trapezoidal method for integrating stiff multibody dynamics with contact, joints, and friction. Int J Numer Methods Eng 66: 1079–1124
Taylor RL, Papadopoulos P (1993) On a finite element method for dynamic contact/impact problems. Int J Numer Methods Eng 36: 2123–2140
Armero F, Petocz E (1998) Formulation and analysis of conserving algorithms for frictionless dynamic contact/impact problems. Comput Methods Appl Mech Eng 158: 269–300
Laursen TA, Love GR (2002) Improved implicit integrators for transient impact problems-geometric admissibility within the conserving framework. Int J Numer Methods Eng 53: 245–274
Krause R, Walloth M (2009) A time discretization scheme based on Rothe’s method for dynamical contact problems with friction. Comput Methods Appl Mech Eng 199: 1–19
Feng ZQ, Joli P, Cros JM, Magnain B (2005) The bi-potential method applied to the modeling of dynamic problems with friction. Comput Mech 36: 375–383
Lee K (1994) A numerical solution for dynamic contact problems satisfying the velocity and acceleration compatibilities on the contact surface. Comput Mech 15: 189–200
Lee K (1997) A numerical method for dynamic analysis of vehicles moving on flexible structures having gaps. Int J Numer Methods Eng 40: 511–531
Lee K (2001) Analysis of dynamic contact between rotating spur gears by finite element and multi-body dynamics techniques. Proc Inst Mech Eng Part C Mech Eng Sci 215: 423–435
Lee K (2009) Numerical analysis for dynamic contact between high-speed wheel and elastic beam with Coulomb friction. Int J Numer Methods Eng 78: 883–900
Vu-Quoc L, Olsson MA (1989) Computational procedure for interaction of high-speed vehicles on flexible structures without assuming known vehicle nominal motion. Comput Methods Appl Mech Eng 76: 207–244
Timoshenko SP, Goodier JN (1970) Theory of elasticity. McGraw-Hill, New York
Johnson KL (1985) Contact mechanics. Cambridge University Press, UK
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lee, K. A stabilized numerical solution for the dynamic contact of the bodies having very stiff constraint on the contact point. Comput Mech 46, 533–543 (2010). https://doi.org/10.1007/s00466-010-0498-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-010-0498-9