Stabilization-free virtual element method for 3D hyperelastic problems

Abstract

In this work, we present a first-order stabilization-free virtual element method (SFVEM) for three-dimensional hyperelastic problems. Different from the conventional virtual element method, which necessitates additional stabilization terms in the bilinear formulation, the method developed in this work operates without the need for any stabilization. Consequently, it proves highly suitable for the computation of nonlinear problems. The stabilization-free virtual element method has been applied in two-dimensional hyperelasticity and three-dimensional elasticity problems. In this work, the format will be applied to three-dimensional hyperelasticity problems for the first time. Similar to the techniques used in the two-dimensional stabilization-free virtual element method, the new virtual element space is modified to allow the computation of the higher-order $L_2$ projection of the gradient. This paper reviews the calculation process of the traditional $\mathcal {H}_1$ projection operator; and describes in detail how to calculate the high-order $L_2$ projection operator for three-dimensional problems. Based on this high-order $L_2$ projection operator, this paper extends the method to more complex three-dimensional nonlinear problems. Some benchmark problems illustrate the capability of the stabilization-free VEM for three-dimensional hyperelastic problems.

1 Introduction

For a wide range of engineering and scientific problems governed by partial differential equations, numerical methods are an effective tool for simulating and solving such problems. The Virtual Element Method (VEM), as introduced in [1, 2], has received more and more attention due to its greater flexibility in the fields of the element shape and the definition of the degrees of freedom. As a generalization of the Finite Element Method (FEM), the virtual element method allows very general arbitrarily shaped elements, which makes the method suitable for calculating some special problems such as crack propagation, hanging nodes, and adaptive meshes. In the framework of structural mechanics, the method has been applied to different fields including linear elastic problems [3,4,5,6,7], hyperelastic materials at finite deformations [8,9,10,11], contact problems [12,13,14,15], phase field fracture [16, 17], elastodynamics problems [18,19,20,21], and finite elastoplastic deformations [22,23,24]. Specific work of VEM in engineering can be found in the latest published VEM book [25]. At the same time, there are also other numerical methods that use polygonal or polyhedral meshes for calculations, such as Polygonal Finite Element Method (PFEM) [26, 27], Discontinuous Galerkin Methods (DG) [28, 29], Polygonal Smoothed Finite Element Method (S-FEM) [30, 31]. However, the above-mentioned methods have general difficulties when dealing with three-dimensional problems. For example, the above polygonal finite element methods have great difficulties when solving nonconvex polyhedrons or dealing with high-order elements. Generally speaking, VEM has higher advantages when dealing with complex-shaped elements and high-order elements.

Given the flexibility of VEM, it is interesting to develop a new virtual element format for three-dimensional hyperelastic solids. According to previous relevant descriptions [1, 2], the main idea of VEM is a split of the variable $u_h$ into a projection part $\Pi u$ and a remainder, that is $u_h = \Pi u+(u_h-\Pi u)$. This formulation requires additional stabilization terms in VEM to ensure that the element stiffness matrix has the correct rank (for elements with more than 4 nodes). The selection of stabilization terms, especially for nonlinear problems, is a complicated issue. Different formulations can be found in [3, 7], which are extended to energy stabilization in [9, 25, 32]. However, a virtual element that does not require any stabilization will be more flexible and reliable for the solution of nonlinear problems.

With this aim, we are going to construct a three-dimensional stabilization-free virtual element method and use it to solve hyperelastic problems. In conventional VEM, the stabilization term is needed because the strain order is too low to accurately describe the energy within the element. By increasing the order of the strain polynomial, the stabilization-free virtual element method (SFVEM) [33] has been recently proposed and has been successfully used in different fields [34,35,36]. However, these applications are usually limited to two-dimensional linear problems. Recently, the author developed SFVEM for hyperelastic problems [37], but it is still for two-dimensional problems. Similar to the two-dimensional problem, by using the high-order $L_2$ projection operator $\Pi _{l,E}^0\nabla$ of the gradient of function in $\mathcal {H}^1(E)$, we can construct a stabilization-free virtual element format for three-dimensional problems. The first work on stabilization-free 3D virtual elements can be found in [38], but it is mainly aimed at heat transfer problems. In this work, the virtual element space is modified to allow the computation of a higher-order $L_2$ projection operator. Based on that the SFVEM for three-dimensional problems will be developed and applied to hyperelasticity problems for the first time. In addition, this work will also use the arc length method to solve unstable structures.

Based on the above description, we can divide the paper into the following parts. In Sect. 2, the governing equations for hyperelastic problems are reviewed. Then, the three-dimensional stabilization-free virtual element spaces will given in Sect. 3 for arbitrary order k. Based on the above definitions, the $\mathcal {H}_1$ projection operator and higher-order $L_2$ projection operator are developed in Sect. 4. The virtual element discretization will be described for 3D hyperelastic problems in Sect. 5. Numerical examples are presented and discussed in Sect. 6. The paper closes with some concluding remarks in Sect. 7.

2 Governing equations for finite elasticity

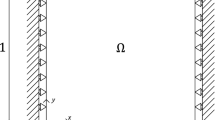
Consider a three-dimensional elastic solid that is deforming from the initial configuration occupying a volume $\mathcal {B}_0\in \mathbb {R}^3$ with boundary $\Gamma _0 = \partial \mathcal {B}_0$ into the current configuration $\mathcal {B}_t$ with boundary $\partial \mathcal {B}_t$ (see Fig. 1). The position $\varvec{x}$ of a material point $\mathcal {P}$ initially at $\varvec{X}$ is given by the motion

$$\begin{aligned} \varvec{x} = \varvec{\varphi }\left( \varvec{X},t\right) = \varvec{X}+\varvec{u}(\varvec{X},t), \end{aligned}$$

(1)

where $\varvec{u}$ is the displacement field. We denote by $\varvec{F}$ the deformation gradient defined by

$$\begin{aligned} \varvec{F} = \text {Grad}\varvec{\varphi } = \varvec{1}+\nabla \varvec{u}, \end{aligned}$$

(2)

where $\varvec{1}$ represents the second-order unity tensor and $\nabla \varvec{u}$ is the displacement gradient with respect to the initial coordinates. Based on $\varvec{F}$, the right Cauchy-Green deformation tensor is given by

$$\begin{aligned} \varvec{C} = \varvec{F}^T\cdot \varvec{F}. \end{aligned}$$

(3)

Further, we can define the Green-Lagrange strain tensor

$$\begin{aligned} \varvec{E} = \frac{1}{2}\left( \varvec{C}-\varvec{1}\right) . \end{aligned}$$

(4)

Fig. 1

Motion of a body from the initial configuration $\mathcal {B}_0$ to the current configuration $\mathcal {B}_t$

For the static case, the equilibrium requires

$$\begin{aligned} -\text {Div}\varvec{P} = \varvec{f}, \end{aligned}$$

(5)

where $\varvec{P}$ is the first Piola–Kirchhoff stress and $\varvec{f}$ is the body force. The Dirichlet and Neumann boundary conditions are

$$\begin{aligned} \varvec{u}&= \bar{\varvec{u}}\quad \text {on}\quad \Gamma _D, \end{aligned}$$

(6)

$$\begin{aligned} \varvec{P}\cdot \varvec{N}&= \bar{\varvec{t}} \quad \text {on}\quad \Gamma _N, \end{aligned}$$

(7)

where $\varvec{N}$ is the outward normal vector of $\partial \mathcal {B}_0$.

The second Piola–Kirchhoff stress is often used in constitutive modeling since it is work conjugated to the Green-Lagrange strain tensor. The second Piola–Kirchhoff stress can be obtained from $\varvec{P}$ as

$$\begin{aligned} \varvec{S} = \varvec{F}^{-1}\cdot \varvec{P}, \end{aligned}$$

(8)

where $\varvec{\sigma }$ is the Cauchy stress tensor (real stress), J is the determinant of the deformation gradient tensor

$$\begin{aligned} J = \text {det}(\varvec{F}). \end{aligned}$$

(9)

The work conjugate relationship can be written as

$$\begin{aligned} \mathcal {W} = \int _{V_0}\delta \varvec{E}:\varvec{S}\textrm{d}V_0=\int _{V_0}\delta \varvec{F}:\varvec{P}\textrm{d}V_0, \end{aligned}$$

(10)

The virtual element formulation for a hyperelastic material can start from the potential energy function directly. By introducing a strain energy function $\Psi (\varvec{u})$ for elastic problems, the second Piola–Kirchhoff stresses follow

$$\begin{aligned} \varvec{S} =2\frac{\partial \Psi (\varvec{u})}{\partial \varvec{C}}. \end{aligned}$$

(11)

For a homogeneous compressible isotropic hyperelastic material, the strain energy function $\Psi (\varvec{u})$ for the Neo-Hookean hyperelastic model can be adopted as

$$\begin{aligned} \Psi = \frac{\mu }{2}\left( I_C-3\right) -\mu \ln J+\frac{\lambda }{2}\left( \ln J\right) ^2, \end{aligned}$$

(12)

where $I_C$ is the first invariant of the right Cauchy-Green tensor in Eq. (3), J is the determinant of $\varvec{F}$, $\lambda$ and $\mu$ are the two Lame parameters.

Considering $\frac{\partial J}{\partial \varvec{C}} = \frac{1}{2}J\varvec{C}^{-1}$, the second Piola–Kirchhoff stress tensor $\varvec{S}$ can be obtained for the Neo-Hookean hyperelastic model (Eq. (12)) as

$$\begin{aligned} \varvec{S}&=2\frac{\partial \Psi }{\partial \varvec{C}} = \mu \varvec{1}-2\mu \frac{1}{J}\frac{\partial J}{\partial \varvec{C}}+2\lambda \left( \ln J\right) \frac{1}{J}\frac{\partial J}{\partial \varvec{C}}\nonumber \\&=\mu \left( \varvec{1}-\varvec{C}^{-1}\right) +\lambda \left( \ln J\right) \varvec{C}^{-1}. \end{aligned}$$

(13)

By differentiating the second Piola–Kirchhoff stress $\varvec{S}$, the constitutive tensor $\varvec{\mathcal {D}}$ can be deduced as

$$\begin{aligned} \varvec{\mathcal {D}} =2\frac{\partial \varvec{S}}{\partial \varvec{C}} = \lambda \varvec{C}^{-1}\otimes \varvec{C}^{-1}+2\left( \mu -\lambda \ln J\right) \varvec{\mathcal {L}}, \end{aligned}$$

(14)

with the components of $\varvec{\mathcal {L}}$

$$\begin{aligned} \mathcal {L}_{IJKL}&= -\frac{\partial \left( \varvec{C}^{-1}\right) _{IJ}}{\partial C_{KL}}\nonumber \\&= \frac{1}{2}\left[ \left( \varvec{C}^{-1}\right) _{IK}\left( \varvec{C}^{-1}\right) _{JL}+\left( \varvec{C}^{-1}\right) _{IL}\left( \varvec{C}^{-1}\right) _{JK}\right] . \end{aligned}$$

(15)

3 3D stabilization-free virtual element spaces

In this part, we describe the basic ideas of the three-dimensional stabilization-free virtual element method (SFVEM).

3.1 Notation

For three-dimensional problems, a decomposition $\mathcal {T}_h=\left\{ \Omega _E\right\} _h$ is introduced where $\Omega _E$ is a partition of the computational domain $\Omega$ into non-overlapping polyhedron elements. For each polyhedron element E with boundary $\partial E$ as shown in Fig. 2, the parameters are given as: volume |E|, barycenter $\varvec{x}_E = (x_E,y_E,z_E)^T$, and diameter $h_E$. Besides, an element face $F\in \partial E$ is a planar and a two-dimensional subset of $\mathbb {R}^3$. We denote the set of polygon faces by $\mathcal {F}_h$ as shown in Fig. 2. By defining a local coordinate system $(\xi ,\eta )$, the parameters for the local polygon face are given as area |F|, barycenter $\varvec{\xi }_F = (\xi _F,\eta _F)^T$, and diameter $h_F=\text {sup}_{\varvec{x},\varvec{y}\in F}|\varvec{x}-\varvec{y}|$. Specific requirements for 3D virtual element mesh can be found in [39].

Fig. 2

A polyhedral element and its polygonal surfaces

For three-dimensional problems ($d=3$), we introduce scaled monomials $\mathcal {M}_k(E)$ as

$$\begin{aligned} \mathcal {M}_k(E):=\left\{ m_\alpha =\left( \frac{\varvec{x}-\varvec{x}_E}{h_E}\right) ^{\varvec{\alpha }}\,\text {for}\,\varvec{\alpha }\in \mathbb {N}^d \text { with }|\varvec{\alpha }|\le k\right\} , \end{aligned}$$

(16)

where $\varvec{\alpha } = (\alpha _1,\alpha _2,\alpha _3)$ is a multiindex and $\varvec{x}^{\varvec{\alpha }}:=x_1^{\alpha _1}\cdots x_1^{\alpha _d}$. The dimension of the given polygonal function space (Eq. (16)) is

$$\begin{aligned} N_k:=\text {dim}\left( \mathbb {P}_k(E)\right) =\frac{(k+1)(k+2)(k+3)}{6} \end{aligned}$$

(17)

Using local coordinates, the scaled monomials $\mathcal {M}^f_k(F)$ for the polygon face F of a polyhedron can be defined as

$$\begin{aligned} \mathcal {M}_k^f(F):=\left\{ m^f_\alpha =\left( \frac{\varvec{\xi }-\varvec{\xi }_F}{h_F}\right) ^{\varvec{\alpha }}\text { for }\varvec{\alpha }\in \mathbb {N}^{d-1} \text { with }|\varvec{\alpha }|\le k\right\} , \end{aligned}$$

(18)

with the dimension

$$\begin{aligned} N_k^f:=\text {dim}\left( \mathbb {P}_k(F)\right) = \frac{(k+1)(k+2)}{2} \end{aligned}$$

(19)

3.2 Virtual element space

For a given three-dimensional polyhedral element E with boundary $\partial E$ and $F\in \partial E$ a polygonal face of E, we start by defining the local lifting spaces on each face F

$$\begin{aligned} \tilde{\mathcal {V}}_k(F)&:=\big \{u_h\in \mathcal {H}^1(F)\cap C^0(F):\Delta _F u_h \nonumber \\&\in \mathbb {P}_{k}(F),u_h|_e\in \mathbb {P}_k(e),e\in \partial F\big \}, \end{aligned}$$

(20)

where $\Delta _F$ is the 2D Laplacian over the face F. In this work, a low-order Ansatz is adopted for the construction of the stabilization-free virtual element formulation ($k=1$) and the scaled monomials $m_\alpha ^f\in \mathcal {M}_k^f(F)$ (see Eq.(18)) have the explicit form as

$$\begin{aligned} m_1^f = 1,\quad m_2^f = \frac{\xi -\xi _F}{h_F}\quad m_3^f = \frac{\eta -\eta _F}{h_F}. \end{aligned}$$

(21)

The degrees of freedom can be selected as the value $u_h(v)$ for the vertice F. We can define the $\mathcal {H}_1$ projection operator $\Pi _{k,F}^\nabla :\tilde{\mathcal {V}}_k(F)\rightarrow \mathbb {P}_k(F)$ using

$$\begin{aligned}&\int _F \nabla _F{\Pi }_{k,F}^\nabla u_h\cdot \nabla _F p\textrm{d}\Omega _F \nonumber \\&\qquad = \int _F \nabla _F u_h\cdot \nabla _F p\textrm{d}\Omega _F,\quad \forall p \in \mathbb {P}_k(F), \end{aligned}$$

(22)

$$\begin{aligned}&P_0\left( \Pi _{k,F}^\nabla u_h-u_h\right) _F = 0. \end{aligned}$$

(23)

Integration by parts allows the evaluation of projection operator $\Pi _{k, F}^\nabla$, details can be found in [37, 40]. The higher-order moments in Eq. (20) can be approximated so the dimension of the function space does not change [41]. Then we can define the two-dimensional virtual element space

$$\begin{aligned} \mathcal {V}^h_k(F)&:=\bigg \{u_h\in \tilde{\mathcal {V}}_k(F): \int _{F}u_h p\textrm{d}\Omega _F\nonumber \\&\quad =\int _F\left( \Pi _{k,F}^{\nabla }u_h p\right) \textrm{d}\Omega _F,\quad \forall p\in \mathbb {P}_k(E) \bigg \}. \end{aligned}$$

(24)

For the 3D polyhedral element E, we consider the preliminary virtual space

$$\begin{aligned} \tilde{\mathcal {V}}_k(E)&:= \big \{u_h\in \mathcal {H}^1(E)\cap C^0(E):\Delta u_h\nonumber \\&\quad \in \mathbb {P}_{k}(E),u_h|_e\in \tilde{\mathcal {V}}_k(F),F\in \partial E\big \}. \end{aligned}$$

(25)

Next, we can compute the $\mathcal {H}_1$ projection operator $\Pi _{k,E}^\nabla :\tilde{\mathcal {V}}_k(E)\rightarrow \mathbb {P}_k(E)$ using

$$\begin{aligned} \int _E \nabla {\Pi }_{k,E}^\nabla u_h\cdot \nabla p\textrm{d}\Omega&= \int _E \nabla u_h\cdot \nabla p\textrm{d}\Omega ,\quad \forall p \in \mathbb {P}_k(E), \end{aligned}$$

(26)

$$\begin{aligned} P_0\left( {\Pi }_{k,E}^\nabla u_h-u_h\right)&= 0. \end{aligned}$$

(27)

Then we can define the local virtual element space

$$\begin{aligned} \mathcal {V}^h_k(E)&:=\bigg \{ u_h\in \tilde{\mathcal {V}}_k(E):\int _Eu_h p\textrm{d}\Omega \nonumber \\&=\int _E\left( \Pi _{k,E}^{\nabla }u_h\right) p\textrm{d}\Omega ,\quad \forall p\in \mathbb {P}_k(E) \bigg \}. \end{aligned}$$

(28)

The projection operator $\Pi _{1, E}^\nabla$ depends only on its vertex values for $k=1$. Thus the function space can be uniquely characterized by the vertex values (named degrees of freedom). According to the above space (28), we can construct a discrete form of the classic three-dimensional VEM. This consistency part requires additional stabilization for a correct rank of the element stiffness matrix.

To construct a virtual element formulation without any stabilization for three-dimensional problems, we need to introduce an additional enhancement space for $k=1$. Inspired by Ref. [42], we define a local enlarged enhancement virtual element space based on the higher-order polynomial projection

$$\begin{aligned} \mathcal {V}_{1,l}(E)&:=\left\{ u_h\in \mathcal {H}^1(E):\Delta u_h\in \mathbb {P}_{l+1}(E),\int _E u_hp\textrm{d}\Omega \right. \nonumber \\&\left. =\int _E\Pi _{1,E}^{\nabla }u_h p_{l+1}\textrm{d}\Omega ,\quad \forall p_{l+1}\in \mathbb {P}_{l+1}(E) \right\} \end{aligned}$$

(29)

Again the degrees of freedom can be selected as the values at $N_E^V$ vertices in E (same as the d.o.f used in $\mathcal {V}^h_k(E)$). The order of the polynomial (l in Eq. (29)) is related to the number of vertices $N_E^V$. For two-dimensional problems, the selection of l to ensure well-posedness can be found in [33, 35, 43, 44]. For three-dimensional problems, the selection of l has been based on an eigenvalue analysis, and the relationship between the order l and the number of vertices $N_E^V$ can be found in our previous work [45]. As discussed in [45], the order l can be selected as $l=1\sim 2$ for most of the elements.

4 Projection operators

The $\mathcal {H}_1$ projection operator $\Pi _{1,F}^\nabla :\tilde{\mathcal {V}}_1(E)\rightarrow \mathbb {P}_1(E)$ was introduced in the previous section. This projection operator is known from conventional VEM where a stabilization term was to be introduced to ensure the correct rank of the element stiffness matrix. In this work, we construct a virtual element formulation without any stabilization for 3D problems. As shown in Eq. (29), the $\mathcal {H}^1$ projection operator is necessary in the local enlarged enhancement virtual element space for the approximation of higher order moments. So in this part, we need to review how to calculate the $\mathcal {H}_1$ projection operator $\Pi _{1, E}^\nabla$ for three-dimensional problems, and further explain how to calculate the $L_2$ projection operator $\varvec{\Pi }_{l,E}^0\nabla$.

4.1 $\mathcal {H}_1$ projection operator on polyhedral elements

In the present work, only the first-order element ($k=1$) is considered. The scaled monomials $m_\alpha \in \mathcal {M}_1(E)$ have the form

$$\begin{aligned} m_1 = 1,\quad m_2 = \frac{x-x_E}{h_E},\quad m_3 = \frac{y-y_E}{h_E},\quad m_4 = \frac{z-z_E}{h_E}. \end{aligned}$$

(30)

According to the previous definition, the projector $\Pi _{1,E}^\nabla :\mathcal {V}_1(E)\rightarrow \mathbb {P}_1(E)$ can be calculated by

$$\begin{aligned} \int _E \nabla \Pi _{1,E}^\nabla u_h\cdot \nabla p\textrm{d}\Omega = \int _E \nabla u_h\cdot \nabla p\textrm{d}\Omega ,\forall p \in \mathbb {P}_1(E) \end{aligned}$$

(31)

with the additional condition

$$\begin{aligned} \sum _{i=1}^{n_E}\left( \Pi _{k,E}^\nabla u_h-u_h\right) = 0, \end{aligned}$$

(32)

where $n_E$ is the number of vertices. Considering the Green formula for Eq. (31), we have

$$\begin{aligned} \int _{E}\nabla \Pi _{1,E}^\nabla u_h\cdot \nabla p\, \textrm{d}\Omega =-\int _{E}u_h\cdot \Delta p\,\textrm{d}\Omega +\int _{\partial E}u_h\cdot \frac{\partial p}{\partial \varvec{n}}\textrm{d}\Gamma , \end{aligned}$$

(33)

where the projection operator $\Pi _{1,E}^\nabla$ can be expanded in a matrix form

$$\begin{aligned} \Pi _{1,E}^\nabla \varvec{\phi }^T= \varvec{m}^T\varvec{\Pi }_{1*,E}^\nabla = \varvec{\phi }^T\varvec{\Pi }_{1,E}^\nabla , \end{aligned}$$

(34)

where $\varvec{\phi }$ is the unknown basis function vector, $\varvec{\Pi }_{1*,E}^\nabla$ is matrix formulation of the Ritz projection operator. Substituting Eq. (34) into Eq. (33), yields

$$\begin{aligned}&\int _{E}\nabla \varvec{m}\cdot \nabla \varvec{m}^T\textrm{d}\Omega \varvec{\Pi }_{1*,E}^\nabla \nonumber \\&\quad =-\int _{E}\Delta \varvec{m}\cdot \varvec{\phi }^T\,\textrm{d}\Omega +\sum _{F\subset \partial E}\int _{F}\left( \nabla \varvec{m}\cdot \varvec{n}_F\right) \varvec{\phi }^T\textrm{d}\Gamma , \end{aligned}$$

(35)

which leads to an equation system for $\varvec{\Pi }_{1*,E}^\nabla$

$$\begin{aligned} \varvec{G}^\nabla \varvec{\Pi }_{1*,E}^\nabla = \varvec{B}^\nabla , \end{aligned}$$

(36)

where

$$\begin{aligned} \varvec{G}^\nabla&:= \int _{E}\nabla \varvec{m}\cdot \nabla \varvec{m}^T\textrm{d}\Omega , \end{aligned}$$

(37)

$$\begin{aligned} \varvec{B}^\nabla&:=\sum _{F\subset \partial E}\int _{F}\left( \nabla \varvec{m}\cdot \varvec{n}_F\right) \varvec{\phi }^T\textrm{d}\Gamma . \end{aligned}$$

(38)

Since the surface F of a polyhedral element E is a polygonal element, see Fig. 2, the shape function $\varvec{\phi }$ on the surface is still unknown. In this aspect, the three-dimensional problem differs from the two-dimensional problem. Based on the definition of the 3D virtual space (Eq. (25)), the unknown shape function $\varvec{\phi }$ in $\varvec{B}^\nabla$ can be calculated by

$$\begin{aligned} \varvec{B}^\nabla&=\sum _{F\subset \partial E}\int _{F}\left( \nabla \varvec{m}\cdot \varvec{n}_F\right) \varvec{\phi }^T\textrm{d}\Gamma \nonumber \\&= \sum _{F\subset \partial E}\left[ \left( \nabla \varvec{m}\cdot \varvec{n}_F\right) \int _F \left( \varvec{m}^f\right) ^T\textrm{d}\Gamma \cdot \varvec{\Pi }_{1*,F}^\nabla \right] , \end{aligned}$$

(39)

where $\varvec{m}^f$ and $\varvec{\Pi }_{1*, F}^\nabla$ are the scaled monomial vector and Ritz projection matrix with respect to local coordinates $(\xi ,\eta )$. For $k=1$, we can directly calculate the matrix $\varvec{G}^\nabla$ through the volume of the unit |E|, and the matrix $\varvec{B}^\nabla$ can be simplified as

$$\begin{aligned} \varvec{B}^\nabla =\sum _{F\subset \partial E}\left[ \left( \nabla \varvec{m}\cdot \varvec{n}_F\right) \cdot [|F|, 0, 0]\cdot \varvec{\Pi }_{1*,F}^\nabla \right] , \end{aligned}$$

(40)

where |F| is the area of F. Considering the consistency condition in Eq. (32), the Ritz projection matrix is obtained by solving Eq. (36).

4.2 $L_2$ projection operator on polyhedral elements

Based on the $L_2(E)$ projection $\varvec{\Pi }_{l,E}^0\nabla$ of the gradient of variables in $\mathcal {V}_{1,l}(E)$ (see Eq. (29)) to $[\mathbb {P}_l(E)]^3$, this projection can be explicitly expressed as

$$\begin{aligned} \int _{E}\varvec{p}_l^T\varvec{\Pi }_{l,E}^0\nabla u_h \textrm{d}\Omega = \int _{E}\varvec{p}_l^T\nabla u_h\textrm{d}\Omega . \end{aligned}$$

(41)

Integrating by parts of the right-hand side of Eq. (41), we can obtain

$$\begin{aligned} \int _{E}\varvec{p}_l^T\nabla u_h\textrm{d}\Omega = \int _{\partial E}\left( \varvec{p}_l^T\cdot \varvec{n}_F\right) u_h\textrm{d}\Gamma -\int _{E}\left( \text {div}\varvec{p}_l\right) u_h\textrm{d}\Omega . \end{aligned}$$

(42)

The higher-order moments can be considered in the function space $\mathcal {V}_{1,l}(E)$ [41], which also means that we need to calculate the $\mathcal {H}_1$ projection operator.

The key idea for the stabilization-free formulation is to use higher-order polynomials for the gradient, which results in a mixed-form method. For the gradient $\nabla u_h$ and the polynomial $\varvec{p}_l$, we follow the construction in [35, 36], the variable field $u_h$ and the gradient can be expanded as

$$\begin{aligned} \varvec{\Pi }_{l,E}^0\nabla u_h= \left( \varvec{N}^p\right) ^T\varvec{\Pi }^m\tilde{\varvec{u}},\quad \varvec{p}_l=\left( \varvec{N}^p\right) ^T\tilde{\varvec{p}}_l, \end{aligned}$$

(43)

where $\varvec{\Pi }^m$ is a matrix form of the projector $\varvec{\Pi }_{l,E}^0\nabla$ and $\varvec{{N}^p}$ is a matrix of complete polynomial of order l

$$\begin{aligned} \left( \varvec{N}^p\right) ^T:= \begin{bmatrix} \varvec{m}_l^T &{} \varvec{0} &{} \varvec{0}\\ \varvec{0} &{} \varvec{m}_l^T &{} \varvec{0}\\ \varvec{0} &{} \varvec{0} &{} \varvec{m}_l^T \end{bmatrix}. \end{aligned}$$

(44)

Substituting Eq. (43) into Eq. (41), considering Eq. (42) and $u_h = \varvec{\phi }^T\tilde{\varvec{u}}$, yields

$$\begin{aligned}&\tilde{\varvec{p}}^T\int _{E}\varvec{N}^p\left( \varvec{N}^p\right) ^T\textrm{d}\Omega \varvec{\Pi }^m\tilde{\varvec{u}}\nonumber \\&\quad = \tilde{\varvec{p}}^T\int _{\partial E}\left( \varvec{N}^p\cdot \varvec{n}_F\right) \varvec{\phi }^T\textrm{d}\Gamma \tilde{\varvec{u}}-\tilde{\varvec{p}}^T\int _{E}\left( \text {div}\varvec{N}^p\right) \varvec{\phi }^T\textrm{d}\Omega \tilde{\varvec{u}}, \end{aligned}$$

(45)

which can be rewritten as

$$\begin{aligned}{} & {} \int _{E}\varvec{N}^p\left( \varvec{N}^p\right) ^T\textrm{d}\Omega \varvec{\Pi }^m\nonumber \\{} & {} \quad = \int _{\partial E}\left( \varvec{N}^p\cdot \varvec{n}_F\right) \varvec{\phi }^T\textrm{d}\Gamma -\int _{E}\left( \text {div}\varvec{N}^p\right) \varvec{\phi }^T\textrm{d}\Omega , \end{aligned}$$

(46)

since the form is true for all $\tilde{\varvec{u}}$ and $\tilde{\varvec{p}}$. Similar to Eq. (35), Eq. (46) leads to the matrix form

$$\begin{aligned} \varvec{G}\varvec{\Pi }^m = \varvec{B}, \end{aligned}$$

(47)

where

$$\begin{aligned} \varvec{G}:= & {} \int _{E}\varvec{N}^p\left( \varvec{N}^p\right) ^T\textrm{d}\Omega , \end{aligned}$$

(48)

$$\begin{aligned} \varvec{B}:= & {} \int _{\partial E}\left( \varvec{N}^p\cdot \varvec{n}_F\right) \varvec{\phi }^T\textrm{d}\Gamma -\int _{E}\left( \text {div}\varvec{N}^p\right) \varvec{\phi }^T\textrm{d}\Omega . \end{aligned}$$

(49)

The matrices $\varvec{B}$ and $\varvec{G}$ are very similar to the matrices used in the $\mathcal {H}_1$ projection matrix, see Eqs. (37) and (38). Between the two matrices mentioned above, matrix $\varvec{G}$ is more straightforward to compute. It involves dividing the polyhedral element into multiple tetrahedral elements (as shown in Fig. 3) and utilizing Gaussian integration at each tetrahedron for the calculation. Since matrix $\varvec{G}$ is the integration of a complete polynomial, the application of the divergence theorem facilitates the conversion of the integral to the surface F and subsequently to the edge e. A detailed exposition of this process can be found in the VEM book [25].

Fig. 3

Polyhedral triangulation and numerical integration

The calculation of matrix $\varvec{B}$ seems to be very complicated because $\varvec{B}$ contains higher-order moments (see Eq. (49)) that have not been defined before (another understanding is, that we do not know the basis function $\varvec{\phi }$ within the element E and on the element boundary F). In order not to increase the degree of freedom, we can change the first-order polynomial $\mathbb {P}_1$ in the boundary element space (see Eqs. (20) and (24)) to an l-order polynomial $\mathbb {P}_l$ and can take advantage of the properties related to the enlarged enhancement virtual element space (low-order mapping operators approximate high-order moments) [41]. Then the matrix $\varvec{B}$ can be written as

$$\begin{aligned} \varvec{B}&=\sum _{F\subset \partial E}\int _e\varvec{N}^p\varvec{n}_F\Pi _{1,f}^\nabla \varvec{\phi }^T\textrm{d}\Gamma -\int _{E}\left( \text {div}\varvec{N}^p\right) \varvec{\phi }^T\varvec{\Pi }_{1,E}^\nabla \textrm{d}\Omega \nonumber \\&=\sum _{F\subset \partial E}\int _e\varvec{N}^p\varvec{n}_F(\varvec{m}_1^f)^T\textrm{d}\Gamma \varvec{\Pi }_{1*,f}^\nabla \nonumber \\&\quad -\int _{E}\left( \text {div}\varvec{N}^p\right) \varvec{m}_1^T\textrm{d}\Omega \,\varvec{\Pi }_{1*,E}^\nabla . \end{aligned}$$

(50)

The integrations in Eq. (50) can be calculated by partitioning F and E into triangles and tetrahedrons and adopting a Gauss quadrature rule.

Substituting matrices $\varvec{G}$ and $\varvec{B}$ into Eq. (47) yields the projection matrix $\varvec{\Pi }^m$

$$\begin{aligned} \varvec{\Pi }^m = \varvec{G}^{-1}\varvec{B}, \end{aligned}$$

(51)

and the gradient of the variable can be approximated by

$$\begin{aligned} \nabla u\approx \varvec{\Pi }_{l,E}^0\nabla u_h= \left( \varvec{N}^p\right) ^T\varvec{\Pi }^m\tilde{\varvec{u}}. \end{aligned}$$

(52)

5 Stabilization-free virtual element method for 3D hyperelastic problems

According to the discussion in the previous section, we can directly use Eq. (52) to approximate the gradient of the variable. Under the premise of choosing an appropriate polynomial order l, the virtual element method format does not require additional stabilization terms. Therefore, when addressing nonlinear problems such as hyperelasticity, we can employ the same framework (calculation process) as in the finite element method. Subsequently, we will follow the basic ideas in continuum mechanics to construct a format for SFVEM to solve this nonlinear problem.

5.1 Lagrange linearized internal virtual work

Recall from Eq. (10) that the internal virtual work can be expressed in a Lagrange form as

$$\begin{aligned} \mathcal {W} = \int _{V_0}\delta \varvec{E}:\varvec{S}\textrm{d}V_0 \end{aligned}$$

(53)

Then, the linearization of the virtual work is obtained from

$$\begin{aligned} \delta \mathcal {W} = \int _{V_0}\delta \varvec{E}:\Delta \varvec{S}\,\textrm{d}V_0+\int _{V_0}\Delta \left( \delta \varvec{E}\right) :\varvec{S}\,\textrm{d}V_0. \end{aligned}$$

(54)

Considering the definition of the Green-Lagrange strain tensor $\varvec{E}$ (Eq. (4)), we have

$$\begin{aligned} \delta \varvec{E} = \frac{1}{2}\left( \delta \varvec{F}^T\cdot \varvec{F}+\varvec{F}^T\cdot \delta \varvec{F} \right) \end{aligned}$$

(55)

and

$$\begin{aligned} \Delta \delta \varvec{E}&= \frac{1}{2}\left( \delta \varvec{F}^T\cdot \Delta \varvec{F}+\Delta \varvec{F}^T\cdot \delta \varvec{F} \right) \nonumber \\&=\frac{1}{2} \left( \delta \varvec{D}^T\Delta \varvec{D}+\Delta \varvec{D}^T\delta \varvec{D} \right) \end{aligned}$$

(56)

where

$$\begin{aligned} \varvec{D} = \frac{\partial \varvec{u}}{\partial \varvec{X}},\quad \varvec{F} = \varvec{1}+\varvec{D}. \end{aligned}$$

(57)

Substituting Eqs. (56) and (57) into Eq. (54) and considering $\Delta \varvec{S} = \mathcal {D}:\Delta \varvec{E}$, the linearization of the virtual work has the formulation as

$$\begin{aligned} \delta \mathcal {W}&= \int _{V_0}\delta \varvec{E}:\Delta \varvec{S}\textrm{d}V_0+\int _{V_0}\varvec{S}:\left( \delta \varvec{D}^T\cdot \Delta \varvec{D}\right) \textrm{d}V_0\nonumber \\&=\int _{V_0}\delta \varvec{E}:\varvec{\mathcal {D}}:\Delta \varvec{E}\textrm{d}V_0+\int _{V_0}\varvec{S}:\left( \delta \varvec{D}^T\cdot \Delta \varvec{D}\right) \textrm{d}V_0, \end{aligned}$$

(58)

where $\mathcal {D}$ is the constitutive tensor given in Eq. (14).

5.2 Virtual element discretization

For three-dimensional problems, utilizing Voigt notation, the Green-Lagrange strain tensor can be written as

$$\begin{aligned} \hat{\varvec{E}} = \begin{bmatrix} E_{XX}&E_{YY}&E_{YY}&2E_{XY}&2E_{YZ}&2E_{ZX} \end{bmatrix}^T, \end{aligned}$$

(59)

and the second Piola–Kirchhoff stress can be written as

$$\begin{aligned} \hat{\varvec{S}} = \begin{bmatrix} S_{XX}&S_{YY}&S_{ZZ}&S_{XY}&S_{YZ}&S_{ZX} \end{bmatrix}^T. \end{aligned}$$

(60)

Besides, the incremental constitutive relationship can be rewritten as

$$\begin{aligned} \Delta \hat{\varvec{S}} = \hat{\varvec{\mathcal {D}}}\cdot \Delta \hat{\varvec{E}}. \end{aligned}$$

(61)

Considering Eq. (52), the gradient of displacement $\varvec{D}$ (defined in Eq. (57)) can be simulated as

$$\begin{aligned} \varvec{D} = \begin{bmatrix} \frac{\partial u}{\partial X} &{} \frac{\partial u}{\partial Y}&{} \frac{\partial u}{\partial Z}\\ \frac{\partial v}{\partial X} &{} \frac{\partial v}{\partial Y}&{} \frac{\partial v}{\partial Z}\\ \frac{\partial w}{\partial X} &{} \frac{\partial w}{\partial Y}&{} \frac{\partial w}{\partial Z} \end{bmatrix} = \left[ \left( \varvec{N}^p\right) ^T\varvec{\Pi }^m\begin{bmatrix} \tilde{\varvec{u}}&\tilde{\varvec{v}}&\tilde{\varvec{w}} \end{bmatrix}\right] ^T, \end{aligned}$$

(62)

and the Green-Lagrange strain tensor can be calculated as

$$\begin{aligned} \Delta \hat{\varvec{E}}&= \varvec{A}_1\left( \varvec{N}^p\right) ^T\varvec{\Pi }^m\Delta \tilde{\varvec{u}}+\varvec{A}_2\left( \varvec{N}^p\right) ^T\varvec{\Pi }^m\Delta \tilde{\varvec{v}}\nonumber \\&\quad +\varvec{A}_3\left( \varvec{N}^p\right) ^T\varvec{\Pi }^m\Delta \tilde{\varvec{w}}\nonumber \\&= \begin{bmatrix} \varvec{A}_1\left( \varvec{N}^p\right) ^T\varvec{\Pi }^m&\varvec{A}_2\left( \varvec{N}^p\right) ^T\varvec{\Pi }^m&\varvec{A}_3\left( \varvec{N}^p\right) ^T\varvec{\Pi }^m \end{bmatrix} \Delta \tilde{\varvec{U}}\nonumber \\&= \varvec{A}\varvec{N}_p^T\varvec{\Pi }_m \Delta \tilde{\varvec{U}}, \end{aligned}$$

(63)

where

$$\begin{aligned} \varvec{A}_1&= \begin{bmatrix} F_{11} &{} 0 &{} 0\\ 0 &{} F_{12} &{} 0 \\ 0 &{} 0 &{} F_{13} \\ F_{12} &{}F_{11}&{} 0 \\ 0 &{} F_{13} &{} F_{12} \\ F_{13} &{}0&{} F_{11} \end{bmatrix}, \varvec{A}_2 = \begin{bmatrix} F_{21} &{} 0 &{} 0\\ 0 &{} F_{22} &{} 0 \\ 0 &{} 0 &{} F_{23} \\ F_{22} &{}F_{21}&{} 0 \\ 0 &{} F_{23} &{} F_{22} \\ F_{23} &{}0&{} F_{21} \end{bmatrix}\nonumber \\ \varvec{A}_3&= \begin{bmatrix} F_{31} &{} 0 &{} 0\\ 0 &{} F_{32} &{} 0 \\ 0 &{} 0 &{} F_{33} \\ F_{32} &{}F_{31}&{} 0 \\ 0 &{} F_{33} &{} F_{32} \\ F_{33} &{}0&{} F_{31} \end{bmatrix}, \end{aligned}$$

(64)

$$\begin{aligned} \varvec{A}&= \begin{bmatrix} \varvec{A}_1&\varvec{A}_2&\varvec{A}_3 \end{bmatrix}, \end{aligned}$$

(65)

$$\begin{aligned} \varvec{N}_p^T&= \begin{bmatrix} \left( \varvec{N}^p\right) ^T &{} &{} \\ {} &{} \left( \varvec{N}^p\right) ^T &{} \\ {} &{} &{} \left( \varvec{N}^p\right) ^T \end{bmatrix}, \varvec{\Pi }_m = \begin{bmatrix} \varvec{\Pi }^m &{} &{} \\ {} &{} \varvec{\Pi }^m &{} \\ {} &{} &{} \varvec{\Pi }^m \end{bmatrix}, \end{aligned}$$

(66)

and

$$\begin{aligned} \Delta \tilde{\varvec{U}} = \begin{bmatrix} \Delta \tilde{\varvec{u}}&\Delta \tilde{\varvec{v}}&\Delta \tilde{\varvec{w}} \end{bmatrix}^T. \end{aligned}$$

(67)

For the last term in Eq. (58), we can define vector $\varvec{\theta }$ as

$$\begin{aligned} \varvec{\theta } = \begin{bmatrix} \frac{\partial u}{\partial X}&\frac{\partial u}{\partial Y}&\frac{\partial u}{\partial Z}&\frac{\partial v}{\partial X}&\frac{\partial v}{\partial Y}&\frac{\partial v}{\partial Z}&\frac{\partial w}{\partial X}&\frac{\partial w}{\partial Y}&\frac{\partial w}{\partial Z} \end{bmatrix}^T, \end{aligned}$$

(68)

and the term $\delta \varvec{\theta }$ can be calculated as

$$\begin{aligned} \Delta \varvec{\theta } = \varvec{N}_p^T\cdot \varvec{\Pi }_m \cdot \Delta \tilde{\varvec{U}}. \end{aligned}$$

(69)

5.3 Element stiffness matrix and internal force

Based on the definition of $\varvec{\theta }$ given in Eq. (68), the last term in Eq. (58) can be written as

$$\begin{aligned} \varvec{S}:\left( \delta \varvec{D}^T\cdot \Delta \varvec{D}\right)&= \delta \varvec{\theta }^T\cdot \varvec{\mathcal {I}}\cdot \Delta \varvec{\theta }\nonumber \\&= \delta \tilde{\varvec{U}}^T\cdot \left( \varvec{\Pi }_m^T\cdot \varvec{N}_p\right) \cdot \varvec{\mathcal {I}}\nonumber \\&\quad \cdot \left( \varvec{N}_p^T\cdot \varvec{\Pi }_m\right) \cdot \Delta \tilde{\varvec{U}}, \end{aligned}$$

(70)

where

$$\begin{aligned} \varvec{\mathcal {I}} = \begin{bmatrix} \varvec{S} &{} &{} \\ {} &{} \varvec{S} &{} \\ {} &{} &{} \varvec{S} \end{bmatrix}. \end{aligned}$$

(71)

Substituting Eq. (70) into Eq. (58), the linearized variation of energy can be written as

$$\begin{aligned} \delta \mathcal {W} = \int _{V_0}\delta \hat{\varvec{E}}^T\cdot \hat{\varvec{\mathcal {D}}}\cdot \Delta \hat{\varvec{E}}\textrm{d}V_0 +\int _{V_0}\delta \varvec{\theta }^T\cdot \varvec{\mathcal {I}}\cdot \Delta \varvec{\theta }\textrm{d}V_0. \end{aligned}$$

(72)

Consider Eqs. (63) and (69), we have

$$\begin{aligned} \delta \mathcal {W}&=\delta \tilde{\varvec{U}}^T\cdot \int _{V_0} \left( \varvec{\Pi }_m^T\cdot \varvec{N}_p\cdot \varvec{A}^T\right) \nonumber \\&\quad \cdot \hat{\varvec{\mathcal {D}}}\cdot \left( \varvec{A}\cdot \varvec{N}_p^T\cdot \varvec{\Pi }_m\right) \textrm{d}V_0\cdot \Delta \tilde{\varvec{U}}\nonumber \\&\quad +\delta \tilde{\varvec{U}}^T\cdot \int _{V_0} \left( \varvec{\Pi }_m^T\cdot \varvec{N}_p\right) \cdot \varvec{\mathcal {I}}\cdot \left( \varvec{N}_p^T\cdot \varvec{\Pi }_m\right) \textrm{d}V_0\cdot \Delta \tilde{\varvec{U}}. \end{aligned}$$

(73)

Then the element tangent stiffness matrix can be obtained by

$$\begin{aligned} \varvec{K}^t_{K2} = \varvec{K}^{t1}_{K2}+\varvec{K}^{t\sigma }_{K2}, \end{aligned}$$

(74)

where

$$\begin{aligned} \varvec{K}^{t1}_{K2} = \varvec{\Pi }_m^T\cdot \int _{V_0} \varvec{N}_p\cdot \varvec{A}^T\cdot \hat{\varvec{\mathcal {D}}}\cdot \varvec{A}\cdot \varvec{N}_p^T \textrm{d}V_0\cdot \varvec{\Pi }_m, \end{aligned}$$

(75)

$$\begin{aligned} \varvec{K}^{t\sigma }_{K2}=\varvec{\Pi }_m^T\cdot \int _{V_0} \varvec{N}_p\cdot \varvec{\mathcal {I}}\cdot \varvec{N}_p^T \textrm{d}V_0\cdot \varvec{\Pi }_m. \end{aligned}$$

(76)

Fig. 4

3D Cook’s membrane problem, a Geometry and boundary condition; b example of a polyhedral swept mesh; c example of a regular mesh

The $\varvec{\Pi }_m$ matrix is calculated and stored before the iteration. In addition, in each nonlinear iteration step, the integral term in the tangent stiffness matrix needs to be calculated based on the current stress state. Similar to before, the integral can be calculated by dividing the polyhedron into tetrahedrons and adopting a Gauss quadrature rule. The internal force is obtained from Eq. (10) as

$$\begin{aligned} \varvec{F}_{\text {int}} = \varvec{\Pi }_m^T\cdot \int _{V_0}\varvec{N}_p\cdot \varvec{A}^T\cdot \hat{\varvec{S}}\textrm{d}V_0. \end{aligned}$$

(77)

At each step, the second Piola–Kirchhoff stress $\hat{\varvec{S}}$ at each interpolation point is calculated and the Cauchy stress $\varvec{\sigma }$ can be calculated as

$$\begin{aligned} \varvec{\sigma } = \frac{1}{J}\varvec{F}\cdot \varvec{S}\cdot \varvec{F}^T. \end{aligned}$$

(78)

6 Numerical examples

6.1 3D Cook’s membrane problem

As a first example, we consider the standard Cook’s membrane bending test with the geometric model illustrated in Fig. 4. The relevant dimensions are $L=48$, $H_1 = 44$, $H_2 = 16$, $B=10$. The left side of the tapered beam is fixed and the right side is applied a constant distributed vertical load $q_y$. The material parameters are selected as $\lambda = 100$ and $\mu = 40$. The distributed vertical load is given as $q_y = 4$.

For SFVEM, it is necessary to ensure that the order of the basis function of the strain mode meets the requirements (the rank of the resulting stiffness matrix is correct). Using an eigenvalue analysis of different polyhedral elements, see [45], a relationship between the number of vertices and the polynomial order l was obtained. Furthermore, we note that while an individual element is rank deficient, the rank of the global stiffness matrix can be correct. In such cases, a low-order polynomial ($l=1$) can be used to avoid the high computational cost caused by the domain integration. The results obtained from polynomials of different orders will be compared in this example.

To compare the performance of SFVEM for 3D hyperelastic problems, the first-order finite element method (Q1) is selected. The convergence is studied here by adopting various meshes using uniform refinement. Four different meshes defined by the parameter N which corresponds to the number of divisions $2^N\times 2^N$ in $L\times H$ are selected. As shown in Fig. 4, two different types of meshes including a polyhedral swept mesh and a hexahedral swept mesh are used in this example. For different meshes, the maximum vertical displacement $u_y$ for different divisions $2^N$ are solved by different methods and compared in Table 1.

Table 1 Maximum vertical displacement $u_y$ for different element division N for polyhedral and regular meshes

Table 1 illustrates that the results calculated by SFVEM for regular meshes are very close to those obtained by FEM. The results depict the same convergence characteristic as SFVEM. Polyhedral meshes do not change this behavior. The order of the polynomial $l=1$ yields already accurate results. Higher-order polynomials are less efficient for the same accuracy. The convergence curves obtained by different methods and different parameters are shown in Fig. 5. Besides, for $l=1$ and $N=4$, the contour plots of displacements $u_y$ and stresses $S_{yx}$ are given in Figs. 6 and 7.

Fig. 5

Maximum value of vertical displacement $u_y$ for different element division $2^N$

Fig. 6

Contour plots of displacement $u_y$ obtained by SFVEM for different meshes, $l=1, N=4$

Fig. 7

Contour plots of stresses $S_{xy}$ obtained by SFVEM for different meshes, $l=1, N=4$

6.2 Punch problem

In this example, a punch problem is selected which is subjected to high compression loading. The geometry and relevant dimensions are given in Fig. 8 as $L_1 = L_2 = 2$, $H=1$. A surface load $P = 300$ is applied on one-quarter of the block and other boundary conditions are given in Fig. 8. The Neo-Hookean material model is used with the Lame constants $\lambda = 400.75$ and $\mu =92.5$.

Fig. 8

Punch problem and boundary boundary conditions

Table 2 Maximum vertical displacement $u_z$ for different element division N for polyhedral and regular meshes

Fig. 9

Minimum value (corner A) of vertical displacement $u_z$ for different element division N

Fig. 10

Contour plots of displacements and stresses obtained by SFVEM with different meshes, a, b displacements $u_z$; c, d stresses $s_{zz}$

Similar to the first example, a numerical convergence study is presented for different meshes. The vertical displacement $u_z$ of point A (as shown in Fig. 8) is reported for mesh refinement parameter N corresponding to a mesh of $N\cdot 2N\cdot 2N$ for regular and polyhedral meshes. For the regular meshes, the order of the strain mode is selected as $l=1$. For the polyhedral meshes, the order of the strain mode is selected as $l=1$ and $l=2$. The first-order finite element method (FEM, Q1) is selected for comparison.

The values of the vertical displacements $u_z$ of point A are calculated and given in Table 2 for regular meshes and polyhedral meshes. For the regular hexahedral mesh, the results obtained by SFVEM are very close to those obtained by FEM, even for coarse meshes. For polyhedral meshes, for strain modes of different orders l, the displacement results obtained are different only in the case of the coarsest mesh ($N=4$). The reason for this difference may be that the mesh size is too large. For other meshes, the displacement results obtained by different orders l are basically the same.

The convergence of the displacement $u_z$ of point A is demonstrated in Fig. 9. For the current material and load boundary conditions, we used a quadratic (Q2) element to calculate a reference solution, which led to $u_z^\text {ref} = -0.6344$ and is illustrated in Fig. 9. It can be seen from the figure that although the results obtained by the hexahedral mesh are in better agreement with the finite element, the results obtained by the polyhedral mesh are closer to the reference solution.

Finally, for $N=10$, the contour plots of displacement $u_z$ and stress $\sigma _{zz}$ obtained by SFVEM on hexahedral mesh ($l=1$) and polyhedral mesh ($l=2$) are depicted in Fig. 10.

Fig. 11

Twisting column: geometry, hexahedral mesh and polyhedral mesh used for the analysis

Fig. 12

Contour plots of displacements $u_y$ obtained by SFVEM with different meshes, a–c hexahedral mesh; d–f polyhedral mesh

6.3 Twisting of a column

In this example, the twisting of a column is used to evaluate the performance of the proposed method under extremely large deformations. The geometry of the problem and the virtual element meshes (including hexahedral meshes and polyhedral meshes) are given in Fig. 11. The bottom nodes are fixed and the top nodes rotate around the Z-axis as:

$$\begin{aligned} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \cos \theta &{} -\sin \theta &{} 0\\ \sin \theta &{} \cos \theta &{} 0\\ 0 &{} 0 &{} 1 \end{bmatrix}\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}, \end{aligned}$$

(79)

where (X, Y, Z) represents the initial configuration, (x, y, z) is the deformed configuration. Besides, $\theta$ represents the angle of rotation for the top surface around the Z-axis.

The material model for this example is assumed as Neo-Hookean hyperelastic with the Lame parameters $\lambda = 100$ and $\mu = 40$. The angle of rotation of the top surface is given as $\theta =\pi$. The order of the polynomial is selected as $l=1$ to save computing time. For different meshes, the deformed shapes and contour plots of displacement $u_y$ are provided in Fig. 12. Again, the regular and polyhedral meshes lead to the same responses.

6.4 Force deformation of round arch

The last example is an arch subjected to a concentrated load. The geometric model and polyhedral mesh are given in Fig. 13. The outer radius of the arch is 100, the inner radius is 95, and the thickness is 10. As shown in Fig. 13, two different boundary conditions are applied. For boundary condition 1, the left side of the model is fixed. For boundary condition 2, the left side of the model is hinged. For two different boundary conditions, the bottom right end of the model is fixed. Nodal forces are applied to the top of the model. The material parameters are assumed as $E=5$ and $\nu = 0.35$.

Fig. 13

Three-dimensional arch geometry and mesh. This problem considers two different boundary conditions: boundary condition 1: the left side of the model is fixed, boundary condition 2: the left side of the model is hinged

This type of structure is geometrically unstable and needs the path-following or arc-length solution method. The basic idea of the arc-length method is to add a constraint condition to the set of nonlinear equations, which is associated with the total load factor $\lambda$. Since the method proposed in this work does not require stabilization, the techniques employed in the nonlinear finite element method can be directly used. For details, see related books on nonlinear finite elements method [46].

For the first type of boundary condition, the initial load factor $\lambda$ is selected as $\lambda =0.2$. For the second type of boundary condition, the initial load factor $\lambda$ is selected as $\lambda =0.02$. The evolution of displacement $u_y$ of point A (as shown in Fig. 13) with respect to the load factor is plotted in Fig. 14 and Fig. 15 for different boundary conditions, respectively.

Fig. 14

Load displacement curve of the round arch with boundary 1

The load-deflection curves obtained with the SFVEM match very well with the solutions obtained by FEM with similar meshes. For the second type of boundary condition, Fig. 15 shows the complex nonlinear behavior (snap-back) of this simple structure. The contour plots obtained under different displacements and different boundary conditions are provided in Fig. 16.

Fig. 15

Load displacement curve of the round arch with boundary 2

Fig. 16

Contour plots of displacement $u_y$ at different times

7 Conclusion

This paper introduces a stabilization-free virtual element method for 3D hyperelastic problems. As an extension to the two-dimensional problem, a first-order three-dimensional virtual element method without any stabilization is presented. This paper discusses in detail the specific calculation process of the traditional first-order $\mathcal {H}_1$ projection operator and the high-order $L_2$ projection operator for three-dimensional polyhedral elements. The $L_2$ projection operators are computed relying on the components of the gradient, and the matrix for strain approximation is directly constructed. As no stability terms are required in SFVEM, hyperelastic problems can be directly solved within the framework following the finite element method. Benchmark examples are used to demonstrate the accuracy of the 3D SFVEM for hyperelastic problems. In addition, this paper also uses the arc-length method to track the complete structural deformation of unstable structures. It can be seen from the numerical examples that when using a hexahedral mesh, the results obtained are similar to FEM. At the same time, SFVEM yields more accurate results for polyhedral meshes. Since no stabilization term is required, the method can be applied to complex multiphysics problems, such as large-strain incompressible electromechanics or electromechanical growth problems in the future.