Localization in log-gamma polymers with boundaries

Abstract

Consider the directed polymer in one space dimension in log-gamma environment with boundary conditions, introduced by Seppäläinen (Ann Probab, 40(1):19–73, 2012). In the equilibrium case, we prove that the end point of the polymer converges in law as the length increases, to a density proportional to the exponent of a zero-mean random walk. This holds without space normalization, and the mass concentrates in a neighborhood of the minimum of this random walk. We have analogous results out of equilibrium as well as for the middle point of the polymer with both ends fixed. The existence and the identification of the limit relies on the analysis of a random walk seen from its infimum.

1 Directed polymers and localization

The directed polymer model was introduced in the statistical physics literature by Huse and Henley [25] to mimic the phase boundary of Ising model in presence of random impurities, and it is frequently used to study the roughness statistics of random interfaces. Later, it has been mathematically formulated as a random walk in a random potential by Imbrie and Spencer [26]. In the $(1+1)$-dimensional lattice polymer case, the random potential is defined by a field of random variables $\{\omega (i,j):(i,j) \in \mathbb {Z}^2\}$ and a polymer $\mathbf{x}=(x_t; t=0,\ldots n)$ is a nearest neighbor up-right path in $\mathbb {Z}^2$ of length n. The weight of a path is equal to the exponent of the sum of the potential it has met on its way. There is a competition between the entropy of paths and the disorder strength, i.e., the inhomogeneities of the potential. If the potential is constant, the path behaves diffusively and spreads smoothly over distances of order of the square root of its length. On the contrary, if the potential has large fluctuations, the path is pinned on sites with large potential values, and it localizes on a few corridors with width of order of unity. An early example where this behavior was observed is the parabolic Anderson model yielding a rigourous framework to analyse intermittency [8]. Recently, significant efforts have been focused on planar polymer models (i.e. $(1+1)$-dimensional) which fall in the KPZ universality class (named after Kardar, Parisi and Zhang), see Corwin’s recent survey [13]. In the line of specific first passage percolation models and interacting particle systems, a few explicitly solvable models were discovered, and they allow for detailed descriptions of new scaling limits and statistics. We namely mention Brownian queues [30], log-gamma polymer [35], KPZ equation [23, 33]. However, the theory of universality classes does not explain the localization phenomena. For instance, the wandering exponent 2 / 3 from the KPZ class accounts for the typical transverse displacement of order $n^{2/3}$ of the polymer of length n, certainly an important information, however different in nature since it addresses the location of the corridor but not its width.

Let us start by defining the model of directed polymers in random environment. For each endpoint (m, n) of the path, we can define a point-to-point partition function

$$\begin{aligned} Z_{m,n}^{\omega }= \sum _{\mathbf{x}} \exp \left\{ \sum _{t=1}^{m+n}\omega (x_t)\right\} , \end{aligned}$$

where the sum is over up-right paths $\mathbf{x}$ that start at (0, 0) and end at (m, n). The model does not have a temperature in the strict sense of statistical mechanics, however the parameter $\mu$ entering below the log-gamma distribution of $\omega$ plays a similar role by tuning the strength of the disorder. The point-to-line partition function is given by

$$\begin{aligned} Z_{n}^{\omega }= \sum _{k=0}^n Z_{k,n-k}^{\omega }. \end{aligned}$$

The point-to-line polymer measure of a path of length n is

$$\begin{aligned} Q_{n}^{\omega }(\mathbf{x})= \frac{1}{Z_{n}^{\omega }} \exp \left\{ \sum _{t=1}^{n}\omega (x_t)\right\} . \end{aligned}$$

It is known that the polymer at a vanishing temperature concentrates on its geodesics. However little information is known on the random geodesics [31], except under assumptions which are often hard to check [15, 19]. A less ambitious way to analyze this localization phenomenon is to consider the endpoint of the path, and study the largest probability for ending at a specific point,

$$\begin{aligned} I_n=\max _{x\in \mathbb {Z}}Q_{n-1}^{\omega }\{x_n=x\}, \end{aligned}$$

(1)

which does not require any information on where the endpoint concentrates. Observe that $I_n$ is small when the measure is spread out, for example if $\omega$ is constant, but $I_n$ should be much larger when $Q_{n}^{\omega }$ concentrates on a small number of paths. In large generality it is proved that the polymer is localized and it is expected from the KPZ scaling that most of the endpoint density lies in a relatively small region around a random point at distance $n^{2/3}$ from the mid-point of the transverse diagonal. The size of this region is much smaller than $n^{2/3}$ and is believed that it is order one. Moreover, Carmona and Hu [7] and Comets, Shiga and Yoshida [10] showed that there is a constant $c_0=c_0(\beta )>0$ such that the event

$$\begin{aligned} \limsup _{n\rightarrow \infty } I_n \ge c_0 \end{aligned}$$

has $\mathbb {P}$-probability one. This property is called endpoint localization. In fact, the Césaro mean of the sequence $I_n$ is a.s. lower bounded by a positive constant. Analyzing terms in semimartingale decompositions, the technique is quite general, but also very circuitous and thus it only provides rough estimates. Recently, Seppäläinen has introduced in [35] a new solvable polymer model with a particular choice of the law of the potential. In this paper, we consider the log-gamma model, taking advantage of its solvability to analyze the mechanism of localization and obtain an explicit description. The model can be defined with boundary conditions (b.c.), i.e., with a different law for vertices inside the quadrant or on the boundary, see (2). From now, we will consider this model. First, it is convenient to introduce multiplicative weights

$$\begin{aligned} Y_{i,j}= e^{\omega (i,j)} , \ (i,j) \in \mathbb {Z}_+^2. \end{aligned}$$

As discovered in the seminal paper [35], some boundary conditions make the model stationary as in Burke’s theorem [32], and further, they make it explicitely sovable. In this setting, the point-to-point partition function for the paths with fixed endpoint is given by

$$\begin{aligned} Z_{m,n}= \sum _{\mathbf{x}\in \Pi _{m,n} }\prod _{t=1}^{m+n} Y_{x_t}, \end{aligned}$$

where $\Pi _{m,n}$ denotes the collection of up-right paths $\mathbf{x}=(x_t)_{0\le t\le m+n}$ in the rectangle $\Lambda _{m,n}=\{0,\dots ,m\}\times \{0,\dots ,n\}$ that go from (0, 0) to (m, n). We assign distinct weight distributions on the boundaries $(\mathbb {N}\times \{0\}) \cup (\{0\}\times \mathbb {N})$ and in the bulk $\mathbb {N}^2$. In order to make it clear, we use the symbols U and V for the weights on the horizontal and vertical boundaries:

$$\begin{aligned} U_{i,0}=Y_{i,0} \quad \hbox {and} \quad V_{0,j}= Y_{0,j} \quad \hbox {for} \quad i,j \in \mathbb {N}:=\{1,2,\ldots \}. \end{aligned}$$

Model b.c.( $\theta )$: Let $\mu >0$ be fixed. For $\theta \in (0,\mu )$, we will denote by b.c.($\theta$) the model with

$$\begin{aligned}&\{U_{i,0}, V_{0,j},Y_{i,j}: i,j \in \mathbb {N}\} \ \hbox {are independent with distributions} \nonumber \\&U_{i,0}^{-1} \sim \hbox {Gamma}(\theta ,1), \quad V_{0,j}^{-1} \sim \hbox {Gamma}(\mu -\theta ,1),\quad Y_{i,j}^{-1} \sim \hbox {Gamma}(\mu ,1).\quad \end{aligned}$$

(2)

where $\hbox {Gamma}(\theta ,r)$ distribution has density $\Gamma (\theta )^{-1}r^{\theta }x^{\theta -1}e^{-rx}$ with $\theta >0, r>0$.

The polymer model with boundary condition possesses a two-dimensional stationarity property. Using this property, Seppäläinen [35] obtains an explicit expression for the variance of the partition function, he proves that the fluctuation exponent of free energy is 1 / 3 and that the exponent for transverse displacement of the path is 2 / 3. This model has soon attracted a strong interest: large deviations of the partition function [21], explicit formula for the Laplace transform of the partition function at finite size [14], GUE Tracy-Widom fluctuations for $Z_n$ at scale $n^{1/3}$ [6], computations of Busemann functions [20].

In fact, the model of directed polymers can be defined in arbitrary dimension $1+d$ and with general environment law, see [26], and we now briefly mention some results for comparison. In contrast with the above results for $d=1$, if the space dimension is large and the potential has small fluctuations—the so-called weak disorder regime—this exponent is 0, and under $Q_n^{\omega }$ the fluctuation of the polymer path is order $\mathcal {O}(n^{1/2})$ with a Brownian scaling limit, see [5, 11, 26]. More precisely, if the space dimension $d\ge 3$ and if the ratio ${\mathbb E} (e^{2 \omega } ) / ({\mathbb E} e^{\omega })^2$ is smaller than the inverse of the return probability for the simple random walk, the end point, rescaled by $n^{-1/2}$, converges to a centered d-dimensional Gaussian vector. Moreover, under the previous assumptions, $I_n \rightarrow 0$ a.s., at the rate $n^{-d/2}$ according to the local limit theorem of [37, 39].

Let us come back to the case $d=1$ of up-right polymer paths, more precisely, to the log-gamma model. We now give a flavour of our results with an explicit limit description of the endpoint distribution under the quenched measure.

$$\begin{aligned} Q_{n}^{\omega }\left\{ x_n=(k,n-k)\right\} =\frac{Z_{k,n-k}}{Z_n}, \quad k=0,\ldots , n. \end{aligned}$$

For each n, denote by

$$\begin{aligned} l_n={\arg \max }\left\{ Z_{k,n-k}; 0 \le k \le n\right\} , \end{aligned}$$

(3)

the location maximizing the above probability, and call it the “favourite endpoint”.

Theorem 1

Consider the model b.c.($\theta$) with $\theta \in (0,\mu )$. Define the end-point distribution $\tilde{\xi }^{(n)}$ centered around its mode, by

$$\begin{aligned} \tilde{\xi }^{(n)}=\left( \tilde{\xi }^{(n)}_k; k \in {\mathbb Z}\right) , \quad \text{ with } \quad \tilde{\xi }^{(n)}_k = Q_{n}^{\omega }\left\{ x_n=(l_n+k,n-l_n-k)\right\} . \end{aligned}$$

Thus, $\tilde{\xi }^{(n)}$ is a random element of the set ${\mathcal M}_1$ of probability measures on ${\mathbb Z}$. Then, as $n \rightarrow \infty$, we have convergence in law

$$\begin{aligned} \tilde{\xi }^{(n)} \mathop {\longrightarrow }\limits ^{\mathcal L} \xi \quad \text{ in } \text{ the } \text{ space } ({\mathcal M}_1, \Vert \cdot \Vert _{TV}), \end{aligned}$$

(4)

where $\Vert \mu -\nu \Vert _{TV}= \sum _k |\mu (k)-\nu (k)|$ is the total variation distance.

The definition of $\xi _k$ is given as a functional of a random walk conditioned to stay positive on ${\mathbb Z}^+$ and conditioned to stay strictly positive on ${\mathbb Z}^-$. The explicit expression for $\xi$ is formula (12) below. The convergence is not strong but only in distribution. The above result yields a complete description of the localization phenomenon revealed in [7, 10]. In particular, the mass of the favourite point is converging in the distributional sense.

Corollary 1

Consider the model b.c.$(\theta )$ from (2). With $I_n$ from (1), it holds

$$\begin{aligned} I_n \mathop {\longrightarrow }\limits ^{\mathcal L} \max \left\{ \frac{\xi _k+\xi _{k+1}}{2}; k \in {\mathbb Z}\right\} >0 , \end{aligned}$$

as $n \rightarrow \infty$. By consequence, $\limsup _n I_n >0 \ \ \mathbb {P}$-a.s.

Moreover, we derive that the endpoint density indeed concentrates in a microscopic region, i.e., of size ${\mathcal O}(1)$, around the favourite endpoint.

Corollary 2

(Tightness of polymer endpoint) Consider the model b.c.$(\theta )$ from (2) with $\theta \in (0,\mu )$. Then we have

$$\begin{aligned} \lim \limits _{K\rightarrow \infty } \limsup _{n\rightarrow \infty } Q_n^{\omega }\left[ \Vert x_n-(l_n,n-l_n)\Vert \ge K\right] =0 \ \ \mathrm{in \ probability.} \end{aligned}$$

(5)

Our results call for a few comments.

Remark 1

(i) Influence of high peaks in the parabolic Anderson model: it is easy to check that the sequence $Z_{m,n}$ is the unique solution of the parabolic Anderson equation

$$\begin{aligned} Z_{m,n}=e^{\omega (m,n)} [Z_{m-1,n}+Z_{m,n-1}] \end{aligned}$$

with initial condition $Z_{0,0}=1$ and boundary conditions $Z_{-1,n}=Z_{m,-1}=0$. Hence, $Z_{m,n}$ can be interpreted as the mean density at time $m+n$ and location (m, n) of a population starting from one individual at the origin, subject to the following discrete dynamics: each particle splits at each integer time into a random number (with mean $2 e^{\omega (m,n)}$ at location (m, n)) of identical individual moving independently, and jumping instantaneously one step upwards or to the right. If $e^{-\omega (m,n)} \sim Gamma(\mu ), e^{-\omega (m,0)} \sim Gamma(\theta ),$ and $e^{-\omega (0,n)} \sim Gamma(\mu -\theta )$, our result applies, and shows that the population concentrates around the highest peak and spreads at distance O(1). In particular, the second high peak does not contribute significantly to the measure, a feature which is believed to hold in small space dimension only. In large time, the population density converges, without any scaling, to a limit distribution given by $\xi$.

(ii) Corollary 2 states uniqueness of the favourite endpoint, in the sense that all the mass is concentrated in the neighborhood of the favourite point $l_n$. This property is analogous to uniqueness of geodesics in planar oriented last passage percolation. We refer to [15, 19] for a detailed and recent account on this and related questions.

Besides the point-to-line polymer measure, we also study in this paper the point-to-point measure, for which the polymer endpoint is prescribed. Under this measure, we obtain similar localization results, that we will state in the next section. They deal with the location in the direction transverse to the overall displacement of the “point in the middle” of the polymer chain, and with the “middle edge”. They are the first results of this nature. The main reason is that the general approach via martingales in [7, 10] fails to apply if the endpoint of the path is fixed. We mention that the alternative method, introduced in [40] to deal with environment without exponential moments, could be applied to point-to-point measures. A similar comment holds for another approach, based on integration by parts, which has been recently introduced in [9] to extend localization results to the path itself—and then reveal the favourite corridors. So far, it is known to apply to Gaussian environment and Poissonian environment [12], but whether it covers the log-gamma case is still open.

As we will see in Sect. 2, the localization phenomena around the favourite point in the log-gamma model directly relates to the problem of splitting a random walk at its local minima. This coupling is also the main tool to study the recurrent random walk in random environment [18] in one dimension. In the literature, it was proved by Williams [41], Bertoin [1–3], Bertoin and Doney [4], Kersting and Memişoǧlu [28] that if the random walk is split at its local minimum, the two new processes will converge in law to certain limits which are related to a process called the random walk conditioned to stay positive/negative. The mechanism is reminiscent of that of the localization in the main valley of the one-dimensional random walk in random environment in the recurrent case, discovered by Sinaï [36] and studied by Golosov [22].

Our results only hold for boundary conditions ensuring stationarity. A possible way towards the model without boundary conditions could be via techniques of tropical combinatorics initiated in [14].

Organization of the paper: In Sect. 2, we recall the basic facts on the log-gamma model and state the main localization results both for point-to-line and point-to-point measures. In Sect. 3, we introduce the important properties of the random walk conditioned to stay positive that we need to define the limits. In Sect. 4 we give the proofs of Theorem 1, Corollaries 1 and 2. The last section contains the complete statements for the point-to-point measure, together with their proofs.

2 Polymer model with boundary conditions and results

2.1 Endpoint under the point-to-line measure

Assume the condition (2). Define for $(m,n)\in \mathbb {Z}_+^2$,

$$\begin{aligned} U_{m,n}= \frac{Z_{m,n}}{Z_{m-1,n}} \quad \hbox {and} \quad V_{m,n}= \frac{Z_{m,n}}{Z_{m,n-1}}. \end{aligned}$$

We can associate the U’s and V’s to edges of the lattice $\mathbb {Z}_+^2$, so that they represent the weight distribution on a horizontal or vertical edge respectively. Let $\mathbf{e_1}, \mathbf{e_2}$ denote the unit coordinate vectors in $\mathbb Z^2$. For an horizontal edge $f=\{y-\mathbf{e_1},y\}$ we set $T_f=U_y$, and $T_f= V_y$ if $f=\{y-\mathbf{e_2},y\}$. Let ${\mathbf z}= (z_k)_{k \in \mathbb {Z}}$ be a nearest-neighbor down-right path in $\mathbb {Z}_+^2$, that is, $z_k \in \mathbb {Z}_+^2$ and $z_k-z_{k-1}=\mathbf{e_1} \ \hbox {or} -\mathbf{e_2}$. Denoting the undirected edges of the path by $f_k=\{z_{k-1},z_k\}$, we then have

$$\begin{aligned} T_{f_k}= \left\{ \begin{array}{ll} U_{z_k}, &{} \hbox {if} \ f_k\ \hbox {is a horizontal edge}\\ V_{z_{k-1}} &{} \hbox {if}\ f_k\ \hbox {is a vertical edge.}\\ \end{array} \right. \end{aligned}$$

Seppäläinen proved [35] that the choice of log-gamma distribution provides a stationary structure to the model:

Fact 1

(Theorem 3.3 in [35]) Assume (2). For any down-right path $(z_k)_{k\in \mathbb {N}}$ in $\mathbb {Z}_+^2$, the variables $\{T_{f_k}: k\in \mathbb {Z}\}$ are mutually independent with marginal distributions

$$\begin{aligned} \begin{aligned} U^{-1}&\sim \hbox {Gamma}(\theta ,1), \ V^{-1}\sim \hbox {Gamma}(\mu -\theta ,1). \end{aligned} \end{aligned}$$

By considering the down-right path along the vertices x with $x\cdot ({\mathbf { e_1+e_2}})=n$, we deduce the following fact, which will be a fundamental ingredient in the next two sections.

Fact 2

For each n, the variables $(U_{k,n-k},V_{k,n-k})_{0\le k\le n}$ are independent, and

$$\begin{aligned} U_{k,n-k}^{-1} \sim \hbox {Gamma}(\theta ,1)\ \ \ V_{k,n-k}^{-1} \sim \hbox {Gamma}(\mu -\theta ,1). \end{aligned}$$

(6)

Now, define for each $1\le k \le n$ the random variable $X_k^n$

$$\begin{aligned} X_k^n= -\log \left( \frac{Z_{k,n-k}}{Z_{k-1,n-k+1}}\right) =-\log \left( \frac{U_{k,n-k}}{V_{k-1,n-k+1}}\right) , \end{aligned}$$

and $X_0^n =0$. By corollary 2, for each n, $(X_k^n)_{1\le k\le n}$ are i.i.d random variables, and satisfy

$$\begin{aligned} \frac{Z_{k,n-k}}{Z_{0,n}}= \exp \left( -\sum _{i=0}^k X_i^n\right) . \end{aligned}$$

(7)

Defining $S_k^n= \sum _{i=1}^k X_i^n$, for $0\le k\le n$, we will express the mass at point $(k,n-k)$ as a function of $S^n$,

$$\begin{aligned} Q_{n}^{\omega }\{x_n=(k,n-k)\} = \frac{Z_{k,n-k}}{\sum _{i=0}^n Z_{i,n-i}} = \frac{1}{\sum _{i=0}^n \exp (-(S_i^n-S_k^n))} \end{aligned}$$

From (7), the favourite point $l_n$ defined in (3) is also the minimum of the random walk,

$$\begin{aligned} l_n={\arg \min }\left\{ S_k^n; 0 \le k \le n\right\} . \end{aligned}$$

(8)

Since we are only interested in the law of $Q_{n}^{\omega }\{x_n=(k,n-k)\}$, in order to simplify the notion, we consider a single set of i.i.d random variables $(X_k)_{k\in \mathbb {Z}_+}$, with the same distribution under $\mathbb {P}$ as $\log (U/V)$, where U and V are independent with the same distribution as in (6). The associated random walk is given by

$$\begin{aligned} S_n=\sum _{i=1}^n X_i, \end{aligned}$$

(9)

and we define

$$\begin{aligned} \xi _k^n= \frac{1}{\sum _{i=0}^n \exp (-(S_i-S_k))}. \end{aligned}$$

Then one can check that for every n:

$$\begin{aligned} (\xi _k^n)_{0\le k\le n} \mathop {=}\limits ^{\mathcal {L}}\left( Q_{n}^{\omega }\{x_n=(k,n-k)\}\right) _{0\le k\le n}, \end{aligned}$$

where $\mathop {=}\limits ^{\mathcal {L}}$ means equality in law. Then instead of considering for each n a new set of i.i.d random variables to calculate $\tilde{\xi }_k^{(n)}$, we just need the n first steps of the random walk $S_n$ to compute the law of $\xi _k^n$. Hence Theorem 1 can be reformulated as follows:

$$\begin{aligned} \left\{ \xi _{\ell _n+k}^n\right\} _{k\in \mathbb {Z}}\mathop {\longrightarrow }\limits ^{\mathcal {L}}\{\xi _k\}_{k\in \mathbb {Z}}, \quad \text{ in } \text{ the } \ell _1-\mathrm{norm}, \end{aligned}$$

(10)

with

$$\begin{aligned} \ell _n=\underset{k\le n}{\arg \min }\ S_k. \end{aligned}$$

(11)

Since the environment has a continuous distribution, the minimum is a.s. unique. The complete construction of the limit $\xi _k$ will be given in Sect. 4 below in two different cases when $\theta =\mu /2$ and $\theta \ne \mu /2$. However, for the convenience of the reader, we give an informal definition, starting with the case $\theta =\mu /2$. Let $(S^\uparrow _k,k \ge 0), (S_k^\downarrow , k \ge 0)$ be two independent processes, with the first one distributed as the random walk S conditioned to be non-negative (forever), and the second one distributed as the random walk S conditioned to be positive (for positive k). Since we condition by a negligible event, the proper definition requires some care, it relies on Doob’s h-transform. Then,

$$\begin{aligned} \xi _k = \left\{ \begin{array}{ll} \frac{ {\exp (-S_k^\uparrow )}}{ 1+\sum _{i=1}^\infty \exp (-S_i^\uparrow )+\sum _{i=1}^\infty \exp (-S_i^\downarrow )}, &{}\quad \hbox {if} \ k\ge 0,\\ \frac{\exp (-S_k^\downarrow )}{ 1+\sum _{i=1}^\infty \exp (-S_i^\uparrow )+\sum _{i=1}^\infty \exp (-S_i^\downarrow )}, &{} \quad \hbox {if} \ k<0. \\ \end{array} \right. \end{aligned}$$

(12)

In the case $\theta <\mu /2$, then $l_n = {\mathcal O}(1)$, but the limit is still given by the formula (12), provided that $S^\downarrow$ has a lifetime (equal to the time for the walk to reach its absolute minimum), after which it is infinite. $S^\uparrow$ is as before, and it is defined in a classical manner. Thus, the concatenated process is simply equal to S with a space shift by its minimum value, and time shift by the time to reach the minimum. The last case $\theta >\mu /2$ is similar under the change $k \mapsto n-k$.

In particular in the equilibrium case $\theta =\mu /2$, $S_k$ is a random walk with expectation zero. By Donsker’s invariance principle, the random walk has a scaling limit,

$$\begin{aligned} \left( \frac{1}{\sqrt{n}}S_{[nt]}\right) _t \mathop {\longrightarrow }\limits ^{\mathcal {L}}(W_t)_t. \end{aligned}$$

with W a Brownian motion with diffusion coefficient $2 \Psi _1(\mu /2)$ (there, $\Psi _1(\theta )= (\log \Gamma )\text {''}(\theta )$ is the trigamma function). By consequence, the scaling limit of the favourite endpoint is easy to compute in the present model with boundary conditions.

Theorem 2

Consider the model b.c.$(\theta )$ from (2).

• (i) When $\theta =\mu /2$, we have

  $$\begin{aligned} \frac{l_n}{n}\mathop {\longrightarrow }\limits ^{\mathcal {L}}\underset{t\in [0,1]}{\arg \min }\ W_t , \end{aligned}$$

  where the limit has the arcsine distribution with density $[\pi \sqrt{s(1-s)}]^{-1}$ on the interval [0, 1].

• (ii) When $\theta <\mu /2$, $n-l_n$ converges in law, so

  $$\begin{aligned} \frac{l_n}{n}\mathop {\longrightarrow }\limits ^{\mathbb {P}} 1, \end{aligned}$$

  though when $\theta >\mu /2$, $l_n$ converges in law, so

  $$\begin{aligned}\frac{l_n}{n}\mathop {\longrightarrow }\limits ^{\mathbb {P}} 0.\end{aligned}$$

In words, the favourite location for the polymer endpoint is random at a macroscopic level in the equilibrium case, and degenerate otherwise. Further, the (doubly random) polymer endpoint $x_n$ has the same asymptotics under $Q_n^\omega$, since, by (5), $x_n/n$ and $l_n/n$ are asymptotic as $n \rightarrow \infty$. These results disagree with KPZ theory, where the endpoint fluctuates at distance $n^{2/3}$ around the diagonal. A word of explanation is necessary. The difference comes from the boundary conditions. In the equilibrium case $\mu /2=\theta$ the direction of the endpoint has a maximal dispersion, though in non equilibrium ones it sticks to one of the coordinate axes. In the model without boundary conditions –that we leave untouched in this paper–, we expect an extra entropy term to come into the play and balance the random walk $S_n$ in the potential, a factor being of magnitude n and quadratic around its minimum (which is the diagonal by symmetry), making the localization happen close to the diagonal and with fluctuations of order $n^{2/3}$.

Finally, we derive a large deviation principle for the endpoint distribution:

Theorem 3

Consider the model b.c.$(\theta )$ from (2).

• (i) Assume $\theta =\mu /2$. In the Skorohod space $D([0,1],\mathbb {R}^+)$ equipped with Skorohod topology,

  $$\begin{aligned} \left( \frac{-1}{\sqrt{n}}\log Q_n^{\omega }\left\{ x_n=([ns], n-[ns])\right\} \right) _{s\in [0,1]} \mathop {\longrightarrow }\limits ^{\mathcal {L}} \left( W(s)-\min _{[0,1]} W\right) _{s\in [0,1]}.\nonumber \\ \end{aligned}$$

  (13)

  Moreover, for all segment $A\subset \{(s,1-s); s \in [0,1]\}$ in the first quadrant,

  $$\begin{aligned} \frac{-1}{\sqrt{n}}\log Q_n^{\omega }(x_n\in nA) \mathop {\longrightarrow }\limits ^{\mathcal {L}} \inf _A W- \min _{[0,1]} W. \end{aligned}$$

  (14)

• (ii) Assume $\theta > \mu /2$. Then, as $n \rightarrow \infty$,

  $$\begin{aligned} - \frac{1}{{n}}\log Q_n^{\omega }\left\{ x_n=([ns], n-[ns]) \right\} \mathop {\longrightarrow }\limits ^{\mathbb {P}} s \vert \Psi _0(\theta )-\Psi _0(\mu -\theta )\vert , \end{aligned}$$

  (15)

  where $\Psi _0(\theta )= (\log \Gamma )'(\theta )$ is the digamma function. Similarly, if $\theta < \mu /2$,

  $$\begin{aligned} - \frac{1}{{n}}\log Q_n^{\omega }\left\{ x_n=([ns], n-[ns])\right\} \mathop {\longrightarrow }\limits ^{\mathbb {P}} (1-s) \vert \Psi _0(\theta )-\Psi _0(\mu -\theta )\vert . \end{aligned}$$

Then, at logarithmic scale, the large deviation probability for the endpoint is of order $\sqrt{n}$ in the equilibrium case, whereas it is of order n otherwise. This is again specific to boundary conditions, since it is shown in [21] for the model without boundaries that the large deviation probabilities have exponential order n with a rate function which vanishes only on the diagonal ($s=1/2$).

2.2 Middle point under the point-to-point measure

In this section, we consider the point-to-point measure with boundary conditions. Fix $\mu >0$, $(p,q)\in (\mathbb {Z}_+^*)^2$ and for each $N\in \mathbb {N}$, let $R_N$ be the rectangle with vertices (0, 0), (0, qN), (pN, 0) and (pN, qN). With some fixed

$$\begin{aligned} \theta _S, \theta _N \in (0,\mu ), \quad \hbox {let} \quad \theta _E=\mu -\theta _N, \; \theta _W=\mu -\theta _S, \end{aligned}$$

and denote $\Theta =(\theta _N, \theta _S, \theta _E, \theta _W)$. To sites (i, j) strictly inside $R_N$ we assign inverse Gamma variables $Y_{i,j}$ with parameter $\mu$, whereas to sites on the boundary we assign inverse Gamma variables with parameter $\theta _N, \theta _S, \theta _E$ or $\theta _W$ depending if the boundary is north, south, east or west.

Model P2P-b.c.( $\Theta$ ): Assume

$$\begin{aligned}&Y_{i,j}: (i,j) \in R_N{\setminus } \{\mathbf{0}, (pN,qN)\} \ \hbox {are independent with} \nonumber \\&Y_{i,0}^{-1} \sim \hbox {Gamma}(\theta _S,1) \text{ for } i \in [1, pN], \quad Y_{pN,j}^{-1} \sim \hbox {Gamma}(\theta _E,1) \text{ for } j \in [1, qN-1],\nonumber \\&Y_{0,j}^{-1} \sim \hbox {Gamma}(\theta _W,1) \text{ for } j \in [1, qN], \quad Y_{i,qN}^{-1} \sim \hbox {Gamma}(\theta _N,1) \text{ for } i \in [1, pN-1],\nonumber \\&Y_{i,j}^{-1} \sim \hbox {Gamma}(\mu ,1) \text{ for } 1\le i \le pN-1 \text{ and } 1\le j \le qN-1. \end{aligned}$$

(16)

The point-to-point polymer measure is the probability measure on $\Pi _{pN,qN}$ given by

$$\begin{aligned} Q_{pN,qN}^{\omega }(\mathbf{x})= \frac{1}{Z_{pN,qN}^{\omega }} \exp \left\{ \sum _{t=1}^{(p+q)N-1}\omega (x_t)\right\} . \end{aligned}$$

For a path $\mathbf{x}\in \Pi _{pN,qN}$ denote by

$$\begin{aligned} t^-=\max \left\{ t: x_t \cdot (q\mathbf{e_1}+p\mathbf{e_2}) \le pqN\right\} \end{aligned}$$

the “time it crosses the transverse diagonal”. The coordinate of the crossing point can be described up to a multiplicative factor by the integer

$$\begin{aligned} F(\mathbf{x})= (x_{t^-}+x_{t^-+1})\cdot (q\mathbf{e_1}-p\mathbf{e_2}) . \end{aligned}$$

(17)

Theorem 4

Consider the model P2P-b.c.$(\Theta )$. Then, there exist a random integer $m_N$ depending on $\omega$ and a random probability measure $\hat{\xi }$ on $\mathbb Z$ such that, as $N \rightarrow \infty$,

$$\begin{aligned} \left( Q_{pN,qN}^{\omega }( F(\mathbf{x})= m_N + k); k \in {\mathbb Z}\right) \mathop {\longrightarrow }\limits ^{\mathcal L} \hat{\xi }, \end{aligned}$$

in the space $({\mathcal M}_1, \Vert \cdot \Vert _{TV})$.

We recall that middle-point localization for the point-to-point measure is not covered by the usual martingale approach to localization, and this result is the first one of this nature. Here also the limit can be described in terms of the minimum of a functional of random walks. The appropriate form of the claim and the limit itself are given in Theorem 3, Sect. 5. We end with a complement.

Theorem 5

Consider the model P2P-b.c.($\Theta$), and recall $m_N$ from Theorem 4.

• (i) When $\theta _N=\theta _S$, as $N \rightarrow \infty$,

  $$\begin{aligned} \frac{m_N}{4Npq}+\frac{1}{2}\mathop {\longrightarrow }\limits ^{\mathcal {L}} \underset{t\in [0,1]}{\arg \min }\ W_t , \end{aligned}$$

  (18)

  where the limit has the arcsine distribution.

• (ii) When $\theta _N < \theta _S$, then $m_N+2pqN$ converges in law, so

  $$\begin{aligned} \frac{m_N}{4Npq}+\frac{1}{2} \mathop {\longrightarrow }\limits ^{\mathbb {P}} 0, \end{aligned}$$

  but when $\theta _N > \theta _S$, $m_N-2pqN$ converges in law, so

  $$\begin{aligned} \frac{m_N}{4Npq}+\frac{1}{2} \mathop {\longrightarrow }\limits ^{\mathbb {P}} 1, \end{aligned}$$

We stress that the equilibrium relation (18) holds whatever p and q are, provided that $\theta _N=\theta _S$.

In order to prove all these results, the direct approach is to understand the growth of the random walk seen from its local minima. In the next section, we will present different results about the decomposition of random walk around its minima.

3 Splitting at the infimum and random walk conditioned to stay positive

Through this section, we will only consider the equilibrium case $\theta =\mu /2$, i.e. when the random walk $S=(S_k, k\ge 0)$ in (9) has mean 0. The problem of path decomposition for Markov chains at its infimum points is well studied in the literature by Williams [41], Bertoin [1–4], Kersting and Memişoǧlu [28]. We will follow the fine approach of Bertoin [3]. We mention at this point that the case of a walk drifting to infinity was considered by Doney [16]. However for our purpose, we do not need such sophisticated results when $\theta$ is different from $\mu /2$.

First we will introduce the random walk conditioned to stay non negative and explain how it relates to the decomposition of random walk at its minimum. Then we present Tanaka’s construction and its consequence on the growth of the walk around the minimum.

3.1 Random walk conditioned to stay non negative

Recall that $S_0=0$. Define the event that the random walk stays non negative

$$\begin{aligned}\Lambda =\{S_k\ge 0\, \text{ for } \text{ all } k\ge 0\}.\end{aligned}$$

As the random walk does not drift to $+ \infty$ this event has probability $\mathbb {P}[\Lambda ]=0$. In order to give a meaning for the conditioning with respect to $\Lambda$, we can approximate $\Lambda$ with some other event $\Lambda _n$. The natural choice here is

$$\begin{aligned} \Lambda _n=\{S_k\ge 0, \, \forall \ 0\le k \le n\}. \end{aligned}$$

and we would like to study the asymptotics for large n of the law of S conditioned by $\Lambda _n$.

Let us introduce some basic notation. For every real number x, we denote by $\mathbb {P}_x$ the law of the random walk S started at x, and we put $\mathbb {P}=\mathbb {P}_0$. Let $\tau$ be the first entrance time in $(-\infty ,0)$:

$$\begin{aligned} \tau =\min \{k\ge 1:S_k<0\}. \end{aligned}$$

In particular $\Lambda _n=\{\tau >n\}$. Let $(H,T)=((H_k,T_k),k\ge 0)$ be the strict ascending ladder point process of the reflected random walk $-S$. That is, $T_0=0$ and, for $k=0,1,\ldots$,

$$\begin{aligned} H_k=-S_{T_k}, \ \ T_{k+1}=\min \{j>T_k:-S_j>H_k\}, \end{aligned}$$

with the convention $H_k=\infty$ when $T_k=\infty$. The variable $H_1$ is called the first strict ascending height of $-S$, they are depicted in Fig. 1. The renewal function associated with $H_1$ is

$$\begin{aligned} V(x)=\sum _{k=0}^{\infty } \mathbb {P}(H_k\le x). \end{aligned}$$

Fig. 1

The strict ascending ladder of the random walk $-S$. Line segments represent jumps. $T_1$ is the first time the walk is positive, $-H_1=-S_{T_1}$ is the value. $T_2$ is the next time the walk takes a larger value, denoted by $-H_2$, etc.

By the duality lemma ([17], Sect. XII.2), we can rewrite the renewal function for $x \ge 0$ as

$$\begin{aligned} V(x)= 1+ \mathbb {E}\left( \sum _{i=1}^{\sigma (0)-1}1_{\{-x\le S_i\}}\right) , \end{aligned}$$

(19)

where

$$\begin{aligned} \sigma (0)=\min \{k\ge 1: S_k\ge 0\}. \end{aligned}$$

Now we define Doob’s h-transform $P_x^V$ of $P_x$ by the function V, i.e., the law of the homogeneous Markov chain on the nonnegative real numbers with transition function:

$$\begin{aligned} p^V(x,y)=\frac{V(y)}{V(x)}p(x,y)1_{\{y \ge 0\}}. \end{aligned}$$

(20)

Here $p, P_x$ denote the transition density and the law of the chain S starting from x. By definition, if $f(S)=f(S_0,S_1,\dots ,S_k)$ is a functional depending only on the k first steps of the random walk, then

$$\begin{aligned} \mathbb {E}_x^V[f(S)]=\frac{1}{V(x)}\mathbb {E}_x[V(S_k)f(S),k<\tau ]. \end{aligned}$$

(We use the standard notation $E[Z,A]=E[Z {\mathbf 1}_A]$ for an integrable r.v. Z and an event A.) We denote by $(S_k^{\uparrow })_{k \ge 0}$ the chain starting from 0,

$$\begin{aligned} \mathbb {E} \left( f\left( S_1^{\uparrow },\ldots ,S_k^{\uparrow }\right) \right) = \mathbb {E}_0^V(f(S)). \end{aligned}$$

(21)

The following result shows that it yields the correct description of the random walk conditioned to stay non negative.

Proposition 1

For a bounded Borel function $f(S)=f(S_1,\ldots ,S_k)$,

$$\begin{aligned} \lim _{n\rightarrow \infty } \mathbb {E}(f(S)\vert \Lambda _n)=\mathbb {E}\left( f\left( S^{\uparrow }\right) \right) . \end{aligned}$$

Proof

First we will prove the following lemma:

Lemma 1

For every $x\ge 0$, we have

$$\begin{aligned} \liminf _{n\rightarrow \infty } \frac{\mathbb {P}_x(\Lambda _n)}{\mathbb {P}(\Lambda _n)}\ge V(x). \end{aligned}$$

Proof of Lemma 1

Recall that $(H_k,T_k)$ denotes the kth ascending ladder point of $-S$. Let $a_{n,k}$ be the event $\{H_k\le x,T_k\le n, T_{k+1}-T_k>n\}$. On the event $a_{n,k}$, we have $\max _{k\in [0,n]}\{-S_k\}=H_k\le x$. It implies that $\min _{k\in [0,n]}S_k+x\ge 0$, and by consequence $\tau >n$ under $\mathbb {P}_x$. Moreover the events $a_{n,k}$ are clearly disjoint, then we have:

$$\begin{aligned} \mathbb {P}_x(\tau >n)\ge \sum _{k=0}^{\infty } \mathbb {P}(a_{n,k}). \end{aligned}$$

By the Markov property at $T_k$, we have:

$$\begin{aligned} \mathbb {P}_x(\tau >n)\ge \mathbb {P}(\tau >n)\sum _{k=0}^{\infty } \mathbb {P}(H_k\le x, T_k\le n). \end{aligned}$$

By monotone convergence,

$$\begin{aligned} \lim _{n\rightarrow \infty } \sum _{k=0}^{\infty } \mathbb {P}(H_k\le x, T_k\le n)=\sum _{k=0}^{\infty }\mathbb {P} (H_k\le x)=V(x). \end{aligned}$$

which yields the lemma. $\square$

Now, we can complete the proof of Proposition 1. Without loss of generality we may assume that $0\le f \le 1$. By the Markov property, for $k\le n$,

$$\begin{aligned} \mathbb {E}(f(S),\Lambda _n)=\mathbb {E}\left( f(S)\mathbb {P}_{S_k}(\Lambda _{n-k}),\tau >k\right) \ge \mathbb {E}\left( f(S)\mathbb {P}_{S_k}(\Lambda _{n}),\tau >k\right) . \end{aligned}$$

We deduce from Lemma 1 and Fatou’s lemma that

$$\begin{aligned} \liminf _{n\rightarrow \infty } \mathbb {E}(f(S)\vert \Lambda _n)\ge \mathbb {E} (f(S)V(S_k),\tau >k)= \mathbb {E}_0^V(f(S)) \end{aligned}$$

since $V(0)=1$. Replacing f by $1-f$, we get

$$\begin{aligned} \limsup _{n\rightarrow \infty } \mathbb {E}(f(S)\vert \Lambda _n)= & {} 1-\liminf _{n\rightarrow \infty } \mathbb {E}((1-f)(S)\vert \Lambda _n)\\\le & {} 1-\mathbb {E}_0^V((1-f)(S))= \mathbb {E}_0^V(f(S)), \end{aligned}$$

which completes the proof of Proposition 1. $\square$

Now we will show that the random walk conditioned stay non negative is the natural limit for the random walk seen from its local minima. Recall $\ell _n$ from (11). The following property is crucial.

Proposition 2

For a bounded function $f(x_1,\ldots ,x_k)$ and $\varepsilon \in (0,1)$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \mathbb {E}\left( f\left( S_{\ell _n+1}-S_{\ell _n},\ldots ,S_{\ell _n+k}-S_{\ell _n}\right) \vert n-\ell _n>n\varepsilon \right) = \mathbb {E}_0^V(f(S)). \end{aligned}$$

Proof

We have

$$\begin{aligned}&\mathbb {E}\left[ f\left( S_{\ell _n+1}-S_{\ell _n},\ldots ,S_{\ell _n+k}-S_{\ell _n}\right) , {n-\ell _n>n\varepsilon }\right] \nonumber \\&\quad = \sum _{i=0}^{ \lceil n-n\varepsilon \rceil -1}\mathbb {E}\left[ f\left( S_{i+1}-S_{i},\ldots ,S_{i+k}-S_{i}\right) , {\ell _n=i}\right] . \end{aligned}$$

(22)

On the other hand we can write the event $\{\ell _n=i\}$ as

$$\begin{aligned} \left\{ \ell _n=i\right\} =\left\{ S_j\ge S_i, \forall j\le i\right\} \cap \left\{ S_j\ge S_i, \forall j\in [ i,n]\right\} . \end{aligned}$$

Both random variables $f(S_{i+1}-S_{i},\ldots ,S_{i+k}-S_{i})$ and $1_{\{S_j\ge S_i, \forall j\in [ i,n]\}}$ are measurable with respect to $\sigma (X_{i+1},\ldots ,X_n)$ and thus are independent of the event $\{S_j\ge S_i, \forall j\le i\}$ which is in $\sigma (X_1,\ldots ,X_i)$. Then we obtain:

$$\begin{aligned}&\mathbb {E}\left[ f\left( S_{i+1}-S_{i},\ldots ,S_{i+k}-S_{i}\right) , {\ell _n=i}\right] \\&\quad =\mathbb {E}\left( f\left( S_{i+1}-S_{i},\ldots ,S_{i+k}-S_{i}\right) 1_{\{S_j\ge S_i, \forall j \in [i,n]\}}\right) \times \mathbb {P}\left( S_j\ge S_i, \forall j\le i\right) . \end{aligned}$$

Applying the Markov property at time $i (0<i<n-n\varepsilon )$, we obtain

$$\begin{aligned}&\mathbb {E}\left[ f\left( S_{i+1}-S_{i},\dots ,S_{i+k}-S_{i}\right) , {\ell _n=i}\right] \nonumber \\&\quad =\mathbb {E}\left[ f\left( S_{1},\ldots ,S_{k}\right) , {\tau > n-i}\right] \times \mathbb {P}\left( S_j\ge S_i, \forall j\le i\right) . \end{aligned}$$

(23)

From Proposition 1, for fixed $\delta >0$, there exists $n(\delta )$ such that for $n\ge n(\delta )$,

$$\begin{aligned} \left| \mathbb {E}\left[ f(S_{1},\ldots ,S_{k}) \vert {\tau > n\varepsilon }\right] - \mathbb {E}_0^V[f(S_1,\ldots ,S_k)]\right| \le \delta . \end{aligned}$$

(24)

Combining (22), (23) and (24), we obtain

$$\begin{aligned}&\mathbb {E}\left[ f\left( S_{\ell _n+1}-S_{\ell _n},\ldots ,S_{\ell _n+k}-S_{\ell _n}\right) ,{n-\ell _n>n\varepsilon }\right] \\&\quad \ge \left( \mathbb {E}_0^V\left[ f\left( S_1,\ldots ,S_k\right) \right] -\delta \right) \\&\qquad \times \sum _{i=0}^{\lceil n-n\varepsilon \rceil -1} \mathbb {P}\left( S_j\ge S_i, \forall j\in [ i,n]\right) \mathbb {P}\left( S_j\ge S_i, \forall j\le i\right) \\&\quad = \left( \mathbb {E}_0^V[f(S_1,\ldots ,S_k)]-\delta \right) \times \mathbb {P}(n-\ell _n\ge n \varepsilon ) . \end{aligned}$$

Thus, for $n>n(\delta )$,

$$\begin{aligned} \mathbb {E}\left( f\left( S_{\ell _n+1}-S_{\ell _n},\ldots ,S_{\ell _n+k}-S_{\ell _n}\right) \vert n-\ell _n>n\varepsilon \right) \ge \mathbb {E}_0^V[f(S_1,\ldots ,S_k)]-\delta , \end{aligned}$$

and by the same argument,

$$\begin{aligned} \mathbb {E}\left( f\left( S_{\ell _n+1}-S_{\ell _n},\ldots ,S_{\ell _n+k}-S_{\ell _n}\right) \vert n-\ell _n>n\varepsilon \right) \le \mathbb {E}_0^V[f(S_1,\ldots ,S_k)]+\delta . \end{aligned}$$

This yields the desired result. $\square$

In the above result we proved convergence of the post-infimum process. Since the random variables X are centered, by considering the reflected random walk $-S$, we derive a similar convergence result for the pre-infimum process to a limit that we now introduce. Since the environment has a density, the model enjoys a simplification: conditioning the walk to be positive is the same as conditioning it to be non-negative. Define the process $(S_k^{\downarrow })$ as the homogeneous Markov chain starting from 0 with transition function $p^{\hat{V}}$ given by (20) with

$$\begin{aligned} \hat{V}(x)=1+ \mathbb {E} \left( \sum _{i=1}^{\hat{\sigma }(0)-1}1_{\{S_i\le x\}}\right) , \quad x \ge 0, \end{aligned}$$

and

$$\begin{aligned} \hat{\sigma }(0)=\min \{k\ge 1: S_k \le 0\}. \end{aligned}$$

Corollary 3

For a bounded function $f(x_1,\dots ,x_k)$ and $\varepsilon \in (0,1)$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \mathbb {E}\left( f\left( S_{\ell _n-1}-S_{\ell _n}, \ldots ,S_{\ell _n-k}-S_{\ell _{n}}\right) \vert \ell _n>n\varepsilon \right) = \mathbb {E}\left( f\left( S_1^{\downarrow },\ldots ,S_k^{\downarrow }\right) \right) . \end{aligned}$$

Since the walk is centered, the event $\{n\varepsilon <\ell _n<n-n\varepsilon \}$ will happen with high probability for $\varepsilon$ small enough. Then Theorem 2 and Corollary 3 imply that

Corollary 4

For fixed K, the following convergence results hold as $n\rightarrow \infty$:

$$\begin{aligned}&\left( S_{\ell _n+k}-S_{\ell _n}\right) _{1\le k\le K}\mathop {\longrightarrow }\limits ^{\mathcal {L}}\left( S_k^\uparrow \right) _{1\le k\le K},\nonumber \\&\left( S_{\ell _n+k}-S_{\ell _n}\right) _{-1\ge k\ge -K}\mathop {\longrightarrow }\limits ^{\mathcal {L}}\left( S_k^\downarrow \right) _{1\le k\le K},\nonumber \\&\left( \sum _{k=-K}^K e^{-\left( S_k-S_{\ell _n}\right) }\right) ^{-1}\mathop {\longrightarrow }\limits ^{\mathcal {L}} \left( 1+ \sum _{k=1}^{K} e^{-S_k^\uparrow }+\sum _{k=1}^K e^{-S_k^\downarrow }\right) ^{-1}. \end{aligned}$$

(25)

3.2 Growth of random walk conditioned to stay positive

In the literature, it is well known that the random walk conditioned to stay positive can be constructed based on an infinite number of time reversal at the ladder time set of the walk $(S,\mathbb {P})$. The first proof is given by Golosov [22] for the case of random walk with expectation zero and later Tanaka [38] gave a proof for more general case. We first present Tanaka’s construction [38], and summarize the results.

Let $\{(H_k^+,\sigma _k^+)\}_{k\ge 0}$ be the sequence of strictly increasing ladder heights and times respectively of $(S,\mathbb {P})$ with $H_0^+=\sigma _0^+=0$. Define $e_1,e_2,\dots$ the sequence of excursions of $(S,\mathbb {P})$ from its supremum that have been time reversed:

$$\begin{aligned} e_n=\left( 0,S_{\sigma _n^+}-S_{\sigma _n^+-1},S_{\sigma _n^+}-S_{\sigma _n^+-2},\dots ,S_{\sigma _n^+}-S_{\sigma _{n-1}^++1},S_{\sigma _n^+}-S_{\sigma _{n-1}^+}\right) , \end{aligned}$$

for $n\ge 1$. Write for convenience $e_n=(e_n(0),e_n(1),\dots ,e_n(\sigma _n^+-\sigma _{n-1}^+))$ as an alternative for the step of each $e_n$. By Markov property, $e_1,e_2,\dots$ are independent copies of $e=(0,S_{\sigma ^+}-S_{\sigma ^+-1},S_{\sigma ^+}-S_{\sigma ^+-2},\dots ,S_{\sigma ^+}-S_{1},S_{\sigma ^+})$ where $\sigma ^+=\inf \{k\ge 0: S_k\in (0,+\infty )\}$ is from (19). Tanaka’s construction for the reflected random walk $(-S)$ consists in the following process $W^{\uparrow }=\{W_n^{\uparrow }: n\ge 0 \}$:

$$\begin{aligned} W_n^{\uparrow }= \left\{ \begin{array}{l@{\quad }l} e_1(n), &{} \hbox {for}\ 0\le n\le \sigma _1^+\\ H_1^+ + e_2(n-\sigma _1^+) &{} \hbox {for}\ \sigma _1^+<n\le \sigma _2^+ \\ \ldots \\ H_{k-1}^++e_k(n-\sigma _{k-1}^+) &{} \hbox {for} \ \sigma _{k-1}^+<n\le \sigma _{k}^+\\ \ldots \end{array} \right. \end{aligned}$$

(26)

Under the condition $\mathbb {P}\{\sigma ^+ <\infty \}=1$, the main theorem in [38] states that $\{W_n^{\uparrow }\}$ is a Markov chain process on $[0,+\infty )$ with transition function $\hat{p}(x,dy)$, which is given by

$$\begin{aligned} \hat{p}(x,dy)= \frac{g(y)}{g(x)} \mathbb {P}(x+X\in dy) 1_{(0,+\infty )}(y) , \end{aligned}$$

where

$$\begin{aligned} g(x)=\mathbb {E} \left[ \sum _{n=0}^{\sigma ^+}1_{\{-x < S_n\}}\right] . \end{aligned}$$

As we consider here log-gamma variables with $\theta =\mu /2$, then we have $\mathbb {P}$-a.s $\sigma ^+=\sigma (0)<1$ and $g=V$ from (19). Therefore the process $W^{\uparrow }$ has the same law as the random walk conditioned to stay non negative, i.e., $S^{\uparrow }$ defined above Proposition 1. This identity provides an elegant way to determine the growth rate of the limit process $S^{\uparrow }$.

Lemma 2

For every $\varepsilon >0$, then we have:

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{S_n^\uparrow }{n^{1/2-\varepsilon }} = +\infty , \ \mathbb {P} -a.s. \end{aligned}$$

As a consequence, for fixed $\delta > 0$ there exists a constant $k=k(\delta )$ such that

$$\begin{aligned} \mathbb {P}\left( S_n^{\uparrow }\ge n^{1/2- \varepsilon },\forall \ n\ge k\right) \ge 1-\delta . \end{aligned}$$

Proof

We follow the lines of [24]. Let $\{M_k^+,v_k^+\}_{k\ge 0}$ be the space-time points of increase of the future minimum of $(W^{\uparrow },\mathbb {P})$. That is, $M_0^+=v_0^+=0$,

$$\begin{aligned} v_k^+= \inf \left\{ n>v_{k-1}^+: \min _{r\ge n}W_r^{\uparrow }=W_n^{\uparrow }\right\} \quad \hbox {and} \quad M_k^+ = W_{v_k^+}^{\uparrow }, \end{aligned}$$

for $k\ge 1$. From the construction of $W^{\uparrow }$, we can deduce that for each path, the sequence $\{(M_k^+,v_k^+)\}_{k\ge 0}$ corresponds precisely to $\{(H_k^+,\sigma _k^+)\}_{k\ge 0}$. Let $L=\{L_n\}_{n\ge 0}$ be the local time at the maximum in $(S,\mathbb {P})$, that is

$$\begin{aligned} L_n=\left| \left\{ k\le n : \max _{i\le k}S_i= S_k\right\} \right| . \end{aligned}$$

Because $W^{\uparrow }$ is obtained by time reversal from S, then L is also the local time at the future minimum of $(W^{\uparrow },\mathbb {P})$. Hence it’s clear that:

$$\begin{aligned} S_n\le H_{L_n}^+=M_{L_n}^+\le W_n^{\uparrow }. \end{aligned}$$

Now we need the following lemma (e.g., Theorem 3 in [24]): $\square$

Lemma 3

Consider the random walk $(S,\mathbb {P})$. Now suppose that $\Phi \downarrow 0$ and that $\mathbb {E}(S_1)=0$ and $\mathbb {E}(S_1^2)<\infty$. Then

$$\begin{aligned} \mathbb {P}_x\left( \max _{k\le n}S_k < \sqrt{n}\Phi (n)\ i.o.\right) =0\quad { or }1. \end{aligned}$$

according to

$$\begin{aligned} \int _1^{\infty } \frac{\Phi (t)}{t} dt < \infty \quad { or} = \infty . \end{aligned}$$

We use the standard notations “i.o.” for “infinitely often” and “ev.” for “eventually”. For $\Phi (n) =n^{-\varepsilon }$, the integral converges and Lemma 3 yields

$$\begin{aligned} 1= & {} \mathbb {P}\left( \max _{i\le n}S_i \ge \sqrt{n}\Phi (n) \ \text {ev}. \right) \\= & {} \mathbb {P}\left( W_n^{\uparrow }\ge \sqrt{n}\Phi (n) \ \mathrm {ev}.\right) . \end{aligned}$$

Again using the fact that we may replace $\Phi$ by $c\Phi$ for any $c>0$, and that the integral in the lemma still converges, it follows easily that

$$\begin{aligned} \liminf _{n\rightarrow \infty } \frac{W_n^{\uparrow }}{ \sqrt{n}\Phi (n)} = \infty , \end{aligned}$$

$\mathbb {P}$-almost surely. As $W^{\uparrow }$ and $S^{\uparrow }$ have the same law under $\mathbb {P}$, we get the first result. Then it’s clear for fixed $\delta$, there exists k such that

$$\begin{aligned} \mathbb {P}\left( S_n^{\uparrow }\ge n^{1/2- \varepsilon },\forall \ n\ge k\right) =\mathbb {P}(A_k)\ge 1-\delta . \end{aligned}$$

$\square$

We complement Lemma 2 with the following version for the conditioned random walk, proved by Ritter [34].

Theorem 6

[34] Fixed $\eta < 1/2$ then:

$$\begin{aligned} \lim _{\delta \rightarrow 0} \inf _n\mathbb {P}\left[ \inf _{k\le n}(S_k-\delta k^\eta )\ge 0|\tau >n\right] =1. \end{aligned}$$

Note now that the time $\ell _n$ of the first minimum of S on [0, n] is such that, for fixed $\varepsilon \in (0,1)$ we have for large n,

$$\begin{aligned} \mathbb {P}\left[ \ell _n<(1-\varepsilon ^2)n\right] >1-\varepsilon . \end{aligned}$$

(27)

Indeed, by the invariance principle of Donsker (1951), $\ell _n/n$ converges in law to the time of the global minimum of the standard Brownian motion on [0, 1], which obeys the arcsine distribution [27, problem 8.18]. Therefore, conditionally on the event $\{\ell _n<(1-\varepsilon ^2)n\}$, Theorem 6 gives us the growth of the random walk after the minimum:

Corollary 5

If $\eta \in (0,1/2)$, then uniformly in n:

$$\begin{aligned} \lim _{\delta \rightarrow 0} \mathbb {P}\left[ S_{k+\ell _n}-S_{\ell _n}>\delta k^\eta \ \,\hbox {for all } k\le n-\ell _n\right] = 1. \end{aligned}$$

Proof

The proof is similar to the proof of Proposition 2. To simplify the notation define

$$\begin{aligned} A_{\delta }=\left\{ S_{k+\ell _n}-S_{\ell _n}>\delta k^\eta \quad \hbox {for all } k\le n-\ell _n\right\} , \end{aligned}$$

and

$$\begin{aligned} A_{\delta ,j}=\left\{ S_{k+\ell _n}-S_{\ell _n}>\delta k^\eta \, \hbox {for all } k\le n-\ell _n, \ell _n=j\right\} . \end{aligned}$$

Then we have

$$\begin{aligned} \mathbb {P}[A_{\delta }]=\sum _{j=1}^{n}\mathbb {P}[A_{\delta ,j}]= \sum _{j=1}^{n}\mathbb {P}\left[ A_{\delta ,j}\vert \ell _n=j\right] \mathbb {P}[\ell _n=j]. \end{aligned}$$

We know that the event $\{\ell _n=i\}$ can be written as

$$\begin{aligned} \left\{ \ell _n=i\right\} =\left\{ S_j\ge S_i, \forall j\le i\right\} \cap \left\{ S_j\ge S_i, \forall j\in [ i,n]\right\} , \end{aligned}$$

Both random variables $A_{\delta ,j}$ and $1_{\{S_j\ge S_i, \forall j\in [ i,n]\}}$ are measurable with respect to $\sigma (X_{i+1},\dots ,X_n)$ and are independent of the event $\{S_j\ge S_i, \forall j\le i\}$. By the Markov property, it follows that

$$\begin{aligned} \mathbb {P}\left[ A_{\delta ,j}\vert \ell _n=j\right] =\mathbb {P}\left[ S_{k}>\delta k^\eta \quad \hbox {for all } k\le n-j\vert \tau >n-j\right] . \end{aligned}$$

For $\varepsilon >0$ by using Theorem 6, there exists $\delta _{\varepsilon }$ and $n_{\varepsilon }$ such that for all $\delta <\delta _{\varepsilon }$, $m> n_{\varepsilon }$

$$\begin{aligned} \mathbb {P}\left[ \inf _{k\le m}(S_k-\delta k^\eta )\ge 0|\tau >m\right] \ge 1-\varepsilon . \end{aligned}$$

By putting $m=n-j$ and summing $j\in \{1,2,\dots ,[(1-\varepsilon )n]\}$ we obtain

$$\begin{aligned} \mathbb {P}[A_{\delta }]\ge (1-\varepsilon )\mathbb {P}[\ell _n<(1-\varepsilon )n]. \end{aligned}$$

So by (27), for n large enough, we have

$$\begin{aligned} \mathbb {P}[A_{\delta }]\ge 1-2\varepsilon , \end{aligned}$$

which implies easily the corollary. $\square$

4 Proof of the main results in the point-to-line case

We split the section according to $\theta =\mu /2$ or not, starting with the first case, which is more involved than the second one. The reason why $\theta =\mu /2$ is special is that the random variable X in (9) is centered, and even symmetric.

4.1 Equilibrium case

In the equilibrium setting $\theta =\mu /2$, we know that the post- and pre-infimum chain converge in law to the random walk conditioned to stay positive. As these limit processes grow fast enough, we can indeed prove that the endpoint densities of the polymer converge when its length goes to infinity. Firstly we consider the distribution at the favourite endpoint, and we later extend the arguments to all the points:

Lemma 4

For $n\rightarrow \infty$,

$$\begin{aligned} \xi _{\ell _n}^n=\left( \sum _{i=0}^n e^{-(S_i-S_{\ell _n})}\right) ^{-1} \mathop {\longrightarrow }\limits ^{\mathcal {L}}\xi _0 =\left( 1+\sum _{i=1}^\infty e^{-S_i^\uparrow }+\sum _{i=1}^\infty e^{-S_i^\downarrow }\right) ^{-1} . \end{aligned}$$

Proof

From Lemma 2, the random walk conditioned to stay positive is lower bounded by some factor of $n^{1/2-\varepsilon }$, thus the random variable $\xi _0$ is well defined and strictly positive. By the continuous mapping theorem, the claim is equivalent to convergence in law of the inverse random variables. Then, in order to prove the lemma, it suffices to show that, for all bounded and uniformly continuous function f, we have

$$\begin{aligned} \mathbb {E}\left[ f\left( \sum _{i=0}^n e^{-(S_i-S_{\ell _n})}\right) \right] \longrightarrow \mathbb {E}\left[ f\left( 1+\sum _{i=1}^\infty e^{-S_i^\uparrow }+\sum _{i=1}^\infty e^{-S_i^\downarrow }\right) \right] \ ,\end{aligned}$$

(28)

as $n \rightarrow \infty$. By (25) in Corollary 4, we already know that, for a fixed K,

$$\begin{aligned} \mathbb {E}\left[ f\left( \sum _{i=\ell _n-K}^{i=\ell _n+K} e^{-(S_i-S_{\ell _n})}\right) \right] \longrightarrow \mathbb {E}\left[ f\left( 1+\sum _{i=1}^K e^{-S_i^\uparrow }+\sum _{i=1}^K e^{-S_i^\downarrow }\right) \right] . \end{aligned}$$

(29)

By uniform continuity, given an $\varepsilon >0$ there exists $\rho >0$ such that $|f(x)-f(y)|<\varepsilon$ for all x, y with $|x-y|< \rho$. Now we will prove that, for all positive $\varepsilon$, we can find finite $K=K(\varepsilon )$ and $n_0(\varepsilon )$ such that for $n \ge n_0(\varepsilon )$, it holds

$$\begin{aligned} \left| \mathbb {E}\left[ f\left( \sum _{i=0}^n e^{-(S_i-S_{\ell _n})}\right) \right] -\mathbb {E}\left[ f\left( \sum _{i=\ell _n-K}^{i=\ell _n+K} e^{-(S_i-S_{\ell _n})}\right) \right] \right| <\varepsilon , \end{aligned}$$

(30)

and

$$\begin{aligned} \left| \mathbb {E}\left[ f \left( 1+\sum _{i=1}^K e^{-S_i^\uparrow }+\sum _{i=1}^K e^{-S_i^\downarrow }\right) \right] -\mathbb {E}\left[ f\left( 1+\sum _{i=1}^\infty e^{-S_i^\uparrow }+\sum _{i=1}^\infty e^{-S_i^\downarrow }\right) \right] \right| <\varepsilon .\nonumber \\ \end{aligned}$$

(31)

Then, by combining (29), (30) and (31) we get (28) and the proof is finished.

In order to get (30), it is enough to prove that for all positive $\rho , \varepsilon$ there exists a finite K such that

$$\begin{aligned} \mathbb {P}\left( \sum _{i=0}^{\ell _n-K}e^{-(S_i-S_{\ell _n})}+\sum _{i=\ell _n+K}^{n}e^{-(S_i-S_{\ell _n})} < \rho \right) > 1-\varepsilon \end{aligned}$$

(32)

for all n large enough, while, in order to get (31), it is enough to prove that for all positive $\rho , \varepsilon$ there exists a finite K such that

$$\begin{aligned} \mathbb {P} \left( \sum _{i \ge K}e^{-S_i^\uparrow }+ \sum _{i \ge K}e^{-S_i^\downarrow } < \rho \right) > 1-\varepsilon \end{aligned}$$

(33)

for all n large enough.

To prove (32), we use Corollary 5: For any fixed $\eta <1/2$, choose $\delta >0$, such that for all $n\in \mathbb {N}$ :

$$\begin{aligned} \mathbb {P}\left[ S_{k+\ell _n}-S_{\ell _n}>\delta k^\eta ; k=1,2,\ldots , n-\ell _n\right] \ge 1-\varepsilon /2. \end{aligned}$$

Because the random variable X is symmetric, the pre-infimum process verifies the same properties, i.e for $n\in \mathbb {N}$:

$$\begin{aligned} \mathbb {P}\left[ S_{\ell _n-k}-S_{\ell _n}>\delta k^\eta ; k=1,\ldots , \ell _n\right] \ge 1-\varepsilon /2. \end{aligned}$$

Then, choosing K such that $\sum _{k=K}^\infty e^{-\delta k^\eta }< \rho /2$ yields (32). A similar argument leads to (33). This completes the proof of the lemma. $\square$

In the course of the proof we have discovered the limit endpoint densities $(\xi _k)_{k\in Z}$ is given by formula (12). Repeating the argument in the proof of Lemma 4, it is straightforward to extend the result to a finite set of points around the maximum point:

Lemma 5

For fixed K, $n\rightarrow \infty$:

$$\begin{aligned} \left( \xi _{\ell _n+k}^n\right) _{-K\le k\le K} \mathop {\longrightarrow }\limits ^{\mathcal {L}}(\xi _k)_{-K\le k\le K} \end{aligned}$$

Proof of Theorem 1 in the case of

$\theta =\mu /2$.

Recall that $\tilde{\xi }^{(n)}$ and $\xi ^n$ have the same law, and that the total variation distance between probability measures on $\mathbb Z$ coincides with the $\ell ^1$-norm. Taking a function $f:\ell ^1\rightarrow R$ bounded and uniformly continuous in the norm $\vert .\vert _1$ and one needs to prove that

$$\begin{aligned} \mathbb {E}\left[ f\left( \left( \xi _{\ell _n+k}^n\right) _{k\in \mathbb {Z}}\right) \right] \rightarrow \mathbb {E}\left[ f\left( (\xi _k)_{k\in \mathbb {Z}}\right) \right] . \end{aligned}$$

(34)

We will use almost the same idea as in the proof of Lemma 4. From Lemma 5 we have, with a slight abuse of notation,

$$\begin{aligned} \mathbb {E}\left[ f\left( \left( \xi _{\ell _n+k}^n\right) _{k\in [-K,K]}\right) \right] \rightarrow \mathbb {E}\left[ f\left( (\xi _k)_{k\in [-K,K]}\right) \right] \end{aligned}$$

(35)

Fixing $\varepsilon >0$, there exists by continuity some $\delta >0$ such that $|x-y|_1<\delta$ implies $|f(x)-f(y)|<\varepsilon$. Hence,

$$\begin{aligned} \mathbb {E} \left[ f\left( \left( \xi _{\ell _n+k}^n\right) _{k\in [-K,K]}\right) -f\left( \left( \xi _{\ell _n+k}^n\right) _{k\in \mathbb {Z}}\right) \right] \le \varepsilon \end{aligned}$$

(36)

provided that

$$\begin{aligned} \mathbb {E}\left[ \sum _{k:|k|>K}\xi _{\ell _n+k}^n \right] \le \delta , \end{aligned}$$

(37)

and similarly for $\xi$ instead of $\xi ^n$. Since $\mathbb {E}[\xi _k]$ is a probability measure on $\mathbb {Z}$, we can take K large enough so that $\mathbb {E}[\sum _{k:|k|>K}\xi _k ]\le \delta$. Then, from Lemma 5, we see that, as $n \rightarrow \infty$,

$$\begin{aligned} \mathbb {E} \left[ \sum _{k:|k|>K}\xi _{\ell _n+k}^n \right]= & {} 1-\mathbb {E}\left[ \sum _{k:|k|\le K}\xi _{\ell _n+k}^n \right] \longrightarrow \mathbb {E}\left[ \sum _{k:|k|>K}\xi _k \right] \\= & {} 1-\mathbb {E}\left[ \sum _{k:|k|\le K}\xi _{k} \right] , \end{aligned}$$

yielding (37). By combining (35) and (36), we obtain (34). $\square$

Proof of Corollary 2

It is enough to note that

$$\begin{aligned} \lim _{n\rightarrow \infty } Q_n^{\omega }[\vert x_n \cdot \mathbf{e_1}-l_n\vert \ge K] = \sum _{k:|k|>K}\xi _k \quad \text{ in } \text{ law }, \end{aligned}$$

which vanishes as $K \rightarrow \infty$. $\square$

Proof of Corollary 1

Recall first that under $Q_{n-1}^\omega$, the steps after the final time $n-1$ are uniformly distributed, and independent from everything else. Then, it is enough to note that

$$\begin{aligned} Q_{n-1}^{\omega }[x_n=x]&= Q_{n-1}^{\omega }[x_{n-1}=x-{\mathbf e_1}, x_{n}-x_{n-1}={\mathbf e_1}] \\&\quad + Q_{n-1}^{\omega }[x_{n-1}=x-{\mathbf e_2}, x_{n}-x_{n-1}={\mathbf e_2}] \\&= \left( Q_{n-1}^{\omega }[x_{n-1}=x-{\mathbf e_1}] + Q_{n-1}^{\omega }[x_{n-1}=x-{\mathbf e_2}] \right) \times \frac{1}{2} \\&\mathop {\longrightarrow }\limits ^\mathcal{L} \frac{\xi _k+\xi _{k+1}}{2}, \end{aligned}$$

with k determined by $(x-{\mathbf e_1})\cdot {\mathbf e_1}= l_{n-1}+k$. $\square$

Now we give the proof for Theorems 2 and 3:

Proof of Theorem 2 for

$\theta =\mu /2$.

First, recall that $l_n$ and $\ell _n$ have the same law, so we can focus on the latter one. By definition of $\ell _n$ and Donsker’s invariance principle, we have directly

$$\begin{aligned} \frac{\ell _n}{n}=\frac{1}{n} \underset{i\in [0,n]}{\arg \min }\ S_i \mathop {\longrightarrow }\limits ^{\mathcal {L}}\underset{t\in [0,1]}{\arg \min }\ W_t. \end{aligned}$$

By Lévy’s arcsine law [29], the location of the minimum of the Brownian motion, i.e. the above limit, has the density $\pi ^{-1}(s(1-s))^{-1/2}$ on the interval [0, 1]. $\square$

Proof of Theorem 3 for

$\theta =\mu /2$.

We can express the first term in (13) as

$$\begin{aligned} \frac{-1}{\sqrt{n}}\log Q_n^{\omega }\left( x_n=([ns],n-[ns])\right) \mathop {=}\limits ^\mathcal{L} \frac{-1}{\sqrt{n}}(S_{[ns]}-S_{\ell _n}){+}\frac{1}{\sqrt{n}}\log \left( \sum _{k=1}^{n}e^{-(S_k-S_{\ell _n})}\right) ,\nonumber \\ \end{aligned}$$

(38)

with $\mathop {=}\limits ^\mathcal{L}$ the equality in law. As the second term in the right-hand side is almost surely dominated by $\frac{\log n}{\sqrt{n}}$, then again, Donsker’s invariance principle yields (13).

On the other hand, let A be an interval. For all $s\in A$, we have

$$\begin{aligned} Q_n^{\omega }\left( x_n=([ns],n-[ns])\right)\le & {} Q_n^{\omega }(x_n\in nA) \\\le & {} n\max _{x\in A}Q_n^{\omega }\left( x_n=([nx],n-[nx])\right) , \end{aligned}$$

which means that

$$\begin{aligned} \max _{x\in A}Q_n^{\omega }\left( x_n=([ns],n-[ns])\right)\le & {} Q_n^{\omega }(x_n\in nA)\\\le & {} n\max _{x\in A}Q_n^{\omega }\left( x_n=([nx],n-[nx])\right) . \end{aligned}$$

From Donsker’s invariance principle it follows

$$\begin{aligned}&\frac{-1}{\sqrt{n}}\max _{x\in A} \log Q_n^{\omega }\left( x_n=([ns],n-[ns])\right) \\&\quad \mathop {=}\limits ^\mathcal{L} \min _{x\in A} \frac{S_{[nx]}-S_{\ell _n}}{\sqrt{n}} + \frac{1}{\sqrt{n}}\log \left( \sum _{k=1}^{n}e^{-(S_k-S_{\ell _n})}\right) \\&\quad \mathop {\longrightarrow }\limits ^{\mathcal {L}} \min _{x\in \overline{A}}W(x) -\min _{[0,1]} W, \end{aligned}$$

which, in turn, yields (14). $\square$

4.2 Non-equilibrium case

Proof of Theorem 1 in the case of

$\theta \ne \mu /2$.

Without loss of generality, we assume that $\theta < \mu /2$, which implies that $m=\mathbb {E}[X]>0$ and the random walk S drifts to $+\infty$. By the law of large number, we have for all $a \in (0,m)$,

$$\begin{aligned} M=\min _n (S_n-na)>-\infty \quad \mathbb {P}-a.s \end{aligned}$$

It follows that $\mathbb {P}$-a.s for every integer n,

$$\begin{aligned} e^{-S_n}\le e^{-na-M} \end{aligned}$$

Then the sum of $e^{-S_n}$ converges $\mathbb {P}$-a.s and we can identify the limit distribution $\xi$ as

$$\begin{aligned} \overline{\xi }_k=\frac{e^{-S_k}}{\sum _{i=0}^{\infty }e^{-S_i}}\,. \end{aligned}$$

Indeed, it is clear that, for $k\in \mathbb {Z}_+$,

$$\begin{aligned} \xi _k^n= \frac{e^{-S_k}}{\sum _{i=0}^{n}e^{-S_i}}\rightarrow \overline{\xi }_k ,\ \ \ \mathbb {P}-a.s \end{aligned}$$

Since the random walk drifts to $+\infty$ the global minimizer

$$\begin{aligned} \ell =\arg \min \{S_k,k\in \mathbb {Z}_+\} \end{aligned}$$

is $\mathbb {P}$-a.s finite. Moreover, for n large enough we have $\ell _n=\ell$, and by centering the measure $\xi ^n$ and $\overline{\xi }$ around $\ell _n$ and $\ell$ respectively, we can easily obtain that

$$\begin{aligned} \tilde{\xi }^{(n)} \mathop {\longrightarrow }\limits ^{\mathcal L} \xi \quad \text{ in } \text{ the } \text{ space } ({\mathcal M}_1, \Vert \cdot \Vert _{TV}), \end{aligned}$$

where $\tilde{\xi }^{(n)}$ is defined as in (4) and $\xi _k=\overline{\xi }_{\ell +k}$. This yields Theorem 1 in the case $\theta <\mu /2$. $\square$

Proof of Theorem 2 for

$\theta \ne \mu /2$.

It is a straightforward consequence of the above, since $\ell _n={\mathcal O}(1)$ if $\theta < \mu /2$ or $n-\ell _n={\mathcal O}(1)$ if $\theta > \mu /2$. $\square$

Proof of Theorem 3 for

$\theta \ne \mu /2$.

Though it was already proved in [21, 35], we give another argument for completeness. Applying the law of large numbers for i.i.d. variables in (38), we directly obtain the claim. $\square$

5 Localization of the point-to-point measure

In this section, we consider the point-to-point measure with mirror boundary conditions. Recall the definition of the model P2P-b.c.$(\Theta )$ from (16).

In this situation, beside the usual partition function $Z_{m,n}$, we will also define the reverse partition function $\tilde{Z}_{m,n}$ for $(m,n) \in R_N$ as

$$\begin{aligned} \tilde{Z}_{m,n}= \sum _{\mathbf{x}\in \tilde{\Pi }_{m,n}^N }\prod _{t=m+n }^{(p+q)N-1} Y_{x_t}, \end{aligned}$$

(39)

where $\tilde{\Pi }_{m,n}^N$ denotes the collection of up-right paths $\mathbf{x}=(x_t; m+n\le t \le (p+q)N)$ in the rectangle $R_N$ that go from (m, n) to (pN, qN). Note that in the reverse partition function we exclude the weight at (pN, qN). Also, it depends on N, p and q, but we omit to indicate it in the notation. Moreover, we can also define the ratios $\tilde{U}$ and $\tilde{V}$ as in the usual case,

$$\begin{aligned} \tilde{U}_{m,n}= & {} \frac{\tilde{Z}_{m,n}}{\tilde{Z}_{m+1,n}} \end{aligned}$$

(40)

$$\begin{aligned} \tilde{V}_{m,n}= & {} \frac{\tilde{Z}_{m,n}}{\tilde{Z}_{m,n+1}} \end{aligned}$$

(41)

If we take the point (pN, qN) as the initial point then the reverse environment $(\tilde{Z},\tilde{U},\tilde{V})$ is also a stationary log-gamma system with boundary conditions. Indeed one sees from (39), (40) and (41) that $\tilde{U}_{m,qN}=Y_{m,qN}$ and $\tilde{V}_{pN,v}=Y_{pN,n}$.

We partition the rectangle $R_N$ according to the lower half space

$$\begin{aligned} H_{p,q}^{-,N}=\left\{ (i_1,i_2)\in \mathbb {Z}^2: qi_1+pi_2\le pqN\right\} \end{aligned}$$

and its complement. In order to simplify the notations, we denote for an edge f with endpoints in $R_N$,

(42)

From Fact 1 of Sect. 2.1 and independence of the weights in $H_{p,q}^{-,N}$ and its complement, for every down-right path z it follows that the variables $\{T_f:f\in z\}$ are mutually independent. We stress that independence relies also on the expressions of $Z_{m,n}$ and $\tilde{Z}_{m',n'}$, where there are no shared weights. The marginal distribution of $T_f$ is given by the stationary structure, it is a log-gamma distribution with the appropriate parameter. Let $\partial H_{p,q}^{-,N}$ be the transverse diagonal in $R_N$, which is given as

Consider the “lower transverse diagonal” given as

$$\begin{aligned} \mathcal {L}_{p,q}^N \ \text{ is } \text{ the } \text{ down-right } \text{ path } \ \mathbf{x}=(x_i): (0,qN)\rightarrow (pN,0) \ \text{ with } x_i\in \partial H_{p,q}^{-,N} , \end{aligned}$$

and the “upper transverse diagonal”,

$$\begin{aligned} \mathcal {U}_{p,q}^N=(1,1)+\mathcal {L}_{p,q}^N, \end{aligned}$$

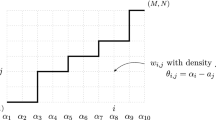
see Fig. 2. Define also the set of up-right edges across the transverse diagonal,

Each up-right path $\mathbf{x}$ that goes from (0, 0) to (pN, qN), intersects the transverse diagonal once and only once. Precisely, the mapping

$$\begin{aligned} \mathbf{x}=(x_j)_j \mapsto G(\mathbf{x})=\langle x_i, x_{i+1}\rangle , \quad \text{ with } \langle x_i, x_{i+1}\rangle \in \mathcal {A}_{p,q}^N , \end{aligned}$$

is well defined, and it indicates where the crossing takes place. (We have $i=t^-$ in (17).) Our main question in this section is the behaviour of the crossing edge when N increases. By definition of the polymer measure, for $\langle z_1,z_2\rangle \in \mathcal {A}_{p,q}^N$ we can write, with the notation $\sum _*$ for the sum over $\mathbf{x}\in \Pi _{pN,qN}, x_{t^-}=z_1, x_{t^-+1}=z_2$,

$$\begin{aligned} Q_{pN,qN}^{\omega }(G(\mathbf{x})=\langle z_1,z_2\rangle )= & {} \frac{1}{Z_{pN,qN}} \; \sum _* \exp \left\{ \sum _{t=1}^{t^-}\omega (x_t)+\sum _{t=t_-+1}^{(p+q)N}\omega (x_t)\right\} \\= & {} \frac{1}{Z_{pN,qN}} \; Z_{z_1} \times \tilde{Z}_{z_2} \times \exp \{ \omega (pN,qN)\}, \end{aligned}$$

where the last factor is the contribution of the last point $x_{(p+q)N}=(pN,qN)$. In view of (40), (41), (42), this term can be expressed as

$$\begin{aligned} Q_{pN,qN}^{\omega }(G(\mathbf{x}) =\langle z_1,z_2\rangle )= & {} \frac{1}{Z_{pN,qN}} \; Z_{0,qN} \times \tilde{Z}_{1,qN} \\&\times \exp \left( -\sum _{\Pi _1(z_1) }\log (T_f) -\sum _{\Pi _2(z_2)} \log (T_f)\right) \\&\times \exp \{ \omega (pN,qN)\}, \end{aligned}$$

where $\Pi _1(z_1)$ is the restriction of $\mathcal {L}_{p,q}^N$ from (0, qN) to $z_1$, and $\Pi _2(z_2)$ is the restriction of $\mathcal {U}_{p,q}^N$ from (1, qN) to $z_2$. Note that, when computing the ratio of the left-hand side for two different values of the crossing edge $\langle z_1,z_2\rangle$, both the first and last lines of the right-hand side cancel. Thus, we consider

$$\begin{aligned} W(\langle z_1,z_2\rangle )=\sum _{\Pi _1(z_1)}\log (T_f) +\sum _{\Pi _2(z_2)} \log (T_f). \end{aligned}$$

Observe that the variables $\{T_f: f\in \Pi _1(z_1)\}$ and $\{T_f: f\in \Pi _2(z_2)\}$ are independent but not identically distributed, so that in order to apply the same method as in previous section, we should divide $\mathcal {U}_{p,q}^N$ and $\mathcal {L}_{p,q}^N$ into identical blocks to obtain a centered random walk. Blocks are shifts of the right triangle with vertices $\mathbf{0}, p\mathbf{e_1}, q\mathbf{e_2}$. Precisely we denote by

$$\begin{aligned} z_1^k=(kp,(N-k)q), \quad \text{ for } 0\le k\le N, \end{aligned}$$

the vertices in $R_N$ which sit on the line of equation $qi_1+pi_2=pqN$, by

$$\begin{aligned} z_2^k=z_1^k+\mathbf{e_1}, \end{aligned}$$

and by $\mathcal {A}$ the set of crossing edges in the basic block $R_1$ shifted by $q\mathbf{e_2}$,

$$\begin{aligned} \mathcal {A}=\left\{ \langle z_1,z_2\rangle \text{ up } \text{ or } \text{ right } \text{ edge: } \ z_1+ q\mathbf{e_2} \in \mathcal {L}_{p,q}^1, \ z_2+q\mathbf{e_2} \in \mathcal {U}_{p,q}^1 , 1 \le z_2 \cdot \mathbf{e_1} \le p\right\} \end{aligned}$$

as shown in Fig. 3. Note that $\langle \mathbf{0},\mathbf{e_1}\rangle \in \mathcal {A}$ and the shifted edge $(p,-q)+ \langle \mathbf{0},\mathbf{e_2}\rangle \in \mathcal {A}$ but . We will use $\mathcal {A}$ and the set $(\langle z_1^k,z_2^k\rangle )_k$ to parametrize the set $\mathcal {A}_{p,q}^N$ as follows. For $\langle z_1,z_2\rangle \in \mathcal {A}_{p,q}^N$ we can find a unique k such that, relative to any coordinate, $z_1$ is between $z_1^k$ and $z_1^{k+1}$. Then by translation, there exists a unique edge $a\in \mathcal {A}$ such that:

$$\begin{aligned} \langle z_1,z_2\rangle =\left\langle z_1^k,z_2^k\right\rangle +a \end{aligned}$$

Fig. 2

Upper and lower “transverse diagonal” with $p=5, q=2, N=4$. Their vertices are indicated by dots and crosses respectively. $H_{p,q}^{-,N}$ is the region below the diagonal. The boundary conditions are indicated on the boundaries of the rectangle

Fig. 3

The set $\mathcal A$ with $p=5, q=2$ contains 7 crossing edges in the first block, indicated by solid lines

On the other hand, we have:

$$\begin{aligned} W_k=W\left( \left\langle z_1^k,z_2^k\right\rangle \right) =\sum _{\Pi _1(z_1^k)}\log (T_f) +\sum _{\Pi _2(z_2^k)} \log (T_f)=\sum _{i=1}^{k} X_i \end{aligned}$$

where

$$\begin{aligned} X_k= \sum _{f\in \Pi _1(z_1^k,z_1^{k+1})} \log (T_f)+\sum _{f\in \Pi _2(z_2^k,z_2^{k+1})} \log (T_f) \end{aligned}$$

(43)

with $\Pi _1(z_1^k,z_1^{k+1})$ the restriction of $\mathcal {L}_{p,q}^N$ from $z_1^k$ to $z_1^{k+1}$ and $\Pi _2(z_2^k,z_2^{k+1})$ the restriction of $\mathcal {U}_{p,q}^N$ from $z_2^k$ to $z_2^{k+1}$.

Let $\mathcal {B}=\{ \text{ edges } \ f \in \Pi _1(z_1^1)\cup \Pi _2(z_2^1)\}$, the edge set of the first block. Then it is clear that the edge set of a general block is a shift of that one,

$$\begin{aligned} \left\{ f \in \Pi _1\left( z_1^k,z_1^{k+1}\right) \cup \Pi _2\left( z_2^k,z_2^{k+1}\right) \right\} = z_1^{k-1}+ \mathcal {B} \end{aligned}$$

By consequence, the variables $(X_i)_{i\le n}$ are i.i.d and moreover

$$\begin{aligned} \mathbb {E}(X_i)= & {} p \left\{ \Psi _0(\theta _S)-\Psi _0(\theta _N)\right\} +q \left\{ \Psi _0(\theta _E)-\Psi _0(\theta _W)\right\} \\&\left\{ \begin{array}{c} =0\\ >0\\ <0 \end{array} \right. \begin{array}{cc} \mathrm{if} &{} \theta _N=\theta _S, \\ \mathrm{if} &{} \theta _N<\theta _S, \\ \mathrm{if} &{} \theta _N>\theta _S. \end{array} \end{aligned}$$

We first consider the case $\theta _N=\theta _S$. Then $W_k$ is a centered random walk and we can define

$$\begin{aligned} {\mathfrak l}_N= \arg \min _{0 \le k < N} W_k \end{aligned}$$

(44)

as in the previous section. Before presenting the key lemma, we introduce the limit law. Denote by $\nu (\cdot | u)$ a regular version of the conditional law of $(W(a), a\in \mathcal {A} )$ given $\sum _{a \in {\mathcal A}} W(a)=u$. Let $(X_i, i \ge 1)$ be an i.i.d. sequence distributed as in (43), and $S^{\uparrow }$ [resp. $S^{\downarrow }$] associated to X [resp., $-X$] as in (21), and $\hat{S}$ the sequence with $\hat{S}_0=0$ and

$$\begin{aligned} \hat{S}_k= \left\{ \begin{array}{ll} S_k^{\uparrow } &{} \hbox {if} \ k > 0\\ S_k^{\downarrow } &{} \hbox {if} \ k<0 \\ \end{array} \right. \end{aligned}$$

Consider also, on the same probability space, a random sequence $(Y_{k,a}: k\in \mathbb {Z}, a\in \mathcal {A})$ such that the vectors ${\mathcal Y}_k=(Y_{k,a}: a\in \mathcal {A})$ are, for $k \in {\mathbb {Z}}$, independent conditionally on $\hat{S}$ with conditional law $\nu (\cdot | \hat{S}_{k+1} -\hat{S}_k)$.

Lemma 6

For fixed $K\in \mathbb {Z}_+$,

$$\begin{aligned} \left[ W\left( \left\langle z_1^{{\mathfrak l}_N+k},z_2^{{\mathfrak l}_N+k}\right\rangle +a\right) -W\left( \left\langle z_1^{{\mathfrak l}_N},z_2^{{\mathfrak l}_N}\right\rangle \right) \right] _{|k|\le K,a\in \mathcal {A}}\mathop {\longrightarrow }\limits ^{\mathcal {L}}(\hat{S}_k+Y_{k,a})_{|k|\le K,a\in \mathcal {A}} . \end{aligned}$$

Proof

Applying Corollary 4 to the centered random walk $W_k$ we obtain for fixed K

$$\begin{aligned} \left[ W\left( \left\langle z_1^{{\mathfrak l}_N+k},z_2^{{\mathfrak l}_N+k}\right\rangle \right) -W\left( \left\langle z_1^{{\mathfrak l}_N},z_2^{{\mathfrak l}_N}\right\rangle \right) \right] _{|k|\le K}\mathop {\longrightarrow }\limits ^{\mathcal {L}}(\hat{S}_k)_{|k|\le K} \end{aligned}$$

(45)

with ${\mathfrak l}_N$ from (44). On the other hand, by independence of the $T_f$’s we know that the vectors

$$\begin{aligned} \left[ W\left( z_1^{k} +a\right) -W\left( \left\langle z_1^k,z_2^k\right\rangle \right) \right] _{a\in \mathcal {A}} \quad \text{ are } \text{ i.i.d. } \text{ for } k\ge 0. \end{aligned}$$

Thus, with $W_k=W(\langle z_1^{k},z_2^{k}\rangle )$, their joint law, conditionally on $(W_k; k \ge 0)$, is $\otimes _k \nu (\cdot | W_{k+1}-W_k)$. Then the result follows from (45). $\square$

Now we can state the main result of our construction, which reformulates Theorem 4 in the equilibrium case.

Proposition 3

Assume $\theta _N=\theta _S$. With the notations of Lemma 6, let

$$\begin{aligned} \xi _{k,a}= \frac{\exp \{-\hat{S}_k- Y_{k,a}\}}{1+\sum _{k=-\infty }^{\infty }\sum _{a\in {\mathcal A}} \exp \{-\hat{S}_k- Y_{k,a}\} } \end{aligned}$$

Then, as $N \rightarrow \infty$,

$$\begin{aligned} \left( Q_{Np,Nq}^{\omega }(G(\mathbf{x})= z_1^{{\mathfrak l}_N+k}+a)\right) _{k\in {\mathbb Z}, a\in \mathcal {A}}\xrightarrow {\mathcal {L}}(\xi _{k,a})_{k\in {\mathbb Z},a\in \mathcal {A}} . \end{aligned}$$

(46)

on the space $(\ell _1( {\mathbb Z}\times \mathcal {A}), |\cdot |_1)$.

Proof

We will use the same method as in the Sect. 4.1 to prove (46). With Lemma 6 at hand, we only need here to control the tail of sums as in (32) and (33). Define

$$\begin{aligned}(l_{N}^*,a_{N}^*)= & {} \arg \min _{(k,a)} \left[ W( z_1^{k}+a)\right] \quad \mathrm{for \ } \in \{0,\ldots ,N-1\} \times {\mathcal A}, \end{aligned}$$

the minimum location of W. Now we consider the process $(k,a) \mapsto W( z_1^{k}+a)$ indexed by integer time $t=kN+\ell$ if a is the $\ell$ element in $\mathcal A$, relative to its infimum, i.e., with the shift $s \mapsto t=s + l_{N}^*\times N+a_{N}^*$. Note that $t \mapsto W( z_1^{k}+a)$ is a sum of independent but not identically distributed random variables, it can be viewed as a Markov chain, which is not time-homogeneous but has periodic transitions with period equal by the cardinality of $\mathcal A$. Then, the law of the post-infimum process

$$\begin{aligned} s \mapsto W\left( z_1^{k}+a\right) - \min _{m,b} W\left( z_1^{m}+b\right) , s \ge 0, \end{aligned}$$

is also a Markov chain with a lifetime, i.e., a Markov chain killed at a stopping time. Similar to Proposition 2, we can prove that the law of this post-infimum process converges as $N \rightarrow \infty$ to a Markov chain on ${\mathbb R}^+$, with non-homogeneous transitions but periodic with period given by the cardinality of $\mathcal A$. The product of N consecutive transition kernels coincides with the one of $S^{\uparrow }$, it is homogeneous. Similar to Theorem 6, we conclude that the post-infimum process grows algebraically: with probability arbitrarily close to 1, we have for some positive $\delta$ and all large N,

$$\begin{aligned} W\left( z_1^{l_{N}^*+k}+a\right) - \min _{m,b} W( z_1^{m}+b) \ge \delta k^\eta , \quad k \in \left\{ 1,\ldots , N-1-l_{N}^*\right\} . \end{aligned}$$

Then, it is plain to check that ${\mathfrak l}_N-l_{N}^*= {\mathcal O}(1)$ in probability using that the former minimizes $W_k=W(\langle z_1^k, z_2^k\rangle )$, and we derive (32) and (33) as well. The rest of the proof follows from similar arguments to those of Theorem 1 in the case of $\theta =\mu /2$ and from Lemma 6. $\square$

Proof of Theorem 4

In the equilibrium case $\theta _N=\theta _S$, the above proposition 3 yields the conclusion by taking

$$\begin{aligned} m_N = \left( z_1^{{\mathfrak l}_N}+z_2^{{\mathfrak l}_N}\right) \cdot \left( q\mathbf{e_1}-p\mathbf{e_2}\right) , \end{aligned}$$

so that any path $\mathbf{x}$ through the edge $\langle z_1^{{\mathfrak l}_N},z_2^{{\mathfrak l}_N} \rangle$ has $F(\mathbf{x})=m_M$.

Consider now the opposite case where, by symmetry, we may assume $\theta _N<\theta _S$ without loss of generality. Then, the walk $(W_k)_{k \ge 0}$ has a global minimum. Interpolating $(W_k)_{k \ge 0}$ with independent pieces with law $\nu$ defined as above, we construct a process $\hat{\xi }$. Repeating the arguments of Sect. 4.2, we check that it is the desired limit. $\square$

Similar to that of Theorem 2, the proof of Theorem 5 is straightforward and left to the reader.