Skip to main content
SpringerLink
Log in

Dynamical stability of the cantilever beam with oscillating length

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

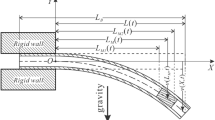
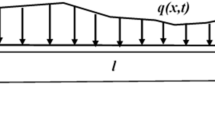
The dynamical stability and transverse vibration of the cantilever beam with oscillating length are analyzed in this study. The differential equation of motion with time-dependent coefficients is discretized by the Galerkin method, and then the method of multiple scales for multi-degree of freedom is applied to investigate the parametric resonances of the cantilever beam with oscillating length. The effects of the oscillation amplitude and frequency on the parametric resonance regions and the tip responses are discussed. Tip responses simulation by Runge–Kutta method confirms the parametric resonance regions obtained by multiple scales method. In addition, the ‘jump’ phenomenon on the tip response of the axially oscillating deploying cantilever beam is also discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Stylianou, M., Tabarrok, B.: Finite element analysis of an axially moving beam. Part I: time integration. J. Sound Vib. 178, 433–453 (1994)

    Article  Google Scholar 

  2. Stylianou, M., Tabarrok, B.: Finite element analysis of an axially moving beam. Part II: stability analysis. J. Sound Vib. 178, 455–481 (1994)

    Article  Google Scholar 

  3. Wang, L.H., Hu, Z.D., Zhong, Z., Ju, J.W.: Hamiltonian dynamic analysis of an axially translating beam featuring time-variant velocity. Acta Mech. 206(3–4), 149–161 (2009)

    Article  MATH  Google Scholar 

  4. Wang, L.H., Hu, Z.D., Zhong, Z., Ju, J.W.: Dynamic analysis of an axially translating viscoelastic beam with an arbitrarily varying length. Acta Mech. 214(3), 225–244 (2010)

    Article  MATH  Google Scholar 

  5. Al-Bedoor, B.O., Khulief, Y.A.: An approximate analytical solution of beam vibrations during axial motion. J. Sound Vib. 192(1), 159–171 (1996)

    Article  Google Scholar 

  6. Chang, J., Lin, W., Huang, C., Choi, S.: Vibration and stability of an axially moving Rayleigh beam. Appl. Math. Model. 34(6), 1482–1497 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Park, S., Yoo, H.H., Chung, J.: Vibrations of an axially moving beam with deployment or retraction. AIAA J. 51(3), 686–696 (2013)

    Article  Google Scholar 

  8. Bao, J., Zhang, P., Zhu, C., Sun, W.: Transverse vibration of flexible hoisting rope with time-varying length. J. Mech. Sci. Technol. 28(2), 457–466 (2014)

    Article  Google Scholar 

  9. Wang, L., Hu, Z., Zhong, Z.: Dynamic analysis of an axially translating plate with time-variant length. Acta Mech. 215(1), 9–23 (2010)

    Article  MATH  Google Scholar 

  10. Zhang, W., Sun, L., Jia, P.: Nonlinear dynamic behaviors of a deploying-and-retreating wing with varying velocity. J. Sound Vib. 332(25), 6785–6797 (2013)

    Article  Google Scholar 

  11. Zaja̧czkowski, J., Lipiński, J.: Instability of the motion of a beam of periodically varying length. J. Sound Vib. 63(1), 9–18 (1979)

    Article  MATH  Google Scholar 

  12. Zaja̧czkowski, J., Yamada, G.: Further results on instability of the motion of a beam of periodically varying length. J. Sound Vib. 68(2), 173–180 (1980)

    Article  MATH  Google Scholar 

  13. Bolotin, V.V.: The Dynamic Stability of Elastic Systems. Holden-Day Inc, San Francisco (1964)

    MATH  Google Scholar 

  14. Zhang, W., Lu, S.F., Yang, X.D.: Analysis on nonlinear dynamics of a deploying composite laminated cantilever plate. Nonlinear Dyn. 76(1), 69–93 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  15. Nayfeh, A.H., Mook, D.T.: Parametrically excitations of linear systems having many degrees of freedom. J. Acoust. Soc. Am. 62, 375–381 (1977)

    Article  MATH  Google Scholar 

  16. Nayfeh, A.H.: Introduction to Perturbation Methods. Wiley, New York (1981)

    MATH  Google Scholar 

  17. Hyun, S.H., Yoo, H.H.: Dynamic modeling and stability analysis of axially oscillating cantilever beams. J. Sound Vib. 228(3), 543–558 (1999)

    Article  Google Scholar 

  18. Chung, J., Jung, D.H., Yoo, H.H.: Stability analysis for the flap wise motion of a cantilever beam with rotary oscillation. J. Sound Vib. 273(5), 1047–1062 (2004)

    Article  Google Scholar 

  19. McIver, D.B.: Hamilton’s principle for systems of changing mass. J. Eng. Math. 7(3), 249–261 (1973)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the supports of the National Natural Science Foundation of China (Nos. 11472211 and 11272254), and the Natural Science Basic Research Plan in Shaanxi Province of China (No. 2015JM1029).

Author information

Authors and Affiliations

  1. School of Mechanical and Precision Instrument Engineering, Xi’ an University of Technology, No. 5 South Jinhua Road, Xi’an, 710048, China

    Yin-lei Huo

  2. Department of Packaging Engineering, Henan University of Science and Technology, No. 263 Kaiyuan Road, Luoyang, 471023, China

    Yin-lei Huo

  3. School of Civil Engineering and Architecture, Xi’ an University of Technology, No. 5 South Jinhua Road, Xi’an, 710048, China

    Zhong-min Wang

Authors
  1. Yin-lei Huo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhong-min Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhong-min Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huo, Yl., Wang, Zm. Dynamical stability of the cantilever beam with oscillating length. Arch Appl Mech 87, 1281–1293 (2017). https://doi.org/10.1007/s00419-017-1249-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-017-1249-6

Keywords

Search

Navigation