Skip to main content
SpringerLink
Log in

Improved solution to the generalized Galilei’s problem with interval loads

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

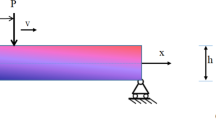
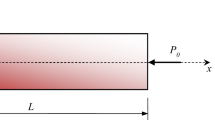
Model of a bar subjected to multiple axial external loads, where load magnitudes are considered as uncertain and represented by intervals, is recently considered by Elishakoff, Gabriele and Wang in this journal. Beside a high complexity of the proposed procedure for computing the intervals of the reaction and of the axial force distribution its assumptions are not always fulfilled and in these cases the obtained interval enclosures are far from the optimal (narrowest) ones. In this work we present a simple and efficient computational model for the reaction and for the axial force distribution which is based on the algebraic extension of classical interval arithmetic. It is proved that this model always yields the narrowest interval enclosure. The new interval model can be generalized and applied to other linear equilibrium equations in mechanics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. For the sake of better understanding, we denote intervals from \(\mathbb {KR}\) by [a]. Of course, \(\mathbf {a}\in \mathbb {IR}\subset \mathbb {KR}\), and thus, \([a]=\mathbf {a}\in \mathbb {KR}\) is a correct assignment.

  2. In the text of this work forces (and other vector quantities) are denoted by drawing a short arrow above the letter used to represent it. This is necessary in order to distinguish vectors from the interval-valued scalars, which are denoted by bold-faced letters, and other real-valued scalars. The magnitude of a vector will be denoted by the corresponding italic-faced letter.

  3. The IEEE interval Std. 1788 does not prescribe functionality for simulating multiplication/division of generalized (Kaucher) intervals.

References

  1. Beer, F.P., Johnston, E.R., Mazurek, D.F., Cornwell, P.J., Eisenberg, E.R.: Vector Mechanics for Engineers: Statics and Dynamics, 9th edn. McGraw-Hill, New York (2010)

    Google Scholar 

  2. Dimitrova, N., Markov, SM., Popova, ED.: Extended interval arithmetics: new results and applications. In: Atanassova, L., Herzberger, J. (eds.) Computer Arithmetic and Enclosure Methods, pp. 225-234. North-Holland (1992)

  3. Elishakoff, I., Gabriele, S., Wang, Y.: Generalized Galileo Galilei problem in interval setting for functionally related loads. Arch. Appl. Mech. 86(7), 1203–1217 (2015)

    Article  Google Scholar 

  4. Heimlich, O.: GNU Octave Interval Package, version 1.1.0, release 2015-08-03. http://octave.sourceforge.net/interval/. Accessed 25 January 2016 (2015)

  5. Hofschuster, W., Krämer, W.: C-XSC 2.0: A C++ library for extended scientific computing. In: Lecture Notes in Computer Science 2991, pp. 15-35. Springer, Heidelberg (2004)

  6. IEEE Standard Association: IEEE Std 1788\(^{{\rm TM}}\)-2015. IEEE Computer Society, IEEE Standard for Interval Arithmetic (2015)

  7. Kaucher, E.: Interval analysis in the extended interval space IR. Comput. Suppl. 2, 33–49 (1980)

    Article  MATH  Google Scholar 

  8. Markov, S.M.: Extended interval arithmetic. Compt. Rend. Acad. bulg. Sci. 30(9), 1239–1242 (1977)

    MathSciNet  MATH  Google Scholar 

  9. Markov, S.M.: On directed interval arithmetic and its applications. J. Univ. Comput. Sci. 1(7), 514–526 (1995)

    MathSciNet  MATH  Google Scholar 

  10. Markov, S.M.: On the foundations of interval arithmetic. In: Alefeld, G., Frommer, A., Lang, B. (eds.) Scientific Computing and Validated Numerics, pp. 307–313. Academie Verlag, Berlin (1996)

    Google Scholar 

  11. Mazandarani, M.: IEEE standard 1788–2015 vs. multidimensional RDM interval arithmetic, posting to IEEE P1788 working group. http://grouper.ieee.org/groups/1788/email/msg08439.html Accessed 25 January 2016 (2015)

  12. Moore, R.E., Kearfott, R.B., Cloud, M.J.: Introduction to Interval Analysis. SIAM Press, Philadelphia (2009)

    Book  MATH  Google Scholar 

  13. Nadezhin, D.Y., Zhilin, S.I.: JInterval library: principles, development, and perspectives. Reliab. Comput. 19, 229–247 (2014)

    MathSciNet  Google Scholar 

  14. Nehmeier, M.: libieeep1788: A C++ Implementation of the IEEE interval standard P1788. In: 2014 IEEE Conference on Norbert Wiener in the 21st Century (21CW), pp. 1–6. doi:10.1109/NORBERT.2014.6893854 (2014)

  15. Neumaier, A.: Computer graphics, linear interpolation, and nonstandard intervals. Manuscript, Univarsität Wien. http://www.mat.univie.ac.at/~neum/ms/nonstandard. Accessed 25 January 2016 (2009)

  16. Popova, ED., Markov, SM.: Towards credible implementation of inner interval operations. In: Sydow, A. (ed.), 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics. Vol. 2 Numerical Mathematics, W&T Verlag, pp 371–376. http://www.math.bas.bg/~epopova/papers/imacs97r. Accessed 25 January 2016 (1997)

  17. Popova, ED., Ullrich, CP.: Directed interval arithmetic in Mathematica. Implementation and applications. Technical Report 96-3, Universität Basel, Switzerland. http://www.math.bas.bg/~epopova/papers/tr96-3. Accessed 25 January 2016 (1996)

  18. Popova, ED.: Interval Model of Equilibrium Equations in Mechanics. In: Freitag, S., Muhanna, R. L., Mullen, R. L. (eds.) Proceedings of REC’2016, Ruhr University Bochum, pp. 241–255. http://rec2016.rub.de/downloads/rec2016_proceedings (2016)

  19. Popova, E.D., Ullrich, C.P.: Generalizing BIAS specification. J. Univ. Comput. Sci. 3(1), 23–41 (1997)

    Google Scholar 

  20. Sainz, MA., Armengol, J., Calm, R., Herrero, P., Jorba, L., Vehi, J.: Modal interval analysis: new tools for numerical information. Lecture Notes in Mathematics 2091, Springer (2014)

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Acad. G. Bonchev Str., Block 8, 1113, Sofia, Bulgaria

    Evgenija D. Popova

Authors
  1. Evgenija D. Popova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Evgenija D. Popova.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Popova, E.D. Improved solution to the generalized Galilei’s problem with interval loads. Arch Appl Mech 87, 115–127 (2017). https://doi.org/10.1007/s00419-016-1180-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-016-1180-2

Keywords

Search

Navigation