1 Introduction

Interest in Cut-off Low (COL) pressure systems has increased in the last decades, in recognition of their importance to precipitation regimes at low-mid latitudes. In particular, precipitation extremes associated with COLs can result in damage and socioeconomic impacts (Llassat et al. 2007; Porcu and Carrassi 2009). Since COLs move slowly, they can result in large accumulated rainfall amounts in a particular location, contributing to flood episodes on different continents (Singleton and Reason 2006a, b; McInnes and Hubbert 2001; Llasat et al. 2007). In particular, deep COLs extending toward the surface are generally associated with wetter conditions (Porcù et al. 2007; Pinheiro et al. 2021a). Moreover, COLs can cause deep intrusions of ozone-rich stratospheric air downward (Ancellet et al. 1994), which can be important at high altitudes as ozone is a pollutant.

COLs are historically identified as closed geopotential height contours in the mid-upper troposphere, associated with high potential vorticity (PV) anomalies cut-off from the stratosphere, as a result of the Rossby wave breaking on the mid-latitude jet (Ndarana and Waugh 2010). COLs typically grow because of the energy imported from the jet streak that propagates eastward along the poleward side of the COL (Ndarana et al. 2020) due to the agestrophic flux convergence, together with baroclinic processes (Gan and Dal Piva 2013, 2016; Pinheiro et al. 2021b), and then decay due to the export of energy downstream (ageostrophic flux divergence), friction and diabatic heating (Kousky and Gan 1981; Hoskins et al. 1985; Fuenzalida et al. 2005; Sakamoto and Takahashi 2005; Cavallo and Hakim 2010).

In the last few years, many studies have been undertaken to demonstrate the climatological features of COLs in both hemispheres, providing new insights in to their spatial distribution and temporal variability. The use of algorithms to objectively identify COLs has facilitated the development of more quantitative studies, mostly based on gridded data (atmospheric reanalysis), indicating that results are sensitive to the chosen identification method (Nieto et al. 2008; Pinheiro et al. 2019) and dataset (Reboita et al. 2010; Pinheiro et al. 2020). More recently, there has been an increasing interest in how climate models simulate COLs, perhaps because changes in the COL behavior may impact regional climate variability. Understanding how well COLs are simulated by climate models is essential for reliable current predictions and future projections. One way to do this is to investigate whether climate models are able to accurately simulate present-day COL characteristics in reasonably good agreement with reanalyses.

While considerable efforts have been made in regional and global climate modeling, there are few studies evaluating the performance of climate models in simulating COLs, with the result that their prediction remains uncertain. An exception is the paper by Bozkurt et al. (2016), in which the relationship of sea surface temperature (SST) anomalies with precipitation was tested using a regional climate model. They compared the simulated COL with observations to show that the warmer SST in the southeast Pacific sector was crucial for the rare event of intense rainfall in the Atacama Desert. Additionally, Reyers and Shao (2019) evaluated the skill of two coupled climate models, which participated in the third phase of the Paleoclimate Modelling Intercomparison Project (PMIP3), in simulating the synoptic conditions associated with COLs located off the coast of Northern Chile. They found that more COLs occurred in the Last Glacial Maximum compared to present-day conditions, due to a decrease of the subtropical jet intensity.

The Coupled Model Intercomparison Project (CMIP) has facilitated the assessment of the impact of past, present and future climate conditions on large and synoptic scale weather patterns (Bellenger et al. 2014; Zappa et al. 2013; Reboita et al. 2019; Harvey et al. 2020), providing an invaluable source for the Intergovernmental Panel on Climate Change (IPCC) Assessment Reports. Data from the sixth generation of CMIP is now available, and represents the current state-of-the-art in global coupled climate modeling. It is important to analyse these outputs and examine whether they are better (or not) in simulating the current climate compared to the predecessor CMIP5 simulations. The most important changes in CMIP6 with respect to the previous version are the increased spatial model resolution and improved model parameterizations and physical processes (Eyring et al. 2016). These improvements will hopefully reduce the model uncertainty and will be critical for better prediction of synoptic-scale features such as COLs, this has been highlighted by recent evidence that the CMIP6 models better represent the location and intensity of extratropical cyclones compared to CMIP5 models (Priestley et al. 2020).

The primary focus of this study is to quantify the ability of the CMIP5 and CMIP6 models in representing the global climatological features of COLs. This will be done by contrasting the results with the latest global reanalysis product ERA5 (Hersbach and Dee 2016). Specifically, we intend to answer the following research questions:

  • Are CMIP6 models better at simulating COLs compared to the CMIP5 models;

  • Does the increased spatial resolution of CMIP6 models result in an improvement in the simulations of COLs in terms of their spatial distribution, number and intensity;

  • What is the inter-model spread in the COL simulations, and what is the overall ranking of model performance for COLs.

The paper continues by describing the reanalysis and model datasets together with the tracking algorithm in Sect. 2. Our results are discussed in Sect. 3, followed by conclusions in Sect. 4.

2 Data and methods

2.1 Models and reanalysis data

Atmospheric reanalysis products have been extensively used to evaluate climate models in simulating current climate conditions. Inconsistences in COL features have been found when COLs have been identified in data from older reanalysis (Reboita et al. 2010), but improvements in the data assimilation and forecast models have reduced the uncertainties in location and intensity of COLs with more recent reanalyses (Pinheiro et al. 2020). The ERA5 is the most recent reanalysis produced by the European Centre for Medium-range Weather Forecasts (ECMWF) (Hersbach and Dee 2016), and will be used here to assess the model results. The most important changes in the ERA5 configuration compared to its predecessor ERA-Interim include a finer spatial spectral resolution (TL639, corresponding ~ 31 km), higher temporal resolution (hourly outputs), higher number of vertical levels (137), and a larger amount of observational data assimilated. ERA5 is based on the Integrated Forecasting System (IFS) model Cycle41r2 with 12-h 4DVar data assimilation.

In this study the present-day historical simulations of 23 CMIP5 models and 23 CMIP6 models, listed in the supplementary Tables S1 and S2, are used. The historical runs are produced using fully coupled ocean–atmosphere climate models, forced by greenhouse gas concentrations, solar forcing, natural and anthropogenic aerosols and land use (Eyring et al. 2016). The historical simulations are available from the mid-nineteenth century to near present, but we restrict our analysis to the period after 1979 to be consistent with the period covered by the reanalysis dataset for the modern satellite era (post-1979), while the end data 2005 was chosen based on the availability of CMIP5 data. The CMIP6, in particular, includes simulations produced as part of the High-Resolution Model Intercomparison Project (HighResMIP, Haarsma et al. 2016), following specific protocols such as incorporating higher resolutions. The standard CMIP6 models have atmospheric resolutions that typically range from ~ 250 to ~ 100 km, but the HighResMIP simulations comprise simulations with considerably higher resolutions (25–50 km), which allows a more detailed investigation of the impact of increased resolution on the simulated characteristics of COLs. Since the CMIP5–CMIP6 models present a wide range of resolutions, it is possible to separate models into “high” and “low” resolution groups, as shown in bold in the Tables S1 and S2. The nominal resolution will be used to categorize models as this attribute does not depend on the grid characteristics, as defined in Appendix 2 in Taylor (2018). The “high” resolution group includes models with nominal resolutions of 100–150 km for CMIP5 and 25–100 km for CMIP6. For the analysis of the large-scale circulation, the data were first regridded to a common horizontal grid using the bilinear interpolation technique.

The CMIP models were chosen based on their data availability at the time of writing, since not all models provide the six-hourly wind fields at upper pressure level (e.g., 250-hPa), which are required to identify and track COLs. We use all available ensemble members to reduce the uncertainty in the analysis (see Table S1 for detail descripts of data). The ensemble mean fields are calculated from the individual model runs where each ensemble model is tracked individually.

2.2 COL tracking and analysis techniques

COLs are identified and tracked using a scheme that has been previously described (Pinheiro et al. 2019, 2020) based on the TRACK algorithm (Hodges 1995, 1999) and is outlined below. The tracking is performed on the relative maxima for the NH and minima for the SH in the six-hourly 250-hPa relative vorticity (\({\xi }_{250}\)). The 250-hPa level was chosen for the tracking due to data availability, and that it is close to the dynamical tropopause level and is the closest level above the 300 hPa, where the highest intensities occur in COLs (Pinheiro et al. 2021a). The 250-hPa zonal and meridional wind speeds are used to compute the \({\xi }_{250}\). The identification process is preceded by spectrally filtering the vorticity field using a triangular truncation 42 (T42) to retain only the synoptic scale features, and this ensures that the features will be focused on a similar spatial scale, irrespective of the model horizontal resolution. The tapering filter of Sardeshmukh and Hoskins (1984) is applied to reduce the Gibbs effect, and the large-scale background is also removed by setting the coefficients of the total wavenumbers less than or equal to five to zero. The extrema (feature points) are determined as off-grid locations using B-spline interpolation and steepest ascent maximization. The tracking is performed on the sphere by first initialising a set of tracks from the feature points using the nearest neighbour method. These tracks are then refined by minimizing a cost function for track smoothness subject to adaptive constraints for displacement and track smoothness. A post-tracking filtering is used to ensure the presence of a cut-off circulation. This is applied to the horizontal wind components, added to the tracks, in four offset points located 5° geodesic from the COL centre, defined as follows: 0° (u < 0), 90° (v > 0), 180° (u > 0), and 270° (v < 0) for the NH; and 0° (u > 0), 90° (v < 0), 180° (u < 0), and 270° (v > 0) for the SH. These conditions reduce the number of open troughs without being too restrictive as in methods based on multiple step schemes (Nieto et al. 2005; Reboita et al. 2010; Pinheiro et al. 2017, 2019). Finally, only the tracks that occur within the 15°–50° latitudinal band from the equator in both hemispheres, and last at least 24 h are retained.

COL diagnostics include their frequency, intensity, life time and seasonality. The spatial statistics are computed using spherical kernel estimators to produce the track density and mean intensity (Hodges 1996). The track density is provided as the number of COLs per season per unit area (5° spherical cap \(\cong \) 106 km2). The mean intensity is computed from all points along the track based on the T42 \({\xi }_{250}\), scaled by -1 in the SH. The spatial diagnostics are examined for each season, but only the mean fields (averaged over all seasons) are shown in the main text for reasons of simplicity and convenience. For each model, the spatial statistics are averaged across all the available ensembles to reduce the uncertainty arising from different model versions. Additional analyses for each season are given as supplementary online material.

The performance of individual climate models in simulating the spatial distribution of COLs (in terms of track density) is evaluated using the Taylor diagram (Taylor 2001), which has been used in other model intercomparison and evaluation studies (Gleckler et al. 2008; Walsh et al. 2013; Langenbrunner and Neelin 2013; Kumar and Sarthi 2019). The Taylor diagram includes widely-used standard statistical metrics such as the standard deviation, correlation, root-mean-square error (RMSE) and unbiased RMSE (ubRMSE) as is in our Taylor diagram. These indices are analysed together with the mean bias and they are all quantified by spatially averaging the mean COL track density over the study area for the reanalysis and climate model simulations. Since the Taylor diagram provides a concise statistical summary of how well climate models reproduce spatial patterns, a skill score method is used by assigning the model’s position (ith ranking position) among all the 46 models from CMIP5 and CMIP6 using the five aforementioned variables, and then averaged over all variables. This allows us to establish the relatively better performing models (i.e., the models with higher ranking scores) for the simulation of COLs.

3 Results

3.1 Spatial distribution of Cut-off Lows

3.1.1 ERA5

Before discussing the results of the model simulations, the global climatology of COLs is presented for the period from 1979 to 2008 using the ERA5 reanalysis to provide a frame of reference. During the 30-year period, the method based on the \({\xi }_{250}\) identifies an average of 575 (440) tracks per year in the NH (SH), which is a larger number than those reported in the literature for methods based on identification using geopotential data and more restrictive criteria (Nieto et al. 2005; Ndarana and Waugh 2010; Reboita et al. 2010; Muñoz et al. 2020). Differences in numbers are expected as for smoother fields such as geopotential weaker COLs are unlikely to be identified, this is compounded by the lack of ground truth to compare with (Pinheiro et al. 2019). The interannual variability of COLs as calculated using a coefficient of variation indicates a small variance (5%) compared to the those observed by Fuenzalida et al. (2005) and Muñoz et al. (2020). Differences may be attributed to either the identification method or dataset as the results from the most recent reanalyses are found to be much better constrained compared to older reanalyses (Pinheiro et al. 2020).

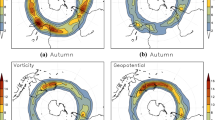
The track density (contours) and mean intensity (colour) are shown in Fig. 1 and provides information on the spatial distribution of COLs for summer and winter in both the NH and SH. Summer and winter were chosen to contrast the periods with highest/lowest frequency and intensity of COLs. By comparing the JJA with DJF, we confirm previous findings that COL systems in both hemispheres are much more frequent in summer (accounting for about one third of the annual mean number of COLs), contrasting with far fewer COLs formed during winter (~ 15% of the annual mean number) when enhanced zonal wind speeds are more frequent in most subtropical and mid-latitude regions, inhibiting the split jet flow, and consequently the Rossby wave breaking (RWB) process, which is generally required for the development of a COL (Peters and Waugh 2003; Ndarana and Waugh 2010). However, deep COLs extending toward the surface are more frequently found in winter (Ndarana et al. 2010; Barnes et al. 2021), when COLs reach their strongest intensities (Pinheiro et al. 2017), but also due to the dynamical tropopause that is closer to the surface compared to other seasons (Kunz et al. 2011).

Fig. 1
figure 1

Track density (contour) and mean intensity (shaded) of 250-hPa relative vorticity for summer and winter in the Northern Hemisphere (NH) and Southern Hemisphere (SH). Track density contours are every 4.0 with the dashed line at 16.0. Mean intensity is suppressed for track density below 1.0. Unit: number per season per unit area (unit area is equivalent to a 5° spherical cap) for track density; and 10–5 s−1 for mean intensity

Full size image

In austral latitudes, COLs are mainly found in the vicinity of the continents in winter, consistent with numerous previous studies (Fuenzalida et al. 2005; Reboita et al. 2010; Ndarana and Waugh 2010; Pinheiro et al. 2017). However, the largest activity of COLs migrates to oceanic areas in summer, where the latent heat release is generally less significant than over the warm continents (Fuenzalida et al. 2005), as diabatic heating has been found to act as a dissipative mechanism in COLs (Sakamoto and Takahashi 2005; Garreaud and Fuenzalida 2007) and tropopause polar vortices (Cavallo and Hakim 2010). The spatial distribution of COLs in the NH is much more asymmetric compared to the SH. In winter, COLs concentrate at three preferred locations: northeastern Atlantic Ocean; Mediterranean Sea and northwestern Africa; and northwestern Pacific Ocean and western North America. During the summer the picture changes as preferred regions for COL development are also found in northeastern China, central Pacific Ocean, and along the Gulf of Mexico and Caribbean Sea region. The prominent Caribbean maximum has also been observed by Wernli and Sprenger (2007) as potential vorticity cutoffs on the 350-K isentropes, but does not appear as an obvious feature in studies where the identification is based on geopotential data (e.g., Nieto et al. 2008; Muñoz et al. 2020), as this field is known to be problematic for identifying and tracking COLs related to the weak geopotential gradients that typically occur at low latitudes (Pinheiro et al. 2019). It is known that the Caribbean is also a region affected by tropical cyclones which occurs most frequently during late summer, and upper-level disturbances such as COLs can act as synoptic-scale precursors to tropical cyclone development (Sadler 1967; Kelley and Mock 1982). The influence of upper-level potential vorticity disturbances on the tropical transition is documented in earlier studies (Emanuel 2005; Galarneau et al. 2015; Bentley et al. 2016) and a possible relationship between COLs and tropical cyclones may be associated with the maximum observed in the Caribbean.

In general, the overall maximum track density located around 30-35oN appears to be associated with COLs developed by RWB, while the mechanism associated with the systems located in more southern latitudes is likely a result of Rossby and mixed Rossby-gravity wave dispersion (Silva Dias et al. 1983). The last type is a tropopause vortex that occurs downstream from upper-level anticyclones, especially during the summer, as discussed in Frank (1970), Kousky and Gan (1981), and Morais et al. (2021).

In Pinheiro et al. (2017), the seasonal COL mean intensity in the SH was analysed using tracking of vorticity minima at 300 hPa using the ERA-Interim reanalysis. As seen in Pinheiro et al. (2017), the main track density (Fig. 1) roughly coincides with regions of maximum intensity in winter in both hemispheres, but the strongest intensities migrate to more poleward latitudes in summer, suggesting that the mechanisms responsible for controlling the COL strength may be subject to the seasonal cycle of the jet streams. The maximum intensities of COLs are found on average at a latitude of about 29° N (29° S) in winter and 43° N (41° S) in summer in the NH (SH), which approximately corresponds to the latitude of maximum zonal winds (not shown). The objective method identifies an average filtered \({\xi }_{250}\) of 7.6 \(\times \) 10–5 s−1 for the NH COLs and − 8.7 \(\times \) 10–5 s−1 for the SH COLs, however, the inter-hemispheric differences in intensity reduces if we consider the latitudinal band 20°–50° N (and 50 –20° S), suggesting that the lower intensities of the NH COLs are partly explained by weak systems located near the equator (particularly in summer) and included in the statistic. The ability of CMIP models to simulate these features will be examined in the next sections.

3.1.2 COLs in the CMIP5 and CMIP6 ensembles

It is important to determine whether changes in the CMIP6 models have resulted in an improved representation of COLs in comparison to their corresponding version in CMIP5 in order to have confidence in how models simulate and predict COLs. Therefore, the ability of the CMIP5 and CMIP6 models to capture the spatial distribution of COLs is examined through the track density averaged over all seasons, using the model historical simulations for the period 1979–2005 and compared to ERA5 for the same period. The diagnosis of the seasonal cycle of the COLs will be discussed in Sect. 3.2. Figure 2 compares the climatology of COLs simulated by the multi-model ensemble mean of the 23 CMIP5 models and the 23 CMIP6 models with the reanalysis data. The analysis is presented for the NH and SH so that the model results for each hemisphere and region can be compared. The CMIP5 and CMIP6 ensemble means of track density (Fig. 2) show that models can reproduce the preferred regions of COL activity, though there is a significant underestimation within the preferred regions. The reduced number of COLs represented by the models can in part be explained by their lower spatial resolution compared with the reanalysis. However, by comparing CMIP5 with CMIP6, we find a reduction in the track density underestimation from 18% (23%) in CMIP5 to 8% (4%) in CMIP6 for the NH (SH) respectively. Moreover, considering the spread among the individual models (see supplementary material, Figs. S1 and S2), the analysis demonstrates an improvement in the inter-model standard deviation which reduces from 0.67 (0.53) in CMIP5 to 0.56 (0.51) in CMIP6 for the NH (SH). While the multi-model ensemble reproduces the regions of high density reasonably well, some models fail to reproduce these features. This is more apparent in CMIP5 (e.g., FGOALS-g2, FGOALS-s2, IPSL-CM5A-LR, IPSL-CM5B-LR, MIROC-ESM), but deficiencies still remain in some CMIP6 models (e.g., IPSL-CM6A-LR, MIROC-ES2L, NorESM2-LM), lowering the confidence in future projections with these models.

Fig. 2
figure 2

Track density of 250-hPa relative vorticity averaged over all seasons for multi-model ensemble mean of a, d the CMIP5 models, b, e the CMIP6 models, and c, f the ERA5 reanalysis. Analysis is performed for a–c NH COLs and d–f SH COLs. Unit is number per season per unit area, where unit area is equivalent to 5° spherical cap

Full size image

Figure 3 shows the multi-model mean bias of the CMIP5 and CMIP6 models relative to ERA5 (model minus ERA5) in terms of track density. To determine the common errors in models, a systematic bias is defined if it is common to all models for each corresponding CMIP phase, which is denoted by stippling the areas where all the models have a bias with the same sign. The spatial pattern of biases in CMIP5 and CMIP6 are similar in each hemisphere, but the magnitude of the mean biases (computed from all grid points in the domain) is substantially lower in CMIP6 than in CMIP5. The largest bias in track density is found in regions of high COL density, where there are too few COLs. In contrast, positive biases are generally found at more equatorward latitudes, which are apparent in South America, the southwestern Atlantic Ocean, and the region extending across the South Indian Ocean, Australia, and eastern and central Pacific Ocean. The equatorward shift of COLs in the climate models is also obvious in the NH from North Africa, extending across the Middle East and India, but the spatial distribution of bias in CMIP6 changes in the North Pacific Ocean which is characterized by too few COLs at more southern latitudes and many more COLs at more northern latitudes. Although biases still persist in CMIP6, there is a reduction of the overall spatial bias and a poleward shift of the COLs in CMIP6 relative to CMIP5 (not shown). For details of the mean track density bias in each individual model, see supplementary material (Figs S5 and S6).

Fig. 3
figure 3

Multi-model mean bias with respect to the ERA5 reanalysis (ensemble mean minus ERA5) for the a, c CMIP5 and b, d CMIP6. Fields are track density for the multi-model mean bias (shaded) and ERA5 for contour intervals 8.0 COL season−1 (5° spherical cap)−1. Stippling denotes areas where the bias of all models has the same sign. Track density is suppressed where values are below 0.25 COL season−1 (5° spherical cap)−1

Full size image

The multi-model mean bias of the mean intensity, as measured by the T42 \({\xi }_{250}\), shows a clear underestimation in CMIP5 in both hemispheres (Fig. 4a, c). The negative bias in the NH (Fig. 4a) generally occurs at more poleward latitudes, in particular from Northeast Asia to North America, and the central Pacific Ocean south to 30oN, where the underestimation occurs during all seasons (not shown). When considering the multi-model mean bias of the mean intensity with respect to CMIP6 (Fig. 4b), we find a reduction of the negative bias in most regions where the CMIP5 fails to simulate the intensities well. In contrast, there are positive biases in central America and from eastern China to the northwestern Pacific Ocean, though with little consensus between the models, which is denoted by the absence of stippling. As with the NH, the intensity of the SH COLs is robustly underestimated by CMIP5 (Fig. 4c), in particular during the austral summer and autumn (not shown). However, there is an overall improvement in the representation of intensities of the SH COLs in CMIP6 (Fig. 4d), since the biases are less prominent and less extensive than those in the corresponding version of CMIP5. In general, we find that the intensity underestimation is reduced by about 7% in CMIP6 compared to CMIP5 in both hemispheres, though there are more pronounced seasonal differences in the simulated intensities in CMIP6, which are underestimated in summer and overestimated in winter (not shown). The underestimation occurs in 96% (91%) of the CMIP5 models, but it decreases to 78% (56%) of the CMIP6 models with regard to NH (SH). This improvement would be even more noticeable if we consider only the higher resolution models in which their representation of the COL intensity performs much better than the lower resolution models. A more detailed discussion of the simulated intensities with respect to model horizontal resolution is given in Sects. 3.2.1 and 3.2.4.

Fig. 4
figure 4

Same as in Fig. 3 but for the mean intensity, scale by − 1 for SH COLs (as they are associated with negative \({\xi }_{250}\)). Unit is 10–5 s−1. The ERA5 climatology is indicated by 8.0 and 10.0 \(\times \) 10–5 s−1 contour intervals. Mean intensity is suppressed for track densities below 0.25

Full size image

3.1.3 Impact of model horizontal resolution

To provide a comparative analysis of how coupled model biases are affected by horizontal resolution, we analyzed the track density bias in two subsets of CMIP6 models from the same modeling centers each including standard and enhanced horizontal resolutions in the atmosphere (see the list of models assessed in the supplementary Table S2). The high-resolution simulations, namely HighResMIP, are based on exactly the same models as for the standard resolution simulations without additional tuning, thereby minimizing differences that could arise from different experimental set-ups and forcings (Haarsma et al. 2016). Figure 5a, b show some improvement in mean bias with the HighResMIP relative to standard resolution simulations in the NH. The negative biases that systematically affect coupled climate models (see Figs. 2 and 3) are reduced in the HighResMIP simulations, particularly in the northeastern Atlantic, southern Europe and north Africa which is likely a result of the enhanced horizontal resolution. The performance of five statistical measures (mean bias, standard deviation, correlation, RMSE and ubRMSE) indicates a clear improvement in COL simulations with HighResMIP over standard resolution models. There is only one standard resolution model (MPI-ESM1-2-HR) that outperforms the corresponding higher resolution version (MPI-ESM1-2-XR), which is the worst HighResMIP model according to the statistical measures. However, improvements are not observed in the North Pacific where biases still remain in the HighResMIP models.

Fig. 5
figure 5

Multi-model mean track density bias for a subset of the CMIP6 models from the same modeling centers corresponding to a, c standard resolution, b, d HighResMIP simulations. Unit is the same as Fig. 3

Full size image

In the SH, improvements between HighResMIP and standard resolution models are less obvious compared to the NH. Perhaps the most remarkable improvement is seen in subtropical South America where the overrepresentation of the COL tracks is reduced in the HighResMIP simulations, which may be associated with a better representation of orographic drag processes in higher-resolution models (Pithan et al. 2016). It is surprising that increasing horizontal resolution does not systematically lead to a larger number of identified tracks, as observed in reanalysis systems (Pinheiro et al. 2020). Overall, our results demonstrate that improving the horizontal resolution impacts positively in the NH, but biases still persist in the SH where errors in the air–sea coupling or the representation of the large-scale circulation may be more problematic (Meehl et al. 2019), while model physics appears to be more important than increased horizontal resolution.

3.1.4 Large-scale circulation bias

Given that most climate models fail to realistically simulate the COL features, even the higher resolution CMIP6 models, it is important to investigate whether the model biases presented in earlier sections can be linked to biases in the large-scale atmospheric circulation. Understanding the factors that influence model bias is essential to gain confidence in climate model projections. Moreover, we intend to verify whether the systematic CMIP5 deficiencies may have evolved or are still persisting in CMIP6. The possible association between the large-scale circulation and the COL activity is investigated by examining the basic state zonal flow defined by the seasonal means of the 250-hPa zonal wind (\({U}_{250}\)) from all model ensemble members and compared to ERA5. Figure 6a, b show that the CMIP5 and CMIP6 multi-model means exhibit an equatorward shift of the NH jet streams relative to ERA5, which is noticeable as a dipole bias with too strong winds on the equatorward side and too weak winds on the poleward side of the climatological jet position. This is an obvious feature in the exit region of the North Atlantic and North Pacific jets, which has previously been observed in CMIP5 (Zappa et al. 2013; Pithan et al. 2016) and still persists in CMIP6. Such biases are present in all seasons, except in summer as shown in the supplementary material (Fig. S11). The enhanced polar jet that extends zonally from the North Atlantic into central Europe leads to a strong underestimation of the COL track density over these areas. The continued presence of the bias indicates that, such under a stronger zonal wind across the North Atlantic and Europe, the COL development will likely be occurring far south of Europe, and not over the Iberian Peninsula, as would be expected.

Fig. 6
figure 6

Zonal windy anomaly at 250-hPa for the multi-model means of THE a, c CMIP5 models and b, d CMIP6 models for the a, b northern hemisphere and c, d Southern hemisphere. Black line contours show ERA5 climatology for the period 1979–2005. Unit is ms−1

Full size image

Figure 6c, d show the multi-model mean bias of the CMIP5 and CMIP6 models, respectively, for the \({U}_{250}\) in the SH. The CMIP5 and CMIP6 models appear to experience a similar bias in the austral jet as found in the NH. The multi-model means of CMIP5 and CMIP6 for the \({U}_{250}\) feature a positive bias on the equatorial side of the exit region of both the polar jet over the South Indian Ocean and the subtropical jet over the South Pacific Ocean, but a notable improvement in the \({U}_{250}\) simulation occurs in CMIP6 with reduced biases compared to CMIP5. The reduced equatorward bias of the CMIP6 models is likely contributing to the decreased bias in COL activity, as shown in Fig. 3c, d. The underestimation in the austral COL activity in locations with high track density, that is more significant in CMIP5, is likely caused by the fact that the simulated zonal flow is accelerated there to values larger than those observed in the reanalysis, in particular in winter and spring (supplementary material, Fig. S12). This highlights the deficiencies in simulating the jet stream that is displaced equatorward relative to observations in the CMIP5 and CMIP6 models.

We suggest that the spatial pattern of bias in track density is connected to that in \({U}_{250}\), since positive (negative) mean track density bias roughly coincide with regions of negative (positive) mean \({U}_{250}\) bias. To gain more insight on the relation between these biases, we compute the inter-model spatial correlation between the \({U}_{250}\) and track density biases area averaged within the 20°–50° N (50°–20° S) latitudinal bands. A weak negative correlation is generally found between the bias in the \({U}_{250}\) and COL track density in both the CMIP5 and CMIP6 models. The multi-model ensemble of CMIP6 (CMIP5) exhibit a correlation of − 0.31 (− 0.22) for the SH and − 0.15 (− 0.17) for the NH, whereas the largest negative correlations occur in autumn in both hemispheres. Looking at each model individually, however, shows there are model differences, as \({U}_{250}\) and track density biases are not correlated in 6 (8) CMIP6 (CMIP5) models in the NH. However, a better agreement is observed in the SH where almost all models present negative correlations.

In summary, our results demonstrate there is a possible link between the spatial distribution of COLs and the jet behavior, which corroborate recent work demonstrating the role of the mid-latitude jet streak on the development of South African COLs (Ndarana et al. 2020). Our results suggest that the simulated zonal wind has improved in the CMIP6 models particularly in summer, due to reduced positive bias in the subtropical jet, which in turn results in an increased number of COLs identified in regions of high track density. However, even though the \({U}_{250}\) bias is a robust feature across the CMIP5 and CMIP6 models, there is a considerable spread in the magnitude and distribution of these biases across the 46 models considered in this paper. For this reason, care is needed in attributing the bias in the COL diagnostics to a single field, such as \({U}_{250}\), as other factors (e.g., cloud radiative forcing) have been found to be important in controlling the position and strength of the extratropical jet streams (Ceppi et al. 2012; Grise and Polvani 2014; Li et al. 2015; Voigt and Shaw 2016). In this regard, recent studies have shown a bias reduction in short wave cloud forcing in CMIP6 models (Kawai et al. 2017, 2019; Voldoire et al. 2019).

3.2 Inter-model spread in the CMIP5 and CMIP6

3.2.1 Number

The COL activity is now further investigated by examining the number of COLs identified in each CMIP5–CMIP6 model against the reanalysis. Figure 7a shows the medians, quartiles, whiskers and outliers (when available) of the percentage difference (with respect to ERA5) in the total number of COLs simulated by the CMIP5 and CMIP6 models. We find that the majority of models underestimate the total number of COLs in both hemispheres as the medians for both CMIP5 and CMIP6 (and the interquartile ranges, except the CMIP6 for the SH) lie entirely below zero. However, there is a wide inter-model spread that exists mainly due to the poor performance of the coarser resolution models, which persist even in CMIP6, though a remarkable improvement has been achieved in CMIP6 with respect to the interquartile distances, in particular in the NH. By comparing CMIP5 and CMIP6, we find a reduction of 39% (35%) in the number of models with percentage change larger than ± 10% for the NH (SH). In CMIP5, six models (FGOALS-g2, GISS-E2-R, IPSL-CM5B-LR, MRI-ESM1, GFDL-ESM2G and GFDL-ESM2M) underestimate the total number of COLs with bias larger than 40%, while only two CMIP6 models (MRI-ESM2-0 and NorESM2-LM) have an underestimation larger than 20%.

Fig. 7
figure 7

Percentage change of COL number with respect to the ERA5 reanalysis in terms of the a total number, b extremes and c, d seasonal variability. White and gray boxes represent the CMIP5 and CMIP6 ensembles, respectively

Full size image

The number of simulated COLs is also analyzed by comparing the seasonal variability. For the NH (Fig. 7c), it can be seen that the CMIP6 models simulate much better the number of COLs in boreal summer, when the median is close to zero, though the smallest inter-model spread (measured by the minimum–maximum and lower quartile-upper quartile differences) occurs in boreal autumn. It was found that the inter-model spread in the simulated number of COLs in the SH (Fig. 7d) is larger than in the NH, particularly in austral winter, contrasting with relatively better models’ performance in austral autumn.

We also examine the ability of models in simulating extreme COLs, defined as those exceeding the threshold of 95th percentile in the maximum along-track \({\xi }_{250}\) relative to the model and reanalysis climatologies. Similar to the total number of COLs, Fig. 7b shows a significant underestimation of the strong COLs with a large dispersion among the models, indicating that the deficiency in representing the number of COLs similarly affects the extremes. However, a reduction in the median bias in CMIP6 (7% in the NH and 17% in the SH) is observed as well as a decrease in the interquartile range (2% in the NH and 24% in the SH) as compared to CMIP5. A closer inspection of individual model performance shows that higher-resolution models generally provide the highest level of global COL activity. Nonetheless, the model resolution is not the only factor that determines model bias, since some high-resolution models such as MRI-ESM2-0 (~ 100 km) and GFDL-CM4 (~ 100 km) underestimate the number of COLs by approximately 10%-20%. In this case, the uncertainties are likely to be attributed to the use of different model physical parameterizations.

3.2.2 Taylor diagram

To examine the level of agreement between reanalysis and individual models, the Taylor diagram is used to further evaluate the simulated spatial patterns of COLs with respect to track density. One difference in the analysis presented here from the standard Taylor diagram is that the mean difference (or bias) is included in our diagrams. In addition, we used the unbiased RMSE (ubRMSE) to remove systematic bias in the CMIP model simulations, as this measure characterizes random errors which occur when biases are present.

Figure 8 shows the performance of each climate model and their ensemble means in both CMIP5 and CMIP6 for the simulations of the COL track density. The normalized standard deviations are generally less spread out than that in the reanalysis. Reduced standard deviation is a result of a smoother track density, which means that COLs are either underestimated in locations of high track density or overestimated in locations of low track density. Most models have standard deviations higher than 0.80 (reference value is 1.0 with respect to reanalysis), in particular from CMIP6. The model with the lowest standard deviation is CNRM-CM6-1-HR, whereas the highest standard deviations are generally observed in the HighResMIP models which are nearly identical with those observed in reanalysis.

Fig. 8
figure 8

Taylor diagram of simulated track density by the a, c CMIP5 models and b, d CMIP6 models for the a, b NH and c, d SH in relation to ERA5. The y axis shows the normalized standard deviation (blue arc), correlation is denoted by the black dashed arc, unbiased root mean square error (ubRMSE) is denoted by solid arc. The mean bias is given in bars below the Taylor diagram

Full size image

Concerning the mean bias, most models systematically underestimate the track density, but there is a general overrepresentation of COLs in the HighResMIP models which are normally more capable in resolving finer-scale features. We find that the multi-model mean bias is substantially reduced in CMIP6 compared to CMIP5, and this is consistent with Fig. 3. Nevertheless, the largest bias is found in CNRM-CM6-1-HR, demonstrating a surprisingly poor ability to detect COLs considering the relatively high horizontal resolution of 50 km. The CMIP6 models generally exhibit high correlations, ranging from 0.88 to 0.98, with an average of 0.94 in the NH, and ranging from 0.80 to 0.95, with an average of 0.91 in the SH. We can see that the CMIP5 models are clearly less accurate in reproducing the spatial patterns compared to the majority of CMIP6 models. The correlation of the CMIP5 simulations with ERA5 varies between 0.82 and 0.95 (average is 0.90) in the NH, and between 0.57 and 0.94 (average is 0.84) in the SH.

The Taylor diagram also includes the ubRMSE, which is another measure of model accuracy. The two models with the lowest ubRMSE values are ECMWF-IFS-HR and GFDL-CM4 (ECMWF-IFS-HR and SAM0-UNICON by considering the RMSE) for the NH, and MIROC6 and MPI-ESM1-2-HR (the same models by considering the RMSE) for the SH. The mean ubRMSE calculated with the CMIP6 models is reduced by 19% (21%) compared to that calculated with the CMIP5 models for the NH (SH).

In general, the CMIP6 models have consistently better agreement with the reanalysis data compared to the CMIP5 models. The inter-model spread in CMIP6 would reduce by omitting the CNRM-CM6-1-HR model, which has the lowest skill of all the CMIP6 models. The results also reinforce that the model performance is affected by their spatial resolution, since models with finer horizontal resolution perform better than those with coarser resolution (see supplementary material—Fig. S15—where the higher and lower horizontal resolution model sets are indicated by blue and red, respectively), particularly in the NH. However, increasing model spatial resolution is not always sufficient to improve simulations. A remarkable example to this finding is CNRM-CM6-1-HR, which is a HighResMIP model that clearly presents an inferior performance with respect to mean bias, standard deviation and ubRMSE (RMSE). Conversely, there are a few CMIP5 models (e.g., ACCESS1-0, ACCESS1-3, HadGEM2-CC and HadGEM2-ES) with relatively low spatial resolutions that outperform some higher resolution CMIP6 models (e.g., BCC-CSM2-MR, CNRM-CM6-1-HR, EC-Earth3, MRI-ESM2-0 and SAM0-UNICON for NH; CNRM-CM6-1-HR for SH) in nearly all metrics. For the NH, the HighResMIP models have a better performance compared to their corresponding standard resolution version, with the exception of MPI-ESM1-2-HR that outperforms the higher resolution version (MPI-ESM1-2-XR) in almost all statistical indices. Despite the robustness of the improved performance of HighResMIP models in the NH, the impact of horizontal resolution on the COL simulations in the SH is much less evident.

An advantage in using the Taylor diagram is that it shows that the multi-model ensemble tends to be more skillful than the average single-model performance. The multi-model superiority is caused by the error cancellation and non-linearity of the diagnostics (Hagedorn et al. 2005). Averaging the skill of the 23 models in both CMIP5 and CMIP6 does not correspond to the skill of the combined models (i.e., the multi-model ensemble), except for the mean bias which is a linear metric. The most outstanding performance of the multi-model ensemble across all simulations is seen in CMIP5 for the SH COLs, where the ubRMSE of the multi-model ensemble is smaller than the best single CMIP5 model.

Considering that the Taylor diagram provides useful information from different statistical measures, a skill score is calculated for each model taking into account the four variables given in the Taylor diagram (mean bias, standard deviation, correlation and ubRMSE) together with RMSE. For example, for the NH the ECMWF-IFS-HR model has the highest ranking score out of 46 models, which was determined by averaging the rank of the five metrics mentioned above. Following this approach, the first four best placed models (by the five-variable average) are, in that order (from the first to fourth best scores): ECMWF-IFS-HR, EC-Earth3P-HR, HadGEM3-GC-HH and CMCC-CM2-VHR4 for the NH; and MIROC6, HadGEM3-GC-HH, ACCESS1-0 and MPI-ESM1-2-HR for the SH. Note that ACCESS1-0 is the only CMIP5 model in the top four model systems for the SH, while the best ranked CMIP5 model for the NH is ACCESS1-3 occupying the 13th place. We find that 15 out of 20 best-ranked models belong to CMIP6, indicating that there is a remarkable improvement from CMIP5 to CMIP6 models in the representation of COLs. The ranking of all models’ performance is given in Table S3 of supplementary material.

3.2.3 Seasonal cycle

We now explore the ability of the CMIP5 and CMIP6 models in capturing the seasonal cycle of COLs. As seen in previous studies (e.g., Nieto et al. 2005; Ndarana and Waugh 2010; Pinheiro et al. 2017; Muñoz et al. 2020) and showed in Fig. 1 of this paper, COL systems exhibit a pronounced seasonal cycle (with larger standard deviation in the NH) with maximum in occurrence during summer and early autumn and minimum in winter and early spring. The weaker zonal circulation observed in summer facilitates the COL development as well as RWB events associated with the 350-K isentropic surface (Postel and Hitchman 1999; Hitchman and Huesmann 2007; Ndarana and Waugh 2011). Figure 9 shows that both CMIP5 and CMIP6 models accurately reproduce the seasonal variation of COLs in both hemispheres, although the multi-model means show a little stronger seasonal cycle compared to ERA5. The CMIP6 has a reduced inter-model spread compared to the CMIP5 by an average of 23% (41%) across the whole monthly distribution for the NH (SH). Models with finer horizontal grid spacing have a better performance than the coarser ones, with higher correlation coefficient and similar standard deviation to observations.

Fig. 9
figure 9

Monthly distribution of Cut-off Lows in the SH (blue) and NH (red) of the multi-model mean of a CMIP5 and b CMIP6. Dashed and solid lines represent multi-model mean for the lower- and higher-resolution models, respectively. Shaded regions indicate the inter-model spread for the CMIP5 and CMIP6 models. Pink and cyan colours represent the ERA5 for the NH and SH, respectively

Full size image

3.2.4 Intensity

According to the analysis presented in this paper, the simulated intensities are improved from CMIP5 to CMIP6. We now investigate whether the CMIP6 models better represent the peak intensity of COLs, and if this is affected by the model spatial resolution. The maximum intensity distribution of COLs observed in ERA5 and simulated by the CMIP5 and CMIP6 models is measured by the maximum (or minimum in the SH, scaled by − 1) along-track T42 vorticity at 250 hPa, as shown in Fig. 10. The reanalysis (black line) shows a positively skewed distribution for the COL intensity in the NH, while the median peak vorticity in the SH shifts to the right, indicating there are more mid-to-strong systems in the SH than in the NH. While the shape of the intensity distribution simulated by the CMIP5 models is similar to that in ERA5, there is a tendency to have too many COLs at the lower end of the distribution and too few COLs at the upper end, which is consistent with the underestimation observed in Fig. 4. There is, however, an improved representation of the intensity distribution in the CMIP6 models that have intensities lying closer to the ERA5 distribution. This improvement is particularly noticeable in the tail of the distribution, associated with the extreme intensities. For example, for the NH (SH) the number of strong COLs with intensities in the range 16–25 \(\times \) 10–5 s−1 is underrepresented by about 48% (46%) in CMIP5 models, but the underestimation is reduced to 4% (5%) in CMIP6 models. Although the underestimation is clearly present in CMIP5, there is a large spread among models, and some of them individually reproduce fairly well the observed intensities, for instance, the MIROC5, MRI-CGCM3, and MRI-ESM1 models, in which their correlation with ERA5 across the intensity distribution is above 0.98 in both hemispheres.

Fig. 10
figure 10

Maximum intensity distribution (based on the T42 vorticity at 250 hPa) of COLs in the a, b NH and c, d SH, for the a, c CMIP5 and b, d CMIP6 multi-models. The gray shaded regions indicate inter-model spread for the CMIP5 and CMIP6 models. The blue and red lines represent the means of high-resolution and low-resolution CMIP5 and CMIP6 models, respectively. The black line represents results from ERA5. Unit is 10–5 s−1, scaled by − 1 for SH

Full size image

One factor that appears to be important in representing the peak intensity of COLs is the model grid spacing. The results show that higher resolution models (blue line) are more accurate in simulating the intensity distribution compared to lower resolution models (red line). This is evident across the two generations of CMIP models, but particularly in CMIP6, where the frequencies closely match the reanalysis, especially with respect to the extremes that are underrepresented even by the higher resolution CMIP5 models. In summary, it is striking how well the COL intensities are represented in the CMIP6 models (relative to CMIP5), where the ensemble spread is reduced across all intensities, though deficiencies still exist in lower-resolution CMIP6 models. This suggests that model horizontal resolution plays an important role in the representation of COL peak intensity.

3.2.5 Life time

Previous studies have shown that the typical life cycle of COLs is characterized by initial growth because of the ageostrophic flux convergence associated with the energy dispersion from upstream systems, and then sustained by baroclinic processes, and a subsequent decay due to the ageostrophic flux divergence, friction and diabatic heating (Garreaud and Fuenzalida 2007; Gan and Piva 2013, 2016; Pinheiro et al. 2021b). The ability of CMIP5–CMIP6 models in simulating the COL life cycle is now investigated using the frequency distribution of lifetimes. The COL lifetime is computed by considering the time from genesis to lysis in each vorticity track, which is generally larger than the mean lifetime found in previous studies in which the identification was based on the geopotential (Fuenzalida et al. 2005; Nieto et al. 2005; Reboita et al. 2010; Favre et al. 2012; Muñoz et al. 2020). The mean lifetime of the 250-hPa vorticity COLs obtained with ERA5 is about 5.8 days in the NH and 4.9 days in the SH, while earlier studies have shown that COLs typically last 2–4 days. This difference is expected as the vorticity field detects more mobile earlier stages of the COL life cycle (Pinheiro et al. 2019).

The lifetime distribution of COLs (Fig. 11) is reasonably well reproduced in the climate models, as the percentage of models with correlations higher than 0.95 are 74% (80%) in CMIP5 and 87% (96%) in CMIP6 for the NH (SH). While the average bias of the COL mean lifetime (i.e., the difference between the multi-model mean and reanalysis) is less than 0.1 day, a few models (e.g., MIROC-ESM, MIROC-ES2L, and CNRM-CM6-1-HR) underestimate the mean lifetime more than 20% relative to ERA5, which may be indicative of either shorter tracks or faster moving systems compared to reanalysis. The most notable discrepancy appears in the MIROC-ESM and MIROC-ES2L as these models simulate unrealistically too many short-lived systems in both hemispheres, while COLs with lifetimes longer than 4 days are underestimated. These differences can partly be attributed to the overestimation of the COL mean speed by the MIROC-ESM and MIROC-ES2L models, due to the simulation of an enhanced subtropical jet as compared to reanalysis (see supplementary material, Figs. S16 and S17). We calculated the difference between the models and ERA5 for the climatological COL mean speed at 250 hPa, and found an overestimation of 1.0 m/s (2.8 m/s) in MIROC-ESM and 1.6 m/s (0.7 m/s) in MIROC-ES2L with respect to the NH (SH), while the average difference (or bias) is generally not large in other models. The model performance does not indicate a clear distinction between high- and low-resolution models, although there is a considerable reduction in the inter-model spread in CMIP6 relative to CMIP5. Interestingly, despite the high resolution of CNRM-CM6-1-HR, this model has a poor skill in simulating the lifetime distribution of NH COLs, presenting the lowest correlation (~ 0.80) among all models. This suggests that other factors besides the model horizontal resolution may affect the accuracy of COL simulations, such as the model parameterizations.

Fig. 11
figure 11

Life time distribution of COLs in the a, b NH and c, d SH, for the a, c CMIP5 and (b, d CMIP6 multi-models. The black line represents results from ERA5, the blue and red lines the high-resolution and low-resolution models, respectively. Unit is day

Full size image

4 Conclusions

This study provides a robust quantitative assessment of 46 coupled climate models (with enough ensemble members) participating in the CMIP5 and CMIP6 experiments for the historical simulations of global COLs, which is considered as one of the most important synoptic-scale systems affecting the weather in subtropical regions. Our motivation is to investigate the ability of the newly available CMIP6 models in representing the climatological features of COLs observed in the ERA5 reanalysis, and to determine whether the simulations have improved from the previous generation of CMIP5 models. This paper provides the opportunity for a better understanding of the systematic deficiencies of models in simulating upper-level winds and their association with COLs, which may be used as a basis for further assessments of the changes and impacts of COLs under future climate conditions.

The main findings of this study are summarized as follows:

  • In general, the CMIP5 and CMIP6 models capture the key features of the spatial distribution of COLs in both hemispheres, though there is a robust underestimation over the locations of maxima in track density. The underrepresentation of COLs demonstrates an overall weak association with the equatorward bias in the extratropical jet that systematically affects models in the NH and SH.

  • The CMIP6 models show a notably improved ability to simulate the COL activity in comparison to the CMIP5 models. A reduction in bias by a factor of four occurs with CMIP6 relative to CMIP5.

  • Our quantitative analysis indicates a considerable inter-model spread and uncertainty in the simulated number of COLs, where higher-resolution models generally provide the highest number of COLs globally. The largest inter-model spread in number is observed in winter, contrasting with better performance in summer in the NH and autumn in the SH.

  • The CMIP6 models tend to underestimate (overestimate) the intensity of COLs in summer (winter), and such biases seem to be related to negative (positive) bias in the mean zonal wind (subtropical jet). This deficiency is partly improved in the CMIP6 models, particularly in summer and winter periods, as previously observed (Bracegirdle et al. 2019).

  • Simulations indicate that biases are affected by model grid spacing, as models with fine horizontal resolutions simulate COLs better than the ones with coarse horizontal resolutions. This is particularly true with regard to the COL intensity, where the high-resolution CMIP6 models reproduce fairly well the peak intensity distribution as compared to ERA5. However, the CMIP5 models struggle to simulate the intensity distributions, particularly with respect to the high-intensity COLs, even the higher resolution CMIP5 models.

  • The monthly distribution of COLs is well represented by the CMIP5 and CMIP6 models, with a seasonal variation slightly less pronounced than observed in reanalysis.

  • The climate models reasonably capture the lifetime distribution of COLs, with reduced skill in MIROC-ESM, MIROC-ES2L and CNRM-CM6-1-HR and minor improvement with CMIP6 models.

The observed systematic weakness in the COL intensity that is found in the CMIP5 models (and also in the relatively coarse-resolution CMIP6 models) has improved in the high-resolution CMIP6 models, supported by the HighResMIP simulations that incorporate models at 25–50 km atmospheric resolution. The community effort in model development, particularly with respect to increasing model spatial resolution, has resulted in a positive impact on the simulation of the COL intensities, which was found to be in better agreement with observations as compared with the coarse resolution models in CMIP5. The smaller differences between CMIP6 models and reanalysis are likely related to improved forecasting capabilities and increased horizontal resolution, in which in HighResMIP models are comparable to that in ERA5, thus facilitating the identification of more of the stronger systems.. Particular care is needed when assessing the impact of model resolution on diagnostics averaged over all seasons, given that the CMIP6 models have intensities underestimated in summer, but overestimated in winter. The overestimation of intensities in winter is likely a result of the stronger jet (and associated vorticity) simulated in regions of high COL track density, indicating an important unrealism in the simulations of the COL intensity in the CMIP6 models.

Looking at each model individually shows that some of them perform better than others, and indicates that the model performance is region dependent. This was demonstrated through a skill score by quantitatively evaluating the spatial model performance of each individual CMIP5 and CMIP6 model. The robustness of the evaluation method was supported by different metrics under consideration, combined to reach a final ranking that may be helpful for climate model users to guide the choice of models in further studies. The overall performance revealed that simulations were significantly improved in CMIP6 that accounts for 75% of the best 20 ranked-models. According to this approach, the highest skill models are, in that order, ECMWF-IFS-HR, EC-Earth3P-HR, HadGEM3-GC-HH and CMCC-CM2-VHR4 for NH, and MIROC6, HadGEM3-GC-HH, ACCESS1-0 and MPI-ESM1-2-HR for SH. Our analysis using the same subset of models indicate that improving horizontal resolution impacts positively in the NH for almost all models, however, the improvements from HighResMIP simulations are relatively modest in the SH.

Despite the difference in model performance, our analysis demonstrates that the use of the multi-model ensemble can be more effective in representing the spatial patterns of COLs rather than using an individual model, as it reduces uncertainties that arise when the output from one model is used. Alternative methods based on statistical weightings could reduce error in multi-model means. A common approach, for example, is the Bayesian model averaging (Duan and Philipps 2010; Shashikanth et al. 2018), where different weights are assigned to models based on their agreement with observations. Another point is that this study is based on a limited number of models in which data were available at the time of writing, therefore more model data might potentially affect the conclusions. Despite this, our conclusions are supported by a robust evidence base that includes 86 ensembles from 23 CMIP6 models and 74 ensembles from 23 CMIP5 models.

The results exhibited in this paper contain several interesting features that summarize the COL behavior in a global perspective, and thus it has only been possible here to present an overview of models’ performance. It is clear from the spatial diagnostics (shown in Figs. 2, 3, 4, 5 and 6) that the model bias varies significantly by region. Local features can be masked by global statistics, therefore future research may focus on regional and seasonal variability. A second important question is whether results are robust to the use of different identification schemes, as differences have been found in numbers and seasonality of COLs between studies using different methods (Wernli and Sprenger 2007; Nieto et al. 2008; Pinheiro et al. 2019). An intercomparison with different methods and/or criteria would be of great value for future research in order to investigate whether results are generalized or affected by the identification method choice. In addition to this question, one crucial aspect of the comparison between methods and datasets lies in the absence of a reference database that could be used as a trustable ground truth to validate against.

In summary, we conclude that the CMIP6 models and their multi-model ensemble means show a significant improvement in simulating the COL characteristics over the subtropical regions in both hemispheres. Improved model physics and increased horizontal and vertical resolutions are some of the likely reasons for improved simulations in CMIP6 that result in a reduction of bias compared to the CMIP5 simulations. A notable improvement is the poleward shift in the COL tracks from CMIP5 to CMIP6 which reduces the large equatorward bias that systematically affects climate models, which can partly be attributed to a better representation of the zonal mean flow in the CMIP6 models. Perhaps the HighResMIP models play the largest role in the improvements seen in the CMIP6, particularly for the NH where higher-resolution simulations lead to a reduction of the large negative bias presented in relatively low-resolution models.

Also of interest, but not discussed here, is the temporal variability of COLs at different time scales and their association with different atmospheric and oceanic climatic modes as discussed previously (Nieto et al. 2007; Singleton and Reason 2007; Risbey et al. 2009; Ndarana and Waugh 2010; Favre et al 2012; Muñoz et al 2020). Understanding the influence of large-scale environmental factors on COL related properties (e.g., location, intensity and precipitation) is a problem of great scientific importance and crucial for understanding the climate and its variation. The simulated response of COL activity to El Niño Southern Oscillation will be discussed in a future paper.