1 Introduction

Seasonal climate prediction aims at predicting the anomalous climate conditions in the next one or several seasons and its accuracy is extremely important for decision making and risk management. In the past two decades, scientists have devoted substantial efforts to developing complex general circulation models (GCMs) to perform seasonal climate prediction (Stockdale et al. 1998; Kanamitsu et al. 2002; Saha et al. 2006, 2014; Luo et al. 2008; Molteni et al. 2011; Merryfield et al. 2013; Liu et al. 2015; MacLachlan et al. 2015). Seasonal prediction using dynamical models is necessarily subject to the errors sources of initial condition and model uncertainties. To mitigate the adverse effects of these uncertainties on the forecasting accuracy, the strategies of single-model ensemble (SME) and multi-model ensemble (MME) forecasting have been widely adopted (Stockdale et al. 1998; Palmer et al. 2004). Based on the multiple forecast realizations from an ensemble, the final prediction can be made in two formats: the deterministic and probabilistic formats. In the field of seasonal climate prediction, deterministic prediction usually refers to an ensemble-mean “point forecast” of a continuous predictand, while probabilistic prediction aims at predicting the occurrence probabilities of some discrete event categories. It has been argued that probabilistic prediction can bring greater economic value for stakeholders than deterministic prediction (Richardson 2006). For this reason, probabilistic prediction is usually deemed to be practically more valuable than deterministic prediction.

Along with developing dynamical forecast models, assessing and understanding model prediction skills is also an important component in the study of dynamical seasonal prediction, since it can provide useful feedbacks for model development. Since dynamical model forecasts can be presented in the two formats, model prediction skill can also be evaluated from two perspectives, the deterministic and probabilistic prediction perspectives. In seasonal climate prediction, the methodology for evaluating the deterministic forecast skill is simple, mainly in terms of the linear correlation between predicted and observed anomalies. Such deterministic skill is also often referred to as correlation or anomaly correlation (AC) skill (Saha et al. 2006). In contrast, the methodologies for evaluating probabilistic forecast skill appear much more complicated. A variety of specific methods have been proposed to measure the probabilistic skill, among which the Brier skill score (BSS) method (Palmer 2000; Kharin and Zwiers 2003a; Wilks 2011) and the relative operating characteristic (ROC) method (Mason and Graham 1999; Palmer 2000; Kharin and Zwiers 2003b; Wilks 2011) appear to be the most commonly used ones. The BSS measures the probabilistic skill based on the relative mean square error criterion. The BSS itself is a measure of overall probabilistic skill and it can be further decomposed into two components, which measure the reliability and resolution attributes of probabilistic skill, respectively (Kharin and Zwiers 2003a). The reliability quantifies how well forecast probabilities match in magnitude the corresponding observed frequencies, whereas the resolution measures how different these observed frequencies are from the climatological probability. The ROC method gauges the probabilistic skill based on comparing the hit rates and the false-alarm rates (Mason and Graham 1999). Essentially, the ROC method measures the discrimination attribute of probabilistic skill, which refers to how different the conditional probabilities of forecasts corresponding to observed event occurrence and nonoccurrence are from each other (Wilks 2011). The attributes of discrimination as well as reliability and resolution represent the most essential aspects of probabilistic forecast quality (Wilks 2011; Jolliffe and Stephenson 2012).

In the past two decades, based on the aforementioned methodologies, many studies have been done for assessing and understanding the seasonal prediction skills of dynamical climate models (Yang et al. 1998; Pavan and Doblas-Reyes 2000; Kirtman 2003; Doblas-Reyes et al. 2003, 2009; Palmer et al. 2004; Hagedorn et al. 2005; Graham et al. 2005; Kang and Shukla 2006; Kirtman and Min 2009; Kharin et al. 2009; Wang et al. 2009; Weisheimer et al. 2009; Zheng et al. 2009; Zheng and Zhu 2010; Chowdary et al. 2010; Philippon et al. 2010; Alessandri et al. 2011; Li et al. 2012; Yang et al. 2012, 2016; Kumar et al. 2013; Yan and Tang 2013; Kirtman et al. 2014; Beraki et al. 2015; Becker and van den Dool 2015; Tippett et al. 2017). While early studies mostly focused on examining the deterministic skill, recent studies have also paid significant attentions on investigating the probabilistic skill.

While the deterministic and probabilistic skills of dynamical seasonal predictions are mostly assessed independently, some studies have put attentions on comparing them and investigating the relationship between them (Wang et al. 2009; Cheng et al. 2010; Alessandri et al. 2011; Sooraj et al. 2012; Yang et al. 2016; Athanasiadis et al. 2017). Actually, in early 1990s, Barnston (1992) noticed their possible existing relationship. It is quite valuable to study the relationship (or lack thereof) between the deterministic and probabilistic skills, since it can offer understanding of the similarities and differences between the two types of seasonal forecasting skills and provide new visions for further understanding the probabilistic forecast skill, which is usually not easy due to the complexity associated with the probabilistic issue. Moreover, from the perspective of practical application, if some specific relationship between the probabilistic and deterministic skills can be identified and established, it can also facilitate comparisons between probabilistic and deterministic assessments of seasonal forecasting capability.

With evaluating the seasonal hindcasts from a MME made of 14 single models, Wang et al. (2009) found that the probabilistic skills of both BSS and ROC show a clear statistical relationship with the corresponding deterministic correlation skill for the seasonal prediction of precipitation and temperature. In analyzing the seasonal prediction skills of three dynamical forecasting systems and their MME, Athanasiadis et al. (2017) found that the probabilistic ROC skill is largely consistent with the corresponding deterministic correlation skill in their large-scale spatial distributions. The forecast skills examined in the above studies are grid point skills calculated over a relatively short period, which may be subject to significant sampling uncertainty, obscuring the underlying true relationship between probabilistic and deterministic skills. Using a longer ensemble hindcast product of five models and evaluating the forecast skills in an area-aggregated way to alleviate the impact of sampling uncertainty, Yang et al. (2016) found that there is no significant relationship between the probabilistic reliability and deterministic correlation skills but instead a strikingly good, quasi-deterministic relationship between the probabilistic resolution and deterministic correlation skills, for the prediction of western North Pacific-East Asian summer monsoon. To further understand the observed relationship between probabilistic and deterministic skills, Yang et al. (2018) presented a theoretical consideration, where the relationship between the resolution and correlation skills was targeted. This theoretical consideration reveals that under certain simplified assumptions, a functional relationship can be analytically derived between the probabilistic resolution and deterministic correlation skills. The theoretical derivations in Yang et al. (2018) were inspired by Kharin and Zwiers (2003a), where a probabilistic interpretation of seasonal potential predictability was proposed based on the BSS methodology. However, since without invoking the perfect model or perfect reliability assumptions, the theoretical framework in Yang et al. (2018) has significant conceptual difference from those in Kharin and Zwiers (2003a) and other previous studies (Kumar et al. 2001; Kumar 2009; Tippett et al. 2010, 2017). This difference has been further discussed in Yang et al. (2019) and Tippett (2019). Since current models are still far from perfect in reproducing the reality, the theoretical framework in Yang et al. (2018) shall be more reasonable and the derived theoretical relationship should be more suitable to represent the realistic situation. In the meantime, the diagnostic analysis in Yang et al. (2018) also confirmed that no necessary relationship exists between the probabilistic reliability and deterministic correlation skills, indicating that the reliability is a fundamental aspect of probabilistic forecast skill that differs from the deterministic skill in dynamical seasonal climate prediction.

As reviewed above, like the resolution skill, the ROC skill was also observed to show a good relationship with the deterministic correlation skill. Considering that the ROC skill reflects the discrimination, another important attribute of probabilistic skill in addition to the resolution and reliability, it is interesting and also necessary to perform an in-depth investigation of its relationship with the deterministic skill from the theoretical point of view. This is the purpose of this study. Specifically, we provide a systematic and in-depth theoretical consideration, which ultimately demonstrates that there is also a theoretically deterministic relationship between the probabilistic ROC skill and the deterministic correlation skill. This theoretically derived relationship can be well validated by GCM dynamical forecasts. The result of this study together with the results of Yang et al. (2018) is expected to contribute to an insightful understanding of the fundamental similarities and difference between probabilistic and deterministic skills in seasonal climate prediction. The paper is structured as follows. Section 2 describes the ROC skill metrics for probabilistic forecasts. The detailed theoretical consideration is presented in Sect. 3. Section 4 focuses on verifying the theoretical consideration through analyzing the seasonal forecasting skills of current GCMs. Summary and discussion are given in Sect. 5.

2 Description of the ROC skill metrics for probabilistic forecasts

The ROC methodology has its origin in the signal detection theory, which reflects the skill of a forecasting system based on comparing the hit rate (HR) and the false-alarm rate (FAR) (Mason and Graham 1999; Kharin and Zwiers 2003b). The HR implies the proportion of events for which a warning was provided correctly, while the FAR implies the proportion of nonevents for which a warning was provided falsely. The ROC skill essentially depends on the extent to which the HR exceeds the corresponding FAR. For probabilistic forecasts, a ROC curve can be constructed to show the different combinations of HRs and FARs given different forecast probability thresholds. On the basis of the ROC curve, a ROC score (ROCS) and ROC skill score (ROCSS) can be defined to quantify the probabilistic ROC skill.

The HRs and FARs that are essential ingredients in the ROC approach can be calculated from 2 × 2 contingency tables. Table 1 shows a standard 2 × 2 contingency table for the simplest case of the binary forecasting, where if an event is predicted to occur, a warning is provided. Here, \(H\) is the number of hits, for which an event occurred and a warning was provided; \(F\) is the number of false alarms, for which an event did not occur but a warning was provided; \(M\) is the number of misses, for which an event occurred but a warning was not provided; and \(C\) is the number of correct rejections, for which an event did not occur and a warning was not provided. Based on the contingency table, the HR and the FAR are defined as

$$HR = \frac{H}{H + M} = \frac{H}{E}{, }$$
(1)
$$FAR = \frac{F}{F + C} = \frac{F}{{E^{\prime}}}{, }$$
(2)

where \(E\) and \(E^{\prime}\) represent the numbers of event occurrences and nonoccurrences, respectively, and the sum of \(E\) plus \(E^{\prime}\) is equal to the total number \(N\) of the forecast-observation pairs. For probabilistic forecasting, a warning can be provided when the forecast probability of an event exceeds some threshold. As such, given a probability threshold pth, a similar 2 × 2 contingency table can be obtained based on the data of forecasts and observations and a corresponding HR and FAR can then be calculated through formulas (1) and (2). Moreover, through successively varying the threshold pth from one towards zero, a set of different pairs of HR and FAR can be finally calculated for probabilistic forecasts.

Table 1 2 × 2 contingency table for the verification of the binary forecasting
Full size table

The ROC curve for probabilistic forecasts is constructed by plotting HRs (vertical axis) versus the corresponding FARs (horizontal axis) in a unit square diagram (also referred to as ROC diagram). The ROC curve displays the full characteristics of HRs versus FARs for different forecast probability thresholds. Based on the ROC curve, the probabilistic ROC skill can be evaluated. If the ROC curve lies above the diagonal line in the diagram, this means that the HRs exceed the FARs, and prediction is skillful. Contrarily, there is no skill or negative skill if the ROC curve coincides with or lies below the diagonal line. The ROCS, which is defined as the area beneath the ROC curve, is commonly used to further quantify the probabilistic ROC skill. The ROCS ranges from 0 to 1 and can be further transformed to the ROCSS that ranges from − 1 to 1 (i.e., having the same range as correlation). The transformation is through the formula \(ROCSS = 2 \times \left( {ROCS - 0.5} \right)\). ROCS (ROCSS) greater than 0.5 (0) indicates a skill, while ROCS (ROCSS) equal to or lower than 0.5 (0) represents no skill or negative skill. In general, the larger the value of the ROCS or ROCSS, the better the probabilistic skill.

3 A theoretical consideration for the relationship between probabilistic ROC skill and deterministic correlation skill

In this section, we present a theoretical consideration for the relationship between probabilistic ROC skill and deterministic correlation (i.e., anomaly correlation; AC) skill in seasonal climate prediction. The prediction object that is focused on is the (seasonal-mean) climate anomalies. The probabilistic ROC skill is considered for the below-normal (BN), near-normal (NN), and above-normal (AN) categories that are defined based on the terciles of the observed climatology and therefore have an equal climatological occurrence probability of \(1/3\). These categories are of particular interest in seasonal climate prediction. Specifically, in this consideration, with certain simplified assumptions, we first derive theoretical expressions for the HR and the FAR, then demonstrate a sole dependence of the ROC curve on the AC, and finally derive and illustrate a theoretical relationship between the ROCS and the AC. The major assumptions used include that the underlying predictive probability density functions (PDFs) are normal, that the variances of the predictive PDFs are invariant from case to case, and that the means of the predictive PDFs and the corresponding observations obey a joint normal distribution. These assumptions were also used in Yang et al. (2018) for deriving the theoretical relationship between the probabilistic resolution and deterministic correlation skills. The assumptions of normal distribution as well as invariant forecast variance have been argued to be in general good approximations for the prediction of seasonal mean atmospheric anomalies (Van den Dool and Toth 1991; Rowell 1998; Kumar et al. 2000; Wilks 2002, 2011; Tang et al. 2008; Weigel et al. 2008, 2009). This theoretical consideration has been initially inspired by the work of Kharin and Zwiers (2003b), but, as will be seen, has great differences from theirs.

3.1 Theoretical expressions for the HR and the FAR

Let \(O\) be a binary random variable for the observed outcome of an event, one for occurrence and zero for nonoccurrence. Suppose that the number of forecast-observation samples is large enough. Then, the HR and FAR in (1) and (2) can be theoretically expressed as the following form:

$$HR = P\left( {{\text{warning|}}O = 1} \right){, }$$
(3)
$$FAR = P\left( {{\text{warning|}}O = 0} \right),$$
(4)

where the notation \(P\left( { \cdot {|} \cdot } \right)\) denotes the conditional probability. For probabilistic forecasting, as stated previously, a warning is provided when the event forecast probability \(p\) exceeds a given threshold pth. Thus, the HR and FAR for probabilistic forecasting can be expressed as a function of the threshold pth as below:

$$HR\left( {p_{th} } \right) = \mathop \int \limits_{{{\Omega }_{p} }}^{{}} f\left( {p{|}O = 1} \right)dp{, }$$
(5)
$$FAR\left( {p_{th} } \right) = \mathop \int \limits_{{\Omega_{p} }}^{{}} f\left( {p{|}O = 0} \right)dp{,}$$
(6)

where \(f\left( {p{|}O} \right)\) represents the conditional PDF of \(p\) given \(O\), and \({\Omega }_{p}\) denotes forecast probabilities \(p > p_{th}\). For the BN and AN categories, the upper bound of the domain \({\Omega }_{p}\) is naturally one. However, note that for the NN category, the domain \({\Omega }_{p}\) is usually upper bounded by a value smaller than one. This is because the maximum possible forecast probabilities for the NN category usually cannot reach one. By invoking the Bayes’ theorem, \(f\left( {p{|}O} \right)\) in (5) and (6) can be expressed as

$$f\left( {p{|}O} \right) = \frac{{P\left( {O{|}p} \right)f_{p} \left( p \right)}}{P\left( O \right)}{, }$$
(7)

where \(P\left( {O{|}p} \right)\) is the conditional probability of \(O\) given \(p\), \(f_{p} \left( p \right)\) represents the marginal PDF of \(p\), and \(P\left( O \right)\) is the marginal probability of \(O\). Substituting (7) into (5) and (6), the HR and FAR can then be expressed as below:

$$HR\left( {p_{th} } \right) = \frac{1}{{P\left( {O = 1} \right)}}\mathop \int \limits_{{{\Omega }_{p} }}^{{}} P\left( {O = 1{|}p} \right)f_{p} \left( p \right)dp{, }$$
(8)
$$\begin{gathered} FAR\left( {p_{th} } \right) = \frac{1}{{P\left( {O = 0} \right)}}\mathop \int \limits_{{\Omega_{p} }}^{{}} P\left( {O = 0{|}p} \right)f_{p} \left( p \right)dp \hfill \\ = \frac{1}{{1 - P\left( {O = 1} \right)}}\mathop \int \limits_{{\Omega_{p} }}^{{}} \left[ {1 - P\left( {O = 1{|}p} \right)} \right]f_{p} \left( p \right)dp{.} \hfill \\ \end{gathered}$$
(9)

For theoretical convenience, we further consider an ideal case with a sufficiently large ensemble size. In this case, the forecast probability \(p\) is not subject to sampling fluctuation, exclusively determined by the underlying predictive PDF. Denote the mean and the variance of the predictive PDF by \(\mu\) and \(\sigma_{e}^{2}\), respectively. If the predictive PDF is a normal distribution that can be fully characterized by its mean and variance, the forecast probability \(p\) is eventually a function of the \(\mu\) and \(\sigma_{e}^{2}\) only. If the forecast variance \(\sigma_{e}^{2}\) is further constant, then the \(HR\left( {p_{th} } \right)\) and \(FAR\left( {p_{th} } \right)\) in (8) and (9) can be rewritten as:

$$HR\left( {p_{th} } \right) = \frac{1}{{P\left( {O = 1} \right)}}\mathop \int \limits_{{{\Omega }_{\mu } }}^{{}} P\left( {O = 1{|}\mu } \right)f_{\mu } \left( \mu \right)d\mu {, }$$
(10)
$$FAR\left( {p_{th} } \right) = \frac{1}{{1 - P\left( {O = 1} \right)}}\mathop \int \limits_{{\Omega_{\mu } }}^{{}} \left[ {1 - P\left( {O = 1{|}\mu } \right)} \right]f_{\mu } \left( \mu \right)d\mu {, }$$
(11)

where \(f_{\mu } \left( \mu \right)\) represents the marginal PDF of \(\mu\) and \({\Omega }_{\mu }\) denotes the domain for all values of \(\mu\) for which \(p > p_{th}\).

Let \(x\) stand for the underlying continuous predictand and \(r\) denote the linear correlation between \(x\) and the predicted signal \(\mu\), i.e., the AC skill. Note that \(x\) and \(\mu\) represent anomalies. As stated in Yang et al. (2018), a standard result in statistics is that if \(\mu\) and \(x\) follow a joint normal distribution, each of \(\mu\) and \(x\) will have a normal marginal distribution itself and the conditional PDF of \(x\) given \(\mu\) (denoted \(f_{x|\mu } \left( {x|\mu } \right)\)) is a normal distribution with mean of \(r\sigma_{x} /\sigma_{\mu } \mu\) and variance of \(\left( {1 - r^{2} } \right)\sigma_{x}^{2}\), where \(\sigma_{x}\) and \(\sigma_{\mu }\) represent the unconditional (climatological) standard deviation of \(x\) and \(\mu\), respectively. Then, the conditional probability \(P\left( {O = 1{|}\mu } \right)\) in (10) and (11) can be evaluated as the integral of \(f_{x|\mu } \left( {x|\mu } \right)\) over the event category interval \(\left( {x_{l} ,x_{r} } \right)\), which can be further expressed as:\({ }P\left( {O = 1{|}\mu } \right) = \Phi \left( {\left( {x_{r} - r\sigma_{x} /\sigma_{\mu } \mu } \right)/\sqrt {\left( {1 - r^{2} } \right)\sigma_{x}^{2} } } \right) - \Phi \left( {\left( {x_{l} - r\sigma_{x} /\sigma_{\mu } \mu } \right)/\sqrt {\left( {1 - r^{2} } \right)\sigma_{x}^{2} } } \right)\), where \(\Phi \left( \cdot \right)\) represents the cumulative distribution function for standard normal distribution. As such, given the defining intervals \(\left( { - \infty ,\sigma_{x} \Phi^{ - 1} \left( {1/3} \right)} \right)\), \(\left( { - \sigma_{x} \Phi^{ - 1} \left( {1/3} \right),\infty } \right)\), and \(\left( {\sigma_{x} \Phi^{ - 1} \left( {1/3} \right), - \sigma_{x} \Phi^{ - 1} \left( {1/3} \right)} \right)\) for the BN, AN, and NN categories, respectively, and letting \(\mu_{s}\) denote the standardized predicted signal \(\mu /\sigma_{\mu }\), the conditional probability \(P\left( {O = 1{|}\mu } \right)\) for these categories, after some manipulations as shown in Yang et al. (2018), can be expressed as:

$$P\left( {O_{BN} = 1{|}\mu } \right) = \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) - r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right){,}$$
(12)
$$P\left( {O_{AN} = 1{|}\mu } \right) = \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) + r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right){,}$$
(13)
$$P\left( {O_{NN} = 1{|}\mu } \right) = 1 - \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) - r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right) - \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) + r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right){,}$$
(14)

where \(\Phi^{ - 1} \left( \cdot \right)\) is the inverse function of \(\Phi \left( \cdot \right)\). As can be explicitly seen from (12), (13), and (14), the conditional probabilities for the three categories turn out to be a function of the standardized predicted signal \(\mu_{s}\) and the AC skill \(r\) only.

Finally, by substituting the explicit expression \(\frac{1}{{\sqrt {2\pi } \sigma_{\mu } }}e^{{ - \frac{1}{2}\mu_{s}^{2} }}\) for normal PDF \(f_{\mu } \left( \mu \right)\) into (10) and (11), invoking the fact that \(P\left( {O = 1} \right) = 1/3\), and changing the integration variable from \(\mu\) to \(\mu_{s}\), we can rewrite the HR and FAR as

$$HR\left( {p_{th} } \right) = \frac{3}{{\sqrt {2\pi } }}\mathop \int \limits_{{{\Omega }_{{\mu_{s} }} }}^{{}} P\left( {O = 1{|}\mu } \right)e^{{ - \frac{1}{2}\mu_{s}^{2} }} d\mu_{s} {,}$$
(15)
$$FAR\left( {p_{th} } \right) = \frac{3}{{2\sqrt {2\pi } }}\mathop \int \limits_{{{\Omega }_{{\mu_{s} }} }}^{{}} \left[ {1 - P\left( {O = 1{|}\mu } \right)} \right]e^{{ - \frac{1}{2}\mu_{s}^{2} }} d\mu_{s} {, }$$
(16)

where \(P\left( {O = 1{|}\mu } \right)\) has the explicit expressions as in (12)–(14) and \({\Omega }_{{\mu_{s} }}\) denotes the domain for all values of \(\mu_{s}\) for which \(p > p_{th}\). Because the entire integrands in (15) and (16) appear as a function of the integration variable \(\mu_{s}\) and \(r\) only, the final integration results will depend on \(r\) and the integration domain \({\Omega }_{{\mu }_{s}}\). As revealed in Appendix A, after denoting the model climatological standard deviation by \({\sigma }_{y}\) and letting \({\rho }_{m}\) represent \({\sigma }_{\mu }/{\sigma }_{y}\) that reflects the model potential predictability, \({\Omega }_{{\mu }_{s}}\) can be established as below: for the BN category, \({\Omega }_{{\mu }_{s}}=(-\infty ,{\mu }_{sth})\) where \({\mu }_{sth}=\left[{{\sigma }_{x}/{\sigma }_{y}\Phi }^{-1}\left(1/3\right)-\sqrt{1-{\rho }_{m}^{2}}{\Phi }^{-1}\left({p}_{th}\right)\right]/{\rho }_{m}\); for the AN category, \({\Omega }_{{\mu }_{s}}=({\mu }_{sth},{ \infty })\) where \(\mu_{sth} = \left[ {\sqrt {1 - \rho_{m}^{2} } \Phi^{ - 1} \left( {p_{th} } \right) - \sigma_{x} /\sigma_{y} \Phi^{ - 1} \left( {1/3} \right)} \right]/\rho_{m}\); for the NN category, \({\Omega }_{{\mu }_{s}}=(-{\mu }_{sth},{\mu }_{sth})\) where \({\mu }_{sth}\) is supposed to be nonnegative and \({\pm \mu }_{sth}\) are two solutions of the \({\mu }_{s}\) for the equation \(1-\Phi \left(\left({{\sigma }_{x}/{\sigma }_{y}\Phi }^{-1}\left(1/3\right)-{\rho }_{m}{\mu }_{s}\right)/\sqrt{1-{\rho }_{m}^{2}}\right)-\Phi \left(\left({{\sigma }_{x}/{\sigma }_{y}\Phi }^{-1}\left(1/3\right)+{\rho }_{m}{\mu }_{s}\right)/\sqrt{1-{\rho }_{m}^{2}}\right)={p}_{th}\). Both the \({\mu }_{sth}\) for the BN and AN categories and the \({\pm \mu }_{sth}\) for the NN category represent the threshold value of \({\mu }_{s}\) corresponding to the probability threshold \({p}_{th}\) in each case. According to the above discussion, we can understand that for any given \(r\), the dependence of the HR and FAR on the \({p}_{th}\) can be transformed to a dependence on the \({\mu }_{sth}\), and the HR and FAR can be formally viewed as a function of \({\mu }_{sth}\) and \(r\) only. Since determining \({\mu }_{sth}\) still requires the knowledge of \({\sigma }_{x}/{\sigma }_{y}\) and \({\rho }_{m}\) in addition to \({ p}_{th}\), the HR and FAR actually also have an underlying dependence on \({\sigma }_{x}/{\sigma }_{y}\) and \({\rho }_{m}\). In conclusion, besides explicitly depending on \({p}_{th}\), the HR and FAR still fundamentally depend on \(r\) as well as \({\sigma }_{x}/{\sigma }_{y}\) and \({\rho }_{m}\).

3.2 Sole dependence of the ROC curve on the AC

Theoretically, the ROC curve is the curve of HR versus FAR when the probability threshold \({p}_{th}\) continuously varies from the maximum value for forecast probability to zero. As noted in the preceding subsection, this maximum value is equal to one for the BN and AN categories and is usually smaller than one for the NN category. We further demonstrate in this subsection that although HR and FAR for individual \({p}_{th}\) fundamentally depend on the AC skill (namely \(r)\) as well as \({\sigma }_{x}/{\sigma }_{y}\) and \({\rho }_{m}\), the theoretical ROC curve, which reflects the “entirety” of HRs versus FARs when the \({p}_{th}\) sequentially takes all the possible values, depends only on the AC. According to (15) and (16) and the associated discussions in the above subsection, the HR and FAR can be understood as a function of \({\mu }_{sth}\) and the AC, where \({\mu }_{sth}\) is further jointly determined by \({p}_{th}\) as well as \({\sigma }_{x}/{\sigma }_{y}\) and \({\rho }_{m}\). However, based on the discussions in Appendix A, it can be revealed that when \({p}_{th}\) varies from the maximum value to zero, the corresponding \({\mu }_{sth}\) for the BN category varies from \(-\infty\) to \(\infty\), the \({\mu }_{sth}\) for the AN category varies from \(\infty\) to \(-\infty\), and the \({\mu }_{sth}\) for the NN category varies from 0 to \(\infty\), all irrespective of how large \({\rho }_{m}\) and \({\sigma }_{x}/{\sigma }_{y}\) are. Therefore, the ROC curve that represents the “entirety” of HRs versus FARs will be independent of \({p}_{th}\), \({\sigma }_{x}/{\sigma }_{y}\), and \({\rho }_{m}\), and solely depend on the AC.

Sequentially taking sufficient values of the \({\mu }_{sth}\) from their continuous varying ranges described above corresponding to the variation of \({p}_{th}\) from the maximum value to zero, and then numerically calculating the integrals in (15) and (16) over varying domains (\({\Omega }_{{\mu }_{s}})\) determined by these different \({\mu }_{sth}\) values, we can numerically obtain sufficient pairs of HRs and FARs and then construct the theoretical ROC curves for the three categories corresponding to any particular AC. As an illustration of the dependence of the theoretical ROC curves on AC, Fig. 1 shows the ROC curves constructed using the above method with AC of ± 0.2, ± 0.5, and ± 0.8, respectively. As can be seen, the ROC curves for the BN and AN categories are identical, which ought to result from the symmetric property of normal distribution. For a positive AC, the ROC curves for all the three categories lie above the diagonal line; the greater the AC is, the more the ROC curves bend towards the upper-left corner of the diagrams. For the same level of the AC skill, the ROC curves for the NN category are significantly closer to the diagonal line that represents the “no-skill” situation than those for the BN and AN categories. This is actually related to the fact that the \(P\left(O=1|\mu \right)\) has a much weaker dependence on the standardized predicted signal \({\mu }_{s}\) for the NN category than for the BN and AN categories, which is also the direct reason why the probabilistic resolution skill is usually lower in the former than in the latter (Yang et al. 2018; Van den Dool and Toth 1991).

Fig. 1
figure 1

Theoretical ROC curves for probabilistic forecasts of a, b the below- or above-normal category and c, d the near-normal category corresponding to values of the deterministic skill of anomaly correlation (\(r\); AC) equal to 0.2, 0.5, and 0.8 (top row) and equal to -0.2, -0.5, and -0.8 (bottom row)

Full size image

For a negative AC, the ROC curves for the BN and AN categories lie below the diagonal line, which indicates a negative ROC skill; the more negative the AC is, the more the ROC curves bend towards the lower-right corner of the diagram, namely the more negative the ROC skill is. In contrast, the ROC curve for the NN category corresponding to a negative AC still lies above the diagonal line and appears to have the same shape as that for the positive AC of the same magnitude. With statistical correction by a regression procedure, bad forecasts with a negative AC could become as skillful as those with a positive AC of the same magnitude. The insensitivity of the ROC skill for the NN category to the sign of AC means that it can automatically recognize the effectively useful information contained in the forecasts with negative ACs. A similar insensitivity to the sign of AC was also found for the probabilistic resolution skill of each category in Yang et al. (2018).

3.3 Theoretical relationship between the ROCS and the AC

Since the ROC curve theoretically depends only on the AC, as demonstrated in the above subsection, the ROCS (namely the ROC score), defined as the area beneath the ROC curve, necessarily depends only on the AC as well. In other words, the ROCS has a deterministic relationship with the AC. This relationship can be revealed by calculating the areas under the theoretical ROC curves numerically. Instead of using this direct method, here we derive an analytical expression for the theoretical relationship between the ROCS and the AC, from which the relationship can be further numerically depicted. The detailed derivations are placed in Appendix B. According to Appendix B, the ROCS for the BN, AN, and NN categories can be expressed explicitly as below:

$$ROCS_{BN} = \frac{9}{4\pi }\mathop \int \limits_{ - \infty }^{\infty } \left[ {\mathop \int \limits_{ - \infty }^{{\mu_{sth} }} \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) - r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right)e^{{ - \frac{1}{2}\mu_{s}^{2} }} d\mu_{s} } \right]\left[ {1 - \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) - r\mu_{sth} }}{{\sqrt {1 - r^{2} } }}} \right)} \right]e^{{ - \frac{1}{2}\mu_{sth}^{2} }} d\mu_{sth} {,}$$
(17)
$$ROCS_{AN} = \frac{9}{4\pi }\mathop \int \limits_{ - \infty }^{\infty } \left[ {\mathop \int \limits_{{\mu_{sth} }}^{\infty } \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) + r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right)e^{{ - \frac{1}{2}\mu_{s}^{2} }} d\mu_{s} } \right]\left[ {1 - \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) + r\mu_{sth} }}{{\sqrt {1 - r^{2} } }}} \right)} \right]e^{{ - \frac{1}{2}\mu_{sth}^{2} }} d\mu_{sth} {,}$$
(18)
$$\begin{gathered} ROCS_{NN} = \frac{9}{\pi }\int_{0}^{\infty } {\left\{ {\mathop \int \limits_{0}^{{\mu_{sth} }} \left[ {1 - \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) - r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right) - \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) + r\mu_{s} }}{{\sqrt {1 - r^{2} } }}} \right)} \right]e^{{ - \frac{1}{2}\mu_{s}^{2} }} d\mu_{s} } \right\}} \hfill \\ \left[ {\Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) - r\mu_{sth} }}{{\sqrt {1 - r^{2} } }}} \right) + \Phi \left( {\frac{{\Phi^{ - 1} \left( {1/3} \right) + r\mu_{sth} }}{{\sqrt {1 - r^{2} } }}} \right)} \right]e^{{ - \frac{1}{2}\mu_{sth}^{2} }} d\mu_{sth} {. } \hfill \\ \end{gathered}$$
(19)

The structures of these expressions clearly imply that the ROCS appears as a function of the AC skill \(r\) only.

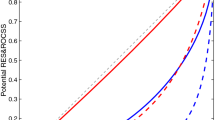
The integral expressions in (17)–(19) can be numerically evaluated, as depicted in Fig. 2. For the BN and AN categories, the ROCS appears as a monotonically increasing function of the AC over the full range of AC values and the functional relationship is quasi-linear and symmetric with respect to the point (0, 0.5) that corresponds to a “no-skill” situation. A positive (negative) AC corresponds to a ROCS larger (smaller) than 0.5 that represents a positive (negative) ROC skill, which is consistent with the previous ROC curve results. Further, it is found that for the BN and AN categories the relationship between the ROCS and the AC highly approaches the linear relation of \(ROCS = 0.5 \times \left( {AC + 1} \right)\). With invoking the formula for the ROCSS (the ROC skill score) shown in Sect. 2, we can have an interesting result that the ROCSS for the BN and AN categories is approximately equal to the AC. For the NN category, the ROCS-AC relationship is considerably nonlinear. Only when AC is positive, the ROCS appears as a monotonically increasing function of the AC. For the same AC, the ROCS is usually noticeably weaker than that for the BN and AN categories, which is also consistent with the previous ROC curve results. When AC is negative, the ROCS-AC relationship appears as a mirror of the relationship when AC is positive, which is consistent with the previous finding that the ROC curve for the NN category is only sensitive to the magnitude of AC.

Fig. 2
figure 2

Theoretical relationship between the probabilistic skill of the ROC score (ROCS) and the deterministic skill of the anomaly correlation (AC). The purple solid curve represents the relationship for the below- or above-normal category, while the purple dashed curve represents the relationship for the near-normal category. The grey dashed line stands for the relation of \(ROCS = 0.5 \times \left( {AC + 1} \right)\), which is approached by the theoretical ROCS-AC relationship for the below- and above-normal categories

Full size image

The formulas from (3) to (11) have been discussed in literature (Kharin and Zwiers 2003b; Palmer et al. 2000). On the basis of (10) and (11) and further considering a perfect model scenario that the model-predicted signal and noise are identical to their true counterparts in the observed system, Kharin and Zwiers (2003b) numerically demonstrated a deterministic relationship of the probabilistic ROC skill with the potential predictability of the observed system. The latter is defined as the ratio of the true predictable signal variance to the total observed variance, which is also equal to the square of the correlation between the true predictable signal and the observed predictand (denoted by \(\rho_{{{\text{pot}}}}\) in Kharin and Zwiers (2003b)). However, this perfect model scenario is in general unrealistic, given that current dynamical climate models still have significant problems in reproducing the observed climate variability. Therefore, the above deterministic link obtained under the perfect model scenario between the probabilistic ROC skill of model forecasts and the potential predictability of the real world would not be able to faithfully reflect the reality. Different from Kharin and Zwiers (2003b), through this theoretical consideration, we have analytically derived a deterministic relationship of the probabilistic ROC skill with the deterministic AC skill that reflects the correlation between the model-predicted signal and the observed predictand. As seen from (12) to (19), our derived theoretical relationship does not rely on whether the model-predicted signal and noise match the true counterparts or not.

4 Verifying the theoretical consideration with GCM seasonal forecasts

In this section, we aim at verifying the theoretical consideration with GCM seasonal forecasts. Specifically, the focus is put on verifying the derived theoretical relationship between the ROCS and the AC. To this end, we use the historical forecast outputs of five coupled GCMs produced by the Ensemble-Based Predictions of Climate Changes and their Impacts (ENSEMBLES; Weisheimer et al. 2009) project. The five models are respectively from the UK Met Office (UKMO), Météo France (MF), the European Centre for Medium-Range Weather Forecasts (ECMWF), the Leibniz Institute of Marine Sciences at Kiel University (IFM-GEOMAR), and the Euro-Mediterranean Centre for Climate Change (CMCC-INGV) in Bologna. The ENSEMBLES dataset contains at-least-7-month-long ensemble seasonal forecasts of multiple variables with nine members for each model, starting on the 1st of February, May, August, and November, respectively, for each year from 1960 to 2005. As in Yang et al. (2018), we focus on analyzing the GCM prediction skills for atmospheric circulation variables of 200- and 500-hPa geopotential heights (G200 and G500) as well as variables of surface air temperature (SAT) and precipitation that are of direct socioeconomic impacts. The “observed” data for calculating skills for G200, G500, and SAT are from the National Centers for Environmental Prediction/National Center for Atmospheric Research Reanalysis product (Kalnay et al. 1996), while the “observed” data for precipitation are from the Climate Prediction Center Merged Analysis of Precipitation data set (CMAP; Xie and Arkin 1996). The precipitation prediction skills are calculated only for the period of 1979–2005, owing to the shorter time coverage of the CMAP data. We only target the 1-month lead forecasts of the seasonal means of December–January–February (DJF), March–April–May (MAM), June–July–August (JJA), and September–October–November (SON). The skills of both the ROCS and the AC are calculated based on the standardized anomalies of model predictions and observation that are defined at each grid point relative to their own local climatologies. To avoid overfitting, the skills are evaluated in a leave-one-out cross-validation manner, i.e., the anomaly is obtained relative to the climatological mean that is calculated with excluding the data for the current year. For the MME, forecasts are generated based on the grand ensemble of the cross-validated single-model standardized anomalies. The probabilistic ROC skills are calculated for the tercile-based categories of the BN, NN, and AN and the predicted probability of one event is estimated as the fraction of ensemble members forecasting the event to occur. As in many other studies, eleven probability threshold values evenly taken from one to zero with interval of 0.1 are empirically selected for calculating multiple pairs of HRs and FARs. We note the fact that, for the NN category, some of the given threshold values may exceed its maximum forecast probability value but does not affect the practical evaluation of its probabilistic ROC skill, since the values of the HRs and FARs associated with these thresholds are necessarily zero, not really contributing in the calculation of the area under the ROC curve.

A skill spatial analysis is first performed. Figure 3 displays the ROCS skill for the BN and AN categories for the prediction of the DJF G200. Since the ROCS skills for these two categories are similar in size, only the averaged skill is shown for simplicity. For all the SMEs and the MME, the overall spatial patterns bear a strong resemblance among each other. The most remarkable feature is a strong skill belt within the tropics (30ºS–30ºN), in which most regions have a ROCS greater than 0.85 or equivalently a ROCSS larger than 0.7. In contrast, the extratropical prediction skill is in general notably weaker. However, a moderately good skill can be seen in some specific extratropical regions such as the Pacific-North American region. The large-scale spatial feature of the ROCS skill is largely consistent with that of the AC skill displayed in Fig. 2 of Yang et al. (2018), which is also very strong in the tropics and generally weak but significant in certain regions in the extratropics. Figure 4 displays the ROCS skill for the NN category. The ROCS for the NN category is noticeably lower than that for the other two categories. However, its distribution still features a distinct contrast between the tropics and the extratropics, fairly resembling that of the AC shown in Yang et al. (2018). It is seen that in terms of the probabilistic ROC skill, the MME seems not very advantageous over all the SMEs. A consistent result was also found in Yang et al. (2016, 2018) for the deterministic correlation skill and the probabilistic resolution skill, which is in contrast to the situation for the probabilistic reliability skill.

Fig. 3
figure 3

Spatial distributions of the probabilistic skill of the ROC score for the prediction of DJF 200-hPa geopotential height at one-month lead by the five models of the ENSEMBLES and their multimodel ensemble (MME) over the period of 1960–2005. The skills shown here are averaged skills for the below- and above-normal categories. The character strings of ECMWF, IFM-GEOMAR, MF, UKMO, and CMCC-INGV denote the acronym names of the five models, respectively (see the main text)

Full size image
Fig. 4
figure 4

As in Fig. 3, but for the predictions for the near-normal category

Full size image

We next focus on quantitatively verifying the theoretical ROCS-AC relationship through analyzing scatterplots. Figure 5 shows the scatterplots of ROCS versus AC using the data of grid point skills for the prediction of the DJF G200, with the theoretical ROCS-AC relationship also plotted for comparison. As seen, the grid point AC skills are mostly non-negative. The scatter patterns show a general covarying tendency of the ROCS with the AC, which is basically consistent with what the theoretical curves indicate. However, the covarying relationship between the ROCS and the AC is obviously far from strong enough to be able to be approximately described as a deterministic relationship as expected by the theory. Yang et al. (2018) found that the relationship between the probabilistic resolution and AC skills of GCM forecasts is either clearly not as strong as expected from their theoretical result, if the examined skills are grid point skills. As discussed in Yang et al. (2018), the significant sampling error in estimating grid point forecast skills due to the small temporal sample size is likely the main reason for this “unsuccessful” validation. This kind of sampling uncertainty in estimating the ROCS skill has been especially pointed out for the ENSO prediction by Kirtman (2003). To better verify the theoretical relationship, we next adopt the strategy used in Yang et al. (2018) to examine the “large sample” zonally aggregated skills for the latitudes between 60°S and 60°N, which are calculated based on pooling together the samples from different locations along the same latitude circles. As seen in Fig. 6a, when the skills are considered in the zonally aggregated sense, the observed relationship between the ROCS and AC for the prediction of the DJF G200 becomes remarkably stronger, capable of being described as a quasi-deterministic relationship, which is greatly consistent in shape with what the theory predicts. As further seen in Fig. 6b–d, the observed ROCS-AC relationships for the prediction of G200 for the MAM, JJA, and SON seasons also agree well with the theoretical result.

Fig. 5
figure 5

Scatterplots of ROC score (ROCS) against anomaly correlation (AC) with using the data of global grid point skills for the prediction of the DJF 200-hPa geopotential height at one-month lead by the ENSEMBLES’ five single-model ensembles (SMEs) and their multimodel ensemble (MME) over 1960–2005 for the a below-normal (BN), b near-normal (NN), and c above-normal (AN) categories. The solid and dashed curves stand for the theoretical ROCS-AC relationships shown only over the AC range that is consistent with the data’s

Full size image
Fig. 6
figure 6

Scatterplots of ROC score (ROCS) against anomaly correlation (AC) with using the data of zonally aggregated skills for the latitudes between 60°S and 60°N for the prediction of 200-hPa geopotential height at one-month lead by the ENSEMBLES’ five single-model ensembles (SMEs) and their multimodel ensemble (MME) for the a DJF, b MAM, c JJA, and d SON seasons over the period of 1960–2005. The left, middle, and right columns are for the below-normal (BN), near-normal (NN), and above-normal (AN) categories, respectively. The solid and dashed curves stand for the theoretical ROCS-AC relationships shown only over the AC range from 0 to 1

Full size image

To further illustrate the consistency of the results for the GCM predictions with the theoretical results, we here give an example analysis of the ROC curve that underlies the calculation of the ROC skill. Figure 7 presents the ROC curve diagrams for the probabilistic forecasts of the DJF G200 aggregated within the tropical region of 30ºS–30ºN and for those aggregated within the midlatitude region of 60ºS–30ºS and 30ºN–60ºN. The aggregated ACs for the tropical prediction for the SMEs and MME vary between 0.7 and 0.8, while the ACs for the midlatitude prediction are between 0.2 and 0.4. As seen, the ROC curves for the BN and AN categories are close to each other for both the tropical and the midlatitude predictions. Further, for each of the BN, AN, and NN categories, the ROC curves for the tropical prediction bend considerably more towards the upper-left corner of the diagrams than those for the midlatitude prediction for all the SMEs and the MME, which illustrates a significant ROC skill contrast between the tropical and midlatitude predictions that is consistent with the contrast seen in the AC. A furthermore visual inspection reveals that the ROC curves for the tropical prediction look like the theoretical curve for AC equal to 0.8 displayed in Fig. 1 and the ROC curves for the midlatitude prediction are like the theoretical curve for AC equal to 0.2 or 0.5. The above ROC curve analysis further verifies the theoretical consideration.

Fig. 7
figure 7

ROC curve diagrams for the probabilistic predictions of the DJF 200-hPa geopotential height at one-month lead aggregated within the tropical region of 30ºS-30ºN (solid curves) and for those aggregated within the midlatitude region of 60ºS-30ºS and 30ºN-60ºN (dashed curves). The blue, green, and red curves are for the below-normal (BN), near-normal (NN), and above-normal (AN) categories, respectively. The character strings of ECMWF, IFM-GEOMAR, MF, UKMO, and CMCC-INGV denote the acronym names of the five models, respectively (see the main text). MME denotes multimodel ensemble

Full size image

The good consistency between the theoretical ROCS-AC relationship and the observed counterpart is not only seen in the prediction of G200. For the prediction of G500, an almost equally good consistency is also seen (figures not shown). Figures 8 and 9 further show the scatterplots of ROCS against AC for the predictions of SAT and precipitation, respectively. For the SAT prediction, the observed ROCS-AC relationship shows a very good consistency with the theoretical counterpart (Fig. 8), which is even better than that for the G200 prediction. In contrast, for the precipitation prediction, the observed ROCS-AC relationship is visibly less consistent with the theoretical counterpart (Fig. 9). As seen in Fig. 9, the scatters for large ACs noticeably spread and deviate downward from the theoretical curve for the BN and AN categories. Yang et al. (2018) also found that the observed relationship between the probabilistic resolution and AC skills for the precipitation prediction, even in the zonally aggregated sense, is still not very consistent with the corresponding theoretical result. As argued in Yang et al. (2018), as compared to other variables, the normal distribution and constant forecast variance assumptions may both be too ideal for the precipitation, which could lead to this unsatisfactory result. Nevertheless, we still can consider the observed ROCS-AC relationship for the zonally aggregated forecast skills of the precipitation as being fairly consistent with the theoretical result, particularly compared to the situation seen previously for the grid point skills. To test the possible effect of the non-normality of the precipitation on the result, following Yang et al. (2018), the Box-Cox transformation technique (Weigel et al. 2009) was further used to transform both the observed and model-predicted precipitation data to be more normal and then the forecast skills using the transformed data were calculated and examined. As displayed in Fig. 10, the observed relationship between the ROCS and AC skills calculated using the transformed data is visibly more consistent with the theoretical result than the original ones. This improvement implies that the non-normality of the precipitation distribution is a main reason why the observed ROCS-AC relationship for the prediction of precipitation is not well consistent with the theoretical result. As shown in Yang et al. (2018), the non-normality also appears as the main reason for the observed resolution-AC relationship for the precipitation failing to closely follow the theoretical expectation.

Fig. 8
figure 8

As in Fig. 6, but for the prediction of surface air temperature at one-month lead

Full size image
Fig. 9
figure 9

As in Fig. 6, but for the prediction of precipitation at one-month lead over the period of 1979–2005

Full size image
Fig. 10
figure 10

As in Fig. 9, but for the forecast skills calculated using the transformed precipitation data that are more normal, which are obtained by applying the Box-Cox transformation technique (see the main text)

Full size image

5 Summary and discussion

Significant interests have been recently placed on investigating the relationship between probabilistic and deterministic skills in dynamical seasonal climate prediction. Based on the BSS methodological framework, Yang et al. (2018) have previously presented a theoretical and diagnostic investigation of the relationships between the probabilistic resolution and reliability skills and the deterministic correlation skill. It was found that a functional relationship can be theoretically derived and practically verified between the resolution skill and the deterministic skill, whereas no good relationship can be identified between the reliability skill and the deterministic skill. In this study, we further present an in-depth study of the relationship between the probabilistic ROC skill and the deterministic skill. The ROC skill measures the discrimination attribute of probabilistic forecast quality, another important aspect in addition to the resolution and reliability. Specifically, the probabilistic ROC skill is quantified based on the ROC curve and the related scores of the ROCS and ROCSS. The ROC skill is considered for the BN, NN, and AN categories defined based on the terciles of the observed climatology.

First, a systematic theoretical consideration has been provided. This consideration is based on the assumptions that predictive PDFs are normal, that predicted noise variance is constant among different cases for a fixed lead time, and that predicted signal and corresponding observation obeys a joint normal distribution. Specifically, based on the above assumptions, we first derive theoretical expressions for the HR and FAR of probabilistic forecasts as a function of the probability threshold \(p_{th}\) and identify their determining factors. Based on these, we then demonstrate and illustrate that the ROC curve, as the curve of HR versus FAR given that \(p_{th}\) varies from the maximum value to zero, has a sole dependence on the AC, the deterministic correlation skill. Based on these preceding results, we finally analytically derive and illustrate a deterministic relationship between the ROCS that measures the area beneath the ROC curve and the AC. The specific shape of the theoretical ROCS-AC relationship depends on which category is considered. For the BN and AN categories, the theoretical relationships are identical and quasi-linear. Further, an approximation to them can be given by \(ROCS = 0.5 \times \left( {AC + 1} \right)\), which also implies that the corresponding ROCSS is approximately equal to the AC. For the NN category, the theoretical relationship is nonlinear and according to this relationship, the ROC skill is insensitive to the sign but only sensitive to the magnitude of the AC. For positive ACs, the corresponding ROCS for the NN category is usually significantly smaller than those for the BN and AN categories. The theoretical ROCS-AC relationship has been argued to exist independent of whether or not the model-predicted signal and noise match the true counterparts in the observed system.

Subsequently, we have focused on verifying the theoretical consideration through analyzing the skills of the GCM seasonal forecasts provided by the ENSEMBLES project. A skill spatial analysis shows that the probabilistic ROC skill of the GCM forecasts is largely consistent in large-scale spatial distribution feature with the corresponding deterministic correlation skill. Further scatterplot analyses find that when considered in a zonally-aggregated sense by which the biasing effect of finite sample size is lessened, the probabilistic ROCS and deterministic AC skills of the GCM dynamical forecasts exhibit a good relationship that, in general, can be characterized as quasi-deterministic, whose specific feature is greatly consistent with that of the theoretically derived relationship. An additional analysis further confirms that the ROC curves for the GCM forecasts show a dependence on the AC that is consistent with what the theory predicts. In brief, the analysis of GCM dynamical forecasts verifies the theoretical result.

To summarize, the most important result of this study is that a deterministic functional relationship between the probabilistic ROC skill and the deterministic correlation skill is theoretically revealed and practically verified in dynamical seasonal climate prediction. One practical use of the revealed theoretical relationship lies in that it can facilitate comparisons between probabilistic and deterministic assessments of seasonal forecasting capability. Especially, as stated above, a simple expression can approximately represent the revealed theoretical relationship for the BN and AN categories, which can further simplify its practical application. Furthermore, the result here together with the previous results of Yang et al. (2018) contribute to an understanding of the fundamental similarities and difference between probabilistic and deterministic skills in seasonal climate prediction. That is, the discrimination and resolution aspects of probabilistic skill are intrinsically equivalent to the deterministic skill, while the reliability aspect of probabilistic skill appears to be the fundamental aspect that differs from the deterministic skill. This understanding undoubtedly can offer potential implications for the study of seasonal probabilistic forecasting in many aspects. In the following, we provide two examples of such implications. One example is on the recalibration in improving seasonal probabilistic forecasts, which has also been discussed in Yang et al. (2018). Previous studies (Doblas-Reyes et al. 2005; Weigel et al. 2009) have shown that simple recalibration via appropriately rescaling dynamical models’ forecasts a posteriori is able to improve the seasonal probabilistic forecast skill. However, the mechanism behind this improvement, to our knowledge, has not been fully understood in theory. Our above understanding of the similarities and difference between the probabilistic and deterministic skills can provide an implication on this issue. That is, only the reliability, rather than the discrimination or the resolution aspect of the probabilistic skill, would be possibly improved by the above recalibration strategy. This is because the latter aspects are intrinsically equivalent to the deterministic correlation skill, which is invariant by rescaling (only the case with positive AC is considered). Another example of such implications is about the specific role of ensemble spread in improving the seasonal probabilistic forecast skill. In ensemble prediction, ensemble spread (variance) is desired to be consistent in magnitude with the mean square error of ensemble mean (MSE) and a deviation of the ensemble spread from the MSE is believed to degrade the seasonal probabilistic forecast skill (Stan and Kirtman 2008). However, which aspect or aspects of the probabilistic skill can be directly influenced by the ensemble spread seems not being widely understood. For example, Stan and Kirtman (2008) seemed surprised by their finding that the probabilistic ROC skill is not reduced by a lack of ensemble spread in studying the ENSO prediction and predictability. However, according to our understanding highlighted above, the discrimination and resolution aspects of the probabilistic skill would not be able to be directly affected by the ensemble spread, since deterministic correlation skill can only be affected by the error in ensemble mean. Only the reliability aspect that has fundamental difference from the deterministic skill could be directly influenced by the ensemble spread. As discussed in Yang et al. (2018), the reliability can be understood as a measure of the conditional bias of probability forecasts, which can be ultimately influenced by the biases in ensemble mean as well as in ensemble spread. Therefore, improving the ensemble spread shall help improve the reliability aspect of the seasonal probabilistic forecast skill.

We note that the deterministic linkage revealed between the probabilistic ROC skill and the deterministic correlation skill in this study may also hint that a deterministic linkage perhaps equally exists between categorical forecast skill and the deterministic skill. Categorical forecast is another kind of forecast format especially preferred in operational centers, which provides an explicit judgement of which category will occur based on the underlying (probabilistic) forecast information. The skill of categorical forecasts is usually measured by the Heidke skill score (HSS; O’Lenic et al. 2008), which was found to have a good correspondence with both the probabilistic ROC skill and the deterministic skill in diagnostic analysis of seasonal forecasts (Peng et al. 2012, 2013; Sooraj et al. 2012). As seen in the formulation of the HSS, the key concept for measuring the categorical forecast skill is that known as “hit” as well, which bears a general similarity to the concept of the hit in the ROC method, despite their formally different definitions. As such, enlightened by the theoretical result of this study, a theoretical linkage between the categorical and deterministic skills of seasonal forecasts seems to be expectable. Actually, Kumar (2009) and Tippett et al. (2010) derived theoretical expressions for the relationship between the HSS and the AC. Nevertheless, their derivations are again based on the perfect model framework. A generalized exploration following the ideas of this study is needed in the future study to investigate and fully understand the relationship between the categorical and deterministic skills in seasonal climate prediction.