Novel dynamical indices for the variations of the western Pacific subtropical high based on three-pattern decomposition of global atmospheric circulation in a warming climate

Abstract

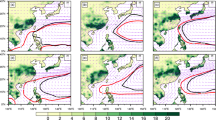
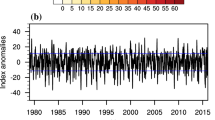
Previous studies have often used the 500 hPa geopotential height to define indices of the western Pacific subtropical high (WPSH). However, some studies reported that global warming caused a significant increase in geopotential height, particularly at the middle and lower latitudes, leading artificial results about long-term trend of the WPSH. To avoid the spurious signals resulting from global warming, this study first redefines the area, intensity, westward ridge point and ridge line indices of the WPSH by adopting the stream function R of horizontal circulation in the three-pattern decomposition of global atmospheric circulation (3P-DGAC). Subsequently, the climatic characteristics of the WPSH in summer are investigated by applying the new indices based on four reanalysis datasets. The results show that the circulation features of the WPSH could be revealed by the stream function R in 3P-DGAC. Moreover, the rain belt over East Asia is located at the northwest periphery of the zero-value isoline of the stream function R. We conclude that the climatological average WPSH is contracted and retreated eastward during 1979–2018 relative to 1948–1978. Nevertheless, by analyzing interdecadal changes of the time series of the new indices during 1948–2018, we find that area and intensity indices decrease with time before the end of 1970s and increase slightly with time after the end of 1970s, the western ridge point index moves eastward with time before the end of the 1970s and moves westward slightly with time after the end of 1970s, as well as there is no obvious interdecadal variations in the ridge line index. Because of the evident dynamical meaning, the stream function R in 3P-DGAC can be used as an objective indicator to describe the interdecadal variation of the WPSH under global warming.

Appendices

Appendix A

1.1 Hypsometric equation

Based on the hypsometric equation (Holton 2004), the geopotential height $\tilde{H}$ for a given pressure level p is approximately represented as follows:

$$\tilde{H} = \frac{{\tilde{R}\overline{T} }}{{{\text{g}}_{0} }}\ln \frac{{P_{S} }}{p},$$

(16)

where

$$\overline{T} = \frac{{\int_{{P_{S} }}^{p} {Td\ln p} }}{{\int_{{P_{S} }}^{p} {d\ln p} }},$$

(17)

$\tilde{R}$ = 287.0 J/(K·kg) is the gas constant of dry air, and g₀ = 9.80665 m s⁻² is the global average of gravity at the mean sea level. $\overline{T}$ stands for the vertical mean temperature between level p and sea level. P_S = 1000 hPa is the sea level pressure, which means $\ln \frac{{P_{S} }}{p} > 0$. Therefore, the increase in $\tilde{H}$ will closely follow the increase in $\overline{T}$.

Appendix B

2.1 Three-pattern decomposition of global atmospheric circulation (3P-DGAC)

The 3P-DGAC method decomposes global atmospheric circulation into three-dimensional (3D) horizontal, meridional, and zonal circulations within three orthogonal planes to acquire a uniform representation of the atmospheric circulation from a global perspective (Hu et al. 2017, 2018a, b). In an effort to solve the problem of inconsistent units in the 3D vorticity vector in the pressure coordinate, the spherical σ-coordinate system is adopted in the 3P-DGAC, that is

$$u^{\prime} = \frac{u}{a},\;v^{\prime} = \frac{v}{a},\; \, \dot{\sigma } = \frac{\omega }{{P_{{\text{S}}} }},\;\sigma \, = \frac{{\text{p}}}{{P_{{\text{S}}} }} \, ,$$

(18)

where a is the radius of the earth, p is the pressure, and P_S = 1000 hPa is the sea level pressure. $(u^{\prime},v^{\prime},\dot{\sigma })$ and (u, v, ω) denote the three velocity components in the spherical σ-coordinate system and spherical p-coordinate system, respectively. Hence, the three-dimensional (3D) velocity field $\vec{V}^{\prime}$ in the spherical σ-coordinate system is denoted as follows:

$$\vec{V}^{\prime}(\lambda ,\theta ,\sigma ) = u^{\prime}(\lambda ,\theta ,\sigma ) \, \vec{i} + v^{\prime}(\lambda ,\theta ,\sigma ) \, \vec{j} + \dot{\sigma }(\lambda ,\theta ,\sigma ) \, \vec{k},$$

(19)

Here, λ is the longitude and θ is the colatitude. The continuity equation of the actual atmosphere can be expressed as follows:

$$\frac{1}{\sin \theta }\frac{{\partial u^{\prime}}}{\partial \lambda } + \frac{1}{\sin \theta }\frac{{\partial (v^{\prime}\sin \theta )}}{\partial \theta } + \frac{{\partial \dot{\sigma }}}{\partial \sigma } = 0.$$

(20)

In terms of the key characteristics of the Rossby, Hadley and Walker circulations, the global horizontal circulation $\vec{V}^{\prime}_{R}$, meridional circulation $\vec{V}^{\prime}_{H}$ and zonal circulation $\vec{V}^{\prime}_{W}$ are defined as follows:

$$\left\{ \begin{gathered} \vec{V}^{\prime}_{R} (\lambda ,\theta ,\sigma ) = u^{\prime}_{R} (\lambda ,\theta ,\sigma )\vec{i} + v^{\prime}_{R} (\lambda ,\theta ,\sigma )\vec{j}, \hfill \\ \vec{V}^{\prime}_{H} (\lambda ,\theta ,\sigma ) = v^{\prime}_{H} (\lambda ,\theta ,\sigma )\vec{j} + \dot{\sigma }_{H} (\lambda ,\theta ,\sigma )\vec{k}, \hfill \\ \vec{V}^{\prime}_{W} (\lambda ,\theta ,\sigma ) = u^{\prime}_{W} (\lambda ,\theta ,\sigma )\vec{i} + \dot{\sigma }_{W} (\lambda ,\theta ,\sigma )\vec{k}. \hfill \\ \end{gathered} \right.$$

(21)

They meet the following continuity equations:

$$\left\{ \begin{gathered} \frac{1}{\sin \theta }\frac{{\partial u^{\prime}_{R} }}{\partial \lambda } + \frac{1}{\sin \theta }\frac{{\partial (v^{\prime}_{R} \sin \theta )}}{\partial \theta } = 0, \hfill \\ \frac{1}{\sin \theta }\frac{{\partial (v^{\prime}_{H} \sin \theta )}}{\partial \theta } + \frac{{\partial \dot{\sigma }_{H} }}{\partial \sigma } = 0, \hfill \\ \frac{1}{\sin \theta }\frac{{\partial u^{\prime}_{W} }}{\partial \lambda } + \frac{{\partial \dot{\sigma }_{W} }}{\partial \sigma } = 0, \hfill \\ \end{gathered} \right.$$

(22)

where R, H and W represent the stream functions of horizontal circulation, meridional circulation and zonal circulation, respectively. Equation (22) guarantees that the components of $\vec{V}^{\prime}_{R}$, $\vec{V}^{\prime}_{H}$ and $\vec{V}^{\prime}_{W}$ can be expressed by the stream functions $R(\lambda ,\theta ,\sigma )$, $H(\lambda ,\theta ,\sigma )$ and $W(\lambda ,\theta ,\sigma )$ as follows:

$$\left\{ \begin{gathered} u^{\prime}_{R} = - \frac{\partial R}{{\partial \theta }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v^{\prime}_{R} = \frac{1}{\sin \theta }\frac{\partial R}{{\partial \lambda }}, \hfill \\ v^{\prime}_{H} = - \frac{\partial H}{{\partial \sigma }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{\sigma }_{H} = \frac{1}{\sin \theta }\frac{\partial (H\sin \theta )}{{\partial \theta }}, \hfill \\ u^{\prime}_{W} = \frac{\partial W}{{\partial \sigma }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{\sigma }_{W} = - \frac{1}{\sin \theta }\frac{\partial W}{{\partial \lambda }}. \hfill \\ \end{gathered} \right.$$

(23)

Since the three-pattern circulations appear in both the low and mid-high latitudes, the actual atmospheric circulation can be represented as the superimposition of the horizontal, meridional, and zonal circulations for large-scale motions, as follows:

$$\vec{V}^{\prime} = \vec{V}^{\prime}_{H} + \vec{V}^{\prime}_{W} + \vec{V}^{\prime}_{R} ,$$

(24)

with the following components:

$$\left\{ \begin{gathered} u^{\prime} = u^{\prime}_{W} + u^{\prime}_{R} = \frac{\partial W}{{\partial \sigma }} - \frac{\partial R}{{\partial \theta }}, \hfill \\ v^{\prime} = v^{\prime}_{R} + v^{\prime}_{H} = \frac{1}{\sin \theta }\frac{\partial R}{{\partial \lambda }} - \frac{\partial H}{{\partial \sigma }}, \hfill \\ \dot{\sigma } = \dot{\sigma }{}_{H} + \dot{\sigma }_{W} = \frac{1}{\sin \theta }\frac{\partial (H\sin \theta )}{{\partial \theta }} - \frac{1}{\sin \theta }\frac{\partial W}{{\partial \lambda }}. \hfill \\ \end{gathered} \right.$$

(25)

Equation (24) or (25) is known as 3P-DGAC.

In comparison with the traditional 2D decomposition of the atmospheric motion into the vortex and divergent components (Holton 2004), the continuity Eq. (22) cannot assure the uniqueness of $R\left( {\lambda ,\theta ,\sigma } \right)$, $H\left( {\lambda ,\theta ,\sigma } \right)$ and $W\left( {\lambda ,\theta ,\sigma } \right)$ since$\vec{V}^{\prime}_{R}$, $\vec{V}^{\prime}_{H}$ and $\vec{V}^{\prime}_{W}$ have three spatial dimensions (Hu et al. 2017, 2018a, b). The following restrict condition is required (Theorems 1 and 2 in Hu et al. 2018a):

$$\frac{1}{\sin \theta }\frac{\partial H}{{\partial \lambda }} + \frac{1}{\sin \theta }\frac{\partial (W\sin \theta )}{{\partial \theta }} + \frac{\partial R}{{\partial \sigma }} = 0.$$

(26)

Equation (26) guarantees both the uniqueness of the stream functions R, H, and W and the physical rationality of 3P-DGAC.

The following equations are obtained by applying Eqs. (25) and (26):

$$\Delta_{3} R = \zeta ,$$

(27)

$$\frac{\partial H}{{\partial \sigma }} = \frac{1}{\sin \theta }\frac{\partial R}{{\partial \lambda }} - v^{\prime},$$

(28)

$$\frac{\partial W}{{\partial \sigma }} = \frac{\partial R}{{\partial \theta }} + u^{\prime},$$

(29)

where $\Delta_{3} = \frac{1}{{\sin^{2} \theta }}\frac{{\partial^{2} }}{{\partial \lambda^{2} }} + \frac{1}{\sin \theta }\frac{\partial }{\partial \theta }(\sin \theta \frac{\partial }{\partial \theta }) + \frac{{\partial^{2} }}{{\partial \sigma^{2} }}$ denotes the 3D Laplacian in the spherical σ-coordinates and $\zeta = \frac{1}{\sin \theta }\frac{\partial v^{\prime}}{{\partial \lambda }} - \frac{1}{\sin \theta }\frac{\partial (u^{\prime}\sin \theta )}{{\partial \theta }}$ represents the vertical vorticity of the actual atmosphere. The stream functions R, H, and W can be acquired by solving Eqs. 27–29. Then the global atmospheric circulation $\vec{V}^{\prime}$ is partitioned into three-pattern circulations$\vec{V}^{\prime}_{R}$, $\vec{V}^{\prime}_{H}$ and $\vec{V}^{\prime}_{W}$ by solving Eq. (23).