1 Introduction

The 2018 IPCC report on a global warming of \(1.5^{\circ }\rm {C}\) (IPCC 2018) made one thing abundantly clear: An increase in global mean temperature of this magnitude would already raise the climate-related risk to human systems, which is partly the result of an amplification of climate and weather extremes. Most likely, there would be an increase in hot extremes in most inhabited areas and, likely, regional increases in the occurrence frequency of heavy precipitation and droughts. Just as concerning, the report indicates that it will require an enormous, global effort to limit \(\rm {CO}_{2}\) emissions to a level that maintains the temperature rise below \(1.5^{\circ }\rm {C}\), relative to pre-industrial levels, requiring zero-emissions by the middle of this century. If this cannot be achieved, global mean temperature will likely increase by more than \(2.0^{\circ }\rm {C}\), further raising the risks resulting from changes in climate extremes from a moderate to a high level.

Human activity affects climate (extremes) not only due to \(\rm {CO}_{2}\) emission but also because of anthropogenic changes in land-cover and land-use. Here, many studies have shown irrigation to be one of the key factors and estimates of its impact on the hydrological cycle place the irrigation-related contribution to present-day terrestrial evapotranspiration as high as 4 % (Gordon et al. 2005; Oki and Kanae 2006). The influence of irrigation on local climate has been the focus of numerous investigations and a profound effect on regional circulations, such as the Indian monsoon, precipitation rates and surface temperatures has been established in a number of model-based regional studies (Adegoke et al. 2003; Douglas et al. 2006; Kueppers et al. 2007; Douglas et al. 2009; Lobell et al. 2009; Saeed et al. 2009; Lee et al. 2009; Niyogi et al. 2010; Lucas-Picher et al. 2011; Harding et al. 2013; Lo and Famiglietti 2013; Huber et al. 2014; Tuinenburg et al. 2014; Alter et al. 2015). But also on the global scale, many studies found irrigation to have a distinct impact on climate (Boucher et al. 2004; Lobell et al. 2006; Sacks et al. 2009; Puma and Cook 2010; Cook et al. 2011, 2014; de Vrese et al. 2016; de Vrese and Hagemann 2017). With respect to temperature extremes, irrigation can be expected to have a predominantly mitigating function as it counters the general trend of global warming by inducing an evaporative cooling at the surface (Thiery et al. 2017; Hauser et al. 2019). However, with respect to hydrological extremes, i.e. floods and droughts, the role of irrigation is less clear. In general, irrigation increases evaporatranspiration and the amount of atmospheric water vapour. This increases precipitation locally, regionally and even in distant locations, which can be beneficial when concurring with a period of drought. However, more saturated soils can also intensify heavy precipitation and prolong the duration of wet spells, thus increasing the occurrence frequency and intensity of meteorological floods (Seneviratne et al. 2010). Furthermore, the irrigation-induced surface cooling may affect regional circulations in a way that leads to a reduction of precipitation in adjacent regions, e.g. in case of the East Asian monsoon (de Vrese et al. 2016). A better understanding of irrigation’s impact on hydrometeorological extremes is not only essential for evaluating its potential to mitigate the negative consequences of global warming but also for estimating the risks that stem from the declining water availability in drying regions.

The present study uses an Earth System Model (ESM), the Max-Planck-Institute for Meteorology’s ESM (de Vrese et al. 2018) (MPI-ESM), to investigate the effect that irrigation has on the occurrence frequency and magnitude of severe and extreme hydrometeorological regimes (SEHRs) during the 21st century. Here, the investigation is focused on irrigation’s theoretical (maximum) impacts on the global scale, with irrigation only limited by the availability of renewable fresh water. This includes irrigation in regions that are currently not irrigated. Thus, rather than the “most-plausible” scenario, we investigate a highly idealized trajectory which allows a more general understanding of irrigation’s climate impact but does not necessarily provide an estimate of real-world potentials. For the first half of the 21st century, the scenario assumes present-day agricultural practices, i.e. cropland areas remain unchanged and the irrigation water demand can be satisfied also from non-renewable sources. During the second half of the century, the cropland area is being maximised under prevailing climatic conditions, which includes the optimization of water extractions for irrigation within hydrologically sustainable limits. As a result, the irrigated area is expanded substantially in arable regions in which there was previously only little irrigation but where sufficient renewable fresh water is available. At the same time, the irrigated area declines in regions where demands can not be sustained from renewable resources, while guaranteeing the environmental flow requirements.

The respective simulations are described in more detail in Sect. 2, together with a brief description of the model development that was required to enable this study. Furthermore, the section discusses the way precipitation percentiles and the Standardized Precipitation Index are used to evaluate the simulations with respect to hydrometeorological extremes. In Sect. 3, we present the results on how irrigation affects the magnitude and occurrence frequencies of SEHRs. To provide a better perspective on the importance of irrigation, we compare the respective impacts to the trends in severe and extreme events that result from the general signal of global warming during the 21st century due to a moderate increase in greenhouse gas (GHG) concentrations, i.e. for the RCP4.5 scenario. In Sect. 4, the main findings are briefly summarized and discussed with respect to their real-world applicability.

2 Methods

2.1 Model and simulations

The MPI-ESM is a state of the art ESM but, as many other models that are used in the 6th phase of the Coupled Model Intercomparison Project (CMIP) (Eyring et al. 2016), the standard version of the MPI-ESM (Raddatz et al. 2007; Jungclaus et al. 2013; Stevens et al. 2013) does not account for the process of irrigation. Furthermore, the spatial extent of croplands is not determined dynamically, accounting for climatic conditions, but prescribed (Hurtt et al. 2011). To estimate the maximum impact of irrigation on climate, we adapted the MPI-ESM and included a model for agricultural land-cover and land-use changes that maximizes the global cropland area under prevailing climatic conditions. This recently developed crop-management scheme determines the extent of irrigated and non-irrigated crops dynamically and includes a new water-management scheme that contains a routine to calculate the environmental flow requirements, a routine to dynamically determine the size of reservoirs and a routine to simulate water withdrawals and releases. A short overview over these schemes is given below, while a more detailed description is provided in de Vrese et al. (2018).

The crop-management scheme determines the spatial extent of cultivated areas as a function of climatic conditions and the available renewable fresh water. In grid-boxes in which climatic conditions allow for a minimum productivity, i.e. where net primary productivity corresponds to a dry yield of at least \(\approx 250\,\text {t}\,\text {(biomass)}\,\rm {km}^{-2}\rm {(canopy)}\,\rm {year}^{-1}\), croplands expand incrementally until the maximum cultivable area is reached, i.e. the surface area not limited by soil or terrain constraints. In regions with a lower productivity, the area under crops declines. The irrigated cropland fraction is determined based on the size of the local water reservoir and the crops’ water requirements in such a way that the water stored in the reservoir should allow irrigation for a growing period of at least 3 months. To ensure that irrigation is hydrologically sustainable, water withdrawals are limited to the fraction of renewable fresh water that exceeds environmental requirements. The latter are assumed to correspond to a third of the unimpaired, long-term mean streamflow (Pastor et al. 2014), i.e. the streamflow that would have occurred in the absence of water withdrawals. The above conditions are checked on an annual basis so that the irrigated and non-irrigated cropland fractions continuously adapt to the prevailing climatic conditions throughout the entire simulation.

Water for irrigation is removed from the river network and stored in a dedicated reservoir, whose size depends on the amount of extractable water (long-term mean). During the growing season, the water can be taken from the reservoir and applied to the soil, from where it evaporates, is taken up by plants and transpired or returned to the river via subsurface runoff. Additionally, the model can be used in a setup in which the crop-management scheme is active but without irrigation so that only the extent of rainfed crops is maximized. Finally, the model can be run in a configuration in which the irrigated and non-irrigated cropland fractions are prescribed and only the water-management scheme is active. In this setup it can also be assumed that water can be added whenever the renewable fresh water does not meet irrigation water requirements. This resembles the use of non-renewable groundwater, which is not explicitly represented in the MPI-ESM. Note that this assumption does not conserve the model’s water balance, however, it best represents the current practice in many irrigated areas where water demands are often satisfied from exhaustible sources (Wada et al. 2012).

We used this adapted model to investigate the climate-agriculture dynamics during the 21st century that develop under a moderate increase in GHG concentrations, i.e. the representative concentration pathway RCP4.5 (Meinshausen et al. 2011; van Vuuren et al. 2011). The pathway assumes a peak in GHG concentrations by the middle of the century and a subsequent stabilization of the radiative forcing at around \(4.5\,\hbox {Wm}^{-2}\). All simulations cover the period 2000–2100 and use a temporal resolution of 450 seconds. They have a horizontal resolution of T63 (\(1.9^{\circ } \times 1.9^{\circ }\)) in the atmosphere and at the land-surface, while the ocean model uses a \(1.5^{\circ }\) resolution. The setup has a vertical resolution of 47 atmospheric model levels, 40 levels in the ocean and 5 soil layers that represent the top 10 m of the soil column. In total we performed 3 sets of two simulations, in which the two simulations differ only due to slight modifications in their initial conditions. The difference between the two simulations is only used to evaluate the model’s internal variability and in the following we consider the mean of the two simulations, for simplicity referring to this mean as one simulation. For the irrigation simulation, the model was run with both new schemes, the crop- and the water-management scheme, active, while for the second, the no-irrigation-simulation, the crop-management scheme is active but without accounting for irrigation. Comparing these two simulations allows to estimate the effect of irrigation on the simulated climate. In the third simulation only the irrigation scheme is active but the cover fractions of irrigated and non-irrigated crops are prescribed (Hurtt et al. 2011), corresponding to the year 2005, while the irrigation water use is not limited to the available, renewable fresh water. As this best resembles the present agricultural practice, this simulation functions as a reference simulation with the help of which also the general trends due to the GHG increase of the RCP4.5 scenario are being evaluated (Table 1).

Table 1 Experimental overview
Full size table

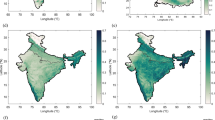
Of these 3 setups, the reference setup is most comparable to the CMIP5 scenario experiments (Taylor et al. 2012a). The respective simulation shows general surface temperature and precipitation patterns that are very similar to those of other CMIP5 models (Fig. 1a,b) (IPCC 2013). Over the oceans, the increase in annual mean temperature is predominantly below 2 K and in the northern Atlantic there is even a distinct temperature decrease, which is also present in simulations with many other models. Over land, the temperature increase is much more pronounced and can reach up to 5 K in the high northern latitudes. Also the changes in precipitation follow a pattern similar to those of other CMIP5 models, with a very strong increase close to the equator, a predominant drying trend in the subtropics and parts of the tropics and a strong increase in mean precipitation rates in high latitudes. Finally, the impacts of irrigation on the mean climate fall within the range estimated by other models that were used to investigate idealized (extreme) irrigation scenarios (Fig. 1c,d) (Lobell et al. 2006; Cook et al. 2011). This gives some confidence that the findings of this study are not limited to the particular physics implementation of the MPI-ESM.

Fig. 1
figure 1

Annual mean surface temperatures and precipitation rates simulated with the MPI-ESM: a Difference in 30-year-mean surface temperature between the period 2000–2029 and 2070–2099 as simulated for the RCP4.5 scenario with the reference model setup (REF). b Same as a, but for mean precipitation. c Difference in 30-year-mean surface temperature (2070–2099) between the idealized simulations with (IR45) and without irrigation (RF45). d Same as c, but for mean precipitation. Non-significant differences (\(\hbox {p} > 0.05\)) are masked in all sub-plots

Full size image
Fig. 2
figure 2

The SPI for one calender month and grid box: a Simulated and fitted (gamma) precipitation distribution in June for a single grid-box (\(42^{\circ }\hbox {N}, 4^{\circ }\hbox {E}\)) as simulated with the reference setup. b Distribution of June-SPIs for the reference simulation. c Time series of June-SPIs for the reference simulation

Full size image

2.2 Analysis

In the following analysis, we focus on precipitation as one of the main drivers of hydrological extremes and we use monthly mean precipitation rates to investigate periods of SEHRs. As a measure for the intensity of extreme conditions we look at the 5th and the 95th percentile of the precipitation distribution which corresponds to the precipitation rates during the 6 driest and 6 wettest months within a ten year period. For the analysis with respect to the occurrence frequency of severe and extreme precipitation rates, we use the Standardized Precipitation Index (SPI) (Lloyd-Hughes and Saunders 2002; Khan et al. 2008). Based on the transformation of a precipitation time series into a standardized normal distribution, the index quantifies the degree of wetness or dryness of each of the records on a scale with eight categories. For this, the index does not use absolute precipitation thresholds but indicates to which degree, given by the number of standard deviations, a certain event deviates from the long-term-mean of the precipitation time series (Table 2). This makes the SPI applicable through a wide range of climate conditions. Based on the SPI, we define severe conditions as either severely (and extremely) wet, i.e. SPI \(\ge 1.5\) or as severely (and extremely) dry SPI \(\le -1.5\). Extreme conditions are defined as a subset of the severe conditions, namely those whose SPI is either \(\ge 2.0\) or \(\le -2.0\). For the study, the index was calculated by fitting a gamma distribution to the precipitation histogram for each grid cell and transforming the resulting cumulative density function into the cumulative density function of the standard normal distribution (Fig. 2a, b). The technical realization of the SPI’s computation was done based on the python package “Standard Precipitation (Evapotranspiration) Index, Version 2” (Nussbaumer 2018) which determines the SPI following Lloyd-Hughes and Saunders (Lloyd-Hughes and Saunders 2002).

Table 2 SPI-classes
Full size table

The SPI can be computed for different time scales all of which have a different relevance for the hydrological cycle, e.g. time scales of a few months are most important for soil moisture and streamflow while longer time scales of up to several years are more relevant for groundwater levels. If the analysis is performed for a sub-annual time scale, the time series only contains the precipitation-sums that cover the same period during each year, i.e. when calculating the SPI for boreal spring, precipitation is summed over the months of March, April and May for each year of the time series. For the present study, we calculate the SPI for each month of the year separately (2c), however, we do not investigate the months individually. Instead we use the number of severely and extremely dry and wet months that occur within a given year or half-year as a measure for the occurrence frequency of severe and extreme regimes (Fig. 3). Note that more information about potential weaknesses of this approach is given in the supplementary material Fig. S3.

Fig. 3
figure 3

Occurrence frequency of sever and extreme conditions: a Number of months per year that are severely dry (\(\hbox {SPI} < -1.5\)) or wet (\(\hbox {SPI} > 1.5\)) and that are extremely dry (\(\hbox {SPI} < -2.0\)) or wet (\(\hbox {SPI} > 2.0\)) for the reference simulation (single grid box at \(42^{\circ }\hbox {N}, 4^{\circ }\hbox {E}\)). b Same as a but only considering the northern hemisphere summer (April–September). c Same as b but for the northern hemisphere winter (October–March). In this grid box there is a statistically significant trend in the number of severely dry months that occur each year and there are positive trends in the number of severely and extremely dry months that occur during summer. In contrast, there are no statistically significant trends for extreme or severe precipitation rates during winter and there are also no statistically significant trends in the number of severely or extremely wet conditions

Full size image

The SPI’s standardized nature has important consequences for the methodology of the present investigation. If sufficiently long time periods are considered, events with a certain level of severity (mild,moderate,severe,extreme) have the same occurrence frequency in any series. This limits the index’s applicability, but the effects due to the increase in GHG concentrations and changes in irrigation can be investigated through the trends they introduce into the precipitation time series. Furthermore, the effect of irrigation on the occurrence of SEHRs can not be obtained by simply evaluating the difference between the SPIs of an irrigation and a no-irrigation simulation, as the magnitude of severe or extreme events differs strongly between the two different precipitation time series. To overcome this issue and make events of a given severity comparable between two time series it is necessary to include a common reference. For the analysis of this study, we constructed the precipitation time series at a given grid-box in a way that the first half (2000–2049) of the series for both, the irrigation and the no-irrigation scenario, contains the records of a common reference. For this we use the first 50 years of the reference simulation, which assumes the present-day agricultural land-use and land-cover for the entire 21st century, i.e. irrigation is limited to the areas that at present are equipped for irrigation but the water withdrawal is not restricted to the streamflow above the environmental flow (see also supplementary material Fig. S4).

Creating the time series in this manner yields three scenarios: The reference scenario in which a “business as usual” agricultural practice is assumed throughout the 21st century (REF) and two scenarios in which agricultural land-use and land-cover are changing for the second half of the century. In these scenarios the extent of cultivated areas is adapted to maximize global crop production under given climatic conditions, with the difference being that in one scenario (IR45) irrigation is maximized within hydrologically sustainable limits, while in the second scenario there is no irrigation (RF45) (Fig. 4). This maximisation of agricultural areas and irrigation was done to capture irrigation’s maximum impact on climate (within hydrologically sustainable limits), while maintaining a similar land-cover distribution in the two scenarios. The maximization of irrigation almost doubles the irrigation quantities, but there are many regions, especially in the sub-tropics, where the irrigation rates are lower than in the reference scenario (for a more detailed description please see supplement S2). For simplicity reasons, we will also refer to IR45 and RF45 as simulations even though the respective time series result from joining the reference and the scenario simulations as described above. In the following we will use REF to evaluate the changes in hydrometeorological extremes that occur due to the increase in GHG concentrations (RCP4.5), while the comparison of IR45 and RF45 allows to investigate the effect of irrigation.

Fig. 4
figure 4

Global irrigation and mean precipitation: a Time series of the global cropland area for the reference scenario (REF), the irrigation scenario (IR45) and the no-irrigation scenario (RF45). b Time series of global irrigation (sum) for the three scenarios. c Time series of global mean precipitation for the three scenarios

Full size image
Fig. 5
figure 5

Relative change in the 5th and 95th precipitation percentiles: a Relative difference in the 5th precipitation percentiles (monthly means) between the periods 2050–2100 and 2000–2050 in REF. b Same as a, but for the 95th percentile. c Same as a, but for the difference between IR45 and RF45 for the period 2050–2100. d Same as c, but for the 95th percentile. Extremely dry regions (annual mean precipitation rates of less than \(0.5\,\hbox {mm day}^{-1}\)) are masked in all plots

Full size image

3 Results

Whether global warming amplifies the magnitude of SEHRs is highly dependant on the location and on the measure that is being considered (Orlowsky and Seneviratne 2011; Sillmann et al. 2013). When looking at the tails of the precipitation distribution, here the 5th (low precipitation) and the 95th percentile (heavy precipitation), we find many areas in which the severity of both low and heavy precipitation periods intensifies due to 21st-century warming. Throughout the Mediterranean, the Middle East and many regions in the Americas and Southern Africa, precipitation rates during the driest months, given by the 5th precipitation percentile, are often by over 30% lower during the second than during the first half of the century (Fig. 5a). At the same time, the precipitation rates during the wettest months—the 95th precipitation percentile—increase by up to 15% in the equatorial region and large areas in high northern latitudes and Asia (Fig. 5b). However, there are also extensive regions especially near the equator, in the high northern latitudes, Eastern and Southeast Asia where the precipitation rates in the driest months are substantially larger, indicating a reduced severity of dry extremes (Note that an overview over regional changes is given in Table 3).

Table 3 Impact on the 5th and 95th precipitation percentiles. The table shows the relative differences [/] in the 5th and 95th precipitation percentile that result from an increase in GHG concentrations (\(\hbox {PP05}_{GHG}\) [5th percentile] and \(\hbox {PP95}_{GHG}\) [95th percentile]) and from irrigation (\(\hbox {PP05}_{IRR}\) [5th percentile] and \(\hbox {PP95}_{IRR}\) [95th percentile])
Full size table

In comparison, the effect of irrigation is much more unidirectional and there are only a few areas where it causes a reduction in the precipitation rates during either the wettest (95th precipitation percentile) or the driest months (5th precipitation percentile). Furthermore, irrigation affects SEHRs over land areas in mid and low latitudes, while most of the large changes that result from the increase in GHG concentrations can be found over the oceans and in high northern latitudes. Agricultural water requirements are highest when soils are dry, making irrigation very effective in modulating precipitation during the driest months (Fig. 5c). For these months, the potential impact of irrigation on precipitation is substantial and in large parts of Europe, the Americas, South-, Central- and Southeast Asia, the respective precipitation rates are twice as large in the irrigation than in the no-irrigation simulation. In these regions, the magnitude of irrigation’s impact on precipitation rates during the driest months is distinctively, often several times, larger than the effect of increasing GHG concentrations; not only in terms of relative differences but also in terms of absolute differences in the precipitation rates (not shown). Furthermore, the irrigation-induced increase in precipitation rates during the driest months often acts against the drying trend which results from the rise in GHG concentrations. On one hand this indicates that, in many regions, the drying trend due to climate change may have been masked by an increase in irrigation, which implies substantial risks for regions that are presently heavily irrigated and rely on extractions from exhaustible groundwater resources. On the other hand it shows that there is a large mitigation potential for areas where currently there is only little irrigation, but where water is readily available.

Fig. 6
figure 6

Zonal mean precipitation and irrigation: a Zonal mean of terrestrial precipitation averaged over the period 2050–2099 for IR45. b Same as a but for irrigation. Note that the amounts (precipitation and irrigation) give the average over the terrestrial surface

Full size image
Fig. 7
figure 7

Difference in trends in the occurrence frequency of severe and extreme precipitation due to irrigation: a Difference in trends—number of severely dry (\(\hbox {SPI} \le -1.5\)) months that occur during summer—between IR45 and RF45. b Same as a, but for winter. c Difference in trends—number of severely wet (\(\hbox {SPI} \ge 1.5\)) months that occur during summer—between IR45 and RF45. d Same as c, but for winter. e Difference in trends—number of extremely dry (\(\hbox {SPI} \le -2.0\))months that occur during summer—between IR45 and RF45. f Same as e, but for winter. g) Difference in trends—number of extremely wet (\(\hbox {SPI} \ge 2.0\)) months that occur during summer—between IR45 and RF45. h Same as g, but for winter. Non-significant differences (\(\hbox {p} > 0.05\)), areas with low precipitation and oceans are masked in all subplots

Full size image
Fig. 8
figure 8

Severely and extremely dry months in the irrigation scenario IR45: a Difference in mean irrigation between the periods 2050-2100 and 2000-2050 for IR45. b Trend in the number of severely dry months during summer for IR45. c Same as b, but for winter. d Trend in the number of extremely dry months during summer for IR45. e Same as d, but for winter

Full size image

However, the impact of irrigation is not only beneficial, as it can also increase in the intensity of wet spells (Fig. 5d). There is substantially less irrigation during months with more intense precipitation (see below), but soils can have a moisture memory of several weeks, allowing irrigation to set conditions that favour precipitation long after the soils were last irrigated (Seneviratne et al. 2006; Stacke and Hagemann 2016). As a consequence, there are regions, especially in the Americas, South Asia and Central Asia, where the precipitation rates during the wettest months increase by up to 20%. Here, the absolute changes in precipitation rates are often larger during the wettest than during the driest months (not shown). While there are areas in South America, South Asia and Central Asia, where irrigation increases the precipitation rates during the wettest months by over \(50\,\hbox {mm month}^{-1}\), the changes in precipitation during the driest month, even in Europe, are mostly below \(25\,\hbox {mm month}^{-1}\).

Additionally, irrigation substantially reduces the terrestrial surface temperatures in many parts of the world (Fig. 1c), offsetting many of the effects of global warming. For example in South-America, the irrigation induced cooling, of about 1K, is comparable to the temperature rise that results from the increase in GHG concentrations. As the precipitation rates over the Pacific ocean are strongly connected to surface temperatures in South America, the irrigation-induced cooling counters the precipitation decrease during the wettest months off the western coast of South America, roughly between \(10^{\circ }\hbox {S} - 30^{\circ }\hbox {S}\), that results from the increase in GHG concentrations (compare Fig. 5b and d). The opposite effect can be seen over the Pacific between roughly between \(10^{\circ }\hbox {N} - 10^{\circ }\hbox {S}\), where the irrigation-related decrease in precipitation during the wettest months reduces the positive signal that results from global warming.

Irrigation and the 21st century warming do not only affect the precipitation rates during severe or extreme periods, but also the frequency with which SEHRs occur. Here, the meaning of the occurrence frequency depends on the measure used to define extreme and severe regimes. In the following, we aim to investigate whether the whole hydrological cycle shifts towards more or towards less extreme conditions. This requires a definition of SEHRs that differs from the measure employed above, i.e. the 5th and 95th precipitation percentile of the full time series. In many places, precipitation rates follow a pronounced cycle with distinct wet- and dry-seasons. Consequently, even a drastic decrease (increase) in precipitation may not result in rates that qualify as severe or extreme conditions if the decrease (increase) occurs during the wetter (drier) period of the year. However, the resulting conditions would have to be considered an extremely arid wet-season (humid dry-season). To account for this effect, we do not evaluate levels of severity based on the entire precipitation distribution, but for each month of the year individually. The following analysis is based on the SPI, which is used to classify degrees of dryness and wetness by whether the precipitation during a given month can be considered severe or extreme, relative to this month’s typical precipitation rates (see Table 2 and Subsect. 2.2).

Additionally we evaluate impacts on the occurrence frequency of SEHRs for the boreal summer half-year (April–September) and the boreal winter half-year (October–March) separately. In the tropics, temperatures allow crops to be cultivated all year round. Here, irrigation is predominantly required to compensate for lower precipitation rates during the dryer season of the year, which for the northern hemisphere encompasses the months October to March and April to September for the southern hemisphere (Fig. 6). In the temperate zones, the cultivation of crops and irrigation is not only determined by the availability of water but also by the annual temperature cycle. The latter limits the growing season for crops and introduces a pronounced annual cycle for potential evaporation. As a consequence irrigation is predominantly required during the warmer periods which do not necessarily encompass the dryer months of the year. This introduces a clear seasonality into the temporal distribution of irrigation and, due to the distribution of the continents, the total amount of irrigation that is employed during the (boreal) summer half-year is almost twice as large as the amount during the winter months. As a consequence, also the impact of irrigation on precipitation extremes differs strongly between the seasons. Note that in the following we will refer to the period of April to September simply as summer, while the period from October to March will be referred to as winter. Finally, a significant fraction of the changes in precipitation occurs over the ocean (Fig. 1, 5), where it may affect the near-surface salinity or even alter the surface albedo, when snow is deposited on sea-ice. However, the resulting feedbacks are substantially smaller than those at the terrestrial surface—where precipitation is a key driver of the vegetation dynamics—and in the following we we will focus our investigation exclusively on land areas.

Increasing GHG concentrations have very little effect on the occurrence frequency of severe- and almost no impact on the occurrence frequency of extreme conditions over terrestrial areas. The only pronounced effects are an increase in severely dry conditions over Europe—including a corresponding decrease in severely wet conditions—and the southern US, as well as an increase in severely wet conditions in central Africa and East Asia (Note that a more detailed description is provided in the supplements Fig. S1 and a overview over regional averages is provided in Table 4).

Table 4 Trends in the occurrence frequency of SEHRs, resulting from increasing GHG concentrations, for SREX–regions
Full size table

In contrast, irrigation has a pronounced effect on the occurrence frequency SEHRs over land (Table5 provides an overview over regional averages). It reduces the occurrence frequency of severely dry months (SDMs) during summer, especially in North America, parts of northern South America, Europe, South Asian and Central Asia (Fig. 7a). These impacts are largest in Europe, where irrigation reduces the trend in the number of dry months that, on average, occur during a given summer by as much as \(-1.5\,\hbox {month year}^{-1}\,\hbox {century}^{-1}\). Here, the impacts of the simulated irrigation are not only two to three times larger in magnitude than those resulting from an increase in GHG concentration – as projected by RCP4.5–, but the affected area is also much more extensive. In contrast, there is only little irrigation in the northern hemisphere during winter and significant reductions in the occurrence frequency of SDMs are mostly limited to South Asia, the Middle East and South America (Fig. 7b). There are also significant impacts of irrigation on the occurrence frequency of extreme conditions and, in Europe, North America, South Asian and Central Asia, there are extensive areas in which irrigation reduces the occurrence frequency of extremely dry summer months by up to \(-0.75\,\hbox {month year}^{-1}\,\hbox {century}^{-1}\) (Fig. 7e,f).

Table 5 Impact of irrigation on the trends in the occurrence frequency of SEHRs for SREX regions
Full size table

There are only few terrestrial areas in which irrigation leads to an increase in the occurrence frequency of SDMs (Fig. 7a,b), with the drying trend most likely being a consequence of the evaporative cooling of the surface. For example, in South and Southeast Asia the irrigation-induced cooling reduces the land-sea thermal contrast weakening the East Asian monsoon, which leads to an increase in summer SDMs in parts of Southeast Asia (de Vrese et al. 2016). Reduced surface temperatures in sub-saharan Africa affect the location of the inter-tropical convergence zone which shifts the temporal distribution of precipitation rates in central Africa, increasing the number of SDMs during summer while reducing it during winter.

With the decreases in the occurrence frequency of SDMs being so much larger than the corresponding increases, both in spatial extent and in magnitude, the effect of irrigation on the occurrence frequency of SDMs is largely beneficial. At the same time, irrigation significantly increases the risks related to heavy precipitation by increasing the occurrence frequency of severely wet month, especially during summer (Fig. 7c,d). However, these detrimental effects are limited to the occurrence of severe events and when looking at the occurrence frequency of extremely wet months there are almost no areas that are significantly affected by irrigation (Fig. 7g,h).

The present findings merely pertain to the theoretical impact of irrigation and not necessarily to what is achievable in the real world. In the irrigation simulation, the expansion of cropland areas and the increase in irrigation in sufficiently productive regions is limited only by the availability of water. In reality however, there are many other, often more restrictive ecological and economic factors that limit the expansion of agricultural areas. It has been suggested that expanding the extent of croplands beyond 15% of the global ice-free land surface could bring the planet to a tipping point, e.g due to hypertrophication resulting from increased use of fertilizers and the loss of biodiversity (Rockström et al. 2009; Steffen et al. 2015). This is a much smaller area than what is transformed into cropland in the irrigation simulation. Consequently, it is very problematic to draw any conclusions about irrigation’s real-world potential to mitigate future droughts, as it is likely that the irrigation simulation overestimates what, in reality, can be converted into irrigated cropland.

However, there are extensive regions where present-day water withdrawals are largely non-sustainable and extraction has already lead to a substantial depletion of groundwater reserves (Taylor et al. 2012b; Wada et al. 2012; Rodell et al. 2018). Especially in South Asian, Central Asia, the Middle East and Southern Europe, it is likely that water availability will be the most restrictive factor, limiting the extent of cultivated areas in the future. This is well captured by the irrigation simulation, in which the water withdrawals and the irrigated area decline substantially in the second half of the century, when the irrigation water use is restricted to the utilizable share of the renewable fresh water (Fig. 8a). In this region, the irrigation simulation represents a highly plausible scenario, namely that non-renewable groundwater will be used to the point of depletion (in the simulation assumed to be in 2050), followed by a sharp decrease in irrigation-rates and a decline in the respective areas. Here, the simulation can indeed indicate the real-world consequences of a (complete) depletion of the non-renewable groundwater resources in regions where present-day water extractions are not sustainable.

The reduction of irrigation rates, especially in South-Asia, has a substantial impact not only on the mean climate but also on the hydrometeorological extremes. Throughout the region, there is a strong increase in surface temperature and distinct regional decreases in annual mean precipitation, which in large areas lead to a reduction in the occurrence frequency of severe summer wet spells (not shown). More importantly, there is also a substantial increase in SDMs during summer in the Mediterranean region, the Middle East, Central Asia and the western parts of South Asia (Fig. 8b). For most parts this increase signifies that by the end of century the average number of SDMs during summer has increased by half a month \(\hbox {year}^{-1}\) while, around the Indus basin and the Caspian Sea, severe summer dryness will (on average) be present every year. For winter, the impact of reduced irrigation rates is much smaller and mostly confined to northern India where the number of SDMs still increases by up to 1 month \(\hbox {year}^{-1}\) during the 21st century (Fig. 8c). For extreme dryness, the spatial pattern is very similar even though the increase in extremely dry months is much smaller. In most places that exhibit a significant increase in extremely dry summer months, the trend is below \(0.5\,\hbox {month year}^{-1}\,\hbox {century}^{-1}\) . However, in parts of India and Pakistan, some of the most densely populated countries in the world, even extreme summer dryness will occur (on average) at least every 2 years (Fig. 8d,e).

4 Discussion

The above results demonstrate irrigation’s strong impact on the occurrence frequency and magnitude of severe and extreme conditions and highlight its theoretical potential to mitigate some of the detrimental effects of global warming. Extreme and severe conditions in large parts of the terrestrial surface in mid and low latitudes are significantly affected by the simulated irrigation and the respective impacts are substantially larger than those resulting from the rise in GHG concentrations. As irrigation almost exclusively leads to a reduced severity and occurrence of severely and extremely dry conditions, it counters the drying trend in many regions in the mid and low latitudes that results from the 21st century warming. At the same time, irrigation does not only have a mitigating effect, but it also substantially increases the occurrence frequency and intensity of severely wet conditions in many regions.

Beyond irrigation’s potential to mitigate severely and extremely dry conditions, we could show the large risks that result from a depletion of non-renewable ground water in heavily irrigated region. That the respective increases in drought frequency are largely attributable to the reduction in irrigation and not to the general signal of 21st century warming, can be seen when comparing the trends of the irrigation simulation (Fig. 8) to those of the reference simulation in which irrigation is not limited to a sustainable level (Fig. S1 a,b,e,f). While the irrigation simulation shows a widespread increase in the number of severely and extremely dry months throughout South Asian and Central Asia, the Middle East, Southern Europe and Northern Africa, these can only be found in Southern Europe and Northern Africa in the reference simulation—in which limitations due to water-availability are not accounted for.

At present, most ESMs and climate models only have a crude representation of the irrigation process – if irrigation is represented at all. Furthermore, the typical ESM-resolution is very coarse in comparison to the characteristic length scales of irrigated areas in many (semi) arid regions. Some of the related issues can be addressed with adequate parametrizations of the sub-grid-scale heterogeneities (de Vrese and Hagemann 2017), but there are two large challenges that have not been addressed so far. On one hand, soil textures vary at very fine spatial scales and irrigated areas are often chosen because of properties, such as the water holding capacity. Thus it must be assumed that there is a spatial correlation between soil properties and arable areas that is not accounted for when irrigated areas make up only a small fraction of a grid-box. Most land surface models, including JSBACH, assume horizontally homogeneous soil characteristics and, at coarse spatial resolution, it is very difficult to simulate a high level of saturation in irrigated areas, without overestimating the irrigation water requirements (de Vrese and Hagemann (2017) and Fig. S2). On the other hand, irrigation in hot and arid environments introduces strong, local contrasts in temperature and humidity—the oasis effect—, that can lead to the development of local circulations, which can not be accounted for at a resolution at which irrigated areas are a sub-grid-scale feature.

However, the largest problem for present day models is to account for water availability and we are not aware of any model that is capable of simulating the changes in irrigation rates that would result from a depletion of exhaustible groundwater resources. Consequently, the respective effects on climate have not been taken into account in any ESM-based study and the increasing risk due to changes in climate extremes has been severely underestimated for vulnerable regions such as South Asia. Admittedly, the present findings are based on simulations that use only one particular ESM, hence they come with some uncertainty attached. But at the least, they demonstrate that an expansion or decline in irrigation may substantially affect the risks connected to hydrometeorological extremes, making irrigation a process that requires more attention from the modelling community and a much more realistic representation in global models.