1 Introduction

The long-term trend in global sea surface temperature (SST) plays a fundamental role in the climate system. Modeling studies indicated that the long-term SST change could affect tropical cyclone frequency and global precipitation. For example, Xie et al. (2010) reported that the enhanced warming over the equatorial Pacific and the Inter-tropical Convergence Zone (ITCZ) anchors increasing local rainfall, and the intensified cooling over the Southern Hemisphere could suppresses tropical cyclone development via reducing the tropical cyclone potential intensity. Cai et al. (2013) suggested that with the enhanced warming in the eastern equatorial Pacific under the future anthropogenic greenhouse gas releasing scenario, the occurrence of extreme El Niño-Southern Oscillation (ENSO) would be doubled. Identifying the underlying long-term global SST change in the recent history can undoubtedly advance our understanding of how the climate system responds to the anthropogenic forcing; it can also provide a benchmark for elucidation of model behaviors under the historical greenhouse gas forcing scenario (e.g., CMIP5 project; Taylor et al. 2012). However, since the long-term trend in global SST could be modulated by internal oscillations from decadal to multi-decadal time scales and these internal variations simulated in models are not necessarily in phase with those in the observations, one cannot directly compare the trends in models and observations over a fixed period and conclude how the model responds to the anthropogenic forcing. It is therefore necessary to explore the uncertainty due to internal variation on trend and to clarify the SST change due to the anthropogenic forcing.

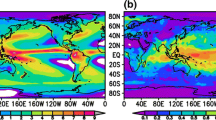
By definition, the sign of the SST change due to the anthropogenic forcing should not change with the prolonging or/and shortening of the record. However, as the magnitude of the linear trend in global SST is generally much smaller than the amplitude of multi-scale internal variation, internal variation can sometimes modulate the sign of the linear trend in regional SST, masking the SST response to the anthropogenic forcing. For example, the linear trend in the zonal SST gradient over the equatorial Pacific was reported to have enhanced over the twentieth century (Luo et al. 2012). However, when using a shorter record starts from the 1950s, the zonal SST gradient over the equatorial Pacific was found to have weakened instead (Tokinaga et al. 2012). L’Heureux et al. (2013) further pointed out that the sign of the linear trend in SST in the central and eastern equatorial Pacific contains strong decadal variability. Using a pair of 100-year records since 1881, the signs of linear trend in the central southern Indian Ocean, the region north of Australia, the eastern off-equatorial Pacific, and the region off California coast can be opposite for two different periods (Fig. 8). Because of this kind of uncertainty in trend estimate, whether the resulting warming trend or/and cooling trend in these regions can be interpreted as the underlying long-term change related to the anthropogenic forcing is far from certain, even when the estimation is based on a 100-year record and when the estimated trend is statistically significant.

It is therefore necessary to find a criterion for determining the uncertainty in the sign of the “estimated” trend. If the de-trended time series is assumed to be independent or uncorrelated, the sign of the “estimated” linear trend estimated by the Ordinary Least-Square (OLS) method can be statistically verified if it passes, for example, the 95% confidence level. This straightforward criterion has been widely used in climate research (e.g., Deser et al. 2010; Luo et al. 2012; Fig. 8). However, a climate variable generally has a serial correlation (von Storch and Zwiers 1999). Assuming the de-trended time series as the first order autoregressive (AR1) process, Weatherhead et al. (1998; W98 hereafter) gave a measurement of the uncertainty of “estimated” linear trend, which depends on the autocorrelation at lag 1 and the variance of the de-trended data. Although this criterion can be easily applied (e.g., Loeb et al. 2007; Wielicki et al. 2013), any departure from the AR1 process makes the criterion in W98 perform poorly (Phojanamongkolkij et al. 2014). Leory et al. (2008; L08 hereafter), on the other hand, gave a criterion when the autocorrelations of the de-trended record at all possible time scales are taken into account. This criterion does not assume any form of the data and is theoretically versatile. However, the difficulty in estimating autocorrelation coefficients at the infinite lags makes it difficult to be used in practice (Phojanamongkolkij et al. 2014).

The aim of this study is to provide a new criterion to scale the uncertainty in the sign of the “estimated” trend, especially for the time series dominated by the oscillatory term. In particular, we will discuss the role of multi-scale internal variation and the role of noise process in the uncertainty of the “estimated” trend, respectively. The rest of the paper is arranged as follows. In Sect. 2, we investigate the theoretical expression of “estimated” trend by the OLS method. A new concept named as the theoretical threshold is introduced to scale the uncertainty in the sign of the “estimated” linear trend related to the oscillatory term. The advantage of this criterion is given by an idealized experiment. In Sect. 3, we apply the new criterion to investigate whether the underlying long-term trend in the global SST since 1881 can be correctly estimated by the OLS method, followed by conclusions and discussion in Sect. 4.

2 Trend evaluation: effects of internal variation on linear trend estimation

2.1 W98 and L08 criteria

Let y(t) be a continuous time series of a climate variable with zero mean. In W98, the linear trend model assumes \(\left( \text{t} \right)=\text{Bt}+\text{N}(\text{t}),\) where B is the “true” linear trend or the long-term linear trend, and N(t) is the term for noise. Considering the associated scale of the fluctuating climate variable, the noise term is assumed to be the AR1 process in W98, that is, \(\text{N}\left( \text{t} \right)={{\rho}_{1}}\text{N}\left( \text{t}-1 \right)+\epsilon (\text{t}),\) where ρ1 and \(\epsilon \left( \text{t} \right)\) denote the autocorrelation of the noise term at lag 1 and white noise, respectively. Let r(L) denote the “estimated” trend. When \(\left\| {{\rho}_{1}} \right\|\) is not close to 1.0, the standard deviation of r(L) used to measure the uncertainty of r(L) can be approximated as:

$${U_{W98}} \approx \sqrt {\frac{{12}}{{{L^3}}}{\sigma ^2}dt\left( {\frac{{1 + {\rho _1}}}{{1 - {\rho _1}}}} \right)}$$
(1)

where \(\sigma\) and \(dt\) are the standard deviation of N(t) and the interval between samples, respectively, and L is the length of the time series. In the case that \(\left\| {{\rho}_{1}} \right\|\) is close to 1.0, the standard deviation of r(L) can be estimated by a more complex formula (see the appendix in W98).

The uncertainty of “estimated” trend proposed in W98 requires only two estimated model parameters (σ and ρ1), making it easy to use. However, the noise term for the climate variable does not always follow the AR1 process. When this happens, \({{\text{U}}_{W98}}\) cannot be used to estimate the uncertainty of “estimated” trend precisely (Phojanamongkolkij et al. 2014).

The criterion shown in L08 does not assume any form for the noise term. Instead, it takes the autocorrelation of N(t) at all lags (from \(-\infty \,\text{to}\,\text{+}\infty\)). The standard deviation of the “estimated” trend r(L) given in L08 is:

$${U_{L08}} \approx \sqrt {\frac{{12}}{{{L^3}}}{\sigma ^2}dt\left( {\mathop \sum \limits_{\mu = - \infty }^{\mu = + \infty } {\rho _\mu }} \right)}$$
(2)

where ρ µ and dt denote the autocorrelation of N(t) at lag µ and the interval between samples, respectively, and σ is the deviation of N(t).

Compared to the criterion proposed in W98, the criterion postulated in L08 is closer to the reality and theoretically versatile. However, the difficulty of estimating the autocorrelation of N(t) at the infinite lag makes it difficult to be applied to finite time series (Phojanamongkolkij et al. 2014). It is noted that when the noise is white (i.e., ρ0 = 1; ρ1 = 0 when i ≠ 0), UW98 and UL08 are identical. In this case, as generally used in climate research, the difference between the “estimated” and the “true” linear trends will be less than 1.96UW98 at the 95% confidence level.

2.2 A new criterion

Here, we propose a new criterion for the uncertainty of “estimated” linear trend by decomposing the noise term N(t) used in W98 into two parts: the part denoting the multi-scale oscillation that can be interpreted as multi-scale internal variation, and the part denoting the possible discontinuity arising from sampling errors and other unexpected fluctuations, which are independent from the multi-scale internal variation:

$$\text{y}\left( \text{t} \right)=\text{Bt}+\mathop{\sum }^{}{{\text{A}}_{\text{i}}}\cdot \sin \left( {{\omega }_{i}}\text{t}+{{\varphi }_{i}} \right)+{{\text{N}}_{t}},$$
(3)

where \(\mathrm{B}\) is the “true” linear trend or the long-term linear trend. A i , ω i and ϕ i are the amplitude, frequency and phase of the ith oscillatory term, respectively. N t represents the unexpected noise.

In W98, the noise term is regarded as the red noise and further assumed as the AR1 process. In our model, the part in the de-trended time series, which shows strong autocorrelation, has been explicitly expressed as the oscillatory term, so the residual part in the de-trended time series is assumed as uncorrelated in a first-order approximation. In other words, N t in Eq. (3) is assumed as white noise. Because the “estimated” linear trend is a linear function of the terms used (Eq. 13 in the appendix), the “estimated” linear trend for Eq. (3) can be written as:

$$\text{r}\left( \text{L} \right)=\text{r}\left( \text{B} \right)+\text{r}\left( \text{O} \right)+\text{r}\left( {{\text{N}}_{t}} \right),$$
(4)

where r(B), r(O) and r(N t ), and denote the part of the linear trend related to the “true” linear trend term, the oscillatory term and the white noise term, respectively. From Eq. (13), we have r(B) = B. The analytical solution for r(O) can also be derived (Eq. 14 in the appendix).

2.2.1 Without the white noise term

Let us first consider a case without the white noise term, that is, N t  = 0. In this case, r(N t ) in Eq. (4) is also equal to zero. The “estimated” linear trend r(L) can be approximated as (Eq. 15 in the appendix):

$$\text{r}\left( \text{L} \right)\cong \text{B}-\frac{6}{{{\text{L}}^{2}}}\mathop{\sum }^{}\frac{{{\text{A}}_{\text{i}}}}{{{\omega }_{i}}}[\text{cos}\left( {{\omega }_{i}}\text{L}+{{\varphi }_{i}} \right)+\text{cos}({{\varphi }_{i}})],$$
(5)

where L is the record length.

From Eq. (5), it is clear that the “estimated” linear trend consists of two terms: One represents the “true” linear trend, and the other denotes the uncertainty of “estimated” linear trend due to the oscillatory term. When A i and ω i are given, the second term will only depend on two parameters. The first parameter is the record length. With the increase of the record length, the uncertainty decreases with the square of the record length. In this sense, the “true” linear trend can be precisely estimated if the record length is long enough. The second parameter is the phase of the oscillatory term. With a different phase of the oscillatory term at the beginning, the “estimated” trend changes nonlinearly. Nevertheless, since the magnitude of the sum of the terms in the bracket cannot be greater than 2, we have:

$$\text{r}\left( \text{L} \right)-B\le \frac{12}{{{\text{L}}^{2}}}\mathop{\sum }^{}\frac{{{\text{A}}_{\text{i}}}}{{{\omega}_{\text{i}}}}$$
(6)

From Eq. (6), it is clear that for a given amplitude, a low-frequency variation (small ωi) will have a larger impact on the “estimated” trend than a high-frequency one (large ωi). Equation (6) also indicates that the difference between the “true” and the “estimated” linear trends is smaller than the theoretical threshold of:

$${{\text{B}}_{t}}=\frac{12}{{{\text{L}}^{2}}}\mathop{\sum }^{}\frac{{{\text{A}}_{\text{i}}}}{{{\omega}_{\text{i}}}}.$$
(7)

Therefore, the “estimated” trend will not give a wrong estimation of the sign of the “true” linear trend once its magnitude exceeds the theoretical threshold. Otherwise, the sign of the “estimated” trend may depend on the phase of the oscillatory term (ϕ i in Eq. 5).

We can also determine the record length required to guarantee the sign of the “true” trend by the OLS method. From Eq. (6), we have:

$$\text{B}-\frac{12}{{{\text{L}}^{2}}}\mathop{\sum }^{}\frac{{{\text{A}}_{\text{i}}}}{{{\omega}_{\text{i}}}}\le \text{r}\left( \text{L} \right)\le \text{B}+\frac{12}{{{\text{L}}^{2}}}\mathop{\sum }^{}\frac{{{\text{A}}_{\text{i}}}}{{{\omega}_{\text{i}}}}.$$
(8)

Therefore, if the “true” linear trend is given, its sign will not be incorrectly estimated by r(L) when the record length L is greater than the critical length of

$${{\text{L}}_{C}}=\sqrt{\frac{12}{\left\| B \right\|}\mathop{\sum }^{}\frac{{{\text{A}}_{\text{i}}}}{{{\omega}_{\text{i}}}}}.$$
(9)

2.2.2 With the white noise term

Theoretically, any continuous time series can be decomposed by a set of oscillatory terms (for example, by Fourier basis functions), and we can use the theoretical threshold to scale the uncertainty of “estimated” trend. However, in practice the observed record is discrete and finite. One thus needs to consider the role of the white noise term N t in Eq. (3), which denotes the part of the record that cannot be fit by the oscillatory term, in the uncertainty of “estimated” trend. From Eq. (1), when ρ1 is set as zero, the standard deviation of r(N t ) can be approximated as:

$$\delta\cong \sqrt{\frac{12}{{{\text{L}}^{3}}}\text{dt}{{\sigma}^{2}}},$$
(10)

where σ denotes the variance associated with N t . δ is referred as the “noise effect” hereafter.

As commonly used in scientific investigation, there is 95% probability that \(\left\| \text{r}\left( {{\text{L}}} \right)-B-{{\text{B}}_{t}} \right\|\le 1.96\delta\). Taking this and referring to Eq. (4), the uncertainty in the sign of the “estimated” trend r(L) can be measured by B t + 1.96δ when a noise term is considered. However, it should be noted that in some extreme cases (which count for 5% cases), \(\left\| \text{r}\left( \text{L} \right)-B \right\|\) could be larger than B t + 1.96δ. Therefore, the uncertainty in the sign of r(L) measured by B t  + δ is from the statistical point of view. Of course, if the noise effect δ is much smaller than the theoretical threshold B t , the uncertainty in the sign of r(L) due to the white noise can be neglected. In this case, the uncertainty in the sign of r(L) can be deterministically scaled by \({\mathrm{B}}_{t}\) alone.

2.3 An idealized example

To illustrate the concept of the theoretical threshold, a simple idealized example is given here. The time series is set as:

$$\text{y}\left( \text{t} \right)=\text{Bt}+100.0\text{sin}\left( 1.0\text{t}+\varphi \right).$$
(11)

The record length is set to 50.0. Note that these parameters are selected for neat display in a figure, though using other parameters will give the same conclusion.

Figure 1 gives the “estimated” linear trend r(L) as a function of the “true” linear trend. With the increase of the “true” linear trend, the “estimated” linear trend linearly increases as suggested by Eq. (5). However, their difference is always smaller than the required theoretical threshold of 0.48. It is clear that the sign of the “estimated” linear trend does not depend on the phase used as long as the magnitude of the “true” trend exceeds the theoretical threshold (green triangles). Otherwise, the sign of the “estimated” linear trend may depend on the phase of the oscillatory term. For example, taking the “true” linear trend as 0.2, one may get a positive “estimated” trend if the oscillatory phase is set to \(\Phi =\frac{3\pi }{4},\) or one may get a negative “estimated” trend if \(\Phi =-\frac{\pi }{4}.\) Therefore, the theoretical threshold does provide a boundary for the magnitude of the “true” trend, which allows its sign to be correctly estimated by the OLS method. From Eq. (6), this is equal to mean that once the magnitude of the “estimated” trend is greater than the theoretical threshold, its sign can be guaranteed as the true sign of the “true” linear trend.

Fig. 1
figure 1

The “estimated” linear trend r(L) as a function of the “true” linear trend B. Red and blue lines denote the “estimated” linear trends when the phase is set as \(-\frac{\pi}{4}\) and \(\frac{3\pi}{4},\) respectively. Grey shading denotes the span of r(L) when using all possible phases from −π to π. The black dashed line denotes r(L) = B. The green triangles denote the theoretical thresholds

Full size image

2.4 Comparing the theoretical threshold and the other criteria

In climate research, the de-trended time series of a given variable, such as SST, is generally dominated by a few modes. For example, the de-trended SST in the eastern equatorial Pacific is dominated by internal variation at the interannual, decadal and interdecadal time scales (as will be shown in Fig. 3). Therefore, it is reasonable to assume the de-trended time series takes the form of Eq. (3). In this case, the uncertainty in the sign of the “estimated” linear trend determined by the theoretical threshold will be more reliable than those determined by the confidence level and the criterion shown in W98 which assume the de-trended data as the white noise on the AR1 process. In addition, unlike the criterion proposed in L08, the theoretical threshold can be easily estimated in practice.

To show the advantage of the theoretical threshold, we analyze the “estimated” linear trend of the following equation:

$$\text{y}\left( \text{t} \right)=0.1\text{t}+6.58\sin \left( 0.2\text{t}+\varphi \right).$$
(12)

The parameters are chosen so that the last point with the “estimated” trend will be equal to the critical length (Eq. 9) when the phase is set to ϕ = 0 (Eq. 16 in the appendix). Note that using other parameters will give a comparable conclusion.

Figure 2 gives the “estimated” trend of Eq. (12) as a function of the record length. As suggested by Eq. (5), the “estimated” trend will nonlinearly approach the “true” trend with increasing record length. Only when the record length is more than the critical length of 62.8, which is estimated by Eq. (9), the sign of the “estimated” trend will be the same as that of the “true” linear trend, which is positive. In practice, the “true” linear trend is unknown. Therefore, if using the criterion of \(\left\| \text{r}(\text{L}) \right\|>~{{\text{B}}_{t}}~\) to justify the sign of the “estimated” trend, the record length needed is 72.

Fig. 2
figure 2

The “estimated” linear trend (red curve) and the range of the theoretical threshold (blue curve) as a function of record length. The vertical green line denotes the critical length

Full size image

However, using other criteria will get an unreliable estimation of the “true” linear trend. Suppose that one only has the record with a length of 30, which is shorter than the required length estimated by the new criterion. The “estimated” linear trend for this short record is −0.350, and the 95% confidence interval is [−0.362, −0.339]. If one justifies the “estimated” linear trend by the 95% confidence test, it will be concluded that the underlying trend in Eq. (12) is a significant negative value. The value of \({{\text{U}}_{W08}}\) and \({{\text{U}}_{L08}}\) are 0.054 and 0.048, respectively, both smaller than the magnitude of the “estimated” trend. As a result, using the criteria proposed in W98 and L08 will lead one to believe that the linear trend underlying in Eq. (12) is negative, which is opposite to the sign of the “true” linear trend (0.1). On the other hand, the required theoretical threshold proposed here is 0.439 when the record length is 30, larger than the magnitude of the “estimated” trend. Therefore, the resulting negative value (−0.350) cannot be fully interpreted as the underlying trend in Eq. (12). This example clearly indicates that the criterion proposed here is more reliable for justifying the sign of the “estimated” trend when the time series is dominated by the oscillatory term. It should be noted that since the autocorrelation at lag 1 is very close to 1.0 for Eq. (12), \({{\text{U}}_{W08}}\) is estimated by the more complex formula shown in the appendix in W98, instead of Eq. (1). To estimate \({{\text{U}}_{L08}},\) following Phojanamongkolkij et al. (2014), the autocorrelation coefficient is set up to \(10{{\log }_{10}}L\) lags.

3 Effect of internal variation on long-term linear trend in global SST

As an application of the criterion proposed in Sect. 2, we now investigate the uncertainty of long-term linear trend in global SST in the recent history. The reconstruction is HadISST1 (Rayner et al. 2003), one of the widely used datasets for climate research. The period is from 1881 to 2013, a total of 1596 monthly records. The SST anomaly is obtained by removing the climatological seasonal mean.

In order to estimate the theoretical threshold for the global SST, we need to know the amplitudes and frequencies for the internal variation at each grid. A widely used method is the fast Fourier transform (FFT). As an example, Fig. 3a gives the time series of SST anomaly in the equatorial Pacific at (120°W, 0°). The amplitudes and periods of all internal variation at this grid identified by the FFT are shown in Fig. 3b. The SST anomaly at this grid has two distinguished spectral peaks: one with periods from 2 to 10 years associated with the ENSO, and the other with a peak at 60 years related to the Pacific Decadal Oscillation (PDO; Mantua et al. 1997) and the Interdecadal Pacific Oscillation (IPO; Power et al. 1999). The spectral peak with periods from 10 to 20 years can also be explained by the PDO (Minobe 1997).

Fig. 3
figure 3

a SST time series at (120°W, 0°). b The power spectrum of SST time series shown in a estimated by the FFT analysis. The vertical red line in b denotes the record length of 133 years

Full size image

Because the record length of the monthly SST data used here is 1596, the longest 2-factoral period identified by the FFT algorithm is 2048 months. Since we cannot fully estimate the oscillation with a period of 2048 months by the 1596-month-long record, only the sinusoids with periods no longer than 1024 months are regarded as internal variation and are used in calculating the theoretical threshold according to Eq. (7). In this case, the frequency of the internal variation satisfies \(\omega \ge \frac{2\pi }{L},\) where L equals 1596. The condition of \(\omega \text{L}\gg 2\) required by Eq. (14) thus can be satisfied. The noise effect that denotes the uncertainty of “estimated” trend due to the white noise is estimated by Eq. (10). The variance of the noise term used in Eq. (10) is assumed as the variance of the time series for simplicity.

Figure 4a gives the theoretical threshold for the global SST trend. We can see that the maximum theoretical threshold with the magnitude of 1.75 °C per century is confined to the western boundary regions. Therefore, only when the magnitude of the “estimated” trend in these regions is larger than 1.75 °C per century, its sign is reliable. In the eastern tropical Pacific and the North Pacific, the required theoretical threshold is about 1.0 °C per century. In general, areas with large theoretical threshold are regions with strong decadal (10–30 years) variability, as implicated by Eq. (7). It is noted that the theoretical thresholds required by the North Pacific is comparable with that required by the eastern equatorial Pacific, the region where ENSO dominates. The reason is that there is strong decadal variability in the North Pacific (Fig. 4a), namely, the PDO (Mantua et al. 1997). The theoretical threshold depends on both amplitude and frequency of local internal variation (Eq. 7). While the amplitude of the decadal SST variability in the North Pacific is smaller than that of ENSO in the eastern equatorial Pacific, its lower frequency could let the North Pacific requires a theoretical threshold as large as that for the eastern tropical Pacific.

Fig. 4
figure 4

a The theoretical threshold (color, unit of °C per century) and the decadal (10–30 years) variability (contour, unit of °C) of global SST linear trend. b The ratio of the noise effect and the theoretical threshold. In a, only areas with SST decadal variability larger than 0.5 °C are shown for neat. The black dots in b denote where the ratio is larger than 0.1

Full size image

The ratio of the noise effect and the theoretical threshold is shown in Fig. 4b. It is clear that in most parts of the global ocean, except for the Mediterranean region, the noise effect counts <10% of the uncertainty of “estimated” trend due to internal variation. We thus could neglect the uncertainty due to the noise term at a good approximation. In this case, the uncertainty of “estimated” linear trend in global SST can be measured by the theoretical threshold.

Figure 5 presents the linear trend in global SST from 1881 to 2013. In most parts of the global ocean, the SST exhibits a warming trend. In the eastern equatorial Pacific and North Atlantic, the trend is negative (cooling). However, the magnitudes of SST trend in most parts of these regions (dotted regions) are smaller than the required theoretical threshold shown in Fig. 4a. Therefore, the positive or/and negative “estimated” trends in these regions may depend on the phase of local multi-scale variation, and thus cannot be fully interpreted as the result of the anthropogenic forcing. Only in the western boundary regions, the tropical Indian Ocean, part of the South Atlantic, and the region between the southern Indian Ocean and the Antarctica, the warming trends found can be treated as the underlying long-term change. Note that except the western boundary regions, most of areas with significant warming trend are regions with relatively weak decadal SST variability (Fig. 4a). The strong warming trend over the western boundary regions is argued to be associated with a synchronous poleward shift and/or intensification of global subtropical western boundary currents in conjunction with a systematic change in winds over both hemispheres (Wu et al. 2012). Du and Xie (2008) suggested that the increased surface relative humidity and stability acted to reduce local evaporation and further amplified SST warming in the twentieth century. Details on the formation of the global warming SST pattern can be found in Xie et al. (2010).

Fig. 5
figure 5

The linear trend in global SST (°C per century) from 1881 to 2013. Each black dot denotes where the magnitude of the linear trend is smaller than the theoretical threshold

Full size image

Assuming the “true” linear trends are those “estimated” trends shown in Fig. 5, we can now estimate the critical length required by global SST. By the definition of the critical length (Eq. 9), it is equivalent to estimate how long the record needs to be to ensure that the sign of the known “true” liner trend that would not be incorrectly estimated by the OLS method. Figure 6 shows the critical length required by global SST. Near the western boundary regions, since the magnitude of the trend is large, records of several decades will be adequate to detect its sign. Also in the South Atlantic, tropical Indian Ocean and the Southern Ocean, the required critical lengths are within the length of the available reconstructions (133 years here). However, in the central southern Indian Ocean, the eastern off-equatorial Pacific and a large area of the North Pacific, one needs a record of about 300 years to ensure the sign of the trend. Apparently, this record length is much longer than the length of currently available reconstructions. For the regions such as the eastern equatorial Pacific, the South Pacific near the Antarctica, the central North Pacific and the North Atlantic, the record length needed to exclude the uncertainty due to multi-scale internal variation is more than 1000 years. For example, the “estimated” SST trend near (120°W, 60°S) is about −0.5 °C per century (Fig. 5). If we are to use this “estimated” trend to represent the “true” trend there, our estimation should be based on a 2000-year record (Fig. 6).

Fig. 6
figure 6

The critical length (units: year) of global SST linear trend

Full size image

Above analyses indicate that the sign of the “estimated” trend in most parts of the global SST is sensitive to the time period used, and thus it may not be a robust trend. We now discuss whether global warming in the recent history is a robust positive trend or not. Figure 7a presents the evolution of global-mean SST anomaly. It is clear that the global-mean SST anomaly exhibits strong interannual variation. Also seen is that there were segments with a sharp warming (for example, periods of 1911–1941 and of 1975–2000) and with a weak warming or slowed-down warming (for example, 1900–1910 and 1940–1950), indicating the internal variation of global-mean SST anomaly at the decadal and interdecadal time scales.

Fig. 7
figure 7

a Global-mean SST anomaly. b The range of theoretical threshold (blue line), the noise effect (green) and the “estimated” linear trend (red line) as a function of the starting year. The ending year is fixed at 2013

Full size image

Figure 7b gives the “estimated” trend of global-mean SST anomaly as a function of the staring year. The ending year used to calculate the “estimated” trend is fixed at 2013. The corresponding theoretical threshold and noise effect, which depend on the record length, are also shown. The “estimated” trend in global-mean SST anomaly is negative or close to zero when the staring year is after 1998, known as the global warming hiatus (Trenberth and Fasullo 2013). With increasing record length, the “estimated” trend in global-mean SST anomaly gradually increases and reaches the maximum of 0.93 °C per century when the starting year is around 1974, the beginning of the second sharp increasing segment in global-mean SST anomaly (Fig. 7a). When the starting year is shifted to an earlier year, the “estimated” linear trend becomes stationary with a magnitude of about 0.5 °C per century.

To clarity whether the sign of the “estimated” trend is robust, we need to compare the magnitude of the “estimated” trend with the required theoretical threshold. Note that the noise effect is very small for global-mean SST anomaly. Because of the strong internal variation in global-mean SST anomaly, especially the variation at the interdecadal time scale, the theoretical threshold is very large when the record length is short. For example, when the record length is 40 years, the theoretical threshold is 2.55 °C per century. Because of this, we cannot use the finding that the 40-year (from 1974 to 2013) trend is 0.93 °C per century to argue that the long-term trend in global-mean SST anomaly was warming, just as we cannot use the negative trend of −0.11 °C per century based on another 40-year record (from 1937 to 1976) to argue that the long-term trend in global-mean SST anomaly was cooling.

However, the theoretical threshold sharply decreases with the square of record length. When the starting year is set before 1924, the magnitude of the positive “estimated” trend will be larger than the corresponding theoretical threshold. Therefore, the warming trend in global-mean SST anomaly can be guaranteed only if the record length is longer than 90 years (1924–2013). Otherwise, namely, when the record length is shorter than 90 years, the sign of the resulting estimated trend may depend on the time period used, just as the case study of the opposite trend based on two 40-years records given above.

As another application of the new criterion proposed here, we explore the contribution of multi-scale variation on the recent global warming hiatus, which started from the early 2000s. The linear trend of global-mean SST in the period of 2000–2013 was 0.148 °C per century. On the other hand, the uncertainties associated with internal variation at interannual (roughly 2–10 years), decadal (10–30 years), multi-decadal (30–70 years), and centennial (more than 70 years) time scales are 0.092, 0.072, 0.176, and 0.069 °C per century, respectively. Apparently, the combined uncertainty due to the interannual and decadal variations (0.092 + 0.072 = 0.164) is larger than the magnitude of the recent hiatus. Therefore, variations at the interannual and decadal time scales are large enough to explain the recent hiatus. The leading modes of global SST at the interannual and decadal time scales are ENSO and PDO, respectively. Many recent studies (e.g., Kosaka and Xie 2013) have shown that the cooling SST in the eastern equatorial Pacific, which is closely related to the negative phase of PDO, can lead to the hiatus.

4 Conclusion and discussion

In this study, we first carried out a theoretical analysis of the linear trend derived by the OLS method. It was found that the uncertainty of “estimated” linear trend consists of two terms: one related to multi-scale internal variation, and the other related to noise. A new theoretical threshold was then introduced to scale the uncertainty in the sign of the “estimated” trend due to the influence from multi-scale internal variation. When the amplitude and frequency of the multi-scale internal variation are given, the sign of the “estimated” trend can be determined for the underlying long-term change once its magnitude is greater than the theoretical threshold. Otherwise, the sign of the “estimated” trend may depend on the phase of the internal variation, namely, the underlying long-term trend may depend on the time period used. Comparing with other widely used criteria, we illustrated that, for the time series that is dominated by the oscillatory term, the criterion proposed in this study is more reliable for justifying the uncertainty in the sign of the “estimated” trend.

We then used this new criterion to discuss the uncertainty of the long-term linear trend in global SST from 1881 to 2013. It was found that the “estimated” warming trends in most parts of the global ocean and the “estimated” cooling trends in the eastern equatorial Pacific and North Atlantic may not represent the signs of the actual underlying long-term changes related to the anthropogenic forcing since their magnitudes are smaller than the required theoretical thresholds. Only in the western boundary regions, the tropical Indian Ocean, part of the South Atlantic, and the region between the southern Indian Ocean and the Antarctica, the “estimated” warming trends found using the 133-year record can represent the true underlying long-term change. We also used this criterion to explore the uncertainty of global-mean SST anomaly in the recent history. We concluded that the global warming since 1881 is a robust trend. Moreover, by comparing the magnitude of global-mean SST trend since 2000 and the uncertainty in trend due to oscillations at different time scales, we suggested the variations at the interannual and decadal time scales are large enough to explain the recent global warming hiatus.

The methods proposed in W98 and L08 were designed to detect climate trends. The main difference between W98/L08 and this study resides in the form of the linear trend model. In W98, the de-trended part of a time series is assumed to follow the AR1 process. Although the uncertainty of the resulting trend can be easily estimated, any departure from the AR1 model will cause the method to perform poorly. While L08 method does not require any form of de-trended part of a time series, the difficulty in estimating autocorrelation coefficients at the infinite lag makes it hard to be used in practice. On the other hand, since distinct multi-scale variation does exist in climate variables, the linear trend model used in the current study is probably closer to the reality. The oscillatory information can be assessed by spectral analysis, making it easy to use in practice. In addition, the model used in this study allows us to estimate the contribution of various oscillatory terms to the uncertainty in trend. For example, we can estimate how strong ENSO and PDO will affect SST trend in the eastern equatorial Pacific, respectively. We will address these issues in our future study.

It should be highlighted here that applying this new criterion to the real data needs a good estimation of the oscillatory component in the time series. Although the FFT analysis is widely used, like any available spectral analysis, it has difficulty in fully assessing the oscillatory components with periods near the record length, or longer. As seen in Eq. (7), the theoretical threshold is a linear combination of oscillatory amplitudes. The confidence level of the theoretical threshold is therefore scaled by the bound of oscillatory amplitudes. As a result, a small deviation of the low-frequent oscillatory amplitude could lead to drastic impacts on the resulting trend (e.g., Harrison and Chiodi 2014). While the current study focused on the superiority of the new criterion in scaling the uncertainty in trend over the existing methods, cautions should be placed on applying this criterion to the real data, especially on the estimation of low-frequency oscillatory component in the data.

Also noted here is the assumption of the white noise in the trend model used here. While we assume the autocorrelation in the data can be completely accounted for by the oscillatory term in the model, observed variability not accounted for by the oscillatory term could be red noise or multiplicative noise rather than white noise. Wuncsh (1999) pointed out the serious problem with statistical tests that assume the white noise type behavior when autocorrelation in fact exists. A more sophisticated model should consider, for example, the AR1 process (W98) as the noise term. The uncertainty due to the noise can then be estimated by Eq. (1) in this case. However, it should be kept in mind that no matter what kind of noise is assumed, there will always be uncertainty with the real data.

In this paper, we argued that large uncertainty of the long-term linear trend in global SST exists based on the HadISST1 reconstruction, which is a widely used interpolated archive. However, as pointed out in many studies, different datasets will give controversial estimations of the sign of the linear trend in regional SST (e.g., Karnauskas et al. 2009; Deser et al. 2010; Tokinaga et al. 2012). In addition, it is suggested that the interpolated archives contain large uncertainty owing to the poor data quality and data assimilation schemes in the record before the early twentieth century (Deser et al. 2010). Applying our new criterion to various SST datasets, especially the un-interpolated archives, will undoubtedly provide a better evaluation of the uncertainty of long-term trend in global SST.

Finally, all our analyses are based on the linear regression model. In reality, the long-term global SST change may contain nonlinear components. Some studies suggested that anthropogenic forcing could lead to decadal SST fluctuations from combined effects of different forcing factors (e.g., Meehl et al. 2009; Ting et al. 2009). In such case, the nonlinear analytical tools will be needed (Wu and Huang 2009). However, when carrying out research within the linear framework, it is recommended that one compare the magnitude of the “estimated” linear trend with its theoretical threshold. If the magnitude of the “estimated” trend is smaller than the corresponding theoretical threshold, one should be cautious when interpreting the sign of the “estimated” trend as the sign of the underlying long-term trend in the record used.