Fractional Cross Intersecting Families

Abstract

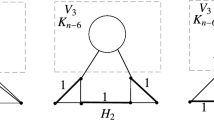
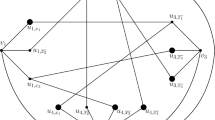
Let $\mathcal {A}=\{A_{1},\ldots ,A_{p}\}$ and $\mathcal {B}=\{B_{1},\ldots ,B_{q}\}$ be two families of subsets of [n] such that for every $i\in [p]$ and $j\in [q]$, $|A_{i}\cap B_{j}|= \frac{c}{d}|B_{j}|$, where $\frac{c}{d}\in [0,1]$ is an irreducible fraction. We call such families $\frac{c}{d}$-cross intersecting families. In this paper, we find a tight upper bound for the product $|\mathcal {A}||\mathcal {B}|$ and characterize the cases when this bound is achieved for $\frac{c}{d}=\frac{1}{2}$. Also, we find a tight upper bound on $|\mathcal {A}||\mathcal {B}|$ when $\mathcal {B}$ is k-uniform and characterize, for all $\frac{c}{d}$, the cases when this bound is achieved.