Fractional Matchings in Graphs from the Spectral Radius

Abstract

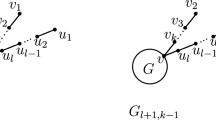
Denote by $\mathcal {G}_{n, \nu ^*}$ $(\mathcal {G}^*_{n,\nu ^*})$ the collection of all (connected) graphs of order n having a fractional matching number $\nu ^*$. This paper characterizes the graphs in $\mathcal {G}_{n,\nu ^*}$ and $\mathcal {G}^*_{n,\nu ^*}$ with the maximum spectral radius, and establishes a lower bound for the spectral radius of graphs of order n to guarantee that their fractional matching numbers are at least $\tau +\frac{1}{2}$. In addition, we explore the relationship between the spectral radius, perfect matching and fractional perfect matching of G. Moreover, we present a spectral condition guaranteeing that the matching number of a graph is at least $k+1$, which generalizes some previous known results.