Smooth estimation of the area under the ROC curve in multistage ranked set sampling

Abstract

The receiver operating characteristic (ROC) curve is an important tool for assessing the discrimination power of a continuous biomarker. The area under the ROC curve is a well-known index for effectiveness of the biomarker. This article deals with estimating the aforesaid measure under a rank-based sampling design called multistage ranked set sampling. A nonparametric estimator using kernel density estimation is developed, and some theoretical results about it are established. Simulation studies show that the proposed estimator can be substantially more efficient than its alternative in simple random sampling. The methodology is illustrated with data from the National Health and Nutrition Examination Survey.

Appendices

Appendix A

Proof of Proposition 2

The identity (5) is a simple application of Proposition 1. So the proof is not detailed here. It is easy to show that

$$\begin{aligned} m^2 n^2 E( \hat{A}^2 )=\alpha _1+\alpha _2+\alpha _3+\alpha _4, \end{aligned}$$

(9)

where

$$\begin{aligned} \alpha _1= & {} E \left\{ \sum _{i \ne i'=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{X_i-Y_j}{t}\right) \Phi \left( \frac{X_{i'}-Y_{j'}}{t}\right) \right\} \nonumber \\= & {} m(m-1)n(n-1) E^2\left\{ \Phi \left( \frac{X-Y}{t}\right) \right\} , \end{aligned}$$

(10)

$$\begin{aligned} \alpha _2= & {} E \left\{ \sum _{i=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{X_i-Y_j}{t}\right) \Phi \left( \frac{X_i-Y_{j'}}{t}\right) \right\} \nonumber \\= & {} m n(n-1) E E^2\Bigg \{ \Phi \left( \frac{X-Y}{t}\right) \Big |X \Bigg \}, \end{aligned}$$

(11)

$$\begin{aligned} \alpha _3= & {} E \left\{ \sum _{j=1}^n \sum _{i \ne i'=1}^m \Phi \left( \frac{X_i-Y_j}{t}\right) \Phi \left( \frac{X_{i'}-Y_j}{t}\right) \right\} \nonumber \\= & {} n m(m-1) E E^2\Bigg \{ \Phi \left( \frac{X-Y}{t}\right) \Big |Y \Bigg \}, \end{aligned}$$

(12)

and

$$\begin{aligned} \alpha _4= E \left\{ \sum _{i=1}^m \sum _{j=1}^n \Phi ^2\left( \frac{X_i-Y_j}{t}\right) \right\} =m n E\left\{ \Phi ^2\left( \frac{X-Y}{t}\right) \right\} . \end{aligned}$$

(13)

Combining (9)–(13) with the expectation of $\hat{A}$, we arrive at (6). Similarly,

$$\begin{aligned} m^2 n^2 E( \hat{A}_{r,s}^2 )=\beta _1+\beta _2+\beta _3, \end{aligned}$$

(14)

where

$$\begin{aligned} \beta _1= & {} E \left\{ \sum _{i \ne i'=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Phi \left( \frac{X_{i'}^{(r)}-Y_{j'}^{(s)}}{t}\right) \right. \nonumber \\&\left. +\, \sum _{j=1}^n \sum _{i \ne i'=1}^m \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Phi \left( \frac{X_{i'}^{(r)}-Y_{j}^{(s)}}{t}\right) \right\} \nonumber \\= & {} E\left( \sum _{i \ne i'=1}^m \sum _{j \ne j'=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} E\Bigg \{ \Phi \left( \frac{X_{i'}^{(r)}-Y_{j'}^{(s)}}{t}\right) \Big | Y_{j'}^{(s)} \Bigg \} \right. \nonumber \\&\left. +\, \sum _{j=1}^n \sum _{i \ne i'=1}^m E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big |Y_{j}^{(s)} \Bigg \} E \Bigg \{ \Phi \left( \frac{X_{i'}^{(r)}-Y_{j}^{(s)}}{t}\right) \Big |Y_{j}^{(s)} \Bigg \} \right) \nonumber \\= & {} E\left( \left[ \sum _{i=1}^m \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right] ^2-\sum _{i=1}^m \sum _{j=1}^n E^2 \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right. \nonumber \\&\left. -\, \sum _{i=1}^m \sum _{j \ne j'=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} E\Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j'}^{(s)}}{t}\right) \Big | Y_{j'}^{(s)} \Bigg \} \right) \nonumber \\= & {} E\left( \left[ \sum _{i=1}^m \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right] ^2 -\sum _{i=1}^m \Bigg [ \sum _{j=1}^n E^2 \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right. \nonumber \\&\left. +\, \sum _{j \ne j'=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} E\Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j'}^{(s)}}{t}\right) \Big | Y_{j'}^{(s)} \Bigg \} \Bigg ] \right) \nonumber \\= & {} E\left( m^2 \left[ \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right] ^2-\sum _{i=1}^m \left[ \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right] ^2 \right) , \end{aligned}$$

(15)

$$\begin{aligned} \beta _2= & {} E \left\{ \sum _{i=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Phi \left( \frac{X_i^{(r)}-Y_{j'}^{(s)}}{t}\right) \right\} \nonumber \\= & {} m E \left\{ \sum _{j \ne j'=1}^n \Phi \left( \frac{X-Y_{j}^{(s)}}{t}\right) \Phi \left( \frac{X-Y_{j'}^{(s)}}{t}\right) \right\} \nonumber \\= & {} m E \left( \sum _{j \ne j'=1}^n E \Bigg \{ \Phi \left( \frac{X-Y_{j}^{(s)}}{t}\right) \Big | X \Bigg \} E \Bigg \{ \Phi \left( \frac{X-Y_{j'}^{(s)}}{t}\right) \Big | X \Bigg \} \right) \nonumber \\= & {} m E \left( \left[ \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X-Y_{j}^{(s)}}{t}\right) \Big | X \Bigg \} \right] ^2 -\sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_{j}^{(s)}}{t} \right) \Big | X \Bigg \} \right) \nonumber \\= & {} m E \left( n^2 E^2 \Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Big | X \Bigg \} -\sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_{j}^{(s)}}{t}\right) \Big | X \Bigg \} \right) , \end{aligned}$$

(16)

and

$$\begin{aligned} \beta _3=E \Bigg \{ \sum _{i=1}^m \sum _{j=1}^n \Phi ^2\left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Bigg \}=m n E\Bigg \{ \Phi ^2\left( \frac{X-Y}{t}\right) \Bigg \}. \end{aligned}$$

(17)

Now, equation (7) is concluded from (14)–(17) and the expectation of $\hat{A}_{r,s}$. $\square$

Proof of Proposition 3

Using equations (6) and (7), one can write

$$\begin{aligned} m^2n^2 \Big [ Var(\hat{A})-Var(\hat{A}_{r,s}) \Big ]=\gamma _1+\gamma _2+\gamma _3, \end{aligned}$$

(18)

where

$$\begin{aligned} \gamma _1= & {} E\left( \sum _{i=1}^m \left[ \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right] ^2 -m \left[ \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X-Y_{j}^{(s)}}{t}\right) \Big | Y_{j}^{(s)} \Bigg \} \right] ^2 \right) \nonumber \\= & {} E\left( \sum _{i=1}^m \left[ \sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t}\right) \Big | Y_j^{(s)} \Bigg \}-\sum _{j=1}^n E \Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t}\right) \Big | Y_j^{(s)} \Bigg \} \right] ^2 \right) , \end{aligned}$$

(19)

$$\begin{aligned} \gamma _2= & {} m n(n-1) E E^2\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Big |X \Bigg \} \nonumber \\&-\,\, m E \Bigg ( n^2 E^2\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Big |X \Bigg \} -\sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Big |X \Bigg \} \Bigg ) \nonumber \\= & {} m E \Bigg ( \sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Big |X \Bigg \}-n E^2\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Big |X \Bigg \} \Bigg )\nonumber \\= & {} m E \Bigg ( \sum _{j=1}^n \left[ E\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Big |X \Bigg \}-E\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Big |X \Bigg \} \right] ^2 \Bigg ), \end{aligned}$$

(20)

and

$$\begin{aligned} \gamma _3= & {} m(m-1)n(n-1) E^2\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Bigg \}+nm(m-1)E E^2\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Big |Y \Bigg \} \nonumber \\&-\,\, m(m-1)E\left( \left[ \sum _{j=1}^n E\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Big |Y_j^{(s)} \Bigg \} \right] ^2 \right) \nonumber \\= & {} m(m-1) \left[ n(n-1) E^2\Bigg \{ \Phi \left( \frac{X-Y}{t} \right) \Bigg \}\right. \nonumber \\&\left. +\,\, E\left( \sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Big |Y_j^{(s)} \Bigg \}-\left[ \sum _{j=1}^n E\left\{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Big |Y_j^{(s)} \right\} \right] ^2 \right) \right] \nonumber \\= & {} m(m-1) \left[ \left( 1-\frac{1}{n}\right) \left( \sum _{j=1}^n E\left\{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \right\} \right) ^2\right. \nonumber \\&\left. -\, \sum _{j \ne j'=1}^n E\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Bigg \} E\Bigg \{ \Phi \left( \frac{X-Y_{j'}^{(s)}}{t} \right) \Bigg \} \right] \nonumber \\= & {} m(m-1) \left[ \sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \Bigg \}-\frac{1}{n} \left( \sum _{j=1}^n E\left\{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) \right\} \right) ^2 \right] \nonumber \\= & {} m (m-1) \sum _{j=1}^n E^2\Bigg \{ \Phi \left( \frac{X-Y_j^{(s)}}{t} \right) -\Phi \left( \frac{X-Y}{t} \right) \Bigg \}. \end{aligned}$$

(21)

The result holds as $\gamma _i$’s are obviously non-negative. $\square$

Proof of Proposition 4

It is enough to show that $Var(\hat{A}_{r,s}) \le Var(\hat{A}_{r-1,s})$ and $Var(\hat{A}_{r,s}) \le Var(\hat{A}_{r,s-1})$. From the expressions of $\beta _i$’s in the Proof of Proposition 2, it can be seen that

$$\begin{aligned} m^2 n^2 E( \hat{A}_{r,s}^2 )= & {} E \left\{ \sum _{i \ne i'=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_{i'}^{(r)}-Y_{j'}^{(s)}}{t} \right) \right. \nonumber \\&+\, \sum _{i=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_i^{(r)}-Y_{j'}^{(s)}}{t} \right) \nonumber \\&+\, \sum _{j=1}^n \sum _{i \ne i'=1}^m \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_{i'}^{(r)}-Y_j^{(s)}}{t} \right) \nonumber \\&\left. +\, \sum _{i=1}^m \sum _{j=1}^n \Phi ^2\left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \right\} . \end{aligned}$$

(22)

We now present some equalities and inequalities which are helpful in proving the desired result. Let $W_{(i)}^{(r-1)}$ be the ith order statistic of an $(r-1)$th stage ranked set sample of size m from f. Then, we have

$$\begin{aligned}&E \left\{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_{i'}^{(r)}-Y_{j'}^{(s)}}{t} \right) \right\} \nonumber \\&\quad = E\Bigg ( E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_{i'}^{(r)}-Y_{j'}^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \}\Bigg ) \nonumber \\&\quad = E \Bigg ( E\Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \} \nonumber \\&\qquad \times \,\, E\Bigg \{ \Phi \left( \frac{X_{i'}^{(r)}-Y_{j'}^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \} \Bigg ) \nonumber \\&\quad = E \Bigg ( E\Bigg \{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \} \nonumber \\&\qquad \times \,\, E\Bigg \{ \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \} \Bigg ) \nonumber \\&\quad \le E\left( E\left\{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \right\} \right) \nonumber \\&\quad = E\left\{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \right\} , \end{aligned}$$

(23)

where the inequality holds because any pair of order statistics in a sample have positive covariance (see Lehmann 1966, for example).

Proceeding in a similar way, we get

$$\begin{aligned}&E \left\{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_{i'}^{(r)}-Y_j^{(s)}}{t} \right) \right\} \nonumber \\&\quad = E\Bigg ( E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_{i'}^{(r)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \}\Bigg ) \nonumber \\&\quad = E\Bigg ( E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \} \nonumber \\&\qquad \times \,\, E \Bigg \{ \Phi \left( \frac{X_{i'}^{(r)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \} \Bigg ) \nonumber \\&\quad = E\Bigg ( E \Bigg \{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \} \nonumber \\&\qquad \times \,\, E \Bigg \{ \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \} \Bigg ) \nonumber \\&\quad \le E\Bigg ( E \Bigg \{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \}\Bigg ) \nonumber \\&\quad = E \Bigg \{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_j^{(s)}}{t} \right) \Bigg \}. \end{aligned}$$

(24)

Finally, a conditioning argument yields

$$\begin{aligned}&E \left\{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_i^{(r)}-Y_{j'}^{(s)}}{t} \right) \right\} \nonumber \\&\quad = E\Bigg ( E \Bigg \{ \Phi \left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{X_i^{(r)}-Y_{j'}^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \}\Bigg ) \nonumber \\&\quad = E\Bigg ( E \Bigg \{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \Big | Y_j^{(s)},Y_{j'}^{(s)} \Bigg \}\Bigg ) \nonumber \\&\quad = E \Bigg \{ \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \Bigg \}, \end{aligned}$$

(25)

and

$$\begin{aligned} E \Bigg \{ \Phi ^2\left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Bigg \}= & {} E\Bigg ( E \Bigg \{ \Phi ^2\left( \frac{X_i^{(r)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \}\Bigg ) \nonumber \\= & {} E\Bigg ( E \Bigg \{ \Phi ^2\left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Big | Y_j^{(s)} \Bigg \}\Bigg ) \nonumber \\= & {} E \Bigg \{ \Phi ^2\left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Bigg \}. \end{aligned}$$

(26)

Combining (22)–(26), it follows that

$$\begin{aligned} m^2 n^2 E( \hat{A}_{r,s}^2 )\le & {} E \Bigg \{ \sum _{i \ne i'=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \nonumber \\&+\, \sum _{i=1}^m \sum _{j \ne j'=1}^n \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_{j'}^{(s)}}{t} \right) \nonumber \\&+\, \sum _{j=1}^n \sum _{i \ne i'=1}^m \Phi \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Phi \left( \frac{W_{(i')}^{(r-1)}-Y_j^{(s)}}{t} \right) \nonumber \\&+\, \sum _{i=1}^m \sum _{j=1}^n \Phi ^2 \left( \frac{W_{(i)}^{(r-1)}-Y_j^{(s)}}{t} \right) \Bigg \} \nonumber \\= & {} m^2 n^2 E( \hat{A}_{r-1,s}^2 ). \end{aligned}$$

(27)

This is to say that $Var(\hat{A}_{r,s}) \le Var(\hat{A}_{r-1,s})$ because the expectation of $\hat{A}_{r,s}$ is fixed for any $r,s\ge 1$. The second part is proved similarly. $\square$

Appendix B

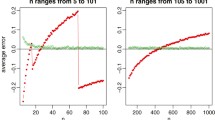
See Figs. 1, 2, 3, 4, 5, 6, 7, 8 and 9.

Fig. 1

Estimated values of RE1 for $m=n=3$ and $\rho _1=\rho _2=1$, when the parent distribution is normal. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 2

Estimated values of RE1 for $m=n=5$ and $\rho _1=\rho _2=1$, when the parent distribution is normal. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 3

Estimated values of RE1 for $m=n=3$ and $\rho _1=\rho _2=1$, when the parent distribution is exponential. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 4

Estimated values of RE1 for $m=n=5$ and $\rho _1=\rho _2=1$, when the parent distribution is exponential. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 5

Estimated values of RE2 for $m=n=3$ and $\rho _1=\rho _2=1$, when the parent distribution is normal. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 6

Estimated values of RE2 for $m=n=5$ and $\rho _1=\rho _2=1$, when the parent distribution is normal. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 7

Estimated values of RE2 for $m=n=3$ and $\rho _1=\rho _2=1$, when the parent distribution is exponential. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 8

Estimated values of RE2 for $m=n=5$ and $\rho _1=\rho _2=1$, when the parent distribution is exponential. Black/solid, blue/dashed, red/dotted, and orange/dotdash curves relate to $r=s=1,2,3,4$, respectively. (Color figure online)

Fig. 9

Estimated values of RE1 and RE2 from the NHANES data using NR and BCV methods. Black/solid, and blue/dashed curves relate to $m=n=3,5$, respectively. (Color figure online)