Abstract
Abreu and Sen (J Econ Theory 50(2):285–299, 1990) provide a necessary condition, called Condition \(\alpha \), which is almost sufficient for a social choice rule to be implementable via subgame perfect equilibria. Yet, it is not straightforward to check the satisfaction of Condition \(\alpha \). We contribute in this direction by establishing a nuanced picture over the subgame perfect implementability of compromise rules, as a function of the compromise threshold. This contrasts with scoring rules that all fail to be subgame perfect implementable and with several Condorcet rules which are subgame perfect implementable.
Similar content being viewed by others
Notes
A social choice rule f is subgame perfect implementable if there exists an extensive form mechanism \(\Gamma \) such that the set of subgame perfect equilibrium outcomes of \(\Gamma \) coincides with the outcome of f for any possible preference profile. As we do not use the definition throughout the paper, we do not give a formal expression, which can be found in Abreu and Sen (1990).
We show, nevertheless, in Sect. 3 that plurality with a runoff is not subgame perfect implementable over the full domain of linear orders.
When singleton-valuedness is imposed, only dictatorial social choice rules are Maskin monotonic (Muller and Satterthwaite 1977). When singleton-valuedness is relaxed and indifferences in individual preferences are ruled out, scoring rules (Erdem and Sanver 2005), Condorcet consistent social choice rules (Jackson 2001; Özkal-Sanver and Sanver 2010) and the majoritarian compromise (Sertel and Yılmaz 1999) fail Maskin monotonicity. When indifferences in individual preferences are allowed, no Pareto optimal social choice rule is Maskin monotonic (Aşan and Sanver 2006).
This negative result covers the plurality rule which we already know from our Proposition 2 on scoring rules.
As we consider SCRs with full range, the definition we adopt is simpler than the original one in Abreu and Sen (1990) which involves the range of the SCR.
With just three alternatives, the case in which we will focus, the class of all scoring rules can be expressed by the family of score vectors (1, \( \lambda ,\) 0) with \(\lambda \in \left[ 0,1\right] \). Note that (1, 0, 0) is the plurality rule, (1, \(\frac{1}{2},\) 0) is the Borda rule and (1, 1, 0) is the antiplurality rule. We write s(x, P) for the score of alternative x at profile P, that is the sum of the scores that x gets from each of the voters. The scoring rule declares as winners the alternatives with the highest score.
The existence of such an n can be seen by observing that the inequality \( \lambda n+1<\) \(\frac{n}{2-\lambda }\) is equivalent to \(\frac{2-\lambda }{ (1-\lambda )^{2}}<n\).
Under plurality with a runoff, each voter announces a ranking of alternatives. The two alternatives with a highest plurality score go to the runoff, the rest of alternatives being removed. In the runoff, the majority winner among the two remaining alternatives is selected, where the majority winner is computed using the initial preference profile. Ties are broken lexicographically according to some linear order.
Under STV, each voter submits a preference ordering over the alternatives. The score of each alternative equals the number of voters who rank that alternative first. STV removes the alternatives with the lowest score and computes the new scores in the preference profile without the removed alternatives and continues until one alternative gets a majority.
This stronger condition requires the same antecedent but a stronger consequence \(f(P)=f(P^{\prime })\) instead of \(f(P)\subseteq f(P^{\prime })\)
This in turn implies that any such \(f_{q}\) fails to be Nash implementable, since Conditions \(\alpha \) is weaker than Maskin monotonicity.
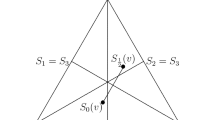
This exemplifies a class of SCRs which are subgame perfect implementable but not Nash implementable, as \(f_{q}\) fails Maskin monotonicity when \(q\ge \frac{n}{2}\). This can be seen through Figure ?? where any \(f_{q}\) with \(q\ge \frac{n}{2}\) picks all three alternatives at profile P and only c at profile \(P^{\prime }\).
If \(r^{*}(P)=1\), \(n(x,1,P^{\prime })\ge n(x,1,P)\ge q\) so that \(x\in f(P)\). This implies that \(n(x,1,P^{\prime })\ge q\) and hence \(x\in f(P^{\prime })\), a contradiction. Thus \(r^{*}(P)\ne 1\). We deduce \( r^{*}(P)\ne 1\) from Brams and Kilgour (2001).
Otherwise, for every \(i\in N\) with \(r(x,P_{i})\in \{2,\ldots ,r^{*}(P)\}\) , we have \(i\notin {\tilde{N}}\), thus \(r(x,P_{i}^{\prime })=1\). Moreover, being in Case B, we have \(r(x,P_{i}^{\prime })=1\) for every \(i\in N\) with \( r(x,P_{i})=1\) as well. Since \(n(x,r^{*}(P),P)\ge q\), it follows that \( n(x,1,P^{\prime })\ge q\) implying \(x\in f(P^{\prime })\), contradicting \( x\in f(P){\setminus } f(P^{\prime })\).
If \(r(b^{\prime },P_{i})\le r^{*}(P)\) for all \(i\in N\), then we proceed to Case B.II.2.
If \(r(y,P_{h^{\prime }}^{\prime })=1\). then we proceed to Case B.II.1.ii.
FB stands for “Fallback Bargaining” which Brams and Kilgour (2001) suggest as a bargaining solution in an environment where agents confront a finite set of alternatives. FB appears in the literature under different names, such as “Rawlsian arbitration rule” in Sprumont (1993), “Kant-Rawls social compromise” in Hurwicz and Sertel (1999) and “unanimity compromise” in Kıbrıs and Sertel (2007).
The only analysis we know in this direction is Vartiainen (2006) which is an incomplete working paper. We thank Hannu Vartiainen for generously providing us with his work.
Interestingly, the set monotonicity condition which ensures the subgame perfect implementability of Condorcet consistent rules has been shown to ensure the Nash implementability of SCRs via set-valued normal form mechanisms in the environments of Bochet and Maniquet (2010) and Özkal-Sanver and Sanver (2006). Moreover, Brandt (2015) shows that a slightly stronger version of that condition, together with particular assumptions on how voters extend their preferences over sets, ensures strategy-proofness of set valued SCRs.
As Merlin et al. (2019) discuss, compromise rules are not Condorcet consistent, nor they can be qualified as scoring rules, although they can be expressed in terms of elementary scoring rules which vary as a function of the preference profile.
Anbarci (2006) does not derive general subgame perfect implementability results, but suggests simple extensive form mechanisms which implements fallback barganing. His analysis inspires a question of interest within the voting context: Our positive results are based on the rather complicated canonical mechanism of Abreu and Sen (1990) which implements any SCR which satisfies the sufficient conditions of subgame perfect implementability. Is there simple mechanisms, specific to each of the SCRs we show to be subgame perfect implementable, which implement the SCR in question? As another analysis in this direction, we have Suh and Wen (2008) who consider matching problems and without deriving general subgame perfect implementability results, suggest a simple extensive form mechanism which implements a given matching solutions under (rather strong) domain restriction assumptions.
Dominance solvable voting schemes are also related to our analysis. As argued by Dutta and Sen (1993), ”a social choice function that can be implemented via backward induction can also be implemented via sophisticated equilibrium”. However, implementability via sophisticated equilibrium and subgame perfect implementability are logically independent.
References
Abreu D, Sen A (1990) Subgame perfect implementation: a necessary and almost sufficient condition. J Econ Theory 50(2):285–299
Anbarci N (2006) Finite alternating-move arbitration schemes and the equal area solution. Theor Decis 61:21–50
Aşan G, Sanver MR (2006) Maskin monotonic aggregation rules. Econ Lett 91(2):179–183
Banks JS (1985) Sophisticated voting outcomes and agenda control. Soc Choice Wel 1(4):295–306
Bassett GW, Persky J (1999) Robust voting. Public Choice 99(3):299–310
Bochet O, Maniquet F (2010) Virtual Nash implementation with admissible support. J Math Econ 46(1):99–108
Brams SJ, Kilgour DM (2001) Fallback bargaining. Group Decis Negot 10(4):287–316
Brandt F (2015) Set-monotonicity implies Kelly-strategy proofness. Soc Choice Welf 45(4):793–804
Congar R, Merlin V (2012) A characterization of the maximin rule in the context of voting. Theor Decis 72(1):131–147
Dutta B (1990) On the tournament equilibrium set. Soc Choice Welf 7(4):381–383
Dutta B, Sen A (1993) Implementing generalized Condorcet social choice functions via backward induction. Soc Choice Welf 10(2):149–160
Erdem O, Sanver MR (2005) Minimal monotonic extensions of scoring rules. Soc Choice Welf 25(1):31–42
Herrero MJ, Srivastava S (1992) Implementation via backward induction. J Econ Theory 56(1):70–88
Horan S (2013) Implementation of majority voting rules. mimeo, Universite de Montréal
Hurwicz L, Sertel MR (1999) Designing mechanisms, in particular for electoral systems: the majoritarian compromise. In: Sertel Murat R (ed) Economic design and behaviour. MacMillan, London
Jackson MO (2001) A crash course in implementation theory. Soc Choice Welf 18(4):655–708
Kıbrıs O, Sertel MR (2007) Bargaining over a finite set of alternatives. Soc Choice Welf 28:421–437
Laffond G, Laslier J-F, Le Breton M (1993) The bipartisan set of a tournament game. Games Econ Behav 5(1):182–201
Laslier JF (1997) Tournament solutions and majority voting. Springer, Berlin
Maskin E (1999) Nash equilibrium and welfare optimality. Rev Econ Stud 66:23–38
Merlin V, Özkal-Sanver I, Sanver MR (2019) Compromise rules revisited. Group Decis Negoc 28:63–78
Moore J, Repullo R (1988) Subgame perfect implementation. Econometrica 56(5):1191–1220
Moulin H (1986) Choosing from a tournament. Soc Choice Welf 3(4):271–291
Muller E, Satterthwaite MA (1977) The equivalence of strong positive association and strategy-proofness. J Econ Theory 14(2):412–418
Nurmi H (1999) Voting paradoxes and how to deal with them. Springer, Berlin
Özkal-Sanver I, Sanver MR (2006) Nash implementation via hyperfunctions. Soc Choice Welf 26(3):607–623
Özkal-Sanver I, Sanver MR (2010) A new monotonicity condition for tournament solutions. Theor Decis 69(3):439–452
Sen A (1987) Two essays in the theory of implementation. PhD thesis, Princeton University
Sertel MR, Yılmaz B (1999) The majoritarian compromise is majoritarian-optimal and subgame-perfect implementable. Soc Choice Welf 16(4):615–627
Smith J (1973) Aggregation of preferences with a variable electorate. Econometrica 41:1027–1041
Sprumont Y (1993) Intermediate preferences and rawlsian arbitration rules. Soc Choice Welf 10:1–15
Suh SC, Wen Q (2008) Subgame perfect implementation of stable matchings in marriage problems. Soc Choice Welf 31(1):163–174
Vartiainen H (2006) A necessary and sufficient condition for two person subgame perfect implementability. mimeo
Vartiainen H (2007a) Subgame perfect implementation: a full characterization. J Econ Theory 133(1):111–126
Vartiainen H (2007b) Subgame perfect implementation of voting rules via randomized mechanisms. Soc Choice Welf 29(3):353–367
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Arunava Sen and Hannu Vartiainen for very fruitful exchanges and two anonymous reviewers for very useful comments. This project has been supported by the ANR-14-CE24-0007-01 (CoCoRICoCoDEC) and the project IDEX ANR-10-IDEX-0001-02 PSL MIFID.
Appendix A: Proof of Lemma A
Appendix A: Proof of Lemma A
By definition, there is some \(i\in {\tilde{N}}\) with \(r(x,P_i)\in \{2, \ldots ,r^*(P)\}\) and some \(h\in N\) with \(r(b,P_h)\in \{r^*(P)+1,\ldots \}\). Thus, \(r(x,P_i)<r(b,P_h)\).
In the sequel of the proof, we write
Observe that \(L(x,P_i)=\{x\} \cup \{a_1,\ldots ,a_{m-r(x,P_i)}\}\) and \( X{\setminus } L(b,P_h)=\{b_1,\ldots ,b_{r(b,P_h)-1}\}\) with \(s<t\) \( \Longrightarrow \) \(a_s P_i a_t\) and \(b_s P_h b_t\). The proof is now divided in two cases: if \(x\in L(x,P_i)\cap (X{\setminus } L(b,P_h))\) and otherwise.
Case 1: Consider first the case where \(x\in L(x,P_i)\cap (X{\setminus } L(b,P_h))\). We will show that \(L(x,P_i)\cap (X{\setminus } L(b,P_h))\ne \{x\}\).
By definition, \(|X{\setminus } L(b,P_h)|=r(b,P_h)-1\). Yet, since \(x\in L(x,P_i)\cap (X{\setminus } L(b,P_h))\) and \(b\not \in X{\setminus } L(b,P_h)\), there are \(r(b,P_h)-2\) different alternatives in \(X{\setminus } L(b,P_h)\) different from b and x. Similarly \(|L(x,P_i)|=m-r(x,P_i)+1\) jointly with \(x\in L(x,P_i)\cap (X{\setminus } L(b,P_h))\) and \(b\not \in X{\setminus } L(b,P_h)\) implies that there are \(m-r(x,P_i)\) different alternatives in \(L(x,P_i)\) different from b and x. However \( m-r(x,P_i)+r(b,P_h)-2=m+(r(b,P_h)-r(x,P_i))-2\ge m-1\) since \( r(x,P_i)<r(b,P_h)\). However, there cannot be \(m-1\) alternatives different from b and x in X. Therefore, there is at least one alternative in common between \(L(x,P_i){\setminus }\{b,x\}\) and \((X{\setminus } L(b,P_h)){\setminus } \{b,x\}\), concluding case 1.
Case 2: Consider now the case that \(x\not \in L(x,P_i)\cap (X{\setminus } L(b,P_h)\).
There are again \(m-r(x,P_{i})\) different alternatives in \(L(x,P_{i})\) which are different from b and x. As \(x\not \in X{\setminus } L(b,P_{h})\), there are now \(r(b,P_{h})\) different alternatives in \(X{\setminus } L(b,P_{h})\) different from b and x. As \(r(x,P_{i})<r(b,P_{h})\), we have \( (m-r(x,P_{i}))+(r(b,P_{h}))>m\) but there cannot be m alternatives different from b and x. Thus \(|L(x,P_{i})\cap (X{\setminus } L(b,P_{h}))|\) \( \ge 2\), as wanted, concluding the proof.
Rights and permissions
About this article
Cite this article
Núñez, M., Sanver, M.R. On the subgame perfect implementability of voting rules. Soc Choice Welf 56, 421–441 (2021). https://doi.org/10.1007/s00355-020-01293-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-020-01293-9