A lightweight convolutional neural network to reconstruct deformation in BOS recordings

Abstract

We introduce a Convolutional Neural Network (CNN) that is specifically designed and trained to post-process recordings obtained by Background Oriented Schlieren (BOS), a popular technique to visualize compressible and convective flows. To reconstruct BOS image deformation, we devised a lightweight network (LIMA) that has comparatively fewer parameters to train than the CNNs that have been previously proposed for optical flow. To train LIMA, we introduce a novel strategy based on the generation of synthetic images from random-irrotational deformation fields, which are intended to mimic those provided by real BOS recordings. This allows us to generate a large number of training examples at minimal computational cost. To assess the accuracy of the reconstructed displacements, we consider test cases consisting of synthetic images with sinusoidal displacement as well as images obtained in the experimental studies of a hot plume in air and a flow past and inside a heated hollow hemisphere. By comparing the reconstructed deformation fields using the LIMA or conventional post-processing techniques used in Direct Image Correlation (DIC) or conventional image cross-correlation, we show that LIMA is more accurate and robust in the synthetic test case. When applied to experimental BOS recordings, all methods provide similar and consistent deformation fields. As LIMA is capable of achieving a comparable or better accuracy at a fraction of the computational costs, it represents a valuable alternative to conventional post-processing techniques for BOS experiments.

1 Introduction

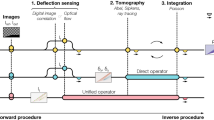
Similar to Schlieren photography, shadowgraphy or interferometry, Background Oriented Schlieren (BOS) Meier (2002) is a density visualization technique that relies on the variation of the optical properties linked to the fluid density. The observed fluid volume is positioned in front of a background pattern and a digital camera records the distortion of the image induced by compressibility or thermal effects. The analysis of the image pair consisting of a reference, undisturbed image and the experiment recording allows the observation of fluid density variations and their motion with time. Typically, the information is reconstructed from the image pairs by means of cross-correlation techniques similar to those employed for Particle Image Velocimetry (PIV) (Raffael et al. 2018) or Digital Image Correlation (DIC) (Vendroux and Knauss 1998; Lu and Cary 2000). A comprehensive review of BOS techniques can be found in Raffel (2015).

Convolutional Neural Network (CNN) architectures have been proposed for optical motion analysis (Dosovitskiy et al. 2015; Hui et al. 2018; Teed and Deng 2020), and more recently for PIV (Rabault et al. 2017; Cai et al. 2019, 2020, 2019; Lee et al. 2017; Yu et al. 2021; Lagemann et al. 2021; Carlier 2005; Gao et al. 2021; Yu et al. 2021; Manickathan et al. 2022; Yu et al. 2022), as an alternative to conventional two-dimensional (2D) image cross-correlation (such as state-of-the-art Window Deformation Iterative Multigrid, WIDIM Scarano and Riethmuller (2000); Schrijer and Scarano (2008); Raffael et al. (2018)). CNNs require very large training sets due to the complexity of the network-parameter space that may include up to millions of free trainable variables. In general, training sets are obtained from numerical solutions of the governing flow equations for particular problems Cai et al. (2019, 2020); Lee et al. (2017), and remain rather limited in size, expensive to generate, and prone to biases. In case of application to BOS recordings, the generation of synthetic datasets to train CNNs is computationally even more challenging as it entails the solution of the ray equations for the specific geometric optics (Grauer et al. 2018), in addition to the numerical solution of complex flow problems.

To overcome these difficulties, we propose a Lightweight Image Matching Architecture (LIMA) for Background Oriented Schlieren (BOS), similar to the one that we have introduced and tested for PIV (Mucignat et al. 2022). Thanks to a considerably leaner architecture, the network has significantly fewer parameters than existing CNNs and may be deployed on a camera with embedded GPU device to enable robust visualization of environmental flows in real-time on low-cost devices. Also, we propose to train the network on a dataset generated by random and random-irrotational deformation fields of a synthetic background pattern, adapting the strategy that we have used to enlarge the training sets for PIV data Manickathan et al. (2022). This allows us to enforce that the deformation fields used for the training process are irrotational (which is an important property of BOS recordings for which we provide a simple proof in Sect. 1), hence, to inform the network about an important characteristic of underlying physical process (physics informed networks are receiving growing attention, see, e.g., Molnar and Grauer (2022); Cai et al. (2021)). As the image deformation fields used to generate the training dataset are obtained through a simple algebraic technique, the generation of a large number of training examples is straightforward and computationally inexpensive.

In this work, we first assess the performance of LIMA for a synthetic BOS case obtained from a 2D sinusoidal image-deformation field; then, we demonstrate the applicability to real experimental recordings by employing LIMA to process experimental BOS images of a hot air plume and of a heated hemispherical cavity exposed to a cross flow in a water tunnel. In all test cases, the results of LIMA are compared with those obtained by state-of-the-art cross correlation methods and by an in house implementation of DIC.

2 The lightweight Image matching architecture (LIMA)

As existing CNNs for optical flow estimation entail a large number of parameters which may require large computational resources, we design a lightweight architecture that has a twofold advantage: it requires smaller training sets, reducing the risk of overfitting, and fewer operations to reconstruct the deformation field, possibly enabling the installation of LIMA on GPU embedded devices for real-time BOS visualization. LIMA is derived from PWCIRRHur and Roth (2019), a version of PWCNet (Sun et al. 2017) that employs the Iterative Residual Refinement (IRR) and has been already used for PIV Manickathan et al. (2022).

Here, the network is made symmetric with respect to the BOS-images pair, and the number of iterative levels is decreased to reduce the dimension of the network parameter space. LIMA has considerably fewer trainable parameters than other CNNs previously proposed for optical flow. Indeed, it has only 1.6 million parameters, as against the 3.6 million of PWCIRRHur and Roth (2019), 5.3 million of RAFTTeed and Deng (2020), 5.37 million of LiteFlowNetHui et al. (2018), 38 million of FlowNetSDosovitskiy et al. (2015)), and 162.5 million of ttFlowNet2Ilg et al. (2017).

2.1 Network architecture

In BOS measurements, a reference background recording, $I_0$, is first acquired at uniform fluid-density conditions (in some cases, it is convenient to define the reference image as the average, or moving average, of multiple images acquired during a time interval at steady-state conditions). When the density varies due to thermal (or compressibility) effects, the fluid acts similarly to a lens and the background Schlieren recording at time t, $I_t$, appears deformed with respect to the reference. Then, the deformation field, $\textrm{d}\varvec{s}$ (expressed in pixels, px) is estimated as

$$\begin{aligned} \textrm{d}\varvec{s} = \mathcal {N}(\textbf{I}), \end{aligned}$$

(1)

where $\mathcal {N}$ represents the CNN operation on the pair of BOS image intensities, $\textbf{I}=(I_0, I_t)^\top$. Since the background typically consists in a dotted pattern, the deformation field is also referred to as the displacement field, because in case of small deformation the dots appear simply displaced with respect to their position in the reference recording.

Fig. 1

LIMA: Lightweight image matching architecture

LIMA infers the deformation using the iterative residual refinement strategy (Hur and Roth 2019), which iteratively corrects and upsamples the deformation at the l-th refinement steps (Fig. 1). First, the multilevel encoder subnetwork, $\mathcal {E}$, constructs the l-level feature map for each image pair,

$$\begin{aligned}&\textbf{F}_0 = \varvec{\mathcal {E}}(I_0), \end{aligned}$$

(2)

$$\begin{aligned}&\textbf{F}_t = \varvec{\mathcal {E}}(I_t), \end{aligned}$$

(3)

where $\textbf{F}_0 = (F_0^1, F_0^2,..., F_0^L)^{\top }$ and $\textbf{F}_t = (F_t^1, F_t^2,..., F_t^L)^{\top }$ are multi-level pyramid feature maps of the image $I_0$ and $I_t$, respectively, so that ${F}_0^l = \mathcal {E}^l(I_0)$ and ${F}_t^l = \mathcal {E}^l(I_t)$ for each $l=1,2,...,L$. At each refinement step l, the encoded feature from the level l is used to infer the deformation with level-specific image resolution. The feature map of image i of level l is then warped using the estimate from the previous level, $l-1$,

$$\begin{aligned} \tilde{F}_i^l = \mathcal {W}\left( F_i^l, \hat{\textrm{d}\varvec{s}}^{l-1}\right) , \end{aligned}$$

(4)

where $\hat{\textrm{d}\varvec{s}}^{l-1}$ is the two-time, i.e., $2\times$, up-sampling of the estimate from the previous level, $\textrm{d}\varvec{s}^{l-1}$, and is constructed to match the resolution of $F_i^l$. Notice that $\mathcal {W}$ is a non-trainable operator which simply warps the feature map by the deformation map using a bi-linear interpolation. As warping is symmetric with respect to $I_0$ and $I_t$, we obtain a central difference image matching which is second-order accurate, as proposed by Wereley and Meinhart Wereley and Meinhart (2001) for classic processing of PIV recordings.

Next, the cost-volume subnetwork, $\mathcal {C}$, construct the cost volume,

$$\begin{aligned} C^l = \mathcal {C}\left( \hat{F}_0^l, \hat{F}_t^l\right) , \end{aligned}$$

(5)

which quantifies the degree of matching between the two warped feature maps at level l. Finally, we correct and refine the deformation estimate for the current level l applying a lightweight decoder subnetwork, $\mathcal {D}$, to the cost volume of level l and to the (upsampled) estimate of the deformation from the previous level $l-1$, i.e.,

$$\begin{aligned} \textrm{d}\varvec{s}^l = \hat{\textrm{d}\varvec{s}}^{l-1} + \mathcal {D}\left( C^l, \hat{\textrm{d}\varvec{s}}^{l-1}\right) . \end{aligned}$$

(6)

As the network architecture is iterative, the final resolution of the output data is determined by the number of of levels. Employing a first layer with kernel of size $64 \times 64$ pixels and reducing the kernel by a factor of $2\times 2$ at each level, a four-level LIMA, for instance, reconstructs an output vector each $4 \times 4$ pixels of the original image. Here, we use a network with two additional levels (hence, a six-level LIMA) to achieve a pixel-level reconstruction of the deformation field. Note that, regardless to the number of iteration levels, the number of trainable parameters remains the same due to the weight-sharing design of the iterative residual refinement architecture (Hur and Roth 2019), hence the GPU memory requirements does not depend on the number of levels. Nevertheless, changing the number of levels requires the network to be retrained. LIMA is implemented using the machine learning library PyTorch (Paszke et al. 2019).

2.2 Random and random-irrotational deformation fields

Fig. 2

Example of a 2D random field from left to right: stream-tracers and distribution of the magnitude of deformation, $|\textrm{d}\varvec{s}_{\textrm{ref}}|$, distribution of the curl component perpendicular to the plane, $(\nabla \times \textrm{d}\varvec{s}_{\textrm{ref}})_z$, and distribution of the divergence, $\nabla \cdot \textrm{d}\varvec{s}_{\textrm{ref}}$

Fig. 3

Example of a random-irrotational field: stream-tracers and distribution of $|\textrm{d}\varvec{s}_{\textrm{ref}}|$, distribution of the curl component perpendicular to the plane, $(\nabla \times \textrm{d}\varvec{s}_{\textrm{ref}})_z$, and distribution of the divergence, $\nabla \cdot \textrm{d}\varvec{s}_{\textrm{ref}}$. Note that the divergence field is same as the pure random one in Fig. 2 but the curl is zero

We consider two different ways to obtain the inexpensive deformation fields that are used to generate the synthetic BOS images for the training set. The first training set employs random deformation fields similar to the random displacement fields used in the kinematic training previously proposed in (Manickathan et al. 2022). This strategy has proven beneficial to construct training sets that achieve state-of-the-art accuracy in PIV-image processing (Manickathan et al. 2022). Each component, $\textrm{d}{s}_{i\in \{x,y\}}$, is obtained independently: first, a scalar random field is sampled from a uniform distribution, $\mathcal {U}(-1,1)$; then, it is passed through a Gaussian filter of size $\sigma$ to introduce a finite correlation length; finally, each component is rescaled to obtain a reference field with a given maximum value. Figure 2 shows an example of such a random field with nonzero curl and divergence. To increase the variability of the deformation fields and enrich the information contained in the training set, both the filter size and the maximum values of each realization are sampled from a uniform distribution, i.e., $\sigma \sim \mathcal {U}[\sigma _{\text {min}},\sigma _{\text {max}}]$ and $\text {max}(ds_\textrm{ref}) \sim \mathcal {U}[{s_\text {min}},s_{\text {max}}]$, respectively.

According to Helmholtz decomposition, any vector field can be described as the sum of an irrotational (curl-free) and a solenoidal (divergence-free) component,

$$\begin{aligned} \textrm{d}\varvec{s} = {-\nabla \phi } + {\nabla \times \varvec{\psi }}, \end{aligned}$$

(7)

where $\phi$ and $\varvec{\psi }$ are the (scalar) potential and the vector potential, respectively. In contrast to BOS recordings which are characterized by an irrotational deformation (see Appendix 1 for a simple proof), random fields, obtained following the procedure to generate the kinematic training dataset (we refer to Manickathan et al. (2022) further details), have nonzero curl. We therefore introduce a second training set that employs irrotational fields to generate the synthetic BOS images.

To define a random-irrotational deformation we could generate a random scalar field, f, and solve Poisson equation, $\nabla ^2 \phi = f$, to obtain the scalar potential and the irrotational deformation $\textrm{d}\varvec{s}=-\nabla \phi$. To avoid the high computational costs due to the presence of the Laplace operator, we directly generate a random potential field, $\phi =f$, and obtain the irrotational deformation as $\textrm{d}\varvec{s}=-\nabla \phi =-\nabla f$. Figure 3 shows an example of a random field with zero curl and nonzero divergence. Notice that if the same random field is used, this computationally inexpensive method leads to less smoother fields than the solution of the Poisson problem, which involves a double integration of the generated random scalar field, possibly leading to more fluctuations in the dataset.

The random potential field is generated following an approach analogous to the generation of each component of the random displacement field (Manickathan et al. 2022): first, a random field is sampled from a uniform distribution, $\mathcal {U}(-1,1)$; then, the spatially uncorrelated random field is passed through a spatial Gaussian filter; and finally, the gradient is calculated and rescaled to obtain a reference field with a certain maximum value. Also for the random-irrotational fields the filter size and the maximum deformation value of each individual realization are sampled from uniform deformation.

2.3 Generation of the synthetic BOS images from the deformation fields

Once a deformation field is obtained, we generate the pairs of images using a Synthetic Image Generator (SIG). First, we create the reference image, $I_0$, by populating the image domain with reference dots. The dot positions are obtained by means of Poisson sampling, conditional on the dot diameter D and the minimum spacing between dots s. Then, to obtain the deformed image, $I_t$, we apply a warping step to $I_0$ according to the reference deformation field. This image manipulation step employs a SINC-8 interpolation scheme to minimize the errors in sampling the original intensity field (Astarita 2007; Armellini et al. 2012).

For each example in the training set, we vary the reference dot properties $D$ and s as reported in Table 1. We remark that the scale factor and the filter size of the deformation field have a uniform random distribution, while for a given dot diameter there is a realizable number of dots, conditional on the minimum allowed dot distance s. We model the effects of image noise by defining a signal-to-noise ratio as the ratio of the image maximum intensity to the variance of a 2D Gaussian distribution $I_{max}/\xi _{\sigma }$. For each image, we sample this distribution and add the resulting scalar field to the images.

2.4 Training strategy and multilevel loss function

LIMA is trained by a supervised learning strategy: the synthetic particle image pairs, $\textbf{I}$, (Sect. 2.3) are the input, whereas the random or random-irrotational fields used to generate the image pairs are the ground truth. The training process seeks the set of network parameters that minimizes the loss function,

$$\begin{aligned} \mathcal {L} = \sum _{l=1}^{L} \lambda ^l \left( \lambda _u |\textrm{d}\varvec{s} - \textrm{d}\varvec{s}_{\textrm{ref}}|+ \lambda _J |\textbf{J}|\right) , \end{aligned}$$

(8)

where the sum is taken over all levels; $\textrm{d}\varvec{s}_{\textrm{ref}}$ is the reference ground-truth deformation: $\textrm{d}\varvec{s}$ the estimated deformation; $\textbf{J}$ is the Jacobian of the estimated deformation; $\lambda ^l$ are the loss weights that control the influence of the estimation at a given level as in Manickathan et al. (2022) (here we use $\lambda ^1 = 0.0025$, $\lambda ^2=0.005$, $\lambda ^3=0.01$, $\lambda ^4=0.02$, $\lambda ^5=0.08$, and $\lambda ^6=0.32$); $\lambda _u$ and $\lambda _J$ are the trade-off weights of deformation and Jacobian, respectively. In this work we use $\lambda _u=1$ and $\lambda _J = 0.1$, notice that the second term of the loss function penalizes fields with large deformation gradients.

Both the random and the random-irrotational training sets comprise 20,000 examples. In Table 1, we report the parameters of the uniform distributions from which we sample the parameters for image generation. We remark that image parameters such as dot size, minimum dot distance, and exposure level are the same for both data sets.

Table 1 Range of properties and parameters used to generate the random deformation field and the synthetic BOS images used to produce the training set

The network is trained for 300 epochs on an Nvidia RTX 3090 TI, which requires approximately 48 h for 20,000 training examples. We note that 20% of the training examples, hence 4,000, are used as validation set. The training uses the Adam optimizer with $\beta _1 = 0.9$, $\beta _2 = 0.999$, a mini-batch size of 4, and an initial learning rate equal to $1 \times 10^{-4}$, which is reduced during the training by means of a ReduceLRonPlateau scheme with a decay rate of 1/5. To improve the generalization of the network, the training set is augmented by means of random translation, scaling, rotation, reflection, brightness change, as in previous studies (Manickathan et al. 2022; Cai et al. 2019, 2020).

3 PIV and DIC processing

In addition to the reconstruction error, calculated for a synthetic data using the reference deformation field or by image matching (Sciacchitano et al. 2013), we also compare the deformation fields reconstructed by LIMA with those obtained by two established methods for image post-processing, namely PIV, employing image cross-correlation with the WIDIM scheme (Scarano 2001), and DIC.

In case of WIDIM, we choose an initial grid of $16\times 16$ pixels, then refined to $8\times 8$, with 2 passes at $50\%$ overlap. Vector validation is performed based on a peak-ratio criterion and a Normalized Median Filter (NMF) with a kernel of $5\times 5$ pixels. Finally, an isotropic denoising step is applied as proposed by Wieneke (2017). The images are processed with a state-of-the-art commercial software package (Davis 10, LaVision).

On the same image dataset, we also apply DIC with a window size of $12\times 12$ pixels and $75\%$ overlap, which allows us to achieve the same final resolution as WIDIM. The processing is performed by means of an in-house code based on Vendroux and Knauss (1998) to which we added the possibility of forcing the reconstruction of an affine transformation, which is also irrotational, by imposing symmetry of the mapping matrix. The remaining transformation coefficients are then obtained by least-squares minimization. The code employs a spline interpolation scheme to manipulate the image intensity field in order to achieve the highest accuracy.

4 Results

To compare the performance of a six-level LIMA, which provides pixel-level resolution, we consider three test cases: (i) a synthetic dataset that has not been used for training; (ii) an heat-driven plume in air; and (iii) a mixed convection experiment performed in a water tunnel, in which, a bottom-heated hemisphere is exposed to a cross flow. For the synthetic test case the ground truth, represented by the reference deformation field used to generate the BOS images, is available and we can readily calculate the reconstruction error. Since no ground truth is available for the experimental test cases, we evaluate the estimates obtained by the different methods by performing an uncertainty assessment by means of image matching (Sciacchitano et al. 2013) as suggested in (Rajendran 2020).

LIMA is compared with the state-of-the-art commercial software for cross-correlation analysis based on WIDIM (Davis 10, LaVision) and with our in-house implementation of the Digital Image Correlation method. Hereafter, we use the subscripts rnd (resp. irr) to indicate the results obtained with LIMA trained with random (resp. random-irrotational) datasets (see Table 1), hence, we write $\textrm{d}\varvec{s}_\mathtt{{rnd}}$ (resp. $\textrm{d}\varvec{s}_\mathtt{{irr}}$) for the estimated deformation fields. Similarly, we use the subscripts cc and dic to indicate the deformation fields obtained by image cross correlation (using the WIDIM scheme and including anisotropic de-noising), hence we write $\textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$, respectively.

4.1 Runtime assessment

Before assessing the accuracy of the estimated deformation fields, we evaluate the runtime of LIMA and compare it with the performance of PWCIRR and WIDIM. Both networks are deployed on the same GPU hardware, consisting of a Nvidia RTX 2080 Ti, whereas WIDIM is GPU-accelerated and has a final resolution of 24x24 (px), 50 % overlap, and an-isotropic de-noising.

We consider different image sizes, ranging from $128\times 128$ to $2048\times 2048$ pixels, as reported in Table 2. For each size we generate 100 image pairs and report the average inference time for PWCIRR, LIMA, and WIDIM. Note that the maximum image size that can be processed by the CNN depends on the number of network parameters and on the available GPU memory. Above a certain limit, the images have to be split into sub-images and processed separately with an obvious increase in computational cost and runtime, resulting from the additional memory transfers. In our case, the maximum image size that can be handled by PWCIRR without splitting is as small as $800 \times 800$ pixels, while LIMA, can process images up to a resolution of $2048 \times 2048$ pixels (4  Mpx), without resorting to image splitting. For an image size of $512\times 512$ pixels, LIMA is 1.4 times faster than PWCIRR, while, for larger image sizes, i.e., $2048\times 2048$ pixels, LIMA has an inference runtime of 1.17 s, which yields a speed up of 4.5 times compared to PWCIRR. Indeed, once image splitting is required, the run-time of PWCIRR and LIMA grows with $N^2$.

If we compare LIMA with WIDIM, the network is always faster as long as no image splitting is required. The computational advantage tends to decrease when the image size increases, and reduces from roughly 4 times for an image of $1024 \times 1024$ pixels to 2.5 times for an image of $2048 \times 2048$ pixels. For an image of $4096 \times 4096$ pixels, which requires image splitting, LIMA has slightly longer runtime than WIDIM. Note that the results reported in Table 2 have been obtained with a python implementation of PWCIRR and LIMA, whereas for WIDIM we used a commercial, compiled package. Preliminary tests with a compiled version of LIMA showed that it is possible to reduce the runtime at least by a factor of 1.5 compared to the python version.

Table 2 Runtime for different image sizes processed with PWCIRR, LIMA, and a commercial GPU implementation of WIDIM with a final grid size of 24x24 px at 50% overlap

4.2 A synthetic case study with sinusoidal deformation

We assess the accuracy of the methods by applying LIMA to synthetic BOS images obtained from sinusoidal deformation fields, i.e.,

$$\begin{aligned} \textrm{d}\varvec{s}_{\textrm{ref}} = A \begin{bmatrix} \sin \left( \frac{2\pi x}{T}\right) \\ \cos \left( \frac{2\pi y}{T}\right) \end{bmatrix}, \end{aligned}$$

(9)

where T (px) is the spatial modulation period, and the amplitude A (px) dictates the maximum magnitude of the field.

Table 3 Range and random deformation field settings and image properties used for test dataset generation

A set of $N=4,000$ image pairs is generated by varying the maximum deformation, the modulation period, and the image parameters (dot diameter, minimum relative distance, exposure level, and signal-to-noise ratio) according to the values given in Table 3. First, the images are preprocessed by applying a sliding minimum subtraction with a kernel size of $16\times 16$ pixels and a local normalization on a kernel of $64\times 64$ pixels; then, all four methods are used to reconstruct the deformation field from each pair of images. For each reconstructed field, we calculate the spatial average of the magnitude of the reconstruction error,

$$\begin{aligned} \epsilon (\textrm{d}\varvec{s})=\overline{|\textrm{d}\varvec{s}-\textrm{d}\varvec{s}_{\textrm{ref}}|}, \end{aligned}$$

(10)

where $\textrm{d}\varvec{s}$ refers to the deformation field estimated by the different methods (i.e., to $\textrm{d}\varvec{s}_\mathtt{{irr}}, \textrm{d}\varvec{s}_\mathtt{{rnd}},\textrm{d}\varvec{s}_\mathtt{{cc}}$, or $\textrm{d}\varvec{s}_\mathtt{{dic}}$) and the bar denotes the spatial averaging. Notice that the spatial average is calculated excluding an outer shell of thickness 24 px in order to remove boundary artifacts that may affect cc and dic.

Fig. 4

Scatter plots of the error of the reconstructed deformation fields. a The spatial average of the errors with respect to the reference, $\epsilon =\overline{|\textrm{d}\varvec{s}-\textrm{d}\varvec{s}_{\textrm{ref}}|}$, of the reconstructed fields $\textrm{d}\varvec{s}_\mathtt{{rnd}}, \textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ are plotted against the average error of $\textrm{d}\varvec{s}_\mathtt{{irr}}$; b the standard deviation of the errors, $\sigma$, of the reconstructed fields $\textrm{d}\varvec{s}_\mathtt{{rnd}}, \textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ are plotted against the standard deviation of the error of $\textrm{d}\varvec{s}_\mathtt{{irr}}$; c the mean, calculated over all the 4,000 samples, of the spatial average of the error is plotted against its standard deviation for all reconstructed fields

In Fig. 4a we plot the spatial average errors of $\textrm{d}\varvec{s}_\mathtt{{rnd}}$, $\textrm{d}\varvec{s}_\mathtt{{dic}}{}$, and $\textrm{d}\varvec{s}_\mathtt{{cc}}$ against the spatial average error of $\textrm{d}\varvec{s}_\mathtt{{irr}}{}$. Points that lay above the bisector of the scatter plot correspond to image pairs for which we obtain smaller reconstruction errors with LIMA trained on the random-irrational dataset than with the other methods. By comparison between the point clouds it is possible to rank the relative accuracy of the other methods. In general, the error associated to $\textrm{d}\varvec{s}_\mathtt{{irr}}$ is lower than the one of the other three methods for the large majority of the samples in the dataset. For instance, only 2% of the image pairs show lower error when processed with CC instead of $\textrm{d}\varvec{s}_\mathtt{{irr}}{}$, while for no image pair a lower error is achieved by means of DIC. On the other end, by using LIMA trained on the random dataset we achieve a better accuracy than with an random-irrotational dataset for about 14% of the samples, mostly characterized by small reconstruction error ($\epsilon < 0.02$ px) for both methods.

In Fig. 4b we compare the standard deviation of the error, $\sigma$, by presenting the scatter plot of $\sigma$ for the reconstructed fields $\textrm{d}\varvec{s}_\mathtt{{rnd}}$, $\textrm{d}\varvec{s}_\mathtt{{dic}}{}$, and $\textrm{d}\varvec{s}_\mathtt{{cc}}$ against $\sigma$ for $\textrm{d}\varvec{s}_\mathtt{{irr}}{}$. Again, LIMA trained on the random-irrotational dataset allows the lowest $\sigma$ values for the majority of the image pairs. In particular, only for 1.5% of the image pairs we obtain a lower variance by processing the data with CC while DIC has yields always to larger errors. At the same time, for about 12% of the image pairs $\sigma$ is lower if LIMA is trained on the random dataset rather than on the random-irrotational dataset.

To compare the statistical robustness of the methods, we calculate the mean error, and its standard deviation, over all the 4’000 image pairs in the synthetic dataset. Recalling that the concept of accuracy (ISO 1994) is based on trueness (i.e., low mean error) and precision (i.e., low variance of the error), in Fig. 4c we plot the mean errors as a function of the standard deviation, i.e., the square root of the variance, for all methods. We observe that LIMA trained on the random-irrotational dataset achieves the highest accuracy, having both the lowest mean error and standard deviation. If compared with CC, LIMA allows a reduction in the mean error (trueness) from 0.061 px to 0.023 px and of the standard deviation from 0.027 px to 0.018 px, if the random-irrotational fields are used for the kinematic training. In contrast, employing the random dataset for the kinematic training of LIMA increases the mean error to 0.031 px and the standard deviation to 0.03 px. When comparing CC (with denoising) with DIC we can observe that the latter is less effective, probably because we employ a code that employs a single pass evaluation. This requires adapting the window size to the specific image parameters (dot size, spacing, mean displacement value), limiting the dynamic range of the reconstructed data.

Fig. 5

Scatter plots of the divergence errors of the reconstructed fields: a The spatial average of the divergence errors with respect to the reference, $\epsilon _{div}=\overline{|\nabla \cdot \textrm{d}\varvec{s}- \nabla \cdot \textrm{d}\varvec{s}_{\textrm{ref}}|}$, of the reconstructed fields $\textrm{d}\varvec{s}_\mathtt{{rnd}},\textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ are plotted against the average divergence error of $\textrm{d}\varvec{s}_\mathtt{{irr}}$; b the standard deviation of the divergence errors, $\sigma _{div}$, of the reconstructed fields $\textrm{d}\varvec{s}_\mathtt{{rnd}},\textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ are plotted against the standard deviation of the diverge error of $\textrm{d}\varvec{s}_\mathtt{{irr}}$; c the mean, calculated over the 4,000 samples, of the spatial average of the divergence error is plotted against its standard deviation for all reconstructed fields

Finally, we consider the spatial average of the error on the reconstructed divergence,

$$\begin{aligned} \epsilon _\textrm{div}(\textrm{d}\varvec{s}) = \overline{|\nabla \cdot \textrm{d}\varvec{s}- \nabla \cdot \textrm{d}\varvec{s}_{\textrm{ref}}|}, \end{aligned}$$

(11)

where again $\textrm{d}\varvec{s}$ refers to the field estimated by the different methods (i.e., to $\textrm{d}\varvec{s}_\mathtt{{irr}}, \textrm{d}\varvec{s}_\mathtt{{rnd}},\textrm{d}\varvec{s}_\mathtt{{cc}}$, or $\textrm{d}\varvec{s}_\mathtt{{dic}}$) and $\textrm{d}\varvec{s}_\textrm{ref}$ is the ground truth. Analogously to the spatial average error, we plot $\epsilon _\textrm{div}(\textrm{d}\varvec{s}_\texttt{rnd})$, $\epsilon _\textrm{div}(\textrm{d}\varvec{s}_\texttt{dic})$, and $\epsilon _\textrm{div}(\textrm{d}\varvec{s}_\textrm{cc})$ against $\epsilon _\textrm{div}(\textrm{d}\varvec{s}_\texttt{irr})$ in Fig. 5a, and the scatter plot of the respective standard deviations is shown in Fig. 5b. As for the average reconstruction error, the fields reconstructed by LIMA trained on the random-irrotational dataset, i.e., $\textrm{d}\varvec{s}_\mathtt{{irr}}$, exhibits the highest trueness (lowest average error) and the highest precision (lowest standard deviation) for the majority of the image pairs in the dataset. This is also confirmed by the plot of the mean divergence errors a function of the standard deviation on the divergence (Fig. 5c), which shows a 36% and 33% reduction in the mean divergence error and its standard deviation, respectively, if LIMA trained on the random-irrotational dataset is used instead of CC.

4.3 Experimental study of a hot-plate thermal plume

To assess the performance of the different methods when applied to experimental image pairs, we first employ BOS to measure the evolution of a thermal plume generated by a square hot plate of 3 cm. The background pattern consists of printed dots with a size of 0.7 mm and an average dot-to-dot distance of 0.3 mm. The pattern is placed 53 cm behind the hot plate and the camera 60 cm in front of it (Fig. 6).

Fig. 6

Left: experimental setup of hot plate thermal plume BOS experiment. Right: example of one BOS recording, showing the deformation of the reference dot pattern

The deformation of the background pattern is imaged at 30 Hz by a Raytrix C42 camera with a resolution of 1920$\times$1080 pixels (8 bits) and a 35 mm lens (f/8) with an exposure time of 30 ms. The resulting dot images have a diameter of about 6 px (Fig. 6). After recording the reference image of the background pattern, the plate temperature is set to $250^{\circ }$C.

Fig. 7

Hot-plate thermal plume; 2D distribution of the magnitude of the deformation fields ($\textrm{d}\varvec{s}_\mathtt{{irr}},\textrm{d}\varvec{s}_\mathtt{{rnd}}, \textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$) reconstructed from one of the BOS recordings at a hot-plate temperature of $250 ^\circ C$

Fig. 8

Hot-plate thermal plume: 2D distribution of the disparity error of $\textrm{d}\varvec{s}_\mathtt{{irr}}$,$\textrm{d}\varvec{s}_\mathtt{{rnd}}$, $\textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ in Fig. 7

The maps in Fig. 7 depict the distribution of $\textrm{d}\varvec{s}_\mathtt{{irr}}$, $\textrm{d}\varvec{s}_\mathtt{{rnd}}$, $\textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ for one of the BOS recordings of the thermal plume. All methods consistently reconstruct the image deformation induced by the temperature fluctuations of buoyant flow with no outlier or artifact. However, $\textrm{d}\varvec{s}_\mathtt{{irr}}{}$, $\textrm{d}\varvec{s}_\mathtt{{rnd}}{}$, and $\textrm{d}\varvec{s}_\mathtt{{cc}}{}$ are much smoother than $\textrm{d}\varvec{s}_\mathtt{{dic}}{}$ to which no denoising is applied and which exhibits salt-and-pepper noise. We also note that the mean of the deformation (averaged over 100 recordings, not shown here for the sake of brevity) reconstructed by the different methods is very similar.

To quantify the uncertainty of the reconstructed fields, we calculate the disparity error, $\epsilon _{d}$, according to Sciacchitano et al. (2013). In Fig. 8, we plot the 2D distributions of the disparity error corresponding to the deformations $\textrm{d}\varvec{s}_\mathtt{{irr}}$,$\textrm{d}\varvec{s}_\mathtt{{rnd}}$, $\textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ in Fig. 7. In general, all methods perform well and $\epsilon _d$ remains always below 0.04 px, except at the edges of the hot plate. LIMA achieves higher accuracy when trained on the random-irrational dataset than when trained on the random dataset; both training datasets allow LIMA to perform better than cross correlation and DIC, in particular in the hot-plume region, where they allow a higher fidelity reconstruction of the flow features. Even far from the hot plate conventional reconstruction methods exhibits larger disparity error (in the order of 0.02$-$0.03 px) in presence of convective structures, whereas the disparity error of LIMA remains in general below 0.01 px.

For all methods we calculate the spatial average of the disparity error, $\overline{\epsilon _d}$, and the standard deviation, $\sigma _d=\left[ {\overline{(\epsilon _d(x)-\overline{\epsilon _d})^2}}\right] ^{1/2}$, in the region depicted by the box in each of the panels in Fig. 7 for 100 BOS recordings. The average disparity is plotted versus its standard deviation in Fig. 9, and the average over the 100 recordings are reported in Table 4. We observe that, as for the synthetic test case, LIMA achieves a higher accuracy than conventional methods, with an error reduction of about 12–17% if the network is trained on the random-irrotational dataset.

Fig. 9

Hot-plate thermal plume. Scatter plot of disparity error $\overline{\epsilon _{d}}$ vs standard deviation, $\sigma _d$, averaged in the region depicted by the dashed-line box in Fig. 7 for all reconstruction methods

Fig. 10

Left: the heated hemisphere in the refractive index-matching (RIM) water tunnel of the Swiss Federal Laboratories for Materials Science and Technology. Right: detail of the reference image close to the edge of the dome. Due to an imperfect refractive index matching and the strong curvature of the FEP layer the dots appear as streaks

4.4 Experimental study of flow past and inside a heated hollow hemisphere

In the second experimental test case, we perform BOS measurements performed in the Refractive Index Matching (RIM) water tunnel of the Swiss Federal Laboratories for Materials Science and Technology. We study the flow past and inside a heated hollow hemisphere, manufactured by thermoforming a Fluorinated Ethylene Propylene (FEP) sheet, in which we place a 5 cm circular heater from Minco (HM6970) (Fig. 10a). A detailed description of the setup can be found in Shah et al. (2023).

The reference background is affixed on one side of the transparent test section, in contact with the plexiglass of the RIM tunnel, and a high-power LED lamp is used to illuminate the BOS target from the back, while a PCO edge 5.5 is used to record the images with a resolution of $2560 \times 2160$ pixels at a frame rate of 20 Hz. To match the refractive index of FEP ($n_\textrm{FEP}=1.3385$), glycerol is added to the water in small increments until the mismatch between the reference BOS images of the target with and without the FEP dome is minimized at a solution temperature of $20 ^{\circ } C$. This is achieved with by adding $5\%$ of glycerol by wt. Due to the strong curvature of the dome and to an imperfect refractive index matching caused by temperature changes, strong distortions of the reference pattern are observed in correspondence with the dome upper boundary, where dots are heavily stretched and appear as streaks (see Fig. 10b).

The experiment is performed at a bulk speed of the water-glycerol mixture of 0.02 m/s, while the temperature of the plate is set to $40 ^{\circ }$C, resulting in a Reynolds number $\mathrm Re=1,000$ and a Richardson number $\mathrm Ri=5.64$ (the dome diameter, $d=5$ cm, is used as characteristic length). As reference image of the background we use the average of 1,000 recordings at test conditions in order to eliminate small background drifts. For all methods we apply the same image pre-processing, which consists of sliding minimum subtraction and normalization with $16 \times 16$ pixels and $64 \times 64$ pixels kernel size, respectively.

Fig. 11

Heated hemisphere: 2D distribution of the magnitude of the deformation fields ($\textrm{d}\varvec{s}_\mathtt{{irr}},\textrm{d}\varvec{s}_\mathtt{{rnd}}, \textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$) reconstructed from a BOS recording at $\mathrm Re = 1,000$ and $\mathrm Ri = 5.64$

Fig. 12

Heated hemisphere: 2D distribution of the residual disparity error $\epsilon _{d}$ calculated for the deformation fields in Fig. 11 ($\textrm{d}\varvec{s}_\mathtt{{irr}},\textrm{d}\varvec{s}_\mathtt{{rnd}}, \textrm{d}\varvec{s}_\mathtt{{cc}}$ and $\textrm{d}\varvec{s}_\mathtt{{dic}}$)

Fig. 13

Heated hemisphere: scatter plot of area averaged disparity error $\overline{\epsilon _{d}}$ vs standard deviation in the region indicated with a dashed line in Fig. 11: left inside the dome, right in the shear layer

Figure 11 shows the 2D distribution of the deformation fields $\textrm{d}\varvec{s}_\mathtt{{irr}}$, $\textrm{d}\varvec{s}_\mathtt{{rnd}}$, $\textrm{d}\varvec{s}_\mathtt{{cc}}$, and $\textrm{d}\varvec{s}_\mathtt{{dic}}$ reconstructed from one of the BOS recordings. All methods are able to reconstruct the convection structures that characterize the buoyant flow. Again, $\textrm{d}\varvec{s}_\mathtt{{dic}}{}$ is affected by salt-and-pepper noise, while the distributions of $\textrm{d}\varvec{s}_\mathtt{{irr}}$, $\textrm{d}\varvec{s}_\mathtt{{rnd}}$, and $\textrm{d}\varvec{s}_\mathtt{{cc}}$ appear very similar (with $\textrm{d}\varvec{s}_\mathtt{{rnd}}$ being slightly less smooth than the other two). Notice that we do not mask the region of the image close to the top of the dome, where the reference dots are heavily distorted. Nevertheless, $\textrm{d}\varvec{s}_\mathtt{{irr}}$ and $\textrm{d}\varvec{s}_\mathtt{{rnd}}$ depict realistic convection structures, suggesting that LIMA trained on datasets containing images of dot-patterns are robust also when applied to estimate deformations from images in which different patterns are used. As for the conventional methods, CC, to which denoising is applied, is also able to reconstruct realistic structures even if the reconstructed fields is less smooth and coarser than $\textrm{d}\varvec{s}_\mathtt{{irr}}$ or $\textrm{d}\varvec{s}_\mathtt{{rnd}}$. On the contrary, DICis strongly affected by salt-and-pepper noise, and it is unable to converge in the vicinity of the top boundary of the hemisphere (the white region in Fig. 11d); also close to the circular heater placed at the bottom, $\textrm{d}\varvec{s}_\mathtt{{dic}}$ exhibits unrealistic and noisy structures.

Also for this test case, we calculate the disparity error ( Sciacchitano et al. (2013)) of the deformations reconstructed from 200 BOS recordings by all four methods. The 2D distributions of the disparity errors corresponding to the deformation fields in Fig. 11 are shown in Fig. 12. The error patterns are similar, with higher disparity in the vicinity of the circular heater plate and close to the top of the dome for all methods. Notice that these regions are characterized by large distortions of the background patters (Fig. 10b), in which dots are not visible, appear as streaks, or are not clearly separated; these conditions do not allow a reliable estimate of the measurement uncertainty, because a small residual mismatch between images of dots is assume to calculate the disparity error, and it is difficult to assess the quality of the reconstructed fields by the disparity error.

To quantitatively compare the performance of the different methods, we calculate the spatial average of the disparity errors, together with their standard deviations, in two sub-regions in which the background reference image is not heavily distorted: one is located in the dome and the other at the shear layer separating form the hemisphere (both sub-regions are highlighted in Fig. 11). The spatial average of the disparity error is rather similar for all methods and fluctuates depending on the specific definition of the sub-regions. In Fig. 13, we plot the spatial average of the disparity errors versus their standard deviations for all methods in the two sub-regions depicted by the box in Fig. 11), whereas the average over the 200 BOS recordings considered are reported in Table 4. In the dome sub-region, the disparity error is up to one order of magnitude higher than in the hot-plate test case. In general, the errors are very similar for all methods, although the scatter plot suggests that CCexhibits consistently higher disparity errors, and that the deformations reconstructed by LIMA are slightly less uncertain, in particular in the shear layer region. We remark, however, that the a-posteriori image matching may not provide a sufficiently reliable estimate of the reconstruction error, because of the difficulty in clearly identifying the intensity peaks of the dot when they are not sufficiently separated in the recorded image. Further investigations that employ different background patters would be probably necessary to clearly assess the relative accuracy of the methods for this flow configuration.

Table 4 Spatial average of the disparity error, $\langle \overline{\epsilon _d}\rangle$, and standard deviation, ${\langle \sigma _d\rangle }$, of all reconstruction methods for the two experimental test cases. For the hot-plate test case the two quantities are the spatial average in the box depicted in Fig. 7 and averaged over 100 recordings; for the heated hollow hemisphere test case we calculate the spatial average in two regions (in the dome and in the shear layer, both depicted in Fig. 11) and we average over 200 recordings

5 Conclusions

By modifying the architecture and the loss function, and by appropriately choosing the training datasets, Convolutional Neural Networks can be adapted to better post-process specific optical-flow data. Here, we have applied the lightweight image matching architecture (LIMA) to reconstruct the image deformation from BOS recordings. To prepare the network for post-processing BOS data, we propose to train LIMA on datasets of synthetic images that are generated from random-irrotational deformation fields. This allows us to teach the CNN to reconstruct fields that comply with the irrotational constraint that characterizes BOS recordings, at least in the limit of small deformations. Analogously to the kinematic training proposed for PIV (Manickathan et al. 2022; Mucignat et al. 2022), this strategy enables to generate large training datasets at minimum computational costs, reducing the risk of overfitting and improving the performance of the network.

Indeed, we demonstrate that LIMA is able to reconstruct accurate deformation fields both from synthetic and experimental test images. By validating the network on a synthetic test case for a wide range of parameters, we show that the error of the reconstructed deformation field is smaller if LIMA is trained on a random-irrotational dataset than on a non-irrotational dataset. Also, both training datasets allow LIMA to achieve a better accuracy than state-of-the-art cross-correlation methods with WIDIM (CC) and Direct Image Correlation (DIC). The error on the deformation fields estimated by LIMA trained on random-irrotational (resp. non-irrotational) is about $70\%$ (resp. 50%) smaller than the error of the deformation estimated by CC(with denoising), which in turns performs better than DIC. Moreover, the CNN allows us to estimate the deformation fields with pixel level resolution, whereas classical methods are limited by the minimum processing window size.

When used on a real experimental set of images, LIMA is able to recover displacement fields that are consistent with those estimated by DIC and CC. It is also capable of reconstruct more realistic convective structures in critical regions, such as strong-convection regions close to the heater or regions where the background pattern is highly distorted. As no reference deformation is available for the experimental test cases, the error of the reconstructed fields is estimated by a-posterior image matching. The calculated disparity errors are very similar for all methods, but suggest that LIMA consistently achieves a slightly higher accuracy than conventional methods. Despite the possible limitation of an accuracy analysis based on the disparity error and the difficulty in clearly ranking the performance of the different methods, the experimental test cases confirm that LIMA is at least as robust as the classical methods, with the additional advantage of being capable of reconstructing the deformation field with pixel-level resolution also from experimental BOS recordings of highly complex flows.

Finally, we remark that our lightweight network has many fewer parameters than other CNNs previously proposed for optical flow post-processing. This can drastically reduce the computational cost and the memory requirements, making it possible to deploy LIMA on GPU embedded devices for fast and robust BOS visualization of convective and compressible flows.

Appendix 1: zero vorticity of BOS displacement fields

We demonstrate an important property of the deformation fields generated in BOS experiments on the image plane. To so, we recall that the horizontal and vertical components due to the Schlieren effect, namely $\textrm{d}s_x$ and $\textrm{d}s_y$, can be expressed as (Eq. 3 in Raffel (2015)):

$$\begin{aligned} \textrm{d}s_x&= K \delta _x, \end{aligned}$$

(A1)

$$\begin{aligned} \textrm{d}s_y&= K \delta _y, \end{aligned}$$

(A2)

where K is a constant that depends on the optical setup and $\delta _x$ and $\delta _y$ are the deflection angles. Thereafter, under the assumption of small deflections, $\delta _x$ and $\delta _y$ can be defined as (Eq. 2 in Raffel (2015):

$$\begin{aligned} \delta _x&= \frac{1}{n_0} \int { \frac{\partial {n}}{ \partial {x}} dz},\end{aligned}$$

(A3)

$$\begin{aligned} \delta _y&= \frac{1}{n_0} \int { \frac{\partial {n}}{ \partial {y}} dz}, \end{aligned}$$

(A4)

and, therefore, BOS quantifies the first spatial derivative of the refractive index n, integrated along each optical ray connecting the camera sensor to the background pattern. The resulting vorticity field can be calculated as

$$\begin{aligned} \omega _{z} =\frac{\partial {s_y}}{\partial {x}}-\frac{\partial {s_x}}{\partial {y}}. \end{aligned}$$

(A5)

Combining the equations above and recalling Leibniz rule, it is easy to prove that the curl of a potential gradient field is zero,

$$\begin{aligned} \omega _{z} = \frac{K}{n_0}\int {\left[ \frac{\partial }{\partial {x}}\left( \frac{\partial {n}}{\partial {y}}\right) -\frac{\partial }{\partial {y}}\left( \frac{\partial {n}}{\partial {x}}\right) \right] dz } = 0. \end{aligned}$$

(A6)

Hence, BOS displacement fields are irrotational and have nonzero divergence in contrast to displacement recorded by velocimetry techniques such as PIV, in which the 3D flow field has zero divergence if compressibility effects can be neglected.