1 Introduction

Aerodynamic forces result from the relative motion of an object in air. These forces are relevant for a multitude of applications, such as aircraft systems, wind turbines and ground transportation. Aerodynamic forces are typically measured by means of wind tunnel experiments (Bacon and Reid 1924; Zdravkovich 1990 among others), where the model is immersed in a uniform air stream within accurately controlled conditions. In other cases, aerodynamic studies are conducted with the object moving in a quiescent fluid. This approach is needed for instance to study the flow behind accelerating objects (Coutanceau and Bouard 1977a) or the development of the wake of an aircraft over a large distance (Scarano et al. 2002; Von Carmer et al. 2008). Furthermore, instructive flow visualizations have been obtained of high-speed flight of a bullet in stagnant air (van Dyke 1982). Aerodynamic investigations for ground vehicles and speed sports such as cycling, skating and skiing require specific arrangements of the wind tunnel (moving floor, model supports) to achieve realistic conditions. Yet, experiments that simulate specific conditions such as curved trajectories, acceleration, or with the athlete in motion remain challenging. In contrast, experiments conducted with the object moving in the laboratory frame of reference are relatively easy to realize and can mimic more closely real-life conditions.

An aspect that has not been sufficiently covered from towed experiments, is the quantitative analysis of the flow field, such to be able to evaluate the aerodynamic forces, the drag in particular. The present work focuses on the latter question to explore the viability of drag estimation from aerodynamic data obtained during towed experiments. The results are intended as a proof-of-concept for applications in automotive industry and speed sports in particular.

In professional cycling the aerodynamic drag is routinely estimated using the mechanical power generated by the rider. These estimates, however, include other forces due to the friction between wheels and ground and other mechanical resistance. Therefore, assumptions need to be made to extract the aerodynamic drag from the total resistance (Grappe et al. 1997). Similar assumptions are made for ground vehicle testing that relies upon constant speed torque measurement (Fontaras et al. 2014) and coast down tests (Howell et al. 2002) of cars and trucks. Instrumentation of a vehicle with pressure taps to measure the overall pressure distribution requires an unrealistic multitude of sensing points. For an athlete, such approach is practically impossible.

Aerodynamic drag measurements based on wake survey are potentially of more general applicability as they do not dependent upon assumptions as discussed above and do not require extensive instrumentation of the model. The approach deals with the determination of the momentum deficit of the flow past the object. The airflow velocity is measured in the wake and the aerodynamic force is obtained from the velocity deficit compared to the incoming stream. This approach has been long practiced in wind tunnels by means of wake rakes (multi-hole Pitot probes; Goett 1939; Guglielmo and Selig 1996). In contrast to using force balances and pressure taps, a wake rake offers the advantage of yielding additional whole-field velocity information in the model’s wake. The identification of the streamwise vortical structures behind cars, for instance, has been among the most significant insights in vehicle aerodynamics in the past decades (Hucho and Sovran 1993). Furthermore, relating changes in the leg orientation of a cyclist to the wake flow topology recently provided new insights for cycling aerodynamics (e.g. Crouch et al. 2014).

Particle image velocimetry (PIV) has been demonstrated as a valid instrument to replace Pitot probes for a stationary object (Kurtulus et al. 2007; Van Oudheusden 2013) as well as for moving objects like rotor blades (Ragni et al. 2011, 2012). More recently, Neeteson et al. (2016) have extended the approach to estimate the drag of a sphere freely falling in water trying to reconstruct the pressure distribution all over its surface.

The present study aim at measuring the aerodynamic drag of transiting objects using tomographic PIV measurements in the wake of the model and invoking the conservation of momentum in a control volume. Because the use of micro-sized droplets as tracers is limited to a relatively small measurement domain (Scarano 2013), using helium-filled soap bubbles (HFSB) is considered essential for the current experiment. The high light scattering efficiency and tracing fidelity of the HFSB (Bosbach et al. 2009; Scarano et al. 2015, among others) allow measurements on the meter scale (Kühn et al. 2011), preluding upscaling applications towards field tests in the automotive and speed sports.

The detailed goal of the present work is to examine the accuracy of a method that measures the aerodynamic drag of a transiting object and to assess its potential applicability for full-scale conditions. For this demonstration, a sphere is towed within a rectangular channel at a velocity of 1.45 m/s (Re = 10,000). Despite the simple geometry, the flow exhibits an unsteady, turbulent wake with complex vortex interactions (e.g. Achenbach 1972; Brücker 2001) mimicking conditions also encountered behind ground vehicles (Ahmed et al. 1984) or cyclists (Crouch et al. 2014). The experiments determine the time-average drag and a detailed comparison is made with data available from literature. The terms contributing to the overall drag are studied separately to identify a criterion for simplified measurement configurations. Finally, the experimental uncertainty related to the tomographic PIV measurements and disturbing factors such as non-homogeneous initial flow conditions, supporting strut and blockage effects are discussed.

2 Working principle

2.1 Drag from a control volume approach

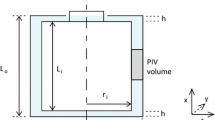
The drag force acting on a body moving in a fluid can be derived by application of the conservation of momentum in a control volume containing this body (Anderson 1991), as visualized in Fig. 1. In the incompressible flow regime, the time dependent drag force acting on the body can be written as:

Fig. 1
figure 1

Schematic description of the control volume approach within a wind-tunnel setting (stationary object)

Full size image
$$D\left( t \right) = \; - \oiiint\nolimits_{v} {\frac{{\partial u}}{{\partial t}}{\rm d}{\text{V}} - \rho {\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} }_{{\text{S}}} \left( {\user2{v} \cdot \user2{n}} \right)u{\rm d}S - {\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} }_{{\text{S}}} ((p{\bf n} - \tau \cdot \user2{n}){\rm d}S)_{x} },$$
(1)

where v is the velocity vector with components [u,v,w] along the coordinate directions [x,y,z] respectively, ρ is the fluid density, p the static pressure and τ the viscous stress tensor. V is the control volume, with S its boundary and n is the outward pointing normal vector.

It can be shown that in most cases of interest the viscous stress is negligible with respect to the other contributions when the control surface is sufficiently far away from the body surface and the boundary is not aligned with the flow shear (Kurtulus et al. 2007). Furthermore, the contour S is defined as the contour abcd, with segments ad and bc approximating streamlines. When the segments ab, ad and bc are taken sufficiently far away from the model, expression (1) can be rewritten such that the only surface integral to be evaluated is that in the wake of the model S wake (segment cd):

$$D\left( t \right) = \; -\oiiint\nolimits_{v} {\frac{{\partial u}}{{\partial t}}{\rm d}{\text{V}} + \rho \mathop {\iint }\nolimits_{{{\text{S}}_{{{\text{wake}}}} }} \left( {U_{\infty } - u} \right)u{\rm d}{\text{S}} + \; \mathop {\iint }\nolimits_{{{\text{S}}_{{{\text{wake}}}} }} \left( {p_{\infty } - p} \right)\;{\rm d}{\text{S}}},$$
(2)

where \(U_{\infty }\) and \(p_{\infty }\) are, the freestream velocity and pressure, respectively.

2.2 Time-average force on a stationary model

The evaluation of the volume integral on the right hand side of Eq. (2) poses the typical problems due to limited optical access all around the object. Evaluating this integral can be avoided by considering the time-average drag instead of its instantaneous value. When decomposing the equation into the Reynolds average components and averaging both sides of the equation, the time-average drag force is obtained with the sole contribution of surface integrals:

$$\bar{D} = \rho \mathop{\iint }\nolimits_{{{\text{S}}_{{wake}} }} \left( {U_{\infty } - \bar{u}} \right)\bar{u}{\rm d}{\text{S}} - \rho \mathop {\iint }\nolimits_{{{\text{S}}_{{wake}} }} \bar{u}^{{{\prime }2}} {\rm d}{\text{S}} + \mathop{\iint }\nolimits_{{{\text{S}}_{{wake}} }} \left( {p_{\infty } - \bar{p}} \right){\rm d}{\text{S}},$$
(3)

where ū is the time-average streamwise velocity and u’ the fluctuating streamwise velocity.

2.3 Time-average forces on a moving model at constant velocity

According to the principle of Galilean invariance, Eq. (3) holds in any reference frame moving at constant velocity. Following Ragni et al. (2011), the time-average drag acting on a model at constant speed U M is expressed as:

$$\bar{D} = \rho \mathop{\iint }\nolimits_{{{\text{S}}_{{{\text{wake}}}} (t)}} \left( {U_{\infty } - (\bar{u} - U_{M} )} \right)(\bar{u} - U_{M} ){\text{dS}} - \rho \mathop {\iint }\nolimits_{{{\text{S}}_{{{\text{wake}}}} (t)}} \bar{u}^{{\prime 2}} {\text{dS}} + \mathop{\iint }\nolimits_{{{\text{S}}_{{{\text{wake}}}} (t)}} \left( {p_{\infty } - \bar{p}} \right){\text{dS}},$$
(4)

where ū is the streamwise velocity measured in the laboratory frame of reference. In the moving frame of reference the freestream velocity stems from the velocity of the model relative to that of its environment \(U_{{{\text{env}}}}\):

$$U_{\infty } = U_{{\text{env}}} - U_{M}.$$
(5)

For perfectly quiescent air U env = 0. During real experiments it may occur that U env is different from zero and cannot be neglected. The value of U env needs therefore to be measured prior to the passage of the model.

Expression (4) allows deriving the time-average drag from velocity and pressure statistics in a cross section of the wake. The time-average pressure is evaluated from the velocity measurements solving the Poisson equation for pressure, according to Van Oudheusden (2013). An accurate evaluation of the pressure in a highly three-dimensional flow requires the estimation of the full velocity gradient tensor components (Ghaemi et al. 2012; Van Oudheusden 2013), which justifies the adoption of the tomographic PIV technique instead of planar stereo-PIV. The measurement volume must be large enough to encompass the full wake and reach the region of steady potential flow at its edges where Dirichlet boundary conditions can be applied based on Bernoulli law. Neumann conditions are prescribed at the inflow and outflow boundaries of the domain. The resulting approach yields the time averaged drag using only the velocity measurements and no other information.

3 Experimental apparatus and procedure

3.1 Measurement system and conditions

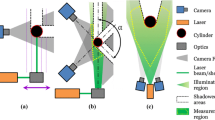
A schematic view of the system devised for the experiments is shown in Fig. 2, with a photograph of the setup in Fig. 3. The apparatus consists of a 170 cm long duct with a squared cross section of 50 × 50 cm2, where the sphere model is towed. Part of the duct has transparent walls for optical access (Fig. 3).

Fig. 2
figure 2

Schematic views of the experimental setup

Full size image
Fig. 3
figure 3

Overview of the experimental system and measurement configuration

Full size image

The model is a smooth sphere of diameter D = 10 cm towed at a constant speed U M  = 1.45 m/s. The model is supported by an aerodynamically shaped strut with 20 mm chord and 3 mm thickness. The strut is 20 cm long and is installed onto a carriage moving on a rail beneath the bottom wall of the duct. The carriage is pulled by a linen wire connected to the shaft of a digitally controlled electric motor (Maxon Motor RE35). Markers on the surface of the sphere track its position during the transit.

The wake behind the sphere starting from rest needs time to reach a fully developed regime. For an impulsively started cylinder at low Reynolds number (Re < 100) it is reported that about 15 cylinder diameters (Coutanceau and Bouard 1977b) are needed before the wake is developed. In the present work a conservative value is taken with the model beginning 25 sphere diameters before the measurement region.

3.2 Tomographic system

The time-resolved tomo-PIV measurements are conducted using neutrally buoyant helium-filled soap bubbles (HFSB, 300 μm diameter) as tracer particles produced with an array of ten generators that yield a total of about 300,000 particles per second. The air, helium and soap fluid flow rates are controlled by a fluid supply unit provided by LaVision GmbH. The average time response of such tracer particles is expected to be below 20 s (Scarano et al. 2015). Considering the relevant flow time scale (D/U M  = 70 ms) the small value of the Stokes number of the tracers indicates their adequacy for the current experiments.

The illumination is provided by a Quantronix Darwin Duo Nd:YLF laser (2 × 25 mJ/pulse at 1 kHz). The laser beam is first shaped into an elliptical cross section and is then cut into a rectangular one with light stops (Fig. 3). The size of the measurement volume is 3 cm × 40 cm × 40 cm in x, y and z direction, respectively, and is located 80 cm from the exit of the duct (Fig. 2). The tomographic imaging system consists of three Photron Fast CAM SA1 cameras (CMOS, 1024 × 1024 pixels, pixel pitch of 20 μm, 12 bits). Each camera is equipped with a 60 mm Nikkor objective set to f/8. The optical magnification is approximately 0.07. In the present conditions, the seeding concentration is approximately 3 particles/cm3 and the imaging density is 0.04 particles/pixel. PIV acquisition is performed within LaVision Davis 8.3 delivering single-exposure frames at a rate of 500 Hz.

3.3 Measurement procedure

The tunnel entrance and exit are closed to confine the HFSB seeding before the transit of the sphere. The exit is closed by a porous curtain, which maintains the seeding tracers inside, but prevents the buildup of an over-pressure. The HFSB generators are operated for approximately two minutes until the steady-state concentration is reached. Approximately quiescent conditions are achieved 30 s after the generators are switched off. The tunnel entrance wall is then opened and the model is put in motion through the duct. Image recording begins 1 s before the sphere passes through the measurement region and stops when it touches the exit curtain. Figure 4 illustrates the motion of the air by particle streaks at three positions of the model; before entering (top), inside (middle) and after leaving the measurement domain (bottom). The measurements are separated by 70 ms (35 frames) and the streaklines are obtained by averaging ten consecutive frames. A relatively high velocity is observed in the center of the measurement region behind the model (bottom image) with quiescent air conditions at the edges. An animation of raw images of the passing sphere is available at the multimedia store of the publisher (Supplementary material 1). The experiment comprises 35 repeated measurements to form a statistical estimate of the flow properties and the associated aerodynamic drag.

Fig. 4
figure 4

Particle streaks for three positions of the sphere passing through the measurement domain. The particle streaks are obtained by averaging over ten consecutive frames. The sphere positions are separated by time increments of 70 ms

Full size image

3.4 Data reduction

The tomographic-PIV data analysis is performed with the LaVision Davis 8.3 software. Image pre-processing comprises background subtraction and Gaussian smoothing. The volume reconstruction and velocity evaluation follows the sequential MTE-MART algorithm (SMTE, Lynch and Scarano 2015), yielding a discretized object with 1074 × 1050 × 72 voxels. The interrogation is based on spatial cross-correlation volumes of 323 voxels with an overlap of 75%. The resulting velocity vector field has a density of 3 vectors/cm. Figure 5 illustrates the reconstructed intensity distribution along the depth. The SMTE algorithm returns a high reconstruction signal-to-noise ratio, indicating that the cross correlation result is not affected by ghost particles effects (Elsinga et al. 2006).

Fig. 5
figure 5

Illumination distribution along the measurement depth (evaluated over an area of 25 × 25 cm2)

Full size image

A Galilean transformation of the instantaneous velocity is performed to represent the measurement in a frame of reference consistent with the object moving at a constant velocity U M . In this frame of reference, the drag is evaluated using Eq. (4). The phase-average velocity field in the laboratory frame of reference, \({\bar{\varvec{v}}}^{*}\) is obtained from the 35 repeated measurements yielding the mean velocity and its fluctuations. A three-dimensional spatial representation of the velocity field in the sphere frame of reference, \({\bar{\varvec{v}}}\) is obtained by considering the linear relation between the streamwise coordinate and the time elapsed after the passage of the sphere:

$${\bar{\varvec{v}}}\left( {x,y,z} \right) = {\bar{\varvec{v}}}^{*} (tU_{M} ,y,z),$$
(6)

where its origin matches the center of the sphere and both coordinate systems coinciding at t = 0. The procedure encompasses the streamwise direction downstream of the sphere from x/D = 0.5 till x/D = 9.5. This approach is illustrated in Fig. 6.

Fig. 6
figure 6

Illustration of the time-average streamlines after streamwise reconstruction of the velocity field (v) (in the sphere frame of reference) from phase-average time-history velocity fields (v *) (in the laboratory reference frame)

Full size image

The Poisson equation for pressure is solved prescribing Neumann conditions on all boundaries. The obtained pressure field is scaled afterwards by a constant value, prescribing the freestream pressure at its top, bottom and side boundaries in the spatial range in which the velocity at these boundaries best matches stagnant conditions (x/D > 4), and excluding a small segment (5 cm wide) in the center of the bottom boundary, which is affected by the wake of the strut.

4 Results

4.1 Instantaneous flow field

At a Reynolds number of 10,000 the wake of a sphere is in the unsteady regime, exhibiting vortex shedding and complex vortex interactions (Bakić et al. 2006). A snapshot of the flow structure will typically yield an asymmetric pattern, while the time-average structure is known to be axi-symmetric. Figure 7 shows the instantaneous velocity field in the laboratory frame of reference in the center YZ-plane at four consecutive time instants. A supplementary animation of the time-resolved velocity field is available as multimedia file (Supplementary material 2). Non-dimensional time is defined as \(t^{{\text{*}}} = {\text{}}t{\text{}}U_{M} /D\). Each increment \(\Delta t^{{\text{*}}} = 1\) corresponds to a translation in space of one sphere diameter in negative x-direction. At t * = 0.5, a region of accelerated flow is visible at the periphery of the wake. Furthermore, a negative peak of streamwise velocity is present in the near wake of the sphere. The maximum velocity deficit decays with time, consistently with the observations from past investigations (Jang and Lee 2008; Constantinescu and Squires 2003).

Fig. 7
figure 7

Instantaneous streamwise velocity u* in the YZ-plane at four time instants, t * = 0.5, t * = 1.5, t * = 2.5 and t * = 3.5. The measurement region is cropped to half its size along y and z for readability

Full size image

4.2 Time-average flow structure

The ensemble-statistics yield the time-average velocity field, the fluctuating velocity and time-average pressure distribution. These terms are inspected to understand how the individual terms from Eq. 4 contribute to the aerodynamic drag. Figure 8 illustrates the streamwise velocity distribution in the separated wake (x/D = 0.85, top) and after the flow reattachment (x/D = 3, bottom). The velocity field in the wake is close to the axi-symmetric condition, with some slight deviations due to the supporting strut (5–10% velocity deficit). The latter will be accounted for in the section on drag derivation. Furthermore, the spatial velocity distribution shows a radial velocity directed towards the flow symmetry axis, decreasing in magnitude at increasing distance from the sphere, which is consistent with literature (e.g. Jang and Lee 2008). The expected flow reversal in the center of the wake is also captured in the present measurement (Fig. 8-top-right).

Fig. 8
figure 8

Time-average velocity vectors in the wake of the sphere at x/D = 0.85 (top-left) and x/D = 3 (bottom-left). Streamwise velocity contours (right). A rectangle (bottom-right) indicates the region where the strut drag is estimated

Full size image

The streamwise velocity contour at x/D = 3 (Fig. 8 bottom-right) shows a slight asymmetry in the spatial velocity distribution outside the wake. At the top of the domain the non-dimensional streamwise velocity is about 0.98, while at the bottom it is 1.01. This asymmetry stems from the flow conditions prior to the transit of the sphere and is ascribed to the motion induced during injection of the HFSB tracers. In the derivation of the aerodynamic drag, the momentum term expresses a deficit in the wake, relative to the fluid momentum prior to the passage of the sphere (Eq. 5). Therefore any residual motion before the passage of the sphere is accounted for the drag evaluation.

The streamwise velocity distribution in the central XY-plane is depicted in Fig. 9. in the spatial range 0.5 < x/D < 3.5. The streamlines pattern yields a reattachment point at about x/D = 1.3, which is consistent with values from literature. Table 1 summarizes the relevant flow properties from other works: Jang and Lee (2008) report a recirculation length, L/D = 1.05 (Re = 11,000) obtained by PIV; Ozgoren et al. (2011) measure a value of about 1.4 (Re = 10,000) by PIV; Bakić et al. (2006) list a value of 1.5 (Re = 51,500) measured by LDV; the numerical work of Yun et al. (2006) and Constantinescu and Squires (2003), both at Re = 10,000, report a significantly longer separated wake with L/D = 1.86 and 2.2, respectively. The variability of the reattachment position can be ascribed to experimental settings, such as the model support (Bakić et al. 2006, use a single rigid support from the back of the sphere; Ozgoren et al. 2011 apply a strut from the top and Jang and Lee suspend the sphere with two thin wires forming an X-shape through the center of the sphere) as well as to the settings of the numerical simulations (i.e. the grid resolution and subgrid-scale modeling for the LES).

Fig. 9
figure 9

Reconstructed spatial distribution of the time-average velocity in the wake of the sphere in the center XY-plane (left) and the center XZ-plane (right). Flow streamlines (top) and contours of streamwise velocity (bottom). The measurement region is cropped along x for readability

Full size image
Table 1 Comparison between present experimental results and values reported in literature
Full size table

The maximum reverse flow velocity measured here is −0.52 occurring at x/D = 0.85 approximately on the symmetry axis (Fig. 9, top), which compares fairly well to the value of −0.4 reported by Constantinescu and Squires (2003) and − 0.427 of Bakić et al. (2006). The location of maximum reverse flow, differs from that reported by Constantinescu and Squires (2003) (x/D = 1.41), presumably due to the larger recirculation length.

Asymmetries in the mean flow are observed in both the vertical plane (Fig. 9, left) and the horizontal plane (Fig. 9-right). These may stem from a number of causes: primarily non-homogeneous flow prior to the passage of the model, but also incomplete statistical convergence and the presence of the strut.

The toroidal structure of the recirculating flow when examined in the XY-cross section yields two foci at about x/D = 0.75 and radial distance r/D = 0.45, (Fig. 9, top-left), which closely correspond with the flow topology reported by Ozgoren et al. (2011). The presence of this vortex structure is less evident in the horizontal center-plane (Fig. 9, top-right), which is ascribed to the reduced precision of the PIV measurements in low velocity regions and the limited size of the statistical ensemble. The recirculation region past a sphere features a circular focus, following Jang and Lee (2008), among others. Figure 10 illustrates that the vorticity magnitude isosurface (value selected at 6.7 rad/s) features an axi-symmetric flow structure with the annular shape shortly interrupted at the position of the supporting strut.

Fig. 10
figure 10

Streamlines of time-average velocity in the recirculation region in the wake of the sphere. Isosurface of vorticity magnitude at 6.7 rad/s (green). Velocity vectors are depicted at x/D = 0.5 and x/D = 3.5 in the at y/D = 0

Full size image

The uncertainty of the time-average velocity, ε v primarily stems from the uncertainty of the measurement of the instantaneous velocity and the size of the ensemble used to estimate the time-average value. Its value decreases with the square root of the number of uncorrelated samples (N = 35 here): \(\varepsilon _{{\mathbf{v}}} = \sigma /\sqrt N\), where σ is the standard deviation of the velocity from the ensemble at the same phase. In the region outside the wake, velocity fluctuations are the smallest, and the standard uncertainty is about 0.3% of the sphere velocity. Inside the wake, the uncertainty attains a maximum level of 6.5% of the sphere velocity (as a result of the velocity fluctuations) at the shear layer locations at x/D = 1. The uncertainty of the mean velocity decreases with the distance from the model as a result of turbulence decay. At x/D = 3 the maximum uncertainty is 3.5% and at x/D = 7 it stays within 1.5%. An overview of the uncertainties of the three velocity components is given in Table 2. These uncertainties provide the baseline information to evaluate the accuracy of the aerodynamic drag estimates addressed in a later section.

Table 2 Uncertainty of the time-average velocity as a percentage of the sphere velocity along the wake
Full size table

4.3 Velocity fluctuations

The distribution of turbulent fluctuations plays a role in the momentum exchange within the wake and needs to be accounted for when evaluating the aerodynamic drag as clear from the formulation in Eq. (4). Figure 11 shows the contour plots of the root-mean-square of the streamwise velocity fluctuations in the center XY-plane (top) and the center XZ-plane (bottom). The velocity fluctuations are rather symmetric in both planes. Their distribution in the XZ-plane compares well to literature data (Jang and Lee 2008; Constantinescu and Squires 2003; Yun et al. 2006), with maxima around x/D = 1 and z/D = ± 0.45, featuring two branches with peak values that diverge from the streamwise axis and decreasing in strength for x/D > 1. The distribution in the XY-plane shows less similarity to literature, likely due to the disturbance of the supporting strut. The local maxima of \(\sqrt {\bar{u}^{{\prime 2}} } /U_{M}\) are between 0.35 and 0.4, within the range reported in literature (Table 1). At x/D = 7, the fluctuations have not decayed yet and exhibit a maximum of about 0.08, indicating that the Reynolds stress term in Eq. (4) still contributes to the drag of the sphere at that distance.

Fig. 11
figure 11

Spatial distribution of streamwise velocity fluctuations in the center XY-plane (top) and the center XZ-plane (bottom)

Full size image

4.4 Pressure reconstruction

The flow past a bluff body generally produces a large base drag resulting from a low-pressure region at the base of the object (Neeteson et al. 2016). After reattachment the pressure recovers towards the free-stream conditions. This variation of the pressure field is investigated to understand its contribution to the aerodynamic drag. Figure 12 depicts the distribution of the mean pressure coefficient in the center XY-plane (top) and the center XZ-plane (bottom). The spatial distribution of the time-average pressure coefficient features a minimum approximately corresponding with the focus of the toroidal recirculation (Fig. 9, bottom-left). At the reattachment point, a region of positive CP is observed. The distribution of pressure shows a slight asymmetry in both planes, but to a lesser extent compared to the velocity fields presented in Figs. 9 and 11. To the best knowledge of the authors, the pressure field in the wake of a sphere has not been evaluated in previous literature, which makes comparisons not possible. The base pressure coefficient estimated from the flow field pressure close to the solid surface is about −0.52 in the present experiment, which is comparatively higher than what is reported by Yun et al. (2006) and Constantinescu and Squires (2003) who report a value of −0.27 and Bakić et al. (2006) with a value of −0.3 at Re = 51,500. Nevertheless, in the current work, the drag is evaluated up to the far wake, where the pressure practically equals that of the quiescent flow and the pressure term is deemed negligible (|C p | < 0.004 at x/D = 7).

Fig. 12
figure 12

Spatial distribution of time-average pressure coefficient in the center XZ-plane (top) and the YZ-plane (bottom)

Full size image

4.5 Aerodynamic drag

Both the model and its strut contribute to the drag. The two contributions need to be separated to obtain solely the sphere drag. The effect of the strut on the flow is visible in Fig. 8 (right). Its drag introduces a bias error for the estimation of the sphere drag. This error can be estimated by a local application of the control volume approach, which considers a region only affected by the strut. The control volume, containing a 2 cm section of the strut (−0.75 < z/D < 0.75 and − 1.4 < y/D < −1.6), is indicated by the dashed line Fig. 8, right-bottom. The contribution is evaluated at a distance of 100 strut diameters behind the model, where the pressure and Reynolds stress terms on the drag can be neglected. Afterwards, the drag of the entire strut is obtained, scaling the drag of the 2 cm section to its full length. The resulting strut drag is 0.0006 N, which is subtracted from the drag of the entire model (0.0056 N).

A second source of bias error for the drag is the finite size of the rectangular channel. Considering a blockage factor of 3.4%, the value of the drag in the experiment overestimates that of a sphere travelling in an unconfined medium (Moradian et al. 2009). The drag is therefore corrected, using the continuity equation (assuming continuous solid blockage), multiplying the measured value by a factor 0.94. The results presented in the remainder of the work refer solely to the drag of the sphere and include the correction for blockage (0.0003 N).

The time-average aerodynamic drag, derived from the velocity statistics, is expected to be independent of the distance between the measurement plane and the sphere. Given the principle stated in Eq. (4) the sum of the three terms on the right hand side is an invariant when considering steady state conditions (assumed after phase-averaging). At sufficient distance from the object, the drag is expected to be dominated solely by the momentum deficit term, as the pressure disturbance and the velocity fluctuations terms decay (Figs. 11, 12). Figure 13 shows the drag coefficient computed in the wake of the model in a streamwise range between x/D = 0.5 and x/D = 9.5. The physical location at which the drag is computed hardly affects the resulting drag coefficient value until x/D = 7, which confirms the solidity of the measurement principle. At x/D = 7, a sudden increase of the momentum contribution is observed, balanced by a negative increase of the pressure term. The latter situation is caused by the sphere hitting the porous curtain placed at the end of the channel. Given the amplitude of these effects, the measurement of the drag is not extended beyond 7 diameters, even though the drag coefficient itself appears to be affected to smaller extent.

Fig. 13
figure 13

Mean drag coefficient evaluated at varying distance behind the sphere; C D and the individual momentum, pressure and Re stress term

Full size image

The momentum term is strongly negative close to the sphere, with a peak at x/D = 0.6, where it acts as a thrust term. Considering Eq. (4), this thrust originates from the reverse flow in the recirculation region and partly from the accelerated flow around the sphere periphery. The contribution of the reverse flow to the thrust ends after reattachment (x/D = 1.3), where the momentum term changes sign and increases to reach a relatively constant value after x/D = 2. The negative contribution of the momentum deficit at small x/D is mostly compensated by the pressure term, which is highest within the first diameter close to the sphere and vanishes after about x/D = 5. The Reynolds normal stresses contribute negatively to the drag by definition. A minimum is observed around x/D = 1, which corresponds to the location of the peaks of streamwise velocity fluctuations in Fig. 11. This term decays more slowly reaching a value of about − 0.05 at x/D = 7. Along the wake the contribution of the Reynolds normal stress is significant and cannot be neglected when computing the aerodynamic drag. This agrees with the study of Balachandar et al. (1997) who evaluated the contribution of the Reynolds normal stress to the wake of two-dimensional bluff bodies and suggested the presence of shear layer interactions in the vortex shedding dynamics.

The discussed spatial development of the different terms, and in particular the pressure, has a practical consequence for the measurement of the aerodynamic drag. As long as the pressure term remains significant (x/D < 5), the full velocity gradient tensor evaluation is needed for accurate pressure reconstruction, requiring tomographic-PIV or other 3D-PIV techniques. Instead, when the pressure term is not significant, stereo-PIV measurements on a single plane may be sufficient for accurate drag evaluation.

The comparison against literature data is made taking into account the main sources of uncertainty.

First, the position along the wake is considered. Although theoretically the drag may be measured at any arbitrary station in the wake, the large velocity fluctuations in the near wake increase the uncertainty of the measured time-average velocity (Table 2) and, therefore, the uncertainty of the pressure and the drag. The large variations observed for x/D < 2 suggest that reliable drag estimates should be obtained at a larger distance from the model. The computed drag coefficient is relatively constant with an average value of 0.47 for x/D > 2.

The statistical uncertainty of the mean drag coefficient, \(\varepsilon _{{\bar{C}_{D} }} N\) mostly stems from variations in the instantaneous drag, caused by large scale fluctuations in the wake. It scales inversely proportional to \(\sqrt{N}\), where N is the statistical ensemble size. The latter can be enlarged by increasing the number of passages of the sphere N P , and the amount of uncorrelated stations selected along the wake N S :

$$N = N_{P} \cdot\,N_{S}.$$
(7)

In the present experiments the statistical ensemble is built from 35 individual passages (N P  = 35) of the sphere and three stations x/D = {5, 6, 7} in the wake (N S  = 3), in the range where the pressure term can be neglected. Considering that the uncertainty of the drag coefficient from a single sample is \(\varepsilon _{{\bar{C}_{D} }} N\) to 0.26, the above condition reduce the statistical uncertainty to approximately \(\varepsilon _{{\bar{C}_{D} }} N\) to 0.026 at 95% coverage factor.

Any further decrease of the uncertainty of the mean drag coefficient relies on the increase of N P and N S . For the latter, the assumption of negligible environmental disturbances during the observation time must hold true. This means that after the passage of the model through the measurement region, momentum is not added by external sources or removed for instance due to wall interactions.

Considering the latter uncertainty, the presented value for the drag coefficient of 0.47 falls within the range of reported values in literature: Moradian et al. (2009) measured a CD of about 0.51 (Re = 22,000) by load cells, Achenbach (1972), a value of 0.5 (Re = 60,000) by strain gauges, while Constantinescu and Squires (2003) and Yun et al. (2006) report a value of 0.39 (Re = 10,000).

Finally, regarding the applicability of the control volume approach to other bluff body flows, it is worth mentioning that the flow over spheres becomes turbulent at a Reynolds number around 800 and remains so afterwards. Hence, the statistical approach to determine the drag can be considered also for experiments at a higher Reynolds number. Therefore, the conclusions drawn from this study can be extrapolated to model geometries other than the sphere under the assumption of similarity in the behavior of the wake.

5 Conclusions

Time resolved tomographic-PIV measurements are conducted to determine the aerodynamic drag of a transiting sphere using the control volume approach in the wake of the model. The concept is demonstrated using a newly developed system to measure the flow over a sphere with a diameter of 10 cm moving at 1.45 m/s. Velocity statistics in the wake of the sphere have been obtained from a set of 35 model transits. The obtained time-average velocity and its fluctuations are used to estimate the flow field pressure. The aerodynamic drag is evaluated via a control volume approach as the sum of these three contributions along the wake behind the sphere. The estimation of the drag coefficient is practically unaffected by the position where the momentum integral is evaluated. In particular, the time-average drag coefficient obtained 2 sphere diameters behind the model falls within the range of reported values in literature.

For practical applications of this approach, it is observed that the pressure term vanishes after 5 diameters, which can greatly simplify the measurement procedure. Three disturbing factors are worth mentioning that may affect the measurement accuracy: the flow conditions prior to the passage of the sphere need to be taken into account in the evaluation; the blockage effect due to the finite channel cross section; the contribution of the supporting strut needs to be subtracted to isolate that of the main object only.