Three-dimensional flow structures and unsteady forces on pitching and surging revolving flat plates

Abstract

Tomographic particle image velocimetry was used to explore the evolution of three-dimensional flow structures of revolving low-aspect-ratio flat plates in combination with force measurements at a Reynolds number of 10,000. Two motion kinematics are compared that result in the same terminal condition (revolution with constant angular velocity and $45^{\circ }$ angle of attack) but differ in the motion during the buildup phase: pitching while revolving at a constant angular velocity; or surging with a constant acceleration at a fixed angle of attack. Comparison of force histories shows that the pitching wing generates considerably higher forces during the buildup phase which is also predicted by a quasi-steady model quite accurately. The difference in the buildup phases affects the force histories until six chords of travel after the end of buildup phase. In both cases, a vortex system that is comprised of a leading-edge vortex (LEV), a tip vortex and a trailing edge vortex is formed during the initial period of the motion. The LEV lifts off, forms an arch-shaped structure and bursts into substructures, which occur at slightly different phases of the motions, such that the revolving–surging wing flow evolution precedes that of the revolving–pitching wing. The delay is shown to be in accordance with the behavior of the spanwise flow which is affected by the interaction between the tip vortex and revolving dynamics. Further analysis shows that the enhanced force generation of the revolving–pitching wing during the pitch-up phase originates from: (1) increased magnitude and growth rate of the LEV circulation; (2) relatively favorable position and trajectory of the LEV and the starting vortex; and (3) generation of bound circulation during the pitching motion, whereas that of the revolving–surging wing is negligible in the acceleration phase.

1 Introduction

The flapping flight of insects and birds is a three-dimensional unsteady phenomenon, which combines pitch, plunge and sweeping motions of the wing, with three-dimensional effects being further enhanced by low values of the wing aspect ratio. This challenging phenomenon has been subject of many studies aiming to characterize the flow structures and force generation on wings undergoing aforementioned motions, especially for the low Reynolds number (Re) conditions typical of animal flight (see Sane 2003; Lehmann 2004, and references therein). Among these, the pitch motion of the wing to high angle of attack has received a special attention as it was shown to enhance the aerodynamic performance by the formation of additional circulation.

One of the earlier studies to investigate the effect of wing rotation on the generation of forces was reported by Dickinson (1994). He performed experiments on a two-dimensional wing model to investigate the effect of wing rotation during the stroke reversal and showed that formation of vortical structures in the rotation phase of the motion increases forces considerably. Hamdani and Sun (2000) studied the fast pitching motion of a two-dimensional airfoil in a constant free-stream by Navier–Stokes simulations. They reported that large aerodynamic forces are generated during the rapid pitch-up which they associated with the formation and motion of new vorticity layers in addition to the previously existing thick vorticity layers. More recently, loading on a rapidly pitching nominally two-dimensional flat plate was studied by Granlund et al. (2013). They showed the effects of the pitch rate and the pitch pivot point location on the time history of lift and drag in conjunction with the flow-field evolution. They found that, similar to unsteady wing theory, the pitch contribution to lift is proportional to the pitch rate and to the distance from the pivot point to the 0.75 chord point. The latter is also in agreement with the results of Sane and Dickinson (2002).

To include three-dimensional effects, Yilmaz and Rockwell (2011) explored the flow structures around a low-aspect-ratio wing with rectangular and elliptical planforms undergoing a pitch-up motion from $0^{\circ }$ to $45^{\circ }$ in a constant free-stream. Flow visualization with particle image velocimetry (PIV) revealed the formation of a significantly three-dimensional leading-edge vortex (LEV) structure. They reported a spanwise flow component with magnitudes larger than the free-stream velocity and which is directed away from the symmetry plane near the leading edge and toward the symmetry plane near the trailing edge in the fully developed state. They also observed distortion of the LEV, which is less pronounced for the elliptical wing associated with different spanwise flow structures.

The aforementioned studies considered the pitch-up motion of a translating wing, yet the natural flapping flight is represented more realistically with revolving motion with the associated occurrence of spanwise variation of the flow. Moreover, Lentink and Dickinson (2009) point to the rotational inertial mechanisms (i.e., centripetal and Coriolis accelerations) in combination with the spanwise flow (Ellington et al. 1996), which are present in the case of revolving wings, as the responsible mechanism for stabilizing the LEV and thus augmenting force generation. Recently, Jardin and David (2014) showed that spanwise gradient of the local wing speed by itself leads to stabilization of the LEV but not to enhanced lift; the latter is observed when including the rotational inertial effects.

The flow and the aerodynamic loading on revolving wings at a constant angle of attack or with combined revolving and pitching motions, particularly in a reciprocating manner with rotation of the wings at the stroke reversals, have been studied extensively in the literature (Ozen and Rockwell 2012, and references therein). Ozen and Rockwell (2012) investigated the flow field around a revolving low-aspect-ratio flat plate experimentally, excluding the transient phase at the start of the motion. They reported a stable LEV for angles of attack from $30^{\circ }$ to $75^{\circ }$ and added that the sectional structure of the LEV at the mid-plane is not affected by the Reynolds number in the range from 3,600 to 14,500 (based on the velocity at the radius of gyration). Venkata and Jones (2013) conducted flow visualizations and force measurements on a revolving wing in the Reynolds number range of 5,000 to 25,000 based on the velocity at 75 % span position. They showed that following the initial noncirculatory peak at the onset of the motion, the forces reach a local maximum after approximately four chords of travel and decrease to steady-state values of the first revolution. Flow visualizations revealed the burst of the LEV at the outboard section of the wing span. Furthermore, Garmann et al. (2013) performed high-fidelity implicit large eddy simulations to resolve the flow around a revolving low-aspect-ratio wing at a constant angle of attack. Their results revealed a coherent vortex system that is generated after the onset of the motion and which stays attached to the wing during the motion. Correspondingly, following the initial fast increase in the wing loading due to angular acceleration of the flat plate, forces grow gradually with the settlement and strengthening of the vortical structures. However, increasing Reynolds number causes vortex breakdown in these structures, in the sense that large-scale coherence gradually gives way to fragmentation and formation of vortical substructures. Nevertheless, the force generation mechanisms appear not to be adversely affected by this loss of coherence of the vortex system, and on the contrary, wing loading is observed to moderately increase with increasing Reynolds number. They indicated that the reversal of the outward spanwise flow in the core of the LEV is correlated with the vortex breakdown and formation of the unsteady substructures. Their analysis further showed that the spanwise pressure gradient and centrifugal forces are the dominant mechanisms in the generation of spanwise flow; whereas Coriolis force is not contributing to the stability of the LEV in their case. They also compared revolving and translating wings and reported that although similar patterns are present at the onset of the motion, the following period of the two motions generate significantly different flow fields. The liftoff and the subsequent breakdown of the LEV were also reported by Carr et al. (2013). They investigated the effect of aspect ratio on the three-dimensional flow structures of revolving wings at 45º angle of attack. Phase-locked, phase-averaged stereo PIV measurements were taken on aspect ratio 2 and 4 flat plates at the Reynolds number of 5,000 based on the tip velocity. They showed that for both aspect ratios, the LEV lifts off from the wing surface and forms an arch-shaped structure in the outer-span region after $20^{\circ }$ rotation. For the aspect ratio 2 plate, breakdown of the outboard LEV and the tip vortex (TV) occurs around the rotation angle of $70^{\circ }$. They observed a stable LEV up to approximately $60\,\%$ span for the complete motion and outward of this position, and the TV and the LEV are indistinguishable. Garmann and Visbal (2014) conducted high-fidelity numerical simulations in order to investigate the flow around revolving wings at different aspect ratios. They mentioned the chordwise growth of the LEV along the span is physically limited by the trailing edge; therefore, the aerodynamic forces saturate with increasing aspect ratio. They also confirmed the importance of the centrifugal forces on the LEV attachment by adding a source term in the governing equations to cancel out centrifugal forces near the wing surface resulting in the propagation of outboard LEV liftoff inward. Recently, Bross and Rockwell (2014) reported flow-field measurements on a simultaneously pitching and revolving wing and discussed the presence of distinctive vortical structures in comparison with translating–pitching and pure revolving wing cases. They showed that the vortex system involving the LEV and the TV preserves its coherence in the case of the revolving–pitching wing, while it is degraded in the case of a pure revolving wing. It is also revealed that compared to the translating–pitching wing case, in which the LEV moves away from the leading-edge region relatively quickly, a more stable vortex structure is present in the revolving–pitching motion.

Whereas previous studies on plates accelerated from rest have extensively documented the aerodynamics and force generation characteristics of both translating–pitching plates and revolving wings at a constant pitch angle, relatively little attention has been paid so far to the comparison with pitching–revolving wings. The specific aim of the current study is, therefore, to experimentally explore flow characteristics of pitching/surging revolving wings, in particular regarding the impact of the wing kinematics in the buildup phase on the vortex formation and time history of the forces for a revolving wing ultimately rotating with constant angular velocity at $45^{\circ }$ angle of attack. In the first case, indicated as revolving pitch, the wing first accelerates up to the terminal velocity while at zero angle of attack and subsequently pitches to $45^{\circ }$. For the second case, referred to as revolving surge, the wing accelerates from rest while at constant angle of attack. Thus, two wing motions result such that the two have the same terminal condition, but with a different transient in the motion buildup phase. The particular objective of the study is to characterize the initial formation, stability and the integrity of the flow structures in conjunction with the variation of the forces and to assess the impact of the buildup phase.

2 Experimental setup and methods

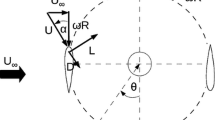
The experiments were performed in a water tank at the Aerodynamics Laboratory of Delft University of Technology (TUDelft). The octagonal water tank (600 mm of diameter and 600 mm of height) is made of Plexiglass allowing full access for illumination and optical imaging (Fig. 1a). A Plexiglass flat plate with sharp edges and a thickness of 3 mm was used as the rectangular wing model. It has chord length $(c)$ of 50 mm, a span length $(b)$ of 100 mm, resulting in an aspect ratio of 2 (Fig. 1b). The wing model was positioned at approximately $5c$ distance from the water surface, $7c$ distance from the bottom wall and $4.2c$ (wing tip to wall) distance from the side wall, and tests were carried out to verify that with these settings the results are not affected by wall or free-surface interference effects. A brushed DC motor with a gearbox (gear ratio of 132:1) that was connected to the main vertical axis (y axis) of the setup drove the wing in revolution. The wing model was pitched about its leading edge (z axis) by a waterproof servo motor that was placed in the servo box which also contains the force sensor.

Fig. 1

a Experimental arrangement in the water tank, b dimensions of the wing model

2.1 Motion kinematics

The three-quarter span length of the wing model was taken as the reference position for defining the terminal velocity $(V_{\rm t})$ and nondimensional parameters, such as convective time $(t^{*}=t \times V_{\rm t}/c)$ and chords travelled ($d^{*}=d/c$ where $d$ is the wing displacement at the reference position). The distance between the root chord and the rotation axis is 35 mm, and the radius of gyration is 90 mm, resulting in a Rossby number of 1.8. The revolving–pitching motion kinematics used in the experiments can be described as follows (Fig. 2a): The motion is initiated by a constant acceleration from rest to $V_{\rm t}=0.2\,{\rm m/s}$ (corresponding to a Reynolds number of 10,000 based on the wing chord length) at an angle of attack $(\alpha )$ of $0^{\circ }$ over $t^{*}=2\,(d^{*}=1$ and the revolution angle $\phi =25.8^{\circ }$); this is then followed by a period in which the wing pitches up to $\alpha =45^{\circ }$ over $t^{*}=1$ $(d^{*}=1)$ at a constant pitch rate ($\dot{\alpha }=3.14$ rad/s corresponding to a nondimensional pitching rate of $k=\dot{\alpha }c/(2V_{\rm t})=0.39$); and the wing continues to revolve at a constant rate at $\alpha =45^{\circ }$. On the other hand, in the revolving–surging motion (Fig. 2b), the wing motion is initiated at $45^{\circ }$ angle of attack with an acceleration period from rest to $V_{\rm t}=0.2$ m/s over $t^{*}=2$ ($d^{*}=1$) after which the wing remains to revolve at a constant angle of attack and constant rate. During the measurements, real-time position and rotational velocity information were acquired from the motor encoder at 33 Hz data acquisition frequency to check the motion kinematics. The accuracy of the brushed DC motor is $0.018c$ (corresponding to $0.46^{\circ }$) in position and $0.0125 V_{\rm t}$ in velocity. In all experiments, the entire travel distance is 14c $(d^{*}=14)$ corresponding to one full revolution. Although the forces were captured for the full motion, flow-field measurements were limited to the first 7c of travel.

2.2 Measurement and estimation of the unsteady forces

Six components of forces and moments were measured by use of a water-submergible ATI Nano17/IP68 force sensor. Force signals were acquired at 2 kHz data acquisition frequency via in-house developed LabVIEW code that also controls the motors and synchronizes the wing motion with the force data acquisition and the PIV measurements. Ensemble averaging of forces and moments was performed over 20 repetitions of the experiments for the pitching case and 50 repetitions for the surging case. The averaged force and moment data were then filtered to remove electrical noise and mechanical vibrations of the driving system as well as the natural frequency of the test rig (16.6 Hz) in the signal, by means of a Chebyshev Type II low-pass filter with a cutoff frequency of 15 Hz. A forward–backward filtering technique was used in order to prevent time shift of the data. Lift and drag are normalized by use of the terminal velocity $V_{\rm t}$ and wing surface area, in order to produce force coefficients ($c_{\rm L}$ and $c_{\rm D}$, respectively). When calculating the measurement uncertainty from the raw unfiltered data and number of repetitions of the experiments, the average uncertainty in the calculated force coefficients is 6 % of the steady-state mean values for the surging case and 12 % for the pitching case with 95 % confidence interval. The increased level of uncertainty in the revolving–pitching motion is caused by the smaller number of repetitions and increased level of vibrations during the pitch-up. However, this calculation of the uncertainty based on the raw signal also includes the contribution of the structural resonance of the test rig due to impulsive start of the motion as well as constant sensor noise. Therefore, the uncertainty in the measurements was also calculated based on the 15-Hz low-pass filtered signal which results in 0.5 and 1.5 % average uncertainties in the revolving–surging and revolving–pitching cases, respectively. These values are considered to be representative for the reported measurement data.

In addition to the measurements, a quasi-steady model (Sane and Dickinson 2002) was used to estimate the evolution of unsteady forces for the given kinematics. In this model, the instantaneous force is composed of three main contributions:

$$\begin{aligned} F_{\rm i}=F_{\rm revolution}+F_{\rm inertial}+F_{\rm rotation} \end{aligned}$$

(1)

The first term on the right-hand side of Eq. 1 stands for the force component due to circulatory effects as a result of the revolving (curvilinear) motion of the wing at a certain angle of attack. Normal and tangential force components were approximated based on steady-state mean values measured on the revolving wing at various angles of attack and Re. Steady-state mean values of force measurements at different angles of attack were interpolated to estimate revolution-related forces during the pitch-up motion. A similar approach was employed for the estimation of the revolving motion component during the acceleration phase of the surging case by use of force measurements performed on a revolving–surging wing at various Re at $45^{\circ }$ angle of attack.

The second term is the force due to inertia of the added mass of the fluid acting normal to the wing surface. It is estimated by use of an approximation derived for an infinitesimally thin two-dimensional plate moving in an inviscid fluid (Sedov 1965) and integrating the sectional values over the spanwise direction. For the rectangular wing model, the equation is simplified as follows:

$$\begin{aligned} F_{\rm inertial}=\rho \frac{\pi }{4} c^{2} \ddot{\phi } \sin {\alpha } \int _{r_{\rm root}}^{r_{\rm tip}} r \, \hbox{d}r + \rho \ddot{\alpha } \frac{\pi }{8} c^{3} b \end{aligned}$$

(2)

where $\rho$ is the fluid density, $\ddot{\phi }$ is the angular acceleration of the revolving motion and $r$ is the spanwise distance from the revolution axis, $\ddot{\alpha }$ is the angular acceleration of the pitch-up motion.

The last term in Eq. 1 is the contribution due to the pitch-up motion of the wing which also acts in the wing-normal direction. The pitching motion results in varying local velocities in the chordwise direction which in turn generates a varying effective angle of attack distribution along the chord. Similar as in the unsteady airfoil theory, this effect can be considered equivalent to adding camber to a nonpitching airfoil such that it imparts an identical downwash distribution along the plate. Likewise, the motion can be decomposed into two parts with regard to the mid-chord position: (1) a uniform motion of the plate at a velocity that is proportional to the pitch rate and the distance between the mid-chord position and the pitching pivot point; (2) a rotational motion of the plate about the mid-chord point. The former generates a uniform downwash distribution along the chordline, the value of which is constant for a constant pitch rate and fixed pitching point. This component can, hence, be interpreted as a dynamic angle of attack effect. The latter motion component induces a downwash that varies linearly with respect to mid-chord point, so that it can be considered as a dynamic camber effect.

Following thin airfoil theory and integrating the sectional contribution over the span of the wing, the theoretical estimation of this circulatory force component is given as (Ellington 1984; Granlund et al. 2013; Sane and Dickinson 2002):

$$\begin{aligned} F_{\rm rotation}=\rho \pi c^{2} \dot{\phi } \dot{\alpha } (0.75-\hat{x}_0) \int _{r_{\rm root}}^{r_{\rm tip}} r \, \hbox{d}r \end{aligned}$$

(3)

where $\dot{\phi }$ is the angular velocity of the revolving motion, $\dot{\alpha }$ is the angular velocity of the pitch-up motion and $\hat{x}_0$ is the nondimensional distance of the pitching pivot point from the leading edge.

Fig. 2

Kinematics of the a revolving–pitching and b revolving–surging motions

2.3 Tomographic particle image velocimetry

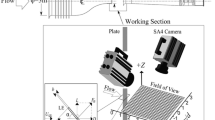
Three-dimensional quantitative information of the flow around the outboard section of the wing model was acquired via phase-locked tomographic PIV (Tomo-PIV) measurements (Scarano 2013). At each run, a double-frame image was captured at a specific phase of the wing motion. Repeated runs were performed with sufficient time intervals to restore quiescent conditions in the water tank. The measurement volume of $90\times 70\times 25$ mm³ in size (Fig. 3a)

Fig. 3

a Sketch of the top view of the experimental setup with camera arrangement, b wing model and measurement volume arrangement

was positioned at two different spanwise locations side by side as shown in Fig. 3b. Then, a Kriging regression technique (Baar et al. 2014) with a correlating length of 2 mm in all directions was used in order to combine the two measurement volumes and to provide a complete visualization of the flow field. The starting position of the wing was adjusted based on the desired measurement phase so as to have the wing oriented normal to the measurement volume during image acquisition. For each measurement phase, the experiments were repeated for three times and vector fields are ensemble-averaged in order to improve signal-to-noise ratio. The volume was illuminated by a double-pulsed Nd:Yag laser at a wavelength of 532 nm. Polyamide spherical particles of 56 μm diameter were employed as tracers at a concentration of 0.4 particles/mm³. The motion of tracer particles was captured by four 12-bit CCD cameras with a resolution of $1{,}376\times 1{,}040$ pixels and a pixel pitch of 6.45 μm. Three cameras were arranged along different azimuthal directions in a horizontal plane at an angle of $45^{\circ }$ with respect to each other while the fourth camera was positioned above the mid-camera in a vertical plane at an angle of $30^{\circ }$ with respect to the horizontal plane (Fig. 3a). Each camera was equipped with a Nikon 60-mm focal length objective with numerical aperture $f\#=11$. Scheimpflug adapters were used on the three off-axis cameras to align the mid-plane of the measurement volume with the focal plane. The digital resolution is 15 pixels/mm, and the average particle image density is approximately 0.04 particles per pixel (ppp). Image preprocessing, volume calibration, self-calibration, reconstruction and three-dimensional cross-correlation-based interrogation were performed in LaVision DaVis 8.1.5. The measurement volume was calibrated by scanning a plate with $9\times 10$ dots through the volume in depth of 25 mm with steps of 5 mm. In each calibration plane, the relation between the physical coordinates and image coordinates is described by a 3rd order polynomial fit. Linear interpolation is then used to find corresponding image coordinates at intermediate z locations. Image preprocessing with background intensity removal, particle intensity normalization and a Gaussian smooth with $3\times 3$ kernel size was performed in order to improve the volume reconstruction process. Particle images were interrogated using windows of final size $32\times 32\times 32$ voxels with an overlap factor of 50 %. The resultant vector spacing is 1.0 mm in each direction forming a dataset of $87\times 68\times 24$ velocity vectors in the measurement volume.

3 Results

3.1 Evolution of unsteady forces

Figure 4 represents the time variation of lift and drag coefficients for both revolving–pitching and revolving–surging motions. Note that for sake of comparison, the origin for the horizontal axis $(d^{*})$ has been defined such that the start of the pitch-up phase for the pitching wing and start of the acceleration phase for the surging wing (i.e., the two buildup phases) match and that for both cases the terminal condition is reached at $d^{*}=1$.

Fig. 4

Temporal evolution of a lift and b drag coefficients for the wings undergoing revolving–pitching (black) and revolving–surging (red) motions with theoretical estimations based on the quasi-steady model (dashed), c tangential (dashed) and normal (full) force coefficients for the wings undergoing revolving–pitching (black) and revolving–surging motions (red)

In the case of revolving–pitching wing motion, during the acceleration phase that precedes the pitch-up, the model experiences very low forces: nominally zero lift due to its zero angle of attack and a slight drag $(c_{\rm D}=0.08)$ which is attributed to added mass and skin friction contributions. This phase is then followed by the pitch-up motion, which is characterized by four prominent features: initial strong rise of the lift coefficient due to noncirculatory effects that is the result of the rotational acceleration at the onset of this phase; persistent and high lift coefficient values which also have an increasing trend during the period of constant pitch rate following the initial noncirculatory peak; nearly linear increase of the drag coefficient as the pitch angle increases; secondary noncirculatory peak in the opposite sense at the end of the motion due to the rotational deceleration of the model. The growth of lift and drag coefficients in this phase of the motion basically originates from the increasing angle of attack which has twofold effects on the force components: It promotes flow separation and growth of the LEV circulation which in turn enhance the circulatory force component; secondly, it results in the tilting of the wing-normal vector toward the horizontal direction so that the drag component of the normal force increases gradually with increasing angle of attack. These features are captured fairly well by the quasi-steady model albeit with a slight over-prediction of the magnitudes. Also, the added mass peaks due to acceleration and deceleration of the wing during the pitch-up motion are not reproduced precisely because the rotational acceleration of the waterproof servo motor is not a controllable and well-defined parameter and it was estimated roughly for the calculations. A further source of discrepancy for the constant velocity pitch-up phase of the motion originates from the fact that the force component due to the revolving motion $(F_{\rm revolution})$ is estimated based on the steady-state force values of experimental cases for wings undergoing revolving motion at various angles of attack. These steady-state values are reached approximately $4c$ of travel after the start of the motion in the experiments, whereas in the model it is assumed that the wing generates that level of circulatory force as soon as it reaches a certain angle of attack during the pitch-up motion. However, it takes a finite time for the growth of circulation so that the wing does not achieve such levels of forces for a given angle of attack immediately. Furthermore, the theoretical estimation of the $F_{\rm rotation}$ is essentially based on the calculation of the bound circulation of a wing with an established Kutta condition during the pitching motion in the context of potential flow theory. However, in reality, the wing does not reach that state in the pitch-up phase (i.e., it does not generate that amount of circulation nor does it fully establish the Kutta condition), which might be considered as another source for the overprediction of the forces. Subsequently, after completion of the pitch-up motion and with the model revolving at a constant rate at $\alpha =45^{\circ }$, force coefficients increase slightly, reaching a maximum at around $d^{*}=5.4$ ($c_{\rm L}=1.10$ and $c_{\rm D}=1.07$). After a following decrease of the forces, more-or-less steady-state values ($c_{\rm L}=0.98$ and $c_{\rm D}=0.96$) are reached at approximately d ^* = 7.

In the revolving–surging wing case, the acceleration phase should in principle display a constant noncirculatory force contribution and gradually increasing circulatory force, while some spurious force peaks can be observed that are attributed to test rig vibrations as a result of the impulsive start of the motion. The force coefficients peak at the end of the acceleration phase, which is then followed by a slight decrease and a subsequent increase due to circulatory effects until they reach maximum values ($c_{\rm L}=1.07$ and $c_{\rm D}=0.99$) after 4.3 chord lengths of travel with respect to the start of the motion. Subsequently, forces decrease to steady-state values which are equal to those of the revolving–pitching wing case. Theoretical estimation of the forces in the acceleration phase of the motion yields reasonable values also for this case. The added mass contribution evident at the very start of the motion is calculated in a reasonable approximation, while the contribution due to the revolving motion (i.e., circulatory component) is estimated less accurately due to the use of steady-state values of revolving wing experiments at different Re, which are higher than those of a wing during the buildup phase of the LEV and associated circulation. This results in overestimation of the lift and drag coefficients.

It is clear that in both cases, mainly normal forces are generated throughout the complete motion, whereas tangential forces remain insignificant (Fig. 4c). During the pitch-up period, the normal force can be considered as superposition of the rotational contribution (calculated as approximately 2.6 by use of the quasi-steady model) and the increasing contribution of the circulatory component with the increasing angle of attack. At smaller angles of attack, a small tangential force is generated (with a maximum of $c_{\rm T}=0.18$) but it vanishes with increasing angle of attack. This force most probably stems from a leading-edge suction effect: A positive tangential force is generated due to acceleration of the fluid around the sharp leading edge which transforms into a normal force component with the increase of angle of attack beyond the static stall limits and formation of the LEV (Gülçat 2010), also known as Polhamus’ leading-edge suction analogy (Polhamus 1971). In the case of the revolving–surging wing, mostly normal forces are generated which is in accordance with the findings of Birch et al. (2004) who showed that even at relatively low Re, the force vector is normal to the wing surface, indicating the dominance of pressure forces. In the post-buildup phase of both motions, the pitching moment displays steady characteristics yielding a stationary center of pressure at approximately $0.4c$ chordwise position.

The most prominent difference between the force histories of the two cases is the substantially different force generation during the initial phases of both motions in which the pitching wing outperforms the surging wing, with the latter hardly reaching the level of steady-state values. In the subsequent phase of both motions, from $d^{*}=1$ until $d^{*}=7$, the two cases display slightly different force histories with the revolving–pitching wing producing higher lift and drag in general. There is a local maximum in the force histories of both cases, appearing earlier for the revolving–surging motion. Apparently, the different start-up of the motion and buildup of the forces affect the evolution of forces and accordingly flow structures at least until six chords of travel after the buildup phase has ended.

3.2 Three-dimensional flow fields

Three-dimensional flow structures around the outboard part of the revolving flat plate are visualized by means of isosurfaces of nondimensional Q criterion $(Q/(V_{\rm t}/c)^{2})$ for both motions. Three-dimensional vortical structures are complemented with contour plots of nondimensional out-of-plane vorticity $(\omega _{z} c/V_{\rm t})$ and out-of-plane velocity (viz. spanwise velocity - $V_{z}/V_{\rm t}$) in the reference plane at 75 % wing span, to facilitate interpretation of the results. Only half of the flat-plate model is depicted in the figures, whereas the spanwise extent of the flow measurement domain ranges from approximately 0.62 to 1.12 of the wing span (see Fig. 3b). The start of the pitch-up phase of the revolving–pitching wing motion is defined as $d^{*}=0$ to match motion kinematics for both cases, similar as in the representation of the force data. The pitch-up phase of the revolving–pitching wing motion is resolved by two instants that are the mid-pitch-up ($d^{*}=0.5$ and $\alpha =22.5^{\circ }$) and the end of the pitch-up ($d^{*}=1$ and $\alpha =45^{\circ }$) in Fig. 5

Fig. 5

Isosurfaces of $Q/(V_{\rm t}/c)^{2}=3.125$ colored by vorticity magnitude (first row), contours of nondimensional out-of-plane vorticity ($\omega _{z} c/V_{\rm t}$) in the reference plane (second row) and contours of nondimensional spanwise velocity ($V_{z}/V_{\rm t}$) in the reference plane (third row) plotted in the buildup phase (the pitch-up phase of the revolving–pitching motion and the acceleration phase of the revolving–surging motion) for the revolving–pitching and revolving–surging cases (the rectangular zone that was used in the calculation of the spanwise vorticity flux is shown in the out-of-plane vorticity plot of the revolving–surging wing case at $d^{*}=1$)

. The subsequent part of the motion is represented by four phases ($d^{*}=2, 3, 4$ and $5$) in Figs. 6 and 8. Likewise, the accelerating part of the revolving–surging case is investigated in two instants corresponding to half-way acceleration ($d^{*}=0.5$, and wing speed $V=0.71V_{\rm t}$) and end of the acceleration ($d^{*}=1$ and $V=V_{\rm t}$) in Fig. 5, whereas the ensuing period of the motion is captured at six consecutive instants ($d^{*}=1.5, 2, 3, 4, 5$ and $6$) in Figs. 6 and 8. Note that every chord of travel in the reference plane corresponds to $\phi =25.8^{\circ }$ of rotation and the wing completes one full revolution approximately at $d^{*}=14$ so that presented data are not affected by the interaction of the wing with its own wake.

Fig. 6

Isosurfaces of $Q/(V_{\rm t}/c)^{2}=3.125$ colored by vorticity magnitude (first row), contours of nondimensional out-of-plane vorticity $(\omega _{z} c/V_{\rm t})$ in the reference plane (second row) and contours of nondimensional spanwise velocity $(V_{z}/V_{\rm t})$ in the reference plane (third row) plotted at two instants ($d^{*}=2$ and 3) for the revolving–pitching and revolving–surging cases

In addition to the visualization of the flow structures, the position and cumulative circulation of the LEV (or LEVs in the case of presence of secondary LEVs) is calculated based on the spanwise component of vorticity $(\varGamma =\iint _A \,\omega _{z} \, \hbox{d}x\, \hbox{d}y)$ in the reference plane and it is nondimensionalized by $V_{\rm t}$ and $c \, (\varGamma ^{*}=\varGamma /(V_{\rm t} c))$. The center of the LEV is tracked by use of the $\gamma _{1}$ scheme, which is primarily based on the topology of the vector field (Graftieaux et al. 2001). As this algorithm is not Galilean invariant, the calculations were performed in a noninertial coordinate system that is moving with the wing. In the case of multiple LEVs present in the flow field, the position of the initial most coherent vortex was registered. In order to define the calculation region for the LEV circulation, the vortex core detection algorithm is employed $(\gamma _{2})$ as described by Graftieaux et al. (2001). Cumulative LEV circulation for each instant of both motions was calculated by integrating the spanwise component of vorticity within the $\gamma _{2}=2/\pi$ contours. Moreover, the flux of the spanwise component of vorticity $(q=\iint _A \,V_{z} \,\omega _{z} \, \hbox{d}x\, \hbox{d}y)$ is calculated at several chordwise-oriented planes in the first measurement volume and nondimensionalized by $V_{\rm t}^{2}c$. The integration was performed on the data points which satisfy the criteria of $\omega _{z}c/V_{\rm t}>1.25$ and $\mid V_{z}/V_{\rm t} \mid >0.01$ (note that the selection of the precise threshold values is not critical and use of different values does not lead to significantly different results). The calculation region was defined as a rectangular zone that is limited by the leading edge and a half-chord distance aft of the trailing edge in $x$ direction. The lower edge in $y$ direction is aligned with the trailing edge position, whereas the upper edge coincides with the border of the field of view (see the spanwise vorticity plot at $d^{*}=1$ of the revolving–surging case in Fig. 5).

3.2.1 Flow-field structure

Temporal evolution of flow structures during the buildup phases of the motions (pitch-up phase in the pitching motion, acceleration phase in the surging motion) are shown in Fig. 5. The flow field around the pitching wing at the mid-pitch-up position $(d^{*}=0.5)$ stands out with well-defined and coherent vortical structures, i.e., a LEV, a TV and a trailing-edge vortex (TEV) as the starting vortex of the motion. These initial structures are all connected to each other and have two-dimensional characteristics at the mid-pitch-up phase with no appreciable spanwise flow pattern present in relation to the vortex positions (see bottom diagram). However, this scene has changed at the end of the pitch-up motion $(d^{*}=1.0)$: The TEV extends toward the wake of the wing model while sustaining its linkage to the TV; the TV has a conical shape with swirling features of small-scale vortical structures which appear around the base of the conical formation and extend along the trailing edge as secondary TEVs (present as a train of vorticity structures in the contour plots of out-of-plane vorticity); the LEV is larger in size and slightly tilted downstream in the inward region of the wing. The vorticity patterns visualized in the reference plane bear a close resemblance to the measurements of a translating–pitching plate under similar conditions, as reported by Yu and Bernal (2013). Although a similar vortex loop structure is observed in the revolving–surging wing motion case, these structures display different characteristics in terms of coherence. Clearly, at the position of $d^{*}=0.5$, the TV already displays slightly fragmented formation which becomes more evident in the following instant ($d^{*}=1$). The TV is divided into swirling features at the bottom side, and these are all connected to a train of co-rotating trailing edge vortices as in the revolving–pitching wing case. Although both cases have similar morphology in terms of vortical structures, it may be observed that in the pitch case, the LEV is positioned closer to the wing surface and the TEV is stronger due to the high trailing edge velocity induced by the pitching motion. Moreover, the evolution of spanwise flow in the reference plane occurs differently. At the mid-pitch position, contours of positive spanwise flow (toward the wing tip) on the upstream side of the wing and negative spanwise flow (toward the wing root) on the downstream side of the wing are present while no considerable spanwise flow occurs around the wing in the reference plane in the middle of the acceleration phase in the revolving–surging motion. As the motion progresses for both cases, the positive spanwise flow pattern appears around the trailing edge on the downstream side of the wing in accordance with the evolution and positioning of the tip vortex.

At the position of $d^{*}=2$, when the constant final motion has been established for one chord of travel (Fig. 6), in the revolving–pitching wing case, the LEV has burst into smaller structures and lifts off from the wing surface. The TV, on the other hand, loses its conical shape and starts segmenting into longitudinal structures extending along the tip. On the inner side of this segmented structure, there is still a coherent vortex formation extending into the wake and connecting to the starting vortex. Previously shed clockwise-rotating secondary TEVs are coupled with the counter-rotating vortical structures which are derived from counterclockwise vorticity formed during the pitch-up motion of the wing. The segmentation of the TV and the burst of the LEV become more significant in the following phase $(d^{*}=3)$. The initial LEV still stays in the vicinity of the wing but is located more downstream of the leading edge, whereas a large segment of the TV also unpins from the wing surface. A similar behavior of the LEV is observed also in the revolving–surging wing case. At $d^{*}=2$, the initial LEV is clearly detached from the wing surface and secondary small-scale vortical structures emanate from the leading edge, which appear as individual blobs in the shear layer extending from the leading edge in the out-of-plane vorticity contours in the reference plane. The TV is more fragmented with respect to that of the revolving–pitching motion, and a series of finger-like corotating TEVs are shed from the trailing edge. At the position of $d^{*}=3$, the vortex formations display less coherent and more chaotic features. Notwithstanding significant differences in the spanwise flow patterns during the buildup phases of both cases, they now generate qualitatively similar flow fields in the reference plane albeit with different magnitudes. In both cases, at $d^{*}=2$, the spanwise flow is confined within the LEV and TEV and it is directed toward the tip. The existence of such a flow pattern can be explained by the three-dimensionality of the vortex system and the associated presence of a pressure gradient in the spanwise direction. As the motion continues and the LEV moves downstream, the spanwise flow pattern that is initially located near the leading edge starts to move along the wing chord toward the trailing edge.

To better visualize the vortex formations at the phase of $d^{*}=2$, when the departure of the initial LEV from the leading edge and instabilities at the substructure level are observed for the first time, close-up views of isosurfaces of Q criterion colored by helicity density are shown in Fig. 7. Helicity density is the dot product of the velocity and vorticity vectors, integral of which is the helicity that is associated to the topology of the vortex lines in terms of having knots or linkages (Moffatt and Tsinober 1992). Helicity density is also used for the detection of the vortex cores (Degani et al. 1990), and nonzero helicity indicates a helical vortex structure with an axial flow. In the case of revolving–pitching motion, the LEV forms an arch-shaped structure with its outboard leg pinned around the wing-tip corner. The inboard structure is not captured due to the limited extent of the measurement domain, but is presumed to display an inner leg reattachment inboards closer to the root. The revolving–surging wing has a similar arch-shaped structure, which was also reported by Garmann et al. (2013) for a lower-aspect-ratio wing and different acceleration kinematics and by Carr et al. (2013) for different acceleration kinematics. However, the outer leg of this structure does not attach to the wing surface at the front corner but slightly more toward the trailing edge (near 0.4c). There are also secondary vortex formations rolling around the lifted-off LEV. In both cases, a helical LEV structure is present with a positive helicity density that is indicative of outward spanwise flow aligned with the vorticity vector (as evident in Fig. 6). This implies flux of vorticity with the axial flow. The occurrence of counter-rotating vortical elements below the TEV in the pitch case and their absence for the surge case, as discussed in relation to Fig. 6, is also evident in the side views of Fig. 7.

Fig. 7

Isosurfaces of $Q/(V_{\rm t}/c)^{2}=5$ colored by helicity density (red positive; blue negative) plotted at the position of $d^{*}=2$ for the revolving–pitching and revolving–surging cases (above top view, below side view)

Fig. 8

Isosurfaces of $Q/(V_{\rm t}/c)^{2}=4.375$ colored by vorticity magnitude (first row), contours of nondimensional out-of-plane vorticity $(\omega _{z} c/V_{\rm t})$ in the reference plane (second row) and contours of nondimensional spanwise velocity $(V_{z}/V_{\rm t})$ in the reference plane (third row) plotted at two instants $(d^{*}=4$ and 5) for the revolving–pitching and revolving–surging cases

Fig. 9

Isosurfaces of spanwise velocity [$V_{z}/V_{\rm t}=-0.25$ (blue) and $V_{z}/V_{\rm t}=0.25$ (yellow)] plotted throughout the motion for the revolving–pitching and revolving–surging cases

In the subsequent phases of the motion, the coherency of the initial vortex system is completely lost and there are small-scale unsteady substructures spread over an increasing part of the measurement volume (Fig. 8). Notwithstanding the obscurity created by these incoherent structures (note that a slightly higher isovalue for the Q criterion is used in Fig. 8 in order to avoid overemphasis of these structures), there are still certain features similar to both cases: feeding of leading-edge vorticity in the form of consecutive longitudinal structures extending along the leading edge; linkage between these secondary leading-edge structures and the vortex formations of the wing tip, which are not attached to the wing surface all along the tip. The contour plots of out-of-plane vorticity in the reference plane show that vorticity layers in the case of revolving–pitching motion tend to be more curved toward the wing in the wake at both instances which can explain generation of higher forces in this case. Arguably, the relative positioning of these vorticity layers will become virtually identical to that of the revolving–surging wing case after approximately $d^{*}=7$ when the two cases display similar steady-state force generation. The spanwise velocity contours also reflect the phase difference between the two cases as at the position of $d^{*}=5$, the streamwise flow pattern is mostly concentrated around the trailing edge for the surging wing, whereas strong spanwise flow is still present up to half-chord length for the pitching wing. However, in general, both cases display similar behavior, which involves the translation of spanwise flow toward the trailing edge as the motion progresses such that there remains no significant spanwise flow pattern around the leading edge.

To complement the planar view of the spanwise flow patterns, a volumetric representation for the different phases is provided by means of isosurfaces of spanwise velocity ($V_{z}/V_{\rm t}=-0.25$ (blue) and $V_{z}/V_{\rm t}=0.25$ (yellow)) in Fig. 9. It is evident that as a result of higher pressure difference (thus higher lift) between the pressure and suction sides of the wing during the pitching motion, a stronger spanwise flow pattern that is dominated by the tip vortex is formed in the pitch-up phase ($d^{*}=0.5$ and 1). The region of strong spanwise flow in the case of the surging wing remains rather confined to the vicinity of the wing tip in accordance with the segmented structure of the tip vortex. At $d^{*}=2$, in the revolving–pitching wing case, the tip vortex is still the dominant factor in the formation of spanwise flow in most part of the measurement volume. However, there appears a flow pattern directed toward the tip in the inner side of the measurement volume around the leading edge, which is formed by the increasing effects of centrifugal forces and spanwise pressure gradient (Garmann et al. 2013), especially around the leading edge due to three-dimensional nature of the LEV. In the case of the revolving–surging wing, this outward flow pattern overcomes the inward flow generated by the tip vortex and extends along the leading edge until the wing tip. As a consequence, the tip vortex loses its coherence and detaches from the wing-tip corner. A similar state is achieved in the case of revolving–pitching wing case after one more chord length of travel $(d^{*}=3)$, which is in correlation with the lag in the temporal evolution of the forces. In the following instants of the motion, the spanwise flow pattern which is confined in the core of the LEV moves toward the trailing edge and secondary consecutive LEVs emanate from the leading edge in both cases. Comparison of Figs. 8 and 9 reveals that in the later phases of the motion, discrete tip vortex formations only emerge at the upper half-chord of the wing, where there is no pattern of outward spanwise flow.

3.2.2 LEV circulation

Comparison of the temporal evolution of the LEV circulation (Fig. 10) reveals that the circulation increases rapidly in the buildup phases of both motions. Yet this increase has a higher pace in the revolving pitching case which results in a larger LEV circulation at the end of the buildup phase. The increasing trend of the circulation during the pitch-up motion is interrupted at the end of the buildup phase. This decline in the progression of the circulation for the revolving–pitching wing is correlated with termination of the pitching motion, the shedding of the counterclockwise leading-edge vorticity from the trailing edge and the liftoff of the LEV at $d^{*}=2$ (see Fig. 6). Once the final motion is settled, both cases display similar values until $d^{*}=4$. The circulation level peaks at this position in the surging case in accordance with the position of the maximum force generation $(d^{*}=4.3)$. In a similar manner, the circulation continues to rise in the case of pitching motion as the maximum force is reached approximately at $d^{*}=5.4$.

Fig. 10

Temporal evolution of the LEV circulation

However, the differences in the temporal evolution of the LEV circulation by themselves are not sufficient to explain the differences in the resultant forces particularly for the buildup phase when significantly larger forces are produced in the revolving–pitching case. The relation between the vorticity (hence, circulation) and force generation can be interpreted by use of the vorticity moment theory described by Wu (1981), which reads for three-dimensional flows:

$$\begin{aligned} {\mathbf{F}}=-\frac{1}{2} \rho \frac{d}{dt} \int _{R_{\rm f}+R_{\rm b}} {\mathbf{p}} \times {\mathbf{\omega}} \, \hbox{d}R + \rho \frac{d}{dt} \int _{R_{\rm b}} {\mathbf{v}} \, \hbox{d}R \end{aligned}$$

(4)

where ${\mathbf{p}}$ is the position vector in a global reference frame, ${\mathbf{\omega}}$ is the vorticity vector, ${\mathbf{v}}$ is the body velocity, and $R_{\rm f}$ and $R_{\rm b}$ are the fluid volume and body volume, respectively. Eq. 4 states that the force exerted on the body can be calculated from the time rate of change of the total first moment of the vorticity field in the complete fluid domain including the body (first term) and the inertial force due to the mass of fluid displaced by the solid body (second term). For thin plates, the contributions from the body integrals can be neglected. Thus, it can be inferred from the first term that it is not only the temporal evolution of total amount of vorticity that affects the force generation, but also the temporal variation of its distribution in the flow field. Moreover, assessment of the resultant force requires consideration of the temporal variation of the moment of the complete vorticity field rather than that of the vorticity accumulated only in the LEV. For instance, in the buildup phases of both motions (Fig. 5), the TEVs are still partially moving with the wing (from $d^{*}=0.5$ to $d^{*}=1$, the starting vortex travels approximately $0.3c$ with the wing for the pitching case and $0.23c$ for the surging case in $x$ direction as calculated in the reference plane) while also growing in strength. Therefore, it is plausible to state that the moment of vorticity of the TEVs is changing in time so that it still contributes to the first term in Eq. 4, in an opposite sense with respect to the LEV in both cases. It should also be noted that the theorem can be applied to the experimental data correctly as long as the field of view of the measurements covers the entire generated vorticity.

In order to better evaluate the effect of the LEV on the force generation, its position is tracked throughout both motions and the diagonal distance between the leading-edge corner and the core of the LEV ($s$) is determined (Fig. 11). It is clear that for most part of the motion, the LEV stays relatively close to the leading edge in the revolving–pitching wing case. After $6c$ of travel in the revolving–surging motion, the initially coherent LEV cannot be captured in the reference plane anymore most probably due to bursting and inclination of the vortex structure with respect to the chordwise-oriented reference plane so that the $\gamma _{1}$ algorithm detects secondary smaller-scale LEVs emanating from the leading edge instead.

Fig. 11

Temporal evolution of the nondimensional distance $(s/c)$ between the leading-edge corner and the core of the LEV

In order to estimate sectional forces from the flow data in the reference plane, the two-dimensional form of Eq. 4 is considered:

$$\begin{aligned} l=-\rho \frac{\hbox{d}}{\hbox{d}t} \int _{A_{{\rm f}}+A_{\rm b}} {\omega _{z}} x \, \hbox{d}A + \rho \frac{\hbox{d}}{{\rm d}t} \int _{A_{{\rm b}}} v \, \hbox{d}A \end{aligned}$$

(5)

where $x$ is the horizontal distance measured from the origin of the global coordinate system, $A_{\rm f}$ and $A_{\rm b}$ are the fluid and body areas, respectively. Obviously, such an analysis can only be performed in the buildup phases of both motions for the present study as these are the only stages of motions when the starting vortex and secondary TEVs could be captured mostly in the field of view. The moment of the spanwise component of vorticity $(|\omega _{z}c/V_{\rm t}|>1.25)$ was calculated in the reference plane with respect to a global coordinate system that was positioned at $1c$ of distance from the leading edge at the start of both buildup phase. By use of the two available time instants of the buildup phases, the corresponding sectional lift coefficients are estimated as 3.38 and 1.15 for the pitching and surging cases, respectively. These values practically correspond to forces at approximately $d^{*}=0.75$ of both motions, whereas the actual measured values are 2.8 and 0.78 for the pitching and surging wings, respectively. Overestimation of the forces is mainly attributed to the use of a two-dimensional approach to calculate sectional lift from the velocity fields in the reference plane which does not account for the three-dimensional effects present in the finite span wing. Additional sources of errors which may contribute to the discrepancy between the calculated and measured values are: (1) the low temporal resolution of tomographic PIV data in the buildup phases of both motions in view of the discrete sampling of the motion, which results in a poor representation of the development in the buildup phases when forces vary significantly in time; (2) not capturing a part of the wake and thus of the trailing edge vorticity at $d^{*}=1$ stage of the pitching wing case (this is compensated for in the present analysis by use of Kelvin’s circulation theorem and locating the “missing circulation” at the centroid of the wake vorticity); and (3) incapability of the current tomographic PIV setup in accurately resolving the velocity field in the close vicinity of the wing due to low effective spatial resolution (interrogation volume size of $2\times 2\times 2\,\hbox {mm}$) when compared to the wing thickness (which is 3 mm). The last subject is of particular importance to account for the bound circulation (in case generated throughout the motion) that can contribute substantially to the temporal variation of the vorticity moment (thus forces) as it translates with the wing. The presence of bound circulation and its contribution to the resultant forces in the buildup phases of both motions are addressed subsequently.

3.2.3 Rotational forces

The revolving–pitching wing generates significantly greater lift in the pitch-up phase with respect to the surging wing in the acceleration phase (approximately 3.6 times that of the surging wing at $d^{*}=0.75$). However, there is not such a significant difference observed in the circulation and trajectory histories of the LEVs. In the above calculation of sectional lift, it was found that the contribution of the LEV to the time rate change of the moment of vorticity term in the pitching case is approximately 1.7 times that of the surging case. However, this ratio does not necessarily reflect directly in the forces because the contribution of negative vorticity emanating from the trailing edge ($20\,\%$ higher in the pitching case) is also influential on the resultant force. Moreover, only 50–60 % of the total positive circulation is accumulated in the LEV defined by the $\gamma _{2}=2/\pi$ contours for the pitching wing case, whereas it reaches $80\,\%$ for the revolving–surging wing in the buildup phase. These differences suggest the generation of bound circulation by the revolving–pitching wing. Bound circulation in the present discussion is understood as the vorticity accumulated in the close vicinity of the plate. This is verified by the use of two methods: (1) comparing the circulation of the LEV with the total circulation of the negative vorticity emanating from the trailing edge; (2) calculating the circulation in an arbitrary contour that includes the complete wing, the LEV and part of the trailing edge vorticity as the line integral of velocity along the contour, then subtracting the LEV and included negative circulation of the trailing edge region to obtain the bound circulation value (Fig. 12).

The first method is principally based on the application of the Kelvin’s circulation theorem that implies conservation of angular momentum such that the total circulation of the flow is constant in time and equal to the initial value of zero as there is no net circulation when the fluid and the wing are at rest. Although the theorem is not strictly valid in a plane of a three-dimensional flow structure, the two-dimensional nature of the vortical structures (i.e., LEV and TEVs) that carry majority of the spanwise vorticity at the early stages of the motion justifies the application of the method in the reference plane in the present study. Furthermore, the second method, which is an application of the Stokes’ theorem, is used as a means of verification.

Fig. 12

Regions of integration for the calculation of the bound circulation in the buildup phases of revolving–pitching (top) and revolving–surging (bottom) cases: (1) Negative spanwise vorticity (blue) is integrated within the red rectangle with a threshold of $\omega _{z}c/V_{t}<-1.25$, whereas positive spanwise vorticity (red) is integrated within $\gamma _{2}=2/\pi$ contours (black) to calculate the LEV circulation; (2) the total circulation is calculated within an arbitrary rectangle (dashed green) by integrating the velocity around the edges

According to Kelvin’s circulation theorem, the circulation of the LEV should be equivalent to that of negative vorticity, in case of zero bound circulation and low levels of vorticity deposited in the feeding shear layer of the leading edge. Indeed for the revolving–surging wing case, both methods yield very small values of positive excessive circulation around the wing $(\varGamma ^{*}<0.08)$ at $d^{*}=0.5$. At the stage of $d^{*}=1$, this value of positive excessive nondimensional circulation calculated by both methods is about 0.3. However, closer inspection reveals that this excessive part originates from the feeding shear layer between the two LEV contours and some layers of vorticity around the LEV contours defined by $\gamma _{2}=2/\pi$ at $d^{*}=1$. Therefore, it is plausible to conclude that the surging wing does not generate appreciable bound circulation in the acceleration phase. This is in accordance with the findings of Pitt Ford and Babinsky (2013), who showed that for the translating wing case at $15^{\circ }$ angle of attack (impulsively accelerated from rest), bound circulation remains relatively small initially and most of the positive circulation is accumulated inside the LEV. Recently, they also showed that the bound circulation is negligible in the first chord and a half of travel after an impulsive start for a flat plate at both $15^{\circ }$ and $45^{\circ }$ angle of attack (Pitt Ford and Babinsky 2014).

On the other hand, comparison of the LEV and negative trailing edge vorticity circulations at the mid-pitch-up phase of the revolving–pitching motion reveals that trailing edge vorticity circulation is roughly twice that of the LEV, whereas they are almost equal in the mid-acceleration phase of the revolving–surging motion. In physical terms, this can be understood as promotion of the trailing edge separation due to the higher trailing edge velocity induced by the pitching motion. Analysis of the flow field by both of the methods shows that the wing has a bound circulation at an equivalent value with the LEV at this instant $(\varGamma _{LEV}^{*}\approx \varGamma _{bound}^{*}=0.5)$. At $d^{*}=1$, a slightly higher bound circulation value is found $(\varGamma _{bound}^{*}=0.6)$, around $80\,\%$ of which is accumulated in the vorticity layer distributed along the chord. Although an accurate quantification is difficult due to the presence of the LEV and the feeding shear layer with positive vorticity (particularly at the end of the buildup phase) around the wing, there is a clear evidence that the pitching wing generates a bound circulation at least roughly at a value of $\varGamma _{bound}^{*}=0.48$. This can also be inferred from the shedding of positive vorticity from the trailing edge after the pitching motion is over (see $d^{*}=2$ of the revolving–pitching motion in Figs. 6 and 7).

In the context of the unsteady thin airfoil theory, as discussed earlier, the prediction of the rotational force is based on the generation of additional bound circulation in order to establish the Kutta condition and can be interpreted as a consequence of dynamic angle of attack and dynamic camber effects. Under the current conditions, with large-scale flow separation present, the increase in the LEV circulation is associated with the dynamic angle of attack effect, whereas the generation of bound circulation can likely be understood as an attempt to satisfy the Kutta condition during the pitching motion although the wing never reaches a fully established state as evident from the continuous shedding of trailing edge vorticity. This may also explain why the theoretical estimation of the rotational circulation (Sane and Dickinson 2002) is significantly higher $(\varGamma _{rot,theo}^{*}=1.7)$ than the bound circulation value measured in the experiments.

Clearly, the increased force generation of the pitching motion under the current conditions originates from relatively favorable characteristics of the LEV and TEV in addition to the generation of bound circulation. The contribution of the LEV is twofold: (1) the higher magnitude of circulation as well as higher growth rate ($\hbox{d}\varGamma ^{*}_{\rm LEV,pitch}/\hbox{d}t^{*}=1.5$ and $\hbox{d}\varGamma ^{*}_{\rm LEV,surge}/\hbox{d}t^{*}=0.8$); (2) the tendency of the LEV to remain closer to the wing. Contrary to the LEV, the starting vortex moves further from the wing in the pitching case (at $1.34c$ and $1.52c$ horizontal distance from the leading edge at $d^{*}=0.5$ and $1$, respectively) than in the surging case ($0.97c$ and $1.24c$, respectively), which reduces its negative effect on the resultant force and yields an enhanced lift. Furthermore, the contribution of the measured bound circulation based on the two-dimensional vorticity moment theory could reach approximately $\Delta {c_{\rm l}}=1$ in the ideal case (assuming that its counterpart with opposite circulation stays stationary at the starting position), which could then account for nearly $50\,\%$ of the difference between the pitching and surging cases. However, this is an optimistic assumption as the TEVs do not fully shed and stay stationary in the global coordinate system during the buildup phase, but rather translate with the wing while increasing in circulation.

3.2.4 Spanwise vorticity flux

Comparison of the flux of the spanwise vorticity component (Fig. 13) also reveals differences in the temporal progression of the flow in the two cases. At the initial stage of both motions ($d^{*}=0.5$ and 1), there is negligible vorticity flux throughout the measurement volume. At $d^{*}=2$ in both motions, the overall magnitude of the flux has increased with a significant spanwise variation. It should be noted that the gradient of the flux in the spanwise direction is the summation of vorticity advection term and stretching term. In the case of a positive spanwise gradient, it can be considered that positive spanwise vorticity is transported in the spanwise direction (Kim and Gharib 2010). However, in the pitch-up case, there is a steep decrease of the flux in the spanwise direction. In the surge case, on the other hand, the flux value increases until 70 % span position and decreases afterward at a relatively low rate. The negative gradient is an indication of vorticity accumulation in a given plane. However, this does not necessarily result in an increase in the circulation values as advection of the vorticity in the in-plane directions and the vortex-tilting mechanisms also affect the resultant change of the vorticity in the plane. For instance, at $d^{*}=2$, the LEV is lifted off from the wing surface forming an arch-shaped structure (see Fig. 7) which contains $x$ and $y$ components in addition to the $z$ component of vorticity. The tilting of the LEV results in the steep decrease of the flux in the spanwise direction. Subsequently, in the revolving–surging motion case, the magnitude of the vorticity flux decreases to a zero level gradually with no significant gradient in the spanwise direction. The revolving–pitching wing, on the other hand, displays different evolution also in terms of vorticity flux such that the magnitude of the flux remains relatively high with respect to the surging case at $d^{*}=3$ and 4 while showing noticeable spanwise variation; at the last position $(d^{*}=5)$, although it levels at zero at the inward stations, the flux value increases toward the tip with a significant gradient.

Fig. 13

Spanwise vorticity flux calculated at different chordwise planes plotted at different phases of a revolving–pitching, b revolving–surging motions

4 Conclusions

The flow field around an accelerated revolving low-aspect-ratio flat-plate wing has been investigated experimentally via tomographic PIV. Two different motion kinematics were used to transfer from rest to the final steady-state condition over one chord length of travel (based on the reference plane position at 75 % wing span): (1) the revolving–pitching motion, in which the wing first accelerates to the terminal velocity at $0^{\circ }$ angle of attack, then pitches up to $45^{\circ }$ about its leading edge with a constant pitch rate (corresponding nondimensional pitch rate k = 0.39); (2) the revolving–surging motion, in which the wing accelerates to the terminal velocity at a constant acceleration rate and at a constant angle of attack. Each motion then continues in revolution with a constant velocity at a fixed angle of attack. The reference terminal velocity is 0.2 m/s in both cases corresponding to a Reynolds number of 10,000. Tomographic PIV measurements were taken in two adjacent volumes, providing a total measurement volume of size $90\times 70\times 50 \, \hbox{mm}^{3}$ (chordwise $\times$ normal $\times$ spanwise). A water-submergible force sensor was used to measure the fluid forces on the wing model.

Comparison of force histories of both cases reveals that, as expected, the wing generates considerably higher lift and drag during the pitch-up motion when compared to the acceleration phase of the revolving–surging motion. The lift coefficient reaches 2.5 times the steady-state value, and drag displays a quasi-linear increase during the pitch-up phase. The quasi-steady model predicts the forces fairly well in terms of temporal variation and magnitude in the buildup phase of both cases. In the post-buildup phase, although the wing moves with the same kinematics in both cases, the revolving–pitching motion continues generating higher lift and drag coefficients until six chords of travel after the end of the pitch-up motion. During this period, both lift and drag peak and subsequently decrease to the steady-state values relatively later (difference of one chord length of travel) in the revolving–pitching wing case. Apparently, the buildup phase of the motion affects the following force evolution in terms of both amplitude and phase of the maximum force generation. Predominantly, wing-normal forces are generated in the post-buildup phase of both motions.

In general, the flow fields during the buildup phases of both kinematics display a vortex system comprising an LEV, a TEV and a TV. This vortex system, especially the tip vortex, shows different characteristics in terms of integrity already in the middle of the buildup phases: The pitching wing generates a conical TV and a well-defined LEV; the surging wing displays a TV with a fragmented structure at the lower half of the vortex. As the wing reaches the end of the acceleration phase, this fragmentation becomes more prominent with swirling features of vortical structures that are linked to secondary trailing edge vortices. The disintegration of the TV also occurs in the case of pitching wing with shedding of secondary trailing edge vortices during the buildup phase; however, it is not as severe as for the surging case. In accordance with what was reported by Carr et al. (2013), the liftoff of the LEV is observed at $d^{*}=1\, (\phi =25.8^{\circ })$ for the first time in the surging case. As of $d^{*}=2$, the flow fields display small-scale substructures appearing in the vortex system in both cases. The arch-shaped LEV is clearly visible at $d^{*}=2$ $(\phi =51.6^{\circ })$ for both cases. The outer leg of this structure is attached at the wing-tip corner in the pitching wing case, whereas it is unpinned from the wing surface and attached back near $40\,\%$ of the chord length in the surging case. Seemingly, the surging wing precedes the pitching wing in terms of flow-field evolution, which is also evident in the isosurfaces of spanwise velocity (Fig. 9): The state of dominant outward spanwise flow driven by the centrifugal forces and pressure gradient in the core of the LEV is reached earlier in the surging wing case. In the following phases of both motions, the spanwise flow pattern which is confined in the core of the LEV moves toward the trailing edge and secondary consecutive LEVs emanate from the leading edge in both cases. In general, the flow fields have then become chaotic and populated with several substructures.

Apparently, the interaction between the tip vortex and the spanwise flow determines the coherence and the attachment of the tip vortex. The formation of a strong TV during the buildup phase of the revolving–pitching wing motion postpones the generation of outward spanwise flow in the post-buildup period, which extends the period the TV stays attached to the wing surface and keeps its integrity. Correspondingly, the segmentation of the LEV occurs at a later phase in the pitching case; however, this does not cause a decrease in the force generation. Nevertheless, the delay in the formation of the spanwise flow affects the force histories such that steady-state values are reached at a later phase for the revolving–pitching wing. Furthermore, the local maxima in the force histories in the post-buildup phase of both motions are aligned with the translation of the spanwise flow pattern toward the trailing edge such that in the period of steady-state force generation, the outward spanwise flow pattern is mostly accumulated around the trailing edge. This state is most probably due to growth of the LEV toward the trailing edge and its inhibition by the trailing edge as recently investigated by Garmann and Visbal (2014). They showed that for revolving wings, the growth of the LEV is almost proportional to the distance from the root and it is constrained by the trailing edge for increasing aspect ratio such that once the LEV reaches the trailing edge and occupies the complete chord, forces level around the steady-state values.

The circulation of the LEV builds up rapidly in the buildup phase in both motions. In the pitching wing case, this increasing trend is interrupted with the end of the pitch-up motion that is also correlated with the shedding of positive leading-edge vorticity from the trailing edge and tilting of the LEV. Subsequently until $d^{*}=5$, both motions generate similar amount of circulation which is altered by the decrease of the circulation level in the revolving–surging motion in accordance with the decay of the forces to the steady-state values. The circulation of the LEV continues to increase in the revolving–pitching case similar to its force history. In order to assess the relation between the vortical structures and force generation, and to identify the phenomenon behind the greater performance of the pitching wing compared to surging wing in terms of force generation, the vorticity moment theory (Wu 1981) was applied on the flow fields in the reference plane during the buildup phase of both motions. It is found that elevated force generation of the pitching motion originates from a number of consequences of the pitching motion: (1) increase in the magnitude and growth rate of the circulation accumulated in the LEV; (2) positioning of the LEV closer to the wing and the starting vortex further away from it; and (3) generation of bound circulation.

Regarding the force prediction models, it is clear that the theoretical model inspired by the unsteady thin airfoil theory captures the general trend and the magnitude of the forces reasonably well despite its two major shortcomings. First, the model estimates the rotational forces due to pitch-up motion based on the generation of bound circulation of an unique value that establishes the Kutta condition. Nevertheless, this does not hold during the pitching motion as shown in the results of the experiments so that the model overestimates the bound circulation. Second, the steady-state values are used for the estimation of instantaneous circulatory forces during the buildup phases, whereas the formation of vortical structures and hence reaching the circulatory steady-state forces take a finite amount of time. This source of deficiency, however, can be scrutinized and possibly be corrected by adding a Wagner-function-like approach for the acceleration phase of the revolving–surging motion. The second theoretical model discussed in the study, based on the vorticity moment theory, provides a means of force prediction once the flow-field information is available. Obviously, this model requires knowledge of the vortex behavior, whereas the quasi-steady model attempts to provide a prediction based on the wing kinematics directly.