Particle tracking velocimetry of the flow field around a collapsing cavitation bubble

Abstract

The velocity field in the vicinity of a laser-generated cavitation bubble in water is investigated by means of particle tracking velocimetry (PTV). Two situations are explored: a bubble collapsing spherically and a bubble collapsing aspherically near a rigid wall. In the first case, the accuracy of the PTV method is assessed by comparing the experimental data with the flow field around the bubble as obtained from numerical simulations of the radial bubble dynamics. The numerical results are matched to the experimental radius–time curve extracted from high-speed photographs by tuning the model parameters. Trajectories of tracer particles are calculated and used to model the experimental process of the PTV measurement. For the second case of a bubble collapsing near a rigid wall, both the bubble shape and the velocity distribution in the fluid around the bubble are measured for different standoff parameters γ at several instants in time. The results for γ > 1 are compared with the corresponding results of a boundary-integral simulation. For both cases, good agreement between simulation and experiment is found.

1 Introduction

Particle image velocimetry (PIV) and particle tracking velocimetry (PTV) are nowadays routinely used to examine small-scale flow fields in microfluidic systems, for example in lab-on-a-chip devices (Santiago et al. 1998; Devasenathipathy et al. 2003; Bown et al. 2006). These systems typically feature small geometrical dimensions and flow velocities, thus low Reynolds numbers, and can be well investigated using conventional microscopic setups. In this work, the flow field around a single cavitation bubble collapsing in water is measured using a PTV technique. This flow is characterized by a large dynamic range of velocities, and quite different time scales and spatial scales, and therefore poses problems for particle-based velocimetry. Furthermore, a relatively large observation distance is needed so as not to disturb the bubble dynamics.

The collapse of cavitation bubbles has been studied extensively over the past few decades both experimentally and numerically (Lauterborn et al. 1999). Special attention has been paid to bubbles collapsing near boundaries (Blake and Gibson 1987), due to their major role in ultrasonic cleaning and cavitation erosion (Philipp and Lauterborn 1998; Krefting et al. 2004). Their shape dynamics has been investigated using high-speed photography in a variety of experimental situations, for example at different distances from a plane rigid boundary (Lauterborn and Bolle 1975; Vogel et al. 1989; Lindau and Lauterborn 2003; Isselin et al. 1998), in front of a convex or concave solid wall (Tomita and Shima 1990), a composite (Tomita and Kodama 2003), an elastic (Brujan et al. 2001) or a free surface (Blake and Gibson 1981). The main physical features of bubble collapse near a wall are shock wave emission and the formation of a liquid jet that penetrates the bubble. If the bubble is close, the jet hits the boundary with a velocity that can exceed 100 m/s (Lauterborn and Bolle 1975; Vogel et al. 1989; Lauterborn 1974). Shock waves emitted upon collapse have been characterized by means of hydrophone measurements and visualization techniques like shadowgraph imaging (Vogel et al. 1989; Lindau and Lauterborn 2003; Isselin et al. 1998; Vogel and Lauterborn 1988a; Shaw et al. 1996). Also, erosion and pit formation on surfaces caused by collapsing bubbles have been studied by correlating their dynamics with damage spots on the surface (Philipp and Lauterborn 1998; Isselin et al. 1998; Tomita and Shima 1986). Numerical work on the interaction of a bubble with nearby boundaries using the boundary-integral method (Blake et al. 1986; Best and Kucera 1992; Robinson et al. 2001) has generally shown good agreement with experimental observations. Computations were performed up to the last stages of collapse (Best 1993; Zhang et al. 1993; Brujan et al. 2002) and beyond (Lee et al. 2007).

A direct measurement of the flow field around a collapsing bubble was presented by Vogel et al. (1989), Vogel and Lauterborn (1988b). They used focused laser pulses to generate bubbles near a solid boundary in water and measured the velocity field by means of a rotating drum camera with up to 10,000 frames per second, which recorded the light scattered from marker particles. The particles with a diameter of 25 μm were illuminated five times per frame with consecutive light pulses of 1 μs duration and 3 μs separation. This work already made use of the reproducibility of the event to interlace image series for better time resolution. With image acquisition by fast CCD cameras and digital image processing, a better spatial coverage is now possible. An improved spatial resolution is obtained here by digitally overlaying frames from separate recordings to increase the density of fluid velocity vectors, again making use of the reproducibility of the bubble experiments.

The flow field around laser-induced bubbles in microfluidic devices has been examined recently (Zwaan et al. 2007). In this case, the observed flow dynamics is mainly two dimensional, due to the strong confinement in the direction of observation.

The objective of this work is twofold. First, the accuracy of a modern particle tracking velocimetry setup in measuring the flow field around collapsing cavitation bubbles is assessed. The motion of the tracer particles is modeled for the test case of spherical bubble collapse for which the fluid motion is known well enough to determine the measurement error caused by the tracers’ velocity lag. Furthermore, PTV measurements of this flow are compared to numerical results to check the overall error. Second, the collapse of a bubble in front of a solid wall is investigated by a combination of short-exposure photography and PTV. Local modeling of the data allows us to interpolate them on a grid to facilitate comparison with numerical simulations and to further analyze the flow data quantitatively (Kröninger 2008).

2 Methods

To obtain comprehensive data on flow field and bubble dynamics, the experiment utilizes a combination of dual-frame imaging of fluorescent particles (PTV) and short-exposure photography of bubbles.

2.1 High-speed photography

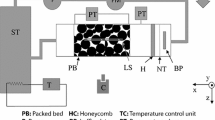
The experimental arrangement is shown in Fig. 1. A laser pulse with energy of a few mJ (wavelength λ = 1,064 nm, duration 8 ns) is focused into a water-filled cuvette (50 × 50 × 50 mm³) by a lens system mounted at the center of one face. The bubble generated at the laser focus is observed with a sensitive Interline-CCD camera (PCO Sensicam qe) equipped with a 60-mm lens (f _# = 2.8) and spacer rings, resulting in a magnification of about 1.7. The filter protects the camera from scattered laser radiation. A flash lamp placed behind a ground glass is used for backlight illumination. As an alternative, a nanosecond LED-flash can be employed to take shadowgrams of possible shock waves. The laser system, flash lamp and the camera electronics are synchronized in order to take pictures (exposure time 500 ns) at well-defined times after bubble generation. By repeating the image acquisition at different time delays, a picture series of the bubble dynamics is compiled. An example of a bubble collapse obtained that way is shown in Fig. 2. Because of an elongated form of the laser plasma, the bubble is slightly asymmetric shortly after the breakdown, but becomes nearly spherical after about 70 μs (first image), when it reaches its maximum radius of approximately 750 μm. The first bubble collapse takes place at t = 140 μs. In the course of the violent collapse and rebound, the onset of shape instabilities generally leads to the bubble’s destruction after the second collapse.

Fig. 1

Experimental setup for bubble generation and short-exposure photography

Fig. 2

Images of an undisturbed bubble collapse. The first picture is taken 70 μs after bubble generation and corresponds to the state of maximum expansion. The time between frames is 10  μs. The series is arranged left to right, top to bottom

Due to fluctuations of the maximum radius the collapse time of the bubbles generated during one run of the experiment may vary within a few percentage. To select images that belong to bubbles of nearly the same size only, a hydrophone is positioned in a corner of the cuvette beneath the water surface to record the shock waves that are emitted at cavity generation and collapse. In this way, the time between bubble inception and first collapse is measured, which is uniquely related to the maximum bubble radius. After recording and digital image processing (equalization of levels), the bubble volume and an effective radius are extracted from the selected images (Geisler 2003).

2.2 Particle tracking velocimetry

Conventional PIV methods that are based on correlation analysis of small interrogation areas cannot be used with this experiment. They require a large number of tracer particles in each area (Raffel et al. 1998) that, given the high magnification needed to capture the flow details, would lead to a prohibitively large density of tracers in the liquid. A high concentration of tracers would deteriorate the image quality and adversely affect the bubble generation by laser breakdown.

With a lower density of tracer particles, these problems are alleviated. Then, however, few tracer particles are visible in an image, which have to be located and traced individually by a PTV algorithm. The resolution of velocity measurements is limited by the displacement of the particles between exposures.

The setup used for the particle tracking measurements is outlined in Fig. 3. It differs slightly from the one shown in Fig. 1. To trace the flow, monodisperse rhodamine-B-labeled polystyrene particles with a diameter of 4.9 μm are suspended in the water. They have a density of ρ_p = 1.05 g/cm³, very near to that of water to follow the flow closely. Their dynamics is modeled in Sect. 2.3.2. Fluorescent particles are used since they allow for better background filtering with respect to the exciting laser light. That way, the camera sensor can be protected effectively from laser light reflected by the bubble surface.

Fig. 3

Experimental setup for the particle tracking velocimetry measurements

The fluorescent particles are excited by two successive laser pulses (wavelength λ = 532 nm, pulse duration = 8  ns) generated by a twin Nd:YAG laser system (PIV 400 Quanta Ray) and recorded on two separate CCD frames. The PIV laser is synchronized with the laser that generates the bubbles. In this way, the instant of flow field observation can be timed accurately relative to the time of bubble nucleation. The number density of tracer particles is chosen to give a maximum change in the particles’ positions that is smaller than the average distance between the particles. The separation of the illuminating laser pulses is adjusted between 1 and about 10 μs, depending on the flow velocities to be measured.

The illuminating laser light, entering at the top, is shaped into a light sheet with a minimum thickness of about 90 μm by a Galilean-type beam compressor and a cylindrical lens (Dantec light sheet optics model 80X70). The waist of the light sheet is centered at the bubble’s position. The depth of field of the camera lens is slightly smaller than the waist thickness. With a diffraction-limited spot size of diameter

$$ d_{\rm diff}=2.44 f_{\#}(M+1)\lambda, $$

(1)

giving d _diff ≈ 11 μm at λ = 584 nm for the lens used, the theoretical depth of field is

$$ \delta_Z=2 f_{\#} d_{\rm diff} (M+1)/M^2, $$

(2)

which yields δ _Z  ≈ 57 μm. Here, M denotes the magnification and f _# is the f-number of the imaging optics.

The filter mounted in front of the camera lens protects the CCD chip from damage by scattered laser radiation (at 532 and 1,064 nm), while the tracers’ fluorescence emission around 584 nm is able to pass the filter without significant absorption.

An example of raw image data acquired with this setup is given in Fig. 4. Only two small, equal sections of size 0.55 mm × 0.74 mm from the total images of a dual-frame set are shown for better visibility of the tracer particles in print. The interframe time is 3 μs. Clearly, the patterns of bright spots appear to be quite similar to the unaided eye, though, e.g., the spot brightness may vary between the two frames, and some defocused particle images appear in the second frame. These features have to be equalized or removed by proper preprocessing of the images.

Fig. 4

Sections of two raw images of the tracer particle field around a bubble collapsing near to a solid boundary taken with a time separation of 3 μs. The bubble’s collapse time is 300 μs; the images are taken 20 μs before collapse. The field of view is about 0.55 mm  ×  0.74  mm. In the lower right part of the image, the bubble is visible

Particle localization and tracking is performed with a Matlab code by Blair and Dufresne. It is an adaptation of an IDL algorithm written by Crocker and Grier (1996). The PTV analysis proceeds in a number of steps. The first step is bandpass filtering of the images, which brings out features that have the size of a well-focused particle image (≈3 pixels). Second, to avoid artefacts, certain image regions are masked, in particular the region where the bubble is located. Reflections of the fluorescing tracers at the bubble surface could otherwise lead to spurious particle detections and false trajectories. Next, the location of the tracer particles is determined with sub-pixel accuracy by searching for local brightness maxima and calculating the center of the intensity distribution at this point.

To determine the tracers’ trajectories, every particle identified on the first frame of a dual-frame set is assigned a particle on the second frame. For every list of assignments thus obtained, the sum of all squared displacements is calculated. The assignment list that minimizes this quantity is assumed to yield the true flow motion. The computation time is reduced by permitting only those assignments that give a displacement smaller than a specified length.

To obtain a comprehensive view of the instantaneous flow field with a sufficiently high density of displacement vectors, the data from several acquisitions with the same timing parameters are combined. Finally, a median validation filter is applied. It removes displacement vectors that deviate too much in length or direction from the median vector, calculated for a circular neighborhood at the considered point. For a better presentation of the results, the dataset can then be interpolated for a uniform grid. The two components of the velocity vectors are treated separately, so that the problem is reduced to modeling a scalar quantity in two dimensions. A fixed number of next neighbors are used to perform a weighted local fit of a linear model for each grid point. The biweight function

$$ w_k=\left( 1- \left({\frac{a_k}{a_{\rm max}}} \right)^2 \right)^2 $$

(3)

is chosen as the weighting function, where w _k denotes the weighting factor for the neighbor at distance a _k to the grid point and a _max is the largest distance found in the set of neighbors. To optimize the number of next neighbors and to check which polynomial order is suited best for the interpolation, a leave-one-out cross-validation is performed on different datasets. Although zero- or second-order polynomial fits give slightly smaller errors in some cases, the linear model performs quite well in all cases. It has the advantage that, compared to the other models, the quality of the fit is nearly constant over a wide range of numbers of next neighbors. In this study, around 20–30 neighbors are used for the fit. Grid points that are farther away from the next data point than the grid spacing are not considered for interpolation.

2.3 Numerical simulations

Numerical simulations of bubble dynamics and of fluid flow around the bubble are compared with the experimental results. In the case of spherically symmetric bubble motion, this comparison allows to assess the accuracy of the PTV method, while in the case of asymmetric bubble collapse, the experimental data serve to validate the simulations.

2.3.1 Spherical bubble dynamics

The radial dynamics of a bubble sufficiently far away from boundaries or obstacles that may disturb the spherical symmetry of the flow can be described by the model of Keller and Miksis (1980), Prosperetti and Lezzi (1986), Parlitz et al. (1990):

$$ \begin{aligned} &\left(1-{\frac{U_{\rm b}}{C}}\right) R_{\rm b}\dot{U}_{\rm b} +{\frac{3}{2}}U_{\rm b}^2 \left(1-{\frac{U_{\rm b}}{3C}} \right) =\cr &\left(1+{\frac{U_{\rm b}}{C}} \right) {\frac{P_R-p_0}{\rho}} + {\frac{R_{\rm b}}{\rho C}} {\frac{{\rm d}(P_R-p_0)}{{\rm d}t}}, \end{aligned} $$

(4)

where R _b and $U_{\rm b}=\dot{R}_{\rm b}$ denote the bubble’s radius and wall velocity, respectively, p ₀ is the ambient pressure and ρ is the density of the liquid. The speed of sound in the liquid, C, is assumed to be constant. This model is of first order in the Mach number, so weak compressibility effects are taken into account. The gas inside the bubble is modeled by the van der Waals law. Thus, the pressure in the liquid at the bubble wall, P _R , is given by

$$ \begin{aligned} P_R&=\left (p_0 - p_{\rm v} +{\frac{2 \sigma}{R_0}} \right) \left({\frac{R_0^3-bR_0^3 }{R_{\rm b}^3-bR_0^3}}\right)^{\kappa}\cr &\quad- {\frac{2\sigma}{R_{\rm b}}} - {\frac{4\mu U_{\rm b}} {R_{\rm b}}} + p_{\rm v}, \end{aligned} $$

(5)

where R ₀ is the equilibrium radius of the bubble. The model takes account of vapor pressure p _v, viscosity μ and surface tension σ of the liquid. The van der Waals parameter is chosen as b = 0.0016, the polytropic exponent as κ = 4/3.

A numerical solution of Eqs. 4 and 5 for initial conditions that yield minimum RMS deviation of the radius–time curve from the experimental data is shown in Fig. 5. As expected, it shows good agreement with the experiment, in particular for the well-measurable large-excursion part of the bubble dynamics. The flow is subsonic during the cycle up to the final moment of collapse. This justifies to treat the liquid as incompressible in the subsequent analysis of the spherically symmetric flow situation. The curve brings out the specific features of bubble dynamics that pose a challenge to particle-based flow measurements: (1) the high dynamic range of flow velocities encountered over time (and over space) and (2) the large acceleration of the fluid on a small time and spatial scale.

Fig. 5

Experimentally measured effective bubble radius (circle), see Fig. 2, and numerical solution of the Keller–Miksis model with initial conditions that give the best fit with the experimental data (solid line)

2.3.2 Dynamics of the tracer particles

Given the radius–time curve of a spherical bubble centered at r = 0 (see Fig. 5) and assuming incompressible flow, the velocity of the fluid, U _f, is given by:

$$ {\mathbf U}_{\rm f}({\mathbf r},t)={\frac{U_{\rm b}(t) R_{\rm b}(t)^2}{|{\mathbf r}|^2}} {\mathbf e}_{\rm r}, $$

(6)

with e _r being the unit vector in the radial direction.

With this information on the flow field, the motion of the tracer particles is calculated numerically using the Basset–Boussinesq–Oseen (BBO) equation. The model assumes that the particles are small, spherical and non-deformable, which is the case in the experiments presented. In the notation of Soo (1967), the BBO equation reads

$$ \begin{aligned} {\frac{4 \pi}{3}} a_{\rm p}^3 \rho_{\rm p} {\frac{{\rm d}{\mathbf U}_{\rm p}}{{\rm d}t_{\rm p}}} &={\frac{4 \pi}{3}} a_{\rm p}^3 \rho_{\rm p} G ({\mathbf U} _{\rm f} - {\mathbf U}_{\rm p}) - {\frac{4 \pi}{3}} a_{\rm p}^3 {\frac{\partial P}{\partial \bf{r}}}\cr &+ {\frac{1}{2}}\,{\frac{4 \pi}{3}} a_{\rm p}^3 \rho_{\rm f} {\frac{{\rm d}}{{\rm d}t_{\rm p}}} ({\mathbf U}_{\rm f} - {\mathbf U}_{\rm p}) + {\mathbf F}_{\rm ext}\cr &+6a_{\rm p}^2 \sqrt{\pi \rho_{\rm f} \mu} \int\limits_{t_{{\rm p}_0}}^{t_{\rm p}} {\frac{({\rm d}/{\rm d}\tau) ({\mathbf U}_{\rm f} - {\mathbf U}_{\rm p})} {\sqrt{t_{\rm p}-\tau}}}{\rm d}\tau \end{aligned}$$

(7)

with

$$ G={\frac{3}{8}} C_D {\frac{\rho_{\rm f}}{\rho_{\rm p}}} {\frac{1}{a_{\rm p}}} |{\mathbf U}_{\rm f}-{\mathbf U}_{\rm p}|. $$

(8)

where U _p denotes the particle velocity, a _p denotes the particle radius, and P denotes the pressure. The density of the particle and the fluid are denoted by ρ_p and ρ_f, respectively. The derivatives d/dt _p refer to the frame of reference moving with the particle, so that

$$ {\frac{{\rm d}U_{\rm f}}{{\rm d}t_{\rm p}}} =\left({\frac{\partial U_{\rm f}}{\partial t}} +U_{\rm p} {\frac{\partial U_{\rm f}}{\partial r}} \right). $$

(9)

The influence of external forces (F _ext) and the history force (integral term in Eq. 7) is neglected. The equation can be used in scalar form due to the spherical symmetry of the system.

Because the Reynolds number Re = 2a _pρ_f|U _f − U _p|/μ may reach values up to the order of 10 in the present experiment, Olson’s parametrizing formula (Graf 1971) is used for the drag coefficient C _D:

$$ C_{\rm D}={\frac{24}{{\rm Re}}} \left ( 1+{\frac{3}{16}} {\rm Re}\right)^{0.5}. $$

(10)

This empirical formula is expected to be valid up to Re ≈ 100.

According to Maxey (1983), the pressure-gradient term in Eq. 7 is given by the acceleration of the fluid:

$$ - {\frac{\partial P}{\partial r}}= {\frac{{\rm d}U_{\rm f}}{{\rm d}t}}\rho_{\rm f}. $$

(11)

The extra term proportional to ∇² U _f in his equation is negligible in our case.

Equation (7) is coupled to the bubble model via Eq. 6. The motion of tracers starting at different distances from the bubble wall is computed. In Fig. 6 (top), some representative results are shown together with the trajectories of ideal fluid elements having the same starting coordinates. As can be seen, the tracers (of diameter 4.9 μm) follow the fluid elements rather well, except those starting in the immediate vicinity of the bubble wall. In the lower plot, the relative error of the tracer velocity compared to the fluid velocity at the tracer’s current position is shown. In all cases, the error remains smaller than 4% up to the short moment of collapse. There, the fluid velocity switches direction and at the moment, when it reaches zero, the error has to diverge. Although it exceeds 4% for a few μs after collapse, the absolute error is quite small and stays below 2.5 m/s for the tracers starting at the bubble wall and below 1 m/s for those farther away. Smaller particles would follow the flow even better but cannot be used in our experiment due to their insufficient fluorescence intensity.

Fig. 6

Tracer dynamics near a spherically collapsing bubble. The gray curve represents the motion of the bubble wall as shown in Fig. 5. Solid curves refer to trajectories of ideal fluid elements for different starting radii from bubble center. In comparison, calculated trajectories of tracer particles are shown (dashed black curves)

The computation of the tracer positions makes it possible to simulate the experimental conditions. Several trajectories of model tracer particles were computed by means of Eq. 7. The radial positions r ₁ and r ₂ at the times of illumination in the real experiment, t ₁ and t ₂, yield the velocity (r ₂ − r ₁)/(t ₂ − t ₁), which is compared with the fluid velocity. In this way, systematic errors resulting from the sampling of the flow field and the inertia of the tracer particles are identified. The sampling time, t ₂ − t ₁, was chosen to yield acceptably small errors. The experience gained for the spherical bubble collapse is used to adjust the sampling times for the aspherical bubble collapse.

2.3.3 Boundary-integral method

A frequently used method to calculate the flow around a bubble collapsing near a surface is the boundary-integral method described by Blake et al. (1986). The fluid surrounding the bubble is treated as incompressible, free of vortices and non-viscous. Therefore, the velocity potential ϕ obeys the Laplace equation

$$ \Updelta \phi = 0. $$

(12)

The content of the bubble is assumed to be an ideal, homogeneous gas described by an adiabatic pressure law. If the boundary conditions are known, the solution of the Eq. 12 yields the velocity of the fluid v(x) = −∇ϕ(x).

The temporal evolution of the velocity field is given by the time-dependent Bernoulli equation

$$ \rho {\frac{\partial \phi}{\partial t}} + \frac{1}{2} \rho |{\mathbf v}|^2 = -p $$

(13)

with the boundary conditions at infinity (x → ∞)

$$ {\mathbf v} \rightarrow 0, \quad p \rightarrow 0, \quad \phi \rightarrow 0. $$

(14)

Using this equation, the temporal evolution of a fluid element and its potential are given by

$$ {\frac{{\rm d}{\mathbf y}}{{\rm d}t}} = {\mathbf v}({\mathbf y}), \quad {\frac{{\rm d} \phi}{{\rm d}t}} = -{\frac{p}{\rho}} + \frac{1}{2} |{\mathbf v}|^2. $$

(15)

The motion of the bubble wall is calculated by alternately performing the following two steps: the velocity on the boundary is determined by solving Eq. 12 with the known shape of the bubble wall and the potential on this boundary. Then, the temporal evolution of the boundary and the potential are computed using Eq. 15.

The solution of Laplace’s equation in the domain Ω can be obtained using the boundary-integral equation

$$ \begin{aligned} &\int\limits_{\partial \Omega} \left( {\frac{\partial \phi}{\partial n}}({\mathbf y}) G({\mathbf x}, {\mathbf y}) - \phi({\mathbf y}) {\frac{\partial G}{\partial n}}({\mathbf x}, {\mathbf y})\right) {\rm d} S({\mathbf y}) \cr &\quad=\phi({\mathbf x}) \cdot {\left\{\begin{array}{ll} 2 \pi & {\mathbf x} \in \partial \Omega,\\ 4 \pi & {\mathbf x} \in \Omega \setminus \partial \Omega. \end{array}\right.} \end{aligned} $$

(16)

G(x, y) denotes Green’s function of the Laplace operator and ∂Ω denotes the domain’s boundary.

If ϕ is given on the boundary, Eq. 16 is a Fredholm integral equation of the first kind with respect to the unknown quantity ∂ϕ/∂n. This equation is solved numerically using a discretization of the boundary in axisymmetric coordinates. The collocation method is applied and an appropriate interpolation of the boundary is implemented. This yields a linear system of equations that can be solved by standard methods. In the case of a flat, rigid boundary, a simple way to avoid parametrizing the wall is to create an image bubble. This second bubble acts as if a wall were present, localized exactly half way between the bubbles.

In order to compare the results of the calculations with the PTV measurements, the fluid velocity at points within the domain Ω is determined. This is done by calculating the velocity potential at any desired point using Eq. 16 with the quantities on the surface already known. The initial state of the bubble is taken to be spherical. Initial radius, initial velocity and the equilibrium radius are obtained from the experiment as described earlier.

3 Results and discussion

3.1 Spherical bubble collapse

In order to assess the accuracy of the PTV method, spherical bubble collapse was investigated first. A bubble with a collapse time of 140 μs, as shown in Fig. 2, was chosen as the test object.

Figure 7 gives the outcome of 10 PTV measurements of the flow velocity at 9 μs before collapse, measured with an interframe time of 8 μs. The magnitude of the velocity is plotted versus the distance r from the bubble’s center (top). The local velocity of the water at time (t ₂ − t ₁)/2 is given for comparison. It is derived with Eq. 6 from the data on bubble wall velocity and radius (see Fig. 5). The bottom figure shows the RMS deviation of the experimental data from the numerical values, calculated at 100 μs intervals. It can be stated that the experimental values are in good agreement with the simple incompressible flow model. Even close to the bubble wall the RMS deviation is smaller than 1 m/s. At higher distances, it drops to a plateau of about 0.07 m/s.

Fig. 7

Flow velocity field at a time 9 μs before collapse (interframe time 8 μs). The magnitudes of the measured velocity vectors (circle) are plotted versus the distance r to the bubble center. They virtually coincide with the numerical results for ideal fluid elements (solid line). The dashed line denotes the position of the bubble wall

Figure 8 shows the result of a second set of measurements carried out at 2 μs before collapse (t ₁ = 137 μs, t ₂ = 139 μs). The same analysis procedures are applied. In this case, the spread of the data is considerably larger. The velocities encountered are higher and the interframe time had to be chosen much smaller to cope with the high acceleration near the wall. Thus, the tracer images are shifted between the frames by a few pixels only, and the limited accuracy of the tracer localization gives rise to a higher noise level. At distances greater than about 1 mm from the bubble center, the displacement gets smaller than 1 pixel, resulting in a bias toward larger velocities. This corresponds to the plateau in the standard deviation of about 0.27 m/s.

Fig. 8

As in Fig. 7, except the time is 2 μs before collapse, and the interframe time is 2 μs

To obtain an estimate of the quality of the tracer localization by the algorithm, a PTV measurement was performed at a small interframe time with the water being at rest. The displacement values were examined to determine the range that contains 68% of all data vectors. A value of 0.13 pixels was found. This corresponds to velocities of 0.24 and 0.06 m/s for interframe times of 2 and 8 μs, respectively, which is nearly exactly the height of the plateaus seen in the corresponding graphs for the RMS deviation.

In the vicinity of the bubble wall, a systematic error becomes prominent, see Fig. 8. At the time of observation, the bubble radius is of the order of the light sheet size. Hence , tracers that are not exactly in the center plane of the illuminated volume have a non-negligible out-of-plane velocity component. Since this component cannot be measured, it biases the results toward smaller velocities. Also, due to the projection effect, the positions of the tracers appear to be closer to the bubble. This explains the large deviations encountered for r ≤ 0.5 mm.

3.2 Bubble in front of a wall

If a bubble is generated in the vicinity of a solid wall, its dynamics can be strongly influenced, depending on its distance d from the boundary and its maximum volume. A frequently used parameter to characterize the collapse geometry is the standoff parameter:

$$ \gamma\,=\,{\frac{d}{R_{\rm max}}}, $$

(17)

where R _max denotes the maximum equivalent radius of the bubble, i.e., the maximum radius of a sphere with the same volume as the cavity. A scaled time, that is commonly used with the boundary-integral method, is introduced for easy comparison of experimental results with calculations:

$$ T={\frac{t}{R_{\rm max}}} \left( {\frac{p_0}{\rho_{\rm f}}}\right)^{1/2} $$

(18)

The main feature of bubble collapse near to a solid wall is the formation of a liquid jet directed toward the boundary that eventually leads to the generation of a vortex ring. A simple explanation for this behavior is given by Benjamin and Ellis (1966), who argued that the only way for the bubble–fluid system to conserve its Kelvin impulse is to generate vorticity. An example for the formation of a jet is given in Fig. 9.

Fig. 9

Photographs (left) and results of the boundary-integral simulation (right) of a bubble generated in the vicinity of a glass wall (located at the bottom of each picture). The first picture at the top corresponds to a time 150 μs after the bubble is generated, whereas the collapse occurs at t = 170 μs. The time between the frames is 5 μs

On the left-hand side, photographs of the last stages of a bubble collapse near a solid boundary are shown, starting 150 μs after bubble generation with an interframe time of 5 μs. The location of the wall, made of glass, is at the bottom of each picture. Shortly after bubble generation, the bubble center has a distance of d = 1.07 mm from the wall. With R _max  value of  0.81  mm, γ is 1.32 for the given data, and the collapse time is t _c = 170 μs (T _c = 2.1). On the right-hand side, with the same scaling and for the same times, the outcome of the boundary-integral simulation is shown. The initial parameters are chosen in a way that the simulation yields the same maximum radius and collapse time as found in the experiment. The dynamics of the phase boundary and the bubble position are in good agreement with the experiment. A similar comparison for γ = 1 can be found in Vogel et al. (1989). There, the experimentally obtained bubble shapes are compared to results from Plesset and Chapman (1971) and Blake et al. (1986). In the latter case, also utilizing the boundary-integral method, good accordance with experiment is found.

Experimental PTV data are compared with the simulated flow field in Figs. 10 and 11. The simulation was run with the same initial values as used before. In Fig. 10, the results of a measurement (gray vectors), performed 10 μs before collapse (t ₁ = 156 μs, t ₂ = 164 μs), are plotted along with the velocity vectors computed with the boundary-integral method (black) at the same points in space and in time. The bubble shape is also shown in the figure for better orientation. The solid boundary is located on the x-axis. At this stage, the bubble has already moved ~0.25 mm toward the boundary and a jet is starting to form at the top of the bubble. A very good match between the experimental and simulation results is found in the whole domain. Note that the averaging process due to the temporal sampling is not taken into account by the numerics, but the averaging does not introduce a significant systematic error in this situation. Near the bubble’s indentation, velocities of up to 6.3 m/s are measured, which is roughly the method’s limit for the given particle density, magnification and interframe time of 8 μs. Possible displacements higher than the mean spacing of the tracer particles have to be filtered out.

Fig. 10

Comparison of experimentally measured velocities (gray vectors) with a boundary-integral simulation (black vectors) for a bubble collapsing in front of a solid boundary (at y = 0 mm) at time t = 160, 10 μs before collapse. The vectors are anchored at their tail points. The shape of the bubble is shown in gray (see Fig. 9)

Fig. 11

As in Fig. 10, except t  = 165, 5 μs before collapse

The outcome of a second measurement at 5 μs before collapse (t ₁ = 163 μs, t ₂ = 167 μs) is shown in Fig. 11. At this instant, shortly before collapse, the jet has formed and is about to hit the lower bubble wall. Jet formation is indicated also by the fact that the velocity vectors near the upper bubble wall are all directed to a point above the bubble’s center. This point is the position of the jet funnel in the numerical results. Due to the smaller interframe time of only 4 μs, it was possible to measure velocities up to 12.1 m/s. Again, the experimental values match the numerical output very well.

In conclusion, the boundary-integral method is able to simulate the given problem for γ ≈ 1.3. Pearson et al. (2004) show that it still yields qualitatively good results down to γ = 0.8. For smaller distances to the wall, the calculations suffer from strong instabilities. Therefore, simulations were not performed for the cases γ = 0.7 and γ = 0.5 now presented.

Figure 12 shows shadowgrams of these bubbles in their state of maximum expansion. The distance of the laser focus (which is still visible on all the images as a bright spot at the center) to the glass wall is the same in both cases. Only the laser energy is changed, resulting in maximum radii of R _max = 0.93 mm (γ = 0.7) and R _max = 1.3 mm (γ = 0.5). Although the collapse times, t _c = 220 μs and t _c = 300 μs, are quite different, the scaled collapse times, T _c = 2.37 and T _c = 2.31, are close. In both the images, the bubble has already touched the glass wall, but the contact angles are different. Apart from the flattening at the surface side, the bubble remains more or less spherical in the case γ = 0.7. For γ = 0.5, however, the bubble attaches to the surface, its bottom part attaining a cone-like shape, while the upper part has a nearly constant curvature. Also, the lower rim of the bubble wall has a much sharper edge. This may be attributed to the fact that the fluid is pushed aside earlier and with a greater pressure from the growing bubble.

Fig. 12

Shadowgrams of two bubbles in front of a glass wall (indicated by the white dotted line) in the state of maximum expansion; left γ = 0.7, right γ = 0.5

In Fig. 13 (γ = 0.7) and Fig. 14 (γ = 0.5), image sequences of the bubble collapse are shown, taken with a constant interframe time of 5 μs. In Fig. 13, for γ = 0.7, the bubble has a cone-like shape with a rounded top (first row) at about 50 μs before collapse. The contact angle between the bubble rim and the glass wall has steepened, compared with Fig. 12. This feature is even more pronounced for γ = 0.5 (Fig. 14). Here, the rim of the bubble starts to move more slowly along the glass wall early during the shrinking phase (second row) leaving a bulge. Theory predicts this behavior from the jet flow directed radially outwards after impact of the jet on the glass wall.

Fig. 13

Shadowgrams of a bubble collapsing in front of a glass wall (indicated by the white dotted line); standoff parameter: γ = 0.7; maximum radius: R _max = 0.93 mm; collapse time: t _col = 220 μs; first frame at 50 μs before collapse, time between frames: 5 μs

Fig. 14

Shadowgrams of a bubble collapsing in front of a glass wall (indicated by the white dotted line); standoff parameter γ = 0.5; maximum radius: R _max = 1.3 mm; collapse time: t _col = 300 μs; first frame at 50 μs before collapse, time between frames: 5 μs

At 25 μs (Fig. 13, 5th frame) and 40 μs (Fig. 14, 3rd frame) before collapse, an indentation appears that indicates the formation of a jet. During the last few microseconds before collapse, the bubble shape becomes unstable. Then the bubble splits into many fragments that collapse and emit shock waves separately. This was also found in other investigations (Philipp and Lauterborn 1998;  Lindau and Lauterborn 2003).

In order to clearly visualize the flow field around the bubble for these two values of the standoff parameter, the results of several PTV flow measurements made at the same time before collapse were merged and interpolated on a regular grid. The resulting vector fields are shown in Fig. 15 for γ = 0.7 and in Fig. 16 for γ = 0.5 as an overlay of the corresponding bubble image.

Fig. 15

Interpolated PTV data of the flow field around the bubble shown in Fig. 13 (γ = 0.7), at times 20 μs before collapse (top), 10 μs before collapse (middle) and immediately at collapse (bottom)

Fig. 16

Interpolated PTV data of the flow field around the bubble shown in Fig. 14 (γ = 0.5), at times 20 μs before collapse (top), 10 μs before collapse (middle) and immediately at collapse (bottom)

For γ = 0.7, the highest velocities are measured at 20 μs before the collapse (Fig. 15, first image). A maximum value of about 30 m/s is found at the entrance of the jet funnel. The velocity of the tip of the jet must be higher, though. Philipp and Lauterborn (1998) obtained a value of 100–140 m/s.

At 10 μs later (Fig. 15, second image), the funnel has broadened. The jet has probably already reached the glass wall so that the inflow is reduced. In contrast, the lateral inflow has increased its velocity. For γ  >  0.6, Lindau and Lauterborn (2003) report the occurrence of a liquid splash. A splash for γ = 0.9 was also predicted by Tong et al. (1999) and observed by Brujan et al. (2002). The lateral inflow beneath the bubble hits the outward flow from the jet. A splash is formed and moves radially outward, roughening the bubble wall along its way.

Another 10 μs later, when the toroidal bubble has collapsed (Fig. 15, third image), the velocity of the central inflow has dropped to about 10–12 m/s. The velocity does not vary much over the inner torus cross section.

A similar flow dynamics is observed for the case γ = 0.5. Here, the maximum inflow velocity occurs at 10 μs before collapse (Fig. 16, second image). The same maximum velocity of about 30 m/s is found above the jet funnel. Note that the velocity at the center of the funnel is slightly smaller than at its edges. This could mean that the tip of the jet has already hit the glass wall, whereas its outer parts did not make contact yet. At collapse (Fig. 16, third image), the velocity of the vertical inflow at the center of the torus bubble has dropped significantly compared to the lateral inflow that still has a velocity of about 15 m/s.

In Fig. 17, path lines of fluid elements are presented. They are calculated using the PTV data of measurements performed at 20, 10, 2 and 0 μs before collapse. The velocity field is interpolated spatially and temporally and used to calculate a smooth trajectory for a number of fluid elements. Again, the corresponding bubble outlines are shown for better orientation. The jet formation is clearly visible at both standoff parameters: the fluid lines above the bubble are delimited by a bell-like shape, its tip pointing in the direction of the bubble indentation. For γ = 0.5, a much broader, stem-like jet profile is seen in the pathline portrait. Because of the high water hammer pressure building up at the center, the fluid is driven radially outward, indicated by the outer path lines being slightly curved to the outside near their termination.

Fig. 17

Path lines of some fluid elements from 20 μs before collapse up to the collapse, obtained from interpolated PTV data as shown in Figs. 15 and 16, respectively. Bubble outlines at times 20, 10 and 0 μs before collapse are shown superimposed in the background. Top γ = 0.7, bottom γ = 0.5

4 Conclusions

It is shown that particle tracking velocimetry is a viable method to measure the flow field around collapsing cavitation bubbles. By a proper choice of the tracer particle diameter and interframe time, a good accuracy of the measurements can be achieved. Thus, the experimental data may serve to validate numerical simulations of this two-phase flow problem in a quantitative way.

With PTV, the collapse of a laser-generated bubble close to a solid wall has been investigated for different values of the standoff parameter, γ. For the case of γ ≈ 1.3, a good agreement between experiment and a boundary-integral simulation is found. Furthermore, the collapse at small γ values, that can hardly be treated numerically by this method, has been studied in detail for the two cases γ = 0.7 and γ = 0.5. The shape dynamics and the interpolated velocity field shortly before collapse as obtained by PTV are presented. They can be processed further to obtain characteristics of the flow field like the vorticity (Kröninger 2008). The results clearly indicate the presence of a ring vortex in the vicinity of the bubble wall shortly before collapse.

A shortcoming of the method presented is that at small bubble diameters comparable to the light sheet thickness, velocities may be underestimated, as the analyzed particles may have a significant out-of-plane velocity component. Further development of the experiment thus aims at stereoscopic observation of the flow to obtain fully three-dimensional information on the velocity. Bubble collapse in more complex, non-axisymmetric geometries can then be studied. Also, the hydrodynamic interaction between two or more bubbles, the generation of streaming motion by bubble pulsations, or flow-bubble interaction in shearing flows, for example, are accessible to experimental investigation by this method. Flows in hydraulic machineries with sufficient repeatability should become measurable with higher spatial resolution, for instance flows in pumps, turbines or around propellors.